
第10卷第4期 智能系统学报 Vol.10 No.4 2015年8月 CAAI Transactions on Intelligent Systems Feh.2015 D0:10.3969/j.issn.1673-4785.201407014 网s络出版地址:http:/www.cnki.net/kcms/detail/23.1538.TP.20150720.0912.004.html 一种基于模糊方法的领导-跟随型多机器人编队控制 吴垠12,刘忠信2,陈增强2,孙青林12 (1.南开大学计算机与控制工程学院,天津300071:2.天津市智能机器人技术重点实验室,天津300071) 摘要:该文采用领导-跟随方式实现多机器人的编队控制针对移动机器人模型复杂性及不确定性等因素,采用不 依赖系统模型的模糊控制方法,对领导者进行路径跟踪控制通过模糊控制器的输出实时调整线速度和角速度,使领 导者能够达到并沿着给定的路径运动同时通过设计合适的控制律使每个跟随者与领导者的相对距离和角度收敛到 给定值,从而达到编队控制效果通过数值仿真及实际的场地实验表明,该算法可有效实现多移动机器人路径跟踪及 编队运动的控制。 关键词:模糊控制:路径跟踪:移动机器人:运动学模型:领导者:跟随者:SBC控制:编队控制 中图分类号:TP18文献标志码:A文章编号:1673-4785(2015)04-0533-08 中文引用格式:吴垠,刘忠信,陈增强,等.一种基于模糊方法的领导-跟随型多机器人编队控制[J].智能系统学报,2015,10(4): 533.540. 英文引用格式:WU Yin,LIU Zhongxin,Chen Zengqiang,etal.Formation control of leader-following type multi-robot based on fuzzy control method [J].CAAI Transactions on Intelligent Systems,2015,10(4):533-540. Formation control of leader-following type multi-robot based on fuzzy control method WU Yin2,LIU Zhongxin,CHEN Zengqiang'2,SUN Qinglin'2 (1.College of Computer and Control Engineering,Nankai University,Tianjin 300071,China;2.Key Laboratory of Intelligent Robot- ics of Tianjin,Tianjin 300071,China) Abstract:The leader-following method is adopted in this paper to achieve formation control of multi-robot.In order to overcome the complexity and uncertainty of mobile robot model,fuzzy control which is independent of system model is chosen as the path tracking strategy for the leader robot.The velocity and angular velocity of the leader are adjusted in real time by the output of fuzzy controller,guaranteeing that the leader can reach and move along the desired path.At the same time,the appropriate control law is designed to make the relative distance and angle be- tween the leader and each follower converge to the given value,so as to achieve the desired formation control.Nu- merical simulations and actual field experiments are provided in this paper,showing the effectiveness of the control strategy in path tracking and the formation control of multiple mobile robots. Keywords:fuzzy control;path following;mobile robot;kinematic model;leader;follower;SBC control;formation control 在实际工程应用中,由于单个智能体自身能力 协同控制吸引了越来越多的研究者。如今,随着研 的局限性,在处理复杂任务或处于复杂环境下仅靠 究的不断深入和发展,多智能体编队协同控制已经 个体行为往往无法解决。人们受到自然界中鱼群、 得到了广泛的应用,如环境勘探、残留有毒物清理、 鸟群等生物种群协作完成捕食、迁移等生物集群协 大型物体运输、搜寻与救援任务等4。而多机器 作行为的启发,将这种生物集群编队协作的特点运 人编队控制是多智能体系统研究中最典型的问题之 用到多智能体系统中)。近年来,多智能体编队 一。同时随着人工智能科学的不断发展,越来越多 的人工智能算法被应用到多智能体系统中来,其中 收稿日期:2014-07-09.网络出版日期:2015-07-20 模糊控制是人工智能研究的热点之一。模糊控制本 基金项目:国家自然科学基金资助项目(61174094,61273138):天津市 自然科学基金资助项目(13 JCYBJC17400,14 JCYBJC18700. 身属于一种非线性控制,它不依赖于被控对象的数 14 JCZDJC39300). 通信作者:刘忠信Email:lzhx@nankai.cdu.cn 学模型。对于模型中具有高度非线性和不确定性因
第 10 卷第 4 期 智 能 系 统 学 报 Vol.10 №.4 2015 年 8 月 CAAI Transactions on Intelligent Systems Feb. 2015 DOI:10.3969 / j.issn.1673⁃4785.201407014 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20150720.0912.004.html 一种基于模糊方法的领导-跟随型多机器人编队控制 吴垠1,2 ,刘忠信1,2 ,陈增强1,2 ,孙青林1,2 (1.南开大学计算机与控制工程学院,天津 300071;2.天津市智能机器人技术重点实验室,天津 300071) 摘 要:该文采用领导-跟随方式实现多机器人的编队控制.针对移动机器人模型复杂性及不确定性等因素,采用不 依赖系统模型的模糊控制方法,对领导者进行路径跟踪控制.通过模糊控制器的输出实时调整线速度和角速度,使领 导者能够达到并沿着给定的路径运动.同时通过设计合适的控制律使每个跟随者与领导者的相对距离和角度收敛到 给定值,从而达到编队控制效果.通过数值仿真及实际的场地实验表明,该算法可有效实现多移动机器人路径跟踪及 编队运动的控制。 关键词:模糊控制;路径跟踪;移动机器人;运动学模型;领导者;跟随者;SBC 控制;编队控制 中图分类号:TP18 文献标志码:A 文章编号:1673⁃4785(2015)04⁃0533⁃08 中文引用格式:吴垠,刘忠信,陈增强,等.一种基于模糊方法的领导-跟随型多机器人编队控制[ J]. 智能系统学报, 2015, 10(4): 533⁃540. 英文引用格式:WU Yin, LIU Zhongxin, Chen Zengqiang, et al .Formation control of leader⁃following type multi⁃robot based on fuzzy control method [J]. CAAI Transactions on Intelligent Systems, 2015, 10(4): 533⁃540. Formation control of leader⁃following type multi⁃robot based on fuzzy control method WU Yin 1,2 , LIU Zhongxin 1,2 , CHEN Zengqiang 1,2 , SUN Qinglin 1,2 (1. College of Computer and Control Engineering, Nankai University, Tianjin 300071, China; 2. Key Laboratory of Intelligent Robot⁃ ics of Tianjin, Tianjin 300071, China) Abstract:The leader⁃following method is adopted in this paper to achieve formation control of multi⁃robot. In order to overcome the complexity and uncertainty of mobile robot model, fuzzy control which is independent of system model is chosen as the path tracking strategy for the leader robot. The velocity and angular velocity of the leader are adjusted in real time by the output of fuzzy controller, guaranteeing that the leader can reach and move along the desired path. At the same time, the appropriate control law is designed to make the relative distance and angle be⁃ tween the leader and each follower converge to the given value, so as to achieve the desired formation control. Nu⁃ merical simulations and actual field experiments are provided in this paper, showing the effectiveness of the control strategy in path tracking and the formation control of multiple mobile robots. Keywords:fuzzy control; path following; mobile robot; kinematic model; leader; follower; SBC control; formation control 收稿日期:2014⁃07⁃09. 网络出版日期:2015⁃07⁃20. 基金项目:国家自然科学基金资助项目( 61174094, 61273138);天津市 自然科学基金资助项目( 13JCYBJC17400, 14JCYBJC18700, 14JCZDJC39300). 通信作者:刘忠信.Email:lzhx@ nankai.edu.cn. 在实际工程应用中,由于单个智能体自身能力 的局限性,在处理复杂任务或处于复杂环境下仅靠 个体行为往往无法解决。 人们受到自然界中鱼群、 鸟群等生物种群协作完成捕食、迁移等生物集群协 作行为的启发,将这种生物集群编队协作的特点运 用到多智能体系统中[1⁃3] 。 近年来,多智能体编队 协同控制吸引了越来越多的研究者。 如今,随着研 究的不断深入和发展,多智能体编队协同控制已经 得到了广泛的应用,如环境勘探、残留有毒物清理、 大型物体运输、搜寻与救援任务等[4⁃5] 。 而多机器 人编队控制是多智能体系统研究中最典型的问题之 一。 同时随着人工智能科学的不断发展,越来越多 的人工智能算法被应用到多智能体系统中来,其中 模糊控制是人工智能研究的热点之一。 模糊控制本 身属于一种非线性控制,它不依赖于被控对象的数 学模型。 对于模型中具有高度非线性和不确定性因

.534. 智能系统学报 第10卷 素以及难以建立模型的被控对象,基于专家经验的 对硬件的依赖,具有良好的可移植性和可扩展性。 模糊控制具有较强的优势[6。模糊控制中的模糊 同时,通过对每个跟随者与领导者之间的相对距离 逻辑是用人类的语言语句表达的,因此,它较为直 和角度φ加以控制,使其收敛到给定值,以此完成编 观,易于人们理解。无论是在科学研究还是工程 队控制效果。 实际运用上都逐渐被广泛应用8。但在实际工程 中模糊控制规则的制定没有统一的模式,往往需要 1机器人模型 丰富的工程实践经验,因此模糊控制器设计较为困 对于作为领导者的移动机器人而言,其运动学 难,且对设计人员的要求较高。同时大量的模糊规 模型只根据自身的位姿信息确定:而对于作为跟随 则使得存贮模糊规则库的计算机内存空间必须足够 者的移动机器人,其运动学模型建立在与领导者的 大,这对于如单片机等内存有限的硬件系统而言,显 位姿信息基础之上,通过与领导者的相对位置和角 然无法满足其内存要求。因此模糊控制系统在可应 度信息来间接描述其自身的位姿信息。 用性、可移植性及扩展性上并不具备优势[0。 1.1领导者运动学模型 大多数基于领导-跟随方式的多机器人系统编 设轮式移动机器人在某一运动时刻t的质心坐 队控制主要工作是设计协同控制律使得各个智能体 标点为M(x,y),此时机器人的速度方向与x轴正 达到并保持给定的期望队形,对于领导者自身的运 方向的夹角为0,如图1所示。机器人在这一时刻 动轨迹往往并不关心[)。随着工程研究的广泛和 的位姿信息由向量q=(x,y,)I确定,机器人的运 深入,在利用多机器人执行编队任务(如多无人水 动信息由向量p=(v,w)T确定,其中v(t)和(t)分 下航行器水下地形测绘,多无人机编队协同打击 别表示机器人在t时刻的线速度和角速度。 等])时,若同时对领导者的运动轨迹加以限制,针 对不同的地形环境对领导者的运动轨迹进行合理规 划后使其沿给定轨迹运动,则可大大提高多机器人 系统编队协同控制在实际应用中的效率及适应和应 变能力。 许多学者做过关于编队控制和路径跟踪的研 究,文献[1]讨论了离散时间下的多机器人编队控 制,通过设计合理的控制律,使每个机器人的位姿信 息与前一个机器人的位姿信息之差收敛到给定期望 队形的编队向量来保证多智能体编队协同运动。文 X 献[14]中提到SBC控制,通过对当前机器人的运动 图1机器人运动学模型 信息加以控制,使当前机器人与参考机器人的相对 Fig.1 Kinematic model of the robot 距离和角度总保持在给定值来完成编队。目前在路 由图1知,机器人的运动学方程可表示为 径跟踪研究中,已有一些学者利用智能控制方法成 x=v·c0s(0) 功解决路径跟踪问题,文献[15]采用预测控制方法 y=v·sin(0) (1) 对机器人进行运动控制,使其达到跟踪给定路径目 的。文献[16]采用遗传控制算法,将机器人运动规 8=w 划转化为非线性控制系统的优化问题,通过不断优 将式(1)用向量形式可表示为g=R()p,其中 化机器人的运动轨迹来完成路径跟踪目的。 cose 0 针对轮式机器人模型高度非线性及运动学和动 R(8)= sin 0 1 (2) 力学模型不易确定等特点,本文采用了不依赖于系 10 统模型的模糊控制方法,通过不断调整机器人的控 1.2跟随者运动学模型 制输入来对每个子目标点实时跟踪,从而实现领导 设2个机器人在t时刻的线速度分别为,(t) 者沿整条期望轨迹运动。本文设计的模糊控制器控 和,(t),它们的运动方向与x轴正方向的夹角为 制规则简单明了,易于理解,且规则数较少,减少了
素以及难以建立模型的被控对象,基于专家经验的 模糊控制具有较强的优势[6] 。 模糊控制中的模糊 逻辑是用人类的语言语句表达的,因此,它较为直 观,易于人们理解[7] 。 无论是在科学研究还是工程 实际运用上都逐渐被广泛应用[8⁃9] 。 但在实际工程 中模糊控制规则的制定没有统一的模式,往往需要 丰富的工程实践经验,因此模糊控制器设计较为困 难,且对设计人员的要求较高。 同时大量的模糊规 则使得存贮模糊规则库的计算机内存空间必须足够 大,这对于如单片机等内存有限的硬件系统而言,显 然无法满足其内存要求。 因此模糊控制系统在可应 用性、可移植性及扩展性上并不具备优势[10⁃11] 。 大多数基于领导⁃跟随方式的多机器人系统编 队控制主要工作是设计协同控制律使得各个智能体 达到并保持给定的期望队形,对于领导者自身的运 动轨迹往往并不关心[12] 。 随着工程研究的广泛和 深入,在利用多机器人执行编队任务(如多无人水 下航行器水下地形测绘,多无人机编队协同打击 等[13] )时,若同时对领导者的运动轨迹加以限制,针 对不同的地形环境对领导者的运动轨迹进行合理规 划后使其沿给定轨迹运动,则可大大提高多机器人 系统编队协同控制在实际应用中的效率及适应和应 变能力。 许多学者做过关于编队控制和路径跟踪的研 究,文献[1]讨论了离散时间下的多机器人编队控 制,通过设计合理的控制律,使每个机器人的位姿信 息与前一个机器人的位姿信息之差收敛到给定期望 队形的编队向量来保证多智能体编队协同运动。 文 献[14]中提到 SBC 控制,通过对当前机器人的运动 信息加以控制,使当前机器人与参考机器人的相对 距离和角度总保持在给定值来完成编队。 目前在路 径跟踪研究中,已有一些学者利用智能控制方法成 功解决路径跟踪问题,文献[15]采用预测控制方法 对机器人进行运动控制,使其达到跟踪给定路径目 的。 文献[16]采用遗传控制算法,将机器人运动规 划转化为非线性控制系统的优化问题,通过不断优 化机器人的运动轨迹来完成路径跟踪目的。 针对轮式机器人模型高度非线性及运动学和动 力学模型不易确定等特点,本文采用了不依赖于系 统模型的模糊控制方法,通过不断调整机器人的控 制输入来对每个子目标点实时跟踪,从而实现领导 者沿整条期望轨迹运动。 本文设计的模糊控制器控 制规则简单明了,易于理解,且规则数较少,减少了 对硬件的依赖,具有良好的可移植性和可扩展性。 同时,通过对每个跟随者与领导者之间的相对距离 l 和角度 φ 加以控制,使其收敛到给定值,以此完成编 队控制效果。 1 机器人模型 对于作为领导者的移动机器人而言,其运动学 模型只根据自身的位姿信息确定;而对于作为跟随 者的移动机器人,其运动学模型建立在与领导者的 位姿信息基础之上,通过与领导者的相对位置和角 度信息来间接描述其自身的位姿信息。 1.1 领导者运动学模型 设轮式移动机器人在某一运动时刻 t 的质心坐 标点为 M(x,y) ,此时机器人的速度方向与 x 轴正 方向的夹角为 θ ,如图 1 所示。 机器人在这一时刻 的位姿信息由向量 q = (x,y,θ) T 确定,机器人的运 动信息由向量 p = (v,w) T 确定,其中 v(t)和 w(t)分 别表示机器人在 t 时刻的线速度和角速度。 图 1 机器人运动学模型 Fig.1 Kinematic model of the robot 由图 1 知,机器人的运动学方程可表示为 x · = v·cos(θ) y · = v·sin(θ) θ · = w ì î í ï ïï ï ï (1) 将式(1)用向量形式可表示为 q · = R (θ) p ,其中 R(θ) = cosθ 0 sin θ 1 0 1 é ë ê ê êê ù û ú ú úú (2) 1.2 跟随者运动学模型 设 2 个机器人在 t 时刻的线速度分别为 v1(t) 和 v2(t) ,它们的运动方向与 x 轴正方向的夹角为 ·534· 智 能 系 统 学 报 第 10 卷

第4期 吴垠,等:一种基于模糊方法的领导-跟随型多机器人编队控制 ·535. 日,和02。以机器人两轮轴心连线的中点为参考点, 令机器人1为领导者,机器人2为跟随者,两机器人 旋转点之间的距离为!,跟随机器人前进方向与两 () P(y) 机器人旋转点连线的夹角为p。如图2所示。 D 机器人1 (领导者) v,(t) () 旋转点 参考点 机器人2 (限随者) 图3领导者向目标点移动 Fig.3 The leader move to the target 令B即为机器人运动方向与目标点的偏离角, 图2跟随者保持队形模型 则B=0-α。选取D与B作为模糊控制器的输入 Fig.2 Formation keeping model of followers 量,机器人的线速度(t)和角速度w(t)作为模糊 需要指出的是,由于当机器人原地旋转时参考 控制器的输出量。通过设计合理的模糊控制规则, 点的线速度始终为零,为研究方便,选取以机器人的 来保证移动机器人在轨迹跟踪的过程总能达到目标 参考点为起点沿机器人前进正方向平移距离d得到 点P,即变量D与B总是趋于零,即可达到机器人实 的机器人的质点作为机器人的旋转点,以此来保证 时跟踪给定轨迹的目的。下面由模糊语言变量分别 机器人运动过程中线速度始终非零。 对2个输入输出变量进行模糊子集的划分,如表1 令y=0,-0,+p,在对跟随者的运动状态进行 和表2所示。 数学描述时,文中采用SBC控制(separation-bearing 表1输入变量D与B的模糊子集划分 control,SBC)方法建立跟随者模型s)。因此对跟 Table 1 The fuzzy subset partition of input variables D andB 随者进行建模时,由跟随者与领导者的相对位置和 距离D 角度B 角度表示的跟随者的运动学方程为 ZE零 NL负大 VN非常近 NM负中 I=v cosy -dw siny -vzcosop dwzsinp (4) NE近 NS负小 1 (vsiny-vsiny-dw cosy do,cospb) ME中等 ZE零 FA远 PS正小 (5) VF非常远 PM正中 2控制算法 EF格外远 PL正大 表2输出变量:与心的模糊子集划分 对领导者采用模糊控制方法,使其能够达到并 Tab.2 Thefuzzy subset partition of output variables v and 沿着给定曲线运动。对跟随者,通过实时控制与领 速度u 角速度e 导者的相对距离和相对角度,使其同时收敛到给定 ZE零 NL负大 值来达到编队控制的目的。 VS非常小 NM负中 2.1基于模糊控制的路径跟踪 SM小 NS负小 将给定曲线分解为若干个目标点,采用模糊控 ME中等 ZE零 制方法使机器人总能到达距当前自身位置距离最近 LA大 PS正小 的目标点。如图3所示,设当前所要到达的目标点 VL非常大 PM正中 为P(x4,ya),移动机器人的质点M与目标点P的 EL极大 PL正大 距离为D,线速度方向水平夹角为0。参考点与目 标点连线的夹角为:
θ 1 和 θ 2 。 以机器人两轮轴心连线的中点为参考点, 令机器人 1 为领导者,机器人 2 为跟随者,两机器人 旋转点之间的距离为 l ,跟随机器人前进方向与两 机器人旋转点连线的夹角为 φ 。 如图 2 所示。 图 2 跟随者保持队形模型 Fig.2 Formation keeping model of followers 需要指出的是,由于当机器人原地旋转时参考 点的线速度始终为零,为研究方便,选取以机器人的 参考点为起点沿机器人前进正方向平移距离 d 得到 的机器人的质点作为机器人的旋转点,以此来保证 机器人运动过程中线速度始终非零。 令 γ = θ2 - θ1 + φ ,在对跟随者的运动状态进行 数学描述时,文中采用 SBC 控制( separation⁃bearing control, SBC)方法建立跟随者模型[15] 。 因此对跟 随者进行建模时,由跟随者与领导者的相对位置和 角度表示的跟随者的运动学方程为 l · = v1 cosγ - dw1 sinγ - v2 cosφ + dw2 sinφ (4) φ · = 1 l (v2 sinγ - v1 sinγ - dw1 cosγ + dw2 cosφ - lw2) (5) 2 控制算法 对领导者采用模糊控制方法,使其能够达到并 沿着给定曲线运动。 对跟随者,通过实时控制与领 导者的相对距离和相对角度,使其同时收敛到给定 值来达到编队控制的目的。 2.1 基于模糊控制的路径跟踪 将给定曲线分解为若干个目标点,采用模糊控 制方法使机器人总能到达距当前自身位置距离最近 的目标点。 如图 3 所示,设当前所要到达的目标点 为 P(xd ,yd ) ,移动机器人的质点 M 与目标点 P 的 距离为 D,线速度方向水平夹角为 θ 。 参考点与目 标点连线的夹角为 α 。 图 3 领导者向目标点移动 Fig.3 The leader move to the target 令 β 即为机器人运动方向与目标点的偏离角, 则 β = θ - α 。 选取 D 与 β 作为模糊控制器的输入 量,机器人的线速度 v(t) 和角速度 w(t) 作为模糊 控制器的输出量。 通过设计合理的模糊控制规则, 来保证移动机器人在轨迹跟踪的过程总能达到目标 点 P,即变量 D 与 β 总是趋于零,即可达到机器人实 时跟踪给定轨迹的目的。 下面由模糊语言变量分别 对 2 个输入输出变量进行模糊子集的划分,如表 1 和表 2 所示。 表 1 输入变量 D 与 β 的模糊子集划分 Table 1 The fuzzy subset partition of input variables D and β 距离 D 角度 β ZE 零 NL 负大 VN 非常近 NM 负中 NE 近 NS 负小 ME 中等 ZE 零 FA 远 PS 正小 VF 非常远 PM 正中 EF 格外远 PL 正大 表 2 输出变量 v 与 w 的模糊子集划分 Tab.2 Thefuzzy subset partition of output variables v and w 速度 v 角速度 w ZE 零 NL 负大 VS 非常小 NM 负中 SM 小 NS 负小 ME 中等 ZE 零 LA 大 PS 正小 VL 非常大 PM 正中 EL 极大 PL 正大 第 4 期 吴垠,等:一种基于模糊方法的领导-跟随型多机器人编队控制 ·535·

·536· 智能系统学报 第10卷 对2个输入变量和输出变量的模糊集合均采取形式 来,它反映了从输入到输出的映射关系。本文对于 较为简单的三角形隶属度函数,简化了设计工作。 模糊规则制定的核心思想是对机器人与目标点的距 在设计夹角B的隶属度函数时,考虑到轮式机器人 离D较大(或较小)时要求由模糊控制器输出一个 的偏离角大多保持在[-90,90]范围内这一实际情 较大(或较小)的线速度(t):同时对机器人与目 况,将属于这一区间的隶属度函数的模糊语言变量 标点的偏离角B较大(或较小)时要求由模糊规则 密度加大。同时对于偏离角较大的情况时,采用最 输出一个较大(或较小)的角速度w(t)。由此可以 大隶属度,使得机器人在实际运动中能够快速调整 保证机器人始终在由一系列目标点构成的给定路径 自身位姿信息,跟踪上给定的路径。选取三角形隶 上运动。本文采用2个输人和输出变量、7个语言 属度函数来限定这些语言变量的值如图4~7所示。 变量模糊集,对输出变量v(t)和w(t)分别进行模 糊控制,两输出变量各自可以归纳出7条模糊规则。 VN NE ME FA VE 1.0 它们的模糊规则形式如下: 变量(t)的模糊规则: 0.5 IF D =D:THEN v is v 变量w(t)的模糊规则: 50 100 150 D/cm IF BB:THEN w is w 图4D隶属度函数 其中D、":、B、0:(i=1,2,…,7)表示在表1 Fig.4 subordinate degree function of D 和表2中4个输入输出变量在第i条规则下各自对 应的语言变量值。 NL NMNSZE PS PM PL 模糊推理方法又称去模糊化方法,常用的模糊推 理算法有重心法(centroid)、面积平分法(bsector)、平 0.5 均最大隶属度法(mom)、最大隶属度取最小值法 (som)等。最常用的去模糊化方法是重心法。这里 0电 -150-100-50 0 50100150 采用重心法计算第i条规则的输出: B/arg 图5B隶属度函数 (t)= ,()/∑min(uehn) (6) i=1 i=1 Fig.5 subordinate degree function of B o(t)=】 ,(o/2min(ue4o) (7) =1 i=1 1.0E VS SM ME 式中:,(t)和w,(t)为第i条规则的输出值,s和 赵 ▣0.5 4o为输人变量的隶属度值。 在路径跟踪控制中,利用Mamdani型这一基本 0 的模糊逻辑系统对领导者运动轨迹加以控制。在设 00.10.20.30.40.50.60.70.80.91.0 wm's 计模糊控制器的过程中,输入输出变量论域范围的选 择至关重要。针对实验中的轮式机器人自身参数的 图6隶属度函数 约束,将线速度的取值限定在区间[0m/s,1m/s]范 Fig.6 subordinate degree function ofv 围内,同时结合实际场地实验情况及一定的容许度等 NM NS' ZE PS PM P 因素,对角速度的取值限定在区间[-4rad/s,4rad/ s]范围内较为合理。对于规则库的制定采用单输入 置 0.5 单输出(single-input single-output,SISO)形式的语言 条件,制定方法简单直观同时由于规则数较少,可有 效节省存放规则表的内存空间,从而极大地减小了对 -2 -1 @/rad-s 硬件的要求,对于存储空间有限的移动机器人具有更 图710隶属度函数 强的可应用性。 Fig.7 subordinate degree function of w 2.2跟随者编队保持 对于模糊规则的制定往往靠专家经验总结而 在图2所描述的对象模型中,令误差向量为
对 2 个输入变量和输出变量的模糊集合均采取形式 较为简单的三角形隶属度函数,简化了设计工作。 在设计夹角 β 的隶属度函数时,考虑到轮式机器人 的偏离角大多保持在 [ - 90,90] 范围内这一实际情 况,将属于这一区间的隶属度函数的模糊语言变量 密度加大。 同时对于偏离角较大的情况时,采用最 大隶属度,使得机器人在实际运动中能够快速调整 自身位姿信息,跟踪上给定的路径。 选取三角形隶 属度函数来限定这些语言变量的值如图 4~7 所示。 图 4 D 隶属度函数 Fig.4 subordinate degree function of D 图 5 β 隶属度函数 Fig.5 subordinate degree function of β 图 6 v 隶属度函数 Fig.6 subordinate degree function of v 图 7 w 隶属度函数 Fig.7 subordinate degree function of w 对于模糊规则的制定往往靠专家经验总结而 来,它反映了从输入到输出的映射关系。 本文对于 模糊规则制定的核心思想是对机器人与目标点的距 离 D 较大(或较小)时要求由模糊控制器输出一个 较大(或较小) 的线速度 v(t) ;同时对机器人与目 标点的偏离角 β 较大(或较小)时要求由模糊规则 输出一个较大(或较小)的角速度 w(t) 。 由此可以 保证机器人始终在由一系列目标点构成的给定路径 上运动。 本文采用 2 个输入和输出变量、7 个语言 变量模糊集,对输出变量 v(t) 和 w(t) 分别进行模 糊控制,两输出变量各自可以归纳出 7 条模糊规则。 它们的模糊规则形式如下: 变量 v(t) 的模糊规则: IF D = D ~ i ,THEN v is v ~ i 变量 w(t) 的模糊规则: IF β = β ~ i ,THEN w is w ~ i 其中 D ~ i 、 v ~ i 、 β ~ i 、 w ~ i (i = 1,2,…,7)表示在表 1 和表 2 中 4 个输入输出变量在第 i 条规则下各自对 应的语言变量值。 模糊推理方法又称去模糊化方法,常用的模糊推 理算法有重心法(centroid)、面积平分法(bsector) 、平 均最大隶属度法(mom) 、最大隶属度取最小值法 (som)等。 最常用的去模糊化方法是重心法。 这里 采用重心法计算第 i 条规则的输出: v(t) = ∑ n i = 1 vi(t) /∑ n i = 1 min(μiβ ,μiD) (6) w(t) = ∑ n i = 1 wi(t) /∑ n i = 1 min(μiβ ,μiD) (7) 式中: vi(t) 和 wi(t) 为第 i 条规则的输出值, μiβ 和 μiD 为输入变量的隶属度值。 在路径跟踪控制中,利用 Mamdani 型这一基本 的模糊逻辑系统对领导者运动轨迹加以控制。 在设 计模糊控制器的过程中,输入输出变量论域范围的选 择至关重要。 针对实验中的轮式机器人自身参数的 约束,将线速度的取值限定在区间[0 m/ s,1 m/ s]范 围内,同时结合实际场地实验情况及一定的容许度等 因素,对角速度的取值限定在区间[ -4 rad / s,4 rad / s] 范围内较为合理。 对于规则库的制定采用单输入 单输出(single⁃input single⁃output, SISO)形式的语言 条件,制定方法简单直观,同时由于规则数较少,可有 效节省存放规则表的内存空间,从而极大地减小了对 硬件的要求,对于存储空间有限的移动机器人具有更 强的可应用性。 2.2 跟随者编队保持 在图 2 所描述的对象模型中,令误差向量为 ·536· 智 能 系 统 学 报 第 10 卷

第4期 吴垠,等:一种基于模糊方法的领导-跟随型多机器人编队控制 .537. [e,e.]=[l4-L,9a-p]。在编队运动过程,若 等号成立。则系统渐近稳定。证毕。 能始终保持每个跟随者与领导者之间的相对距离L 该编队算法实现过程较为简便且思路清晰,易 和角度p均收敛到给定值(l4,P),即满足 于接受。通过改变期望距离L和角度P:的值,可以 lim(e,)=0,lim(e.)=0 完成任意编队队形要求,具有较好的灵活性。由于 即可达到编队控制目标。 在编队运动的过程中,所有跟随者都只与领导者进 设计闭环控制律: 行通信,因此在编队运动过程中随时加入新的跟随 v=Pasiny -p cosy (8) 者,不会对现有队形产生影响,且对跟随者的数量没 1 有限制,体现该算法良好的扩展性。 w,=dp:siny+p,eosy) (9) 同时也注意到,在计算跟随者的控制律时,其控 其中 制律高度依赖于领导者模型。在通信过程中由于噪 p=dwzsing vzcosop a (la-) (10) 声干扰或通信延迟等因素影响,一旦领导者的位姿 P2 vzsing dwzcoso-al(oa-)-lw2 信息不能准确地被跟随者获取时,跟随者便立即无 (11) 法完成与领导者的编队协同控制。因此,这就要求 则有下面的结论。 领导者在通信传输方面具有较高的精度及较强的稳 定理1对于任意给定参数满足a1、α>0,若 定性。 跟随机器人的控制律采用式(8)和(9),则有1im 3仿真研究 (e,)=0和lim(e.)=0同时成立,即多机器人系统可 以实现稳定的编队。 3.1基于MATLAB的数值仿真 为了验证该算法的有效性,采用MATLAB软件 证明构造李雅普诺夫函数V= 对 进行对多机器人系统进行数字仿真测试。领导者给 求导并代入运动学方程(4)和(5),得 定路径分别选取为直线y=0,y=x和圆x2+y2= 4。领导者与跟随者初始位置信息随机给定。2个 V=erer +eee= 跟随者编队期望距离和角度(1,p)分别为(1.5, (1-1)1-(-)= 90°),(1.5,-90),即跟随者分别位于领导者的两 -(-1)(v cosy dw siny -vcoso dwzsing)- 侧并与领导者保持1.5m的距离。 图8~10为多机器人的运动轨迹。从图中可以 ()(vsing-d cosy- 看出,开始时每个智能体的起始位置随机分布,由编 v sing dw,cosop -lw2) 队控制算法对每个智能体加以控制。从图中可以看 将控制律式(8)和(9)代入: 出经过一段时间后每个智能体均逐步达到了各自期 i=-(1)(p:simycosy -Prcos'y-dsinysiny 1 望的位置并同时保持期望的队形运动。 智能体编队运动轨迹 p,cosy)-t,cosp+dl,sing)-(pa-p)(v.sing- 2.0r GivenPath Leader 1.5 Followerl 1 1.0 Followey Pasin+p,sin ycosy-dcosysin 0.5 P2 cos T)+dwzcoso -lw2)= -((-p-v2coso dwzsing)- -0.5 1 -1.0h (e:-p)7(,sinp-p+de;cos-h,) -1.5 将式(10)、(11)代入并进一步整理可得 -2.04 -2 0 2468101214 x/m V=-a,(4-l)2-a2(pa-p)2= 图8领导者给定路径为直线y=0时的编队运动轨迹 -aei-aze Fig.8 Formation trajectory when the given path of leader is the straight liney =0 由a1、a2>0可知,V≤0当且仅当e1=0、e。=0时
[el,eφ] T = [l d - l,φd - φ] T 。 在编队运动过程,若 能始终保持每个跟随者与领导者之间的相对距离 l 和角度 φ 均收敛到给定值 (l d ,φd ) ,即满足 lim t→¥ (el) = 0,lim t→¥ (eφ) = 0 即可达到编队控制目标。 设计闭环控制律: v1 = ρ2 sinγ - ρ1 cosγ (8) w1 = 1 d (ρ1 sinγ + ρ2 cosγ) (9) 其中 ρ1 = dw2 sinφ - v2 cosφ - α1(l d - l) (10) ρ2 = v2 sinφ + dw2 cosφ - α2 l(φd - φ) - lw2 (11) 则有下面的结论。 定理 1 对于任意给定参数满足 α1 、α2 > 0,若 跟随机器人的控制律采用式(8) 和(9),则有 lim t→¥ (el) = 0 和 lim t→¥ (eφ)= 0 同时成立,即多机器人系统可 以实现稳定的编队。 证明 构造李雅普诺夫函数 V = 1 2 e 2 l + 1 2 e 2 φ ,对 v 求导并代入运动学方程(4)和(5),得 V · = el e · l + eφ e · φ = - (l d - l)l · - (φd - φ)φ · = - (l d - l)(v1 cosγ - dw1 sinγ - v2 cosφ + dw2 sinφ) - (φd - φ) 1 l (v2 sinφ - dw1 cos γ - v1 sinφ + dw2 cosφ - lw2 ) 将控制律式(8)和(9)代入: V · = - (l d - l)(ρ2 sinγcosγ - ρ1 cos 2 γ - dsinγ 1 d (ρ1 sinγ + ρ2 cosγ) - v2 cos φ + dw2 sinφ) - (φd - φ) 1 l (v2 sinφ - ρ2 sin 2 γ + ρ1 sin γcos γ - dcosγ 1 d (ρ1 sinγ + ρ2 cos Τ) + dw2 cosφ - lw2 ) = - (l d - l)( - ρ1 - v2 cosφ + dw2 sinφ) - (φd - φ) 1 l (v2 sin φ - ρ2 + dw2 cos φ - lw2 ) 将式(10)、(11)代入并进一步整理可得 V · = - α1(l d - l) 2 - α2(φd - φ) 2 = - α1 e 2 l - α2 e 2 φ x 由 α1 、α2 > 0 可知, V · ≤ 0 当且仅当 el = 0、eφ = 0 时 等号成立。 则系统渐近稳定。 证毕。 该编队算法实现过程较为简便且思路清晰,易 于接受。 通过改变期望距离 l d 和角度 φd 的值,可以 完成任意编队队形要求,具有较好的灵活性。 由于 在编队运动的过程中,所有跟随者都只与领导者进 行通信,因此在编队运动过程中随时加入新的跟随 者,不会对现有队形产生影响,且对跟随者的数量没 有限制,体现该算法良好的扩展性。 同时也注意到,在计算跟随者的控制律时,其控 制律高度依赖于领导者模型。 在通信过程中由于噪 声干扰或通信延迟等因素影响,一旦领导者的位姿 信息不能准确地被跟随者获取时,跟随者便立即无 法完成与领导者的编队协同控制。 因此,这就要求 领导者在通信传输方面具有较高的精度及较强的稳 定性。 3 仿真研究 3.1 基于 MATLAB 的数值仿真 为了验证该算法的有效性,采用 MATLAB 软件 进行对多机器人系统进行数字仿真测试。 领导者给 定路径分别选取为直线 y = 0, y = x 和圆 x 2 + y 2 = 4。 领导者与跟随者初始位置信息随机给定。 2 个 跟随者编队期望距离和角度( l , φ ) 分别为(1.5, 90°),(1.5,-90°),即跟随者分别位于领导者的两 侧并与领导者保持 1.5 m 的距离。 图 8~10 为多机器人的运动轨迹。 从图中可以 看出,开始时每个智能体的起始位置随机分布,由编 队控制算法对每个智能体加以控制。 从图中可以看 出经过一段时间后每个智能体均逐步达到了各自期 望的位置并同时保持期望的队形运动。 图 8 领导者给定路径为直线 y = 0 时的编队运动轨迹 Fig. 8 Formation trajectory when the given path of leader is the straight line y = 0 第 4 期 吴垠,等:一种基于模糊方法的领导-跟随型多机器人编队控制 ·537·

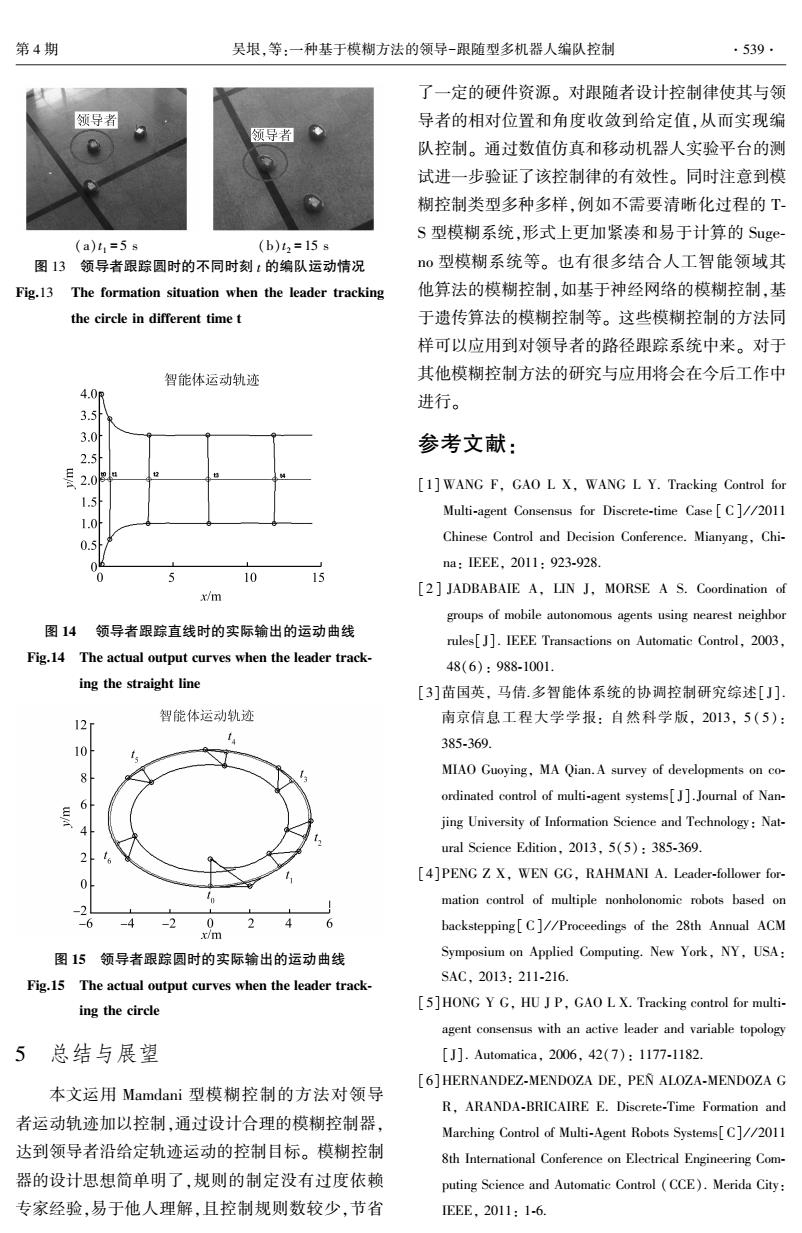
.538. 智能系统学报 第10卷 智能体编队运动轨迹 分别选取Amigo机器人在t,和t,这2个不同时刻的 14 实际场地运动情况,如图12、13所示。图14、15是 由移动机器人码盘采回的实际运动数据所绘制的运 8 动轨迹图,并在图中分别给出几种不同时刻机器人 6 的队形保持情况,如图中黑色实线所示。在图14和 4 2 图15中标注的机器人在t1、,时刻的编队运动情况 分别与图12和图13中的t1、t,时刻一一对应。可 -202468101214 以看出,在实际场地实验中,当给定轨迹为直线和圆 x/m 时,采用该算法,领导者能够完成跟踪给定路径的要 图9领导者给定路径为斜线y=x时的编队运动轨迹 求,同时跟随者能够较快地达到并保持给定编队队 Fig.9 Formation trajectory when the given path of 形。由数字仿真和实际场地实验共同表明,该算法 leader is the diagonal line y =x 能够很好地完成所要求的控制目标,具有一定的有 智能体编队运动轨迹 效性。 3 开始 初始化 由规划路径产生目标点序列 跟随者接收信息 计算模糊控制输入 计算距离和角度 -3 模糊控制器 计算y,w -4-3-2-10123456 x/m 获得模糊控制输出,w 驱动Amigoi运动 图10领导者给定路径为圆x2+y2-4时的编队运动轨迹 Fig.10 Formation trajectory when the given path of 驱动Amigo运动 、循环结束 leader is the circlex2+y2=4 获得Amigo当前位姿信息 Y 停止运动 3.2基于轮式机器人的相关实验 为了进一步验证该编队控制算法的有效性,并 循环结束 从实际应用的角度出发,采用轮式移动机器人进行 图11程序流程图 实际场地实验。 Fig.11 The program flow chart 本实验采用的是美国ActivMedia Robotics公司 生产的Amigo移动机器人作为实验平台。首先利用 该公司提供的配套仿真软件MobileSim进行仿真测 试,再利用Amigo机器人进行实际场地实验。主程 领导者 领导者 序流程图如图11。 本实验采用3个Amigo机器人分2组进行,第 一组实验的领导者给定路径为直线y=2,2个跟随 者与领导者的期望距离均为1m,期望角度分别为 (a)t,=58 (b)2=15s 90°和-90°,即分别位于领导者的左右两侧。第2组 图12领导者跟踪直线时的不同时刻t的编队运动情况 实验的领导者给定路径为圆x2+(y-5)2=25,两 Fig.12 The formation situation when the leader tracking 跟随者的期望距离均为1m,期望角度分别为90°和 the straight line in different time t 0,即2个跟随者分别位于领导者的正前方和左侧
图 9 领导者给定路径为斜线 y = x 时的编队运动轨迹 Fig. 9 Formation trajectory when the given path of leader is the diagonal line y = x 图 10 领导者给定路径为圆 x 2 + y 2 = 4 时的编队运动轨迹 Fig.10 Formation trajectory when the given path of leader is the circle x 2 + y 2 = 4 3.2 基于轮式机器人的相关实验 为了进一步验证该编队控制算法的有效性,并 从实际应用的角度出发,采用轮式移动机器人进行 实际场地实验。 本实验采用的是美国 ActivMedia Robotics 公司 生产的 Amigo 移动机器人作为实验平台。 首先利用 该公司提供的配套仿真软件 MobileSim 进行仿真测 试,再利用 Amigo 机器人进行实际场地实验。 主程 序流程图如图 11。 本实验采用 3 个 Amigo 机器人分 2 组进行,第 一组实验的领导者给定路径为直线 y = 2,2 个跟随 者与领导者的期望距离均为 1 m,期望角度分别为 90°和-90°,即分别位于领导者的左右两侧。 第 2 组 实验的领导者给定路径为圆 x 2 + (y - 5) 2 = 25,两 跟随者的期望距离均为 1 m,期望角度分别为 90°和 0,即 2 个跟随者分别位于领导者的正前方和左侧。 分别选取 Amigo 机器人在 t 1和 t 2这 2 个不同时刻的 实际场地运动情况,如图 12、13 所示。 图 14、15 是 由移动机器人码盘采回的实际运动数据所绘制的运 动轨迹图,并在图中分别给出几种不同时刻机器人 的队形保持情况,如图中黑色实线所示。 在图 14 和 图 15 中标注的机器人在 t 1 、t 2时刻的编队运动情况 分别与图 12 和图 13 中的 t1、t 2时刻一一对应。 可 以看出,在实际场地实验中,当给定轨迹为直线和圆 时,采用该算法,领导者能够完成跟踪给定路径的要 求,同时跟随者能够较快地达到并保持给定编队队 形。 由数字仿真和实际场地实验共同表明,该算法 能够很好地完成所要求的控制目标,具有一定的有 效性。 图 11 程序流程图 Fig.11 The program flow chart (a)t 1 = 5 s (b)t 2 = 15 s 图 12 领导者跟踪直线时的不同时刻 t 的编队运动情况 Fig.12 The formation situation when the leader tracking the straight line in different time t ·538· 智 能 系 统 学 报 第 10 卷
第4期 吴垠,等:一种基于模糊方法的领导-跟随型多机器人编队控制 ·539. 了一定的硬件资源。对跟随者设计控制律使其与领 领导者 导者的相对位置和角度收敛到给定值,从而实现编 领导者 队控制。通过数值仿真和移动机器人实验平台的测 试进一步验证了该控制律的有效性。同时注意到模 糊控制类型多种多样,例如不需要清晰化过程的T s型模糊系统,形式上更加紧凑和易于计算的Suge (a)t1=58 (b)t2=158 图13领导者跟踪圆时的不同时刻:的编队运动情况 o型模糊系统等。也有很多结合人工智能领域其 Fig.13 The formation situation when the leader tracking 他算法的模糊控制,如基于神经网络的模糊控制,基 the circle in different time t 于遗传算法的模糊控制等。这些模糊控制的方法同 样可以应用到对领导者的路径跟踪系统中来。对于 智能体运动轨迹 其他模糊控制方法的研究与应用将会在今后工作中 4.0R 进行。 3.5 参考文献: 2.0 [1]WANG F,GAO L X,WANG L Y.Tracking Control for 1.5 Multi-agent Consensus for Discrete-time Case [C]//2011 1.0 0.5 Chinese Control and Decision Conference.Mianyang,Chi- 0 na:EEE,2011:923-928. 10 [2]JADBABAIE A,LIN J,MORSE A S.Coordination of x/m groups of mobile autonomous agents using nearest neighbor 图14领导者跟踪直线时的实际输出的运动曲线 rules[J].IEEE Transactions on Automatic Control,2003, Fig.14 The actual output curves when the leader track- 48(6):988-1001. ing the straight line [3]苗国英,马倩.多智能体系统的协调控制研究综述[J]: 智能体运动轨迹 12T 南京信息工程大学学报:自然科学版,2013,5(5): 10 385-369. MIAO Guoying,MA Qian.A survey of developments on co- ordinated control of multi-agent systems[J].Journal of Nan- 目 6 jing University of Information Science and Technology:Nat- ural Science Edition,2013,5(5):385-369. 2 [4]PENG Z X,WEN GG,RAHMANI A.Leader-follower for- 0 mation control of multiple nonholonomic robots based on 2 -2 024 6 backstepping[C]//Proceedings of the 28th Annual ACM r/m 图15领导者跟踪圆时的实际输出的运动曲线 Symposium on Applied Computing.New York,NY,USA: Fig.15 The actual output curves when the leader track- SAC,2013:211-216. ing the circle [5]HONG Y G,HU J P,GAO L X.Tracking control for multi- agent consensus with an active leader and variable topology 5总结与展望 [J].Automatica.,2006,42(7):1177-1182. [6]HERNANDEZ-MENDOZA DE,PEN ALOZA-MENDOZA G 本文运用Mamdani型模糊控制的方法对领导 R,ARANDA-BRICAIRE E.Discrete-Time Formation and 者运动轨迹加以控制,通过设计合理的模糊控制器, Marching Control of Multi-Agent Robots Systems[C]//2011 达到领导者沿给定轨迹运动的控制目标。模糊控制 8th International Conference on Electrical Engineering Com- 器的设计思想简单明了,规则的制定没有过度依赖 puting Science and Automatic Control (CCE).Merida City: 专家经验,易于他人理解,且控制规则数较少,节省 EEE,2011:1-6
(a)t 1 = 5 s (b)t 2 = 15 s 图 13 领导者跟踪圆时的不同时刻 t 的编队运动情况 Fig.13 The formation situation when the leader tracking the circle in different time t 图 14 领导者跟踪直线时的实际输出的运动曲线 Fig.14 The actual output curves when the leader track⁃ ing the straight line 图 15 领导者跟踪圆时的实际输出的运动曲线 Fig.15 The actual output curves when the leader track⁃ ing the circle 5 总结与展望 本文运用 Mamdani 型模糊控制的方法对领导 者运动轨迹加以控制,通过设计合理的模糊控制器, 达到领导者沿给定轨迹运动的控制目标。 模糊控制 器的设计思想简单明了,规则的制定没有过度依赖 专家经验,易于他人理解,且控制规则数较少,节省 了一定的硬件资源。 对跟随者设计控制律使其与领 导者的相对位置和角度收敛到给定值,从而实现编 队控制。 通过数值仿真和移动机器人实验平台的测 试进一步验证了该控制律的有效性。 同时注意到模 糊控制类型多种多样,例如不需要清晰化过程的 T⁃ S 型模糊系统,形式上更加紧凑和易于计算的 Suge⁃ no 型模糊系统等。 也有很多结合人工智能领域其 他算法的模糊控制,如基于神经网络的模糊控制,基 于遗传算法的模糊控制等。 这些模糊控制的方法同 样可以应用到对领导者的路径跟踪系统中来。 对于 其他模糊控制方法的研究与应用将会在今后工作中 进行。 参考文献: [1] WANG F, GAO L X, WANG L Y. Tracking Control for Multi⁃agent Consensus for Discrete⁃time Case [ C] / / 2011 Chinese Control and Decision Conference. Mianyang, Chi⁃ na: IEEE, 2011: 923⁃928. [2 ] JADBABAIE A, LIN J, MORSE A S. Coordination of groups of mobile autonomous agents using nearest neighbor rules[J]. IEEE Transactions on Automatic Control, 2003, 48(6): 988⁃1001. [3]苗国英, 马倩.多智能体系统的协调控制研究综述[ J]. 南京信息工程大学学报: 自然科学版, 2013, 5 ( 5): 385⁃369. MIAO Guoying, MA Qian.A survey of developments on co⁃ ordinated control of multi⁃agent systems[J].Journal of Nan⁃ jing University of Information Science and Technology: Nat⁃ ural Science Edition, 2013, 5(5): 385⁃369. [4]PENG Z X, WEN GG, RAHMANI A. Leader⁃follower for⁃ mation control of multiple nonholonomic robots based on backstepping[ C] / / Proceedings of the 28th Annual ACM Symposium on Applied Computing. New York, NY, USA: SAC, 2013: 211⁃216. [5]HONG Y G, HU J P, GAO L X. Tracking control for multi⁃ agent consensus with an active leader and variable topology [J]. Automatica, 2006, 42(7): 1177⁃1182. [6]HERNANDEZ⁃MENDOZA DE, PEÑ ALOZA⁃MENDOZA G R, ARANDA⁃BRICAIRE E. Discrete⁃Time Formation and Marching Control of Multi⁃Agent Robots Systems[C] / / 2011 8th International Conference on Electrical Engineering Com⁃ puting Science and Automatic Control (CCE). Merida City: IEEE, 2011: 1⁃6. 第 4 期 吴垠,等:一种基于模糊方法的领导-跟随型多机器人编队控制 ·539·

.540. 智能系统学报 第10卷 [7]ARAI T,PAGELLO E,PARKER L E.Guest editorial ad- IEEE International Conference on Robotics and Automa- vances in multirobotsystems[J].IEEE Transactions on Ro- tion.Scottsdale.AZ:IEEE,1989:1277-1282 botics and Automation,2002,18(5):655-661. [16]吴瑾斐,秦东兴,刘俊.四轮式移动机器人非完整运动 [8]刘曙光,魏俊民,竺志超.模糊控制技术[M].北京:中 控制[J].电子科技大学学报,2007,36(2):301-304. 国纺织出版社,2001:1-8. WU Jinfei,QIN Dongxing,LIU Jun.Nonholonomic motion LIU Shuguang,WEI Junmin,ZHU Zhichao.Fuzzy control control of four-wheeled mobile robot[J].Journal of Univer- technology[M].Beijing:China Textile Press,2001:1-8. sity of Electronic Science and Technology of China,2007, [9]孙德丰.MATLAB模糊系统设计[M].北京:国防工业出 36(2):301-304. 版社,2009. [17]汪超,唐勇奇.基于独立C代码的模糊控制器应用程 SUN DefengThe design of Fuzzy Systems[M].Beijing:Na- 序设计[J].计算机技术与发展,2009,19(5):242-244. tional Defence Industry Press,2009. WANG Chao,TANG Yongqi.Programmer of fuzzy control- [10]HSU Y-C,CHEN G R,LI H X.A Fuzzy adaptive varia- ler based on stand-alone C-Code[J].Computer Technology ble structure controller with application to robot manipula- and Development,2009,19(5):242-244. tors[J].IEEE Transactions on Systems,Man,and Cyber- 作者简介: netics-Part B:Cybernetics,2001,31(3):331-340. 吴垠,男,1989年生,硕士研究生, [11]骆德渊,刘荣,李纪文.采用模糊逻辑的移动机器人轨 主要研究方向为多智能体系统控制、人 迹跟踪[J].电子科技大学学报,2008,37(6):943-947. 工智能系统与控制。 LUO Deyuan,LIU Rong,LI Jiwen.Path tracking of mo- bile robots using fuzzy logic[J].Journal of University of E- lectronic Science and Technology of China,2008,37(6): 943-947. 刘忠信,男,1975年生,教授,博士 [12]陈杨杨,田玉平.多智能体沿多条给定路径编队运动的 生导师,中国人工智能学会智能空天系 有向协同控制[J].自动化学报,2009,35(12):1541- 统专业委员会委员、中国智能物联系统 1549. 建模与仿真专业委员会委员,主要研究 CHEN Yangyang,TIAN Yuping.Directed coordinated con- 方向为多智能体系统、复杂动态网络、 trol for multi-agent formation motion on a set of given 计算机控制与管理。 curves[J].ActaAutomaticaSinica,2009,37(12):1541- 1549. 陈增强,男,1964年生,教授,博士 [13]徐国焯.多UUV编队路径跟踪控制研究[D].哈尔滨:哈 生导师,中国系统仿真学会理事、中国 尔滨工程大学,2012:12.54. 自动化学会控制理论与应用专业委 XUGuozhuo.Research on path following control for Multi- 员会委员、中国自动化学会过程控制专 业委员会委员、中国优选法统筹法与经 UUV formation [D].Harbin:Harbin Engineering Univer- 济数学研究会复杂系统专业委员会理事、天津市自动化学会 sity,2012:12-54. 理事、天津市图形图像学会理事,主要研究方向为智能预测 [14]FIERRO R,SONG P,DAS Aet al.Cooperative Control of 控制、混沌系统与复杂动态网络、多智能体系统控制。曾担 Robot Formations M ]Philadelphia,US:Springer, 任国家863计划项目、国家自然科学基金项目及省部级科研 2002.66:73-93. 项目10余项。发表学术论文100余篇,被SCI和EI收录10 [15]CROWLEY J L.Asynchronous control of orientation and 0多篇次。 displacement in a robot vehicle C//Proceeding of 1989 [责任编辑:李雪莲]
[7]ARAI T, PAGELLO E, PARKER L E. Guest editorial ad⁃ vances in multirobotsystems[ J]. IEEE Transactions on Ro⁃ botics and Automation, 2002, 18(5): 655⁃661. [8]刘曙光, 魏俊民, 竺志超. 模糊控制技术[M]. 北京: 中 国纺织出版社, 2001: 1⁃8. LIU Shuguang, WEI Junmin, ZHU Zhichao. Fuzzy control technology[M]. Beijing: China Textile Press, 2001: 1⁃8. [9]孙德丰. MATLAB 模糊系统设计[M].北京: 国防工业出 版社, 2009. SUN DefengThe design of Fuzzy Systems[M]. Beijing: Na⁃ tional Defence Industry Press, 2009. [10]HSU Y ⁃C, CHEN G R, LI H X. A Fuzzy adaptive varia⁃ ble structure controller with application to robot manipula⁃ tors[J]. IEEE Transactions on Systems, Man, and Cyber⁃ netics⁃Part B: Cybernetics, 2001, 31(3): 331⁃340. [11]骆德渊, 刘荣, 李纪文. 采用模糊逻辑的移动机器人轨 迹跟踪[J].电子科技大学学报, 2008, 37(6): 943⁃947. LUO Deyuan, LIU Rong, LI Jiwen. Path tracking of mo⁃ bile robots using fuzzy logic[J].Journal of University of E⁃ lectronic Science and Technology of China,2008, 37(6): 943⁃947. [12]陈杨杨, 田玉平.多智能体沿多条给定路径编队运动的 有向协同控制[ J].自动化学报, 2009, 35(12): 1541⁃ 1549. CHEN Yangyang, TIAN Yuping. Directed coordinated con⁃ trol for multi⁃agent formation motion on a set of given curves[J]. ActaAutomaticaSinica, 2009, 37(12): 1541⁃ 1549. [13]徐国焯.多 UUV 编队路径跟踪控制研究[D].哈尔滨:哈 尔滨工程大学, 2012:12⁃54. XUGuozhuo. Research on path following control for Multi⁃ UUV formation [D]. Harbin: Harbin Engineering Univer⁃ sity, 2012: 12⁃54. [14]FIERRO R, SONG P, DAS Aet al. Cooperative Control of 2002, 66: 73⁃93. [15] CROWLEY J L. Asynchronous control of orientation and displacement in a robot vehicle [C] / / Proceeding of 1989 IEEE International Conference on Robotics and Automa⁃ tion. Scottsdale, AZ: IEEE, 1989: 1277⁃1282. [16]吴瑾斐, 秦东兴, 刘俊.四轮式移动机器人非完整运动 控制[J]. 电子科技大学学报, 2007, 36(2): 301⁃304. WU Jinfei, QIN Dongxing, LIU Jun. Nonholonomic motion control of four⁃wheeled mobile robot[J]. Journal of Univer⁃ sity of Electronic Science and Technology of China, 2007, 36(2): 301⁃304. [17]汪超, 唐勇奇. 基于独立 C 代码的模糊控制器应用程 序设计[J].计算机技术与发展, 2009, 19(5): 242⁃244. WANG Chao, TANG Yongqi. Programmer of fuzzy control⁃ ler based on stand⁃alone C⁃Code[J]. Computer Technology and Development, 2009, 19(5): 242⁃244. 作者简介: 吴垠,男,1989 年生,硕士研究生, 主要研究方向为多智能体系统控制、人 工智能系统与控制。 刘忠信,男,1975 年生,教授,博士 生导师,中国人工智能学会智能空天系 统专业委员会委员、中国智能物联系统 建模与仿真专业委员会委员,主要研究 方向为多智能体系统、复杂动态网络、 计算机控制与管理。 陈增强,男,1964 年生,教授,博士 生导师,中国系统仿真学会理事、中国 业委员会委员、中国优选法统筹法与经 济数学研究会复杂系统专业委员会理事、天津市自动化学会 理事、天津市图形图像学会理事,主要研究方向为智能预测 Robot Formations [ M ]. Philadelphia, US: Springer, 任国家 863 计划项目、国家自然科学基金项目及省部级科研 [责任编辑:李雪莲 项目 10 余项。 发表学术论文 100 余篇,被 SCI和 EI 收录 10 0多篇次。 ] ·540· 智 能 系 统 学 报 第 10 卷 自动化学会控制理论与应用专 业委 员会委员、中国自动化学会过程控制专 控制、混沌系统与复杂动态网络、多智能体系统控制。 曾担