机器学习：基于改进的遗传算法的模糊聚类算法编辑部

第10卷第4期 智能系统学报 Vol.10 No.4 2015年8月 CAAI Transactions on Intelligent Systems Aug.2015 D0:10.3969/j.issn.1673-4785.201503033 网络出版地址：http://www.cnki.net/kcms/detail/23.1538.tp.20150709.1649.001.html 基于改进的遗传算法的模糊聚类算法 张永库1，尹灵雪2，孙劲光 (1.辽宁工程技术大学电子与信息工程学院，辽宁葫芦岛125105；2.辽宁工程技术大学研究生学院，辽宁葫芦岛 125105) 摘要：针对传统的模糊C均值聚类(fuz四yC-means clustering)算法容易陷入局部最优解，并且对初始值敏感的缺 陷，提出一种基于改进的遗传算法的模糊聚类算法。该算法针对遗传算法的早熟问题提出一种改进的遗传算法，并 将其应用于FCM算法，来寻找全局最优的聚类中心。实验表明，该算法与基于传统遗传算法的FCM算法相比，具有 更强的寻优能力，更优的聚类效果。 关键词：模糊C均值算法：聚类分析：遗传算法：动态分析：模糊聚类：初始值：避免早熟；全局最优：局部最优 中图分类号：TP18文献标志码：A文章编号：1673-4785(2015)04-0627-09 中文引用格式：张永库，尹灵雪，孙劲光.基于改进的遗传算法的模糊聚类算法[J].智能系统学报，2015,10(4)：627-635. 英文引用格式：ZHANG Yongku,YIN Lingxue,.SUN Jinguang..Fuz四clustering algorithm based on improved genetic algorithm[J]. CAAI Transactions on Intelligent Systems,2015,10(4):627-635. Fuzzy clustering algorithm based on the improved genetic algorithm ZHANG Yongku',YIN Lingxue2,SUN Jinguang (1.College of Electronics and Information Engineering,Liaoning Technical University,Liaoning 125105,China;2.Institute of Gradu- ate,Liaoning Technical University,Liaoning 125105,China) Abstract:The traditional fuzzy C-means(FCM)clustering algorithm is prone to fall into the solution of local opti- mum and is sensitive to initial value.Aiming at these drawbacks,a fuzzy C-means based on the improved genetic algorithm is presented.The improved genetic algorithm is employed to optimise the FCM algorithm,finding the cluster center of the global optimum.Finally,the experimental results show that compared with the traditional FCM,the proposed algorithm has stronger optimisation ability and better clustering effect Keywords:fuzzy C-means clustering;cluster analysis;genetic algorithm;dynamic analysis;fuzzy clustering;initial values;premature contraction avoidance;global optimum;local optimum 作为一种无监督的学习方法，聚类分析被视为 的，那么对其进行划分界限明确的聚类分析显然是 机器学习研究以及数据挖掘应用中的一个主要内 不恰当的。L.A.Zedeh提出了一种用模糊集理论来 容。它仅根据在数据中发现的描述对象及其关系的 解决的聚类问题，即模糊聚类分析。在大量的模糊 信息，将数据对象分组，其目标是，组内的对象相互 聚类算法中，应用的最为广泛的算法便是基于目标 之间是相似的，而不同组中的对象是不同的)。由 函数的模糊C均值算法(FCM)。FCM作为聚类分 于现实生活中许多问题是在类属方面存在模糊性 析中的一个重要研究领域，目前针对其研究的应用 已经非常广泛。但该算法易陷入局部最优解和对初 收稿日期：2015-03-18.网络出版日期：2015-07-02 基金项目：国家自然科学基金资助项目(61172144)：国家科技支撑计划 始值敏感[)。文献[3]提出将遗传算法(genetic al-- 资助项目(2013BAH12F02):辽宁省教育厅科学研究一般资 gorithm)应用于FCM,利用GA的全局搜索性能去确 助项目(L201432). 通信作者：尹灵雪.E-mail:ykx19910708@163.com 定最佳聚类数并寻找到全局最优聚类中心，即GA

第 １０ 卷第 ４ 期 智 能 系 统 学 报 Ｖｏｌ．１０ №．４ ２０１５ 年 ８ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ａｕｇ． ２０１５ ＤＯＩ：１０．３９６９ ／ ｊ．ｉｓｓｎ．１６７３⁃４７８５．２０１５０３０３３ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ｔｐ．２０１５０７０９．１６４９．００１．ｈｔｍｌ 基于改进的遗传算法的模糊聚类算法 张永库１ ，尹灵雪２ ，孙劲光１ （１．辽宁工程技术大学 电子与信息工程学院，辽宁 葫芦岛 １２５１０５；２． 辽宁工程技术大学 研究生学院，辽宁 葫芦岛 １２５１０５） 摘 要：针对传统的模糊 Ｃ 均值聚类（ ｆｕｚｚｙ Ｃ⁃ｍｅａｎｓ ｃｌｕｓｔｅｒｉｎｇ）算法容易陷入局部最优解，并且对初始值敏感的缺 陷，提出一种基于改进的遗传算法的模糊聚类算法。 该算法针对遗传算法的早熟问题提出一种改进的遗传算法，并 将其应用于 ＦＣＭ 算法，来寻找全局最优的聚类中心。 实验表明，该算法与基于传统遗传算法的 ＦＣＭ 算法相比，具有 更强的寻优能力，更优的聚类效果。 关键词：模糊 Ｃ 均值算法；聚类分析；遗传算法；动态分析；模糊聚类；初始值；避免早熟；全局最优；局部最优 中图分类号： ＴＰ１８ 文献标志码：Ａ 文章编号：１６７３⁃４７８５（２０１５）０４⁃０６２７⁃０９ 中文引用格式：张永库，尹灵雪，孙劲光． 基于改进的遗传算法的模糊聚类算法［Ｊ］． 智能系统学报， ２０１５， １０（４）： ６２７⁃６３５． 英文引用格式：ＺＨＡＮＧ Ｙｏｎｇｋｕ，ＹＩＮ Ｌｉｎｇｘｕｅ，ＳＵＮ Ｊｉｎｇｕａｎｇ． Ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ｂａｓｅｄ ｏｎ ｉｍｐｒｏｖｅｄ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ［Ｊ］． ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ， ２０１５， １０（４）： ６２７⁃６３５． Ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ｂａｓｅｄ ｏｎ ｔｈｅ ｉｍｐｒｏｖｅｄ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ ＺＨＡＮＧ Ｙｏｎｇｋｕ １ ，ＹＩＮ Ｌｉｎｇｘｕｅ ２ ，ＳＵＮ Ｊｉｎｇｕａｎｇ １ （ １． Ｃｏｌｌｅｇｅ ｏｆ Ｅｌｅｃｔｒｏｎｉｃｓ ａｎｄ Ｉｎｆｏｒｍａｔｉｏｎ Ｅｎｇｉｎｅｅｒｉｎｇ， Ｌｉａｏｎｉｎｇ Ｔｅｃｈｎｉｃａｌ Ｕｎｉｖｅｒｓｉｔｙ， Ｌｉａｏｎｉｎｇ １２５１０５， Ｃｈｉｎａ； ２． Ｉｎｓｔｉｔｕｔｅ ｏｆ Ｇｒａｄｕ⁃ ａｔｅ， Ｌｉａｏｎｉｎｇ Ｔｅｃｈｎｉｃａｌ Ｕｎｉｖｅｒｓｉｔｙ， Ｌｉａｏｎｉｎｇ １２５１０５， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｔｈｅ ｔｒａｄｉｔｉｏｎａｌ ｆｕｚｚｙ Ｃ⁃ｍｅａｎｓ（ＦＣＭ） ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ｉｓ ｐｒｏｎｅ ｔｏ ｆａｌｌ ｉｎｔｏ ｔｈｅ ｓｏｌｕｔｉｏｎ ｏｆ ｌｏｃａｌ ｏｐｔｉ⁃ ｍｕｍ ａｎｄ ｉｓ ｓｅｎｓｉｔｉｖｅ ｔｏ ｉｎｉｔｉａｌ ｖａｌｕｅ． Ａｉｍｉｎｇ ａｔ ｔｈｅｓｅ ｄｒａｗｂａｃｋｓ， ａ ｆｕｚｚｙ Ｃ⁃ｍｅａｎｓ ｂａｓｅｄ ｏｎ ｔｈｅ ｉｍｐｒｏｖｅｄ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ ｉｓ ｐｒｅｓｅｎｔｅｄ． Ｔｈｅ ｉｍｐｒｏｖｅｄ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ ｉｓ ｅｍｐｌｏｙｅｄ ｔｏ ｏｐｔｉｍｉｓｅ ｔｈｅ ＦＣＭ ａｌｇｏｒｉｔｈｍ， ｆｉｎｄｉｎｇ ｔｈｅ ｃｌｕｓｔｅｒ ｃｅｎｔｅｒ ｏｆ ｔｈｅ ｇｌｏｂａｌ ｏｐｔｉｍｕｍ． Ｆｉｎａｌｌｙ， ｔｈｅ ｅｘｐｅｒｉｍｅｎｔａｌ ｒｅｓｕｌｔｓ ｓｈｏｗ ｔｈａｔ ｃｏｍｐａｒｅｄ ｗｉｔｈ ｔｈｅ ｔｒａｄｉｔｉｏｎａｌ ＦＣＭ， ｔｈｅ ｐｒｏｐｏｓｅｄ ａｌｇｏｒｉｔｈｍ ｈａｓ ｓｔｒｏｎｇｅｒ ｏｐｔｉｍｉｓａｔｉｏｎ ａｂｉｌｉｔｙ ａｎｄ ｂｅｔｔｅｒ ｃｌｕｓｔｅｒｉｎｇ ｅｆｆｅｃｔ Ｋｅｙｗｏｒｄｓ：ｆｕｚｚｙ Ｃ⁃ｍｅａｎｓ ｃｌｕｓｔｅｒｉｎｇ； ｃｌｕｓｔｅｒ ａｎａｌｙｓｉｓ； ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ； ｄｙｎａｍｉｃ ａｎａｌｙｓｉｓ； ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ；ｉｎｉｔｉａｌ ｖａｌｕｅｓ； ｐｒｅｍａｔｕｒｅ ｃｏｎｔｒａｃｔｉｏｎ ａｖｏｉｄａｎｃｅ； ｇｌｏｂａｌ ｏｐｔｉｍｕｍ； ｌｏｃａｌ ｏｐｔｉｍｕｍ 收稿日期：２０１５⁃０３⁃１８． 网络出版日期：２０１５⁃０７⁃０２． 基金项目：国家自然科学基金资助项目（６１１７２１４４）；国家科技支撑计划 资助项目（２０１３ＢＡＨ１２Ｆ０２）；辽宁省教育厅科学研究一般资 助项目（Ｌ２０１４３２）． 通信作者：尹灵雪． Ｅ⁃ｍａｉｌ：ｙｌｘ１９９１０７０８＠ １６３．ｃｏｍ． 作为一种无监督的学习方法，聚类分析被视为 机器学习研究以及数据挖掘应用中的一个主要内 容。 它仅根据在数据中发现的描述对象及其关系的 信息，将数据对象分组，其目标是，组内的对象相互 之间是相似的，而不同组中的对象是不同的［１］ 。 由 于现实生活中许多问题是在类属方面存在模糊性 的，那么对其进行划分界限明确的聚类分析显然是 不恰当的。 Ｌ．Ａ．Ｚｅｄｅｈ 提出了一种用模糊集理论来 解决的聚类问题，即模糊聚类分析。 在大量的模糊 聚类算法中，应用的最为广泛的算法便是基于目标 函数的模糊 Ｃ 均值算法（ ＦＣＭ）。 ＦＣＭ 作为聚类分 析中的一个重要研究领域，目前针对其研究的应用 已经非常广泛。 但该算法易陷入局部最优解和对初 始值敏感［２］ 。 文献［３］提出将遗传算法（ ｇｅｎｅｔｉｃ ａｌ⁃ ｇｏｒｉｔｈｍ）应用于 ＦＣＭ，利用 ＧＡ 的全局搜索性能去确 定最佳聚类数并寻找到全局最优聚类中心，即 ＧＡ⁃

·628. 智能系统学报 第10卷 FCM算法[)。近些年来，GA-FCM算法得到了十分 为了使目标函数J在已经给定的约束条件下取 广泛的应用46]，众多学者针对GA-FCM提出了改 得极小值，FCM算法基本步骤如下： 进的算法，LIU Su-hua)等将模拟退火算法引入了 1)随机生成c个聚类中心{A1,A2,…,A}。 GA中，以此来改进GA的早熟问题，进而获得较好 2)根据式(4)，计算求得隶属矩阵U,使其符合 的聚类效果，与此同时改进GA的交叉算子和变异 式(1)中的约束条件。 算子。Feryel Souami等提出的文献[8]使用了一种 3)根据式(2)计算目标函数值。若它小于某个 新的适应度函数，从而避免了存储和计算隶属度矩 阵在效率上的浪费[)。 确定的阈值，或者它相对上一次目标函数值的改变 量小于某一个给定阈值，则算法终止。 这些算法用不同的方法来对GA-FCM进行了 改进并且取得了良好的效果。为了进一步优化GA 4)用式(3)计算得到新的聚类中心。返回2)。 FCM所达到的聚类效果，改进GA所存在的早熟问 2遗传算法 题，本文通过对GA的选择算子进行改进，并非每次 循环都进行选择，而是通过目前种群中个体的多样 John H.Holland在20世纪60年代提出遗传算 性动态决定选择操作是否发生，进而提出了一个新 法，该算法是一种基于遗传学中的自然选择和适者 的Dynamic GA-FCM算法，改进了GA的早熟问题， 生存机制而产生的简单、强健、有效的优化技术。 通过人工数据以及经典数据集的仿真实验，表明本 GA中所求问题的可行解使用个体即染色体来表 文所提出的改进方法确实具有更佳的聚类性能。 示，并且每一个体以STRING类型进行编码，该算法 以遗传学为基础，每一个体都按照提前设计好的适 1FCM算法 应度函数来计算该个体的适应度值，然后按照优胜 模糊C均值聚类(FCM)最早是由JAMES C. 劣汰原则并且通过全局并行搜索来不断地获得更加 BEZDEK等人在参考文献[9]中提出来的，FCM算法 优秀的个体，进而获得更加优秀的种群山。编码的 基于模糊划分，用隶属度来确定每一个数据，点属于某 方法、对种群的初始化、设计适应度函数、遗传算子 一个聚类的程度，最终实现被划分到同一簇的对象之 以及各个参数的设置，以上5部分是遗传算法的主 间相似度最大，而不同簇之间的相似度最小)。 要部分[1。 它把向量x,(i=1,2,…,n)分为c组V={V, 而上述提到的遗传算子，其中主要包括选择算 V2,…,V},并求出每一组的聚类中心A={A1,A2 …,A},每一个向量x用值在0~1的隶属度来表示 子、交叉算子、和变异算子。以下为基本遗传算法的 其属于各个组的程度。一个数据集的隶属度之和恒 步骤： 等于1。即隶属度矩阵U必须满足如下条件： 1)随机产生染色体种群，每一个染色体都代表 一个所求解问题的解决方案。 ∑4g=1,j=1,2,…,n (1) 2)计算种群中每一个染色体的适应度值。 当“：=1时表示第j个对象完全属于第i个类， 3)重复以下步骤，直到完成一个新的种群的产生。 u:=0时表示第j个对象完全不属于第i个类。 ①根据每个个体的适应度值从种群中选择2个 FCM的目标函数为 父代染色体。适应度值越高，被选中作为父代染色 JU,AA…,A)=∑，=∑∑gd(2) 体的概率越大。 i=1 i=1 ②给定一个交叉概率P.,若2个父代染色体交 d,=‖A:-x,‖为第i个聚类中心和第j个数据点 叉则形成新的子代染色体。若未发生交叉，则其子 之间的欧几里德距离：其中入∈[1，∞)，它是一个 代染色体与父代染色体相同。 加权指数。在式(1)约束条件下对式(2)应用拉格 朗日乘法，求导得： 4)用新产生的种群代替原来的种群。 5)给定一个变异概率Pm,种群中每个个体以该 概率发生变异，产生新的子代。 A,=ii (3) 6)用新产生的种群代替原来的种群。 7)如果新种群满足了终止条件，则跳出循环， 1 并且返回种群中的最佳解决方案，得到所求问题的 d 72/A-1) (4) 最优解。 8)回到2)

ＦＣＭ 算法［３］ 。 近些年来，ＧＡ⁃ＦＣＭ 算法得到了十分 广泛的应用［４⁃６］ ，众多学者针对 ＧＡ⁃ＦＣＭ 提出了改 进的算法，ＬＩＵ Ｓｕ⁃ｈｕａ ［７］ 等将模拟退火算法引入了 ＧＡ 中，以此来改进 ＧＡ 的早熟问题，进而获得较好 的聚类效果，与此同时改进 ＧＡ 的交叉算子和变异 算子。 Ｆｅｒｙｅｌ Ｓｏｕａｍｉ 等提出的文献［８］使用了一种 新的适应度函数，从而避免了存储和计算隶属度矩 阵在效率上的浪费［８］ 。 这些算法用不同的方法来对 ＧＡ⁃ＦＣＭ 进行了 改进并且取得了良好的效果。 为了进一步优化 ＧＡ⁃ ＦＣＭ 所达到的聚类效果，改进 ＧＡ 所存在的早熟问 题，本文通过对 ＧＡ 的选择算子进行改进，并非每次 循环都进行选择，而是通过目前种群中个体的多样 性动态决定选择操作是否发生，进而提出了一个新 的 Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ 算法，改进了 ＧＡ 的早熟问题， 通过人工数据以及经典数据集的仿真实验，表明本 文所提出的改进方法确实具有更佳的聚类性能。 １ ＦＣＭ 算法 模糊 Ｃ 均值聚类（ ＦＣＭ） 最早是由 ＪＡＭＥＳ Ｃ． ＢＥＺＤＥＫ 等人在参考文献［９］中提出来的，ＦＣＭ 算法 基于模糊划分，用隶属度来确定每一个数据点属于某 一个聚类的程度，最终实现被划分到同一簇的对象之 间相似度最大，而不同簇之间的相似度最小［１］ 。 它把向量 ｘｉ（ｉ ＝ １，２，…，ｎ） 分为 ｃ 组 Ｖ ＝ ｛Ｖ１ ， Ｖ２ ，…，Ｖｃ｝， 并求出每一组的聚类中心 Ａ ＝ ｛Ａ１ ，Ａ２ ， …，Ａｃ｝ ，每一个向量 ｘｉ 用值在 ０～１ 的隶属度来表示 其属于各个组的程度。 一个数据集的隶属度之和恒 等于 １。 即隶属度矩阵 Ｕ 必须满足如下条件： ∑ ｃ ｉ ＝ １ ｕｉｊ ＝ １，∀ｊ ＝ １，２，…，ｎ （１） 当 ｕｉｊ ＝ １ 时表示第 ｊ 个对象完全属于第 ｉ 个类， ｕｉｊ ＝ ０ 时表示第 ｊ 个对象完全不属于第 ｉ 个类。 ＦＣＭ 的目标函数为 Ｊ（Ｕ，Ａ１ ，Ａ２ ，…，Ａｃ） ＝ ∑ ｃ ｉ ＝ １ Ｊｉ ＝ ∑ ｃ ｉ ＝ １ ∑ ｎ ｊ ｕ λ ｉｊ ｄ ２ ｉｊ （２） ｄｉｊ ＝ ‖Ａｉ － ｘｊ‖ 为第 ｉ 个聚类中心和第 ｊ 个数据点 之间的欧几里德距离；其中 λ ∈ ［１， ∞ ） ，它是一个 加权指数。 在式（１） 约束条件下对式（２） 应用拉格 朗日乘法，求导得： Ａｉ ＝ ∑ ｎ ｊ ＝ １ ｕ λ ｉｊ ｘｊ ∑ ｎ ｊ ＝ １ ｕ λ ｉｊ （３） ｕｉｊ ＝ １ ∑ ｃ ｋ ＝ １ ｄｉｊ ｄｋｊ é ë ê ê ù û ú ú ２／ （λ－１） （４） 为了使目标函数 Ｊ 在已经给定的约束条件下取 得极小值，ＦＣＭ 算法基本步骤如下： １）随机生成 ｃ 个聚类中心 ｛Ａ１ ，Ａ２ ，…，Ａｃ｝ 。 ２）根据式（４），计算求得隶属矩阵 Ｕ，使其符合 式（１）中的约束条件。 ３）根据式（２）计算目标函数值。 若它小于某个 确定的阈值，或者它相对上一次目标函数值的改变 量小于某一个给定阈值，则算法终止。 ４）用式（３）计算得到新的聚类中心。 返回 ２）。 ２ 遗传算法 Ｊｏｈｎ Ｈ． Ｈｏｌｌａｎｄ 在 ２０ 世纪 ６０ 年代提出遗传算 法，该算法是一种基于遗传学中的自然选择和适者 生存机制而产生的简单、强健、有效的优化技术［１０］ 。 ＧＡ 中所求问题的可行解使用个体即染色体来表 示，并且每一个体以 ＳＴＲＩＮＧ 类型进行编码，该算法 以遗传学为基础，每一个体都按照提前设计好的适 应度函数来计算该个体的适应度值，然后按照优胜 劣汰原则并且通过全局并行搜索来不断地获得更加 优秀的个体，进而获得更加优秀的种群［１１］ 。 编码的 方法、对种群的初始化、设计适应度函数、遗传算子 以及各个参数的设置，以上 ５ 部分是遗传算法的主 要部分［１２］ 。 而上述提到的遗传算子，其中主要包括选择算 子、交叉算子、和变异算子。 以下为基本遗传算法的 步骤： １）随机产生染色体种群，每一个染色体都代表 一个所求解问题的解决方案。 ２） 计算种群中每一个染色体的适应度值。 ３）重复以下步骤，直到完成一个新的种群的产生。 ①根据每个个体的适应度值从种群中选择 ２ 个 父代染色体。 适应度值越高，被选中作为父代染色 体的概率越大。 ②给定一个交叉概率 Ｐｃ，若 ２ 个父代染色体交 叉则形成新的子代染色体。 若未发生交叉，则其子 代染色体与父代染色体相同。 ４） 用新产生的种群代替原来的种群。 ５）给定一个变异概率 Ｐｍ ，种群中每个个体以该 概率发生变异，产生新的子代。 ６）用新产生的种群代替原来的种群。 ７）如果新种群满足了终止条件，则跳出循环， 并且返回种群中的最佳解决方案，得到所求问题的 最优解。 ８）回到 ２）。 ·６２８· 智 能 系 统 学 报 第 １０ 卷

第4期 张永库，等.基于改进的遗传算法的模糊聚类算法 ·629. 3.2适应度函数 Dynamic GA-FCM 对于所求解问题，解决方案的好坏通过每一个 GA-FCM算法虽然在一定程度上改善了模糊C 个体的适应度值来评价。而适应度值则是根据事先 均值算法对初始聚类中心敏感的问题，但遗传算法的 定义好的适应度函数计算得到的。 早熟问题却严重影响了聚类算法的准确性]。在传 传统GA-FCM算法的适应度函数需要使用隶 统的GA-FCM算法中，由于早熟问题而产生的局部最 属度矩阵，而每次循环中，隶属度矩阵的更新花费大 优聚类中心，可能会降低该算法聚类的质量。 量的时间，在很大程度上降低了算法的效率，为了解 基于以上问题，本文将传统遗传算法进行改进， 决这一问题，Hathaway和Bezdek基于式(2)提出了 目的是降低其发生早熟现象的概率，从而提高聚类 一个新的FCM目标函数的形式，Feryel Souami就是 的质量。早熟问题发生的最主要原因就是选择的速 基于该目标函数以及Frigui所提出的竞争凝聚 度过快，而产生新个体的速度过慢15]。在遗传算法 (competitive agglomeration)算法，提出了一个新的适 中，新个体的产生是通过交叉算子和变异算子来实 应度函数[]，该适应度函数定义如下： 现，因此可以通过增加交叉和变异算子实现的次数 1 F= (5) 来加快产生新个体的速度，但同时，若种群中个体的 R*(t) 多样性过高，即产生新个体的速度过快，又会导致种 f(t)=1-a*exp(-t/b) (6) 群中个体所保存的解决方案的信息将会被丢失，并 式中：t为种群解决方案的代数，a、b为2个常量。 且很难实现最终的收敛，或收敛的速度过慢。为了 能够平衡种群中个体的多样性和稳定性，本文将遗 R=∑（∑(d,4)1-) (7) 传算法中的选择算子进行改进，使其根据当前种群 其中，d可以是欧几里得距离，也可以是其他距离。 中个体的多样性，来自适应的调整选择的速度。进 在本文中，使用了欧几里得距离，1为模糊指数。 而保证种群中个体的多样性保持在适当的水平，不 3.3 选择操作 会过高，也不会过低。由于传统的GA-FCM每次计 选择操作就是从种群中选择适应度值较高的个 算适应度函数值时都需要计算隶属度矩阵，这大大 体，将其保留到下一代种群，适应度值越高的个体 增加了实现算法所用的时间，在本算法中，采用了 被保留到下一代的概率就越高，反之则越小，选择操 Feryel Souami等提出的新的适应度函数公式()，计 作使种群中个体的适应度值不断的接近于最优解。 算适应度时不再计算隶属度矩阵，缩短了算法所用 本文使用轮盘赌选择法。该方法是一种回放式随机 时间20。 采样法，种群中每一个个体被选择的概率为 3.1染色体编码和初始种群产生 染色体编码有很多种方式，本文采用了浮点数 p(ind,)=F(ind,)/F(ind.) (8) k=1 编码。初始种群的产生采用了随机生成，方法为：在 式中：F(ind:)为第i个个体的适应度值， 所给出的参与聚类分析的n个样本点中，随机的抽 取c个样本点，将其作为c个聚类的聚类中心，并通 F(ind)为种群中所有个体，即m个个体的适应 =1 过染色体表示出来，其中c为聚类数。即1条染色 度值之和。 体可以使用由c个基因位组成的浮点码串{A1,A2, 3.4交叉操作 A3,…,A}表示，重复进行m次(m为种群大小)， 本文算法采用了离散重组的一点交叉，假设有染 得到初始种群。如图1所示，为一个由4个二维聚 色体对x(t)=(x1,x2,…,xm,…,xc),x(t)= 类中心组成的染色体，其中A1A2(Hi=1,2,…,c) （61,x2,…,x,…,xc)。其中i∈(1,2，…，c）,t 皆为浮点数。 为遗传算法迭代次数。每个染色体的任意2个相邻 A11A12 A21A22A31A32 A41A42 基因位之间设立一个交叉点，从左到右依次为1,2， …,c-1,总共c-1个不同的交叉点。每一对染色体以 P概率来进行交叉，在c-1个交叉点中随机的选择一 Al A2 A3 A4 染色体 点，交换2个染色体自该交叉点以后的所有基因。 聚类中心为有2维特征的{A1,A2,A3,A4} 3.5变异操作 图1染色体的表示方式 对每一个个体的每一个基因位，产生随机数P, Fig.1 Representation of a chromosome 当p<P时，对此基因位进行随机变异操作，在参与

３ Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ ＧＡ⁃ＦＣＭ 算法虽然在一定程度上改善了模糊 Ｃ 均值算法对初始聚类中心敏感的问题，但遗传算法的 早熟问题却严重影响了聚类算法的准确性［１３］ 。 在传 统的 ＧＡ⁃ＦＣＭ 算法中，由于早熟问题而产生的局部最 优聚类中心，可能会降低该算法聚类的质量［１４］ 。 基于以上问题，本文将传统遗传算法进行改进， 目的是降低其发生早熟现象的概率，从而提高聚类 的质量。 早熟问题发生的最主要原因就是选择的速 度过快，而产生新个体的速度过慢［１５］ 。 在遗传算法 中，新个体的产生是通过交叉算子和变异算子来实 现，因此可以通过增加交叉和变异算子实现的次数 来加快产生新个体的速度，但同时，若种群中个体的 多样性过高，即产生新个体的速度过快，又会导致种 群中个体所保存的解决方案的信息将会被丢失，并 且很难实现最终的收敛，或收敛的速度过慢。 为了 能够平衡种群中个体的多样性和稳定性，本文将遗 传算法中的选择算子进行改进，使其根据当前种群 中个体的多样性，来自适应的调整选择的速度。 进 而保证种群中个体的多样性保持在适当的水平，不 会过高，也不会过低。 由于传统的 ＧＡ⁃ＦＣＭ 每次计 算适应度函数值时都需要计算隶属度矩阵，这大大 增加了实现算法所用的时间，在本算法中，采用了 Ｆｅｒｙｅｌ Ｓｏｕａｍｉ 等提出的新的适应度函数公式［８］ ，计 算适应度时不再计算隶属度矩阵，缩短了算法所用 时间［２０］ 。 ３．１ 染色体编码和初始种群产生 染色体编码有很多种方式，本文采用了浮点数 编码。 初始种群的产生采用了随机生成，方法为：在 所给出的参与聚类分析的 ｎ 个样本点中，随机的抽 取 ｃ 个样本点，将其作为 ｃ 个聚类的聚类中心，并通 过染色体表示出来，其中 ｃ 为聚类数。 即 １ 条染色 体可以使用由 ｃ 个基因位组成的浮点码串 ｛Ａ１ ，Ａ２ ， Ａ３ ，…，Ａｃ｝ 表示，重复进行 ｍ 次（ｍ 为种群大小）， 得到初始种群。 如图 １ 所示，为一个由 ４ 个二维聚 类中心组成的染色体，其中 Ａｉ１ 、Ａｉ２（∀ｉ ＝ １，２，…，ｃ） 皆为浮点数。 图 １ 染色体的表示方式 Ｆｉｇ．１ Ｒｅｐｒｅｓｅｎｔａｔｉｏｎ ｏｆ ａ ｃｈｒｏｍｏｓｏｍｅ ３．２ 适应度函数 对于所求解问题，解决方案的好坏通过每一个 个体的适应度值来评价。 而适应度值则是根据事先 定义好的适应度函数计算得到的。 传统 ＧＡ⁃ＦＣＭ 算法的适应度函数需要使用隶 属度矩阵，而每次循环中，隶属度矩阵的更新花费大 量的时间，在很大程度上降低了算法的效率，为了解 决这一问题，Ｈａｔｈａｗａｙ 和 Ｂｅｚｄｅｋ 基于式（２）提出了 一个新的 ＦＣＭ 目标函数的形式，Ｆｅｒｙｅｌ Ｓｏｕａｍｉ 就是 基于该目标函数以及 Ｆｒｉｇｕｉ 所提出的竞争凝聚 （ｃｏｍｐｅｔｉｔｉｖｅ ａｇｇｌｏｍｅｒａｔｉｏｎ）算法，提出了一个新的适 应度函数［１９］ ，该适应度函数定义如下： Ｆ ＝ １ Ｒ∗ｆ ２ （ｔ） （５） ｆ（ｔ） ＝ １ － ａ∗ｅｘｐ（ － ｔ ／ ｂ） （６） 式中：ｔ 为种群解决方案的代数， ａ、ｂ 为 ２ 个常量。 Ｒ ＝ ∑ ｎ ｊ ＝ １ （∑ ｃ ｉ ＝ １ （ｄ（ｘｊ，Ａｉ）） １／ （１－ｌ） ） １－ｌ （７） 其中，ｄ 可以是欧几里得距离，也可以是其他距离。 在本文中，使用了欧几里得距离， ｌ 为模糊指数。 ３．３ 选择操作 选择操作就是从种群中选择适应度值较高的个 体，将其保留到下一代种群，适应度值越高的个体， 被保留到下一代的概率就越高，反之则越小，选择操 作使种群中个体的适应度值不断的接近于最优解。 本文使用轮盘赌选择法。 该方法是一种回放式随机 采样法，种群中每一个个体被选择的概率为 ｐ（ｉｎｄｉ） ＝ Ｆ（ｉｎｄｉ） ／∑ ｍ ｋ ＝ １ Ｆ（ｉｎｄｋ） （８） 式 中： Ｆ（ｉｎｄｉ） 为 第 ｉ 个 个 体 的 适 应 度 值， ∑ ｍ ｋ ＝ １ Ｆ（ｉｎｄｋ） 为种群中所有个体，即 ｍ 个个体的适应 度值之和。 ３．４ 交叉操作 本文算法采用了离散重组的一点交叉，假设有染 色体 对 ｘａ（ｔ） ＝ （ｘａ１ ，ｘａ２ ，…，ｘａｉ，…，ｘａｃ），ｘｂ（ｔ） ＝ （ｘｂ１ ，ｘｂ２ ，…，ｘｂｉ， …，ｘｂｃ） 。 其中 ｉ ∈ （１，２，…，ｃ） ， ｔ 为遗传算法迭代次数。 每个染色体的任意 ２ 个相邻 基因位之间设立一个交叉点，从左到右依次为 １，２， …，ｃ－１，总共 ｃ－１ 个不同的交叉点。 每一对染色体以 Ｐｃ概率来进行交叉，在 ｃ－１ 个交叉点中随机的选择一 点，交换 ２ 个染色体自该交叉点以后的所有基因。 ３．５ 变异操作 对每一个个体的每一个基因位，产生随机数 ｐ， 当 ｐ ＜ Ｐｍ 时，对此基因位进行随机变异操作，在参与 第 ４ 期 张永库，等． 基于改进的遗传算法的模糊聚类算法 ·６２９·

·630 智能系统学报 第10卷 聚类分析的样本集中随机的抽取一个对象，代替此基 的动态选择可以动态的调整种群收敛速度。将上述 因位的基因，作为新聚类中心，生成下一代种群。 过程不断循环，最终求得全局最优解。 变异概率Pm一般很小，通常在0.001~0.1，如果 算法的步骤为： 变异概率过大，就会破坏很多优良个体，可能无法得 1)参数初始化，种群大小m,交叉概率P.,变异 到最优解，而如果变异概率过小，个体则无法变异到 概率Pm,聚类数c; 更优的解，导致算法收敛速度变慢，只能达到局部最 2)初始化由m个个体组成的初始种群，每个个 优解。 体由c个聚类中心组成： 3.6保持种群多样性 3)对于每一个个体，用式(5)~(7)计算该个 在聚类分析中，传统的遗传算法当种群中各个 体的适应度值F(ind:),其中i=1,2,…,m: 体的目标函数值趋向一致或者趋向局部最优时，对 4)根据适应度值F(ind,)用式(9)、(10)计算 于交叉算子以及变异算子来说，不易生成新的最优 出种群中个体的多样性度量值Stddev(P)是否大于 个体的结构，因而搜索范围将局限于局部最优的区 最低多样性度量值Std,若是，则执行5)，否则执 域，只能取得局部最优的结果，即早熟。针对这一问 行6)： 题，在本算法中，当种群中的各个体其目标函数值趋 5)根据适应度值F(ind:),用式(8)计算出选 向一致时，根据种群的多样性度量值，动态决定选择 择概率，执行选择操作； 操作是否发生，而非每次循环都进行选择，只有当种 6)对种群中各个体执行交叉和变异操作产生 群的多样性度量值大于所期望的最低多样性度量值 新个体： 时，才进行选择操作。 7)将新个体代替原个体保留在种群中： 本算法采用标准偏差法(standard deviation)来 8)若在一定迭代次数L内种群的性能没有改 度量种群的多样性，标准偏差法是Kenny Q.Zhu在 进或达到了最大迭代次数t,跳出循环，否则执行步 文献[16]中所介绍的。根据该方法，种群的多样性 骤3)。 度量值为 3.8算法复杂性分析 算法的时间复杂度可以用来度量算法运行的时 stddev(P)= (9) m-1 间，表示算法计算效率的高低，其大小反映了算法性 式中：m为种群大小，f为第i个个体的适应度值，f 能的优劣，不考虑硬件及环境因素，假设每一次执行 为种群中所有个体适应度值的平均值。 时硬件条件和环境条件是相同的，设有n个待聚类 而最低多样性度量值，本算法根据Kim Nguyen 对象，聚类中心个数为c,种群大小为m,算法的迭 等在文献[17]所提出的模型，将其定义为 代次数为L,则本文算法的时间复杂度为O(Lncm), Std(b)=Std(0)x exp(-b) (10) 以下为对时间复杂度的说明。 式中：Std(0)为种群初始多样性度量值，b为种群 1)以算法的一次迭代为例，从待聚类的n个对 当前的迭代次数。 象中随机选取m个个体作为初始种群，其中每个个 3.7 Dynamic GA-FCM算法描述 体由c个对象组成，代表c个聚类中心，其时间复杂 Dynamic GA-FCM算法的思想是先随机选择m 度为O(cm)。 个个体，组成大小为m的种群，然后计算种群的多 2)求解种群中每个个体适应度时，需要遍历 样性度量值，若种群的多样性小于给定阈值，则不进 个待聚类对象与该个体所代表的c个聚类中心的距 行选择操作，对种群中的个体不断的循环进行交叉 离矩阵Dxm,其时间复杂度为O(c),由于需要计 操作和变异操作，增加种群中个体的多样性，直至种 算种群中m个个体的适应度，那么该步骤总共消耗 群多样性大于给定阈值。当种群多样性度量值大于 的时间为O(ncm)。 阈值时，则按照原遗传算法的流程，顺序进行选择、 3)计算种群中个体的多样性度量值Stddev(P) 交叉、以及变异操作。交叉算子和变异算子的作用 需要对种群中所有个体的适应度进行遍历，时间复 是产生新的个体，每次交叉变异结束，用新个体代替 杂度为0(m)。 原个体保留在种群中。通过该种思想，使种群中个 4)选择操作需要计算种群中每个个体的选择 体的多样性动态控制选择算子实现的速度。由于选 概率并根据选择概率重新选择m个个体，时间复杂 择算子的作用主要是实现种群的收敛，故通过本文 度为0(2m)

聚类分析的样本集中随机的抽取一个对象，代替此基 因位的基因，作为新聚类中心，生成下一代种群。 变异概率 Ｐｍ一般很小，通常在 ０．００１～０．１，如果 变异概率过大，就会破坏很多优良个体，可能无法得 到最优解，而如果变异概率过小，个体则无法变异到 更优的解，导致算法收敛速度变慢，只能达到局部最 优解。 ３．６ 保持种群多样性 在聚类分析中，传统的遗传算法当种群中各个 体的目标函数值趋向一致或者趋向局部最优时，对 于交叉算子以及变异算子来说，不易生成新的最优 个体的结构，因而搜索范围将局限于局部最优的区 域，只能取得局部最优的结果，即早熟。 针对这一问 题，在本算法中，当种群中的各个体其目标函数值趋 向一致时，根据种群的多样性度量值，动态决定选择 操作是否发生，而非每次循环都进行选择，只有当种 群的多样性度量值大于所期望的最低多样性度量值 时，才进行选择操作。 本算法采用标准偏差法（ ｓｔａｎｄａｒｄ ｄｅｖｉａｔｉｏｎ） 来 度量种群的多样性，标准偏差法是 Ｋｅｎｎｙ Ｑ． Ｚｈｕ 在 文献［１６］中所介绍的。 根据该方法，种群的多样性 度量值为 ｓｔｄｄｅｖ（Ｐ） ＝ ∑ ｍ ｉ ＝ １ （ｆ ｉ － ｆ － ） ２ ｍ － １ （９） 式中：ｍ 为种群大小， ｆ ｉ为第 ｉ 个个体的适应度值， ｆ － 为种群中所有个体适应度值的平均值。 而最低多样性度量值，本算法根据 Ｋｉｍ Ｎｇｕｙｅｎ 等在文献［１７］所提出的模型，将其定义为 Ｓｔｄｍｉｎ（ｂ） ＝ Ｓｔｄｍｉｎ（０） × ｅｘｐ（ － ｂ） （１０） 式中：Ｓｔｄｍｉｎ（０）为种群初始多样性度量值，ｂ 为种群 当前的迭代次数。 ３．７ Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ 算法描述 Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ 算法的思想是先随机选择 ｍ 个个体，组成大小为 ｍ 的种群，然后计算种群的多 样性度量值，若种群的多样性小于给定阈值，则不进 行选择操作，对种群中的个体不断的循环进行交叉 操作和变异操作，增加种群中个体的多样性，直至种 群多样性大于给定阈值。 当种群多样性度量值大于 阈值时，则按照原遗传算法的流程，顺序进行选择、 交叉、以及变异操作。 交叉算子和变异算子的作用 是产生新的个体，每次交叉变异结束，用新个体代替 原个体保留在种群中。 通过该种思想，使种群中个 体的多样性动态控制选择算子实现的速度。 由于选 择算子的作用主要是实现种群的收敛，故通过本文 的动态选择可以动态的调整种群收敛速度。 将上述 过程不断循环，最终求得全局最优解。 算法的步骤为： １）参数初始化，种群大小 ｍ，交叉概率 Ｐｃ，变异 概率 Ｐｍ ，聚类数 ｃ； ２）初始化由 ｍ 个个体组成的初始种群，每个个 体由 ｃ 个聚类中心组成； ３） 对于每一个个体，用式（５） ～ （７） 计算该个 体的适应度值 Ｆ（ｉｎｄｉ） ，其中 ｉ ＝ １，２，…，ｍ； ４） 根据适应度值 Ｆ（ｉｎｄｉ） 用式（９）、（１０）计算 出种群中个体的多样性度量值 Ｓｔｄｄｅｖ（Ｐ）是否大于 最低多样性度量值 Ｓｔｄｍｉｎ ，若是，则执行 ５），否则执 行 ６）； ５）根据适应度值 Ｆ（ｉｎｄｉ） ，用式（８） 计算出选 择概率，执行选择操作； ６）对种群中各个体执行交叉和变异操作产生 新个体； ７）将新个体代替原个体保留在种群中； ８）若在一定迭代次数 Ｌ 内种群的性能没有改 进或达到了最大迭代次数 ｉｔ，跳出循环，否则执行步 骤 ３）。 ３．８ 算法复杂性分析 算法的时间复杂度可以用来度量算法运行的时 间，表示算法计算效率的高低，其大小反映了算法性 能的优劣，不考虑硬件及环境因素，假设每一次执行 时硬件条件和环境条件是相同的，设有 ｎ 个待聚类 对象，聚类中心个数为 ｃ，种群大小为 ｍ，算法的迭 代次数为 Ｌ，则本文算法的时间复杂度为 Ｏ（Ｌｎｃｍ）， 以下为对时间复杂度的说明。 １）以算法的一次迭代为例，从待聚类的 ｎ 个对 象中随机选取 ｍ 个个体作为初始种群，其中每个个 体由 ｃ 个对象组成，代表 ｃ 个聚类中心，其时间复杂 度为 Ｏ（ｃｍ）。 ２）求解种群中每个个体适应度时，需要遍历 ｎ 个待聚类对象与该个体所代表的 ｃ 个聚类中心的距 离矩阵 Ｄｃ × ｎ ，其时间复杂度为 Ｏ（ ｎｃ），由于需要计 算种群中 ｍ 个个体的适应度，那么该步骤总共消耗 的时间为 Ｏ（ｎｃｍ）。 ３）计算种群中个体的多样性度量值 Ｓｔｄｄｅｖ（Ｐ） 需要对种群中所有个体的适应度进行遍历，时间复 杂度为 Ｏ（ｍ）。 ４）选择操作需要计算种群中每个个体的选择 概率并根据选择概率重新选择 ｍ 个个体，时间复杂 度为 Ｏ（２ｍ）。 ·６３０· 智 能 系 统 学 报 第 １０ 卷

第4期 张永库，等.基于改进的遗传算法的模糊聚类算法 ·631 5)交叉操作过程中，需要对种群中m个个体进 6 行遍历，时间复杂度为O(m)。 6)变异操作同样要遍历种群中m个个体，时间 4202 复杂度为O(m)。 7)在每一次迭代完成后需要判断是否已经达 6 8-6-4-202468 到终止条件，此操作的时间复杂度为O(1)。 属性 通过以上的分析可以得到1)~7)的时间复杂 (a)数据集正确聚类结果 度为O(5m+cm+ncm+1)。整体算法的迭代次数为 L,则本文算法的整体运行时间为O((5m+cm+ncm+ 6 1)L)。当数据规模逐渐增大，即n趋于无穷大时， 本文算法的时间复杂度为O(Lncm)。 4202 4实验结果与分析 28-6-4-202468 属性1 为检验Dynamic GA-FCM算法的有效性以及可 行性，将Dynamic GA-FCM算法、传统GA-FCM算法、 (b)传统GA-FCM算法 K-means算法以及Helo'Ina Alves Arnaldo等人在文献 6 [18]所提出的改进FCM算法进行性能比较，分别选 用人工数据集、UCI数据集以及数字数据集进行测 试。Dynamic GA-FCM和传统GA-FCM算法中模糊 指数l=2,种群个体总数m=100,种群最大迭代次 8-6-4-202468 数it=100,变异概率P。=0.05,交叉概率P.=0.8。 属性1 4.1人工数据实验 (c)k-means算法 本节将人工数据分成2组，以测试Dynamic GA- 6 FCM算法的性能，表一给出了人工数据集的性质。 420 表1人工数据集的数据特征 Tablel Artificial data sets characteristics 4 数据集 对象数/个维数类个数 -8-6-4-202468 属性1 Longl 1000 (d)文献[13]算法 Spiral 1000 2 6 Lineblobs 266 3 Squarel 1000 4 4202 4.1.1人工数据集1 人工数据集I是3个具有复杂的流形分布的数 -8-6-4-202468 属性1 据集，分别为数据集Longl,Spiral以及Lineblobs。 (e)本文算法 以下分别展示了上述3种算法对人工数据集I的聚 图2不同算法对Spiral的聚类结果 类结果，使数据分布情况及聚类效果更为直观的显 Fig.2 Clustering results on Spiral 现。对于每个数据集，独立运行了50次。表2列出 1.4r 了各个算法在求解以上3个聚类问题时得到的聚类 1.0 0.8 的正确率平均值。从表2中的统计数据和如图2~4 9 所示的聚类结果可以清楚的看到，对于Longl,Spi- 国0.2 ral和Lineblobs这3个具有明显的流形分布特点的 -0.2 数据集，本文所提出的算法在总体上较之其他的3 -04-3-2-1012345 属性1 种算法，聚类效果更优。 (a)数据集正确聚类结果

５）交叉操作过程中，需要对种群中 ｍ 个个体进 行遍历，时间复杂度为 Ｏ（ｍ）。 ６）变异操作同样要遍历种群中 ｍ 个个体，时间 复杂度为 Ｏ（ｍ）。 ７）在每一次迭代完成后需要判断是否已经达 到终止条件，此操作的时间复杂度为 Ｏ（１）。 通过以上的分析可以得到 １） ～ ７）的时间复杂 度为 Ｏ（５ｍ＋ｃｍ＋ｎｃｍ＋１）。 整体算法的迭代次数为 Ｌ，则本文算法的整体运行时间为 Ｏ（（５ｍ＋ｃｍ＋ｎｃｍ＋ １）Ｌ）。 当数据规模逐渐增大，即 ｎ 趋于无穷大时， 本文算法的时间复杂度为 Ｏ（Ｌｎｃｍ）。 ４ 实验结果与分析 为检验 Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ 算法的有效性以及可 行性，将 Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ 算法、传统 ＧＡ⁃ＦＣＭ 算法、 Ｋ⁃ｍｅａｎｓ 算法以及 Ｈｅｌｏ′ｌｎａ Ａｌｖｅｓ Ａｒｎａｌｄｏ 等人在文献 ［１８］所提出的改进 ＦＣＭ 算法进行性能比较，分别选 用人工数据集、ＵＣＩ 数据集以及数字数据集进行测 试。 Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ 和传统 ＧＡ⁃ＦＣＭ 算法中模糊 指数 ｌ ＝ ２，种群个体总数 ｍ ＝ １００，种群最大迭代次 数 ｉｔ ＝ １００，变异概率 Ｐｍ ＝ ０．０５，交叉概率 Ｐｃ ＝ ０．８。 ４．１ 人工数据实验 本节将人工数据分成 ２ 组，以测试 Ｄｙｎａｍｉｃ ＧＡ⁃ ＦＣＭ 算法的性能，表一给出了人工数据集的性质。 表 １ 人工数据集的数据特征 Ｔａｂｌｅ１ Ａｒｔｉｆｉｃｉａｌ ｄａｔａ ｓｅｔｓ ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ 数据集 对象数／ 个 维数 类个数 Ｌｏｎｇ１ １ ０００ ２ ２ Ｓｐｉｒａｌ １ ０００ ２ ２ Ｌｉｎｅｂｌｏｂｓ ２６６ ２ ３ Ｓｑｕａｒｅ１ １ ０００ ２ ４ ４．１．１ 人工数据集 Ｉ 人工数据集 Ｉ 是 ３ 个具有复杂的流形分布的数 据集，分别为数据集 Ｌｏｎｇ１，Ｓｐｉｒａｌ 以及 Ｌｉｎｅｂｌｏｂｓ。 以下分别展示了上述 ３ 种算法对人工数据集 Ｉ 的聚 类结果，使数据分布情况及聚类效果更为直观的显 现。 对于每个数据集，独立运行了 ５０ 次。 表 ２ 列出 了各个算法在求解以上 ３ 个聚类问题时得到的聚类 的正确率平均值。 从表 ２ 中的统计数据和如图 ２～４ 所示的聚类结果可以清楚的看到，对于 Ｌｏｎｇ１，Ｓｐｉ⁃ ｒａｌ 和 Ｌｉｎｅｂｌｏｂｓ 这 ３ 个具有明显的流形分布特点的 数据集，本文所提出的算法在总体上较之其他的 ３ 种算法，聚类效果更优。 （ａ） 数据集正确聚类结果 （ｂ） 传统 ＧＡ⁃ＦＣＭ 算法 （ｃ） ｋ⁃ｍｅａｎｓ 算法 （ｄ） 文献［１３］算法 （ｅ） 本文算法 图 ２ 不同算法对 Ｓｐｉｒａｌ 的聚类结果 Ｆｉｇ．２ Ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ Ｓｐｉｒａｌ （ａ） 数据集正确聚类结果 第 ４ 期 张永库，等． 基于改进的遗传算法的模糊聚类算法 ·６３１·

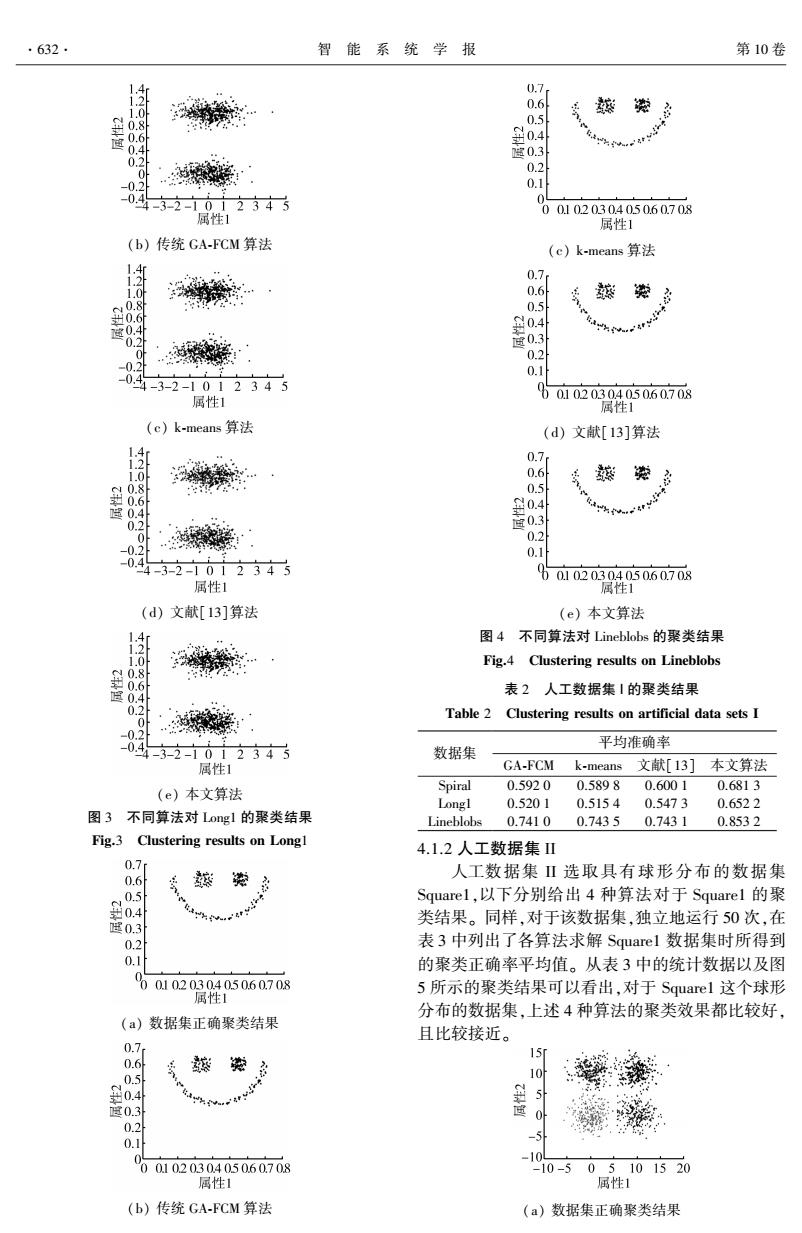
.632 智能系统学报 第10卷 0.7 0.6 蒸 数 0.5 0.4 0.4 03 这0.3 0.2 -02 0.1 0.4 -21012345 001020304050.60.708 屈性1 属性1 (b)传统GA-FCM算法 (c)k-means算法 0.7 0.6 数 8 0.5 0 0.4 0 度0.3引 0.2 0.2 0.1 -0. 4-3-2-1012345 属性1 601020304050.60.708 属性1 (c)k-means算法 (d)文献[13]算法 1.4 1.2 0.7 1.0 0.6 染 0.8 0.5 0.6 0.4 0.4 0.2 度0.3 0.2 -0.2 0.1 -0.4 -3-2-1012345 属性1 0601020304050.60.708 属性1 (d)文献[13]算法 (e)本文算法 图4不同算法对Lineblobs的聚类结果 Fig.4 Clustering results on Lineblobs 0.8 0.6 表2人工数据集1的聚类结果 0.4 0.2 Table 2 Clustering results on artificial data sets I 0 -0.2 -0. 平均准确率 4-3-2-1012345 数据集 属性1 GA-FCMk-means文献[I3]本文算法 0.5920 0.5898 0.6001 0.6813 (e)本文算法 Spiral Longl 0.5201 0.5154 0.5473 0.6522 图3不同算法对Longl的聚类结果 Lineblobs 0.7410 0.7435 0.7431 0.8532 Fig.3 Clustering results on Longl 4.1.2人工数据集Ⅱ 0.7 人工数据集Ⅱ选取具有球形分布的数据集 0.6 类 Square1,以下分别给出4种算法对于Squarel的聚 类结果。同样，对于该数据集，独立地运行50次，在 0.3 0.2 表3中列出了各算法求解Squarel数据集时所得到 0.1 的聚类正确率平均值。从表3中的统计数据以及图 0010203040.5060.708 5所示的聚类结果可以看出，对于Squarel这个球形 属性1 分布的数据集，上述4种算法的聚类效果都比较好， (a)数据集正确聚类结果 且比较接近。 0.7 0.6 10 a 度0.3 04 0.2 0.1 -1 00102030405060.708 -10-505101520 属性1 属性1 (b)传统GA-FCM算法 (a)数据集正确聚类结果

（ｂ） 传统 ＧＡ⁃ＦＣＭ 算法 （ｃ） ｋ⁃ｍｅａｎｓ 算法 （ｄ） 文献［１３］算法 （ｅ） 本文算法 图 ３ 不同算法对 Ｌｏｎｇ１ 的聚类结果 Ｆｉｇ．３ Ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ Ｌｏｎｇ１ （ａ） 数据集正确聚类结果 （ｂ） 传统 ＧＡ⁃ＦＣＭ 算法 （ｃ） ｋ⁃ｍｅａｎｓ 算法 （ｄ） 文献［１３］算法 （ｅ） 本文算法 图 ４ 不同算法对 Ｌｉｎｅｂｌｏｂｓ 的聚类结果 Ｆｉｇ．４ Ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ Ｌｉｎｅｂｌｏｂｓ 表 ２ 人工数据集 Ｉ 的聚类结果 Ｔａｂｌｅ ２ Ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ ａｒｔｉｆｉｃｉａｌ ｄａｔａ ｓｅｔｓ Ｉ 数据集 平均准确率 ＧＡ⁃ＦＣＭ ｋ⁃ｍｅａｎｓ 文献［１３］ 本文算法 Ｓｐｉｒａｌ ０．５９２ ０ ０．５８９ ８ ０．６００ １ ０．６８１ ３ Ｌｏｎｇ１ ０．５２０ １ ０．５１５ ４ ０．５４７ ３ ０．６５２ ２ Ｌｉｎｅｂｌｏｂｓ ０．７４１ ０ ０．７４３ ５ ０．７４３ １ ０．８５３ ２ ４．１．２ 人工数据集 ＩＩ 人工数据集 ＩＩ 选取具有球形分布的数据集 Ｓｑｕａｒｅ１，以下分别给出 ４ 种算法对于 Ｓｑｕａｒｅ１ 的聚 类结果。 同样，对于该数据集，独立地运行 ５０ 次，在 表 ３ 中列出了各算法求解 Ｓｑｕａｒｅ１ 数据集时所得到 的聚类正确率平均值。 从表 ３ 中的统计数据以及图 ５ 所示的聚类结果可以看出，对于 Ｓｑｕａｒｅ１ 这个球形 分布的数据集，上述 ４ 种算法的聚类效果都比较好， 且比较接近。 （ａ） 数据集正确聚类结果 ·６３２· 智 能 系 统 学 报 第 １０ 卷

第4期 张永库，等.基于改进的遗传算法的模糊聚类算法 ·633 15 类正确率平均值。从实验结果中可以看到，对于 10 ris,TAE,Glass这3个UCI数据集，本文算法较之另 5 外3种算法更优，说明本文的算法对于现实世界的 5 数据聚类的问题有着很好的性能。 -1 表4UC数据集的数据特征 10-5 05101520 属性1 Table 4 UCI data sets characteristics (b)传统GA-FCM算法 数据集 对象数/个维数类个数 TAE 151 6 Glass 214 10 7 10 Iris 150 3 表5在UC1数据集下的聚类结果 Table 5 Clustering results on UCI data sets -10-5 05101520 平均准确率 属性1 数据集 GA-FCMk-means文献[I3]本文算法 (c)k-means算法 Iris 0.8102 0.8079 0.8935 0.9039 TAE 0.7016 0.6997 0.7626 0.8024 15 Glass 0.7325 0.7225 0.8030 0.8172 10 4.3数字数据集实验 0 为了进一步评估算法的性能，本文又在著名的 USPS和MNIST2个数字数据集上基于归一化互信息 -10 (normalized mutual information,NMl),进行了4种算 -10-5 0 5101520 属性1 法的对比实验。NMI是一个外部评价标准，用其来评 (d)文献「131算法 价在某个数据集上的聚类结果与这一数据集的真实 15 划分的相近程度，NMI越大，说明聚类性能越好。 10 4.3.1USPS数据集 5 USPS数据集总共有9298个16×16维的灰度 0 图像样本，其中2007个为测试样本，其余为训练样 -10 本。本实验选取所有测试样本作为聚类分析数据 -10-505101520 属性1 集，分别执行以下4组实验： (e)本文算法 USPS-O8:包含数字0、8的灰度图像测试样本； 图4不同算法对Squarel的聚类结果 USPS-358:包含数字3,5、8的灰度图像测试样本： Fig.4 Clustering results on Squarel USPS-1234:包含数字1、2、3、4的灰度图像测 表3人工数据集Ⅱ的聚类结果 试样本； Table 3 Clustering results on artificial data sets II USPS-024679:包含数字0、2、4、6、7、9的灰度 平均准确率 图像测试样本。 数据集 GA-FCM k-means文献[13] 本文算法 其中USPS-08和USPS-358这2组数据较难识 MNIST 0.9900 0.9900 0.9900 0.9900 别，USPS-1234和USPS-024679则相对容易一些。 对每组数据独立的运行50次后，表6给出了 4.2UCI数据实验 NMI标准下4种算法的实验结果。 此外，选择了3个UCI数据集分别的对4种算 表64组USPS数据集在NMI标准下的实验结果 法进行了测试，以便更加全面的考察算法的性能。 Table 6 Four clustering results on USPS at the NMI standard 数据集来自http://archive.ics.uci.edu/ml/,分别为 数据集 GA-FCMk-means文献[l3]本文算法 lris数据集、Glass数据集以及Teaching Assistant E USPS-08 0.6764 0.6121 0.6814 0.7321 valuation数据集，表4给出了UCI数据集的性质。 USPS-358 0.5253 0.4821 0.5218 0.5594 对每个数据集独立的运行50次后，表5分别列 USPS-1234 0.7523 0.7247 0.7607 0.8007 出了各个算法在求解这3个聚类问题时所得到的聚 USPS-024679 0.7013 0.7042 0.7098 0.7456

（ｂ） 传统 ＧＡ⁃ＦＣＭ 算法 （ｃ） ｋ⁃ｍｅａｎｓ 算法 （ｄ） 文献［１３］算法 （ｅ） 本文算法 图 ４ 不同算法对 Ｓｑｕａｒｅ１ 的聚类结果 Ｆｉｇ．４ Ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ Ｓｑｕａｒｅ１ 表 ３ 人工数据集 ＩＩ 的聚类结果 Ｔａｂｌｅ ３ Ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ ａｒｔｉｆｉｃｉａｌ ｄａｔａ ｓｅｔｓ ＩＩ 数据集 平均准确率 ＧＡ⁃ＦＣＭ ｋ⁃ｍｅａｎｓ 文献［１３］ 本文算法 ＭＮＩＳＴ ０．９９０ ０ ０．９９０ ０ ０．９９０ ０ ０．９９０ ０ ４．２ ＵＣＩ 数据实验 此外，选择了 ３ 个 ＵＣＩ 数据集分别的对 ４ 种算 法进行了测试，以便更加全面的考察算法的性能。 数据集来自 ｈｔｔｐ： ／ ／ ａｒｃｈｉｖｅ．ｉｃｓ． ｕｃｉ． ｅｄｕ ／ ｍｌ ／ ，分别为 Ｉｒｉｓ 数据集、Ｇｌａｓｓ 数据集以及 Ｔｅａｃｈｉｎｇ Ａｓｓｉｓｔａｎｔ Ｅ⁃ ｖａｌｕａｔｉｏｎ 数据集，表 ４ 给出了 ＵＣＩ 数据集的性质。 对每个数据集独立的运行 ５０ 次后，表 ５ 分别列 出了各个算法在求解这 ３ 个聚类问题时所得到的聚 类正确率平均值。 从实验结果中可以看到，对于 Ｉ⁃ ｒｉｓ，ＴＡＥ，Ｇｌａｓｓ 这 ３ 个 ＵＣＩ 数据集，本文算法较之另 外 ３ 种算法更优，说明本文的算法对于现实世界的 数据聚类的问题有着很好的性能。 表 ４ ＵＣＩ 数据集的数据特征 Ｔａｂｌｅ ４ ＵＣＩ ｄａｔａ ｓｅｔｓ ｃｈａｒａｃｔｅｒｉｓｔｉｃｓ 数据集 对象数／ 个 维数 类个数 ＴＡＥ １５１ ６ ３ Ｇｌａｓｓ ２１４ １０ ７ Ｉｒｉｓ １５０ ４ ３ 表 ５ 在 ＵＣＩ 数据集下的聚类结果 Ｔａｂｌｅ ５ Ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ ＵＣＩ ｄａｔａ ｓｅｔｓ 数据集 平均准确率 ＧＡ⁃ＦＣＭ ｋ⁃ｍｅａｎｓ 文献［１３］ 本文算法 Ｉｒｉｓ ０．８１０ ２ ０．８０７ ９ ０．８９３ ５ ０．９０３ ９ ＴＡＥ ０．７０１ ６ ０．６９９ ７ ０．７６２ ６ ０．８０２ ４ Ｇｌａｓｓ ０．７３２ ５ ０．７２２ ５ ０．８０３ ０ ０．８１７ ２ ４．３ 数字数据集实验 为了进一步评估算法的性能，本文又在著名的 ＵＳＰＳ 和 ＭＮＩＳＴ ２ 个数字数据集上基于归一化互信息 （ｎｏｒｍａｌｉｚｅｄ ｍｕｔｕａｌ ｉｎｆｏｒｍａｔｉｏｎ，ＮＭＩ），进行了 ４ 种算 法的对比实验。 ＮＭＩ 是一个外部评价标准，用其来评 价在某个数据集上的聚类结果与这一数据集的真实 划分的相近程度，ＮＭＩ 越大，说明聚类性能越好。 ４．３．１ ＵＳＰＳ 数据集 ＵＳＰＳ 数据集总共有 ９ ２９８ 个 １６ × １６ 维的灰度 图像样本，其中 ２ ００７ 个为测试样本，其余为训练样 本。 本实验选取所有测试样本作为聚类分析数据 集，分别执行以下 ４ 组实验： ＵＳＰＳ⁃０８：包含数字 ０ 、８ 的灰度图像测试样本； ＵＳＰＳ⁃３５８：包含数字 ３、５ 、８ 的灰度图像测试样本； ＵＳＰＳ⁃１２３４：包含数字 １、２、３、４ 的灰度图像测 试样本； ＵＳＰＳ⁃０２４６７９：包含数字 ０、２、４、６、７、９ 的灰度 图像测试样本。 其中 ＵＳＰＳ⁃０８ 和 ＵＳＰＳ⁃３５８ 这 ２ 组数据较难识 别，ＵＳＰＳ⁃１２３４ 和 ＵＳＰＳ⁃０２４６７９ 则相对容易一些。 对每组数据独立的运行 ５０ 次后，表 ６ 给出了 ＮＭＩ 标准下 ４ 种算法的实验结果。 表 ６ ４ 组 ＵＳＰＳ 数据集在 ＮＭＩ 标准下的实验结果 Ｔａｂｌｅ ６ Ｆｏｕｒ ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ ＵＳＰＳ ａｔ ｔｈｅ ＮＭＩ ｓｔａｎｄａｒｄ 数据集 ＧＡ⁃ＦＣＭ ｋ⁃ｍｅａｎｓ 文献［１３］ 本文算法 ＵＳＰＳ⁃０８ ０． ６７６ ４ ０．６１２ １ ０．６８１ ４ ０．７３２ １ ＵＳＰＳ⁃３５８ ０．５２５ ３ ０．４８２ １ ０．５２１ ８ ０．５５９ ４ ＵＳＰＳ⁃１２３４ ０．７５２ ３ ０．７２４ ７ ０．７６０ ７ ０．８００ ７ ＵＳＰＳ⁃０２４６７９ ０．７０１ ３ ０．７０４ ２ ０．７０９ ８ ０．７４５ ６ 第 ４ 期 张永库，等． 基于改进的遗传算法的模糊聚类算法 ·６３３·

·634. 智能系统学报 第10卷 实验结果表明，本文算法的NMI值比比另外3 ences,1984,10(2/3):191-203 种算法的对应值大，这说明本文算法在USPS数据集 [7]LIU Zhide,CHEN Jiabin,SONG Chunlei.A new RBF neu- 上的聚类划分结果，相比另外3种算法，有所提高。 ral network with GA-based fuzzy c-means clustering[C]// 4.3.2 MNIST数据集 Chinese Control and Decision Conference.Guilin,China, MNIST数据集中每个字符标准化为16×16的 2009:208-211. [8]HOLLAND J H.Adaptation in Natural and Artificial Sys- 灰度图像，总共有70000个样例。对于0~9每一个 tems:An Introductory Analysis with Applications to Biolo- 数字都选取200个字符用于实验，独立运行50次 gy,Control,and Artificial Intelligence[M].Cambridge: 后，表7为4种算法的实验结果 MIT Press,1992:95-110. 从实验结果可以看出，本文算法在NMI上优于 [9]WANG Jianxin.Reducing the overlap among hierarchical 其他3种算法。 clusters with a GA-based approach[C]//2009 1st Interna- 表7 MNIST数据集在NMI标准下的实验结果 tional Conference on Information Science and Engineering. Table 7 Clustering results on MNIST Nanjing,China,2009:924-927. 数据集GA-FCM k-means文献[13]本文算法 [10]MENENDEZ H D,BARRERO D F,CAMACHO D.A MNIST0.54230.52410.60420.6687 multi-objective genetic graph-based clustering algorithm with memory optimization [C]//2013 IEEE Congress on 5结束语 Evolutionary Computation.Cancun,Mexico,2013:3174- 3181. 本文为了克服传统的基于GA的FCM算法中 [11]RAZIZADEH N,BADAMCHIZAEH M A,GHASEM- 存在的早熟问题，在GA中通过种群中个体的多样 POUR M S G.A new GA based method for improving hy- 性来动态的控制GA选择算子实现的速度，即动态 brid clustering[C]//2013 21st Iranian Conference on E- 控制了收敛速度，进而设计了Dynamic GA-FCM算 lectrical Engineering.Mashhad,Iran,2013:1-6. 法。通过与传统GA-FCM算法、K-means算法以及 [12]NGUYEN DD,NGO L T.Multiple kernel interval type-2 Helo'na Alves Arnaldo等在文献[l8]所提出的改进 fuzzy c-means clustering[C]//IEEE International Confer- FCM算法进行对比实验，实验结果表明，本文提出 ence on Fuzzy Systems (FUZZ).Hyderabad,India, 2013:1-8. 的Dynamic GA-FCM算法具有更好的聚类效果。 [13]ARNALDO H A,BEDREGAL B R C.A new way to obtain 参考文献： the initial centroid clusters in fuzzy c-means algorithm [C]//2013 2nd Workshop-School on Theoretical Computer [l]TAN Pangning,STEINBACH M,KUMAR V.数据挖掘导 Science (WEIT).Rio Grande,Brazil,2013:139-144. 论[M].北京：人民邮电出版社，2006：298-320 [14]NGUYEN D H M,WONG K P.Controlling diversity of ev- [2]GAO Yunguang,WANG Shicheng,LIU Shunbo.Automatic olutionary algorithms[C]//Proceedings of the 2nd Interna- clustering based on GA-FCM for patter recognition[C]// tional Conference on Machine Learning and Cybernetics. Computational Intelligence and Design.Changsha,China, Guilin,China,2003:775-780. 2009:146-149. [15]ZHU K Q.Population diversity in genetic algorithm for ve- [3]VIJAYACHITRA S,TAMILARASI A,KASTHURI N.Mul- hicle routing problem with time windows[C]//European tiple input single output (MISO)process optimization using Conference on Machine Learning.Pisa,Italy,2004:537- [C]//International Conference on Education Technology 547. and Computer.Singapore,2009:248-252. [16]CHENG SS,CHAO Y H,WANG H M,et al.A proto- [4]LIU Suhua,HOU Huifang.A combination of mixture genetic types-embedded genetic K-means algorithm[C]//18th In- algorithm and fuzzy c-means clustering C//IEEE Interna- ternational Conference on Pattern Recognition.Hong Kong, tional Symposium on IT in Medicine Education.Ji'nan, China,2006:724-727. China,2009:254-258. [17]REZAEE M R,LELIEVELDT B P F,REIBER J H C.A [5]BELAHBIB F Z B,SOUAMI F.Genetic algorithm clustering new cluster validity indexes for the fuzzy c-mean[J].Pat- for color image quantization[C]//2011 3rd European Work- tern Recognition Letters,1998,19(3-4):237-246. shop on Visual Information Processing.Paris,French, [18 BANDYOPADHYAY S,MAULIK U.An evolutionary 2011：83-87. technique based on K-means algorithm for optimal cluste- [6]BEZDEK J C,EHRLICH R,FULL W.FCM:the fuzzy c- ring in RN[J].Information Sciences,2002,146(1-4): means clustering algorithm[J].Computers and Geosci- 221-237

实验结果表明，本文算法的 ＮＭＩ 值比比另外 ３ 种算法的对应值大，这说明本文算法在 ＵＳＰＳ 数据集 上的聚类划分结果，相比另外 ３ 种算法，有所提高。 ４．３．２ ＭＮＩＳＴ 数据集 ＭＮＩＳＴ 数据集中每个字符标准化为 １６×１６ 的 灰度图像，总共有 ７０ ０００ 个样例。 对于 ０～９ 每一个 数字都选取 ２００ 个字符用于实验，独立运行 ５０ 次 后， 表 ７ 为 ４ 种算法的实验结果 从实验结果可以看出，本文算法在 ＮＭＩ 上优于 其他 ３ 种算法。 表 ７ ＭＮＩＳＴ 数据集在 ＮＭＩ 标准下的实验结果 Ｔａｂｌｅ ７ Ｃｌｕｓｔｅｒｉｎｇ ｒｅｓｕｌｔｓ ｏｎ ＭＮＩＳＴ 数据集 ＧＡ⁃ＦＣＭ ｋ⁃ｍｅａｎｓ 文献［１３］ 本文算法 ＭＮＩＳＴ ０．５４２ ３ ０． ５２４ １ ０．６０４ ２ ０．６６８ ７ ５ 结束语 本文为了克服传统的基于 ＧＡ 的 ＦＣＭ 算法中 存在的早熟问题，在 ＧＡ 中通过种群中个体的多样 性来动态的控制 ＧＡ 选择算子实现的速度，即动态 控制了收敛速度，进而设计了 Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ 算 法。 通过与传统 ＧＡ⁃ＦＣＭ 算法、Ｋ⁃ｍｅａｎｓ 算法以及 Ｈｅｌｏ′ｌｎａ Ａｌｖｅｓ Ａｒｎａｌｄｏ 等在文献［１８］所提出的改进 ＦＣＭ 算法进行对比实验，实验结果表明，本文提出 的 Ｄｙｎａｍｉｃ ＧＡ⁃ＦＣＭ 算法具有更好的聚类效果。 参考文献： ［１］ＴＡＮ Ｐａｎｇｎｉｎｇ， ＳＴＥＩＮＢＡＣＨ Ｍ， ＫＵＭＡＲ Ｖ． 数据挖掘导 论［Ｍ］． 北京： 人民邮电出版社， ２００６： ２９８⁃３２０． ［２］ＧＡＯ Ｙｕｎｇｕａｎｇ， ＷＡＮＧ Ｓｈｉｃｈｅｎｇ， ＬＩＵ Ｓｈｕｎｂｏ． Ａｕｔｏｍａｔｉｃ ｃｌｕｓｔｅｒｉｎｇ ｂａｓｅｄ ｏｎ ＧＡ⁃ＦＣＭ ｆｏｒ ｐａｔｔｅｒｎ ｒｅｃｏｇｎｉｔｉｏｎ［ Ｃ］ ／ ／ Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ ａｎｄ Ｄｅｓｉｇｎ． Ｃｈａｎｇｓｈａ， Ｃｈｉｎａ， ２００９： １４６⁃１４９． ［３］ＶＩＪＡＹＡＣＨＩＴＲＡ Ｓ， ＴＡＭＩＬＡＲＡＳＩ Ａ， ＫＡＳＴＨＵＲＩ Ｎ． Ｍｕｌ⁃ ｔｉｐｌｅ ｉｎｐｕｔ ｓｉｎｇｌｅ ｏｕｔｐｕｔ （ＭＩＳＯ） ｐｒｏｃｅｓｓ ｏｐｔｉｍｉｚａｔｉｏｎ ｕｓｉｎｇ ［ Ｃ］ ／ ／ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｅｄｕｃａｔｉｏｎ Ｔｅｃｈｎｏｌｏｇｙ ａｎｄ Ｃｏｍｐｕｔｅｒ． Ｓｉｎｇａｐｏｒｅ， ２００９： ２４８⁃２５２． ［４］ＬＩＵ Ｓｕｈｕａ， ＨＯＵ Ｈｕｉｆａｎｇ． Ａ ｃｏｍｂｉｎａｔｉｏｎ ｏｆ ｍｉｘｔｕｒｅ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ ａｎｄ ｆｕｚｚｙ ｃ⁃ｍｅａｎｓ ｃｌｕｓｔｅｒｉｎｇ［Ｃ］ ／ ／ ＩＥＥＥ Ｉｎｔｅｒｎａ⁃ ｔｉｏｎａｌ Ｓｙｍｐｏｓｉｕｍ ｏｎ ＩＴ ｉｎ Ｍｅｄｉｃｉｎｅ ＆ Ｅｄｕｃａｔｉｏｎ． Ｊｉ′ｎａｎ， Ｃｈｉｎａ， ２００９： ２５４⁃２５８． ［ ５］ＢＥＬＡＨＢＩＢ Ｆ Ｚ Ｂ， ＳＯＵＡＭＩ Ｆ． Ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ ｃｌｕｓｔｅｒｉｎｇ ｆｏｒ ｃｏｌｏｒ ｉｍａｇｅ ｑｕａｎｔｉｚａｔｉｏｎ［Ｃ］ ／ ／ ２０１１ ３ｒｄ Ｅｕｒｏｐｅａｎ Ｗｏｒｋ⁃ ｓｈｏｐ ｏｎ Ｖｉｓｕａｌ Ｉｎｆｏｒｍａｔｉｏｎ Ｐｒｏｃｅｓｓｉｎｇ． Ｐａｒｉｓ， Ｆｒｅｎｃｈ， ２０１１： ８３⁃８７． ［６］ＢＥＺＤＥＫ Ｊ Ｃ， ＥＨＲＬＩＣＨ Ｒ， ＦＵＬＬ Ｗ． ＦＣＭ： ｔｈｅ ｆｕｚｚｙ ｃ⁃ ｍｅａｎｓ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ［ Ｊ ］． Ｃｏｍｐｕｔｅｒｓ ａｎｄ Ｇｅｏｓｃｉ⁃ ｅｎｃｅｓ， １９８４， １０（２ ／ ３）： １９１⁃２０３． ［７］ＬＩＵ Ｚｈｉｄｅ， ＣＨＥＮ Ｊｉａｂｉｎ， ＳＯＮＧ Ｃｈｕｎｌｅｉ． Ａ ｎｅｗ ＲＢＦ ｎｅｕ⁃ ｒａｌ ｎｅｔｗｏｒｋ ｗｉｔｈ ＧＡ⁃ｂａｓｅｄ ｆｕｚｚｙ ｃ⁃ｍｅａｎｓ ｃｌｕｓｔｅｒｉｎｇ［Ｃ］ ／ ／ Ｃｈｉｎｅｓｅ Ｃｏｎｔｒｏｌ ａｎｄ Ｄｅｃｉｓｉｏｎ Ｃｏｎｆｅｒｅｎｃｅ． Ｇｕｉｌｉｎ， Ｃｈｉｎａ， ２００９： ２０８⁃２１１． ［８］ ＨＯＬＬＡＮＤ Ｊ Ｈ． Ａｄａｐｔａｔｉｏｎ ｉｎ Ｎａｔｕｒａｌ ａｎｄ Ａｒｔｉｆｉｃｉａｌ Ｓｙｓ⁃ ｔｅｍｓ： Ａｎ Ｉｎｔｒｏｄｕｃｔｏｒｙ Ａｎａｌｙｓｉｓ ｗｉｔｈ Ａｐｐｌｉｃａｔｉｏｎｓ ｔｏ Ｂｉｏｌｏ⁃ ｇｙ， Ｃｏｎｔｒｏｌ， ａｎｄ Ａｒｔｉｆｉｃｉａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ ［ Ｍ］． Ｃａｍｂｒｉｄｇｅ： ＭＩＴ Ｐｒｅｓｓ， １９９２： ９５⁃１１０． ［９］ ＷＡＮＧ Ｊｉａｎｘｉｎ． Ｒｅｄｕｃｉｎｇ ｔｈｅ ｏｖｅｒｌａｐ ａｍｏｎｇ ｈｉｅｒａｒｃｈｉｃａｌ ｃｌｕｓｔｅｒｓ ｗｉｔｈ ａ ＧＡ⁃ｂａｓｅｄ ａｐｐｒｏａｃｈ［Ｃ］ ／ ／ ２００９ １ｓｔ Ｉｎｔｅｒｎａ⁃ ｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｉｎｆｏｒｍａｔｉｏｎ Ｓｃｉｅｎｃｅ ａｎｄ Ｅｎｇｉｎｅｅｒｉｎｇ． Ｎａｎｊｉｎｇ， Ｃｈｉｎａ， ２００９： ９２４⁃９２７． ［１０］ ＭＥＮＥＮＤＥＺ Ｈ Ｄ， ＢＡＲＲＥＲＯ Ｄ Ｆ， ＣＡＭＡＣＨＯ Ｄ． Ａ ｍｕｌｔｉ⁃ｏｂｊｅｃｔｉｖｅ ｇｅｎｅｔｉｃ ｇｒａｐｈ⁃ｂａｓｅｄ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ｗｉｔｈ ｍｅｍｏｒｙ ｏｐｔｉｍｉｚａｔｉｏｎ ［ Ｃ］ ／ ／ ２０１３ ＩＥＥＥ Ｃｏｎｇｒｅｓｓ ｏｎ Ｅｖｏｌｕｔｉｏｎａｒｙ Ｃｏｍｐｕｔａｔｉｏｎ． Ｃａｎｃｕｎ， Ｍｅｘｉｃｏ， ２０１３： ３１７４⁃ ３１８１． ［ １１ ］ ＲＡＺＩＺＡＤＥＨ Ｎ， ＢＡＤＡＭＣＨＩＺＡＥＨ Ｍ Ａ， ＧＨＡＳＥＭ⁃ ＰＯＵＲ Ｍ Ｓ Ｇ． Ａ ｎｅｗ ＧＡ ｂａｓｅｄ ｍｅｔｈｏｄ ｆｏｒ ｉｍｐｒｏｖｉｎｇ ｈｙ⁃ ｂｒｉｄ ｃｌｕｓｔｅｒｉｎｇ［Ｃ］ ／ ／ ２０１３ ２１ｓｔ Ｉｒａｎｉａｎ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｅ⁃ ｌｅｃｔｒｉｃａｌ Ｅｎｇｉｎｅｅｒｉｎｇ． Ｍａｓｈｈａｄ， Ｉｒａｎ， ２０１３： １⁃６． ［１２］ＮＧＵＹＥＮ Ｄ Ｄ， ＮＧＯ Ｌ Ｔ． Ｍｕｌｔｉｐｌｅ ｋｅｒｎｅｌ ｉｎｔｅｒｖａｌ ｔｙｐｅ⁃２ ｆｕｚｚｙ ｃ⁃ｍｅａｎｓ ｃｌｕｓｔｅｒｉｎｇ［Ｃ］ ／ ／ ＩＥＥＥ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒ⁃ ｅｎｃｅ ｏｎ Ｆｕｚｚｙ Ｓｙｓｔｅｍｓ （ ＦＵＺＺ ）． Ｈｙｄｅｒａｂａｄ， Ｉｎｄｉａ， ２０１３： １⁃８． ［１３］ＡＲＮＡＬＤＯ Ｈ Ａ， ＢＥＤＲＥＧＡＬ Ｂ Ｒ Ｃ． Ａ ｎｅｗ ｗａｙ ｔｏ ｏｂｔａｉｎ ｔｈｅ ｉｎｉｔｉａｌ ｃｅｎｔｒｏｉｄ ｃｌｕｓｔｅｒｓ ｉｎ ｆｕｚｚｙ ｃ⁃ｍｅａｎｓ ａｌｇｏｒｉｔｈｍ ［Ｃ］ ／ ／ ２０１３ ２ｎｄ Ｗｏｒｋｓｈｏｐ⁃Ｓｃｈｏｏｌ ｏｎ Ｔｈｅｏｒｅｔｉｃａｌ Ｃｏｍｐｕｔｅｒ Ｓｃｉｅｎｃｅ （ＷＥＩＴ）． Ｒｉｏ Ｇｒａｎｄｅ， Ｂｒａｚｉｌ， ２０１３： １３９⁃１４４． ［１４］ＮＧＵＹＥＮ Ｄ Ｈ Ｍ， ＷＯＮＧ Ｋ Ｐ． Ｃｏｎｔｒｏｌｌｉｎｇ ｄｉｖｅｒｓｉｔｙ ｏｆ ｅｖ⁃ ｏｌｕｔｉｏｎａｒｙ ａｌｇｏｒｉｔｈｍｓ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ２ｎｄ Ｉｎｔｅｒｎａ⁃ ｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｍａｃｈｉｎｅ Ｌｅａｒｎｉｎｇ ａｎｄ Ｃｙｂｅｒｎｅｔｉｃｓ． Ｇｕｉｌｉｎ， Ｃｈｉｎａ， ２００３： ７７５⁃７８０． ［１５］ＺＨＵ Ｋ Ｑ． Ｐｏｐｕｌａｔｉｏｎ ｄｉｖｅｒｓｉｔｙ ｉｎ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｖｅ⁃ ｈｉｃｌｅ ｒｏｕｔｉｎｇ ｐｒｏｂｌｅｍ ｗｉｔｈ ｔｉｍｅ ｗｉｎｄｏｗｓ ［ Ｃ］ ／ ／ Ｅｕｒｏｐｅａｎ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｍａｃｈｉｎｅ Ｌｅａｒｎｉｎｇ． Ｐｉｓａ， Ｉｔａｌｙ， ２００４： ５３７⁃ ５４７． ［１６］ＣＨＥＮＧ Ｓ Ｓ， ＣＨＡＯ Ｙ Ｈ， ＷＡＮＧ Ｈ Ｍ， ｅｔ ａｌ． Ａ ｐｒｏｔｏ⁃ ｔｙｐｅｓ⁃ｅｍｂｅｄｄｅｄ ｇｅｎｅｔｉｃ Ｋ⁃ｍｅａｎｓ ａｌｇｏｒｉｔｈｍ［Ｃ］ ／ ／ １８ｔｈ Ｉｎ⁃ ｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｐａｔｔｅｒｎ Ｒｅｃｏｇｎｉｔｉｏｎ． Ｈｏｎｇ Ｋｏｎｇ， Ｃｈｉｎａ， ２００６： ７２４⁃７２７． ［１７］ＲＥＺＡＥＥ Ｍ Ｒ， ＬＥＬＩＥＶＥＬＤＴ Ｂ Ｐ Ｆ， ＲＥＩＢＥＲ Ｊ Ｈ Ｃ． Ａ ｎｅｗ ｃｌｕｓｔｅｒ ｖａｌｉｄｉｔｙ ｉｎｄｅｘｅｓ ｆｏｒ ｔｈｅ ｆｕｚｚｙ ｃ⁃ｍｅａｎ［ Ｊ］． Ｐａｔ⁃ ｔｅｒｎ Ｒｅｃｏｇｎｉｔｉｏｎ Ｌｅｔｔｅｒｓ， １９９８， １９（３⁃４）： ２３７⁃２４６． ［ １８ ］ ＢＡＮＤＹＯＰＡＤＨＹＡＹ Ｓ， ＭＡＵＬＩＫ Ｕ． Ａｎ ｅｖｏｌｕｔｉｏｎａｒｙ ｔｅｃｈｎｉｑｕｅ ｂａｓｅｄ ｏｎ Ｋ⁃ｍｅａｎｓ ａｌｇｏｒｉｔｈｍ ｆｏｒ ｏｐｔｉｍａｌ ｃｌｕｓｔｅ⁃ ｒｉｎｇ ｉｎ ＲＮ［Ｊ］． Ｉｎｆｏｒｍａｔｉｏｎ Ｓｃｉｅｎｃｅｓ， ２００２， １４６（１⁃４）： ２２１⁃２３７． ·６３４· 智 能 系 统 学 报 第 １０ 卷

第4期 张永库，等.基于改进的遗传算法的模糊聚类算法 .635. [19]SABAU A S.Variable density based genetic clustering 统”、“滑坡灾害远程智能监测系统”等10余项课题，获市科 [C]//2012 14th International Symposium on Symbolic 技进步一等奖1项，市科技进步二等奖4项、辽宁省教学成 and Numeric Algorithms for Scientific Computing (SYN- 果一等奖1项。 ASC).Timisoara,Romania,2012:200-206. 尹灵雪，女，1991年生，硕士研究生 [20]XIAO Huiming.Application in performance assessment of 主要研究方向为数据处理和数据挖掘。 the clinical department in hospital based on fuzzy cluster and genetic algorithm[C]//2014 International Conference on Computational Intelligence and Communication Net- works.Bhopal,India,2014:1057-1061. 孙劲光，女，1962年生，教授，博士， 作者简介： 主要研究方向为图形图像和多媒体、数 张永库，男，1972年生，副教授，主 据处理和数据挖掘。 要研究方向为图形图像和多媒体、数据 处理和数据挖掘，先后主持和参加“唐 钢集团庙沟铁矿管理信息系统”、“基于 点模型的布尔运算和混合建模技术”、 [责任编辑：郑可为] “义煤集团医疗保险管理系 2015年第13届文档分析与识别国际会议 2015 13th International Conference on Document Analysis and Recognition (ICDAR) ICDAR is the premier international forum for researchers and practitioners in the document analysis community for identifying,encouraging and exchanging ideas on the state-of-the-art technology in document analysis,under- standing,retrieval,and performance evaluation.The term document in the context of ICDAR encompasses a broad range of documents from historical forms such as palm leaves and papyrus to traditional documents and modern multi- media documents. Areas: 1)Character and symbol recognition 2)Printed/Handwritten text recognition 3)Graphics analysis and recognition 4)Document analysis 5)Document understanding 6)Historical documents and digital libraries 7)Document based forensics 8)Camera and video based scene text analysis Website:http://2015.icdar.org/

［１９］ ＳＡＢＡＵ Ａ Ｓ． Ｖａｒｉａｂｌｅ ｄｅｎｓｉｔｙ ｂａｓｅｄ ｇｅｎｅｔｉｃ ｃｌｕｓｔｅｒｉｎｇ ［Ｃ］ ／ ／ ２０１２ １４ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｓｙｍｐｏｓｉｕｍ ｏｎ Ｓｙｍｂｏｌｉｃ ａｎｄ Ｎｕｍｅｒｉｃ Ａｌｇｏｒｉｔｈｍｓ ｆｏｒ Ｓｃｉｅｎｔｉｆｉｃ Ｃｏｍｐｕｔｉｎｇ （ ＳＹＮ⁃ ＡＳＣ）． Ｔｉｍｉｓｏａｒａ， Ｒｏｍａｎｉａ， ２０１２： ２００⁃２０６． ［２０］ＸＩＡＯ Ｈｕｉｍｉｎｇ． Ａｐｐｌｉｃａｔｉｏｎ ｉｎ ｐｅｒｆｏｒｍａｎｃｅ ａｓｓｅｓｓｍｅｎｔ ｏｆ ｔｈｅ ｃｌｉｎｉｃａｌ ｄｅｐａｒｔｍｅｎｔ ｉｎ ｈｏｓｐｉｔａｌ ｂａｓｅｄ ｏｎ ｆｕｚｚｙ ｃｌｕｓｔｅｒ ａｎｄ ｇｅｎｅｔｉｃ ａｌｇｏｒｉｔｈｍ［Ｃ］ ／ ／ ２０１４ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ ａｎｄ Ｃｏｍｍｕｎｉｃａｔｉｏｎ Ｎｅｔ⁃ ｗｏｒｋｓ． Ｂｈｏｐａｌ， Ｉｎｄｉａ， ２０１４： １０５７⁃１０６１． 作者简介： 张永库，男，１９７２ 年生，副教授，主 要研究方向为图形图像和多媒体、数据 处理和数据挖掘，先后主持和参加“唐 钢集团庙沟铁矿管理信息系统”、“基于 点模型的布尔运算和混合建模技术”、 “义煤集团医疗保险管理系 统”、“滑坡灾害远程智能监测系统”等 １０ 余项课题，获市科 技进步一等奖 １ 项、市科技进步二等奖 ４ 项、辽宁省教学成 果一等奖 １ 项。 尹灵雪，女，１９９１ 年生，硕士研究生， 主要研究方向为数据处理和数据挖掘。 孙劲光，女，１９６２ 年生，教授，博士， 主要研究方向为图形图像和多媒体、数 据处理和数据挖掘。 ［责任编辑：郑可为］ ２０１５ 年第 １３ 届文档分析与识别国际会议 ２０１５ １３ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｄｏｃｕｍｅｎｔ Ａｎａｌｙｓｉｓ ａｎｄ Ｒｅｃｏｇｎｉｔｉｏｎ （ＩＣＤＡＲ） ＩＣＤＡＲ ｉｓ ｔｈｅ ｐｒｅｍｉｅｒ ｉｎｔｅｒｎａｔｉｏｎａｌ ｆｏｒｕｍ ｆｏｒ ｒｅｓｅａｒｃｈｅｒｓ ａｎｄ ｐｒａｃｔｉｔｉｏｎｅｒｓ ｉｎ ｔｈｅ ｄｏｃｕｍｅｎｔ ａｎａｌｙｓｉｓ ｃｏｍｍｕｎｉｔｙ ｆｏｒ ｉｄｅｎｔｉｆｙｉｎｇ， ｅｎｃｏｕｒａｇｉｎｇ ａｎｄ ｅｘｃｈａｎｇｉｎｇ ｉｄｅａｓ ｏｎ ｔｈｅ ｓｔａｔｅ⁃ｏｆ⁃ｔｈｅ⁃ａｒｔ ｔｅｃｈｎｏｌｏｇｙ ｉｎ ｄｏｃｕｍｅｎｔ ａｎａｌｙｓｉｓ， ｕｎｄｅｒ⁃ ｓｔａｎｄｉｎｇ， ｒｅｔｒｉｅｖａｌ， ａｎｄ ｐｅｒｆｏｒｍａｎｃｅ ｅｖａｌｕａｔｉｏｎ． Ｔｈｅ ｔｅｒｍ ｄｏｃｕｍｅｎｔ ｉｎ ｔｈｅ ｃｏｎｔｅｘｔ ｏｆ ＩＣＤＡＲ ｅｎｃｏｍｐａｓｓｅｓ ａ ｂｒｏａｄ ｒａｎｇｅ ｏｆ ｄｏｃｕｍｅｎｔｓ ｆｒｏｍ ｈｉｓｔｏｒｉｃａｌ ｆｏｒｍｓ ｓｕｃｈ ａｓ ｐａｌｍ ｌｅａｖｅｓ ａｎｄ ｐａｐｙｒｕｓ ｔｏ ｔｒａｄｉｔｉｏｎａｌ ｄｏｃｕｍｅｎｔｓ ａｎｄ ｍｏｄｅｒｎ ｍｕｌｔｉ⁃ ｍｅｄｉａ ｄｏｃｕｍｅｎｔｓ． Ａｒｅａｓ： １）Ｃｈａｒａｃｔｅｒ ａｎｄ ｓｙｍｂｏｌ ｒｅｃｏｇｎｉｔｉｏｎ ２）Ｐｒｉｎｔｅｄ ／ Ｈａｎｄｗｒｉｔｔｅｎ ｔｅｘｔ ｒｅｃｏｇｎｉｔｉｏｎ ３）Ｇｒａｐｈｉｃｓ ａｎａｌｙｓｉｓ ａｎｄ ｒｅｃｏｇｎｉｔｉｏｎ ４）Ｄｏｃｕｍｅｎｔ ａｎａｌｙｓｉｓ ５）Ｄｏｃｕｍｅｎｔ ｕｎｄｅｒｓｔａｎｄｉｎｇ ６）Ｈｉｓｔｏｒｉｃａｌ ｄｏｃｕｍｅｎｔｓ ａｎｄ ｄｉｇｉｔａｌ ｌｉｂｒａｒｉｅｓ ７）Ｄｏｃｕｍｅｎｔ ｂａｓｅｄ ｆｏｒｅｎｓｉｃｓ ８）Ｃａｍｅｒａ ａｎｄ ｖｉｄｅｏ ｂａｓｅｄ ｓｃｅｎｅ ｔｅｘｔ ａｎａｌｙｓｉｓ Ｗｅｂｓｉｔｅ： ｈｔｔｐ：／ ／ ２０１５．ｉｃｄａｒ．ｏｒｇ ／ 第 ４ 期 张永库，等． 基于改进的遗传算法的模糊聚类算法 ·６３５·