
第10卷第4期 智能系统学报 Vol.10 No.4 2015年8月 CAAI Transactions on Intelligent Systems Feh.2015 D0:10.3969/j.issn.1673-4785.201503045 网络出版地址:htp:/www.cmki.net/kcms/detail/23.1538.TP.20150720.0910.001.html 柔性流水车间排产问题的一种协同 进化CGA求解方法 韩忠华123,朱一行,史海波23,林硕,董晓婷 (1.沈阳建筑大学信息与控制工程学院,辽宁沈阳110168:2.中国科学院沈阳自动化研究所,辽宁沈阳110016:3. 中国科学院网络化控制系统重点实验室,辽宁沈阳110016) 摘要:为了解决柔性流水车间排产优化问题(flexible flow shop scheduling problem,FFSP),设计了一种动态协同进 化紧致遗传算法(dynamic co--evolution compact genetic algorithm,DCCGA)作为全局优化算法。DCCGA算法基于FF- SP特点,构建了描述问题解空间分布的概率模型,并对标准紧致遗传算法(compact genetic algorithm,CGA)的进化机 制以及个体选择方式进行了改进。在其进化过程中,2个概率模型结合最优个体继承策略协同进化,并以一定的频 率进行种群基因分布信息的交流,提高了算法进化过程中的种群基因信息多样性,增强了优良进化趋势的稳定性以 及算法持续进化的能力。设计实验对DCCGA算法中新引入的重要参数进行了分析和探讨,确定了最佳参数值。最 后,采用不同规模的FFSP实例对DCCGA算法进行测试,与已有算法进行对比分析,验证了DCCGA算法对于解决 FFSP的有效性。 关键词:双概率模型:动态协同进化:最优个体继承策略:紧致遗传算法:柔性流水车间 中图分类号:TH186文献标志码:A文章编号:1673-4785(2015)04-0562-07 中文引用格式:韩忠华,朱一行,史海波,等柔性流水车间排产问题的一种协同进化CG4求解方法[J].智能系统学报,2015,10 (4):562-568. 英文引用格式:HAN Zhonghua,ZHU Yihang,SHI Haibo,etal.Aco-evolution CGA solution for the flexible flow shop scheduling problem[J].CAAI Transactions on Intelligent Systems,2015,10(4):562-568. A co-evolution CGA solution for the flexible flow shop scheduling problem HAN Zhonghua2.3,ZHU Yihang ',SHI Haibo2.3,LIN Shuo',DONG Xiaoting (1.Faculty of Information and Control Engineering,Shenyang Jianzhu University,Shenyang 110168.China;2.Shenyang Institute of Automation,CAS,Shenyang 110016,China;3.Key Laboratory of Networked Control System,CAS,Shenyang 110016,China) Abstract:In order to solve the flexible flow shop scheduling problem(FFSP),a dynamic co-evolution compact genetic algorithm (DCCGA)is designed as the global optimization algorithm.In DCCGA,a probabilistic model is constructed to describe the distribution of solutions of the problem,and two modifications are incorporated in the standard compact ge- netic algorithm(CGA)for improving the evolutionary mechanism and individual selection method.DCCGA's evolutionary process is led by two probabilistic models,which contains the optimal individual inheritance strategy,and communicates with each other at a certain frequency with the population genetic information.Hence,the diversity of the population ge- netic information is improved during the process,and also the stability of good evolutionary trend and the capacity of continuous evolution are greatly strengthened at the same time.Moreover,the suitable parameter value is suggested based on relative experiments.And,DCCGA is measured by the benchmark problems with comparison of several effective algo- rithm s.The results show that DCCGA is feasible for solving FFSP. Keywords:bi-probabilistic models;dynamic co-evolution;optimal individual inheritance strategy;compact genetic algorithm;flexible flow shop 收稿日期:2015-03-29.网络出版日期:2015-07-20. 在化学工程、机械制造与半导体封装等行业中, 基金项目:中科院重点实验室开放课题资助:国家重大科技专项资助项 目(2011ZX02601-005). 普遍存在着一类复杂的排产优化问题,即柔性流水 通信作者:朱一行.E-mail:zhuyihangl123@hotmail.com
第 10 卷第 4 期 智 能 系 统 学 报 Vol.10 №.4 2015 年 8 月 CAAI Transactions on Intelligent Systems Feb. 2015 DOI:10.3969 / j.issn.1673⁃4785.201503045 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20150720.0910.001.html 柔性流水车间排产问题的一种协同 进化 CGA 求解方法 韩忠华1,2,3 ,朱一行1 ,史海波2,3 ,林硕1 ,董晓婷1 (1.沈阳建筑大学 信息与控制工程学院,辽宁 沈阳 110168;2. 中国科学院 沈阳自动化研究所,辽宁 沈阳 110016;3. 中国科学院 网络化控制系统重点实验室,辽宁 沈阳 110016) 摘 要:为了解决柔性流水车间排产优化问题(flexible flow shop scheduling problem, FFSP),设计了一种动态协同进 化紧致遗传算法(dynamic co-evolution compact genetic algorithm, DCCGA)作为全局优化算法。 DCCGA 算法基于 FF⁃ SP 特点,构建了描述问题解空间分布的概率模型,并对标准紧致遗传算法(compact genetic algorithm, CGA)的进化机 制以及个体选择方式进行了改进。 在其进化过程中,2 个概率模型结合最优个体继承策略协同进化,并以一定的频 率进行种群基因分布信息的交流,提高了算法进化过程中的种群基因信息多样性,增强了优良进化趋势的稳定性以 及算法持续进化的能力。 设计实验对 DCCGA 算法中新引入的重要参数进行了分析和探讨,确定了最佳参数值。 最 后,采用不同规模的 FFSP 实例对 DCCGA 算法进行测试,与已有算法进行对比分析,验证了 DCCGA 算法对于解决 FFSP 的有效性。 关键词:双概率模型;动态协同进化;最优个体继承策略;紧致遗传算法;柔性流水车间 中图分类号:TH186 文献标志码:A 文章编号:1673⁃4785(2015)04⁃0562⁃07 中文引用格式:韩忠华,朱一行,史海波,等.柔性流水车间排产问题的一种协同进化 CGA 求解方法[ J]. 智能系统学报, 2015, 10 (4): 562⁃568. 英文引用格式:HAN Zhonghua, ZHU Yihang,SHI Haibo, et al .A co⁃evolution CGA solution for the flexible flow shop scheduling problem[J]. CAAI Transactions on Intelligent Systems, 2015, 10(4): 562⁃568. A co⁃evolution CGA solution for the flexible flow shop scheduling problem HAN Zhonghua 1,2,3 , ZHU Yihang 1 ,SHI Haibo 2,3 , LIN Shuo 1 , DONG Xiaoting 1 (1. Faculty of Information and Control Engineering, Shenyang Jianzhu University, Shenyang 110168, China; 2. Shenyang Institute of Automation, CAS, Shenyang 110016, China; 3. Key Laboratory of Networked Control System, CAS, Shenyang 110016, China) Abstract:In order to solve the flexible flow shop scheduling problem (FFSP), a dynamic co⁃evolution compact genetic algorithm (DCCGA) is designed as the global optimization algorithm. In DCCGA, a probabilistic model is constructed to describe the distribution of solutions of the problem, and two modifications are incorporated in the standard compact ge⁃ netic algorithm (CGA) for improving the evolutionary mechanism and individual selection method. DCCGA's evolutionary process is led by two probabilistic models, which contains the optimal individual inheritance strategy, and communicates with each other at a certain frequency with the population genetic information . Hence, the diversity of the population ge⁃ netic information is improved during the process, and also the stability of good evolutionary trend and the capacity of continuous evolution are greatly strengthened at the same time. Moreover, the suitable parameter value is suggested based on relative experiments. And, DCCGA is measured by the benchmark problems with comparison of several effective algo⁃ rithm s. The results show that DCCGA is feasible for solving FFSP. Keywords:bi⁃probabilistic models; dynamic co⁃evolution; optimal individual inheritance strategy; compact genetic algorithm; flexible flow shop 收稿日期:2015⁃03⁃29. 网络出版日期:2015⁃07⁃20. 基金项目:中科院重点实验室开放课题资助; 国家重大科技专项资助项 目(2011ZX02601⁃005). 通信作者:朱一行. E⁃mail:zhuyihang1123@ hotmail.com. 在化学工程、机械制造与半导体封装等行业中, 普遍存在着一类复杂的排产优化问题,即柔性流水

第4期 韩忠华,等:柔性流水车间排产问题的一种协同进化CGA求解方法 ·563. 车间排产优化问题(flexible flow shop scheduling 1 问题描述 problem,FFSP)。FFSP通常可描述为:n个工件需 要进行2道或2道以上工序的加工,每道工序中至 问题描述所涉及的主要参数为:n表示工件的 少存在一台相同并行机,至少有一道工序中存在2 总数量,J,表示工件i的编号i∈{1,2,,n},m表 台或2台以上相同并行机,已知各个工件在各道工 示加工的工序总数,O表示第j道工序,j∈ 序中的加工时间,根据优化目标求解最优排产方 {1,2,,m},M表示第j道工序的并行机数,S为 案。FFSP同时囊括了经典Flow-shop的多工序 工件J:在O中的加工起始时间,T,为工件J:在O 特点以及Parallel shop的多并行机特点,较二阶段 中的加工所需时间,C,为工件J:在O中的加工完 的流水车间排产问题更为复杂,属于一类NP-hard 成时间,C为最大完成时间。 问题3)。FSP于l989年被Sriskandarajah首次提 结合以上参数,本文研究的柔性流水车间排产 出,由于其重要的应用价值和学术意义,该问题的研 优化问题(flexible flow shop scheduling problem,FF 究引起了学者们极大的兴趣,Orhan Engin对遗传算 SP)可描述为:n个工件需要进行m道工序的加工, 法(genetic algorithm,GA)的变异操作进行了改进, 第j道工序中并行机数为M:,且至少存在一道工序 用于解决F℉SP,其实验结果表明所提的方法在一定 中M,≥2,同一工序中同一工件在任意并行机上的 程度上提高了GA算法解决FFSP的效率[);M.R. 加工时间相同,所有工件依据加工流程依次经过各 Singh针对FFSP,以最小化makespan为优化目标, 加工工序,已知各个工件在各道工序中的加工所需 提出一种改进的粒子群优化算法(particle swarm 时间,通过优化算法获取相对于优化目标最优的排 optimization,PS0)【6;Y.Xu结合所设计的排产规 产结果,包括工位分配、加工顺序以及在其加工流程 则,提出一个基于改进的免疫算法(immune algo- 上每个工序的开工时间、完工时间。 rithm)的FFSP解决方法[1:王圣尧将分布估计算 1.1基本假设与约束 法(estimation of distribution algorithm,EDA)引入 式(1)、(2)为以最大完工时间作为评价指标: 到排产调度领域中,用于优化FFSP的makespan最 minCma (1)》 小化问题[)等。从已有FFSP研究文献看,目前FF- Cmm max(Ci.mC2.C.) (2) SP的解决方法主要为群体进化算法,同时一些基于 式(3)表示同一道工序中工件的完工时间和开始加 概率统计学思想的新型算法,如EDA算法等也开始 工时间的关系: 逐渐引起人们的关注。 C=S+Twi∈{1,2,…,n}j∈{1,2,…,m}(3) 紧致遗传算法(compact genetic algorithm, 式(4)表示同一工件在相邻工序间加工的先后 CGA)属于一种变量无关的分布估计算法[),于 制约关系: 1998年被美国UIUC大学Haik教授首次提出o。 C-1≤Sie{1,2,…,n}je{1,2…,m}(4) CGA算法的进化过程较为简单,首先根据概率模型 FFSP研究的假设条件各工件在各道工序可 生成2个个体,再从中择优作为依据引导概率模型 选择任意并行机进行加工,一台并行机同一时刻只 更新,依次迭代。因此,该算法计算量小,优化速度 能对应加工一个工件,一个工件同一时刻只能在一 非常快。但是同时作为一种分布估计算法,CGA算 台并行机上加工,工件的加工过程不可中断,工序间 法在进化过程中依然存在着种群基因信息多样性缺 的缓冲区为无限缓冲区。 失的问题,其进化往往以早熟收敛结束2。目前 CGA算法的应用主要集中在硬件处理、控制等领 2 动态协同进化紧致遗传算法 域1],在排产优化领域的应用还相对较少[16。 在标准紧致遗传算法(CGA)每代进化过程中 本文针对FSP多任务、多工序、多并行机的特 (如图1所示),首先根据概率模型生成2个新个 点及CGA算法易早熟收敛的局限性,对CGA算法 体,再从中择优作为依据更新概率模型。该过程中 的进化过程进行改进,以最小化makespan为优化指 存在2个问题,1)由于CGA算法每代用于引导概率 标,提出了基于动态协同进化紧致遗传算法(dy 模型更新的个体单一,种群基因信息在经过几代进 namic co-evolution compact genetic algorithm,DC- 化后,会迅速失去多样性,导致算法早熟收敛:2)由 CGA)的FFSP解决方案。 于CGA算法基于概率模型的个体生产方式存在较
车间 排 产 优 化 问 题 ( flexible flow shop scheduling problem, FFSP)。 FFSP 通常可描述为: n 个工件需 要进行 2 道或 2 道以上工序的加工,每道工序中至 少存在一台相同并行机,至少有一道工序中存在 2 台或 2 台以上相同并行机,已知各个工件在各道工 序中的加工时间,根据优化目标求解最优排产方 案[1] 。 FFSP 同时囊括了经典 Flow⁃shop [2] 的多工序 特点以及 Parallel shop 的多并行机特点,较二阶段 的流水车间排产问题更为复杂,属于一类 NP⁃hard 问题[3] 。 FFSP 于 1989 年被 Sriskandarajah [4]首次提 出,由于其重要的应用价值和学术意义,该问题的研 究引起了学者们极大的兴趣,Orhan Engin 对遗传算 法(genetic algorithm, GA)的变异操作进行了改进, 用于解决 FFSP,其实验结果表明所提的方法在一定 程度上提高了 GA 算法解决 FFSP 的效率[5] ;M.R. Singh 针对 FFSP,以最小化 makespan 为优化目标, 提出一种改进的粒子群优化算法 ( particle swarm optimization, PSO) [6] ;Y. Xu 结合所设计的排产规 则,提出一个基于改进的免疫算法 ( immune algo⁃ rithm) 的 FFSP 解决方法[ 7 ] ;王圣尧将分布估计算 法 ( estimation of distribution algorithm, EDA) 引入 到排产调度领域中,用于优化 FFSP 的 makespan 最 小化问题[8]等。 从已有 FFSP 研究文献看,目前 FF⁃ SP 的解决方法主要为群体进化算法,同时一些基于 概率统计学思想的新型算法,如 EDA 算法等也开始 逐渐引起人们的关注。 紧 致 遗 传 算 法 ( compact genetic algorithm, CGA) 属于一种变量无关的分布估计算法[9] , 于 1998 年被美国 UIUC 大学 Harik 教授首次提出[10] 。 CGA 算法的进化过程较为简单,首先根据概率模型 生成 2 个个体,再从中择优作为依据引导概率模型 更新,依次迭代。 因此,该算法计算量小,优化速度 非常快。 但是同时作为一种分布估计算法,CGA 算 法在进化过程中依然存在着种群基因信息多样性缺 失的问题,其进化往往以早熟收敛结束[11⁃12] 。 目前 CGA 算法的应用主要集中在硬件处理、控制等领 域[13⁃15] ,在排产优化领域的应用还相对较少[16] 。 本文针对 FFSP 多任务、多工序、多并行机的特 点及 CGA 算法易早熟收敛的局限性,对 CGA 算法 的进化过程进行改进,以最小化 makespan 为优化指 标,提出了基于动态协同进化紧致遗传算法( dy⁃ namic co⁃evolution compact genetic algorithm, DC⁃ CGA)的 FFSP 解决方案。 1 问题描述 问题描述所涉及的主要参数为:n 表示工件的 总数量,Ji 表示工件 i 的编号 i∈{1,2,...,n} ,m 表 示加 工 的 工 序 总 数, Oj 表 示 第 j 道 工 序, j ∈ {1,2,...,m} ,Mj 表示第 j 道工序的并行机数,Si,j为 工件 Ji 在 Oj 中的加工起始时间,Ti,j为工件 Ji 在 Oj 中的加工所需时间,Ci,j为工件 Ji 在 Oj 中的加工完 成时间,Cmax为最大完成时间。 结合以上参数,本文研究的柔性流水车间排产 优化问题 (flexible flow shop scheduling problem, FF⁃ SP)可描述为:n 个工件需要进行 m 道工序的加工, 第 j 道工序中并行机数为 Mj,且至少存在一道工序 中 Mj≥2,同一工序中同一工件在任意并行机上的 加工时间相同,所有工件依据加工流程依次经过各 加工工序,已知各个工件在各道工序中的加工所需 时间,通过优化算法获取相对于优化目标最优的排 产结果,包括工位分配、加工顺序以及在其加工流程 上每个工序的开工时间、完工时间。 1.1 基本假设与约束 式(1)、(2)为以最大完工时间作为评价指标: minCmax (1) Cmax = max(C1,m ,C2,m ,...,Cn,m ) (2) 式(3)表示同一道工序中工件的完工时间和开始加 工时间的关系: Ci,j = Si,j + Ti,j i ∈ {1,2,...,n} ,j ∈ {1,2,...,m} (3) 式(4)表示同一工件在相邻工序间加工的先后 制约关系: Ci,j-1 ≤ Si,j i ∈ {1,2,...,n} ,j ∈ {1,2,...,m} (4) FFSP 研究的假设条件 各工件在各道工序可 选择任意并行机进行加工,一台并行机同一时刻只 能对应加工一个工件,一个工件同一时刻只能在一 台并行机上加工,工件的加工过程不可中断,工序间 的缓冲区为无限缓冲区。 2 动态协同进化紧致遗传算法 在标准紧致遗传算法(CGA) 每代进化过程中 (如图 1 所示),首先根据概率模型生成 2 个新个 体,再从中择优作为依据更新概率模型。 该过程中 存在 2 个问题,1)由于 CGA 算法每代用于引导概率 模型更新的个体单一,种群基因信息在经过几代进 化后,会迅速失去多样性,导致算法早熟收敛;2)由 于 CGA 算法基于概率模型的个体生产方式存在较 第 4 期 韩忠华,等:柔性流水车间排产问题的一种协同进化 CGA 求解方法 ·563·
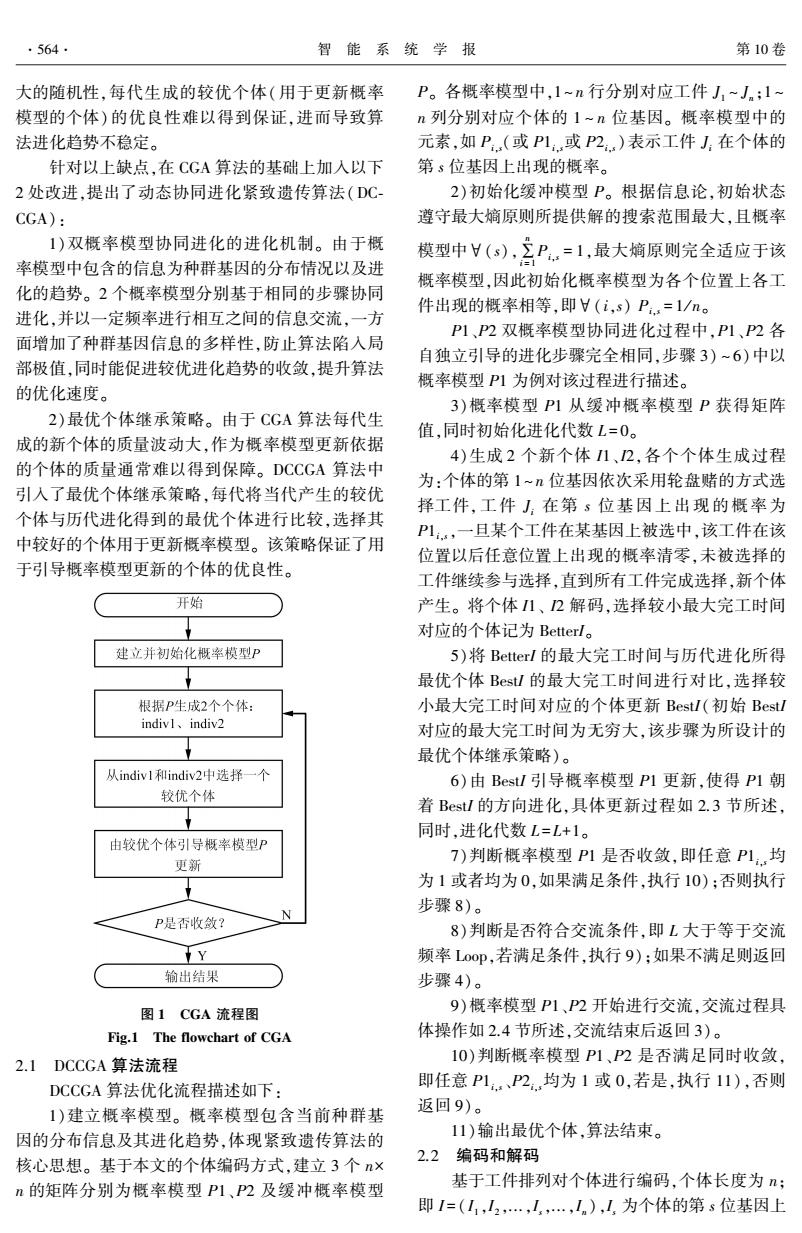
.564. 智能系统学报 第10卷 大的随机性,每代生成的较优个体(用于更新概率 P。各概率模型中,1~n行分别对应工件J1~J:1~ 模型的个体)的优良性难以得到保证,进而导致算 n列分别对应个体的1~n位基因。概率模型中的 法进化趋势不稳定。 元素,如P(或P1.或P2)表示工件J:在个体的 针对以上缺点,在CGA算法的基础上加入以下 第s位基因上出现的概率。 2处改进,提出了动态协同进化紧致遗传算法(DC 2)初始化缓冲模型P。根据信息论,初始状态 CGA): 遵守最大嫡原则所提供解的搜索范围最大,且概率 1)双概率模型协同进化的进化机制。由于概 率模型中包含的信息为种群基因的分布情况以及进 模型中(s),P=1,最大熵原则完全适应于该 概率模型,因此初始化概率模型为各个位置上各工 化的趋势。2个概率模型分别基于相同的步骤协同 件出现的概率相等,即H(i,s)P.=1/no 进化,并以一定频率进行相互之间的信息交流,一方 P1、P2双概率模型协同进化过程中,P1、P2各 面增加了种群基因信息的多样性,防止算法陷入局 自独立引导的进化步骤完全相同,步骤3)~6)中以 部极值,同时能促进较优进化趋势的收敛,提升算法 概率模型P1为例对该过程进行描述。 的优化速度。 3)概率模型P1从缓冲概率模型P获得矩阵 2)最优个体继承策略。由于CGA算法每代生 值,同时初始化进化代数L=0。 成的新个体的质量波动大,作为概率模型更新依据 4)生成2个新个体1、2,各个个体生成过程 的个体的质量通常难以得到保障。DCCGA算法中 为:个体的第1~n位基因依次采用轮盘赌的方式选 引入了最优个体继承策略,每代将当代产生的较优 择工件,工件J在第s位基因上出现的概率为 个体与历代进化得到的最优个体进行比较,选择其 P1:,一旦某个工件在某基因上被选中,该工件在该 中较好的个体用于更新概率模型。该策略保证了用 位置以后任意位置上出现的概率清零,未被选择的 于引导概率模型更新的个体的优良性。 工件继续参与选择,直到所有工件完成选择,新个体 开始 产生。将个体1、2解码,选择较小最大完工时间 对应的个体记为Betterl。 建立并初始化概率模型P 5)将Better/的最大完工时间与历代进化所得 最优个体Best/的最大完工时间进行对比,选择较 根据P生成2个个体: 小最大完工时间对应的个体更新Best/(初始Best/ indivl、indiv2 对应的最大完工时间为无穷大,该步骤为所设计的 最优个体继承策略)。 从indiv1和indiv.2中选择一个 6)由Best/引导概率模型P1更新,使得P1朝 较优个体 着Best/的方向进化,具体更新过程如2.3节所述, 同时,进化代数L=L+1。 由较优个体引导概率模型P 更新 7)判断概率模型P1是否收敛,即任意P1,均 为1或者均为0,如果满足条件,执行10):否则执行 步骤8)。 P是否收敛? 8)判断是否符合交流条件,即L大于等于交流 Y 频率Loop叩,若满足条件,执行9);如果不满足则返回 输出结果 步骤4)。 图1CGA流程图 9)概率模型P1、P2开始进行交流,交流过程具 Fig.1 The flowchart of CGA 体操作如2.4节所述,交流结束后返回3)。 2.1 DCCGA算法流程 10)判断概率模型P1、P2是否满足同时收敛, DCCGA算法优化流程描述如下: 即任意P1、P2:.均为1或0,若是,执行11),否则 1)建立概率模型。概率模型包含当前种群基 返回9)。 因的分布信息及其进化趋势,体现紧致遗传算法的 11)输出最优个体,算法结束。 核心思想。基于本文的个体编码方式,建立3个n× 2.2编码和解码 n的矩阵分别为概率模型P1、P2及缓冲概率模型 基于工件排列对个体进行编码,个体长度为; 即1=(1,山2,…,,…,1),为个体的第s位基因上
大的随机性,每代生成的较优个体(用于更新概率 模型的个体) 的优良性难以得到保证,进而导致算 法进化趋势不稳定。 针对以上缺点,在 CGA 算法的基础上加入以下 2 处改进,提出了动态协同进化紧致遗传算法(DC⁃ CGA): 1)双概率模型协同进化的进化机制。 由于概 率模型中包含的信息为种群基因的分布情况以及进 化的趋势。 2 个概率模型分别基于相同的步骤协同 进化,并以一定频率进行相互之间的信息交流,一方 面增加了种群基因信息的多样性,防止算法陷入局 部极值,同时能促进较优进化趋势的收敛,提升算法 的优化速度。 2)最优个体继承策略。 由于 CGA 算法每代生 成的新个体的质量波动大,作为概率模型更新依据 的个体的质量通常难以得到保障。 DCCGA 算法中 引入了最优个体继承策略,每代将当代产生的较优 个体与历代进化得到的最优个体进行比较,选择其 中较好的个体用于更新概率模型。 该策略保证了用 于引导概率模型更新的个体的优良性。 图 1 CGA 流程图 Fig.1 The flowchart of CGA 2.1 DCCGA 算法流程 DCCGA 算法优化流程描述如下: 1)建立概率模型。 概率模型包含当前种群基 因的分布信息及其进化趋势,体现紧致遗传算法的 核心思想。 基于本文的个体编码方式,建立 3 个 n× n 的矩阵分别为概率模型 P1、P2 及缓冲概率模型 P。 各概率模型中,1~ n 行分别对应工件 J1 ~ Jn ;1 ~ n 列分别对应个体的 1 ~ n 位基因。 概率模型中的 元素,如 Pi,s(或 P1i,s或 P2i,s)表示工件 Ji 在个体的 第 s 位基因上出现的概率。 2)初始化缓冲模型 P。 根据信息论,初始状态 遵守最大熵原则所提供解的搜索范围最大,且概率 模型中∀(s),∑ n i = 1 Pi,s = 1,最大熵原则完全适应于该 概率模型,因此初始化概率模型为各个位置上各工 件出现的概率相等,即∀(i,s) Pi,s = 1 / n。 P1、P2 双概率模型协同进化过程中,P1、P2 各 自独立引导的进化步骤完全相同,步骤 3) ~ 6)中以 概率模型 P1 为例对该过程进行描述。 3)概率模型 P1 从缓冲概率模型 P 获得矩阵 值,同时初始化进化代数 L = 0。 4)生成 2 个新个体 I1、I2,各个个体生成过程 为:个体的第 1~ n 位基因依次采用轮盘赌的方式选 择工件, 工件 Ji 在第 s 位基因上出现的概率为 P1i,s,一旦某个工件在某基因上被选中,该工件在该 位置以后任意位置上出现的概率清零,未被选择的 工件继续参与选择,直到所有工件完成选择,新个体 产生。 将个体 I1、 I2 解码,选择较小最大完工时间 对应的个体记为 BetterI。 5)将 BetterI 的最大完工时间与历代进化所得 最优个体 BestI 的最大完工时间进行对比,选择较 小最大完工时间对应的个体更新 BestI(初始 BestI 对应的最大完工时间为无穷大,该步骤为所设计的 最优个体继承策略)。 6)由 BestI 引导概率模型 P1 更新,使得 P1 朝 着 BestI 的方向进化,具体更新过程如 2.3 节所述, 同时,进化代数 L = L+1。 7)判断概率模型 P1 是否收敛,即任意 P1i,s均 为 1 或者均为 0,如果满足条件,执行 10);否则执行 步骤 8)。 8)判断是否符合交流条件,即 L 大于等于交流 频率 Loop,若满足条件,执行 9);如果不满足则返回 步骤 4)。 9)概率模型 P1、P2 开始进行交流,交流过程具 体操作如 2.4 节所述,交流结束后返回 3)。 10)判断概率模型 P1、P2 是否满足同时收敛, 即任意 P1i,s、P2i,s均为 1 或 0,若是,执行 11),否则 返回 9)。 11)输出最优个体,算法结束。 2.2 编码和解码 基于工件排列对个体进行编码,个体长度为 n; 即 I = (I1 ,I2 ,...,Is,...,In ),Is 为个体的第 s 位基因上 ·564· 智 能 系 统 学 报 第 10 卷

第4期 韩忠华,等:柔性流水车间排产问题的一种协同进化CGA求解方法 ·565· 所记录的工件J:。 种情况:(a)、当MaxP1、MaxP2之和大于1时根据 个体的解码分为2个阶段,在首道工序中,根据 式(8)、(10)操作。(b)、当MaxP1、MaxP2之和不大 个体包含的信息(即工件首道工序的加工顺序)将 于1时根据式(9)和(10)操作。 工件依次进行分配,并基于最先空闲机器(ista- MaxP1 Exceed/2,i MaxNuml vailable machine first,.FAMF)原则为工件安排工位 MaxP2 Exceed/2,i MaxNum2 (8) 进行加工。在第2道及其后续工序则按先入先出 0,否则 (first in first out,FIFO)原则安排工件进行加工。 MaxP1,i MaxNuml 2.3概率模型更新方式 P..=MaxP2,i MaxNum2 (9) 以概率模型P1引导的进化过程为例,概率模 Exceed/(n-2),否则 型的更新操作阐述如下:由最优个体Best/引导概 Exceed =11 MaxPI MaxP2I (10)》 率模型P1进行更新,使得概率模型朝着最优个体 式(8)、(10)中MaxNum1、MaxNum2分别为MaxP1、 Best/的方向发展。更新操作由P1的第l~n列依 MaxP2对应的工件编号:Exceed为MaxP1、MaxP2 次进行,式(5)为第s列的更新操作。 之和与1的差的绝对值,式(8)表明,当MaxP1、 (PI St ,Best/=i MaxP2之和大于1时,调整MaxP1、MaxP2后,分别 P1= (5) (P1.-St/(n 1),Bestl,i 为PmPavam2.赋值,其余第s列中的元素全 式(5)中L为进化代数:S∈(0,1)为学习参数,通 设为0:式(9)表明,当MaxP1、MaxP2之和小于1 时,直接将MaxP1、MaxP2分别赋值给Pmls 常取S0=2示,学习系数K为正整数:Beal,为Beal Pmum2其余第s列中的元素则全赋值为Exceed/ 第s位基因上的工件;式(5)表明当Beat/,为工件J (n-2)。 时,概率模型P1的第s列中,P1加上学习系数S, 3仿真实验 其他元素均减去S/(n-1)。 越界处理若出现P1>1,则取P1.=1:P1 动态协同进化紧致遗传算法(DCCGA)基于 <0,则取P1=0。 MATLAB2012b实现,运行于Window?7操作系统,处 2.4双概率模型信息交流过程 理器为Core i5,CPU2.40Hz,内存为4GB的PC机。 双概率模型信息交流过程为DCCGA算法的重 3.1算法参数设置 要环节,概率模型P1、P2每进化Loop代,进行一次 参数的设置对于一个算法的性能有着至关重要 交流,交流结果记录在缓冲概率模型P中。每次交 的意义。交流频率Loop、学习系数K是DCCGA算 流由2个概率模型相应的第1~n列依次进行,以其 法中2个新引入的参数,通过设计实验,测试两者取 中第s列为例,交流过程阐述如下: 值变化对DCCGA算法寻优性能以及收敛速度的影 首先分别获取P1、P2第s列中的最大值,即个 响,进而确定最佳参数值。参数Loo即,K分别取4 体第s位基因上出现概率最大的工件的概率值分别 种水平,如表1所示。DCCGA算法在每组参数下运 记为MaxP1,MaxP2。 行20次,取最大完工时间Cm平均值CAVG以及 1)当MaxP1、MaxP2对应同一个工件时,根据 进化代数平均值LAVG作为评价指标,CAVG越 式(6)和(7)进行操作: 大表明算法的平均优化性能越高,LAVG越小则表 MaxP max(MaxP1,MaxP2) (6) 明算法的平均优化速度越快。采用规模为15个工 (MaxP,i=MaxNum 件5道工序的标准实例来进行实验,实验结果如表 P.=1-MaxP)/(n-1),香则 (7) 2所示,各参数不同水平的平均结果如表3。根据表 式(6)中MaxP为MaxP1、MaxP2中最大值,式 3,各参数对DCCGA算法性能影响的趋势如图3。 表1参数水平 (7)中MaxNum为MaxP1、MaxP2共同对应的工件 Table 1 The levels of each parameters 编号:P为缓冲概率模型P中i行s列的元素的值。 式(7)表明当MaxP1、MaxP2对应为同一工件时,缓 水 平 参数 冲概率模型P的第s列中,Pam=MaxP,即 2 3 4 MaxNum在第s位基因上出现概率取MaxP,其余第s K 4 5 6 列中的元素均设为(1-MaxP)/(n-I)。 Loop 5 10 15 20 2)当MaxP1、MaxP2对应不同工件时,分以下2
所记录的工件 Ji。 个体的解码分为 2 个阶段,在首道工序中,根据 个体包含的信息(即工件首道工序的加工顺序) 将 工件依次进行分配,并基于最先空闲机器( first a⁃ vailable machine first, FAMF)原则为工件安排工位 进行加工。 在第 2 道及其后续工序则按先入先出 (first in first out, FIFO)原则安排工件进行加工。 2.3 概率模型更新方式 以概率模型 P1 引导的进化过程为例,概率模 型的更新操作阐述如下:由最优个体 BestI 引导概 率模型 P1 进行更新,使得概率模型朝着最优个体 BestI 的方向发展。 更新操作由 P1 的第 1 ~ n 列依 次进行,式(5)为第 s 列的更新操作。 P1 L+1 i,s = P1 L i,s + St P1 L i,s - St / (n - 1) { ,BestIs = i ,BestIs ≠ i (5) 式(5)中 L 为进化代数;St∈(0,1)为学习参数,通 常取 St = 1 2K ,学习系数 K 为正整数;BeatIs 为 BeatI 第 s 位基因上的工件;式(5)表明当 BeatIs 为工件 Ji 时,概率模型 P1 的第 s 列中,P1i,s加上学习系数 St, 其他元素均减去 St / (n-1)。 越界处理 若出现 P1i,s>1,则取 P1i,s = 1;P1i,s <0,则取 P1i,s = 0。 2.4 双概率模型信息交流过程 双概率模型信息交流过程为 DCCGA 算法的重 要环节,概率模型 P1、P2 每进化 Loop 代,进行一次 交流,交流结果记录在缓冲概率模型 P 中。 每次交 流由 2 个概率模型相应的第 1 ~ n 列依次进行,以其 中第 s 列为例,交流过程阐述如下: 首先分别获取 P1、P2 第 s 列中的最大值,即个 体第 s 位基因上出现概率最大的工件的概率值分别 记为 MaxP1,MaxP2。 1)当 MaxP1、MaxP2 对应同一个工件时,根据 式(6)和(7)进行操作: MaxP = max(MaxP1,MaxP2) (6) Pi,s = MaxP,i = MaxNum {(1 - MaxP) / (n - 1),否则 (7) 式(6)中 MaxP 为 MaxP1、MaxP2 中最大值,式 (7)中 MaxNum 为 MaxP1、MaxP2 共同对应的工件 编号;Pi,s为缓冲概率模型 P 中 i 行 s 列的元素的值。 式(7)表明当 MaxP1、MaxP2 对应为同一工件时,缓 冲概 率 模 型 P 的 第 s 列 中, PMaxNum,s = MaxP, 即 JMaxNum在第 s 位基因上出现概率取 MaxP,其余第 s 列中的元素均设为(1-MaxP) / (n-1)。 2)当 MaxP1、MaxP2 对应不同工件时,分以下 2 种情况:(a)、 当 MaxP1、MaxP2 之和大于 1 时根据 式(8)、(10)操作。 (b)、当 MaxP1、MaxP2 之和不大 于 1 时根据式(9)和(10)操作。 Pi,s = MaxP1 - Exceed / 2,i = MaxNum1 MaxP2 - Exceed / 2,i = MaxNum2 0,否则 ì î í ïï ïï (8) Pi,s = MaxP1,i = MaxNum1 MaxP2,i = MaxNum2 Exceed / (n - 2),否则 ì î í ïï ïï (9) Exceed =| 1 - MaxP1 - MaxP2 | (10) 式(8)、(10)中 MaxNum1、MaxNum2 分别为 MaxP1、 MaxP2 对应的工件编号;Exceed 为 MaxP1、MaxP2 之和与 1 的差的绝对值,式( 8) 表明,当 MaxP1、 MaxP2 之和大于 1 时,调整 MaxP1、MaxP 2 后,分别 为 PMaxNum1,s、PMaxNum2,s 赋值,其余第 s 列中的元素全 设为 0;式(9) 表明,当 MaxP1、MaxP2 之和小于 1 时,直接将 MaxP1、 MaxP2 分别赋 值 给 PMaxNum1,s、 PMaxNum2,s其余第 s 列中的元素则全赋值为 Exceed / (n-2)。 3 仿真实验 动态协同进化紧致遗传算法( DCCGA) 基于 MATLAB2012b 实现,运行于 Window7 操作系统,处 理器为 Core i5,CPU2.40 Hz,内存为 4 GB 的 PC 机。 3.1 算法参数设置 参数的设置对于一个算法的性能有着至关重要 的意义。 交流频率 Loop、学习系数 K 是 DCCGA 算 法中 2 个新引入的参数,通过设计实验,测试两者取 值变化对 DCCGA 算法寻优性能以及收敛速度的影 响,进而确定最佳参数值。 参数 Loop, K 分别取 4 种水平,如表 1 所示。 DCCGA 算法在每组参数下运 行 20 次,取最大完工时间 Cmax平均值 CmaxAVG 以及 进化代数平均值 LAVG 作为评价指标,CmaxAVG 越 大表明算法的平均优化性能越高,LAVG 越小则表 明算法的平均优化速度越快。 采用规模为 15 个工 件 5 道工序的标准实例来进行实验,实验结果如表 2 所示,各参数不同水平的平均结果如表 3。 根据表 3,各参数对 DCCGA 算法性能影响的趋势如图 3。 表 1 参数水平 Table 1 The levels of each parameters 参数 水 平 1 2 3 4 K 4 5 6 7 Loop 5 10 15 20 第 4 期 韩忠华,等:柔性流水车间排产问题的一种协同进化 CGA 求解方法 ·565·
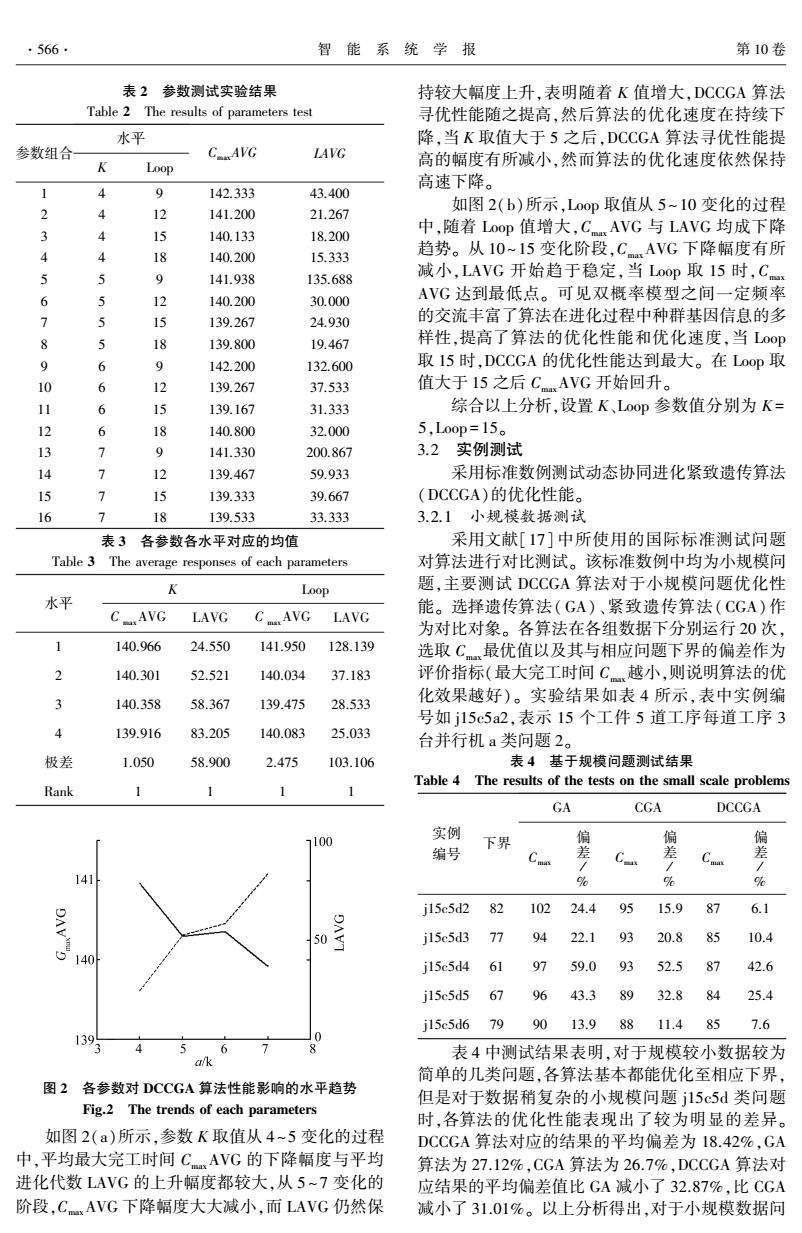
·566 智能系统学报 第10卷 表2参数测试实验结果 持较大幅度上升,表明随着K值增大,DCCGA算法 Table 2 The results of parameters test 寻优性能随之提高,然后算法的优化速度在持续下 水平 降,当K取值大于5之后,DCCGA算法寻优性能提 参数组合 CAVG LAVG K Loop 高的幅度有所减小,然而算法的优化速度依然保持 高速下降。 1 4 9 142.333 43.400 2 4 12 141.200 21.267 如图2(b)所示,Loop取值从5~10变化的过程 3 5 140.133 18.200 中,随着Loop值增大,CAVG与LAVG均成下降 18 140.200 15.333 趋势。从10~15变化阶段,CAVG下降幅度有所 5 5 9 141.938 135.688 减小,LAVG开始趋于稳定,当Loop取15时,C 6 12 140.200 30.000 AVG达到最低点。可见双概率模型之间一定频率 7 5 139.267 24.930 的交流丰富了算法在进化过程中种群基因信息的多 8 5 8 139.800 19.467 样性,提高了算法的优化性能和优化速度,当Loop 9 6 9 142.200 132.600 取15时,DCCGA的优化性能达到最大。在Loop取 10 6 12 139.267 37.533 值大于15之后CAVG开始回升。 11 6 5 139.167 31.333 综合以上分析,设置K、Loop参数值分别为K= 18 140.800 32.000 5,L0op=15。 13 1 9 141.330 200.867 3.2实例测试 14 > 12 139.467 59.933 采用标准数例测试动态协同进化紧致遗传算法 15 > 15 139.333 39.667 (DCCGA)的优化性能。 16 7 18 139.533 33.333 3.2.1小规模数据测试 表3 各参数各水平对应的均值 采用文献[17]中所使用的国际标准测试问题 Table 3 The average responses of each parameters 对算法进行对比测试。该标准数例中均为小规模问 K Loop 题,主要测试DCCGA算法对于小规模问题优化性 水平 CAVG 能。选择遗传算法(GA)、紧致遗传算法(CGA)作 LAVG CAVG LAVG 为对比对象。各算法在各组数据下分别运行20次, 140.966 24.550 141.950 128.139 选取C最优值以及其与相应问题下界的偏差作为 2 140.301 52.521 140.034 37.183 评价指标(最大完工时间C越小,则说明算法的优 3 140.358 58.367 139.475 28.533 化效果越好)。实验结果如表4所示,表中实例编 号如j15c5a2,表示15个工件5道工序每道工序3 4 139.916 83.205 140.083 25.033 台并行机a类问题2。 极差 1.050 58.900 2.475 103.106 表4基于规模问题测试结果 Table 4 The results of the tests on the small scale problems Rank 1 1 1 GA CGA DCCGA 100 实例 下界 偏 偏 偏 编号 % % % j15e5d2 82 102 24.4 95 15.9 87 6.1 50 j15c5d3 77 94 22.1 93 20.8 85 10.4 j15c5d4 61 97 59.0 93 52.5 87 42.6 jl5c5d5 67 96 43.3 89 32.8 84 25.4 j15c5d679 9013.98811.485 7.6 139 表4中测试结果表明,对于规模较小数据较为 简单的几类问题,各算法基本都能优化至相应下界, 图2各参数对DCCGA算法性能影响的水平趋势 但是对于数据稍复杂的小规模问题j15c5d类问题 Fig.2 The trends of each parameters 时,各算法的优化性能表现出了较为明显的差异。 如图2(a)所示,参数K取值从4~5变化的过程 DCCGA算法对应的结果的平均偏差为18.42%,GA 中,平均最大完工时间CAVG的下降幅度与平均 算法为27.12%,CGA算法为26.7%,DCCGA算法对 进化代数LAVG的上升幅度都较大,从5~7变化的 应结果的平均偏差值比GA减小了32.87%,比CGA 阶段,CAVG下降幅度大大减小,而LAVG仍然保 减小了31.01%。以上分析得出,对于小规模数据问
表 2 参数测试实验结果 Table 2 The results of parameters test 参数组合 水平 K Loop CmaxAVG LAVG 1 4 9 142.333 43.400 2 4 12 141.200 21.267 3 4 15 140.133 18.200 4 4 18 140.200 15.333 5 5 9 141.938 135.688 6 5 12 140.200 30.000 7 5 15 139.267 24.930 8 5 18 139.800 19.467 9 6 9 142.200 132.600 10 6 12 139.267 37.533 11 6 15 139.167 31.333 12 6 18 140.800 32.000 13 7 9 141.330 200.867 14 7 12 139.467 59.933 15 7 15 139.333 39.667 16 7 18 139.533 33.333 表 3 各参数各水平对应的均值 Table 3 The average responses of each parameters 水平 K Loop C maxAVG LAVG C maxAVG LAVG 1 140.966 24.550 141.950 128.139 2 140.301 52.521 140.034 37.183 3 140.358 58.367 139.475 28.533 4 139.916 83.205 140.083 25.033 极差 1.050 58.900 2.475 103.106 Rank 1 1 1 1 图 2 各参数对 DCCGA 算法性能影响的水平趋势 Fig.2 The trends of each parameters 如图 2(a)所示,参数 K 取值从 4~5 变化的过程 中,平均最大完工时间 CmaxAVG 的下降幅度与平均 进化代数 LAVG 的上升幅度都较大,从 5 ~ 7 变化的 阶段,CmaxAVG 下降幅度大大减小,而 LAVG 仍然保 持较大幅度上升,表明随着 K 值增大,DCCGA 算法 寻优性能随之提高,然后算法的优化速度在持续下 降,当 K 取值大于 5 之后,DCCGA 算法寻优性能提 高的幅度有所减小,然而算法的优化速度依然保持 高速下降。 如图 2(b)所示,Loop 取值从 5~ 10 变化的过程 中,随着 Loop 值增大,CmaxAVG 与 LAVG 均成下降 趋势。 从 10~15 变化阶段,CmaxAVG 下降幅度有所 减小,LAVG 开始趋于稳定,当 Loop 取 15 时,Cmax AVG 达到最低点。 可见双概率模型之间一定频率 的交流丰富了算法在进化过程中种群基因信息的多 样性,提高了算法的优化性能和优化速度,当 Loop 取 15 时,DCCGA 的优化性能达到最大。 在 Loop 取 值大于 15 之后 CmaxAVG 开始回升。 综合以上分析,设置 K、Loop 参数值分别为 K = 5,Loop = 15。 3.2 实例测试 采用标准数例测试动态协同进化紧致遗传算法 (DCCGA)的优化性能。 3.2.1 小规模数据测试 采用文献[17] 中所使用的国际标准测试问题 对算法进行对比测试。 该标准数例中均为小规模问 题,主要测试 DCCGA 算法对于小规模问题优化性 能。 选择遗传算法(GA)、紧致遗传算法(CGA) 作 为对比对象。 各算法在各组数据下分别运行 20 次, 选取 Cmax最优值以及其与相应问题下界的偏差作为 评价指标(最大完工时间 Cmax越小,则说明算法的优 化效果越好)。 实验结果如表 4 所示,表中实例编 号如 j15c5a2,表示 15 个工件 5 道工序每道工序 3 台并行机 a 类问题 2。 表 4 基于规模问题测试结果 Table 4 The results of the tests on the small scale problems 实例 编号 下界 GA CGA DCCGA Cmax 偏 差 / % Cmax 偏 差 / % Cmax 偏 差 / % j15c5d2 82 102 24.4 95 15.9 87 6.1 j15c5d3 77 94 22.1 93 20.8 85 10.4 j15c5d4 61 97 59.0 93 52.5 87 42.6 j15c5d5 67 96 43.3 89 32.8 84 25.4 j15c5d6 79 90 13.9 88 11.4 85 7.6 表 4 中测试结果表明,对于规模较小数据较为 简单的几类问题,各算法基本都能优化至相应下界, 但是对于数据稍复杂的小规模问题 j15c5d 类问题 时,各算法的优化性能表现出了较为明显的差异。 DCCGA 算法对应的结果的平均偏差为 18.42%,GA 算法为 27.12%,CGA 算法为 26.7%,DCCGA 算法对 应结果的平均偏差值比 GA 减小了 32.87%,比 CGA 减小了 31.01%。 以上分析得出,对于小规模数据问 ·566· 智 能 系 统 学 报 第 10 卷
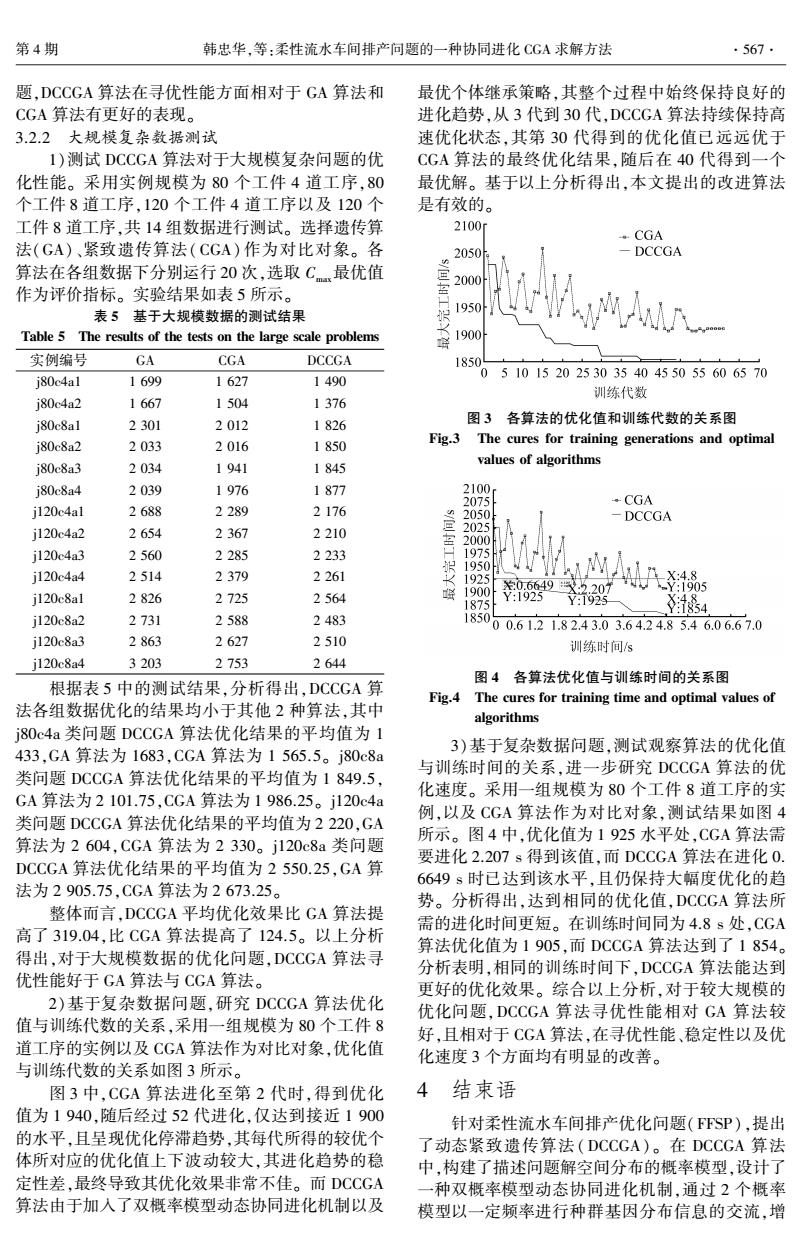
第4期 韩忠华,等:柔性流水车间排产问题的一种协同进化CGA求解方法 ·567. 题,DCCGA算法在寻优性能方面相对于GA算法和 最优个体继承策略,其整个过程中始终保持良好的 CGA算法有更好的表现。 进化趋势,从3代到30代,DCCGA算法持续保持高 3.2.2大规模复杂数据测试 速优化状态,其第30代得到的优化值已远远优于 I)测试DCCGA算法对于大规模复杂问题的优 CGA算法的最终优化结果,随后在40代得到一个 化性能。采用实例规模为80个工件4道工序,80 最优解。基于以上分析得出,本文提出的改进算法 个工件8道工序,120个工件4道工序以及120个 是有效的。 工件8道工序,共14组数据进行测试。选择遗传算 2100 CGA 法(GA)、紧致遗传算法(CGA)作为对比对象。各 2050 -DCCGA 算法在各组数据下分别运行20次,选取C最优值 200( 作为评价指标。实验结果如表5所示。 表5基于大规模数据的测试结果 1950 Table 5 The results of the tests on the large scale problems 1900 实例编号 GA CGA DCCGA 1850 0510152025303540455055606570 j80c4al 1699 1627 1490 j80c4a2 训练代数 1667 1504 1376 j80c8al 2301 2012 1826 图3各算法的优化值和训练代数的关系图 j80c8a2 2033 2016 1850 Fig.3 The cures for training generations and optimal j80c8a3 2034 1941 1845 values of algorithms j80c8a4 2039 1976 1877 2100 2075 CGA j120c4al 2688 2289 2176 2050 -DCCGA i120c4a2 2654 2367 2210 2025 2000 j120c4a3 2560 2285 2233 1975 1950 j120c4a4 2514 2379 2261 1925 1X4.8 :1905 j120c8al 30.6649X.2.207 2826 2725 2564 1900 Y:1925 1875 :1925 184 j120c8a2 2731 2588 2483 1850 00.61.21.82.43.03.64.24.85.46.06.67.0 j120c8a3 2863 2627 2510 训练时间s i120c8a4 3203 2753 2644 图4各算法优化值与训练时间的关系图 根据表5中的测试结果,分析得出,DCCGA算 Fig.4 The cures for training time and optimal values of 法各组数据优化的结果均小于其他2种算法,其中 algorithms j80c4a类问题DCCGA算法优化结果的平均值为1 433,GA算法为1683,CGA算法为1565.5。j80c8a 3)基于复杂数据问题,测试观察算法的优化值 类问题DCCGA算法优化结果的平均值为1849.5, 与训练时间的关系,进一步研究DCCGA算法的优 GA算法为2101.75,CGA算法为1986.25。j120c4a 化速度。采用一组规模为80个工件8道工序的实 类问题DCCGA算法优化结果的平均值为2220,GA 例,以及CGA算法作为对比对象,测试结果如图4 算法为2604,CGA算法为2330。j120c8a类问题 所示。图4中,优化值为1925水平处,CGA算法需 要进化2.207s得到该值,而DCCGA算法在进化0. DCCGA算法优化结果的平均值为2550.25,GA算 6649s时已达到该水平,且仍保持大幅度优化的趋 法为2905.75,CGA算法为2673.25。 势。分析得出,达到相同的优化值,DCCGA算法所 整体而言,DCCGA平均优化效果比GA算法提 需的进化时间更短。在训练时间同为4.8s处,CGA 高了319.04,比CGA算法提高了124.5。以上分析 算法优化值为1905,而DCCGA算法达到了1854。 得出,对于大规模数据的优化问题,DCCGA算法寻 分析表明,相同的训练时间下,DCCGA算法能达到 优性能好于GA算法与CGA算法。 更好的优化效果。综合以上分析,对于较大规模的 2)基于复杂数据问题,研究DCCGA算法优化 优化问题,DCCGA算法寻优性能相对GA算法较 值与训练代数的关系,采用一组规模为80个工件8 好,且相对于CGA算法,在寻优性能、稳定性以及优 道工序的实例以及CGA算法作为对比对象,优化值 化速度3个方面均有明显的改善。 与训练代数的关系如图3所示。 图3中,CGA算法进化至第2代时,得到优化 4 结束语 值为1940,随后经过52代进化,仅达到接近1900 针对柔性流水车间排产优化问题(FFSP),提出 的水平,且呈现优化停滞趋势,其每代所得的较优个 了动态紧致遗传算法(DCCGA)。在DCCGA算法 体所对应的优化值上下波动较大,其进化趋势的稳 中,构建了描述问题解空间分布的概率模型,设计了 定性差,最终导致其优化效果非常不佳。而DCCGA 一种双概率模型动态协同进化机制,通过2个概率 算法由于加入了双概率模型动态协同进化机制以及 模型以一定频率进行种群基因分布信息的交流,增
题,DCCGA 算法在寻优性能方面相对于 GA 算法和 CGA 算法有更好的表现。 3.2.2 大规模复杂数据测试 1)测试 DCCGA 算法对于大规模复杂问题的优 化性能。 采用实例规模为 80 个工件 4 道工序,80 个工件 8 道工序,120 个工件 4 道工序以及 120 个 工件 8 道工序,共 14 组数据进行测试。 选择遗传算 法(GA)、紧致遗传算法(CGA) 作为对比对象。 各 算法在各组数据下分别运行 20 次,选取 Cmax最优值 作为评价指标。 实验结果如表 5 所示。 表 5 基于大规模数据的测试结果 Table 5 The results of the tests on the large scale problems 实例编号 GA CGA DCCGA j80c4a1 1 699 1 627 1 490 j80c4a2 1 667 1 504 1 376 j80c8a1 2 301 2 012 1 826 j80c8a2 2 033 2 016 1 850 j80c8a3 2 034 1 941 1 845 j80c8a4 2 039 1 976 1 877 j120c4a1 2 688 2 289 2 176 j120c4a2 2 654 2 367 2 210 j120c4a3 2 560 2 285 2 233 j120c4a4 2 514 2 379 2 261 j120c8a1 2 826 2 725 2 564 j120c8a2 2 731 2 588 2 483 j120c8a3 2 863 2 627 2 510 j120c8a4 3 203 2 753 2 644 根据表 5 中的测试结果,分析得出,DCCGA 算 法各组数据优化的结果均小于其他 2 种算法,其中 j80c4a 类问题 DCCGA 算法优化结果的平均值为 1 433,GA 算法为 1683,CGA 算法为 1 565.5。 j80c8a 类问题 DCCGA 算法优化结果的平均值为 1 849.5, GA 算法为 2 101.75,CGA 算法为 1 986.25。 j120c4a 类问题 DCCGA 算法优化结果的平均值为 2 220,GA 算法为 2 604,CGA 算法为 2 330。 j120c8a 类问题 DCCGA 算法优化结果的平均值为 2 550.25,GA 算 法为 2 905.75,CGA 算法为 2 673.25。 整体而言,DCCGA 平均优化效果比 GA 算法提 高了 319.04,比 CGA 算法提高了 124.5。 以上分析 得出,对于大规模数据的优化问题,DCCGA 算法寻 优性能好于 GA 算法与 CGA 算法。 2)基于复杂数据问题,研究 DCCGA 算法优化 值与训练代数的关系,采用一组规模为 80 个工件 8 道工序的实例以及 CGA 算法作为对比对象,优化值 与训练代数的关系如图 3 所示。 图 3 中,CGA 算法进化至第 2 代时,得到优化 值为 1 940,随后经过 52 代进化,仅达到接近 1 900 的水平,且呈现优化停滞趋势,其每代所得的较优个 体所对应的优化值上下波动较大,其进化趋势的稳 定性差,最终导致其优化效果非常不佳。 而 DCCGA 算法由于加入了双概率模型动态协同进化机制以及 最优个体继承策略,其整个过程中始终保持良好的 进化趋势,从 3 代到 30 代,DCCGA 算法持续保持高 速优化状态,其第 30 代得到的优化值已远远优于 CGA 算法的最终优化结果,随后在 40 代得到一个 最优解。 基于以上分析得出,本文提出的改进算法 是有效的。 图 3 各算法的优化值和训练代数的关系图 Fig.3 The cures for training generations and optimal values of algorithms 图 4 各算法优化值与训练时间的关系图 Fig.4 The cures for training time and optimal values of algorithms 3)基于复杂数据问题,测试观察算法的优化值 与训练时间的关系,进一步研究 DCCGA 算法的优 化速度。 采用一组规模为 80 个工件 8 道工序的实 例,以及 CGA 算法作为对比对象,测试结果如图 4 所示。 图 4 中,优化值为 1 925 水平处,CGA 算法需 要进化 2.207 s 得到该值,而 DCCGA 算法在进化 0. 6649 s 时已达到该水平,且仍保持大幅度优化的趋 势。 分析得出,达到相同的优化值,DCCGA 算法所 需的进化时间更短。 在训练时间同为 4.8 s 处,CGA 算法优化值为 1 905,而 DCCGA 算法达到了 1 854。 分析表明,相同的训练时间下,DCCGA 算法能达到 更好的优化效果。 综合以上分析,对于较大规模的 优化问题,DCCGA 算法寻优性能相对 GA 算法较 好,且相对于 CGA 算法,在寻优性能、稳定性以及优 化速度 3 个方面均有明显的改善。 4 结束语 针对柔性流水车间排产优化问题(FFSP),提出 了动态紧致遗传算法(DCCGA)。 在 DCCGA 算法 中,构建了描述问题解空间分布的概率模型,设计了 一种双概率模型动态协同进化机制,通过 2 个概率 模型以一定频率进行种群基因分布信息的交流,增 第 4 期 韩忠华,等:柔性流水车间排产问题的一种协同进化 CGA 求解方法 ·567·

·568. 智能系统学报 第10卷 加了算法在进化过程中种群基因信息的多样性,并 [11]DELAOSSA L,GAMEZ JA,MATEO J L,et al.Avoiding 结合局部最优个体继承策略以巩固进化优势,保持 premature convergence in estimation of distribution algo- 进化活力。通过实验对DCCGA算法中新引入的参 rithms[C]//IEEE Congress on Evolutionary Computation, 数进行了分析和探讨,确定了最佳参数值。 2009.Trondheim:IEEE,2009:455-462. 基于多组不同规模的FFSP实例的对比测试结 [12]LEE JY,KIM M S,LEE J J.Compact Genetic Algorithms 果表明,DCCGA算法在优化性能、优化速度与寻优 using belief vectors[J].Applied Soft Computing,2011, 11(4):3385-3401. 稳定性等方面均优于CGA算法,能有效地解决F℉ [13]GALLAGHER J C,VIGRAHAM S,KRAMER G.A family SP这类复杂问题。下一步工作目标是在不影响算 of compact genetic algorithms for intrinsic evolvable hard- 法优化效率的前提下,通过完善协同进化机制、增加 ware[J].IEEE Transactions on Evolutionary Computation, 参与进化的个体数量等方式,进一步提高算法的全 2004,8(2):111-126. 局搜索性能。 [14 MORENO-ARMENDARIZ M A,CRUZ-CORTES N, DUCHANOY C A,et al.Hardware implementation of the 参考文献: elitist compact Genetic Algorithm using Cellular Automa- [1]RUIZ R,VAZQUEZ-RODRIGUEZ J A.The hybrid flow ta pseudo-random number generator[J].Computers E. shop scheduling problem[J].European Journal of Opera- lectrical Engineering,2013,39(4):1367-1379. [15]NAKATA M,LANZI P L,TAKADAMA K.Simple com- tional Research,2010,205(1):1-18. [2]JOHNSON S M.Optimal two-and three-stage production pact genetic algorithm for XCS[C]//2013 IEEE Congress schedules with setup times included[J].Naval Research on Evolutionary Computation (CEC).Cancun:IEEE, Logistics Quarterly,1954,1(1):61-68. 2013:1718-1723. [3]HOOGEVEEN J A,LENSTRA J K,VELTMAN B.Preemp- [16]刘昶,李冬,彭慧,等.求解混合流水生产线调度问题 tive scheduling in a two-stage multiprocessor flow shop is 的变量相关EDA算法[J].计算机集成制造系统, NP-hard[J].European Journal of Operational Research, 2014:(1):15-18. 1996,89(1):172-175. LIU Chang,LI Dong,PENG Hui,et al.An EDA algo- [4]SRISKANDARAJAH C,SETHI S P.Scheduling algorithms rithm with correlated variables for solving hybrid flow-shop for flexible flowshops:worst and average case performance scheduling problem [J].Computer Integrated Manufactur- [J].European Journal of Operational Research,1989,43 ing Systems,2014:(1):15-18. [17]CARLIER J,NERON E.An exact method for solving the (2):143-160. [5]ENGIN O,CERAN G.YILMAZ M K.An efficient genetic multi-processor flow-shop J ]RAIRO-Operations Re- search,2000,34(1):1-25. algorithm for hybrid flow shop scheduling with multiproces- 作者简介: sor task problems[]].Applied Soft Computing,2011,11 (3):3056-3065. 韩忠华,男,1977年生,教授博士,主 要研究方向为生产与运作管理、企业自动 [6]SINGH M R,MAHAPATRA SS.A swarm optimization ap- 化系统集成技术、车间排产与生产调度算 proach for flexible flow shop scheduling with multiprocessor 法,主持和参与国家、省、市科研项目40 tasks[J].The International Journal of Advanced Manufac- turing Technology,2012,62(1/2/3/4):267-277. 余项。获得辽宁省科学技术奖二等奖1 项,沈阳市科技进步一等奖2项,辽宁省 [7]XU Y,WANG L,WANG S Y,et al.An effective immune algorithm based on novel dispatching rules for the flexible 自然学术成果奖二等奖2项,沈阳市自然 学术成果奖二等奖1项,沈阳市自然学术成果奖三等奖2项。 flow-shop scheduling problem with multiprocessor tasks[J]. 发表学术论文100余篇,被EI收录40余篇。参编著作4部。 The International Journal of Advanced Manufacturing Tech- nology,2013,67(1/2/3/4):121-135. 朱一行,男,1990年生,硕士研究 [8]王圣尧,王凌,许烨.求解相同并行机混合流水线车间 生,主要研究方向为生产排产与生产调 调度问题的分布估计算法[],计算机集成制造系统, 度优化算法。 2013,19(6):1304-1312. WANG Shengyao,WANG Ling,XU Ye.Estimation of dis- tribution algorithm for solving hybrid flow-shop scheduling problem with identical parallel machine [J].Computer Inte- grated Manufacturing Systems,2013,19 (6):1304-1312. 史海波,男,1966年生,研究员,博 [9]王圣尧,王凌,方晨,等.分布估计算法研究进展[J] 土生导师,博士,主要研究方向为生产 控制与决策,2012,27(7):961-966,974. 与运作管理理论、制造过程建模与仿真 WANG Shengyao,WANG Ling,FANG Chen,et al.Ad- 技术,主持并参与多项国家863项目、 vances in estimation of distribution algorithmsJ.Control 国家重点科技攻关项目和中国科学院 and Decision,2012,27(7):961-966,974. 知识创新工程重大项目。曾获机械 [10]HARIK G R,LOBO F G,GOLDBERG D E.The compact 部科技进步特等奖1项,省部级科技进步二等奖1项,发表学 genetic algorithm[J].IEEE Transactions on Evolutionary 术论文20余篇。 Computation,1999,3(4):287-297. [责任编辑:李雪莲]
[责任编辑:李雪莲] 加了算法在进化过程中种群基因信息的多样性, 知识创 新 工 程 重 大 项 目。 部科技进步特等奖1项,省部级科技进步二等奖 1 项,发表学 术论文 20余篇。 曾 获机械 并 结合局部最优个体继承策略以巩固进化优势,保持 进化活力。 通过实验对 DCCGA 算法中新引入的参 数进行了分析和探讨,确定了最佳参数值。 基于多组不同规模的 FFSP 实例的对比测试结 果表明,DCCGA 算法在优化性能、优化速度与寻优 稳定性等方面均优于 CGA 算法,能有效地解决 FF⁃ SP 这类复杂问题。 下一步工作目标是在不影响算 法优化效率的前提下,通过完善协同进化机制、增加 参与进化的个体数量等方式,进一步提高算法的全 局搜索性能。 参考文献: [1] RUIZ R, VÁZQUEZ⁃RODRÍGUEZ J A. The hybrid flow shop scheduling problem[ J]. European Journal of Opera⁃ tional Research, 2010, 205(1): 1⁃18. [2] JOHNSON S M. Optimal two⁃and three⁃stage production schedules with setup times included [ J]. Naval Research Logistics Quarterly, 1954, 1(1): 61⁃68. [3]HOOGEVEEN J A, LENSTRA J K, VELTMAN B. Preemp⁃ tive scheduling in a two⁃stage multiprocessor flow shop is NP⁃hard [ J]. European Journal of Operational Research, 1996, 89(1): 172⁃175. [4]SRISKANDARAJAH C, SETHI S P. Scheduling algorithms for flexible flowshops: worst and average case performance [J]. European Journal of Operational Research, 1989, 43 (2): 143⁃160. [5]ENGIN O, CERAN G, YILMAZ M K. An efficient genetic algorithm for hybrid flow shop scheduling with multiproces⁃ sor task problems[ J]. Applied Soft Computing, 2011, 11 (3): 3056⁃3065. [6]SINGH M R, MAHAPATRA S S. A swarm optimization ap⁃ proach for flexible flow shop scheduling with multiprocessor tasks[ J]. The International Journal of Advanced Manufac⁃ turing Technology, 2012, 62(1 / 2 / 3 / 4): 267⁃277. [7]XU Y, WANG L, WANG S Y, et al. An effective immune algorithm based on novel dispatching rules for the flexible flow⁃shop scheduling problem with multiprocessor tasks[ J]. The International Journal of Advanced Manufacturing Tech⁃ nology, 2013, 67(1 / 2 / 3 / 4): 121⁃135. [8]王圣尧, 王凌, 许烨. 求解相同并行机混合流水线车间 调度问题的分布估计算法[ J]. 计算机集成制造系统, 2013, 19(6): 1304⁃1312. WANG Shengyao, WANG Ling, XU Ye. Estimation of dis⁃ tribution algorithm for solving hybrid flow⁃shop scheduling problem with identical parallel machine [J]. Computer Inte⁃ grated Manufacturing Systems, 2013, 19 (6): 1304⁃1312. [9]王圣尧, 王凌, 方晨,等. 分布估计算法研究进展 [ J]. 控制与决策, 2012, 27(7): 961⁃966, 974. WANG Shengyao, WANG Ling, FANG Chen, et al. Ad⁃ vances in estimation of distribution algorithms [ J]. Control and Decision, 2012, 27(7): 961⁃966, 974. [10]HARIK G R, LOBO F G, GOLDBERG D E. The compact genetic algorithm[ J]. IEEE Transactions on Evolutionary Computation, 1999, 3(4): 287⁃297. [11]DELAOSSA L, GÁMEZ J A, MATEO J L, et al. Avoiding premature convergence in estimation of distribution algo⁃ rithms[C] / / IEEE Congress on Evolutionary Computation, 2009. Trondheim: IEEE, 2009: 455⁃462. [12]LEE J Y, KIM M S, LEE J J. Compact Genetic Algorithms using belief vectors [ J]. Applied Soft Computing, 2011, 11(4): 3385⁃3401. [13]GALLAGHER J C, VIGRAHAM S, KRAMER G. A family of compact genetic algorithms for intrinsic evolvable hard⁃ ware[J]. IEEE Transactions on Evolutionary Computation, 2004, 8(2): 111⁃126. [ 14 ] MORENO⁃ARMENDÁRIZ M A, CRUZ⁃CORTÉS N, DUCHANOY C A, et al. Hardware implementation of the elitist compact Genetic Algorithm using Cellular Automa⁃ ta pseudo⁃random number generator[J]. Computers & E⁃ lectrical Engineering, 2013, 39(4): 1367⁃1379. [15]NAKATA M, LANZI P L, TAKADAMA K. Simple com⁃ pact genetic algorithm for XCS[C] / / 2013 IEEE Congress on Evolutionary Computation ( CEC ). Cancun: IEEE, 2013: 1718⁃1723. [16]刘昶, 李冬, 彭慧,等. 求解混合流水生产线调度问题 的变量相关 EDA 算法[ J]. 计算机集成制造系统, 2014:(1):15⁃18. LIU Chang, LI Dong, PENG Hui, et al. An EDA algo⁃ rithm with correlated variables for solving hybrid flow⁃shop scheduling problem [ J]. Computer Integrated Manufactur⁃ ing Systems, 2014:(1):15⁃18. [17]CARLIER J, NÉRON E. An exact method for solving the multi⁃processor flow⁃shop [ J ]. RAIRO⁃Operations Re⁃ search, 2000, 34(1): 1⁃25. 作者简介: 韩忠华,男,1977 年生,教授,博士,主 要研究方向为生产与运作管理、企业自动 化系统集成技术、车间排产与生产调度算 法,主持和参与国家、省、市科研项目 40 余项。 获得辽宁省科学技术奖二等奖 1 项,沈阳市科技进步一等奖 2 项,辽宁省 自然学术成果奖二等奖 2 项,沈阳市自然 学术成果奖二等奖 1 项,沈阳市自然学术成果奖三等奖 2 项。 发表学术论文 100 余篇,被 EI 收录 40 余篇。 参编著作 4 部。 朱一行,男,1990 年生,硕士研究 生,主要研究方向为生产排产与生产调 度优化算法。 史海波,男,1966 年生,研究员,博 士生导师,博士,主要研究方向为生产 与运作管理理论、制造过程建模与仿真 技术,主持并参与多项国家 863 项目、 国家重点科技攻关项目和中国科学院 ·568· 智 能 系 统 学 报 第 10 卷