
第10卷第3期 智能系统学报 Vol.10 No.3 2015年6月 CAAI Transactions on Intelligent Systems Jun.2015 D0:10.3969/j.issn.1673-4785.201404010 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20150409.1657.001.html 一种改进的人工鱼群优化算法 吴昌友 (山东工商学院管理科学与工程学院,山东烟台264005) 摘要:对人工鱼群优化算法的觅食行为、群聚行为、追尾行为和公告板设置等基本原理进行分析,指出算法在 复杂优化问题上产生初始人工鱼群难和陷入局部最优解的原因,提出了改进人工鱼群优化算法,给出了初始 人工鱼群产生的方法,在人工鱼群优化算法的觅食行为、群聚行为、追尾行为中引人了自适应移动步长,同时 在算法中引入变异策略,避免算法陷入局部最优,提高全局寻优能力。最后通过对4个测试函数进行实验,对 于函数∫和f来说,虽然改进的人工鱼群算法和标准人工鱼群算法都达到了最优值,但是改进的人工鱼群 算法收敛的速度更快:函数来说,标准人工鱼群算法运行多次都陷入最优解,无法找到全局最优解。因此, 实验说明了改进算法的有效性与精确性。 关键词:人工鱼群优化算法:觅食:群聚;追尾:移动步长:变异策略 中图分类号:TP18文献标志码:A文章编号:1673-4785(2015)03-0465-05 中文引用格式:吴昌友.一种新的改进人工鱼群优化算法[J].智能系统学报,2015,10(3):465-469. 英文引用格式:WU Changyou.An improved artificial fish swarm optimization algorithm[J].CAAI Transactions on Intelligent Sys- tems,2015,10(3):465-469. An improved artificial fish swarm optimization algorithm WU Changyou School of Management Science and Engineering,Shandong Institute of Business And Technology,Yantai 264005,China) Abstract:In this paper,the basic principles of artificial fish's behaviors of prey,swarm,follow and bulletin board set were analyzed.Investigations were conducted to explore the reasons why it is difficult to produce the initial artifi- cial fish swarm,and why it always falls into local optional solution.The proposed solution improves the artificial fish algorithm with the method of the produce of initial artificial fish swarm,in the artificial fish's behaviors of prey, swarm and follow introduced the adaptive mobile step length with mutation strategy into the artificial fish at the same time,avoiding fish caught in local optima,improving the ability of global optimization.Finally,through the experi- ment of the 4 test functions concluded that as for the function of f,f and f,while the improved artificial fish swarm algorithm and artificial fish swarm algorithm have reached the optimal value,but the convergence of the im- proved artificial fish swarm algorithm is faster.As to the function of f,the standard artificial fish swarm algorithm run in to the optimal solution in several times'operation and the global optimal solution cannot be found.Therefore, the experiment shows the effectiveness and accuracy of the improved algorithm. Keywords:artificial fish swarm optimization algorithm;prey;swarm;follow;moving step length;mutation strategy 人工鱼群优化算法是李晓磊提出的一种智能优 化算法,该算法通过模拟鱼群的觅食、聚群、追尾等 收稿日期:2014-04-08.网络出版日期:2015-04-09. 行为,实现集群智能的一种优化方法,具有较强的鲁 基金项目:国家自然科学基金资助项目(71272122,71373148):山东 棒性和并行分布处理能力等优点[)。该算法与遗 省社科规划项目(13DGLJ05):山东能源经济协同创新中 心资助项目(2014sDXT005);山东省软科学项目 传算法和粒子群优化算法一样容易陷入局部最优解 (2014RKB01021). 和收敛速度慢,这些问题引起了广大学者们的注意, 通信作者:吴昌友.E-mail:wuchangyou_81@163.com
第 10 卷第 3 期 智 能 系 统 学 报 Vol.10 №.3 2015 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2015 DOI:10.3969 / j.issn.1673⁃4785.201404010 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150409.1657.001.html 一种改进的人工鱼群优化算法 吴昌友 (山东工商学院 管理科学与工程学院,山东 烟台 264005) 摘 要:对人工鱼群优化算法的觅食行为、群聚行为、追尾行为和公告板设置等基本原理进行分析,指出算法在 复杂优化问题上产生初始人工鱼群难和陷入局部最优解的原因,提出了改进人工鱼群优化算法,给出了初始 人工鱼群产生的方法,在人工鱼群优化算法的觅食行为、群聚行为、追尾行为中引入了自适应移动步长,同时 在算法中引入变异策略,避免算法陷入局部最优,提高全局寻优能力。 最后通过对 4 个测试函数进行实验,对 于函数 f 1 、f 2和 f 4来说,虽然改进的人工鱼群算法和标准人工鱼群算法都达到了最优值,但是改进的人工鱼群 算法收敛的速度更快;函数 f 3来说,标准人工鱼群算法运行多次都陷入最优解,无法找到全局最优解。 因此, 实验说明了改进算法的有效性与精确性。 关键词:人工鱼群优化算法;觅食;群聚;追尾;移动步长;变异策略 中图分类号:TP18 文献标志码:A 文章编号:1673⁃4785(2015)03⁃0465⁃05 中文引用格式:吴昌友. 一种新的改进人工鱼群优化算法[J]. 智能系统学报, 2015, 10(3): 465⁃469. 英文引用格式:WU Changyou. An improved artificial fish swarm optimization algorithm[J]. CAAI Transactions on Intelligent Sys⁃ tems, 2015, 10(3): 465⁃469. An improved artificial fish swarm optimization algorithm WU Changyou (School of Management Science and Engineering, Shandong Institute of Business And Technology, Yantai 264005, China) Abstract:In this paper, the basic principles of artificial fish's behaviors of prey, swarm, follow and bulletin board set were analyzed. Investigations were conducted to explore the reasons why it is difficult to produce the initial artifi⁃ cial fish swarm, and why it always falls into local optional solution. The proposed solution improves the artificial fish algorithm with the method of the produce of initial artificial fish swarm, in the artificial fish's behaviors of prey, swarm and follow introduced the adaptive mobile step length with mutation strategy into the artificial fish at the same time, avoiding fish caught in local optima, improving the ability of global optimization. Finally, through the experi⁃ ment of the 4 test functions concluded that as for the function of f 1 , f 2 and f 4 , while the improved artificial fish swarm algorithm and artificial fish swarm algorithm have reached the optimal value, but the convergence of the im⁃ proved artificial fish swarm algorithm is faster. As to the function of f 3 , the standard artificial fish swarm algorithm run in to the optimal solution in several times' operation and the global optimal solution cannot be found. Therefore, the experiment shows the effectiveness and accuracy of the improved algorithm. Keywords:artificial fish swarm optimization algorithm; prey; swarm; follow; moving step length; mutation strategy 收稿日期:2014⁃04⁃08. 网络出版日期:2015⁃04⁃09. 基金项目:国家自然科学基金资助项目( 71272122,71373148);山东 省社科规划项目( 13DGLJ05);山东能源经济协同创新中 心 资 助 项 目 ( 2014SDXT005 ); 山 东 省 软 科 学 项 目 (2014RKB01021). 通信作者:吴昌友. E⁃mail: wuchangyou_81@ 163.com. 人工鱼群优化算法是李晓磊提出的一种智能优 化算法,该算法通过模拟鱼群的觅食、聚群、追尾等 行为,实现集群智能的一种优化方法,具有较强的鲁 棒性和并行分布处理能力等优点[1-3] 。 该算法与遗 传算法和粒子群优化算法一样容易陷入局部最优解 和收敛速度慢,这些问题引起了广大学者们的注意

466 智能系统学报 第10卷 分别提出了改进策略3)。如范玉军4为了防止 N8,表明伙伴中心X:有较多食物并且不拥挤,并且 群体中最优个体的退化,提出最优个体保留策略对 有F(X。)>F(X),则X向伙伴中心X前进一步; 觅食行为进行改进,同时对聚群行为和追尾行为进 否则继续执行觅食行为,其计算过程如式(2)所示。 行改进,使全局最优值更快地突现出来,从而加速了 swarm()= 全局搜索。刘佳[s)利用模拟退火算法中的Metropo- X+Y·A·(X-X),n,F(X) s判别准则对人工鱼群算法中的觅食行为进行改 prey(X), else 进。柳毅提出动态调整人工鱼移动步长、视野范 (2) 围和邻域值等方法来提高人工鱼群算法的寻优能 3)追尾行为。 力。张严刃采用特殊觅食行为,约束群聚行为的拥 假设第i条鱼第t时刻状态为X,在其感知距 挤度区间,协调移动策略,进而保障每条鱼的成功觅 食,避免鱼群出现早熟现象。曲良东[⑧劉利用进化策 离r范围内的最优邻居状态为X,并且X在其 略、粒子群算法中的信息策略加入到人工鱼群算法 感知距离范围内有nmm条鱼。如果F(X)> 中,并在理论上证明该算法的收敛性。彭勇9)提出 F(X)且nsF(X:)(3) 人工鱼群算法。 prey(X), else 1人工鱼群算法的基本原理 4)公告板设置。 人工鱼群在优化寻优过程中,设置公告板,在公 设X=(x1,x2,…,x,)为人工鱼群个体向量,其 告板中记录鱼群的最优位置和每条鱼寻优过程中的 中n为各条鱼寻优的变量个数,即待优化问题的变 最优位置。在每次觅食行为、群聚行为和追尾行为 量个数,F=(X)为某条鱼当前位置的食物浓度, 完毕后都要检查自身位置和公告板的位置,如果自 其中F为目标函数,D,=IX,-X‖表示第i条鱼 身的位置优于公告板的位置,则更新公告板。 和第j条鱼之间的距离,r表示人工鱼的感知距离, 2改进人工鱼群算法 人工鱼只能在其感知距离内发生觅食行为,入为人 工鱼移动的步长,8表示拥挤度因子。其人工鱼群 2.1初始人工鱼群的产生 算法的基本原理如下。 初始人工鱼群的产生方法一般有2种,一种是 1)觅食行为。 在可行域范围内按均匀分布随机产生,另一种方法 假设第i条鱼第t时刻状态为X,在其感知距 是人为给定的初始种群,对于复杂的多约束优化 离r内随机产生一个新的状态X:,如果F(X)> 问题,往往很难人为给定初始种群。所以在应用中 F(X)则向X前进一步:反之则重新随机产生X:, 通常都是采用第1种方法产生的。对于无约束问 判断是否满足条件,经过M次后,如果仍不满足条 题,随机产生方法是可行的,但是对于复杂的多约束 件,则随机移动一步,其计算过程如式(1)所示: 优化问题,往往初始种群的产生需要大量的时间。 prey()= 本文给出约束问题人工鱼群初始个体产生如下,假 X:+y·A·(X-X),F(X)>F(X) 设[a,b]为人工鱼群个体向量X=(x1,x2,…,xk, …,xn)中变量x的下限值和上限值。首先采用随 X+y·入, F(X)≤F(X) 机的方法产生一个初始可行的人工鱼,其计算如 (1) 式(4)所示: 式中:y表示符合均匀分布[0,1]之间的随机数。 X=a+rand·(b-a) (4) 2)群聚行为。 判断是否可行域界点,如果是则按式(4) 假设第i条鱼第t时刻的状态为X:,在其感知 重新产生,直至产生X为可行域内点。对于第2 距离r范围内的人工鱼群数目为n,,如果满足n,< 条初始人工鱼X:同样采用式(4)产生,并判断
分别提出了改进策略[3-13] 。 如范玉军[4] 为了防止 群体中最优个体的退化,提出最优个体保留策略对 觅食行为进行改进,同时对聚群行为和追尾行为进 行改进,使全局最优值更快地突现出来,从而加速了 全局搜索。 刘佳[5]利用模拟退火算法中的 Metropo⁃ lis 判别准则对人工鱼群算法中的觅食行为进行改 进。 柳毅[6]提出动态调整人工鱼移动步长、视野范 围和邻域值等方法来提高人工鱼群算法的寻优能 力。 张严[7]采用特殊觅食行为,约束群聚行为的拥 挤度区间,协调移动策略,进而保障每条鱼的成功觅 食,避免鱼群出现早熟现象。 曲良东[8] 利用进化策 略、粒子群算法中的信息策略加入到人工鱼群算法 中,并在理论上证明该算法的收敛性。 彭勇[9] 提出 了动态调整人工鱼视野和步长的方法,解决了人工 鱼群算法的全局搜索能力和局部搜索能力的矛盾。 从以上的学者的研究成果可以看出,主要是从陷入 局部最优解而提出改进的,而没有对初始鱼群的产 生进行研究,而本文提出一种新的初始鱼群产生方 法,并同时采用自适应移动步长和变异策略,来改进 人工鱼群算法。 1 人工鱼群算法的基本原理 设 X = (x1 ,x2 ,…,xn ) 为人工鱼群个体向量,其 中 n 为各条鱼寻优的变量个数,即待优化问题的变 量个数, F = f(X) 为某条鱼当前位置的食物浓度, 其中 F 为目标函数, Dij = ‖Xi - Xj‖ 表示第 i 条鱼 和第 j 条鱼之间的距离, r 表示人工鱼的感知距离, 人工鱼只能在其感知距离内发生觅食行为, λ 为人 工鱼移动的步长, δ 表示拥挤度因子。 其人工鱼群 算法的基本原理如下。 1)觅食行为。 假设第 i 条鱼第 t 时刻状态为 X t i ,在其感知距 离 r 内随机产生一个新的状态 X t j ,如果 F(X t j ) > F(X t i) 则向 X t j 前进一步;反之则重新随机产生 X t i , 判断是否满足条件,经过 M 次后,如果仍不满足条 件,则随机移动一步,其计算过程如式(1)所示: prey(X t i) = X t i + γ·λ·(X t j - X t i), F(X t j ) > F(X t i) X t i + γ·λ, F(X t j ) ≤ F(X t i) ì î í ïï ïï (1) 式中: γ 表示符合均匀分布[0,1]之间的随机数。 2)群聚行为。 假设第 i 条鱼第 t 时刻的状态为 X t i ,在其感知 距离 r 范围内的人工鱼群数目为 nr ,如果满足 nr < Nδ ,表明伙伴中心 X t c 有较多食物并且不拥挤,并且 有 F(Xc) > F(Xi) ,则 X t i 向伙伴中心 X t c 前进一步; 否则继续执行觅食行为,其计算过程如式(2)所示。 swarm(X t i) = X t i + γ·λ·(X t c - X t i),nr < Nδ,F(X t c) > F(X t i) prey(X t i), else { (2) 3)追尾行为。 假设第 i 条鱼第 t 时刻状态为 X t i ,在其感知距 离 r 范围内的最优邻居状态为 X t max ,并且 X t max 在其 感知距离范围内有 nmax 条鱼。 如果 F( X t max) > F(X t i) 且 nmax < Nδ ,则说明 X t max 位置优于 X t i ,并且 在其附近有较多食物并且不拥挤,则向伙伴 X t max 前 进一步;否则继续执行觅食行为,其计算过程如式 (3)所示。 follow(X t i) = X t i + γ·λ·(X t max - X t i), nr < Nδ,F(X t max) > F(X t i) prey(X t i), else ì î í ï ï ï ï (3) 4)公告板设置。 人工鱼群在优化寻优过程中,设置公告板,在公 告板中记录鱼群的最优位置和每条鱼寻优过程中的 最优位置。 在每次觅食行为、群聚行为和追尾行为 完毕后都要检查自身位置和公告板的位置,如果自 身的位置优于公告板的位置,则更新公告板。 2 改进人工鱼群算法 2.1 初始人工鱼群的产生 初始人工鱼群的产生方法一般有 2 种,一种是 在可行域范围内按均匀分布随机产生,另一种方法 是人为给定的初始种群[14] ,对于复杂的多约束优化 问题,往往很难人为给定初始种群。 所以在应用中 通常都是采用第 1 种方法产生的。 对于无约束问 题,随机产生方法是可行的,但是对于复杂的多约束 优化问题,往往初始种群的产生需要大量的时间。 本文给出约束问题人工鱼群初始个体产生如下,假 设 [ak,bk] 为人工鱼群个体向量 X = (x1 ,x2 ,…,xk, …,xn ) 中变量 xk 的下限值和上限值。 首先采用随 机的方法产生一个初始可行的人工鱼 X 0 1 ,其计算如 式(4)所示: X 0 1 = a + rand·(b - a) (4) 判断 X 0 1 是否可行域界点,如果是则按式( 4) 重新产生,直至产生 X 0 1 为可行域内点。 对于第 2 条初始人工鱼 X 0 2 同样采用式( 4) 产生,并判断 ·466· 智 能 系 统 学 报 第 10 卷

第3期 吴昌友:一种改进的人工鱼群优化算法 ·467· X?是否满足约束条件(即是否在可行域内),如 足F(X)>F(X:),则采用式(13)增大入值,按 果满足则产生第3条人工鱼X,如果不满足则按 式(15)进行前进,直到找不到更优的状态。 式(5)进行产生。 follow(:)=+( (15) X=X9+。·(X-X) (5) 2.5变异策略的引入 式中:入。表示[0,1]之间的一个常数。 为了避免人工鱼群算法在优化后期陷入局部最 如果新产生的X满足约束条件,则按式(4)产 优解,以及保持鱼群分布的多样性,本文引入了变异 生第3条人工鱼,否则将缩小入。至入,并将入 策略。如果连续几次找不到更好的人工鱼状态,则 代入式(7)重新产生X。 进行变异,设其变异概率为P,则变异的人工鱼数 为mP。,其变异的计算过程如式(16)所示。 A1=Ao/2 (6) X=X+A,·(X-X) (7) X=[x]= 重新判断新产生的X是否满足约束条件,如果 g+r(6-x),rg>0.5 还不满足条件,则继续缩小入,其按式(8)计算,将 x9-r(x9-),F(X),则X代替X,否则保持 -25≤x1,x2≤25 X状态。 3 X=X+入·(X-X) (9) ma听≤)=(05++°+(金+》 入=入/2 (10) -6.15≤x1,x2≤6.15 如果状态X满足约束条件,并且F(X)> minf.(1,k)=∑[号-10cos(2m,)+10] F(X),则增大入值,继续在该方向上寻找较优的 i=1 状态,其计算如式(11)和(12)所示。 -5.12≤x:≤5.12,i=1,2,…,n 入仁2入 (11) 测试函数~f的三维立体图如图1所示。从 X=X+入·(X-X:) (12) 测试函数的三维立体图可以看出,函数∫为单峰函 如果找到新的状态X:比原来的状态X:还好, 数,非凸的病态函数,在x2=x处有1条长长的深 则继续增大入值,按式(11)和(12)继续搜索寻找, 谷,当最优点取(1,1)时,函数得到全局最小值0:函 直到不如原来的状态好,则停止寻找,此时将用较优 数方,的全局最小值附近有多个极小点,当最优点取 的X代替X,完成觅食行为。 (0,0)时,函数得到全局最小值0:函数5只有1个 2.3群聚行为的改进 全局最优点(0,0),其函数值为3600,还有4个局 如果第i条鱼第t时刻的状态为X,根据群 部最优点。函数f:有大量的极值,当最优点取(0, 0)时,函数得到全局最小值0。 聚行为如果满足F(X)>F(X),则应该增大入 采用标准人工鱼群算法和改进人工鱼群算法对 值,按照式(13)和(14)进行前进,直到找不到更 以上4个函数进行测试实验,其参数设置如初始人 优的状态。 A-2 (13) 工鱼群总数V=50:最大运行次数=30,W2= swam(X)=X:+入·(X。-X;) 50,N=50,Na=30;最大试探次数M=15:拥挤 (14) 2.4追尾行为的改进 度因子8=0.618:人工鱼移动的步长入=0.2;感知距 追尾行为与群聚行为的改进思路相同,如果满 离r=1.5,h2=4,T=1,rha=1
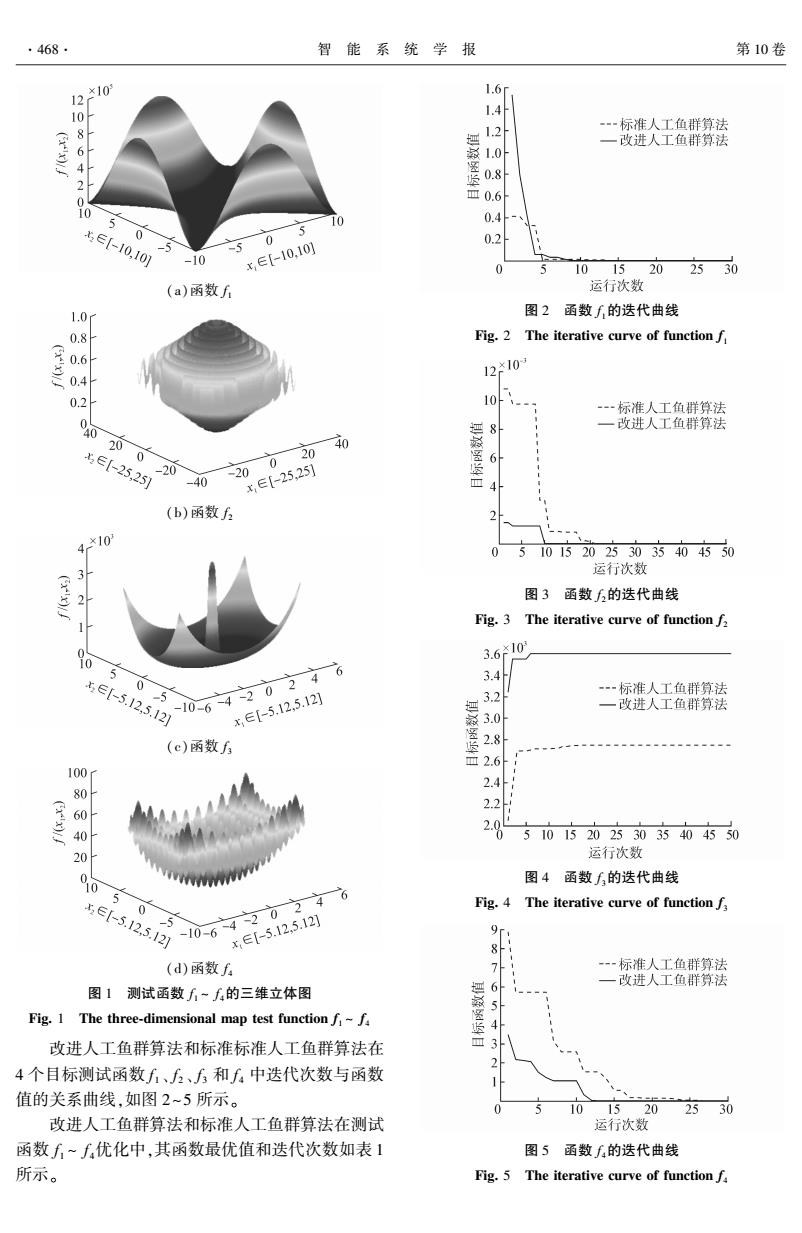
X 0 2 是否满足约束条件( 即是否在可行域内) ,如 果满足则产生第 3 条人工鱼 X 0 3 ,如果不满足则按 式( 5)进行产生 X 0 2 。 X 0 2⇐ X 0 1 + λ0·(X 0 2 - X 0 1 ) (5) 式中: λ0 表示[0,1]之间的一个常数。 如果新产生的 X 0 2 满足约束条件,则按式(4)产 生第 3 条人工鱼 X 0 3 ,否则将缩小 λ0 至 λ1 ,并将 λ1 代入式(7)重新产生 X 0 2 。 λ1 = λ0 / 2 (6) X 0 2⇐ X 0 1 + λ1·(X 0 2 - X 0 1 ) (7) 重新判断新产生的 X 0 2 是否满足约束条件,如果 还不满足条件,则继续缩小 λ1 ,其按式(8)计算,将 λ1 代入式(7)重新产生 X 0 2 。 不断地减小 λ1 直至使 X 0 2 满足约束条件。 λ1⇐λ1 / 2 (8) 对于其他的人工鱼的产生方法与第 2 条人工鱼 产生方法相同,共产生 N 条初始人工鱼。 2.2 觅食行为的改进 假设第 i 条鱼第 t 时刻状态为 X t i ,在其感知距 离 r 内随机产生一个新的状态 X t j ,如果不满足约束 条件,则将新的状态 X t j 向状态 X t i 移动,不断地减小 λ 值,使其满足约束条件,其计算如式(9)和(10)所 示,如果 F(X t j ) > F(X t i) ,则 X t j 代替 X t i ,否则保持 X t i 状态。 X t j⇐ X t i + λ·(X t j - X t i) (9) λ⇐λ / 2 (10) 如果状态 X t j 满足约束条件,并且 F( X t j ) > F(X t i) ,则增大 λ 值,继续在该方向上寻找较优的 状态,其计算如式(11)和(12)所示。 λ⇐2λ (11) X t j⇐ X t j + λ·(X t j - X t i) (12) 如果找到新的状态 X t j 比原来的状态 X t i 还好, 则继续增大 λ 值,按式(11)和(12)继续搜索寻找, 直到不如原来的状态好,则停止寻找,此时将用较优 的 X t j 代替 X t i ,完成觅食行为。 2.3 群聚行为的改进 如果第 i 条鱼第 t 时刻的状态为 X t i ,根据群 聚行为如果满足 F(Xc) > F(Xi) ,则应该增大 λ 值,按照式( 13)和( 14) 进行前进,直到找不到更 优的状态。 λ⇐2λ (13) swarm(X t i) = X t c + λ·(X t c - X t i) (14) 2.4 追尾行为的改进 追尾行为与群聚行为的改进思路相同,如果满 足 F(X t max) > F(X t i) ,则采用式(13)增大 λ 值,按 式(15)进行前进,直到找不到更优的状态。 follow(X t i) = X t max + λ·(X t max - X t i) (15) 2.5 变异策略的引入 为了避免人工鱼群算法在优化后期陷入局部最 优解,以及保持鱼群分布的多样性,本文引入了变异 策略。 如果连续几次找不到更好的人工鱼状态,则 进行变异,设其变异概率为 Pm ,则变异的人工鱼数 为 mPm ,其变异的计算过程如式(16)所示。 X t i = [x (t) ij ] = x (t) ij + rij(bj - x (t) ij ), x (t) ij - rij(x (t) ij - aj), 0.5x (t) ij + 0.25(bj + aj), ì î í ï ï ï ï rij > 0.5 rij < 0.5 rij = 0.5 , j = 1,2,…,n (16) 3 仿真实验 为了验改进的人工鱼群算法的有效性,选取 4 个测试函数进行仿真实验,其测试函数如下: minf 1(x1 ,x2 ) = 100 × (x 2 1 - x2 ) 2 + (1 - x1 ) 2 - 10 ≤ x1 ,x2 ≤ 10 minf 2(x1 ,x2 ) = sin 2 x 2 1 + x 2 2 - 0.5 [1.0 + 0.001 × (x 2 1 + x 2 2 )] 2 + 0.5 - 25 ≤ x1 ,x2 ≤ 25 maxf 3(x1 ,x2 ) = ( 3 0.05 + (x 2 1 + x 2 2 ) 2 ) 2 + (x 2 1 + x 2 2 ) 2 - 6.15 ≤ x1 ,x2 ≤ 6.15 minf 4(x1 ,x2 ) = ∑ n i = 1 [x 2 i - 10cos(2πxi) + 10] - 5.12 ≤ xi ≤ 5.12, i = 1,2,…,n 测试函数 f 1 ~ f 4 的三维立体图如图 1 所示。 从 测试函数的三维立体图可以看出,函数 f 1 为单峰函 数,非凸的病态函数,在 x2 = x 2 1 处有 1 条长长的深 谷,当最优点取(1,1)时,函数得到全局最小值 0;函 数 f 2 的全局最小值附近有多个极小点,当最优点取 (0,0)时,函数得到全局最小值 0;函数 f 3 只有 1 个 全局最优点(0,0),其函数值为 3 600,还有 4 个局 部最优点。 函数 f 4 有大量的极值,当最优点取(0, 0)时,函数得到全局最小值 0。 采用标准人工鱼群算法和改进人工鱼群算法对 以上 4 个函数进行测试实验,其参数设置如初始人 工鱼群总数 N = 50;最大运行次数 N f1 max = 30, N f2 max = 50, N f3 max = 50, N f4 max = 30;最大试探次数 M = 15;拥挤 度因子 δ = 0.618;人工鱼移动的步长 λ = 0.2;感知距 离 rf1 = 1.5, rf2 = 4, rf3 = 1, rf4 = 1。 第 3 期 吴昌友:一种改进的人工鱼群优化算法 ·467·
·468 智能系统学报 第10卷 10 1.6 12 10 --标准人工鱼群算法 86 一改进人工鱼群算法 4 0 立0.6 0.4 05 x,∈[-10,10] 50 0.2 -10 x,∈-10,101 0 1015202530 (a)函数 运行次数 1.0 图2函数f的迭代曲线 0.8 Fig.2 The iterative curve of functionf 0.6 12*103 0.4 0.2 ··标准人工鱼群算法 一改进人工鱼群算法 20020 -20020 40 x3∈[-25,25 -40 x,∈-25,25] 4 (b)函数方 2 ×10 4 05101520253035404550 运行次数 2 图3函数的迭代曲线 Fig.3 The iterative curve of function f 0 3.610 05 1064之0之46 3.4 x∈[-5.12,5.12 --标准人工鱼群算法 x,∈-5.12,5.12] 3.2 一改进人工鱼群算法 3.0 (c)函数f 2.8 100 2.4 2.2 0 5101520253035404550 20 运行次数 0 图4函数f,的迭代曲线 5 x∈[-5.12,5.12 05 10-6广4之0之¥6 Fig.4 The iterative curve of functionf x,∈-5.125.12] (d)函数f 7 --标准人工鱼群算法 ·改进人工鱼群算法 图1测试函数f~f的三维立体图 6 5 Fig.1 The three-dimensional map test functionf~f 4 改进人工鱼群算法和标准标准人工鱼群算法在 3 2 4个目标测试函数方、方、f方和f中迭代次数与函数 值的关系曲线,如图2~5所示。 10 1520 2530 改进人工鱼群算法和标准人工鱼群算法在测试 运行次数 函数f~f优化中,其函数最优值和迭代次数如表1 图5函数∫:的迭代曲线 所示。 Fig.5 The iterative curve of function fa
(a)函数 f 1 (b)函数 f 2 (c)函数 f 3 (d)函数 f 4 图 1 测试函数 f 1 ~ f 4的三维立体图 Fig. 1 The three⁃dimensional map test function f1 ~ f4 改进人工鱼群算法和标准标准人工鱼群算法在 4 个目标测试函数 f 1 、 f 2 、 f 3 和 f 4 中迭代次数与函数 值的关系曲线,如图 2~5 所示。 改进人工鱼群算法和标准人工鱼群算法在测试 函数 f 1 ~ f 4优化中,其函数最优值和迭代次数如表 1 所示。 图 2 函数 f 1的迭代曲线 Fig. 2 The iterative curve of function f1 图 3 函数 f 2的迭代曲线 Fig. 3 The iterative curve of function f2 图 4 函数 f 3的迭代曲线 Fig. 4 The iterative curve of function f3 图 5 函数 f 4的迭代曲线 Fig. 5 The iterative curve of function f4 ·468· 智 能 系 统 学 报 第 10 卷
第3期 吴昌友:一种改进的人工鱼群优化算法 ·469 表1改进和标准人工鱼群算法的最优值和迭代次数比较 artificial fish-school algorithm [J].Journal of Chongqing Table 1 The optimal value of improved and standard AFSA Normal University,2007,24(3):23-26. [5]刘佳,刘丽娜,李靖.基于模拟退火算法的改进人工鱼群 and the comparison of the number of iterations 算法研究[J].计算机仿真,2011,28(10):195-198. 标准人工鱼群算法 改进人工鱼群算法 函数 LIU Jia,LIU Lina,LI Jing.Research of improved artificial 最优值 迭代次数 最优值 迭代次数 fish swarm algorithm based on simulated annealing algorithm 0 14 0 8 [J].Computer Simulation,2011,28(10):195-198. f 0 21 0 10 [6]柳毅求解模糊需求可回程取货车辆路径问题的改进工 6 鱼群算法[J].模式识别与人工智能,2010,23(4):560 2748.8 50 3600 6 564. g 0 27 0 13 LIU Yi.Improved artificial fish swarm algorithm for vehicle routing problem with backhaul and fuzzy demand[J].Pat- 由图2~5和表1可以看出,改进的人工鱼群算 tern Recognition Artificial Intelligence,2010,23(4): 法无论在优化速度和优化精度明显好于标准的人工 560-564 鱼群算法,对于函数f、方和f来说,虽然改进的人 [7]张严,楚晓丽.一种改进的人工鱼群算法[J刀]计算机系统 应用,2011,20(5):199-201. 工鱼群算法和标准人工鱼群算法都达到了最优值, ZHANG Yan,CHU Xiaoli.Advanced artificial fish swarm 但是改进的人工鱼群算法收敛的速度较快:对于函 algorithm[J].Computer Systems Applications,2011,20 数方来说,标准人工鱼群算法运行多次都陷入最优 (5):199-201. 解,无法找到全局最优解。综上所述,搜索目标函数 [8]曲良东,何登旭.基于自适应高斯变异的人工鱼群算法 全局最优值,标准人工鱼群算法不是陷入局部极值, [J].计算机工程,2009,35(15):182-189. 就是计算逐步趋于停顿,而改进标准人工鱼群算法 QU Liangdong,HE Dengxu.Artificial fish-school algorithm 则表现出更为强大的搜索能力、更快的收敛速度以 based on adaptive Gauss mutation[J].Computer Engineer- 及更为准确的计算精度。 ing,2009,35(15):182-189. [9]彭勇,唐国磊,薛志春.基于改进人工鱼群算法的梯级水 4结束语 库群优化调度[J].系统工程理论与实践,2011,31(6): 1118-1126. 对于标准人工鱼群算法容易陷入局部极小点和 PENG Yong,TANG Guolei,XUE Zhichun.Optimal opera- 收敛速度慢等特点,本文提出了一种改进的人工鱼 tion of cascade reservoirs based on improved artificial fish 群算法。在人工鱼群算法应用复杂的约束条件下, swarm algorithm[J].Systems Engineering-Theory Prac- 很难产生可行的初始人工鱼群,本文给出了初始人 tice,2011,31(6):1118-1126. 工鱼群的产生方法,大大提高初始人工鱼群产生速 [10]SHEN Wei,GUO Xiaopen,WU Chao,et al.Forecasting 度,并提出了自适应步长,加速人工鱼群算法的收敛 stock indices using radial basis function neural networks optimized by artificial fish swarm algorithm[J].Knowl- 速度,同时为了保证人工鱼群的多样性,避免陷入局 edge-Based Systems,2011,24(3):378-385. 部最优解,引进了变异策略。从测试实验的结果可 [11]WANG Cuiru,ZHOU Chunlei,MA Jianwei.An improved 以看出,改进人工鱼群算法是可行的。 artificial fish-swarm algorithm and its application in feed- 参考文献: forward neural networks[C]//Proceedings of 2005 Interna- tional Conference on Machine Learning and Cybernetics. [1]李晓磊,钱积新基于分解协调的人工鱼群优化算法研究 Guangzhou,China.2005,5:2890-2894. [J].电路与系统学报,2003,8(1):1-6. [12]FARZI S.Efficient job scheduling in grid computing with LI Xiaolei,OIAN Jixin.Studies on artificial fish swarm opti- modified artificial fish swarm algorithm[].International mization algorithm based on decomposition and coordination Journal of Computer Theory and Engineering,2009,1 techniques[J].Journal of Circuits and Systems,2003,8 (1):13-18. (1):1-6. [13]LUO Yi,ZHANG Juntao,LI Xinxin.The optimization of [2]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模 PID controller parameters based on artificial fish swarm al- 式:鱼群算法[J].系统工程理论与实践,2002,22(11): gorithm[C]//2007 IEEE International Conference on Au- 32-38. tomation and Logistics.Ji'nan,China,2007:1058-1062. LI Xiaolei,SHAO Zhijiang,QIAN Jixin.An optimizing [14]吴昌友,王福林,马力.一种新的改进粒子群优化算法 method based on autonomous animals fish-swarm algorithm [J].控制工程,2010,17(5):359-362. [J].Systems Engineering-Theory Practice,2002,22 WU Changyou,WANG Fulin,MA Li.An improved parti- (11):32.38. cle swarm optimization algorithm[J].Control Engineering [3]李晓磊,路飞,田国会,等组合优化问题的人工鱼群算法 of China,2010,17(5):359-362. 应用J刀.山东大学学报:工学版,2004,34(5):64-67. 作者简介: LI Xiaolei,LU Fei,TIAN Guohui,et al.Applications of ar- 吴昌友,男,1981年生,副教授,博 tificial fish school algorithm in combinatorial optimization 士,主要研究方向为系统工程和人工智 problems[J].Journal of Shangdong University:Engineering 能算法。主持和参与省部级项目6项」 Science,.2004,34(5):64-67. 发表学术论文30余篇,出版专著1部. [4]范玉军,王冬冬,孙明明改进的人工鱼群算法[J].重庆 主编教材1部。 师范大学学报,2007,24(3):23-26. FAN Yujun,WANG Dongdong,SUN Mingming.Improved
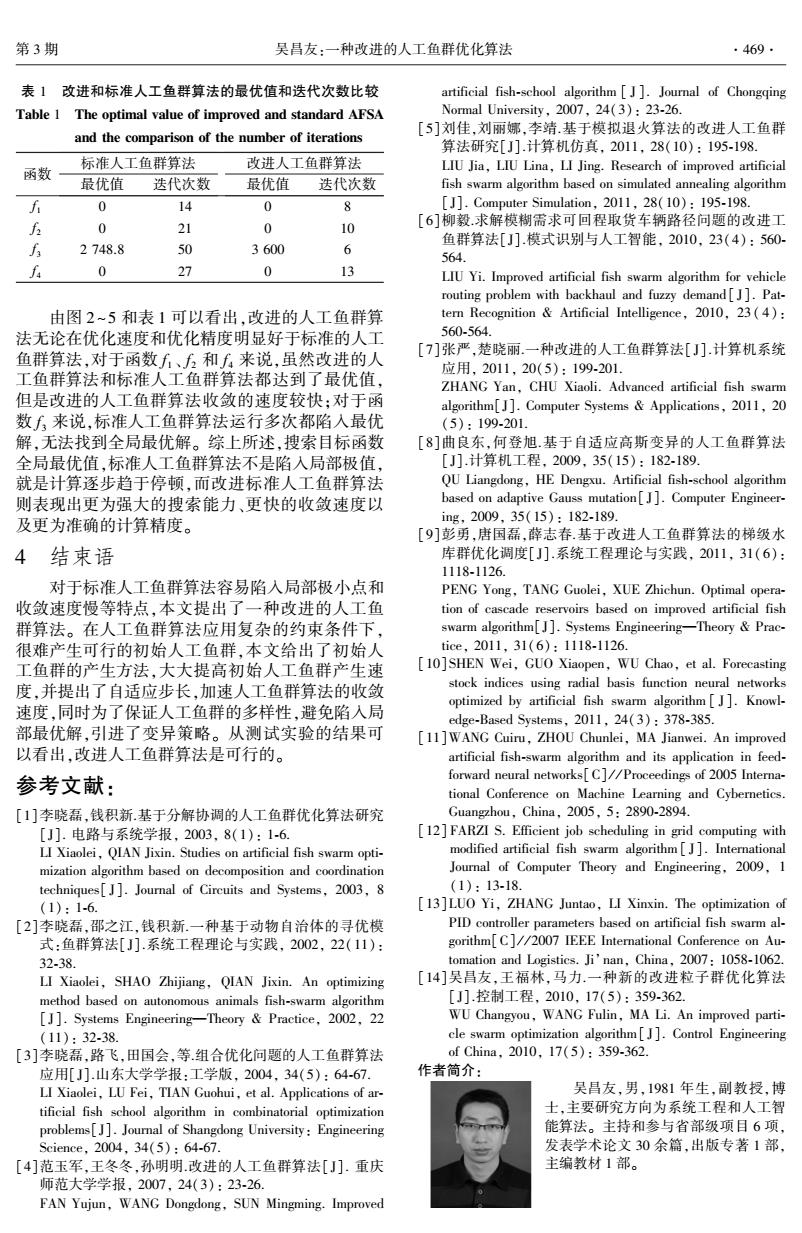
表 1 改进和标准人工鱼群算法的最优值和迭代次数比较 Table 1 The optimal value of improved and standard AFSA and the comparison of the number of iterations 函数 标准人工鱼群算法 最优值 迭代次数 改进人工鱼群算法 最优值 迭代次数 f 1 0 14 0 8 f 2 0 21 0 10 f 3 2 748.8 50 3 600 6 f 4 0 27 0 13 由图 2~5 和表 1 可以看出,改进的人工鱼群算 法无论在优化速度和优化精度明显好于标准的人工 鱼群算法,对于函数 f 1 、 f 2 和 f 4 来说,虽然改进的人 工鱼群算法和标准人工鱼群算法都达到了最优值, 但是改进的人工鱼群算法收敛的速度较快;对于函 数 f 3 来说,标准人工鱼群算法运行多次都陷入最优 解,无法找到全局最优解。 综上所述,搜索目标函数 全局最优值,标准人工鱼群算法不是陷入局部极值, 就是计算逐步趋于停顿,而改进标准人工鱼群算法 则表现出更为强大的搜索能力、更快的收敛速度以 及更为准确的计算精度。 4 结束语 对于标准人工鱼群算法容易陷入局部极小点和 收敛速度慢等特点,本文提出了一种改进的人工鱼 群算法。 在人工鱼群算法应用复杂的约束条件下, 很难产生可行的初始人工鱼群,本文给出了初始人 工鱼群的产生方法,大大提高初始人工鱼群产生速 度,并提出了自适应步长,加速人工鱼群算法的收敛 速度,同时为了保证人工鱼群的多样性,避免陷入局 部最优解,引进了变异策略。 从测试实验的结果可 以看出,改进人工鱼群算法是可行的。 参考文献: [1]李晓磊,钱积新.基于分解协调的人工鱼群优化算法研究 [J]. 电路与系统学报, 2003, 8(1): 1⁃6. LI Xiaolei, QIAN Jixin. Studies on artificial fish swarm opti⁃ mization algorithm based on decomposition and coordination techniques[ J]. Journal of Circuits and Systems, 2003, 8 (1): 1⁃6. [2]李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模 式:鱼群算法[J].系统工程理论与实践, 2002, 22(11): 32⁃38. LI Xiaolei, SHAO Zhijiang, QIAN Jixin. An optimizing method based on autonomous animals fish⁃swarm algorithm [J]. Systems Engineering—Theory & Practice, 2002, 22 (11): 32⁃38. [3]李晓磊,路飞,田国会,等.组合优化问题的人工鱼群算法 应用[J].山东大学学报:工学版, 2004, 34(5): 64⁃67. LI Xiaolei, LU Fei, TIAN Guohui, et al. Applications of ar⁃ tificial fish school algorithm in combinatorial optimization problems[J]. Journal of Shangdong University: Engineering Science, 2004, 34(5): 64⁃67. [4]范玉军,王冬冬,孙明明.改进的人工鱼群算法[ J]. 重庆 师范大学学报, 2007, 24(3): 23⁃26. FAN Yujun, WANG Dongdong, SUN Mingming. Improved artificial fish⁃school algorithm [ J ]. Journal of Chongqing Normal University, 2007, 24(3): 23⁃26. [5]刘佳,刘丽娜,李靖.基于模拟退火算法的改进人工鱼群 算法研究[J].计算机仿真, 2011, 28(10): 195⁃198. LIU Jia, LIU Lina, LI Jing. Research of improved artificial fish swarm algorithm based on simulated annealing algorithm [J]. Computer Simulation, 2011, 28(10): 195⁃198. [6]柳毅.求解模糊需求可回程取货车辆路径问题的改进工 鱼群算法[J].模式识别与人工智能, 2010, 23(4): 560⁃ 564. LIU Yi. Improved artificial fish swarm algorithm for vehicle routing problem with backhaul and fuzzy demand[ J]. Pat⁃ tern Recognition & Artificial Intelligence, 2010, 23 ( 4): 560⁃564. [7]张严,楚晓丽.一种改进的人工鱼群算法[ J].计算机系统 应用, 2011, 20(5): 199⁃201. ZHANG Yan, CHU Xiaoli. Advanced artificial fish swarm algorithm[J]. Computer Systems & Applications, 2011, 20 (5): 199⁃201. [8]曲良东,何登旭.基于自适应高斯变异的人工鱼群算法 [J].计算机工程, 2009, 35(15): 182⁃189. QU Liangdong, HE Dengxu. Artificial fish⁃school algorithm based on adaptive Gauss mutation[ J]. Computer Engineer⁃ ing, 2009, 35(15): 182⁃189. [9]彭勇,唐国磊,薛志春.基于改进人工鱼群算法的梯级水 库群优化调度[J].系统工程理论与实践, 2011, 31(6): 1118⁃1126. PENG Yong, TANG Guolei, XUE Zhichun. Optimal opera⁃ tion of cascade reservoirs based on improved artificial fish swarm algorithm[J]. Systems Engineering—Theory & Prac⁃ tice, 2011, 31(6): 1118⁃1126. [10]SHEN Wei, GUO Xiaopen, WU Chao, et al. Forecasting stock indices using radial basis function neural networks optimized by artificial fish swarm algorithm [ J]. Knowl⁃ edge⁃Based Systems, 2011, 24(3): 378⁃385. [11]WANG Cuiru, ZHOU Chunlei, MA Jianwei. An improved artificial fish⁃swarm algorithm and its application in feed⁃ forward neural networks[C] / / Proceedings of 2005 Interna⁃ tional Conference on Machine Learning and Cybernetics. Guangzhou, China, 2005, 5: 2890⁃2894. [12] FARZI S. Efficient job scheduling in grid computing with modified artificial fish swarm algorithm [ J]. International Journal of Computer Theory and Engineering, 2009, 1 (1): 13⁃18. [13]LUO Yi, ZHANG Juntao, LI Xinxin. The optimization of PID controller parameters based on artificial fish swarm al⁃ gorithm[C] / / 2007 IEEE International Conference on Au⁃ tomation and Logistics. Ji’nan, China, 2007: 1058⁃1062. [14]吴昌友,王福林,马力.一种新的改进粒子群优化算法 [J].控制工程, 2010, 17(5): 359⁃362. WU Changyou, WANG Fulin, MA Li. An improved parti⁃ cle swarm optimization algorithm[ J]. Control Engineering of China, 2010, 17(5): 359⁃362. 作者简介: 吴昌友,男,1981 年生,副教授,博 士,主要研究方向为系统工程和人工智 能算法。 主持和参与省部级项目 6 项, 发表学术论文 30 余篇,出版专著 1 部, 主编教材 1 部。 第 3 期 吴昌友:一种改进的人工鱼群优化算法 ·469·