
第10卷第3期 智能系统学报 Vol.10 No.3 2015年6月 CAAI Transactions on Intelligent Systems Jun.2015 D0:10.3969/j.issn.1673-4785.201404041 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20150603.1623.002.html 投球机器人模糊PID控制 赵新华,王璞,陈晓红 (1.哈尔滨工程大学自动化学院,黑龙江哈尔滨150001;2.哈尔滨船舶锅炉涡轮机研究所,黑龙江哈尔滨150036) 摘要:针对智能投球机器人在轨迹跟踪过程中存在响应慢、跟踪精度低的问题,采用PD控制和模糊PD控制2 种控制方法提高系统的响应速度及控制精度。对二连杆投球机器人进行了详细的运动学建模,建立了机械臂的动 力学模型,联立得约束矩阵方程:然后分别选用PD控制和模糊PD控制对二连杆投球机器人运动轨迹进行控制。 在MATLAB环境下利用SimMechanics对系统数学模型和2种控制方案进行仿真,数值实验结果表明,模糊PID控制 具有更好的控制效果。 关键词:机器人:投球机器人;PD:模糊PD;动力学模型:约束矩阵:轨迹跟踪 中图分类号:TP18文献标志码:A文章编号:1673-4785(2015)03-0399-08 中文引用格式:赵新华,王璞,陈晓红.投球机器人模糊PD控制[J].智能系统学报,2015,10(3):399-406. 英文引用格式:ZHAO Xinhua,WANG Pu,CHEN Xiaohong.Fuzzy PID control of pitching robots[J].CAAI Transactions on In- telligent Systems,2015,10(3):399-406 Fuzzy PID control of pitching robots ZHAO Xinhua',WANG Pu',CHEN Xiaohong? (1.College of Automation,Harbin Engineering University,Harbin 150001,China;2.Harbin Marine Boiler and Turbine Research In- stitute,Harbin 150036,China) Abstract:The PID and fuzzy PID controls were exploited to improve the control performance of the system for sol- ving the problems of the slow response and low accuracy in the trajectory tracking of the pitching robot.Kinematics modeling of a dual-arm pitching robot was built.The dynamic model of the robotic arm was established and the con- straint matrix equation was obtained by simultaneous equations.The PID and fuzzy PID controls were selected to control the trajectory of the dual-arm pitching robot.The mathematical model of the system was simulated using Sim- Mechanics and the comparison of the two kinds of control schemes was completed using MATLAB.The numerical simulation results showed that the fuzzy PID control has a better effect. Keywords:robot;pitching robot;PID;fuzzy PID;dynamics model;constraint matrix;trajectory tracking 智能投球机器人是一个由微处理器控制,集环 干扰因素,机器人的运动具有时变、非线性、干扰大 境感知、避障、行走、投球等功能于一体的智能机器 和不确定等特性,传统的PD控制器已不能达到较 人。对于投球机器人来说,运动控制的目的就是使 好的控制效果。近几年,机器人智能控制在理论 之能精确并且快速地实现机械臂转角运动。传统的 和应用方面都取得较大的进展[)。在模糊控制方 机器人运动控制常采用PD控制器。由于各种 面,由J.J.Buckley等论证了模糊系统的逼近特 性[4」,E.H.Mamdan首次将模糊理论运用于一台实 收稿日期:2014-04-22.网络出版日期:2015-06-03. 基金项目:黑龙江省博士后科研启动基金资助项目(3236310224) 际机器人,使模糊控制技术在机器人中的应用得以 通信作者:赵新华.E-mail:zhaoxinhua@hrbeu.cu.cn
第 10 卷第 3 期 智 能 系 统 学 报 Vol.10 №.3 2015 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2015 DOI:10.3969 / j.issn.1673⁃4785.201404041 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150603.1623.002.html 投球机器人模糊 PID 控制 赵新华1 ,王璞1 ,陈晓红2 (1.哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001; 2.哈尔滨船舶锅炉涡轮机研究所,黑龙江 哈尔滨 150036) 摘 要:针对智能投球机器人在轨迹跟踪过程中存在响应慢、跟踪精度低的问题,采用 PID 控制和模糊 PID 控制 2 种控制方法提高系统的响应速度及控制精度。 对二连杆投球机器人进行了详细的运动学建模,建立了机械臂的动 力学模型,联立得约束矩阵方程;然后分别选用 PID 控制和模糊 PID 控制对二连杆投球机器人运动轨迹进行控制。 在 MATLAB 环境下利用 SimMechanics 对系统数学模型和 2 种控制方案进行仿真,数值实验结果表明,模糊 PID 控制 具有更好的控制效果。 关键词:机器人;投球机器人;PID;模糊 PID;动力学模型;约束矩阵;轨迹跟踪 中图分类号:TP18 文献标志码:A 文章编号:1673⁃4785(2015)03⁃0399⁃08 中文引用格式:赵新华,王璞,陈晓红. 投球机器人模糊 PID 控制[J]. 智能系统学报, 2015, 10(3): 399⁃406. 英文引用格式:ZHAO Xinhua, WANG Pu, CHEN Xiaohong. Fuzzy PID control of pitching robots[J]. CAAI Transactions on In⁃ telligent Systems, 2015, 10(3): 399⁃406 Fuzzy PID control of pitching robots ZHAO Xinhua 1 , WANG Pu 1 , CHEN Xiaohong 2 (1. College of Automation, Harbin Engineering University, Harbin 150001, China; 2. Harbin Marine Boiler and Turbine Research In⁃ stitute, Harbin 150036, China) Abstract:The PID and fuzzy PID controls were exploited to improve the control performance of the system for sol⁃ ving the problems of the slow response and low accuracy in the trajectory tracking of the pitching robot. Kinematics modeling of a dual⁃arm pitching robot was built. The dynamic model of the robotic arm was established and the con⁃ straint matrix equation was obtained by simultaneous equations. The PID and fuzzy PID controls were selected to control the trajectory of the dual⁃arm pitching robot. The mathematical model of the system was simulated using Sim⁃ Mechanics and the comparison of the two kinds of control schemes was completed using MATLAB. The numerical simulation results showed that the fuzzy PID control has a better effect. Keywords:robot; pitching robot; PID; fuzzy PID; dynamics model; constraint matrix; trajectory tracking 收稿日期:2014⁃04⁃22. 网络出版日期:2015⁃06⁃03. 基金项目:黑龙江省博士后科研启动基金资助项目(3236310224). 通信作者:赵新华. E⁃mail: zhaoxinhua@ hrbeu.edu.cn. 智能投球机器人是一个由微处理器控制,集环 境感知、避障、行走、投球等功能于一体的智能机器 人。 对于投球机器人来说,运动控制的目的就是使 之能精确并且快速地实现机械臂转角运动。 传统的 机器人运动控制常采用 PID 控制器[1] 。 由于各种 干扰因素,机器人的运动具有时变、非线性、干扰大 和不确定等特性,传统的 PID 控制器已不能达到较 好的控制效果[2] 。 近几年,机器人智能控制在理论 和应用方面都取得较大的进展[3] 。 在模糊控制方 面,由 J. J. Buckley 等论证了模糊系统的逼近特 性[4] ,E. H. Mamdan 首次将模糊理论运用于一台实 际机器人,使模糊控制技术在机器人中的应用得以

·400· 智能系统学报 第10卷 展现)。文献[6]针对移动机器人在传统控制器控 yp =lsin 0 lzsin(0 +0) (3) 制下自主运动时出现的不稳定状况,将模糊控制策 对末端坐标进行积分得到末端速度方程: 略引入移动机器人运动控制系统中。通过分析比较 xa=-l1m1sin81-2(ω1+w2)sin(8+82)(4) 不同的控制方法,设计了由速度误差率和速度误差 y'm=l101c0s81+l2(ω1+w2)os(6+62)(5) 变化率为输入、电机输出功率为输出的双输入单输 式中:w1=0'1,02=8'2,将式(4)和(5)整理并写成 出模糊逻辑控制器。文献[7]模仿人工预瞄驾驶行 如下矩阵形式(即雅克比矩阵[]): 为,提出了移动机器人运动控制的模糊控制方法,实 验表明,该模糊控制方法可保证移动机器人快速、准 确地沿着各种参考轨迹行走,且具有良好的鲁棒性。 式中:S1=sin01,C,=cos01,S2=sin82,C2=cos62, 文献[8]在智能轮椅机器人中使用超声波的探测距 S12=sin(01+02),Ce=cos(01+02)。 离作为输入信号,经模糊控制技术处理后,输出机器 对二连杆机械臂末端速度方程(3)~(4)进行 人左右轮的转动速度来实现超声波避障。 求导得到末端加速度方程: 本文首先对二连杆投球机器人进行运动学建 x”+(l1S1+l2S2)a1+l2S12a2= 模,然后在此基础上对机器人的控制方法进行了研 -[(l,C1+l2C2)w21+l2C12w2+2l2w1ω2C2] 究,通过PID和模糊PID2种控制方法,实现二连杆 投球机器人运动轨迹的有效控制,用MATLAB软件 (7) 进行仿真,并对仿真结果进行对比分析。 y”d+(l1S1+l2S12)a1+l2S12a2= -[(L1S1+l2S12)w21=l2S12w22+2l2w1w2S12] 1二连杆投球机器人的运动学建模 (8) 1.1二连杆机械臂 式中:a1=0”1,2=0"”2,二连杆机械臂质心位置的 机械手臂是机器人重要构成部件。图1为二杆 加速度与关节处的变量之间关系如下: 机械臂结构图,其中日,和6,分别为关节1、2转角, (Ac +rS=-rCWi L1和2分别为第1、2根杆的长度,r,为关节1到第1 (9) (Aay-riCia1=-rSwi 根杆质心的距离,12为关节2到第2根杆质心的距 A2+(l1S+T2S2)a1+T2S2a2= 离,M.为负载质量。 (L1C1+l2C12)w21+l2C12w2+2l1w1ω2C2(10) A+(L1C,+r2C2)a1+r2C12a2= (化+,5a)a+4soa+2以@,o,Sa(1) 分别对机械臂两连杆的隔离体[o]进行力及力矩的 分析,求得机械臂的动力学方程。 1.2机械臂动力学方程 首先,对二连杆平面投球机器人的第1根连杆 应用牛顿定律,受力分析如图2所示。 图1二连杆机械臂结构 Fig.1 Dual-arm mechanical structure 式(1)是二连杆机械臂的矢量方程,其中R,、 R,是沿T1和T2方向上的矢量,R为合成矢量。由 于在二连杆机械臂中,各连杆的长度保持不变,但它 18 们各自的方位却随机构的运动而改变,所以矢量方 程对时间求导将闭环矢量方程分解成2个标量表达 图2第1根连杆受力分析 式,分别沿x、y方向分解。 Fig.2 The first arm force analysis R=R+R2 (1) R相应于x和y的坐标方程为 图2中,FoF2.分别代表第1根杆2端所受x x=l1c0s8+l2c0s(81+02) (2) 方向的力,F,、F,分别代表第1根杆2端所受y方
展现[5] 。 文献[6]针对移动机器人在传统控制器控 制下自主运动时出现的不稳定状况,将模糊控制策 略引入移动机器人运动控制系统中。 通过分析比较 不同的控制方法,设计了由速度误差率和速度误差 变化率为输入、电机输出功率为输出的双输入单输 出模糊逻辑控制器。 文献[7]模仿人工预瞄驾驶行 为,提出了移动机器人运动控制的模糊控制方法,实 验表明,该模糊控制方法可保证移动机器人快速、准 确地沿着各种参考轨迹行走,且具有良好的鲁棒性。 文献[8]在智能轮椅机器人中使用超声波的探测距 离作为输入信号,经模糊控制技术处理后,输出机器 人左右轮的转动速度来实现超声波避障。 本文首先对二连杆投球机器人进行运动学建 模,然后在此基础上对机器人的控制方法进行了研 究,通过 PID 和模糊 PID2 种控制方法,实现二连杆 投球机器人运动轨迹的有效控制,用 MATLAB 软件 进行仿真,并对仿真结果进行对比分析。 1 二连杆投球机器人的运动学建模 1.1 二连杆机械臂 机械手臂是机器人重要构成部件。 图 1 为二杆 机械臂结构图,其中 θ1 和 θ2 分别为关节 1、2 转角, l 1 和 l 2 分别为第 1、2 根杆的长度, r1 为关节 1 到第 1 根杆质心的距离, r2 为关节 2 到第 2 根杆质心的距 离, Mpl 为负载质量。 图 1 二连杆机械臂结构 Fig. 1 Dual⁃arm mechanical structure 式(1) 是二连杆机械臂的矢量方程,其中 R1 、 R2 是沿 r1 和 r2 方向上的矢量, Rpl 为合成矢量。 由 于在二连杆机械臂中,各连杆的长度保持不变,但它 们各自的方位却随机构的运动而改变,所以矢量方 程对时间求导将闭环矢量方程分解成 2 个标量表达 式,分别沿 x、y 方向分解。 Rpl = R1 + R2 (1) Rpl 相应于 x 和 y 的坐标方程为 xpl = l 1 cos θ1 + l 2 cos(θ1 + θ2 ) (2) ypl = l 1 sin θ1 + l 2 sin(θ1 + θ2 ) (3) 对末端坐标进行积分得到末端速度方程: x′pl = - l 1ω1 sin θ1 - l 2(ω1 + ω2)sin(θ1 + θ2) (4) y′pl = l 1ω1 cos θ1 + l 2(ω1 + ω2 )cos(θ1 + θ2 ) (5) 式中: ω1 = θ′1 ,ω2 = θ′2 ,将式(4)和(5)整理并写成 如下矩阵形式(即雅克比矩阵[9] ): x′pl y′pl é ë ê ê ù û ú ú = - l 1 S1 - l 2 S12 - l 2 S12 l 1C1 + l 2C12 l 2C12 é ë ê ê ù û ú ú ω1 ω2 é ë ê ê ù û ú ú (6) 式中: S1 = sin θ1,C1 = cos θ1,S2 = sin θ2,C2 = cos θ2, S12 = sin(θ1 + θ2),C12 = cos(θ1 + θ2) 。 对二连杆机械臂末端速度方程(3) ~ (4) 进行 求导得到末端加速度方程: x″pl + (l 1 S1 + l 2 S12 )α1 + l 2 S12α2 = - [(l 1C1 + l 2C12 )ω21 + l 2C12ω22 + 2l 2ω1ω2C12 ] (7) y″pl + (l 1 S1 + l 2 S12 )α1 + l 2 S12α2 = - [(l 1 S1 + l 2 S12 )ω21 = l 2 S12ω22 + 2l 2ω1ω2 S12 ] (8) 式中: α1 = θ″1 ,α2 = θ″2 ,二连杆机械臂质心位置的 加速度与关节处的变量之间关系如下: Ac1x + r1 S1α1 = - r1C1ω 2 1 Ac1y - r1C1α1 = - r1 S1ω 2 1 { (9) Ac2x + (l 1 S1 + r2 S12 )α1 + r2 S12α2 = (l 1C1 + l 2C12 )ω21 + l 2C12ω22 + 2l 1ω1ω2C12 (10) Ac2y + (l 1C1 + r2C12 )α1 + r2C12α2 = (l 1 S1 + l 2 S12 )ω21 + l 2 S12ω22 + 2l 2ω1ω2 S12 (11) 分别对机械臂两连杆的隔离体[10] 进行力及力矩的 分析,求得机械臂的动力学方程。 1.2 机械臂动力学方程 首先,对二连杆平面投球机器人的第 1 根连杆 应用牛顿定律[11] ,受力分析如图 2 所示。 图 2 第 1 根连杆受力分析 Fig. 2 The first arm force analysis 图 2 中,F01x、F21x分别代表第 1 根杆 2 端所受 x 方向的力,F01y、F21y分别代表第 1 根杆 2 端所受 y 方 ·400· 智 能 系 统 学 报 第 10 卷
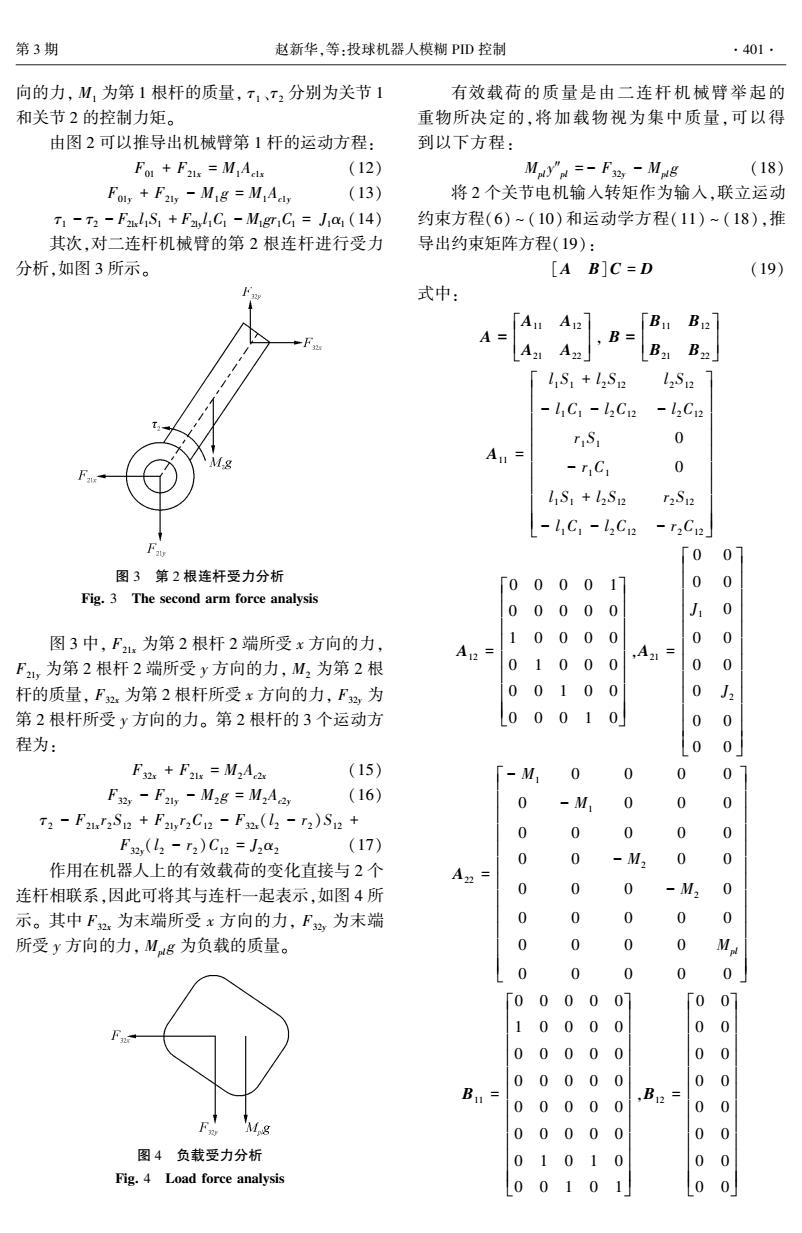
第3期 赵新华,等:投球机器人模糊PD控制 ·401· 向的力,M1为第1根杆的质量,T1、T2分别为关节1 有效载荷的质量是由二连杆机械臂举起的 和关节2的控制力矩。 重物所决定的,将加载物视为集中质量,可以得 由图2可以推导出机械臂第1杆的运动方程: 到以下方程: Fo F2is =MAcls (12) My"=-F32 Mig (18) Foly F2y -Mig =MAcy (13) 将2个关节电机输入转矩作为输入,联立运动 T1-T2 -F2S +Fa,hC-Migr C Jia (14) 约束方程(6)~(10)和运动学方程(11)~(18),推 其次,对二连杆机械臂的第2根连杆进行受力 导出约束矩阵方程(19): 分析,如图3所示。 [A B]C=D (19) 式中: AA 「B1B12 A= ,B= B21 Bz IS+S LS -l1C1-l2C2-l2C12 rSI 0 A1= -r,C1 0 S+lS r2S12 -l1C1-l2C12 -r2C12 「0 01 图3第2根连杆受力分析 「0000 11 0 0 Fig.3 The second arm force analysis 00000 1 0 图3中,F为第2根杆2端所受x方向的力, 100 0 0 0 0 ,A21= F,为第2根杆2端所受y方向的力,M2为第2根 01 00 0 0 0 杆的质量,F2为第2根杆所受x方向的力,F热为 001 00 0 J2 第2根杆所受y方向的力。第2根杆的3个运动方 0 0010 0 0 程为: 0 0 Fxs F21s M2Aos (15) -M 0 0 0 0 Fx2y -F2y -M2g M,Aey (16) 0 -M, 0 0 0 T2-F22S12+F2wr2C12-F2(l23-T2)S12+ 0 0 0 F2,(l2-r2)C2=J2a2 (17) 0 0 -M 0 作用在机器人上的有效载荷的变化直接与2个 A2= 连杆相联系,因此可将其与连杆一起表示,如图4所 0 0 0 -M. 0 示。其中F为末端所受x方向的力,F动为末端 0 0 0 0 所受y方向的力,Mg为负载的质量。 0 0 0 0 0 0 0 0 「000001 「0 07 1000 0 0 0 000 00 0 0 0 0000 0 0 B1= 00000 ,B12= 0 0 Mg 000 0 0 0 0 图4负载受力分析 0 101 0 0 Fig.4 Load force analysis 0 0101 0 0
向的力, M1 为第 1 根杆的质量, τ1 、τ2 分别为关节 1 和关节 2 的控制力矩。 由图 2 可以推导出机械臂第 1 杆的运动方程: F01 + F21x = M1Ac1x (12) F01y + F21y - M1 g = M1Ac1y (13) τ1 - τ2 - F21x l 1S1 + F21y l 1C1 - M1gr1C1 = J1α1 (14) 其次,对二连杆机械臂的第 2 根连杆进行受力 分析,如图 3 所示。 图 3 第 2 根连杆受力分析 Fig. 3 The second arm force analysis 图 3 中, F21x 为第 2 根杆 2 端所受 x 方向的力, F21y 为第 2 根杆 2 端所受 y 方向的力, M2 为第 2 根 杆的质量, F32x 为第 2 根杆所受 x 方向的力, F32y 为 第 2 根杆所受 y 方向的力。 第 2 根杆的 3 个运动方 程为: F32x + F21x = M2Ac2x (15) F32y - F21y - M2 g = M2Ac2y (16) τ2 - F21x r2 S12 + F21y r2C12 - F32x(l 2 - r2 )S12 + F32y(l 2 - r2 )C12 = J2α2 (17) 作用在机器人上的有效载荷的变化直接与 2 个 连杆相联系,因此可将其与连杆一起表示,如图 4 所 示。 其中 F32x 为末端所受 x 方向的力, F32y 为末端 所受 y 方向的力, Mplg 为负载的质量。 图 4 负载受力分析 Fig. 4 Load force analysis 有效载荷的质量是由二连杆机械臂举起的 重物所决定的,将加载物视为集中质量,可以得 到以下方程: Mpl y″pl = - F32y - Mplg (18) 将 2 个关节电机输入转矩作为输入,联立运动 约束方程(6) ~ (10)和运动学方程(11) ~ (18),推 导出约束矩阵方程(19): [A B]C = D (19) 式中: A = A11 A12 A21 A22 é ë ê ê ù û ú ú , B = B11 B12 B21 B22 é ë ê ê ù û ú ú A11 = l 1 S1 + l 2 S12 l 2 S12 - l 1C1 - l 2C12 - l 2C12 r1 S1 0 - r1C1 0 l 1 S1 + l 2 S12 r2 S12 - l 1C1 - l 2C12 - r2C12 é ë ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú A12 = 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 é ë ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ,A21 = 0 0 0 0 J1 0 0 0 0 0 0 J2 0 0 0 0 é ë ê ê ê ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú ú ú ú A22 = - M1 0 0 0 0 0 - M1 0 0 0 0 0 0 0 0 0 0 - M2 0 0 0 0 0 - M2 0 0 0 0 0 0 0 0 0 0 Mpl 0 0 0 0 0 é ë ê ê ê ê ê ê ê ê ê ê ê êê ù û ú ú ú ú ú ú ú ú ú ú ú úú B11 = 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1 0 1 é ë ê ê ê ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú ú ú ú ,B12 = 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 é ë ê ê ê ê ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú ú ú ú ú 第 3 期 赵新华,等:投球机器人模糊 PID 控制 ·401·

.402. 智能系统学报 第10卷 00 LS -l1C1 定积分时间常数T,最后确定微分时间常数T,通 0 00 -1 0 常为0即可。 0 00 0 -1 2.2模糊PD控制 B21= 000r2S12 -T2C12 2.2.1模糊控制基本原理 000 0 0 模糊控制的核心是模糊控制器,而模糊控制器 LM 00 0 0 的关键是模糊控制规则的确定,即模糊控制规则 0 0 表)。模糊控制系统框图如图5所示,把误差e及 1 0 其变化率e作为模糊控制器的输入,把控制量u作 0 1 为模糊控制器的输出,得 B2= (2-2)S2-(l2-r2)C2 u=F(e,e) (21) 0 0 1 糊 模 被 C=[C C:C]T e C,=[a1a]' 对象 dw'dt 制算法 C2 [Aar Acy Ads Ay Apr A 图5模糊控制器基本结构 C=[Fou Foly Fa Fay Fx F] Fig.5 The basic structure of the fuzzy controller -[(I C +lCp)o+lCpo+2@@Ce] -[(l,S1+l2S2)ω,2+l2Sw22+22ω,w2S2] 二连杆平面机器人2个关节预定角度和码 与实际角度0,和0,的误差e及其变化率e.作为控制 -nCiw2 器输入,输出为驱动关节转矩T。 -nSo 2.2.2输入量的模糊化 -[(L,C1+T2Ce)w12+r,C2w22+2,ωwC2] 精确输入量e和e.分别乘以量化因子k.和k。 -[(HS:+raSp)w+r2Spo2+20@Sp] 以转换到各自的论域范围。设模糊控制器的输入量 D= 0 标准域均为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5 Mg 6}。输入量论域划分成7个模糊子集,即{NB,NM, T1-T2 -Migr C NS,ZO,PS,PM,PB}。模糊子集的隶属函数采用高 0 斯函数,函数曲线如图6所示。 Mg plot poinits:181 FIS Variables ☒1. Membership function plots T2 NBX NMX NSX ZOX PSX PMX PB 0 e Mug -4 -2 0 2 2二连杆投球机器人的控制方法 input variable"e" 图6隶属函数曲线 分别采用PD控制和模糊PD控制对二连杆 投球机器人进行运动轨迹控制。 Fig.6 Membership functions curve 2.1PID控制 2.2.2输入量的模糊化 PD控制策略其结构简单、稳定性好、可靠性 规则选取的总体原则是:当误差较大时,选择控 高2]。式(20)为PID控制标准公式,其中U(t)为 制量以消除误差为主:当误差较小时,选择控制量要 PD控制器输出,K。为比例放大系数,T为积分常 防止超调,以系统的稳定性为主。 数,T为微分放大系数,e为偏差信号。 输出变量与输入变量取一样的模糊子集,即u= )=×++ de (20) {NB,NM,NS,ZO,PS,PM,PB},同样采用高斯隶属 函数。e和e分别定义为7个模糊子集、49条规则, PD参数设置:首先确定比例增益K。,而后确 如表1所示
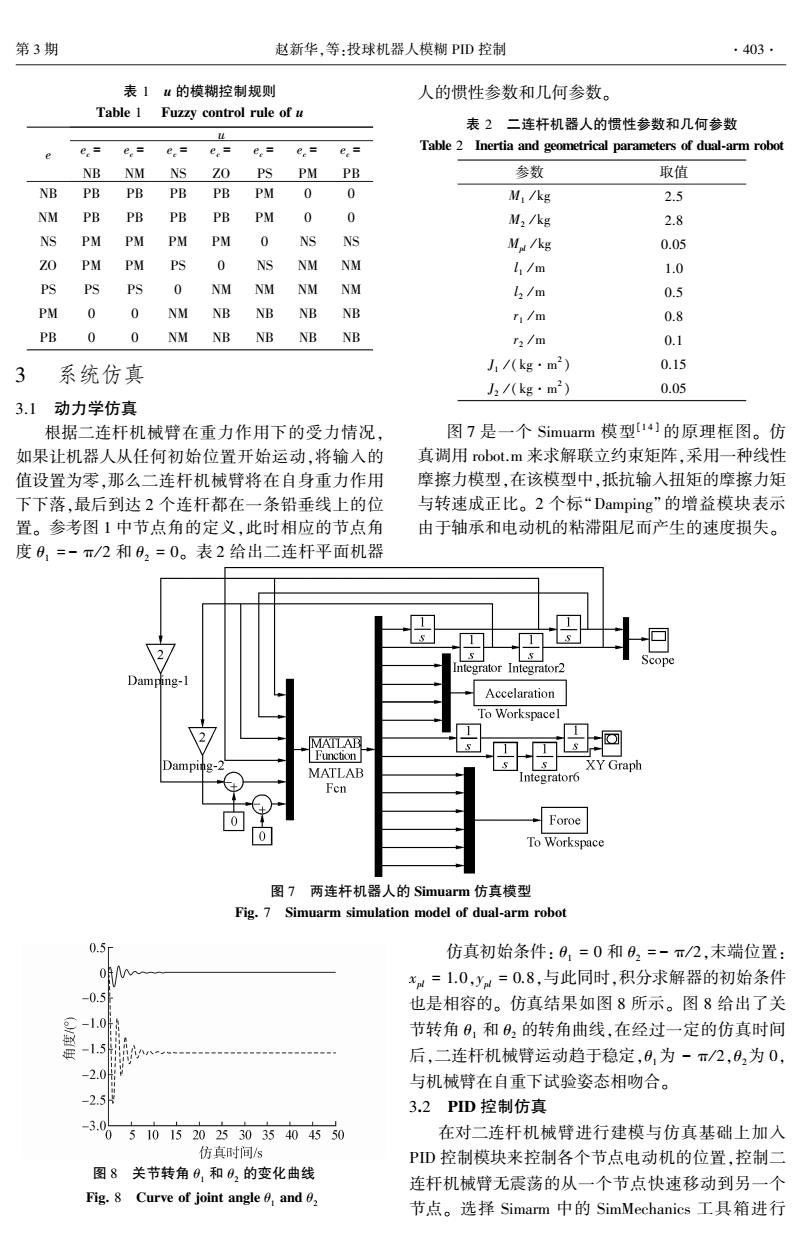
B21 = 0 0 0 l 1 S1 - l 1C1 0 0 0 - 1 0 0 0 0 0 - 1 0 0 0 r2 S12 - r2C12 0 0 0 0 0 Mpl 0 0 0 0 é ë ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú B22 = 0 0 1 0 0 1 (l 2 - r2 )S12 - (l 2 - r2 )C12 1 0 0 1 é ë ê ê ê ê ê ê ê ê ù û ú ú ú ú ú ú ú ú C = [C1 C2 C3 ] T C1 = [α1 α2 ] T C2 = [Ac1x Ac1y Ac2x Ac2y Aplx Aply ] T C3 = [F01x F01y F21x F21y F32x F32y ] T D = - [(l 1C1 + l 2C12)ω 2 1 + l 2C12ω 2 2 + 2l 2ω1ω2C12] - [(l 1S1 + l 2S12)ω1 2 + l 2S12ω2 2 + 2l 2ω1ω2S12] - r1C1ω1 2 - r1S1ω1 2 - [(l 1C1 + r2C12)ω1 2 + r2C12ω2 2 + 2r2ω1ω2C12] - [(l 1S1 + r2S12)ω1 2 + r2S12ω2 2 + 2r2ω1ω2S12] 0 M1g τ1 - τ2 - M1gr1C1 0 M2g τ2 0 - Mplg é ë ê ê ê ê ê ê ê ê ê ê ê ê ê ê ê ê ê ê ê ê ê êê ù û ú ú ú ú ú ú ú ú ú ú ú ú ú ú ú ú ú ú ú ú ú úú 2 二连杆投球机器人的控制方法 分别采用 PID 控制和模糊 PID 控制对二连杆 投球机器人进行运动轨迹控制。 2.1 PID 控制 PID 控制策略其结构简单、稳定性好、可靠性 高[12] 。 式(20)为 PID 控制标准公式,其中 U(t) 为 PID 控制器输出, Kp 为比例放大系数,Ti为积分常 数,Td为微分放大系数,e 为偏差信号。 U(t) = Kp × e + 1 Ti ∫edt + Td de dt é ë ê ê ù û ú ú (20) PID 参数设置:首先确定比例增益 Kp ,而后确 定积分时间常数 Ti,最后确定微分时间常数 Td ,通 常为 0 即可。 2.2 模糊 PID 控制 2.2.1 模糊控制基本原理 模糊控制的核心是模糊控制器,而模糊控制器 的关键是模糊控制规则的确定,即模糊控制规则 表[13] 。 模糊控制系统框图如图 5 所示,把误差 e 及 其变化率 ec作为模糊控制器的输入,把控制量 u 作 为模糊控制器的输出,得 u = F(e,ec) (21) 图 5 模糊控制器基本结构 Fig. 5 The basic structure of the fuzzy controller 二连杆平面机器人 2 个关节预定角度 θ d 1 和 θ d 2 与实际角度 θ1和 θ2的误差 e 及其变化率 ec作为控制 器输入,输出为驱动关节转矩 τ。 2.2.2 输入量的模糊化 精确输入量 e 和 ec分别乘以量化因子 ke 和 kec 以转换到各自的论域范围。 设模糊控制器的输入量 标准域均为{-6,-5,-4,-3,-2,-1,0,1,2,3,4,5, 6}。 输入量论域划分成 7 个模糊子集,即{NB,NM, NS,ZO,PS,PM,PB}。 模糊子集的隶属函数采用高 斯函数,函数曲线如图 6 所示。 图 6 隶属函数曲线 Fig. 6 Membership functions curve 2.2.2 输入量的模糊化 规则选取的总体原则是:当误差较大时,选择控 制量以消除误差为主;当误差较小时,选择控制量要 防止超调,以系统的稳定性为主。 输出变量与输入变量取一样的模糊子集,即 u = {NB,NM,NS,ZO,PS,PM,PB},同样采用高斯隶属 函数。 e 和 ec分别定义为 7 个模糊子集、49 条规则, 如表 1 所示。 ·402· 智 能 系 统 学 报 第 10 卷
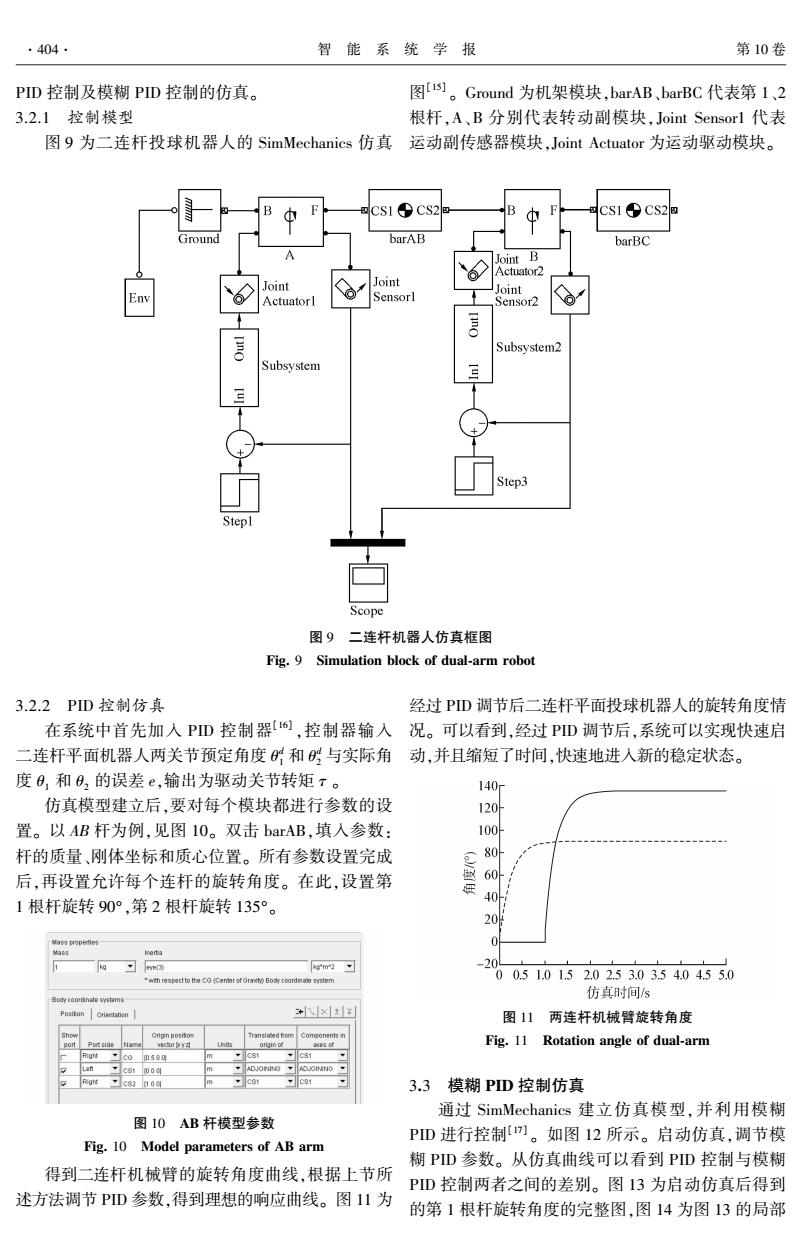
第3期 赵新华,等:投球机器人模糊PD控制 ·403· 表1“的模糊控制规则 人的惯性参数和几何参数。 Table 1 Fuzzy control rule of u 表2二连杆机器人的惯性参数和几何参数 e.= e,= e=e.=e= e= e= Table 2 Inertia and geometrical parameters of dual-arm robot NB NM NS ZO PS PM PB 参数 取值 NB PBPB PB PB PM 0 0 M,/kg 2.5 NM PB PB PB PB PM 0 0 M2/kg 2.8 NS PMPM PM PM 0 NS NS Mu/kg 0.05 PMPM PS 0 Ns NM NM 1/m 1.0 PS PS PS 0 NM NM NM NM 12/m 0.5 PM 00 NM NB NB NB NB r/m 0.8 PB 0 NB NB NB NB r2/m 0.1 3 系统仿真 1/(kg·m2) 0.15 J2/(kg·m2) 0.05 3.1动力学仿真 根据二连杆机械臂在重力作用下的受力情况, 图7是一个Simuarm模型14]的原理框图。仿 如果让机器人从任何初始位置开始运动,将输入的 真调用robot..m来求解联立约束矩阵,采用一种线性 值设置为零,那么二连杆机械臂将在自身重力作用 摩擦力模型,在该模型中,抵抗输入扭矩的摩擦力矩 下下落,最后到达2个连杆都在一条铅垂线上的位 与转速成正比。2个标“Damping”的增益模块表示 置。参考图1中节点角的定义,此时相应的节点角 由于轴承和电动机的粘滞阻尼而产生的速度损失。 度0,=-π/2和02=0。表2给出二连杆平面机器 1 2 ntegrator Integrator2 Damping-1 Accelaration To Workspacel MATLAB Function Dampi中g-2 MATLAB s XY Graph Integrator6 Fcn Foroe 0 To Workspace 图7两连杆机器人的Simuarm仿真模型 Fig.7 Simuarm simulation model of dual-arm robot 0.5m 仿真初始条件:0,=0和0,=-π/2,末端位置: x。=1.0,y=0.8,与此同时,积分求解器的初始条件 -0.51 也是相容的。仿真结果如图8所示。图8给出了关 -1.0 节转角0,和02的转角曲线,在经过一定的仿真时间 -1.5 后,二连杆机械臂运动趋于稳定,01为-π/2,0,为0, -2.0 与机械臂在自重下试验姿态相吻合。 -2.5R 3.2PD控制仿真 -3. 05101520253035404550 在对二连杆机械臂进行建模与仿真基础上加入 仿真时间s PD控制模块来控制各个节点电动机的位置,控制二 图8关节转角6,和0,的变化曲线 连杆机械臂无震荡的从一个节点快速移动到另一个 Fig.8 Curve of joint angle 6,and 0, 节点。选择Simarm中的SimMechanics工具箱进行
表 1 u 的模糊控制规则 Table 1 Fuzzy control rule of u e u ec = NB ec = NM ec = NS ec = ZO ec = PS ec = PM ec = PB NB PB PB PB PB PM 0 0 NM PB PB PB PB PM 0 0 NS PM PM PM PM 0 NS NS ZO PM PM PS 0 NS NM NM PS PS PS 0 NM NM NM NM PM 0 0 NM NB NB NB NB PB 0 0 NM NB NB NB NB 3 系统仿真 3.1 动力学仿真 根据二连杆机械臂在重力作用下的受力情况, 如果让机器人从任何初始位置开始运动,将输入的 值设置为零,那么二连杆机械臂将在自身重力作用 下下落,最后到达 2 个连杆都在一条铅垂线上的位 置。 参考图 1 中节点角的定义,此时相应的节点角 度 θ1 = - π/ 2 和 θ2 = 0。 表 2 给出二连杆平面机器 人的惯性参数和几何参数。 表 2 二连杆机器人的惯性参数和几何参数 Table 2 Inertia and geometrical parameters of dual⁃arm robot 参数 取值 M1 / kg 2.5 M2 / kg 2.8 Mpl / kg 0.05 l 1 / m 1.0 l 2 / m 0.5 r1 / m 0.8 r2 / m 0.1 J1 / (kg·m 2 ) 0.15 J2 / (kg·m 2 ) 0.05 图 7 是一个 Simuarm 模型[1 4 ] 的原理框图。 仿 真调用 robot.m 来求解联立约束矩阵,采用一种线性 摩擦力模型,在该模型中,抵抗输入扭矩的摩擦力矩 与转速成正比。 2 个标“Damping”的增益模块表示 由于轴承和电动机的粘滞阻尼而产生的速度损失。 图 7 两连杆机器人的 Simuarm 仿真模型 Fig. 7 Simuarm simulation model of dual⁃arm robot 图 8 关节转角 θ1 和 θ2 的变化曲线 Fig. 8 Curve of joint angle θ1 and θ2 仿真初始条件: θ1 = 0 和 θ2 = - π/ 2,末端位置: xpl = 1.0,ypl = 0.8,与此同时,积分求解器的初始条件 也是相容的。 仿真结果如图 8 所示。 图 8 给出了关 节转角 θ1 和 θ2 的转角曲线,在经过一定的仿真时间 后,二连杆机械臂运动趋于稳定,θ1为 - π/ 2,θ2为 0, 与机械臂在自重下试验姿态相吻合。 3.2 PID 控制仿真 在对二连杆机械臂进行建模与仿真基础上加入 PID 控制模块来控制各个节点电动机的位置,控制二 连杆机械臂无震荡的从一个节点快速移动到另一个 节点。 选择 Simarm 中的 SimMechanics 工具箱进行 第 3 期 赵新华,等:投球机器人模糊 PID 控制 ·403·
·404. 智能系统学报 第10卷 PID控制及模糊PID控制的仿真。 图s。Ground为机架模块,barAB、barBC代表第1,2 3.2.1控制模型 根杆,A、B分别代表转动副模块,Joint Sensorl代表 图9为二连杆投球机器人的SimMechanics仿真 运动副传感器模块,Joint Actuator为运动驱动模块。 CS1 CS2 CS1 CS2 Ground barAB barBC Joint B Actuator2 Joint Joint Sensorl Joint Env Actuatorl Sensor2 Subsystem2 Subsystem Step3 Step】 Scope 图9二连杆机器人仿真框图 Fig.9 Simulation block of dual-arm robot 3.2.2PID控制仿真 经过PD调节后二连杆平面投球机器人的旋转角度情 在系统中首先加入PD控制器6,控制器输入况。可以看到,经过PD调节后,系统可以实现快速启 二连杆平面机器人两关节预定角度和与实际角动,并且缩短了时间,快速地进入新的稳定状态。 度日,和0,的误差e,输出为驱动关节转矩r。 140 仿真模型建立后,要对每个模块都进行参数的设 120- 置。以AB杆为例,见图10。双击barAB,填入参数: 100 杆的质量、刚体坐标和质心位置。所有参数设置完成 后,再设置允许每个连杆的旋转角度。在此,设置第 60 1根杆旋转90°,第2根杆旋转135°。 0 grm的- -20 00.51.01.52.02.53.03.54.04.55.0 h ect to the0Ce ror的B0dn3tm dycoorsnatnstams 仿真时间s *国 图11两连杆机械臂旋转角度 Fig.11 Rotation angle of dual-arm cS2 Hoo C31 3.3模糊PD控制仿真 通过SimMechanics建立仿真模型,并利用模糊 图10AB杆模型参数 PD进行控制7)。如图12所示。启动仿真,调节模 Fig.10 Model parameters of AB arm 糊PD参数。从仿真曲线可以看到PD控制与模糊 得到二连杆机械臂的旋转角度曲线,根据上节所 PD控制两者之间的差别。图13为启动仿真后得到 述方法调节PD参数,得到理想的响应曲线。图11为 的第1根杆旋转角度的完整图,图14为图13的局部
PID 控制及模糊 PID 控制的仿真。 3.2.1 控制模型 图 9 为二连杆投球机器人的 SimMechanics 仿真 图[15] 。 Ground 为机架模块,barAB、barBC 代表第 1、2 根杆,A、B 分别代表转动副模块,Joint Sensor1 代表 运动副传感器模块,Joint Actuator 为运动驱动模块。 图 9 二连杆机器人仿真框图 Fig. 9 Simulation block of dual⁃arm robot 3.2.2 PID 控制仿真 在系统中首先加入 PID 控制器[16] ,控制器输入 二连杆平面机器人两关节预定角度 θ d 1 和 θ d 2 与实际角 度 θ1 和 θ2 的误差 e,输出为驱动关节转矩 τ 。 仿真模型建立后,要对每个模块都进行参数的设 置。 以 AB 杆为例,见图 10。 双击 barAB,填入参数: 杆的质量、刚体坐标和质心位置。 所有参数设置完成 后,再设置允许每个连杆的旋转角度。 在此,设置第 1 根杆旋转 90°,第 2 根杆旋转 135°。 图 10 AB 杆模型参数 Fig. 10 Model parameters of AB arm 得到二连杆机械臂的旋转角度曲线,根据上节所 述方法调节 PID 参数,得到理想的响应曲线。 图 11 为 经过 PID 调节后二连杆平面投球机器人的旋转角度情 况。 可以看到,经过 PID 调节后,系统可以实现快速启 动,并且缩短了时间,快速地进入新的稳定状态。 图 11 两连杆机械臂旋转角度 Fig. 11 Rotation angle of dual⁃arm 3.3 模糊 PID 控制仿真 通过 SimMechanics 建立仿真模型,并利用模糊 PID 进行控制[17] 。 如图 12 所示。 启动仿真,调节模 糊 PID 参数。 从仿真曲线可以看到 PID 控制与模糊 PID 控制两者之间的差别。 图 13 为启动仿真后得到 的第 1 根杆旋转角度的完整图,图 14 为图 13 的局部 ·404· 智 能 系 统 学 报 第 10 卷

第3期 赵新华,等:投球机器人模糊PD控制 ·405 放大图。图15为第2根杆旋转角度的完整图,图16角度的局部放大图可以看到,模糊PD控制要比PID 为图15的局部放大图。从图14和图16两根杆旋转 控制的定位更加精确。 Inl K 1 Outl du/dt Add M duldt Zero-order Derivativel' hold Fuzzy logic controller 图12第1、2根杆模糊PD模块 Fig.12 Fuzzy PID block of the first and second arm 100 135.15- 80 60 135.10 40H 年 20 135.05 一模糊PID ----PID 2 3 45 仿真时间s 135.00 4.99994.99995 5 5 图13第1根杆旋转角度完整图 仿真时间s Fig.13 The complete graph of the first arm rotation angle 图16第2根杆旋转角度局部放大图 Fig.16 Partial enlarged drawing of the second arm rotation angle 90.20r 模糊PID 4结束语 ---PD 通过对二连杆投球机器人运动学方程和动力学 90.15 方程的推导,得到了二连杆投球机器人的动态数学模 型,此建模过程简单、方便、有效,便于进行动力学分 析和控制问题的研究。把得到的二连杆投球机器人 90.10 5 5 5 的数学模型嵌入到MATLAB仿真中,得到二连杆机 仿真时间s 图14第1根杆旋转角度局部放大图 器人的运动情况,并在仿真过程中加入了PD模块 Fig.14 Partial enlarged drawing of the first arm rotation angle 和模糊PID模块,仿真结果得出模糊PID控制精确 性更高。本设计仅对二连杆投球机器人进行了建模 140 与仿真,下一步将对整体系统进行进一步的研究。 100 参考文献: 60 [1]范永,谭民.机器人控制器的现状及展望[J刀].机器人, 20 一模糊PID 1999(1):75-80. ----PID FAN Yong,TAN Min.Current state and tendencies in the de- -20 0 23 4 velopment of robot controller[J].Robot,1999(1):75-80. 仿真时间s [2]张锐,吴成东.机器人智能控制研究进展[J].沈阳建筑 图15第2根杆旋转角度完整图 工程学院学报:自然科学版,2003,11(1):61-65. Fig.15 The complete graph of the second arm rotation angle ZHANG Rui,WU Chengdong.Some recent progress in robot-
放大图。 图 15 为第 2 根杆旋转角度的完整图,图 16 为图 15 的局部放大图。 从图 14 和图 16 两根杆旋转 角度的局部放大图可以看到,模糊 PID 控制要比 PID 控制的定位更加精确。 图 12 第 1、2 根杆模糊 PID 模块 Fig. 12 Fuzzy PID block of the first and second arm 图 13 第 1 根杆旋转角度完整图 Fig. 13 The complete graph of the first arm rotation angle 图 14 第 1 根杆旋转角度局部放大图 Fig. 14 Partial enlarged drawing of the first arm rotation angle 图 15 第 2 根杆旋转角度完整图 Fig. 15 The complete graph of the second arm rotation angle 图 16 第 2 根杆旋转角度局部放大图 Fig. 16 Partial enlarged drawing of the second arm rotation angle 4 结束语 通过对二连杆投球机器人运动学方程和动力学 方程的推导,得到了二连杆投球机器人的动态数学模 型,此建模过程简单、方便、有效,便于进行动力学分 析和控制问题的研究。 把得到的二连杆投球机器人 的数学模型嵌入到 MATLAB 仿真中,得到二连杆机 器人的运动情况,并在仿真过程中加入了 PID 模块 和模糊 PID 模块,仿真结果得出模糊 PID 控制精确 性更高。 本设计仅对二连杆投球机器人进行了建模 与仿真,下一步将对整体系统进行进一步的研究。 参考文献: [1]范永, 谭民. 机器人控制器的现状及展望[ J]. 机器人, 1999(1): 75⁃80. FAN Yong, TAN Min. Current state and tendencies in the de⁃ velopment of robot controller[J]. Robot, 1999(1): 75⁃80. [2]张锐, 吴成东. 机器人智能控制研究进展[ J]. 沈阳建筑 工程学院学报:自然科学版, 2003, 11(1): 61⁃65. ZHANG Rui, WU Chengdong. Some recent progress in robot⁃ 第 3 期 赵新华,等:投球机器人模糊 PID 控制 ·405·

·406· 智能系统学报 第10卷 ic intelligent control[J].Journal of Shenyang Architectural[ll]陆佑方,冯冠民,齐朝晖.柔性机械臂动力学与控制建 and Civil Engineering Institute,2003,11(1):61-65. 模的若干基本问题[J].机器人,1993,15(2):52-59. [3]蔡自兴,陈海燕,魏世勇.智能控制工程研究的进展[J] LU Youfang,FENG Guanmin,QI Zhaohui.Application of 控制工程,2003,10(1):15-20. artificial neural networks in dynamic identification and posi- CAI Zixing,CHEN Haiyan,WEI Shiyong.Recent advances tion control of robot manipulators[J.Robot,1993,15(2): in research of intelligent control engineering[J].Control En- 52.59. gineering of China.2003,10(1):15-20. [12]吴宏鑫,沈少萍.PD控制应用与理论依据[J].控制工 [4]贾玉赞.浅议智能机器人发展及应用[J].太原科技. 程,2003,37(1):6-10. 2003,5(3):20-26. WU Hongxin,SHEN Shaoping.Basis of theory and applica- JIA Yuzan.Development of intellectual robot and its applica- tions on PID control [J].Control Engineering of China, tion[J].Taiyuan Science and Technology,2003,5(3):20- 2003,37(1):6-10. 26. [13]陆磊.模糊控制在轮式机器人上的应用J].微型电脑应 [5]吴向阳,戴先中,孟正大.分布式机器人控制器体系结构 用,2010,26(12):31-33. 的研究[J].东南大学学报:自然科学版,2003,33(Su LU Lei.Application of fuzzy-PID controller in moble robot pl.):200-204. []Microcomputer Applications,2010,26(12):31-33. WU Xiangyang,DAI Xianzhong,MENG Zhengda.Research[l4]阎绍泽,刘又午,张铁民.柔性机械臂动力特性的实验 on distributed architecture of robot controller[]].Journal of 研究[J].河北工业大学学报,1996,25(11):12-16. Southeast University:Natural Science Edition,2003,33(Su- YAN Shaoze,LIU Youwu,ZHANG Tiemin.Experimental pl.):200-204. study on dynamic performances of flexible manipulators[J]. [6]谭宝成,程智远,牟云霞,等。移动机器人模糊控制系统 Journal of Hebei University of Technology,1996,25(11): 的设计[J].西安工业大学学报,2007,27(4):366-370. 12-16. TAN Baocheng,.CHENG Zhiyuan,.MOU Yunxia,etal.De[l5]孙奎,谢宗武,刘宏.一种新的机器人动力学仿真分析 sign of mobile robot control system based on fuzzy control[J]. 方法[J].机械设计与制造,2008,5(9):163-165. Journal of Xi'an Technological University,2007,27(4): SUN Kui,XIE Zongwu,LIU Hong.The dynamics simula- 366-370. tion analysis of a four DOF manipulator [J].Machinery De- [7]李庆中,顾伟康,叶秀清,等.移动机器人模糊控制方法 sign Manufacture,2008,5(9):163-165. 研究[J刀].仪器仪表学报,2002,23(5):480-484. [16]The Mathworks Inc.SimMechanics user's guide[M].Na- LI Qingzhong,GU Weikang,YE Xiuqing,et al.Study on tick,USA:The Mathworks Inc.,2002:22-27. fuzzy control method for mobile robots[J].Chinese Journal of[l7]苗敬利.模糊控制和传统PID控制的仿真研究[J].微软 Scientific Instrument,2002,23(5):480-484. 计算机信息,2003,4(7):18-24. [8]李余庆,刘继忠,张华.模糊控制在机器人超生避障系统 MIAO Jingli.The simulation study between fuzzy control and 的应用[J].机器人技术,2009,25(52):216-218. PID control[J].Microcomputer Information,2003,4(7): LI Yuqing,LIU Jizhong,ZHANG Hua.Application of fuzzy 18-24. control in ultrasound obstacle avoidance system for robot[]]. 作者简介: Robot Technology,2009,25(52):216-218. 赵新华,女,1980年生,讲师,主要 [9]樊晓平,徐建闽.柔性机器人的动力学建模及其仿真[J] 研究方向为超空泡航行体、AUV的动 控制理论与应用,1997,5(6):60-69. 力学及智能控制方法。发表学术论文 FAN Xiaoping,XU Jianmin.Dynamic modeling and simula- 10余篇。 tion of flexible robotic manipulators[].Control Theory and Applications,1997,5(6):60-69. [l0]田永利,邹慧君,郭为忠,等.基于Matlab-Sim Mechanics 的机电产品组成建模与仿真技术研究[J].机械设计与 王璞,男,1994年生,主要研究方向 为机器人智能控制。 研究,2002,19(12):10-12. TIAN Yongli,ZOU Huijun,GUO Weizhong,et al.Study on modeling and simulation methods for constitution objects of mechatronic products based on Matlab-Sim Mechanics[J]. Machine Design and Research,2002,19(12):10-12
ic intelligent control [ J]. Journal of Shenyang Architectural and Civil Engineering Institute, 2003, 11(1): 61⁃65. [3]蔡自兴, 陈海燕, 魏世勇. 智能控制工程研究的进展[J]. 控制工程, 2003, 10(1): 15⁃20. CAI Zixing, CHEN Haiyan, WEI Shiyong. Recent advances in research of intelligent control engineering[ J]. Control En⁃ gineering of China, 2003, 10(1): 15⁃20. [4]贾玉赞. 浅议智能机器人发展及应用[ J]. 太原科技, 2003, 5(3): 20⁃26. JIA Yuzan. Development of intellectual robot and its applica⁃ tion[J]. Taiyuan Science and Technology, 2003, 5(3): 20⁃ 26. [5]吴向阳, 戴先中, 孟正大. 分布式机器人控制器体系结构 的研究[J]. 东南大学学报:自然科学版, 2003, 33( Su⁃ pl.): 200⁃204. WU Xiangyang, DAI Xianzhong, MENG Zhengda. Research on distributed architecture of robot controller[ J]. Journal of Southeast University: Natural Science Edition, 2003, 33(Su⁃ pl.): 200⁃204. [6]谭宝成, 程智远, 牟云霞, 等. 移动机器人模糊控制系统 的设计[J]. 西安工业大学学报, 2007, 27(4): 366⁃370. TAN Baocheng, CHENG Zhiyuan, MOU Yunxia, et al. De⁃ sign of mobile robot control system based on fuzzy control[J]. Journal of Xi’ an Technological University, 2007, 27 ( 4): 366⁃370. [7]李庆中, 顾伟康, 叶秀清, 等. 移动机器人模糊控制方法 研究[J]. 仪器仪表学报, 2002, 23(5): 480⁃484. LI Qingzhong, GU Weikang, YE Xiuqing, et al. Study on fuzzy control method for mobile robots[J]. Chinese Journal of Scientific Instrument, 2002, 23(5): 480⁃484. [8]李余庆, 刘继忠, 张华. 模糊控制在机器人超生避障系统 的应用[J]. 机器人技术, 2009, 25(52): 216⁃218. LI Yuqing, LIU Jizhong, ZHANG Hua. Application of fuzzy control in ultrasound obstacle avoidance system for robot[ J]. Robot Technology, 2009, 25(52): 216⁃218. [9]樊晓平, 徐建闽. 柔性机器人的动力学建模及其仿真[ J]. 控制理论与应用, 1997, 5(6): 60⁃69. FAN Xiaoping, XU Jianmin. Dynamic modeling and simula⁃ tion of flexible robotic manipulators[ J]. Control Theory and Applications, 1997, 5(6): 60⁃69. [10]田永利, 邹慧君, 郭为忠, 等. 基于 Matlab⁃Sim Mechanics 的机电产品组成建模与仿真技术研究[ J]. 机械设计与 研究, 2002, 19(12): 10⁃12. TIAN Yongli, ZOU Huijun, GUO Weizhong, et al. Study on modeling and simulation methods for constitution objects of mechatronic products based on Matlab⁃Sim Mechanics [ J]. Machine Design and Research, 2002, 19(12): 10⁃12. [11]陆佑方, 冯冠民, 齐朝晖. 柔性机械臂动力学与控制建 模的若干基本问题[J]. 机器人, 1993, 15(2): 52⁃59. LU Youfang, FENG Guanmin, QI Zhaohui. Application of artificial neural networks in dynamic identification and posi⁃ tion control of robot manipulators[J]. Robot, 1993, 15(2): 52⁃59. [12]吴宏鑫, 沈少萍. PID 控制应用与理论依据[ J]. 控制工 程, 2003, 37(1): 6⁃10. WU Hongxin, SHEN Shaoping. Basis of theory and applica⁃ tions on PID control [ J ]. Control Engineering of China, 2003, 37(1): 6⁃10. [13]陆磊. 模糊控制在轮式机器人上的应用[J]. 微型电脑应 用, 2010, 26(12): 31⁃33. LU Lei. Application of fuzzy⁃PID controller in moble robot [J]. Microcomputer Applications, 2010, 26(12): 31⁃33. [14]阎绍泽, 刘又午, 张铁民. 柔性机械臂动力特性的实验 研究[J]. 河北工业大学学报, 1996, 25(11): 12⁃16. YAN Shaoze, LIU Youwu, ZHANG Tiemin. Experimental study on dynamic performances of flexible manipulators[ J]. Journal of Hebei University of Technology, 1996, 25(11): 12⁃16. [15]孙奎, 谢宗武, 刘宏. 一种新的机器人动力学仿真分析 方法[J]. 机械设计与制造, 2008, 5(9): 163⁃165. SUN Kui, XIE Zongwu, LIU Hong. The dynamics simula⁃ tion analysis of a four DOF manipulator [J]. Machinery De⁃ sign & Manufacture, 2008, 5(9): 163⁃165. [16] The Mathworks Inc. SimMechanics user's guide[M]. Na⁃ tick, USA: The Mathworks Inc., 2002: 22⁃27. [17]苗敬利. 模糊控制和传统 PID 控制的仿真研究[J]. 微软 计算机信息, 2003, 4(7): 18⁃24. MIAO Jingli. The simulation study between fuzzy control and PID control[J]. Microcomputer Information, 2003, 4( 7): 18⁃24. 作者简介: 赵新华,女,1980 年生,讲师,主要 研究方向为超空泡航行体、AUV 的动 力学及智能控制方法。 发表学术论文 10 余篇。 王璞,男,1994 年生,主要研究方向 为机器人智能控制。 ·406· 智 能 系 统 学 报 第 10 卷