
第10卷第3期 智能系统学报 Vol.10 No.3 2015年6月 CAAI Transactions on Intelligent Systems Jun.2015 D0:10.3969/j.issn.1673-4785.201405008 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20150529.1021.001.html 四旋翼飞行器自适应反演姿态控制 马正华,张倩倩,陈岚萍 (常州大学信息科学与工程学院,江苏常州213164) 摘要:为了解决四旋冀飞行器控制系统的姿态稳定控制问题,首先根据牛顿第二定律和欧拉方程建立了四旋翼飞 行器运动学模型,并针对姿态控制问题对模型进行简化,然后把姿态控制系统分成3个二阶子系统,运用反演法对 各个子系统分别设计,进一步运用自适应控制律引入积分项,补偿由模型简化引起的模型误差,从而提高系统对外 部扰动和系统模型不确定性的鲁棒性。最后通过Mtlb仿真验证出,改进的自适应积分反演控制器在四旋翼的姿 态控制中对外部干扰信号有较强抑制作用,可以保证在模型参数不确定的情况下的全局稳定性。 关键词:四旋翼飞行器:运动学模型:自适应反演控制:姿态控制;反演法:自适应控制 中图分类号:TP391.9文献标志码:A文章编号:1673-4785(2015)03-0454-06 中文引用格式:马正华,张倩倩,陈岚萍.四旋翼飞行器自适应反演姿态控制[J].智能系统学报,2015,10(3):454-459. 英文引用格式:MA Zhenghua,ZHANG Qianqian,CHEN Lanping.Attitude control of quadrotor aircraft via adaptive back-step ping control[J].CAAI Transactions on Intelligent Systems,2015,10(3):454-459. Attitude control of quadrotor aircraft via adaptive back-stepping control MA Zhenghua,ZHANG Qiangian,CHEN Lanping College of Information Science and Engineering,Changzhou University,Changzhou 213164,China) Abstract:In order to solve the stabilized attitude control problem of quadrotor aircraft,a kinematics model is estab- lished according to Newton's second law and Euler equation.Next,the model is simplified to solve the attitude con- trol problem.After that,the attitude control system is divided into 3 second-order subsystems and each subsystem is designed by the back-stepping control method.Next,an integral term is introduced by applying the adaptive control law to compensate the errors caused by simplified model,thereby improving robustness of the system against exter- nal disturbance and uncertainty of the system model.The simulation results using Matlab show that the stabilized at- titude control of quadrotor aircraft has a strong inhibitory effect using the improved adaptive integral back-stepping controller and it guarantees global stability in the case of uncertain model parameters. Keywords:quadrotor aircraft;kinematics modeling;adaptive back-stepping control;attitude control;back-step- ping;adaptive control 近年来,对小型无人驾驶飞行器(micro air vehi- 器更具有吸引力)。MAV当前主要包括固定翼、扑 cle,MAV)和微型无人驾驶飞行器的设计和研究有了 翼和微型旋翼3种形式。其中四旋翼飞行器由4个 飞速的发展,特别随着微机电系统(micro--electro-me- 螺旋桨对称分布,静态盘旋的稳定性更好,更容易实 chanical system,MEMS)的发展,小型无人驾驶飞行 现机型的微小型化。由于其起降和自由悬停的特点, 特别适合在近地面环境中执行军事、民事等任务(如 收稿日期:2014-05-13.网络出版日期:2015-05-29. 基金项目:国家白然科学基金资助项目(61201096):常州市科技计划 航拍摄影、环境监测和灾情巡查等)。然而四旋翼飞 项目(CJ20110023,CM20123006). 通信作者:张倩倩.E-mail:zqg.08312102@163,com. 行器系统作为一个复杂的非线性系统,它的输入变量
第 10 卷第 3 期 智 能 系 统 学 报 Vol.10 №.3 2015 年 6 月 CAAI Transactions on Intelligent Systems Jun. 2015 DOI:10.3969 / j.issn.1673⁃4785.201405008 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150529.1021.001.html 四旋翼飞行器自适应反演姿态控制 马正华,张倩倩,陈岚萍 (常州大学 信息科学与工程学院,江苏 常州 213164) 摘 要:为了解决四旋翼飞行器控制系统的姿态稳定控制问题,首先根据牛顿第二定律和欧拉方程建立了四旋翼飞 行器运动学模型,并针对姿态控制问题对模型进行简化,然后把姿态控制系统分成 3 个二阶子系统,运用反演法对 各个子系统分别设计,进一步运用自适应控制律引入积分项,补偿由模型简化引起的模型误差,从而提高系统对外 部扰动和系统模型不确定性的鲁棒性。 最后通过 Matlab 仿真验证出,改进的自适应积分反演控制器在四旋翼的姿 态控制中对外部干扰信号有较强抑制作用,可以保证在模型参数不确定的情况下的全局稳定性。 关键词:四旋翼飞行器;运动学模型;自适应反演控制;姿态控制;反演法;自适应控制 中图分类号:TP391.9 文献标志码:A 文章编号:1673⁃4785(2015)03⁃0454⁃06 中文引用格式:马正华,张倩倩,陈岚萍. 四旋翼飞行器自适应反演姿态控制[J]. 智能系统学报, 2015, 10(3): 454⁃459. 英文引用格式:MA Zhenghua, ZHANG Qianqian, CHEN Lanping. Attitude control of quadrotor aircraft via adaptive back⁃step⁃ ping control[J]. CAAI Transactions on Intelligent Systems, 2015, 10(3): 454⁃459. Attitude control of quadrotor aircraft via adaptive back⁃stepping control MA Zhenghua, ZHANG Qianqian, CHEN Lanping (College of Information Science and Engineering, Changzhou University, Changzhou 213164, China) Abstract:In order to solve the stabilized attitude control problem of quadrotor aircraft, a kinematics model is estab⁃ lished according to Newton's second law and Euler equation. Next, the model is simplified to solve the attitude con⁃ trol problem. After that, the attitude control system is divided into 3 second⁃order subsystems and each subsystem is designed by the back⁃stepping control method. Next, an integral term is introduced by applying the adaptive control law to compensate the errors caused by simplified model, thereby improving robustness of the system against exter⁃ nal disturbance and uncertainty of the system model. The simulation results using Matlab show that the stabilized at⁃ titude control of quadrotor aircraft has a strong inhibitory effect using the improved adaptive integral back⁃stepping controller and it guarantees global stability in the case of uncertain model parameters. Keywords:quadrotor aircraft; kinematics modeling; adaptive back⁃stepping control; attitude control; back⁃step⁃ ping; adaptive control 收稿日期:2014⁃05⁃13. 网络出版日期:2015⁃05⁃29. 基金项目:国家自然科学基金资助项目(61201096);常州市科技计划 项目(CJ20110023, CM20123006). 通信作者:张倩倩. E⁃mail: zqq.08312102@ 163,com. 近年来,对小型无人驾驶飞行器(micro air vehi⁃ cle, MAV)和微型无人驾驶飞行器的设计和研究有了 飞速的发展,特别随着微机电系统(micro⁃electro⁃me⁃ chanical system, MEMS)的发展,小型无人驾驶飞行 器更具有吸引力[1] 。 MAV 当前主要包括固定翼、扑 翼和微型旋翼 3 种形式。 其中四旋翼飞行器由 4 个 螺旋桨对称分布,静态盘旋的稳定性更好,更容易实 现机型的微小型化。 由于其起降和自由悬停的特点, 特别适合在近地面环境中执行军事、民事等任务(如 航拍摄影、环境监测和灾情巡查等)。 然而四旋翼飞 行器系统作为一个复杂的非线性系统,它的输入变量

第3期 马正华,等:四旋翼飞行器自适应反演姿态控制 ·455. 和输出变量之间具有强耦合性。系统本身的不确定 {p,0,亚y。 性及外部的干扰,会给系统的控制带来很大的问题。 当四旋翼无人机在无风及慢速飞行的情况下, 因此需要设计一种合理的控制策略。 先忽略阻力系数对四旋翼飞行器的影响,根据牛顿 在四旋翼飞行器的控制研究中,反演设计方法 运动定理和欧拉方程,四旋翼姿态变化所受力矩和 得到了越来越多的国内外研究机构和高校的重视。 表述为向量形式M=d dt ,具体展开为 近十几年来,反演设计方法作为非线性反馈控制系 统的一种递归设计方法,已经成为不确定非线性系 J2=-2×J2+M+4 (1) 统控制的有效方法之一。传统的反演设计方法基本 9r(.-I,)1 原理是将复杂的非线性系统分解为简单的子系统, 2×J2 9 1,9 pr(I -1.) (2) 然后从系统输出开始为每个子系统设计李雅普诺夫 函数和虚拟控制量]。此反演设计过程清晰、系统 pq(I,-1) 化、结构化、易于实现,但也有潜在的问题,推导出的 lb(w1-02) 表达式复杂,抗干扰性不强)。 M,= lb(o号-心) (3) 本文结合四旋翼飞行器控制系统自身的特点对 d(子+o号-o号-2) 传统的反演控制系统进行改进,运用自适应控制律 式中:2=(P,9,)T为欧拉角在三坐标轴角速度分 引入积分项,补偿由模型简化引起的模型误差。由 量,M为四旋翼飞行器所受转动力矩,J=diag(I, 于四旋翼飞行器姿态控制是整个控制系统的基础, 1,,),旋翼提供的升力与升力系数b及转速的平 机体位置的变化都是由姿态变化引起的,本文重点 方成正比,!为旋翼力臂长,4∈R"表示外部扰动信 将所设计的控制器运用到姿态稳定控制当中。 号,包括建模误差、参数变化以及其他不确定因素。 1动力学建模 根据欧拉角与机体坐标系角速度间关系[5): (pC。+qSgS。+rC.S)/Ce 本文目的是设计四旋翼姿态控制器,因此只建 qC。-S, 4 立四旋翼姿态运动模型。由图1可以看出四旋翼飞 (gS。+rC.)/Ca 行器的4只螺旋桨是对称分布的,其中1号和Ⅲ号 螺旋桨在电机驱动下逆时针转动,Ⅱ号和IV号螺旋 定义控制量U=[U,U2U3]如下: 桨顺时针转动,这样可将每个螺旋桨所产生的反扭 U1=F4-F2=b(o子-w) 矩抵消掉4。 U2=F3-F1=b(o-u) 0=F1+F3-F2-F4=d(w+o--0) 电机川 (5) 由式(1)~(5)可得机体的简化模型为 电机 K X. =(Ψ1-I)+lU,)/八 电机 0=(o亚(L,-1)+lU02)/L, (6) Ψ=(o(L.-1,)+U3)/1 电机IV 2控制器设计 2.1反演控制器设计 反演控制器的设计过程是通过逐步构造中间量 图1四旋翼飞行器动力学示意 :=x:一x-1完成的,其中x-1是第i-1步的虚拟控 Fig.1 Schematic diagram of quadrotor aircraft dynamics 制量,最后的虚拟控制量x:是施加于系统实际控制 量u的一部分6。 首先定义基本的坐标系和相应的表示符号,如 本文姿态控制器采用反演设计方法,为进行系 图1。机体坐标系(X。,Y。,Z)是原点在四旋翼重 统设计,对系统进行必要的假设。 心的右手直角正交系统,用于确定飞行器在空中的 假设1输入指令x及其n阶导数是存在且有 姿势。四旋翼的飞行姿态由3个欧拉角描述Φ= 界的
和输出变量之间具有强耦合性。 系统本身的不确定 性及外部的干扰,会给系统的控制带来很大的问题。 因此需要设计一种合理的控制策略。 在四旋翼飞行器的控制研究中,反演设计方法 得到了越来越多的国内外研究机构和高校的重视。 近十几年来,反演设计方法作为非线性反馈控制系 统的一种递归设计方法,已经成为不确定非线性系 统控制的有效方法之一。 传统的反演设计方法基本 原理是将复杂的非线性系统分解为简单的子系统, 然后从系统输出开始为每个子系统设计李雅普诺夫 函数和虚拟控制量[2] 。 此反演设计过程清晰、系统 化、结构化、易于实现,但也有潜在的问题,推导出的 表达式复杂,抗干扰性不强[3] 。 本文结合四旋翼飞行器控制系统自身的特点对 传统的反演控制系统进行改进,运用自适应控制律 引入积分项,补偿由模型简化引起的模型误差。 由 于四旋翼飞行器姿态控制是整个控制系统的基础, 机体位置的变化都是由姿态变化引起的,本文重点 将所设计的控制器运用到姿态稳定控制当中。 1 动力学建模 本文目的是设计四旋翼姿态控制器,因此只建 立四旋翼姿态运动模型。 由图 1 可以看出四旋翼飞 行器的 4 只螺旋桨是对称分布的,其中 I 号和 III 号 螺旋桨在电机驱动下逆时针转动,II 号和 IV 号螺旋 桨顺时针转动,这样可将每个螺旋桨所产生的反扭 矩抵消掉[4] 。 图 1 四旋翼飞行器动力学示意 Fig. 1 Schematic diagram of quadrotor aircraft dynamics 首先定义基本的坐标系和相应的表示符号,如 图 1。 机体坐标系 Xb,Yb,Zb ( ) 是原点在四旋翼重 心的右手直角正交系统,用于确定飞行器在空中的 姿势。 四旋翼的飞行姿态由 3 个欧拉角描述 Φ = {φ,θ,Ψ} 。 当四旋翼无人机在无风及慢速飞行的情况下, 先忽略阻力系数对四旋翼飞行器的影响,根据牛顿 运动定理和欧拉方程,四旋翼姿态变化所受力矩和 表述为向量形式 M = dH dt ,具体展开为 JΩ · = - Ω × JΩ + Mf + Δ (1) Ω × JΩ = p q r é ë ê ê ê ù û ú ú ú × Ix p Iy q Iz r é ë ê ê ê ê ù û ú ú ú ú = qr Iz - Iy ( ) pr Ix - Iz ( ) pq Iy - Ix ( ) é ë ê ê ê ê ù û ú ú ú ú (2) Mf = lb w 2 4 - w 2 2 ( ) lb w 2 3 - w 2 1 ( ) d w 2 1 + w 2 3 - w 2 2 - w 2 4 ( ) é ë ê ê ê ê ù û ú ú ú ú (3) 式中: Ω = (p,q,r) T 为欧拉角在三坐标轴角速度分 量, Mf 为四旋翼飞行器所受转动力矩, J = diag(Ix, Iy,Iz) ,旋翼提供的升力与升力系数 b 及转速的平 方成正比,l 为旋翼力臂长, Δ∈ R n 表示外部扰动信 号,包括建模误差、参数变化以及其他不确定因素。 根据欧拉角与机体坐标系角速度间关系[5] : φ · θ · Ψ · é ë ê ê ê ê ù û ú ú ú ú = pCθ + qSθSφ + rCφ Sθ ( ) / Cθ qCφ - rSφ qSφ + rCφ ( ) / Cθ é ë ê ê ê ê ù û ú ú ú ú (4) 定义控制量 U = [U1 U2 U3 ] 如下: U1 = F4 - F2 = b w 2 4 - w 2 2 ( ) U2 = F3 - F1 = b w 2 3 - w 2 1 ( ) U3 = F1 + F3 - F2 - F4 = d w 2 1 + w 2 3 - w 2 2 - w 2 4 ( ) (5) 由式(1) ~ (5)可得机体的简化模型为 φ ¨ = θ · Ψ · Iy - Iz ( ) + lU1 ( ) / Ix θ ¨ = φ · Ψ · Iz - Ix ( ) + lU2 ( ) / Iy Ψ ¨ = φ · θ · Ix - Iy ( ) + U3 ( ) / Iz (6) 2 控制器设计 2.1 反演控制器设计 反演控制器的设计过程是通过逐步构造中间量 zi = xi - x v i-1 完成的,其中 x v i-1 是第 i - 1 步的虚拟控 制量,最后的虚拟控制量 x v n 是施加于系统实际控制 量 u 的一部分[6] 。 本文姿态控制器采用反演设计方法,为进行系 统设计,对系统进行必要的假设。 假设 1 输入指令 xd 及其 n 阶导数是存在且有 界的[7] 。 第 3 期 马正华,等:四旋翼飞行器自适应反演姿态控制 ·455·

·456. 智能系统学报 第10卷 假设2外部扰动信号4是有界的,且上界4, 量U2,U3。这2个通道控制器的设计过程与此类似,设 是未知的,4|0 (11) 则 模型参数不确定情况下的鲁棒性,引入积分项,= (a)=-a (12) e,()d 22=2- (13) 角速度跟踪误差为 选取二阶李雅普诺夫函数[1-): e2=v-Ud=v+Ce1+入,51-y, (17) 1 V%)=2份+) (14) 由式(16)和(17)可得 e1=e2-ce1-入 (18) 对其求导,得 选择李雅普诺夫函数: V(a1,21)=22(a1x4x6+bU2)-1斤 -z2[元h-a1(a2+a1a1)]z1a2(15〉 (19) 令(211)=-a1-a,则结合式(7) V=e1·e1=ee2-cei-15i (20) (15)可得 对角速度跟踪误差进行求导,得 0=6-ax-a,+)-] e2=i+c(u-少)+入51-y, (21) 引入积分项后,扩展的李雅普诺夫函数为 由李雅普诺夫函数可知,通过上述设计步骤得到 的闭环系统渐近稳定。将俯仰角变量x;=日,x4= ++ 21 代人名2=[氏元]”和偏航角变量x=少,x。== ve,e)=入5ae av av av 乎代入水=[氏】「,按上述相似步骤便可得控制 +ei de +e2 de2
假设 2 外部扰动信号 Δ 是有界的,且上界 Δv 是未知的, Δ < Δv 。 为了方便起见,参考文献[8-9]将动力学模型公 式转换成一阶空间表达式 X · = f(X,U) ,其中状态量 X = x1 x2 … x [ 6 ] = φ φ · θ θ · Ψ Ψ · [ ] , 控制量 U = [U1 U2 U3 ] 。 根据四旋翼数学模型 可知,系统为欠驱动系统。 它只有 4 个控制输入,姿 态控制部分中横滚角、俯仰角和偏航角 3 个自由度为 受控变量。 为了更简单有效控制,将姿态控制回路划 分为 3 个二阶控制器,分别是横滚角、俯仰角、偏航角 控制 3 个通道。 针对四旋翼姿态数学模型,下面以一个横滚角 φ 控制器为例,忽略外部扰动信号 Δ ,设计反演控 制器为 X · 1 = x2 a1 x4 x6 + b1U1 { (7) 式中: X · 1 = x · 1 x · 2 [ ] T , x1 = φ , x2 = x · 1 = φ · , b1 = l / Ix , a1 = Iy - Iz ( ) / Ix 。 首先设置目标值与实际值之差: z1 = x1d - x1 (8) 根据李雅普诺夫相关理论,选取正定且一阶导 数半负定的李雅普诺夫函数 V(z1 ) [10] : V(z1 ) = 1 2 z 2 1 (9) V · z1 ( ) = z1 z · 1 = z1 x · 1d - x · 1 ( ) (10) 选取一个虚拟量 x v 1 ,使 z1 稳定: x v 1 = x · 1d + α1 z1 ,α1 > 0 (11) 则 V · z1 ( ) = - α1 z 2 1 (12) z2 = x2 - x v 1 (13) 选取二阶李雅普诺夫函数[11-13] : V z1 ,z2 ( ) = 1 2 z 2 1 + z 2 2 ( ) (14) 对其求导,得 V · z1 ,z1 ( ) = z2 a1 x4 x6 + b1U2 ( ) - α1 z 2 1 - - z2 x ¨ d1 - α1 z2 + α1 z1 [ ( ) ] z1 z2 (15) 令 V · z1 ,z1 ( ) = - α1 z 2 1 - α2 z 2 2 ,则结合式( 7) ~ (15)可得 U1 = 1 b1 z1 - a1 x4 x6 - α1 z2 + α1 z1 ( ) - α2 z2 [ ] 由李雅普诺夫函数可知,通过上述设计步骤得到 的闭环系统渐近稳定。 将俯仰角变量 x3 = θ , x4 = x · 3 代入 X · 2 = x · 3 x · 4 [ ] T 和偏航角变量 x5 = Ψ,x6 = x · 5 = Ψ · 代入 X · 3 = x · 5 x · 6 [ ] T ,按上述相似步骤便可得控制 量 U2,U3。 这 2 个通道控制器的设计过程与此类似,设 计过程就不再赘述,只给出了最后得出的反演控制律: U2 = 1 b2 z3 - a3 x2 x6 - α3 z4 + α3 z3 ( ) - α4 z4 [ ] U3 = 1 b3 z5 - a5 x2 x4 - α5 z6 + α5 z5 ( ) - α6 z6 [ ] 式中: z3 = θd - θ = x3d - x3 , z4 = x4 - x · 3d - α3 z3 z5 = Ψd - Ψ = x5d - x5 , z6 = x6 - x · 5d - α5 z5 2.2 自适应律设计 针对通常反演控制器不具备自适应能力,且由 于外部扰动和系统模型的不确定性,控制效果有时 可能不理想,提出将自适应控制的相关理论与反演 控制相结合,设计出一种自适应反演控制器,引入积 分项,将此控制器应用在对四旋翼飞行器的控制上。 同样以横滚角 φ 为例,将姿态角子系统的动力 学方程(7)写为二阶一般形式: y ¨ = bU + Ξ + Γ 式中: y 表示横滚角子系统的状态变量; b 是常数, 表示转动惯量; U 是控制输入; Ξ 表示机体陀螺效 应; Γ 表示模型误差变量估计器。 定义横滚角跟踪误差,给出一个横滚角参考信 号 yr ,以角速度 vref 为虚拟控制输入[14-15] : e1 = y - yr, e · 1 = v - y · r vref = - c1 e1 + y · r - λ1 ξ1 (16) 式中: c1 、 λ1 均大于零。 同时,为增强系统在干扰和 模型参数不确定情况下的鲁棒性,引入积分项 ξ1 = ∫ t 0 e1(τ)dτ 。 角速度跟踪误差为 e2 = v - vref = v + c1 e1 + λ1 ξ1 - y · r (17) 由式(16)和(17)可得 e · 1 = e2 - c1 e1 - λ1 ξ1 (18) 选择李雅普诺夫函数: V1 = 1 2 e 2 1 (19) V · 1 = e1·e · 1 = e1 e2 - c1 e 2 1 - λ1 ξ1 (20) 对角速度跟踪误差进行求导,得 e · 2 = v · + c1 v - y · r ( ) + λ1 ξ1 - y ¨ r (21) 引入积分项后,扩展的李雅普诺夫函数为 V e1 ,e2 ( ) = λ1 2 ξ 2 1 + 1 2 e 2 1 + 1 2 e 2 2 V · e1 ,e2 ( ) = λ1 ξ1 ∂V ∂ξ1 + e1 ∂V ∂e1 + e2 ∂V ∂e2 ·456· 智 能 系 统 学 报 第 10 卷

第3期 马正华,等:四旋翼飞行器自适应反演姿态控制 ·457. 式中:V(e1,e2)满足(e1,e2)=-ce-c2e≤0,结 表1仿真模型参数 合式(16)~(21),得到控制输入: Table 1 Parameters of simulation model 参数 值 参数 值 u=6[1-c+,)e+(%+e)e]+ m/kg 0.4 &1 5 名-6A+元-且-刀 1/mm 0.3 2 R/m 0.15 由于不知道T的真实值,利用估计值T代替, 1./(kg·m2) 0.114 4 设计自适应控制律如下: I,/(kg·m2) 0.114 Os “=0-后+A6+6+lt 1/(kg·m2) 0.156 &s 2-6A6+.-三-刀 3.1稳定控制实验 首先检验算法对飞行器的姿态稳定控制效果, 再次使用李雅普诺夫函数,扩展参数估计误差, 不考虑四旋翼模型中的未建模项和干扰项,设定参 构造系统控制的自适应律: 数得到自适应反演控制器3个姿态角响应仿真结果 ++-n 入 如图2所示,观察可知四旋翼三姿态角能够在2s 内快速稳定地调整到平衡状态。 e)-6i+n(+的 15 20 25 30 U/s (22) (a)o 式中:入,、Y,是正常数限制估计收敛速度。选择估 计参数T自适应律。 10 15 2025 30 dr t/s =-Ye2,T=-y52 (23) (b)0 式中:5:=。ea(r)dr。 10 15202530 t/s 通过式(22)和(23),最终得到横滚角P的自适 (c)平 应控制输人表示为 图23通道姿态角响应控制效果 1 Fig.2 Control effect of the attitude subsystem u=6[(1-c+A,)e+(o,+6)e]+ 图3为四旋翼自适应反演控制器4个螺旋桨的 名-GA++元-到 (24) 旋转速度。由图3可知当四旋翼稳定在悬停状态 时,电机的转速大约为210rad/s,该值小于电机的 由以上分析可知,式(6)描述的四旋翼飞行器 最大转速。 姿态控制数学模型在自适应反演控制律式(24)的 300 -300 作用下,能够跟踪误差达到全局渐进稳定状态6。 ·200 ·200 同理,俯仰角日和偏航角乎的自适应律设计也有相 10 似的过程,在此不再赘述。 翠 0 102030 翠 0 102030 3实验验证 tis tis (a)电机山 (b)电机II 300m →300r 为验证所设计方法的有效性,在MATLAB中搭 ·200: ·200 建了四旋翼飞行器的仿真模型并进行2组实验。令 100 里10 四旋翼的初始状态为x,=[111],控制的目的 是使四旋翼最终稳定在原点,即x=[000], 群 0 1020 30 0 1020.30 元4=0。设置采样时间t=2ms,Y1=1,入1=1,参数 (c)电机III (d)电机IV 估计的初值T。=2。仿真模型参数及控制器参数值 图34个螺旋桨的旋转速度 见表1。 Fig.3 Rotate speed of rotors
式中: V e1 ,e2 ( ) 满足 V · e1 ,e2 ( ) = - c1 e 2 1 - c2 e 2 2 £0,结 合式(16) ~ (21),得到控制输入: u = 1 b 1 - c 2 1 + λ1 ( ) e1 + c1 + c2 ( ) e2 [ ] + 1 b - c1λ1 ξ1 + y ¨ r [ - Ξ - Γ] 由于不知道 Γ 的真实值,利用估计值 Γ ^ 代替, 设计自适应控制律如下: u = 1 b 1 - c 2 1 + λ1 ( ) e1 + c1 + c2 ( ) e2 [ ] + 1 b - c1λ1 ξ1 + y ¨ r - Ξ - Γ ^ [ ] 再次使用李雅普诺夫函数,扩展参数估计误差, 构造系统控制的自适应律: V e1 ,e2 ( ) = λ1 2 ξ 2 1 + 1 2 e 2 1 + 1 2 e 2 2 + 1 2γ1 Γ ^ ( - Γ) 2 V · e1 ,e2 ( ) = - c1 e 2 1 - c2 e 2 2 + Γ ^ ( - Γ) e2 + 1 γ1 dΓ ^ dt æ è ç ö ø ÷ (22) 式中: λ1 、 γ1 是正常数限制估计收敛速度。 选择估 计参数 Γ ^ 自适应律。 dΓ ^ dt = - γ1 e2 , Γ ^ = - γ1 ξ2 (23) 式中: ξ2 = ∫ t 0 e2(τ)dτ 。 通过式(22)和(23),最终得到横滚角 φ 的自适 应控制输入表示为 u = 1 b 1 - c 2 1 + λ1 ( ) e1 + c1 + c2 ( ) e2 [ ] + 1 b - c1λ1 ξ1 + γ1 ξ2 + y ¨ r [ - Ξ] (24) 由以上分析可知,式(6)描述的四旋翼飞行器 姿态控制数学模型在自适应反演控制律式(24) 的 作用下,能够跟踪误差达到全局渐进稳定状态[16] 。 同理,俯仰角 θ 和偏航角 Ψ 的自适应律设计也有相 似的过程,在此不再赘述。 3 实验验证 为验证所设计方法的有效性,在 MATLAB 中搭 建了四旋翼飞行器的仿真模型并进行 2 组实验。 令 四旋翼的初始状态为 x1 = [1 1 1] T , 控制的目的 是使四旋翼最终稳定在原点,即 xd = [0 0 0] T , x · d = 0。 设置采样时间 t = 2 ms, γ1 = 1, λ1 = 1,参数 估计的初值 Γ ^ 0 = 2。 仿真模型参数及控制器参数值 见表 1。 表 1 仿真模型参数 Table 1 Parameters of simulation model 参数 值 参数 值 m/ kg 0.4 α1 5 l / mm 0.3 α2 8 R/ m 0.15 α3 5 Ix / (kg·m 2 ) 0.114 α4 8 Iy / (kg·m 2 ) 0.114 α5 2 Iz / (kg·m 2 ) 0.156 α6 1 3.1 稳定控制实验 首先检验算法对飞行器的姿态稳定控制效果, 不考虑四旋翼模型中的未建模项和干扰项,设定参 数得到自适应反演控制器 3 个姿态角响应仿真结果 如图 2 所示,观察可知四旋翼三姿态角能够在 2 s 内快速稳定地调整到平衡状态。 图 2 3 通道姿态角响应控制效果 Fig. 2 Control effect of the attitude subsystem 图 3 为四旋翼自适应反演控制器 4 个螺旋桨的 旋转速度。 由图 3 可知当四旋翼稳定在悬停状态 时,电机的转速大约为 210 rad / s,该值小于电机的 最大转速。 图 3 4 个螺旋桨的旋转速度 Fig. 3 Rotate speed of rotors 第 3 期 马正华,等:四旋翼飞行器自适应反演姿态控制 ·457·
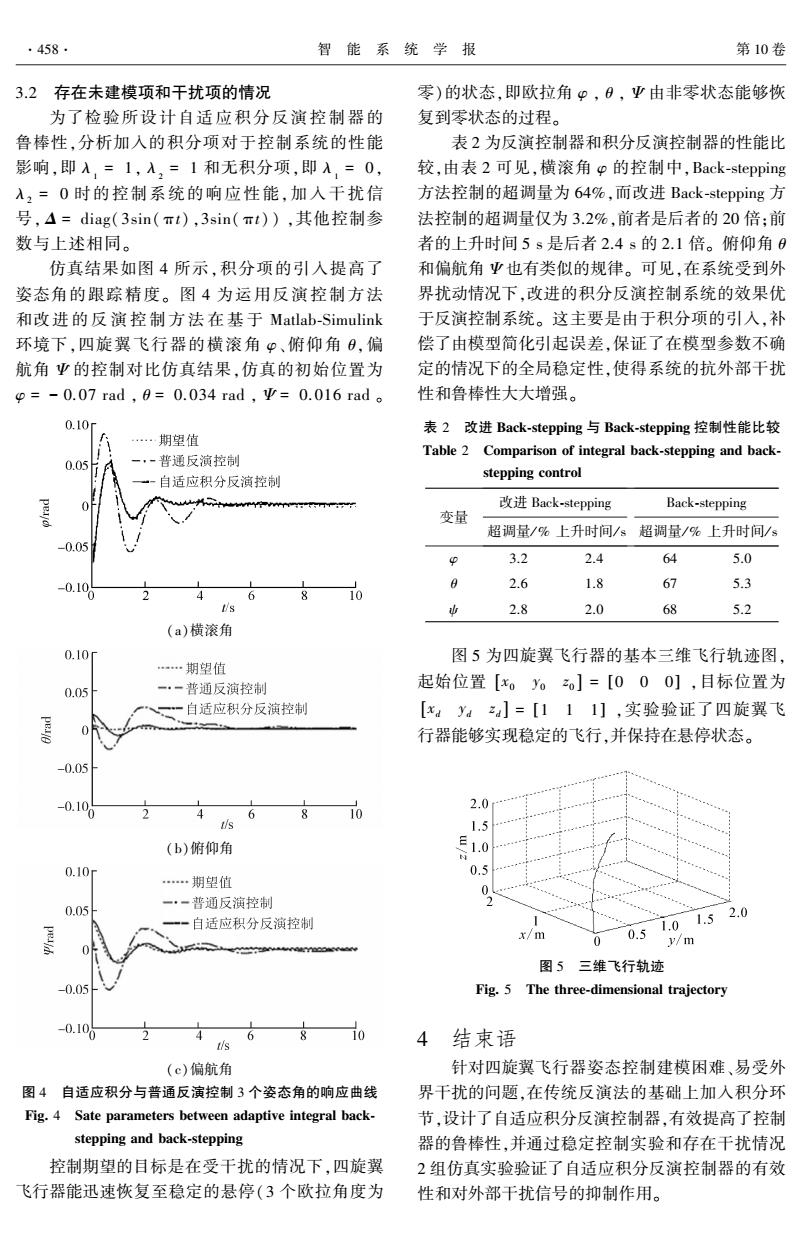
.458. 智能系统学报 第10卷 3.2存在未建模项和干扰项的情况 零)的状态,即欧拉角φ,日,亚由非零状态能够恢 为了检验所设计自适应积分反演控制器的 复到零状态的过程。 鲁棒性,分析加入的积分项对于控制系统的性能 表2为反演控制器和积分反演控制器的性能比 影响,即入,=1,入,=1和无积分项,即入,=0, 较,由表2可见,横滚角p的控制中,Back-stepping 入,=0时的控制系统的响应性能,加入干扰信 方法控制的超调量为64%,而改进Back-stepping方 号,A=diag(3sin(Tt),3sin(Tt)),其他控制参 法控制的超调量仅为3.2%,前者是后者的20倍:前 数与上述相同。 者的上升时间5s是后者2.4s的2.1倍。俯仰角0 仿真结果如图4所示,积分项的引入提高了 和偏航角平也有类似的规律。可见,在系统受到外 姿态角的跟踪精度。图4为运用反演控制方法 界扰动情况下,改进的积分反演控制系统的效果优 和改进的反演控制方法在基于Matlab-Simulink 于反演控制系统。这主要是由于积分项的引入,补 环境下,四旋翼飞行器的横滚角φ、俯仰角日,偏 偿了由模型简化引起误差,保证了在模型参数不确 航角亚的控制对比仿真结果,仿真的初始位置为 定的情况下的全局稳定性,使得系统的抗外部干扰 p=-0.07rad,9=0.034rad,Ψ=0.016rad。 性和鲁棒性大大增强。 0.10 表2改进Back-stepping与Back-stepping控制性能比较 …期望值 Table 2 Comparison of integral back-stepping and back- 0.05 一·-普通反演控制 自适应积分反演控制 stepping control 0 改进Back-stepping Back-stepping 变量 超调量/%上升时间/s超调量/%上升时间/s -0.05 3.2 2.4 64 5.0 0.106 2.6 1.8 67 5.3 4 6 8 10 s 2.8 2.0 68 5.2 (a)横滚角 0.10 图5为四旋翼飞行器的基本三维飞行轨迹图, …期望值 0.05 一·一普通反演控制 起始位置[x。y。】=[000],目标位置为 自适应积分反演控制 [x4ya]=[111],实验验证了四旋翼飞 行器能够实现稳定的飞行,并保持在悬停状态。 -0.05 0.106 2.0 6 s 1.5 (b)俯仰角 三1.0 ” 0.10 0.5 …期望值 0- 一·一普通反演控制 2 0.05 2.0 自适应积分反演控制 x/m 0 0.51.01.5 y/m 图5三维飞行轨迹 -0.05 Fig.5 The three-dimensional trajectory -0.105 6 10 s 4 结束语 (c)偏航角 针对四旋翼飞行器姿态控制建模困难、易受外 图4自适应积分与普通反演控制3个姿态角的响应曲线 界干扰的问题,在传统反演法的基础上加入积分环 Fig.4 Sate parameters between adaptive integral back- 节,设计了自适应积分反演控制器,有效提高了控制 stepping and back-stepping 器的鲁棒性,并通过稳定控制实验和存在干扰情况 控制期望的目标是在受干扰的情况下,四旋翼 2组仿真实验验证了自适应积分反演控制器的有效 飞行器能迅速恢复至稳定的悬停(3个欧拉角度为 性和对外部干扰信号的抑制作用
3.2 存在未建模项和干扰项的情况 为了检验所设计自适应积分反演控制器的 鲁棒性,分析加入的积分项对于控制系统的性能 影响,即 λ1 = 1, λ2 = 1 和无积分项,即 λ1 = 0, λ2 = 0 时的控制系统的响应性能,加入干扰信 号, Δ = diag( 3sin(πt) ,3sin(πt) ) ,其他控制参 数与上述相同。 仿真结果如图 4 所示,积分项的引入提高了 姿态角的跟踪精度。 图 4 为运用反演控制方法 和改进 的 反 演 控 制 方 法 在 基 于 Matlab⁃Simulink 环境下,四旋翼飞行器的横滚角 φ、俯仰角 θ,偏 航角 Ψ 的控制对比仿真结果,仿真的初始位置为 φ = - 0.07 rad , θ = 0.034 rad , Ψ = 0.016 rad 。 (a)横滚角 (b)俯仰角 (c)偏航角 图 4 自适应积分与普通反演控制 3 个姿态角的响应曲线 Fig. 4 Sate parameters between adaptive integral back⁃ stepping and back⁃stepping 控制期望的目标是在受干扰的情况下,四旋翼 飞行器能迅速恢复至稳定的悬停(3 个欧拉角度为 零)的状态,即欧拉角 φ , θ , Ψ 由非零状态能够恢 复到零状态的过程。 表 2 为反演控制器和积分反演控制器的性能比 较,由表 2 可见,横滚角 φ 的控制中,Back⁃stepping 方法控制的超调量为 64%,而改进 Back⁃stepping 方 法控制的超调量仅为 3.2%,前者是后者的 20 倍;前 者的上升时间 5 s 是后者 2.4 s 的 2.1 倍。 俯仰角 θ 和偏航角 Ψ 也有类似的规律。 可见,在系统受到外 界扰动情况下,改进的积分反演控制系统的效果优 于反演控制系统。 这主要是由于积分项的引入,补 偿了由模型简化引起误差,保证了在模型参数不确 定的情况下的全局稳定性,使得系统的抗外部干扰 性和鲁棒性大大增强。 表 2 改进 Back⁃stepping 与 Back⁃stepping 控制性能比较 Table 2 Comparison of integral back⁃stepping and back⁃ stepping control 变量 改进 Back⁃stepping 超调量/ % 上升时间/ s Back⁃stepping 超调量/ % 上升时间/ s φ 3.2 2.4 64 5.0 θ 2.6 1.8 67 5.3 ψ 2.8 2.0 68 5.2 图 5 为四旋翼飞行器的基本三维飞行轨迹图, 起始位置 x0 y0 z [ 0 ] = [0 0 0] ,目标位置为 xd yd z [ d ] = [1 1 1] ,实验验证了四旋翼飞 行器能够实现稳定的飞行,并保持在悬停状态。 图 5 三维飞行轨迹 Fig. 5 The three⁃dimensional trajectory 4 结束语 针对四旋翼飞行器姿态控制建模困难、易受外 界干扰的问题,在传统反演法的基础上加入积分环 节,设计了自适应积分反演控制器,有效提高了控制 器的鲁棒性,并通过稳定控制实验和存在干扰情况 2 组仿真实验验证了自适应积分反演控制器的有效 性和对外部干扰信号的抑制作用。 ·458· 智 能 系 统 学 报 第 10 卷

第3期 马正华,等:四旋翼飞行器自适应反演姿态控制 459. 12]PALUNKO P,FIERRO F.Adaptive control of a quadrotor 参考文献: with dynamic changes in the center of gravity[C]//Pro- [1]MUNGUIA R,GRAU A.An attitude and heading reference ceedings of the 18th IFAC World Congress.Milano,Italy, system AHRS)based in a dual filter [C]//2011 IEEE 2011:2626-2631. Conference on Emerging Technologies Factory Automation [13]ALTUG E,OSTROWSKI J P,TAYLOR C J.Quadrotor ETFA).Toulouse,French.2011:1-8. control using dual camera visual feedback C ]//2003 [2]LEISHMAN J G.The breguet-richet quad-rotor helicopter of IEEE International Conference on Robotics Automation. 1907[J].AHS International Directory,2001:1-4. Taipei,China:4294-4299. [3]BOUABDALLAH S,SIEGWART R.Full Control of a [14]JONES D I,WHITWORTHB CC,EARPC G K,et al.A quadrotor[C]//Proceedings of the IEEE/RSJ International laboratory test-bed for an automated power line inspection Conference on Intelligent Robots and Systems.San Diego, system[J].Control Engineering Practice,2005,13(7): USA:EEE,2007:153-158. 835-851. [4]GONZALEZ-VAZQUEZ S,MORENO-VALENZUELA J.A [15]HAMEL T,MAHONY R,LOZANO R,et al.Dynamic new nonlinear Pl/PID controller for quadrotor posture regu- modeling and configuration stabilization for an X4-Flyer lationC//2010 Electronics,Robotics and Automotive [C]//Proceeding of IFAC 15th Triennial World Congress. Mechanics Conference.Morelos,Mexico,2010:642-647. Barcelona,Spain,2002:665-670. [5]乔维维.四旋冀飞行器飞行控制系统研究与仿真[D]. [16]ZHANG Y M,CHAMSEDDINE A,RABBATH C A,et al. 太原:中北大学,2012:157-168. Development of advanced FDD and FTC,techniques with QIAO Weiwei.Research and simulation on four rotor heli- application to an unmanned quadrotor helicopter testbed copter flight control system[D].Taiyuan,China:North U. [J].Journal of the Franklin Institute,2013,350(9): niversity of China,2012:157-168. 2396-2422. [6]岳基隆.四旋翼无人机自适应控制方法研究[D].长沙: 作者简介: 国防科学技术大学,2010:128-135. 马正华,男,1962年生,教授,主要 YUE Jilong.Research on adaptive control method for 研究方向为嵌入式系统应用、计算机控 quadrotor UAV[D].Changsha,China:National University 制技术、电力电子技术,曾获江苏省科 of Defense Technology,2007:128-135. 技进步三等奖2项,中国机械工业联合 [7]SALIH A L,MOGHAVVEMI M,MOHAMED H A F,et al. 会科技进步三等奖1项。发表学术论 Flight PID controller design for a UAV quadrotor[]Scien- 文100余篇。 tific Research and Essays,2010,5(23):3660-3667. [8]毕胜.变结构飞行器的多刚体建模和姿态控制[D].合 张倩倩,女,1988年生,硕士研究 肥:中国科学技术大学,2011:5-20. 生,主要研究方向为计算机软件与理 BI Sheng.Multi-rigid-body modeling and attitude control of 论、无人机控制系统。 variable structure aircraft[D].Hefei,China:University of Science and Technology of China,2011:5-20. [9]LEE H.Robust adaptive fuzzy control by backstepping for a class of MIMO nonlinear systems[]].IEEE Transactions on Fuzzy Systems,2011,19(2):265-275. 陈岚萍,女,1974年生,副教授,博 [10]YOON S H,KIM Y D,PARK S H.Constrained adaptive 士,主要研究方向为复杂系统稳定性与 backstepping controller design for aircraft landing in wind 跟踪控制、生产过程的优化控制及运动 disturbance and actuator stuckJ.International Journal of 轨迹跟踪控制。完成或参与国家、省级 Aeronautical and Space Sciences,2012,13(1):74-89. 课题项目4项,主持或参与其他各级各 [11]BOUSSERHANE I K,Hazzab A,MAZARI B,et al.Mov- 类课题5项。发表学术论文20余篇. er position control of linear induction motor drive using a- 被SCI检索3篇、EI检索10篇。 daptive backstepping controller with integral action [J]. Tamkang Journal of Science and Engineering,2010,12 (1):17-18
参考文献: [1]MUNGUIA R, GRAU A. An attitude and heading reference system ( AHRS) based in a dual filter [ C] / / 2011 IEEE Conference on Emerging Technologies & Factory Automation (ETFA). Toulouse, French, 2011: 1⁃8. [2]LEISHMAN J G. The breguet⁃richet quad⁃rotor helicopter of 1907[J]. AHS International Directory, 2001: 1⁃4. [3 ] BOUABDALLAH S, SIEGWART R. Full Control of a quadrotor[C] / / Proceedings of the IEEE/ RSJ International Conference on Intelligent Robots and Systems. San Diego, USA: IEEE, 2007: 153⁃158. [4] GONZÁLEZ⁃VÁZQUEZ S, MORENO⁃VALENZUELA J. A new nonlinear PI/ PID controller for quadrotor posture regu⁃ lation [ C] / / 2010 Electronics, Robotics and Automotive Mechanics Conference. Morelos, Mexico, 2010: 642⁃647. [5]乔维维. 四旋翼飞行器飞行控制系统研究与仿真[D]. 太原: 中北大学, 2012: 157⁃168. QIAO Weiwei. Research and simulation on four rotor heli⁃ copter flight control system[D]. Taiyuan, China: North U⁃ niversity of China, 2012: 157⁃168. [6]岳基隆. 四旋翼无人机自适应控制方法研究[D]. 长沙: 国防科学技术大学, 2010: 128⁃135. YUE Jilong. Research on adaptive control method for quadrotor UAV[D]. Changsha, China: National University of Defense Technology, 2007: 128⁃135. [7]SALIH A L, MOGHAVVEMI M, MOHAMED H A F, et al. Flight PID controller design for a UAV quadrotor[J]. Scien⁃ tific Research and Essays, 2010, 5(23): 3660⁃3667. [8]毕胜. 变结构飞行器的多刚体建模和姿态控制[D]. 合 肥: 中国科学技术大学, 2011: 5⁃20. BI Sheng. Multi⁃rigid⁃body modeling and attitude control of variable structure aircraft[D]. Hefei, China: University of Science and Technology of China, 2011: 5⁃20. [9]LEE H. Robust adaptive fuzzy control by backstepping for a class of MIMO nonlinear systems[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(2): 265⁃275. [10]YOON S H, KIM Y D, PARK S H. Constrained adaptive backstepping controller design for aircraft landing in wind disturbance and actuator stuck[J]. International Journal of Aeronautical and Space Sciences, 2012, 13(1): 74⁃89. [11]BOUSSERHANE I K, Hazzab A, MAZARI B, et al. Mov⁃ er position control of linear induction motor drive using a⁃ daptive backstepping controller with integral action [ J ]. Tamkang Journal of Science and Engineering, 2010, 12 (1): 17⁃18. [12]PALUNKO P, FIERRO F. Adaptive control of a quadrotor with dynamic changes in the center of gravity [ C] / / Pro⁃ ceedings of the 18th IFAC World Congress. Milano, Italy, 2011: 2626⁃2631. [13] ALTUG E, OSTROWSKI J P, TAYLOR C J. Quadrotor control using dual camera visual feedback [ C ] / / 2003 IEEE International Conference on Robotics & Automation. Taipei, China: 4294⁃4299. [14]JONES D I, WHITWORTHB C C, EARPC G K, et al. A laboratory test-bed for an automated power line inspection system[J]. Control Engineering Practice, 2005, 13( 7): 835⁃851. [15] HAMEL T, MAHONY R, LOZANO R, et al. Dynamic modeling and configuration stabilization for an X4⁃Flyer [C] / / Proceeding of IFAC 15th Triennial World Congress. Barcelona, Spain, 2002: 665⁃670. [16]ZHANG Y M, CHAMSEDDINE A, RABBATH C A, et al. Development of advanced FDD and FTC, techniques with application to an unmanned quadrotor helicopter testbed [J]. Journal of the Franklin Institute, 2013, 350 ( 9): 2396⁃2422. 作者简介: 马正华,男,1962 年生,教授,主要 研究方向为嵌入式系统应用、计算机控 制技术、电力电子技术,曾获江苏省科 技进步三等奖 2 项,中国机械工业联合 会科技进步三等奖 1 项。 发表学术论 文 100 余篇。 张倩倩,女,1988 年生,硕士研究 生,主要研究方向为计算机软件与理 论、无人机控制系统。 陈岚萍,女,1974 年生,副教授,博 士,主要研究方向为复杂系统稳定性与 跟踪控制、生产过程的优化控制及运动 轨迹跟踪控制。 完成或参与国家、省级 课题项目 4 项,主持或参与其他各级各 类课题 5 项。 发表学术论文 20 余篇, 被 SCI 检索 3 篇、EI 检索 10 篇。 第 3 期 马正华,等:四旋翼飞行器自适应反演姿态控制 ·459·