智能系统：一种未知环境下机器人多目标跟踪算法

第10卷第3期 智能系统学报 Vol.10 No.3 2015年6月 CAAI Transactions on Intelligent Systems Jun.2015 D0:10.3969/j.issn.1673-4785.201405051 网s络出版地址：http://www.cnki.net/kcms/detail/23.1538.tp.20150508.1546.002.html 一种未知环境下机器人多目标跟踪算法 伍明，李琳琳，魏振华，汪洪桥 (第二炮兵工程大学指挥信息工程系，陕西西安710025) 摘要：针对未知环境下移动机器人多目标跟踪问题，设计了一种基于联合概率数据关联的粒子滤波算法。该算法 利用联合概率数据关联方法对Rao-Blackwellized粒子滤波算法进行改进，使机器人能够完成未知环境条件下对自身 状态、环境特征状态和多目标状态的在线联合估计。算法将系统状态变量分为代表多目标、环境特征状态的线性变 量和代表机器人状态的非线性变量，并利用联合概率数据关联Kalman滤波和粒子滤波对系统状态进行更新。通过 仿真实验证明了该算法对机器人状态、环境特征状态以及多目标状态的估计准确性，验证了算法对未知环境下多目 标的跟踪能力。 关键词：机器人；同时定位与地图构建；多目标跟踪；粒子滤波：联合概率数据关联：Rao-Blackwellised粒子滤波；Ka- man滤波 中图分类号：TP242.6文献标志码：A文章编号：1673-4785(2015)03-0448-06 中文引用格式：伍明，李琳琳，魏振华，等.一种未知环境下机器人多目标跟踪算法[J].智能系统学报，2015,10(3)：448453. 英文引用格式：WU Ming,LI Linlin,VEI Zhenhua,etal.A robot multi-object tracking algorithm in unknown environments[J]. CAAI Transactions on Intelligent Systems,2015,10(3):448-453. A robot multi-object tracking algorithm in unknown environments WU Ming,LI Linlin,WEI Zhenhua,WANG Hongqiao (Command Information Engineering Department,The Second Artillery Engineering College,Xian 710025,China) Abstract:In this paper,a particle filtering algorithm based on the joint integrated probabilistic data association (JIPDA)is proposed in order to solve the problem of motile robot multi-object tracking in unknown environments. The Rao-Blackwellized particle filtering is reconstructed based on the JIPDA in the new algorithm.It allows the ro- bot to estimate joint states of itself,environment features and multi-object states simultaneously.The algorithm di- vides the system variables into two parts:the lineal variable representing multi-object and environment feature states,and the non-linear variable representing robot states.The system state is updated by JIPDA Kalman filtering and particle filtering.Estimation precision of robot states,environment feature states and multi-object states is veri- fied by simulation results,verifying the ability of multi-object tracking in unknown environments. Keywords:robot;simultaneous localization and mapping(SLAM);multi-object tracking;particle filtering;joint integrated probabilistic data association JIPDA);Rao-Blackwellized particle filtering;Kalman filtering 机器人同时定位与地图构建问题(simultaneous 独立问题加以研究，而对于某些实际任务，需要将 localization and mapping,SLAM)和目标跟踪问题 SLAM和OT问题作为耦合问题来处理，例如未知环 (object tracking,OT)在机器人学界通常被作为2个 境下目标跟踪任务山、未知环境下机器人围捕任 务[2-别。此类任务要求机器人在未知环境条件下对 收稿日期：2014-05-23.网络出版日期：2015-05-08. 基金项目：国家白然科学基金资助项目(61202332)：陕西省自然科学 目标进行定位和追踪，也就是说，算法需要对机器人 基础研究计划项目(2013JQ8030). 状态、环境特征状态以及目标状态进行同步估计。 通信作者：伍明.E-mail:hyacinth531@163.com

第 １０ 卷第 ３ 期 智 能 系 统 学 报 Ｖｏｌ．１０ №．３ ２０１５ 年 ６ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ｊｕｎ． ２０１５ ＤＯＩ：１０．３９６９ ／ ｊ．ｉｓｓｎ．１６７３⁃４７８５．２０１４０５０５１ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ｔｐ．２０１５０５０８．１５４６．００２．ｈｔｍｌ 一种未知环境下机器人多目标跟踪算法 伍明，李琳琳，魏振华，汪洪桥 （第二炮兵工程大学 指挥信息工程系，陕西 西安 ７１００２５） 摘 要：针对未知环境下移动机器人多目标跟踪问题，设计了一种基于联合概率数据关联的粒子滤波算法。 该算法 利用联合概率数据关联方法对 Ｒａｏ⁃Ｂｌａｃｋｗｅｌｌｉｚｅｄ 粒子滤波算法进行改进，使机器人能够完成未知环境条件下对自身 状态、环境特征状态和多目标状态的在线联合估计。 算法将系统状态变量分为代表多目标、环境特征状态的线性变 量和代表机器人状态的非线性变量，并利用联合概率数据关联 Ｋａｌｍａｎ 滤波和粒子滤波对系统状态进行更新。 通过 仿真实验证明了该算法对机器人状态、环境特征状态以及多目标状态的估计准确性，验证了算法对未知环境下多目 标的跟踪能力。 关键词：机器人；同时定位与地图构建；多目标跟踪；粒子滤波；联合概率数据关联；Ｒａｏ⁃Ｂｌａｃｋｗｅｌｌｉｓｅｄ 粒子滤波；Ｋａｌ⁃ ｍａｎ 滤波 中图分类号：ＴＰ２４２．６ 文献标志码：Ａ 文章编号：１６７３⁃４７８５（２０１５）０３⁃０４４８⁃０６ 中文引用格式：伍明，李琳琳，魏振华，等． 一种未知环境下机器人多目标跟踪算法［Ｊ］． 智能系统学报， ２０１５， １０（３）： ４４８⁃４５３． 英文引用格式：ＷＵ Ｍｉｎｇ， ＬＩ Ｌｉｎｌｉｎ， ＷＥＩ Ｚｈｅｎｈｕａ， ｅｔ ａｌ． Ａ ｒｏｂｏｔ ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ ａｌｇｏｒｉｔｈｍ ｉｎ ｕｎｋｎｏｗｎ ｅｎｖｉｒｏｎｍｅｎｔｓ［Ｊ］． ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ， ２０１５， １０（３）： ４４８⁃４５３． Ａ ｒｏｂｏｔ ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ ａｌｇｏｒｉｔｈｍ ｉｎ ｕｎｋｎｏｗｎ ｅｎｖｉｒｏｎｍｅｎｔｓ ＷＵ Ｍｉｎｇ， ＬＩ Ｌｉｎｌｉｎ， ＷＥＩ Ｚｈｅｎｈｕａ， ＷＡＮＧ Ｈｏｎｇｑｉａｏ （Ｃｏｍｍａｎｄ Ｉｎｆｏｒｍａｔｉｏｎ Ｅｎｇｉｎｅｅｒｉｎｇ Ｄｅｐａｒｔｍｅｎｔ， Ｔｈｅ Ｓｅｃｏｎｄ Ａｒｔｉｌｌｅｒｙ Ｅｎｇｉｎｅｅｒｉｎｇ Ｃｏｌｌｅｇｅ， Ｘｉａｎ ７１００２５， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｉｎ ｔｈｉｓ ｐａｐｅｒ， ａ ｐａｒｔｉｃｌｅ ｆｉｌｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ｂａｓｅｄ ｏｎ ｔｈｅ ｊｏｉｎｔ ｉｎｔｅｇｒａｔｅｄ ｐｒｏｂａｂｉｌｉｓｔｉｃ ｄａｔａ ａｓｓｏｃｉａｔｉｏｎ （ＪＩＰＤＡ） ｉｓ ｐｒｏｐｏｓｅｄ ｉｎ ｏｒｄｅｒ ｔｏ ｓｏｌｖｅ ｔｈｅ ｐｒｏｂｌｅｍ ｏｆ ｍｏｔｉｌｅ ｒｏｂｏｔ ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ ｉｎ ｕｎｋｎｏｗｎ ｅｎｖｉｒｏｎｍｅｎｔｓ． Ｔｈｅ Ｒａｏ⁃Ｂｌａｃｋｗｅｌｌｉｚｅｄ ｐａｒｔｉｃｌｅ ｆｉｌｔｅｒｉｎｇ ｉｓ ｒｅｃｏｎｓｔｒｕｃｔｅｄ ｂａｓｅｄ ｏｎ ｔｈｅ ＪＩＰＤＡ ｉｎ ｔｈｅ ｎｅｗ ａｌｇｏｒｉｔｈｍ． Ｉｔ ａｌｌｏｗｓ ｔｈｅ ｒｏ⁃ ｂｏｔ ｔｏ ｅｓｔｉｍａｔｅ ｊｏｉｎｔ ｓｔａｔｅｓ ｏｆ ｉｔｓｅｌｆ， ｅｎｖｉｒｏｎｍｅｎｔ ｆｅａｔｕｒｅｓ ａｎｄ ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ｓｔａｔｅｓ ｓｉｍｕｌｔａｎｅｏｕｓｌｙ． Ｔｈｅ ａｌｇｏｒｉｔｈｍ ｄｉ⁃ ｖｉｄｅｓ ｔｈｅ ｓｙｓｔｅｍ ｖａｒｉａｂｌｅｓ ｉｎｔｏ ｔｗｏ ｐａｒｔｓ： ｔｈｅ ｌｉｎｅａｌ ｖａｒｉａｂｌｅ ｒｅｐｒｅｓｅｎｔｉｎｇ ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ａｎｄ ｅｎｖｉｒｏｎｍｅｎｔ ｆｅａｔｕｒｅ ｓｔａｔｅｓ， ａｎｄ ｔｈｅ ｎｏｎ⁃ｌｉｎｅａｒ ｖａｒｉａｂｌｅ ｒｅｐｒｅｓｅｎｔｉｎｇ ｒｏｂｏｔ ｓｔａｔｅｓ． Ｔｈｅ ｓｙｓｔｅｍ ｓｔａｔｅ ｉｓ ｕｐｄａｔｅｄ ｂｙ ＪＩＰＤＡ Ｋａｌｍａｎ ｆｉｌｔｅｒｉｎｇ ａｎｄ ｐａｒｔｉｃｌｅ ｆｉｌｔｅｒｉｎｇ． Ｅｓｔｉｍａｔｉｏｎ ｐｒｅｃｉｓｉｏｎ ｏｆ ｒｏｂｏｔ ｓｔａｔｅｓ， ｅｎｖｉｒｏｎｍｅｎｔ ｆｅａｔｕｒｅ ｓｔａｔｅｓ ａｎｄ ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ｓｔａｔｅｓ ｉｓ ｖｅｒｉ⁃ ｆｉｅｄ ｂｙ ｓｉｍｕｌａｔｉｏｎ ｒｅｓｕｌｔｓ， ｖｅｒｉｆｙｉｎｇ ｔｈｅ ａｂｉｌｉｔｙ ｏｆ ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ ｉｎ ｕｎｋｎｏｗｎ ｅｎｖｉｒｏｎｍｅｎｔｓ． Ｋｅｙｗｏｒｄｓ：ｒｏｂｏｔ； ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏｃａｌｉｚａｔｉｏｎ ａｎｄ ｍａｐｐｉｎｇ （ ＳＬＡＭ）； ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ； ｐａｒｔｉｃｌｅ ｆｉｌｔｅｒｉｎｇ； ｊｏｉｎｔ ｉｎｔｅｇｒａｔｅｄ ｐｒｏｂａｂｉｌｉｓｔｉｃ ｄａｔａ ａｓｓｏｃｉａｔｉｏｎ （ＪＩＰＤＡ）； Ｒａｏ⁃Ｂｌａｃｋｗｅｌｌｉｚｅｄ ｐａｒｔｉｃｌｅ ｆｉｌｔｅｒｉｎｇ； Ｋａｌｍａｎ ｆｉｌｔｅｒｉｎｇ 收稿日期：２０１４⁃０５⁃２３． 网络出版日期：２０１５⁃０５⁃０８． 基金项目：国家自然科学基金资助项目（６１２０２３３２）；陕西省自然科学 基础研究计划项目（２０１３ＪＱ８０３０）． 通信作者：伍明． Ｅ⁃ｍａｉｌ： ｈｙａｃｉｎｔｈ５３１＠ １６３．ｃｏｍ． 机器人同时定位与地图构建问题（ ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏｃａｌｉｚａｔｉｏｎ ａｎｄ ｍａｐｐｉｎｇ， ＳＬＡＭ） 和目标跟踪问题 （ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ， ＯＴ）在机器人学界通常被作为 ２ 个 独立问题加以研究，而对于某些实际任务，需要将 ＳＬＡＭ 和 ＯＴ 问题作为耦合问题来处理，例如未知环 境下目标跟踪任务［１］ 、未知环境下机器人围捕任 务［２－３］ 。 此类任务要求机器人在未知环境条件下对 目标进行定位和追踪，也就是说，算法需要对机器人 状态、环境特征状态以及目标状态进行同步估计

第3期 伍明，等：一种未知环境下机器人多目标跟踪算法 449. Wang等首先对该问题进行了研究并提出一种基 值序列，称该值B:为关联系数。 于扫描点匹配的解决方法，由于该方法采用的是 假设该估计问题为马尔可夫过程，对式(3)进 ICP(iterative closest point)匹配算法，因此无法描述 行如下推导： 机器人和目标的不确定性和相关性，并且存在累积 误差[s-刃。Vu等运用全局邻域法(global nearest p(9.l)=p(0l,,n neighborhood,GNN)进行动态物体检测，并用EKF p(91,x 对运动物体进行跟踪。伍明等[8]提出了基于卡尔 p(10i,Xg)·p(0.:IX) (4) 曼滤波框架的单目标跟踪算法，实现了机器人同时 p() 定位、地图构建与多目标跟踪(simultaneous localiza- 式中：p(416,X)代表在关联事件日：条件下获 tion,mapping and multi-objects tracking,SLOMMOT) 得4观测值的相似度，p(0:I)代表在多目标状 的对象状态耦合估计。现有上述方法并未考虑机器 态为X的条件下关联事件0：发生的可能性概率， 人未知环境下多目标跟踪问题，然而对于该问题的 假设该值是恒定值。p((!X)是归一化因子，由此 研究能够有效扩展已有方法的应用前景，使相关算 可得 法更具实用价值。 B.=p(9.1)c 针对SLOMMOT问题提出了一种基于联合概率 p(410.,XW)=p(z1X) (5) 数据关联(joint integrated probabilistic data associa- 由贝叶斯定理可得目标1：在k时刻状态估计为 tion,JIPDA)的粒子滤波算法，算法采用Rao-Black- p()=()p() wellized粒子滤波框架，并利用PDA解决多目标跟 p(|-1.r) 踪问题。首先对未知环境下机器人多目标跟踪问题 (6) 的相关模型进行描述，然后给出基于联合概率数据 式中：p(41-)是归一化因子，记作a。由 关联粒子滤波算法的具体处理过程，最后通过仿真 Chapman-Kolmogorov等式可得 实验验证算法对机器人状态、多目标状态和环境特 p(X12-1,)= 征状态估计的有效性，并分析粒子数对机器人和目 p(X1X-1,2-1.)·p(X-11-1)dX-(7) 标定位准确性的影响。 式(7)表示目标状态的预测过程。由于不能确 1问题描述及联合概率数据关联 定目标观测值和目标的对应关系，此处利用加权和 多目标数据关联目的是确定目标观测值和每个 的形式来表示式(7)，即 目标的对应关系，假设在k时刻，系统得到：个目 p()=aBp()p() 标观测值，记为 i=1 4={球，，…， (1) (8) 而k时刻n个目标的状态集合为 式中：p(z1X,l.r)p(X|-1T)可以用EKF X={X,X,,X} (2) (extended Kalman filter)的预测和更新步骤来解决。 未知环境下多目标跟踪算法目的是机器人在SLAM 2 联合概率数据关联粒子滤波的多目 的同时追踪定位这n个移动目标。 联合概率数据关联滤波由Musicki等[)首先提 标SLAMOT实现 出，JPDA能够解决多目标跟踪问题，该方法对每个 为了解决未知环境下机器人多目标追踪问题， 目标产生一个跟踪滤波器，每次迭代时考虑所有目 在基于Rao-Blackwellised粒子滤波的单目标SLAM- 标观测值-跟踪滤波器组合情况，并用全部目标观 0T算法基础上，修改粒子群结构如下： 测值对每个跟踪滤波器进行更新。 P= 假设关联事件0：代表关联关系(，i)∈{1， {x,x,P,x,P,,X,p} 2,,n}×{1,2,,n}发生，即目标观测值分量z Robot Multiobjects Landmarks 和目标t:状态相对应。首先计算观测值z由目 (9) 标t:引发的后验概率： 式中：x代表k时刻粒子i对应的机器人状态， B.:=p(01.r) (3) X9、P为k时刻粒子i代表的标志柱m的状态 式中：上标k代表截止k时刻为止的所有目标观测 均值和协方差阵，X、P为k时刻粒子i代表的多

Ｗａｎｇ 等［４］首先对该问题进行了研究并提出一种基 于扫描点匹配的解决方法，由于该方法采用的是 ＩＣＰ（ｉｔｅｒａｔｉｖｅ ｃｌｏｓｅｓｔ ｐｏｉｎｔ）匹配算法，因此无法描述 机器人和目标的不确定性和相关性，并且存在累积 误差［５－７］ 。 Ｖｕ 等［１］ 运用全局邻域法（ ｇｌｏｂａｌ ｎｅａｒｅｓｔ ｎｅｉｇｈｂｏｒｈｏｏｄ， ＧＮＮ）进行动态物体检测，并用 ＥＫＦ 对运动物体进行跟踪。 伍明等［８］ 提出了基于卡尔 曼滤波框架的单目标跟踪算法，实现了机器人同时 定位、地图构建与多目标跟踪（ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏｃａｌｉｚａ⁃ ｔｉｏｎ， ｍａｐｐｉｎｇ ａｎｄ ｍｕｌｔｉ⁃ｏｂｊｅｃｔｓ ｔｒａｃｋｉｎｇ， ＳＬＯＭＭＯＴ） 的对象状态耦合估计。 现有上述方法并未考虑机器 人未知环境下多目标跟踪问题，然而对于该问题的 研究能够有效扩展已有方法的应用前景，使相关算 法更具实用价值。 针对 ＳＬＯＭＭＯＴ 问题提出了一种基于联合概率 数据关联（ ｊｏｉｎｔ ｉｎｔｅｇｒａｔｅｄ ｐｒｏｂａｂｉｌｉｓｔｉｃ ｄａｔａ ａｓｓｏｃｉａ⁃ ｔｉｏｎ， ＪＩＰＤＡ）的粒子滤波算法，算法采用 Ｒａｏ⁃Ｂｌａｃｋ⁃ ｗｅｌｌｉｚｅｄ 粒子滤波框架，并利用 ＩＰＤＡ 解决多目标跟 踪问题。 首先对未知环境下机器人多目标跟踪问题 的相关模型进行描述，然后给出基于联合概率数据 关联粒子滤波算法的具体处理过程，最后通过仿真 实验验证算法对机器人状态、多目标状态和环境特 征状态估计的有效性，并分析粒子数对机器人和目 标定位准确性的影响。 １ 问题描述及联合概率数据关联 多目标数据关联目的是确定目标观测值和每个 目标的对应关系，假设在 ｋ 时刻，系统得到 ｎｋ 个目 标观测值，记为 ｚ Ｔ ｋ ＝ ｛ｚ Ｔ１ ｋ ， ｚ Ｔ２ ｋ ， ．．．，ｚ Ｔｎ ｋ ｋ ｝ （１） 而 ｋ 时刻 ｎ 个目标的状态集合为 Ｘ Ｔ ｋ ＝ ｛Ｘ ｔ１ ｋ ， Ｘ ｔ２ ｋ ， ．．．， Ｘ ｔｎ ｋ ｝ （２） 未知环境下多目标跟踪算法目的是机器人在 ＳＬＡＭ 的同时追踪定位这 ｎ 个移动目标。 联合概率数据关联滤波由 Ｍｕｓｉｃｋｉ 等［９］ 首先提 出，ＪＩＰＤＡ 能够解决多目标跟踪问题，该方法对每个 目标产生一个跟踪滤波器，每次迭代时考虑所有目 标观测值－跟踪滤波器组合情况，并用全部目标观 测值对每个跟踪滤波器进行更新。 假设关联事件 θｊ，ｉ 代表关联关系 （ｊ，ｉ） ∈ ｛１， ２，．．．，ｎｋ｝ × ｛１，２，．．．，ｎ｝ 发生，即目标观测值分量 ｚ Ｔｊ ｋ 和目标 ｔ ｉ 状态 Ｘ ｔ ｉ ｋ 相对应。 首先计算观测值 ｚ Ｔｊ ｋ 由目 标 ｔ ｉ 引发的后验概率： βｊ，ｉ ＝ ｐ（θｊ，ｉ ｜ ｚ ｋ，Ｔ ） （３） 式中：上标 ｋ 代表截止 ｋ 时刻为止的所有目标观测 值序列，称该值 βｊ，ｉ 为关联系数。 假设该估计问题为马尔可夫过程，对式（３） 进 行如下推导： ｐ（θｊ，ｉ ｜ ｚ ｋ，Ｔ ） ＝ ｐ（θｊ，ｉ ｜ ｚ Ｔ ｋ ， ｚ ｋ－１，Ｔ ） ＝ Ｍａｒｋｏｖ ｐ（θｊ，ｉ ｜ ｚ Ｔ ｋ ， Ｘ Ｔ ｋ ） ＝ Ｂａｙｅｓ ｐ（ｚ Ｔ ｋ ｜ θｊ，ｉ， Ｘ Ｔ ｋ ）·ｐ（θｊ，ｉ ｜ Ｘ Ｔ ｋ ） ｐ（ｚ Ｔ ｋ ｜ Ｘ Ｔ ｋ ） （４） 式中： ｐ（ｚ Ｔ ｋ ｜ θｊ，ｉ，Ｘ Ｔ ｋ ） 代表在关联事件 θｊ，ｉ 条件下获 得 ｚ Ｔ ｋ 观测值的相似度， ｐ（θｊ，ｉ ｜ Ｘ Ｔ ｋ ） 代表在多目标状 态为 Ｘ Ｔ ｋ 的条件下关联事件 θｊ，ｉ 发生的可能性概率， 假设该值是恒定值。 ｐ（ｚ Ｔ ｋ ｜ Ｘ Ｔ ｋ ） 是归一化因子，由此 可得 βｊ，ｉ ＝ ｐ（θｊ，ｉ ｜ ｚ ｋ，Ｔ ） ∝ ｐ（ｚ Ｔ ｋ ｜ θｊ，ｉ，Ｘ Ｔ ｋ ） ＝ ｐ（ｚ Ｔｊ ｋ ｜ Ｘ ｔ ｉ ｋ ） （５） 由贝叶斯定理可得目标 ｔ ｉ 在 ｋ 时刻状态估计为 ｐ（Ｘ ｔ ｉ ｋ ｜ ｚ ｋ，Ｔ ） ＝ ｐ（ｚ Ｔ ｋ ｜ Ｘ ｔ ｉ ｋ ， ｚ ｋ－１，Ｔ ）·ｐ（Ｘ ｔ ｉ ｋ ｜ ｚ ｋ－１，Ｔ ） ｐ（ｚ Ｔ ｋ ｜ ｚ ｋ－１，Ｔ ） （６） 式中： ｐ（ｚ Ｔ ｋ ｜ ｚ ｋ－１，Ｔ ） 是归一化因子， 记作 α 。 由 Ｃｈａｐｍａｎ⁃Ｋｏｌｍｏｇｏｒｏｖ 等式可得 ｐ（Ｘ ｔ ｉ ｋ ｜ ｚ ｋ－１，Ｔ ） ＝ ∫ｐ（Ｘ ｔ ｉ ｋ ｜ Ｘ ｔ ｉ ｋ－１ ，ｚ ｋ－１，Ｔ ）·ｐ（Ｘ ｔ ｉ ｋ－１ ｜ ｚ ｋ－１，Ｔ ）ｄＸ ｔ ｉ ｋ－１ （７） 式（７）表示目标状态的预测过程。 由于不能确 定目标观测值和目标的对应关系，此处利用加权和 的形式来表示式（７），即 ｐ（Ｘ ｔ ｉ ｋ ｜ ｚ ｋ，Ｔ ） ＝ α∑ ｍｋ ｊ ＝ １ βｊ，ｉ ｐ（ｚ Ｔｊ ｋ ｜ Ｘ ｔ ｉ ｋ ，ｚ ｋ－１，Ｔ ）ｐ（Ｘ ｔ ｉ ｋ ，ｚ ｋ－１，Ｔ ） （８） 式中： ｐ（ｚ Ｔｊ ｋ ｜ Ｘ ｔ ｉ ｋ ，ｚ ｋ－１，Ｔ ）ｐ（Ｘ ｔ ｉ ｋ ｜ ｚ ｋ－１，Ｔ ） 可以用 ＥＫＦ （ｅｘｔｅｎｄｅｄ Ｋａｌｍａｎ ｆｉｌｔｅｒ） 的预测和更新步骤来解决。 ２ 联合概率数据关联粒子滤波的多目 标 ＳＬＡＭＯＴ 实现 为了解决未知环境下机器人多目标追踪问题， 在基于 Ｒａｏ⁃Ｂｌａｃｋｗｅｌｌｉｓｅｄ 粒子滤波的单目标 ＳＬＡＭ⁃ ＯＴ 算法基础上，修改粒子群结构如下： ｐ ｓ ｋ ＝ ｛Ｘ Ｒ，ｉ } ｋ Ｒｏｂｏｔ ，Ｘ Ｔ，ｉ ｋ ，Ｐ Ｔ，ｉ } ｋ Ｍｕｌｔｉ⁃ｏｂｊｅｃｔｓ ，Ｘ ｌｍ１ ，ｉ ｋ ，Ｐ ｌｍ１ ，ｉ ｋ ， ．．．， Ｘ ｌｍｍ，ｉ ｋ ， Ｐ ｌｍｍ，ｉ þ ï ï ï ï ï ý ï ï ï ï ïｋ ü Ｌａｎｄｍａｒｋｓ ｝ Ｎｓ ｉ ＝ １ （９） 式中： Ｘ Ｒ，ｉ ｋ 代表 ｋ 时刻粒子 ｉ 对应的机器人状态， Ｘ ｌｍｊ ，ｉ ｋ 、Ｐ ｌｍｊ ，ｉ ｋ 为 ｋ 时刻粒子 ｉ 代表的标志柱 ｌｍｊ 的状态 均值和协方差阵， Ｘ Ｔ，ｉ ｋ 、Ｐ Ｔ，ｉ ｋ 为 ｋ 时刻粒子 ｉ 代表的多 第 ３ 期 伍明，等：一种未知环境下机器人多目标跟踪算法 ·４４９·

·450· 智能系统学报 第10卷 个目标均值和协方差阵集合，即x={X,X, 整个方法的时间复杂度为O(N·b(M+1)), ,X},P={P,P,,P}。 其中N为粒子个数，M+1为环境特征和机器人个 机器人单目标Rao-Blackwellised粒子滤波运用 数之和。该计算复杂度为M+1的线性复杂度，因 传统粒子滤波完成机器人状态估计，并对每一个粒 此能够满足计算效率要求。 子包含的标志柱、目标状态均值和协方差运用EKF 3实验结果及分析 进行估计。当涉及多个目标的追踪时，需要运用联 合概率数据关联方法对原算法进行改进。 下面通过仿真实验验证多目标追踪PFJPDA_ 未知环境下多目标跟踪算法粒子权值目标部分 SLAMOT算法的有效性，并分析粒子数对于机器人 推导如下： 和目标定位准确性的影响，实验在MATLAB7.5环 心=p(1X,X,X,…,X)= 境下进行。 p(z,z,…,z1X-,X,X,…,X)= 3.1算法跟踪结果 假设运行环境范围为100m×100m,机器人同 p(z1X,X,,…,)· 时追踪3个自左向右运动的目标，机器人控制输入 p(z1x,X,X,,X)· 噪声为diag(0.3m,0.0872rad),目标运动符合定 速模型，目标运动不确定系数为0.4。机器人将根据 p(z1X,X,X,…,X) 目标位置计算控制量并向目标构成的三角形中心运 Πp(z1x,,X,,X)(10) 动。实验共进行20次仿真，其中一次仿真总体结果 i=1 如图1所示。 式中：z代表系统对目标的第j个观测值并假设目 标观测值之间相互独立，X代表粒子i对机器人 目标、机器人实际轨迹 的状态估计，代表粒子i对目标t:的状态估计。 目标、机器人估计轨迹 由于并不能确定观测值和目标的对应关系，因此用 80标1起点 加权和的形式表示式(10)，得 70 o=p(1x,x,x空，，)= 60有标2起点 50 日标3起 i鸟Rp(1X,）（ 40 30 式中：a=1V∑B,为归一化因子，B,由式(5)给出。 20 10 环境特征实际位置 机器人起点 最后介绍目标更新过程，利用式(8)对粒子i对 0 1020304050607080 应的t。目标状态进行更新： X/m p(Xm12.r)= 图1 PFJPDA_SLAMOT算法多目标跟踪仿真结果 Fig.1 The results of simulation about multi-object 2gp(1Xp(x1 (12)》 tracking using PFJPDA_SLAMOT 式中：a=V三B.为归一化因子，数代表时 仿真中粒子数为50，图1显示了此次运行的总 刻粒子i包含的目标tm状态，z代表k时刻对目标 体情况，图2显示了相应区域的局部放大图，其中实 的第j个观测值，β同样由式(5)给出。式(12)的 线轨迹代表对机器人和目标的估计轨迹，虚线轨迹 p(zIX)p(XIX)部分可以通过EKF得 代表机器人和目标的实际运动轨迹。线段代表机器 到：首先由目标状态转移函数得到k时刻目标t。的 人当前对标志柱的观测值。星号代表标志柱的真实 预测状态X,和协方差矩阵P1,之后在更新阶 分布，标志柱周围的粒子群代表对标志柱位置的粒 段，利用目标的观测函数和实际目标观测值z对目 子群估计。 从图2可见，算法能够较好地对3个目标和机器 标预测状态进行矫正，以得到更新的目标状态X 人进行定位。本次仿真中对机器人位置估计的误差 和协方差矩阵P,该过程与单目标跟踪算法类 似，参见文献[8]，此处不再详细介绍。 均值和方差分别为0.452和0.117。对目标1位置估 计的误差均值和方差分别为0.923和0.353。对目标

个目标均值和协方差阵集合，即 Ｘ Ｔ，ｉ ｋ ＝ ｛Ｘ ｔ１ ，ｉ ｋ ， Ｘ ｔ２ ，ｉ ｋ ， ．．．， Ｘ ｔｎ ，ｉ ｋ ｝ ， Ｐ Ｔ，ｉ ｋ ＝ ｛Ｐ ｔ１ ，ｉ ｋ ， Ｐ ｔ２ ，ｉ ｋ ， ．．．， Ｐ ｔｎ ，ｉ ｋ ｝ 。 机器人单目标 Ｒａｏ－Ｂｌａｃｋｗｅｌｌｉｓｅｄ 粒子滤波运用 传统粒子滤波完成机器人状态估计，并对每一个粒 子包含的标志柱、目标状态均值和协方差运用 ＥＫＦ 进行估计。 当涉及多个目标的追踪时，需要运用联 合概率数据关联方法对原算法进行改进。 未知环境下多目标跟踪算法粒子权值目标部分 推导如下： ｗ Ｔ，ｉ ｋ ＝ ｐ（ｚ Ｔ ｋ ｜ Ｘ Ｒ，ｉ ｋ ， Ｘ ｔ１ ，ｉ ｋ ， Ｘ ｔ２ ，ｉ ｋ ， ．．．， Ｘ ｔｎ ，ｉ ｋ ） ＝ ｐ（ｚ Ｔ１ ｋ ，ｚ Ｔ２ ｋ ，．．．，ｚ Ｔｎ ｋ ｋ ｜ Ｘ Ｒ，ｉ ｋ ，Ｘ ｔ１ ，ｉ ｋ ，Ｘ ｔ２ ，ｉ ｋ ，．．．，Ｘ ｔｎ ，ｉ ｋ ） ＝ Ｉｎｄｅｐｅｎｄｅｎｔ ｐ（ｚ Ｔ１ ｋ ｜ Ｘ Ｒ，ｉ ｋ ， Ｘ ｔ１ ，ｉ ｋ ， Ｘ ｔ２ ，ｉ ｋ ， ．．．， Ｘ ｔｎ ，ｉ ｋ ）· ｐ（ｚ Ｔ２ ｋ ｜ Ｘ Ｒ，ｉ ｋ ， Ｘ ｔ１ ，ｉ ｋ ， Ｘ ｔ２ ，ｉ ｋ ， ．．．， Ｘ ｔｎ ，ｉ ｋ ）· ︙ ｐ（ｚ Ｔｎ ｋ ｋ ｜ Ｘ Ｒ，ｉ ｋ ， Ｘ ｔ１ ，ｉ ｋ ， Ｘ ｔ２ ，ｉ ｋ ， ．．．， Ｘ ｔｎ ，ｉ ｋ ） ＝ ∏ ｎｋ ｊ ＝ １ ｐ（ｚ Ｔｊ ｋ ｜ Ｘ Ｒ，ｉ ｋ ， Ｘ ｔ１ ，ｉ ｋ ， Ｘ ｔ２ ，ｉ ｋ ， ．．．， Ｘ ｔｎ ，ｉ ｋ ） （１０） 式中： ｚ Ｔｊ ｋ 代表系统对目标的第 ｊ 个观测值并假设目 标观测值之间相互独立， Ｘ Ｒ，ｉ ｋ 代表粒子 ｉ 对机器人 的状态估计， Ｘ ｔ ｊ ，ｉ ｋ 代表粒子 ｉ 对目标 ｔ ｊ 的状态估计。 由于并不能确定观测值和目标的对应关系，因此用 加权和的形式表示式（１０），得 ｗ Ｔ，ｉ ｋ ＝ ∏ ｎｋ ｊ ＝ １ ｐ（ｚ Ｔｊ ｋ ｜ Ｘ Ｒ，ｉ ｋ ， Ｘ ｔ１ ，ｉ ｋ ， Ｘ ｔ２ ，ｉ ｋ ， ．．．， Ｘ ｔｎ ，ｉ ｋ ） ＝ ∏ ｎｋ ｊ ＝ １ ∑ ｎ ｌ ＝ １ αｊ·βｊ，ｔ ｌ·ｐ（ｚ Ｔｊ ｋ ｜ Ｘ Ｒ，ｉ ｋ ， Ｘ ｔ ｌ ，ｉ ｋ ） （１１） 式中： αｊ ＝ １／∑ ｎ ｉ ＝ １ βｊ，ｔ ｉ 为归一化因子， βｊ，ｔ ｌ 由式（５）给出。 最后介绍目标更新过程，利用式（８）对粒子 ｉ 对 应的 ｔｍ 目标状态进行更新： ｐ（Ｘ ｔｍ，ｉ ｋ ｜ ｚ ｋ，Ｔ ） ＝ α∑ ｎｋ ｊ ＝ １ βｊ，ｔｍ ｐ（ｚ Ｔｊ ｋ ｜ Ｘ ｔｍ，ｉ ｋ ）ｐ（Ｘ ｔｍ，ｉ ｋ ｜ Ｘ ｔｍ，ｉ ｋ－１ ） （１２） 式中： α ＝ １ ／∑ ｎｋ ｉ ＝ １ βｉ，ｔｍ 为归一化因子， Ｘ ｔｍ，ｉ ｋ 代表 ｋ 时 刻粒子 ｉ 包含的目标 ｔｍ 状态， ｚ Ｔｊ ｋ 代表 ｋ 时刻对目标 的第 ｊ 个观测值， βｊ，ｔｍ 同样由式（５）给出。 式（１２）的 ｐ（ｚ Ｔｊ ｋ ｜ Ｘ ｔｍ，ｉ ｋ ）ｐ（Ｘ ｔｍ，ｉ ｋ ｜ Ｘ ｔｍ，ｉ ｋ－１ ） 部分可以通过 ＥＫＦ 得 到：首先由目标状态转移函数得到 ｋ 时刻目标 ｔｍ 的 预测状态 Ｘ ｔｍ，ｉ ｋ｜ ｋ－１ 和协方差矩阵 Ｐ ｔｍ，ｉ ｋ｜ ｋ－１ ，之后在更新阶 段，利用目标的观测函数和实际目标观测值 ｚ Ｔｊ ｋ 对目 标预测状态进行矫正，以得到更新的目标状态 Ｘ ｔｍ，ｉ ｋ 和协方差矩阵 Ｐ ｔｍ，ｉ ｋ ，该过程与单目标跟踪算法类 似，参见文献［８］，此处不再详细介绍。 整个方法的时间复杂度为 Ｏ（Ｎ·ｌｂ（Ｍ ＋ １）） ， 其中 Ｎ 为粒子个数， Ｍ ＋ １ 为环境特征和机器人个 数之和。 该计算复杂度为 Ｍ ＋ １ 的线性复杂度，因 此能够满足计算效率要求。 ３ 实验结果及分析 下面通过仿真实验验证多目标追踪 ＰＦＪＰＤＡ＿ ＳＬＡＭＯＴ 算法的有效性，并分析粒子数对于机器人 和目标定位准确性的影响，实验在 ＭＡＴＬＡＢ ７．５ 环 境下进行。 ３．１ 算法跟踪结果 假设运行环境范围为 １００ ｍ × １００ ｍ，机器人同 时追踪 ３ 个自左向右运动的目标，机器人控制输入 噪声为 ｄｉａｇ（０．３ ｍ，０．０８７２ ｒａｄ） ，目标运动符合定 速模型，目标运动不确定系数为 ０．４。 机器人将根据 目标位置计算控制量并向目标构成的三角形中心运 动。 实验共进行 ２０ 次仿真，其中一次仿真总体结果 如图 １ 所示。 图 １ ＰＦＪＰＤＡ＿ＳＬＡＭＯＴ 算法多目标跟踪仿真结果 Ｆｉｇ． １ Ｔｈｅ ｒｅｓｕｌｔｓ ｏｆ ｓｉｍｕｌａｔｉｏｎ ａｂｏｕｔ ｍｕｌｔｉ⁃ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ ｕｓｉｎｇ ＰＦＪＰＤＡ＿ＳＬＡＭＯＴ 仿真中粒子数为 ５０，图 １ 显示了此次运行的总 体情况，图 ２ 显示了相应区域的局部放大图，其中实 线轨迹代表对机器人和目标的估计轨迹，虚线轨迹 代表机器人和目标的实际运动轨迹。 线段代表机器 人当前对标志柱的观测值。 星号代表标志柱的真实 分布，标志柱周围的粒子群代表对标志柱位置的粒 子群估计。 从图 ２ 可见，算法能够较好地对 ３ 个目标和机器 人进行定位。 本次仿真中对机器人位置估计的误差 均值和方差分别为 ０．４５２ 和 ０．１１７。 对目标 １ 位置估 计的误差均值和方差分别为 ０．９２３ 和 ０．３５３。 对目标 ·４５０· 智 能 系 统 学 报 第 １０ 卷

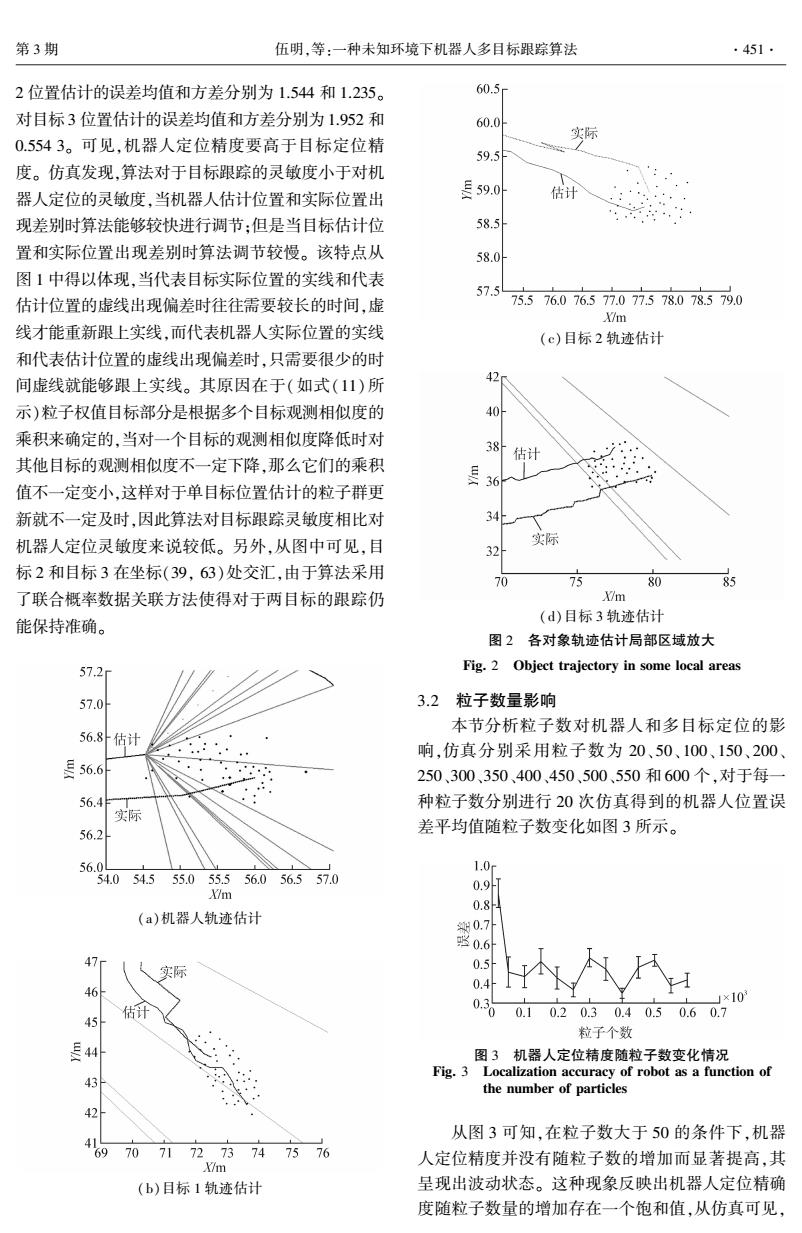
第3期 伍明，等：一种未知环境下机器人多目标跟踪算法 ·451· 2位置估计的误差均值和方差分别为1.544和1.235。 60.5 对目标3位置估计的误差均值和方差分别为1.952和 60.0 实际 0.5543。可见，机器人定位精度要高于目标定位精 59.5 度。仿真发现，算法对于目标跟踪的灵敏度小于对机 器人定位的灵敏度，当机器人估计位置和实际位置出 复59.0 估计 现差别时算法能够较快进行调节：但是当目标估计位 58.5 置和实际位置出现差别时算法调节较慢。该特点从 58.0h 图1中得以体现，当代表目标实际位置的实线和代表 57.57 估计位置的虚线出现偏差时往往需要较长的时间，虚 5.576.076.577.077.578.078.579.0 X/m 线才能重新跟上实线，而代表机器人实际位置的实线 (c)目标2轨迹估计 和代表估计位置的虚线出现偏差时，只需要很少的时 间虚线就能够跟上实线。其原因在于（如式(11）所 2 示)粒子权值目标部分是根据多个目标观测相似度的 40 乘积来确定的，当对一个目标的观测相似度降低时对 38 估计 其他目标的观测相似度不一定下降，那么它们的乘积 36 值不一定变小，这样对于单目标位置估计的粒子群更 新就不一定及时，因此算法对目标跟踪灵敏度相比对 34H 机器人定位灵敏度来说较低。另外，从图中可见，目 32 实际 标2和目标3在坐标(39,63)处交汇，由于算法采用 70 分 80 85 了联合概率数据关联方法使得对于两目标的跟踪仍 Xm 能保持准确。 (d)目标3轨迹估计 图2各对象轨迹估计局部区域放大 572 Fig.2 Object trajectory in some local areas 57.0 3.2粒子数量影响 本节分析粒子数对机器人和多目标定位的影 56.8估计 响，仿真分别采用粒子数为20、50、100、150、200、 里56.6 250、300、350、400、450、500、550和600个，对于每一 56.4 种粒子数分别进行20次仿真得到的机器人位置误 实际 56.2 差平均值随粒子数变化如图3所示。 56. 1.0 54.054.555.055.556.056.557.0 0.9 m 0.8 (a)机器人轨迹估计 0.7 路0.6 实际 0.5 0.4 46 估印 45 0.30 1×10 0.10.20.30.40.50.60.7 粒子个数 三44 图3机器人定位精度随粒子数变化情况 Fig.3 Localization accuracy of robot as a function of 43 the number of particles 42 从图3可知，在粒子数大于50的条件下，机器 6970717273747576 人定位精度并没有随粒子数的增加而显著提高，其 X/m (b)目标1轨迹估计 呈现出波动状态。这种现象反映出机器人定位精确 度随粒子数量的增加存在一个饱和值，从仿真可见

２ 位置估计的误差均值和方差分别为 １．５４４ 和 １．２３５。 对目标 ３ 位置估计的误差均值和方差分别为 １．９５２ 和 ０．５５４ ３。 可见，机器人定位精度要高于目标定位精 度。 仿真发现，算法对于目标跟踪的灵敏度小于对机 器人定位的灵敏度，当机器人估计位置和实际位置出 现差别时算法能够较快进行调节；但是当目标估计位 置和实际位置出现差别时算法调节较慢。 该特点从 图 １ 中得以体现，当代表目标实际位置的实线和代表 估计位置的虚线出现偏差时往往需要较长的时间，虚 线才能重新跟上实线，而代表机器人实际位置的实线 和代表估计位置的虚线出现偏差时，只需要很少的时 间虚线就能够跟上实线。 其原因在于（如式（１１）所 示）粒子权值目标部分是根据多个目标观测相似度的 乘积来确定的，当对一个目标的观测相似度降低时对 其他目标的观测相似度不一定下降，那么它们的乘积 值不一定变小，这样对于单目标位置估计的粒子群更 新就不一定及时，因此算法对目标跟踪灵敏度相比对 机器人定位灵敏度来说较低。 另外，从图中可见，目 标 ２ 和目标 ３ 在坐标（３９， ６３）处交汇，由于算法采用 了联合概率数据关联方法使得对于两目标的跟踪仍 能保持准确。 （ａ）机器人轨迹估计 （ｂ）目标 １ 轨迹估计 （ｃ）目标 ２ 轨迹估计 （ｄ）目标 ３ 轨迹估计 图 ２ 各对象轨迹估计局部区域放大 Ｆｉｇ． ２ Ｏｂｊｅｃｔ ｔｒａｊｅｃｔｏｒｙ ｉｎ ｓｏｍｅ ｌｏｃａｌ ａｒｅａｓ ３．２ 粒子数量影响 本节分析粒子数对机器人和多目标定位的影 响，仿真分别采用粒子数为 ２０、５０、１００、１５０、２００、 ２５０、３００、３５０、４００、４５０、５００、５５０ 和 ６００ 个，对于每一 种粒子数分别进行 ２０ 次仿真得到的机器人位置误 差平均值随粒子数变化如图 ３ 所示。 图 ３ 机器人定位精度随粒子数变化情况 Ｆｉｇ． ３ Ｌｏｃａｌｉｚａｔｉｏｎ ａｃｃｕｒａｃｙ ｏｆ ｒｏｂｏｔ ａｓ ａ ｆｕｎｃｔｉｏｎ ｏｆ ｔｈｅ ｎｕｍｂｅｒ ｏｆ ｐａｒｔｉｃｌｅｓ 从图 ３ 可知，在粒子数大于 ５０ 的条件下，机器 人定位精度并没有随粒子数的增加而显著提高，其 呈现出波动状态。 这种现象反映出机器人定位精确 度随粒子数量的增加存在一个饱和值，从仿真可见， 第 ３ 期 伍明，等：一种未知环境下机器人多目标跟踪算法 ·４５１·

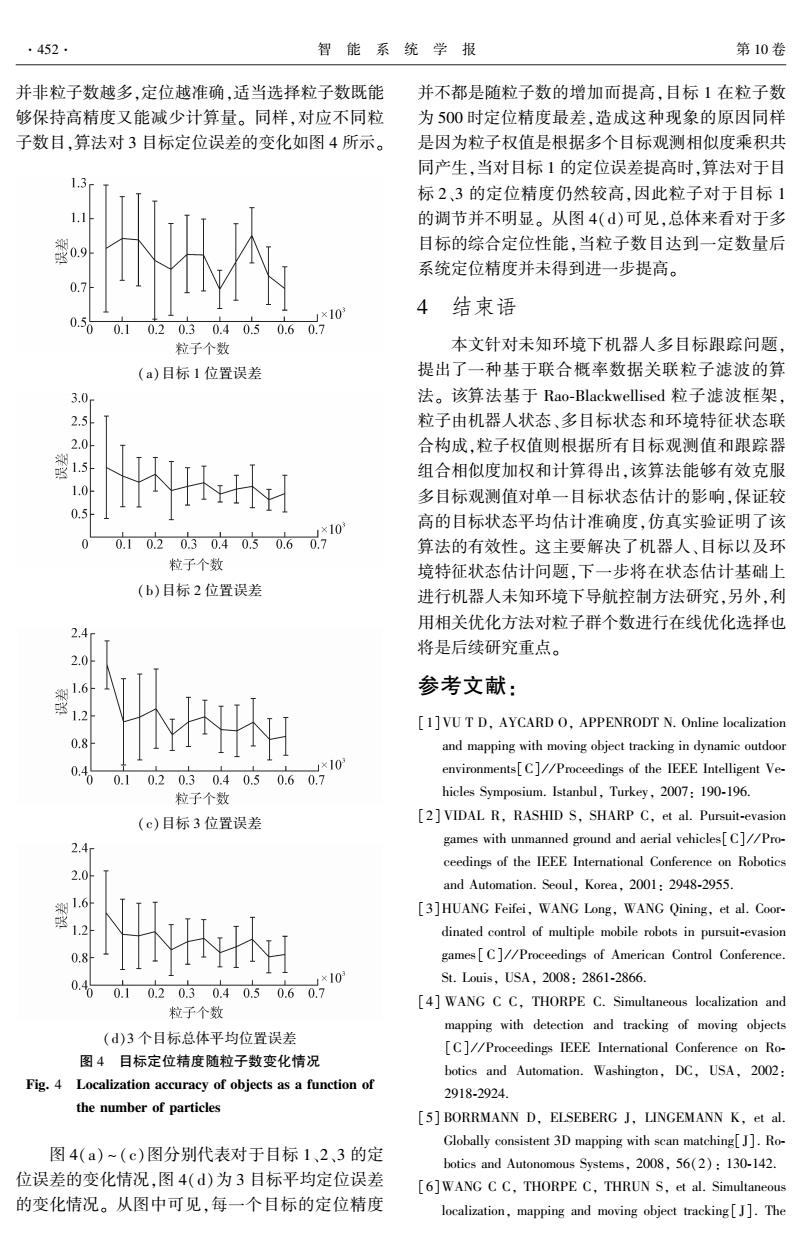
.452. 智能系统学报 第10卷 并非粒子数越多，定位越准确，适当选择粒子数既能 并不都是随粒子数的增加而提高，目标1在粒子数 够保持高精度又能减少计算量。同样，对应不同粒 为500时定位精度最差，造成这种现象的原因同样 子数目，算法对3目标定位误差的变化如图4所示。 是因为粒子权值是根据多个目标观测相似度乘积共 同产生，当对目标1的定位误差提高时，算法对于目 标2、3的定位精度仍然较高，因此粒子对于目标1 的调节并不明显。从图4()可见，总体来看对于多 目标的综合定位性能，当粒子数目达到一定数量后 系统定位精度并未得到进一步提高。 ×10 4结束语 0.10.20.30.40.50.60.7 粒子个数 本文针对未知环境下机器人多目标跟踪问题， (a)目标1位置误差 提出了一种基于联合概率数据关联粒子滤波的算 3.0 法。该算法基于Rao-Blackwellised粒子滤波框架. 粒子由机器人状态、多目标状态和环境特征状态联 20 合构成，粒子权值则根据所有目标观测值和跟踪器 组合相似度加权和计算得出，该算法能够有效克服 10 多目标观测值对单一目标状态估计的影响，保证较 0.5 高的目标状态平均估计准确度，仿真实验证明了该 应040610 算法的有效性。这主要解决了机器人、目标以及环 粒子个数 境特征状态估计问题，下一步将在状态估计基础上 (b)目标2位置误差 进行机器人未知环境下导航控制方法研究，另外，利 用相关优化方法对粒子群个数进行在线优化选择也 2.4 将是后续研究重点。 2.0 参考文献： 1 [1]VU T D,AYCARD O,APPENRODT N.Online localization and mapping with moving object tracking in dynamic outdoor 0.6 1×10 environments[C]//Proceedings of the IEEE Intelligent Ve- 0.1 0.20.30.40.50.60.7 粒子个数 hicles Symposium.Istanbul,Turkey,2007:190-196. (c)目标3位置误差 [2]VIDAL R,RASHID S,SHARP C,et al.Pursuit-evasion 2.4 games with unmanned ground and aerial vehicles[C]//Pro- ceedings of the IEEE International Conference on Robotics 2.0 and Automation.Seoul,Korea,2001:2948-2955. 型 [3]HUANG Feifei,WANG Long,WANG Qining,et al.Coor- 1.2 dinated control of multiple mobile robots in pursuit-evasion 0.8 games[C]//Proceedings of American Control Conference. St.Louis,USA,2008:2861-2866. 0.10.20.30.40.50.60.7 4]WANG CC.THORPE C.Simultaneous localization and 粒子个数 mapping with detection and tracking of moving objects (d)3个目标总体平均位置误差 [C//Proceedings IEEE International Conference on Ro- 图4目标定位精度随粒子数变化情况 botics and Automation.Washington,DC,USA,2002: Fig.4 Localization accuracy of objects as a function of 2918-2924. the number of particles [5]BORRMANN D,ELSEBERG J,LINGEMANN K,et al. Globally consistent 3D mapping with scan matching[J].Ro- 图4(a)~(c)图分别代表对于目标1、2、3的定 botics and Autonomous Systems,2008,56(2):130-142. 位误差的变化情况，图4(d)为3目标平均定位误差 [6]WANG CC,THORPE C,THRUN S,et al.Simultaneous 的变化情况。从图中可见，每一个目标的定位精度 localization,mapping and moving object tracking[J].The

并非粒子数越多，定位越准确，适当选择粒子数既能 够保持高精度又能减少计算量。 同样，对应不同粒 子数目，算法对 ３ 目标定位误差的变化如图 ４ 所示。 （ａ）目标 １ 位置误差 （ｂ）目标 ２ 位置误差 （ｃ）目标 ３ 位置误差 （ｄ）３ 个目标总体平均位置误差 图 ４ 目标定位精度随粒子数变化情况 Ｆｉｇ． ４ Ｌｏｃａｌｉｚａｔｉｏｎ ａｃｃｕｒａｃｙ ｏｆ ｏｂｊｅｃｔｓ ａｓ ａ ｆｕｎｃｔｉｏｎ ｏｆ ｔｈｅ ｎｕｍｂｅｒ ｏｆ ｐａｒｔｉｃｌｅｓ 图 ４（ａ） ～ （ｃ）图分别代表对于目标 １、２、３ 的定 位误差的变化情况，图 ４（ｄ）为 ３ 目标平均定位误差 的变化情况。 从图中可见，每一个目标的定位精度 并不都是随粒子数的增加而提高，目标 １ 在粒子数 为 ５００ 时定位精度最差，造成这种现象的原因同样 是因为粒子权值是根据多个目标观测相似度乘积共 同产生，当对目标 １ 的定位误差提高时，算法对于目 标 ２、３ 的定位精度仍然较高，因此粒子对于目标 １ 的调节并不明显。 从图 ４（ｄ）可见，总体来看对于多 目标的综合定位性能，当粒子数目达到一定数量后 系统定位精度并未得到进一步提高。 ４ 结束语 本文针对未知环境下机器人多目标跟踪问题， 提出了一种基于联合概率数据关联粒子滤波的算 法。 该算法基于 Ｒａｏ⁃Ｂｌａｃｋｗｅｌｌｉｓｅｄ 粒子滤波框架， 粒子由机器人状态、多目标状态和环境特征状态联 合构成，粒子权值则根据所有目标观测值和跟踪器 组合相似度加权和计算得出，该算法能够有效克服 多目标观测值对单一目标状态估计的影响，保证较 高的目标状态平均估计准确度，仿真实验证明了该 算法的有效性。 这主要解决了机器人、目标以及环 境特征状态估计问题，下一步将在状态估计基础上 进行机器人未知环境下导航控制方法研究，另外，利 用相关优化方法对粒子群个数进行在线优化选择也 将是后续研究重点。 参考文献： ［１］ＶＵ Ｔ Ｄ， ＡＹＣＡＲＤ Ｏ， ＡＰＰＥＮＲＯＤＴ Ｎ． Ｏｎｌｉｎｅ ｌｏｃａｌｉｚａｔｉｏｎ ａｎｄ ｍａｐｐｉｎｇ ｗｉｔｈ ｍｏｖｉｎｇ ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ ｉｎ ｄｙｎａｍｉｃ ｏｕｔｄｏｏｒ ｅｎｖｉｒｏｎｍｅｎｔｓ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ＩＥＥＥ Ｉｎｔｅｌｌｉｇｅｎｔ Ｖｅ⁃ ｈｉｃｌｅｓ Ｓｙｍｐｏｓｉｕｍ． Ｉｓｔａｎｂｕｌ， Ｔｕｒｋｅｙ， ２００７： １９０⁃１９６． ［２］ ＶＩＤＡＬ Ｒ， ＲＡＳＨＩＤ Ｓ， ＳＨＡＲＰ Ｃ， ｅｔ ａｌ． Ｐｕｒｓｕｉｔ⁃ｅｖａｓｉｏｎ ｇａｍｅｓ ｗｉｔｈ ｕｎｍａｎｎｅｄ ｇｒｏｕｎｄ ａｎｄ ａｅｒｉａｌ ｖｅｈｉｃｌｅｓ［Ｃ］ ／ ／ Ｐｒｏ⁃ ｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ＩＥＥＥ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｒｏｂｏｔｉｃｓ ａｎｄ Ａｕｔｏｍａｔｉｏｎ． Ｓｅｏｕｌ， Ｋｏｒｅａ， ２００１： ２９４８⁃２９５５． ［３］ＨＵＡＮＧ Ｆｅｉｆｅｉ， ＷＡＮＧ Ｌｏｎｇ， ＷＡＮＧ Ｑｉｎｉｎｇ， ｅｔ ａｌ． Ｃｏｏｒ⁃ ｄｉｎａｔｅｄ ｃｏｎｔｒｏｌ ｏｆ ｍｕｌｔｉｐｌｅ ｍｏｂｉｌｅ ｒｏｂｏｔｓ ｉｎ ｐｕｒｓｕｉｔ⁃ｅｖａｓｉｏｎ ｇａｍｅｓ［ Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ Ａｍｅｒｉｃａｎ Ｃｏｎｔｒｏｌ Ｃｏｎｆｅｒｅｎｃｅ． Ｓｔ． Ｌｏｕｉｓ， ＵＳＡ， ２００８： ２８６１⁃２８６６． ［４］ ＷＡＮＧ Ｃ Ｃ， ＴＨＯＲＰＥ Ｃ． Ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏｃａｌｉｚａｔｉｏｎ ａｎｄ ｍａｐｐｉｎｇ ｗｉｔｈ ｄｅｔｅｃｔｉｏｎ ａｎｄ ｔｒａｃｋｉｎｇ ｏｆ ｍｏｖｉｎｇ ｏｂｊｅｃｔｓ ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ＩＥＥＥ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｒｏ⁃ ｂｏｔｉｃｓ ａｎｄ Ａｕｔｏｍａｔｉｏｎ． Ｗａｓｈｉｎｇｔｏｎ， ＤＣ， ＵＳＡ， ２００２： ２９１８⁃２９２４． ［５］ ＢＯＲＲＭＡＮＮ Ｄ， ＥＬＳＥＢＥＲＧ Ｊ， ＬＩＮＧＥＭＡＮＮ Ｋ， ｅｔ ａｌ． Ｇｌｏｂａｌｌｙ ｃｏｎｓｉｓｔｅｎｔ ３Ｄ ｍａｐｐｉｎｇ ｗｉｔｈ ｓｃａｎ ｍａｔｃｈｉｎｇ［Ｊ］． Ｒｏ⁃ ｂｏｔｉｃｓ ａｎｄ Ａｕｔｏｎｏｍｏｕｓ Ｓｙｓｔｅｍｓ， ２００８， ５６（２）： １３０⁃１４２． ［６］ＷＡＮＧ Ｃ Ｃ， ＴＨＯＲＰＥ Ｃ， ＴＨＲＵＮ Ｓ， ｅｔ ａｌ． Ｓｉｍｕｌｔａｎｅｏｕｓ ｌｏｃａｌｉｚａｔｉｏｎ， ｍａｐｐｉｎｇ ａｎｄ ｍｏｖｉｎｇ ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ［ Ｊ］． Ｔｈｅ ·４５２· 智 能 系 统 学 报 第 １０ 卷

第3期 伍明，等：一种未知环境下机器人多目标跟踪算法 .453. Interational Journal of Robotics Research,2007,26(9): 作者简介： 889-916. 伍明，男，1981年生，讲师，博士，主 [7]WAN Kaowei,WANG CC,TON T T.Weakly interacting 要研究方向为自主机器人控制、多机器 object tracking in indoor environments[C]//Proceedings of 人协作、机器人环境构建。发表学术论 the IEEE International Conference on Advanced Robotics 文10余篇，其中被EI检索8篇。 and Its Social Impacts.Taipei,China,2008:1-6. [8]伍明，孙继银.基于扩展式卡尔曼滤波的移动机器人未 知环境下动态目标跟踪[J].机器人，2010,32(3)：334 343. 李琳琳，女，1974年生，副教授，博 WU Ming,SUN Jigen.Extended Kalman filter based moving 士，主要研究方向为信息栅格技术、多 object tracking by mobile robot in unknown environment[]]. 传感器网络、物联网。主持国家高技术 Robot,2010,32(3):334-343. 研究项目1项，发表学术论文20余篇， [9]MUSICKI D,EVANS R.Joint integrated probabilistic data 其中被EI检索12篇。 association-JIPDA[J].IEEE Transactions on Aerospace and Electronic Systems,2004,40(3):1093-1099. 第3届亚洲模式识别会议 3rd Asian Conference on Pattern Recognition The 3rd IAPR Asian Conference on Pattern Recognition (ACPR2015),sponsored by the International Association of Pat- tern Recognition (IAPR)and supported by the Malaysian Image Analysis and Machine Intelligence Association (MIAMI) and IEEE Computational Intelligence Society (CIS)Malaysia Chapter will be held on November 3-6,2015,Kuala Lum- pur,Malaysia.The First Asian Conference on Pattern Recognition (ACPR2011)was held at Beijing,China;while the second series (ACPR2013)was held at Okinawa,Japan. ACPR2015 is a high quality,biennial single-track conference,comprising oral presentations and poster sessions.ACPR aims at providing one major international forum for researchers in pattern recognition and related fields to share their new ideas and achievements.Submissions from other than the Asia-Pacific regions are also highly encouraged. ACPR2015 solicits high-quality original research for publication in its main conference and co-located workshops.All ac- cepted papers will be included in IEEE Xplore and Indexed by EI.Topics of interest include all aspects of pattern recogni- tion including,but not limited to: A)Computer Vision and Robot Vision; B)Pattern Recognition and Machine Learning; C)Signal Processing (signal,speech,image); D)Media Processing and Interaction (video,document,medical,biometrics,HCI,VR). Important Dates: Full Paper Submission FIRM Deadline):July 10,2015-23:59 (PST) Decisions to Authors:August 31,2015 Camera Ready:September 25,2015 Author Registration:September 25,2015 Workshops/Tutorials:November 3,2015 Main Conference:November 4-6,2015 Website:http://acpr2015.org/

Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｊｏｕｒｎａｌ ｏｆ Ｒｏｂｏｔｉｃｓ Ｒｅｓｅａｒｃｈ， ２００７， ２６（ ９）： ８８９⁃９１６． ［７］ＷＡＮ Ｋａｏｗｅｉ， ＷＡＮＧ Ｃ Ｃ， ＴＯＮ Ｔ Ｔ． Ｗｅａｋｌｙ ｉｎｔｅｒａｃｔｉｎｇ ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ ｉｎ ｉｎｄｏｏｒ ｅｎｖｉｒｏｎｍｅｎｔｓ［Ｃ］ ／ ／ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ ＩＥＥＥ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ａｄｖａｎｃｅｄ Ｒｏｂｏｔｉｃｓ ａｎｄ Ｉｔｓ Ｓｏｃｉａｌ Ｉｍｐａｃｔｓ． Ｔａｉｐｅｉ， Ｃｈｉｎａ， ２００８： １⁃６． ［８］伍明， 孙继银． 基于扩展式卡尔曼滤波的移动机器人未 知环境下动态目标跟踪［Ｊ］． 机器人， ２０１０， ３２（３）： ３３４⁃ ３４３． ＷＵ Ｍｉｎｇ， ＳＵＮ Ｊｉｇｅｎ． Ｅｘｔｅｎｄｅｄ Ｋａｌｍａｎ ｆｉｌｔｅｒ ｂａｓｅｄ ｍｏｖｉｎｇ ｏｂｊｅｃｔ ｔｒａｃｋｉｎｇ ｂｙ ｍｏｂｉｌｅ ｒｏｂｏｔ ｉｎ ｕｎｋｎｏｗｎ ｅｎｖｉｒｏｎｍｅｎｔ［Ｊ］． Ｒｏｂｏｔ， ２０１０， ３２（３）： ３３４⁃３４３． ［９］ ＭＵŠＩＣＫＩ Ｄ， ＥＶＡＮＳ Ｒ． Ｊｏｉｎｔ ｉｎｔｅｇｒａｔｅｄ ｐｒｏｂａｂｉｌｉｓｔｉｃ ｄａｔａ ａｓｓｏｃｉａｔｉｏｎ—ＪＩＰＤＡ［ Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ａｅｒｏｓｐａｃｅ ａｎｄ Ｅｌｅｃｔｒｏｎｉｃ Ｓｙｓｔｅｍｓ， ２００４， ４０（３）： １０９３⁃１０９９． 作者简介： 伍明，男，１９８１ 年生，讲师，博士，主 要研究方向为自主机器人控制、多机器 人协作、机器人环境构建。 发表学术论 文 １０ 余篇，其中被 ＥＩ 检索 ８ 篇。 李琳琳，女，１９７４ 年生，副教授，博 士，主要研究方向为信息栅格技术、多 传感器网络、物联网。 主持国家高技术 研究项目 １ 项，发表学术论文 ２０ 余篇， 其中被 ＥＩ 检索 １２ 篇。 第 ３ 届亚洲模式识别会议 ３ｒｄ Ａｓｉａｎ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｐａｔｔｅｒｎ Ｒｅｃｏｇｎｉｔｉｏｎ Ｔｈｅ ３ｒｄ ＩＡＰＲ Ａｓｉａｎ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｐａｔｔｅｒｎ Ｒｅｃｏｇｎｉｔｉｏｎ （ＡＣＰＲ２０１５）， ｓｐｏｎｓｏｒｅｄ ｂｙ ｔｈｅ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ａｓｓｏｃｉａｔｉｏｎ ｏｆ Ｐａｔ⁃ ｔｅｒｎ Ｒｅｃｏｇｎｉｔｉｏｎ （ＩＡＰＲ） ａｎｄ ｓｕｐｐｏｒｔｅｄ ｂｙ ｔｈｅ Ｍａｌａｙｓｉａｎ Ｉｍａｇｅ Ａｎａｌｙｓｉｓ ａｎｄ Ｍａｃｈｉｎｅ Ｉｎｔｅｌｌｉｇｅｎｃｅ Ａｓｓｏｃｉａｔｉｏｎ （ＭＩＡＭＩ） ａｎｄ ＩＥＥＥ Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ Ｓｏｃｉｅｔｙ （ＣＩＳ） Ｍａｌａｙｓｉａ Ｃｈａｐｔｅｒ ｗｉｌｌ ｂｅ ｈｅｌｄ ｏｎ Ｎｏｖｅｍｂｅｒ ３－６， ２０１５， Ｋｕａｌａ Ｌｕｍ⁃ ｐｕｒ， Ｍａｌａｙｓｉａ． Ｔｈｅ Ｆｉｒｓｔ Ａｓｉａｎ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｐａｔｔｅｒｎ Ｒｅｃｏｇｎｉｔｉｏｎ （ＡＣＰＲ２０１１） ｗａｓ ｈｅｌｄ ａｔ Ｂｅｉｊｉｎｇ， Ｃｈｉｎａ； ｗｈｉｌｅ ｔｈｅ ｓｅｃｏｎｄ ｓｅｒｉｅｓ （ＡＣＰＲ２０１３） ｗａｓ ｈｅｌｄ ａｔ Ｏｋｉｎａｗａ， Ｊａｐａｎ． ＡＣＰＲ２０１５ ｉｓ ａ ｈｉｇｈ ｑｕａｌｉｔｙ， ｂｉｅｎｎｉａｌ ｓｉｎｇｌｅ⁃ｔｒａｃｋ ｃｏｎｆｅｒｅｎｃｅ， ｃｏｍｐｒｉｓｉｎｇ ｏｒａｌ ｐｒｅｓｅｎｔａｔｉｏｎｓ ａｎｄ ｐｏｓｔｅｒ ｓｅｓｓｉｏｎｓ． ＡＣＰＲ ａｉｍｓ ａｔ ｐｒｏｖｉｄｉｎｇ ｏｎｅ ｍａｊｏｒ ｉｎｔｅｒｎａｔｉｏｎａｌ ｆｏｒｕｍ ｆｏｒ ｒｅｓｅａｒｃｈｅｒｓ ｉｎ ｐａｔｔｅｒｎ ｒｅｃｏｇｎｉｔｉｏｎ ａｎｄ ｒｅｌａｔｅｄ ｆｉｅｌｄｓ ｔｏ ｓｈａｒｅ ｔｈｅｉｒ ｎｅｗ ｉｄｅａｓ ａｎｄ ａｃｈｉｅｖｅｍｅｎｔｓ． Ｓｕｂｍｉｓｓｉｏｎｓ ｆｒｏｍ ｏｔｈｅｒ ｔｈａｎ ｔｈｅ Ａｓｉａ⁃Ｐａｃｉｆｉｃ ｒｅｇｉｏｎｓ ａｒｅ ａｌｓｏ ｈｉｇｈｌｙ ｅｎｃｏｕｒａｇｅｄ． ＡＣＰＲ２０１５ ｓｏｌｉｃｉｔｓ ｈｉｇｈ⁃ｑｕａｌｉｔｙ ｏｒｉｇｉｎａｌ ｒｅｓｅａｒｃｈ ｆｏｒ ｐｕｂｌｉｃａｔｉｏｎ ｉｎ ｉｔｓ ｍａｉｎ ｃｏｎｆｅｒｅｎｃｅ ａｎｄ ｃｏ－ｌｏｃａｔｅｄ ｗｏｒｋｓｈｏｐｓ． Ａｌｌ ａｃ⁃ ｃｅｐｔｅｄ ｐａｐｅｒｓ ｗｉｌｌ ｂｅ ｉｎｃｌｕｄｅｄ ｉｎ ＩＥＥＥ Ｘｐｌｏｒｅ ａｎｄ Ｉｎｄｅｘｅｄ ｂｙ ＥＩ． Ｔｏｐｉｃｓ ｏｆ ｉｎｔｅｒｅｓｔ ｉｎｃｌｕｄｅ ａｌｌ ａｓｐｅｃｔｓ ｏｆ ｐａｔｔｅｒｎ ｒｅｃｏｇｎｉ⁃ ｔｉｏｎ ｉｎｃｌｕｄｉｎｇ， ｂｕｔ ｎｏｔ ｌｉｍｉｔｅｄ ｔｏ： Ａ） Ｃｏｍｐｕｔｅｒ Ｖｉｓｉｏｎ ａｎｄ Ｒｏｂｏｔ Ｖｉｓｉｏｎ； Ｂ） Ｐａｔｔｅｒｎ Ｒｅｃｏｇｎｉｔｉｏｎ ａｎｄ Ｍａｃｈｉｎｅ Ｌｅａｒｎｉｎｇ； Ｃ） Ｓｉｇｎａｌ Ｐｒｏｃｅｓｓｉｎｇ （ｓｉｇｎａｌ， ｓｐｅｅｃｈ， ｉｍａｇｅ）； Ｄ） Ｍｅｄｉａ Ｐｒｏｃｅｓｓｉｎｇ ａｎｄ Ｉｎｔｅｒａｃｔｉｏｎ （ｖｉｄｅｏ， ｄｏｃｕｍｅｎｔ， ｍｅｄｉｃａｌ， ｂｉｏｍｅｔｒｉｃｓ， ＨＣＩ， ＶＲ）． Ｉｍｐｏｒｔａｎｔ Ｄａｔｅｓ： Ｆｕｌｌ Ｐａｐｅｒ Ｓｕｂｍｉｓｓｉｏｎ （ＦＩＲＭ Ｄｅａｄｌｉｎｅ）： Ｊｕｌｙ １０， ２０１５－２３：５９ （ＰＳＴ） Ｄｅｃｉｓｉｏｎｓ ｔｏ Ａｕｔｈｏｒｓ： Ａｕｇｕｓｔ ３１， ２０１５ Ｃａｍｅｒａ Ｒｅａｄｙ： Ｓｅｐｔｅｍｂｅｒ ２５， ２０１５ Ａｕｔｈｏｒ Ｒｅｇｉｓｔｒａｔｉｏｎ： Ｓｅｐｔｅｍｂｅｒ ２５， ２０１５ Ｗｏｒｋｓｈｏｐｓ／ Ｔｕｔｏｒｉａｌｓ： Ｎｏｖｅｍｂｅｒ ３， ２０１５ Ｍａｉｎ Ｃｏｎｆｅｒｅｎｃｅ： Ｎｏｖｅｍｂｅｒ ４－６， ２０１５ Ｗｅｂｓｉｔｅ： ｈｔｔｐ： ／ ／ ａｃｐｒ２０１５．ｏｒｇ ／ 第 ３ 期 伍明，等：一种未知环境下机器人多目标跟踪算法 ·４５３·