
第10卷第5期 智能系统学报 Vol.10 No.5 2015年10月 CAAI Transactions on Intelligent Systems 0ct.2015 D0I:10.11992/is.201406028 网s络出版t地址:htp:/ww.cmki.net/kcms/detail/23.1538.tp.20150930.1556.004.html 改进粒子群算法的PD神经网络解耦控制 于立君,陈佳,刘繁明,王辉 (哈尔滨工程大学自动化学院,黑龙江哈尔滨150001) 摘要:综合减摇控制系统存在非线性、多变量、强耦合等因素,会导致减摇系统达不到最佳控制状态。利用粒子群 算法具有对整个空间进行高效搜索以及PD神经网络的自适应特点,提出一种改进粒子群算法,以解决粒子群算法 中存在算法精度不高、粒子易陷入局部极小值等问题,并提高PD神经网络训练速度和训练精度,便于参数寻优。 仿真结果表明,改进的粒子群算法具有一定优越性,将其运用到综合减摇控制系统解耦控制器设计中,能够有效地 减小船舶横摇,达到较好的控制效果。 关键词:粒子群算法:综合减摇系统:PD神经网络:解耦控制:仿真分析 中图分类号:TH186文献标志码:TP18文章编号:1673-4785(2015)05-0699-06 中文引用格式:于立君,陈佳,刘繁明,等.改进粒子群算法的PD神经网络解耦控制[J].智能系统学报,2015,10(5):699-704. 英文引用格式:YU Lijun,CHEN Jia,LIU Fanming,etal.An improved particle swarm optimization for PID neural network de- coupling control[J].CAAI Transactions on Intelligent Systems,2015,10(5):699-704. An improved particle swarm optimization for PID neural network decoupling control YU Lijun,CHEN Jia,LIU Fanming,WANG Hui (College of Automation,Harbin Engineering University,Harbin 150001,China) Abstract:The integrated ship stabilization system has nonlinear,multi-variable and strong coupling characteristics, which may hinder the system from reaching the best control state.An improved particle swarm algorithm is proposed based on the characteristics of particle swarm optimization(PSO)algorithm,which can search the parameter space efficiently,along with its associated PID artificial neuron network that has self-regulation and adaptability.The im- proved particle swarm algorithm can overcome disadvantages in former particle swarm algorithms such as low preci- sion,the particles tend to fall into extremely small values,and so on.In addition,the improved algorithm can in- crease the training speed and precision of the PID nerve network,which facilitates parameter optimization.The sim- ulation results show that the improved PSO has certain advantages,it can reduce ship rolling,and can achieve ex- cellent control effects when it is applied to the design of the decoupling control of an integrated stabilization control system. Keywords:particle swarm algorithms;integrate stabilization system;PID neural network;decoupling control;sim- ulation analysis 综合减摇控制系统具有非线性强、控制变量多、中[],将在很大程度上提高多变量耦合系统的控制 耦合性强、结构复杂且时变等特点[山,这些因素的效果。近年来,由于粒子群算法具有易实现、通用性 存在使得传统控制器在系统应用中有一定的局限 强、收敛速度快等特点,被广泛应用到各个领域 性,其应用的有效性也会受到很大的限制。因此,选 中[3)。同时针对标准粒子群算法存在的缺陷,为 择合理的解耦控制算法并有效地应用到控制器设计 了提高粒子群算法的性能,国内外研究学者在算法 收稿日期:2014-06-17.网络出版日期:2015-09-30. 的惯性权重、加速度系数因子等方面提出了许多改 基金项目:中央高校自由探素计划资助项目(HEUC℉0414O6). 进方法。胡建秀等[6提出了一种线性微分递减策 通信作者:于立君.E-mail:yulijun@hrbeu.edu.cn
第 10 卷第 5 期 智 能 系 统 学 报 Vol.10 №.5 2015 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2015 DOI:10.11992 / tis.201406028 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20150930.1556.004.html 改进粒子群算法的 PID 神经网络解耦控制 于立君,陈佳,刘繁明,王辉 (哈尔滨工程大学 自动化学院, 黑龙江 哈尔滨 150001) 摘 要:综合减摇控制系统存在非线性、多变量、强耦合等因素,会导致减摇系统达不到最佳控制状态。 利用粒子群 算法具有对整个空间进行高效搜索以及 PID 神经网络的自适应特点,提出一种改进粒子群算法,以解决粒子群算法 中存在算法精度不高、粒子易陷入局部极小值等问题,并提高 PID 神经网络训练速度和训练精度,便于参数寻优。 仿真结果表明,改进的粒子群算法具有一定优越性,将其运用到综合减摇控制系统解耦控制器设计中,能够有效地 减小船舶横摇,达到较好的控制效果。 关键词:粒子群算法;综合减摇系统;PID 神经网络;解耦控制;仿真分析 中图分类号:TH186 文献标志码:TP18 文章编号:1673⁃4785(2015)05⁃0699⁃06 中文引用格式:于立君,陈佳,刘繁明,等. 改进粒子群算法的 PID 神经网络解耦控制[J]. 智能系统学报, 2015, 10(5): 699⁃704. 英文引用格式:YU Lijun, CHEN Jia, LIU Fanming, et al. An improved particle swarm optimization for PID neural network de⁃ coupling control[J]. CAAI Transactions on Intelligent Systems, 2015, 10(5): 699⁃704. An improved particle swarm optimization for PID neural network decoupling control YU Lijun, CHEN Jia, LIU Fanming, WANG Hui (College of Automation, Harbin Engineering University, Harbin 150001, China) Abstract:The integrated ship stabilization system has nonlinear, multi⁃variable and strong coupling characteristics, which may hinder the system from reaching the best control state. An improved particle swarm algorithm is proposed based on the characteristics of particle swarm optimization (PSO) algorithm, which can search the parameter space efficiently, along with its associated PID artificial neuron network that has self⁃regulation and adaptability. The im⁃ proved particle swarm algorithm can overcome disadvantages in former particle swarm algorithms such as low preci⁃ sion, the particles tend to fall into extremely small values, and so on. In addition, the improved algorithm can in⁃ crease the training speed and precision of the PID nerve network, which facilitates parameter optimization. The sim⁃ ulation results show that the improved PSO has certain advantages, it can reduce ship rolling, and can achieve ex⁃ cellent control effects when it is applied to the design of the decoupling control of an integrated stabilization control system. Keywords:particle swarm algorithms; integrate stabilization system; PID neural network; decoupling control; sim⁃ ulation analysis 收稿日期:2014⁃06⁃17. 网络出版日期:2015⁃09⁃30. 基金项目:中央高校自由探索计划资助项目(HEUCF041406). 通信作者:于立君. E⁃mail:yulijun@ hrbeu.edu.cn. 综合减摇控制系统具有非线性强、控制变量多、 耦合性强、结构复杂且时变等特点[1] ,这些因素的 存在使得传统控制器在系统应用中有一定的局限 性,其应用的有效性也会受到很大的限制。 因此,选 择合理的解耦控制算法并有效地应用到控制器设计 中[2] ,将在很大程度上提高多变量耦合系统的控制 效果。 近年来,由于粒子群算法具有易实现、通用性 强、收敛速度快等特点, 被广泛应用到各个领域 中[3⁃5] 。 同时针对标准粒子群算法存在的缺陷,为 了提高粒子群算法的性能,国内外研究学者在算法 的惯性权重、加速度系数因子等方面提出了许多改 进方法。 胡建秀等[6] 提出了一种线性微分递减策

·700 智能系统学报 第10卷 略方法,用以提高算法的收敛速度。但是该算法会 在迭代过程中出现进入局部极值区域就难以跳出的 B=le VAraK.Kp 问题。陈水利等刀提出了一种非线性调整加速度 系数因子的策略,可使算法以最快速度搜索到最优 aC.K.Kp C=lp.V-A, 解所在的区域。经过验证该方法能够得到较理想的 对式(1)进行无量纲化可得 效果,但是由于后期种群的多样性的丧失,容易造成 中+2中+w中-B吃-a,2=K 早熟收敛。Alireza]在传统粒子群优化方法的基础 (2) (2+2u,2+wz-b,Φ-Rw中=0 上提出了具有适应变异机制和动态惯性权重系数的 2N, b2 2N.+B 算法,以增强算法的全局搜索能力,并提高准确性。 式中22pS入b2元2,004 算法对动态权重的惯性系数进行了改进,却没考虑 2pigSoR P.Sob2 Dh'+A 加速度因子对算法的影响。本文针对上述改进粒子 a+,+CB=,+,+Cg=1+,+C。 群算法中仍然存在的问题,提出了一种新的改进时 由式(2)可以看出综合减摇控制系统中存在着 变加速度系数的粒子群算法,将该算法与标准粒子 耦合项,而这种耦合影响是由船舶横摇角中及它的 群算法进行比较,并应用到综合减摇控制系统解耦 二阶导数中所引起的。因此,需要选取合适的控制 控制器设计中,验证了改进算法的有效性。 算法对系统进行解耦控制,进而消除减摇系统中存 1综合减摇耦合系统数学模型分析 在的耦合影响,达到提高综合减摇系统性能的目的。 改进粒子群算法的PD神经网络 综合减摇控制系统中,当横摇角较小时,可以把 2 船舶一减摇水舱系统看作是一个受激励的二自由度 解耦控制 振动系统,把减摇鳍的扶正力矩K=A中+Bd+C中 2.1改进粒子群算法 引入到该系统,可以建立综合减摇系统运动的微分 改进粒子群算法分析步骤如下。 方程[9.o」 粒子群的进化方程川可描述为 V(t+1)=ωV(t)+ [(I1+J,+C)中+(2N。+B)中+(Dh'+A)中- cir(t)(pbest;(t)-X:(t))+ (3) p,Sobz-2p gSoRz Dh'aosin @t c2r2(t)(gbest;(t)-X;(t)) 2pSo入2+2N,2+2p,gS2-p,Sob2中-2p,gSRb=0 X,(t+1)=X(t)+V(t+1) (4) (1) 式中:ω为惯性权重,描述的是粒子上一次运行速度 对当前次运行速度的影响[)。V,(t)表示第i个粒 式中:I1=I+△1,I和△1分别为相对于过船舶重心的 子在第t次迭代过程中的速度矢量,X,(t)表示第i 纵轴惯量和附加惯量;2N。为船舶阻尼力矩;D为排 个粒子在第t次迭代过程中的位置矢量,pbest,(t)、 水量:h'为稳心高;S。为边舱自由液面面积;S为沿 gbest,(t)分别代表第i个粒子在第t次迭代后该粒 水舱轴线的法线方向的局部截面积:r为微质量d 子的历史最优点和种群历史最优点。方程中参数 的质心到横摇轴的距离:y为r与d之间的夹角:dl 为迭代次数,1、2为[0,1]的随机数,用来保持种群 为液体微体积沿水舱轴线的长度:!为型水舱轴线 个体的多样性。c2为加速度系数因子,可以 长度:4,=厂二!为舱内水柱相当长度心: 使粒子向自己的历史最优点和种群历史最优点靠 近,通常取值在0~4之间。 Ratnaweera等[i4、乔俊飞等ti]提出了一种参数 reos ydl为水舱轴线对横摇轴的静压力矩;J,= 自调整策略,在进化过程中,通过调整加速度系数动 P,,Sdl为舱内液体对横摇轴的质量惯性矩;R为 态调节算法的局部和全局搜索能力。对于时变加速 度系数,调节公式定义如下: 边舱中至船舶纵中刨面的水平距离:N。为船舶阻尼 c1=(cy-ci)×t/Tms+ci (5) 系数;P,为海水密度;V为航速;A为鳍的投影面积; c2=(c2y-ca)×t/Tmx+c2z (6) aC,/aa为升力系数斜率; 式中:c:cy、c2和c2均为常数,1是当前的迭代次 数,T是最大的迭代次数。 本文在此基础上做如下修改,提出一种改进的
略方法,用以提高算法的收敛速度。 但是该算法会 在迭代过程中出现进入局部极值区域就难以跳出的 问题。 陈水利等[7] 提出了一种非线性调整加速度 系数因子的策略,可使算法以最快速度搜索到最优 解所在的区域。 经过验证该方法能够得到较理想的 效果,但是由于后期种群的多样性的丧失,容易造成 早熟收敛。 Alireza [8]在传统粒子群优化方法的基础 上提出了具有适应变异机制和动态惯性权重系数的 算法,以增强算法的全局搜索能力,并提高准确性。 算法对动态权重的惯性系数进行了改进,却没考虑 加速度因子对算法的影响。 本文针对上述改进粒子 群算法中仍然存在的问题,提出了一种新的改进时 变加速度系数的粒子群算法,将该算法与标准粒子 群算法进行比较,并应用到综合减摇控制系统解耦 控制器设计中,验证了改进算法的有效性。 1 综合减摇耦合系统数学模型分析 综合减摇控制系统中,当横摇角较小时,可以把 船舶—减摇水舱系统看作是一个受激励的二自由度 振动系统,把减摇鳍的扶正力矩 Kc = Aϕ + Bϕ · + Cϕ ¨ 引入到该系统,可以建立综合减摇系统运动的微分 方程[9⁃10] : (I1 + Jt + C)ϕ ¨ + (2Nϕ + B)ϕ · + (Dh′ + A)ϕ - ρtS0 b 2 z ¨ - 2ρtgS0Rz = Dh′a0 sin ωt 2ρtS0λt z ¨ + 2Nt z · + 2ρtgS0 z - ρtS0 b 2ϕ ¨ - 2ρtgS0Rϕ = 0 ì î í ï ï ï ï (1) 式中:I1 = I+ΔI,I 和 ΔI 分别为相对于过船舶重心的 纵轴惯量和附加惯量;2Nϕ 为船舶阻尼力矩;D 为排 水量;h′为稳心高;S0 为边舱自由液面面积;S 为沿 水舱轴线的法线方向的局部截面积;r 为微质量 dm 的质心到横摇轴的距离;γ 为 r 与 d 之间的夹角;dl 为液体微体积沿水舱轴线的长度;l 为型水舱轴线 长度; λt = 1 2 ∫ l 0 S0 S dl 为舱内水柱相当长度;b 2 = ∫ l 0 rcos γdl 为水舱轴线对横摇轴的静压力矩;Jt = ρt ∫ l 0 r 2 Sdl 为舱内液体对横摇轴的质量惯性矩; R 为 边舱中至船舶纵中刨面的水平距离;Nϕ 为船舶阻尼 系数;ρt 为海水密度;V 为航速;Af 为鳍的投影面积; ∂Cy / ∂α 为升力系数斜率; A = l f ρtV 2 AF ∂Cy ∂α KhKI B = l f ρtV 2 AF ∂Cy ∂α KhKP C = l f ρtV 2 AF ∂Cy ∂α KhKD 对式(1)进行无量纲化可得 ϕ ¨ + 2vϕϕ · + ω 2 ϕϕ - βz ¨ - at z = Kω z ¨ + 2vt z . + ω 2 t z - btϕ¨ - Rω 2 t ϕ = 0 { (2) 式中:2vt = 2Nt 2ρtS0λt ;bt = b 2 2λt ;2vϕ = 2Nϕ +B (I1 +Jt +C) ;ω 2 t = g λt ; αt = 2ρtgS0R (I1 +Jt +C) ;β = ρtS0 b 2 (I1 +Jt +C) ;ω 2 ϕ = Dh′+A (I1 +Jt +C) 。 由式(2)可以看出综合减摇控制系统中存在着 耦合项,而这种耦合影响是由船舶横摇角 ϕ 及它的 二阶导数 ϕ ¨ 所引起的。 因此,需要选取合适的控制 算法对系统进行解耦控制,进而消除减摇系统中存 在的耦合影响,达到提高综合减摇系统性能的目的。 2 改进粒子群算法的 PID 神经网络 解耦控制 2.1 改进粒子群算法 改进粒子群算法分析步骤如下。 粒子群的进化方程[11]可描述为 Vi(t + 1) = ωVi(t) + c1 r1(t)(pbest i(t) - Xi(t)) + (3) c2 r2(t)(gbest i(t) - Xi(t)) Xi(t + 1) = Xi(t) + Vi(t + 1) (4) 式中:ω 为惯性权重,描述的是粒子上一次运行速度 对当前次运行速度的影响[12] 。 Vi( t)表示第 i 个粒 子在第 t 次迭代过程中的速度矢量,Xi( t)表示第 i 个粒子在第 t 次迭代过程中的位置矢量,pbest i( t)、 gbest i(t)分别代表第 i 个粒子在第 t 次迭代后该粒 子的历史最优点和种群历史最优点。 方程中参数 t 为迭代次数,r1 、r2 为[0,1]的随机数,用来保持种群 个体的多样性[13] 。 c1 、c2 为加速度系数因子,可以 使粒子向自己的历史最优点和种群历史最优点靠 近,通常取值在 0~4 之间。 Ratnaweera 等[14] 、乔俊飞等[15]提出了一种参数 自调整策略,在进化过程中,通过调整加速度系数动 态调节算法的局部和全局搜索能力。 对于时变加速 度系数,调节公式定义如下: c1 = (c1f - c1i) × t / Tmax + c1i (5) c2 = (c2f - c2i) × t / Tmax + c2i (6) 式中:c1i、c1f、c2i 和 c2f 均为常数,t 是当前的迭代次 数,Tmax是最大的迭代次数。 本文在此基础上做如下修改,提出一种改进的 ·700· 智 能 系 统 学 报 第 10 卷

第5期 于立君,等:改进粒子群算法的PD神经网络解耦控制 ·701· 时变加速度系数的粒子群算法,定义加速度系数公 根据表1中的数据可以得到该减摇系统具体表 式如下: 达式为 c1=(cu-cy)x exp[-(4t/Tms)2]+cu(7) W(s)=(0.8866s3+0.2746s2+0.5863s)/(5.06× c2=(cx-c2y)×exp[-(4t/Tmr)2]+c2y(8) 式中:c:和c2分别是加速度系数c1和c2的初始值。 10-6s3+4.829×10-4s4+0.02767s3+0.4075s2+ c和c2分别是加速度系数c,和c2的最终值。则改 4.772s+2) (12) 变加速度系数后,粒子群算法更新方程如下: 本文选取综合减摇控制系统性能指标函数为 V(t+1)=w×V(t)+ (ct-cy)×exp[-(4t/Tm)2]+cy)× [p,(t)-p.(t)]2(13) r:x (pbest;(t)-X(t))+ (9) (cy-cr)×exp[-(4t/Tm)2]+c2r)× 式中:E:为输出横摇角的误差平方和,9,(t)为预测 r2 x (gbest (t)-X:(t)) 输出横摇角,9(t)为实际输出横摇角,n为训练样 改进粒子群算法流程如图1所示。 本数。粒子群中个体的适应度函数选为 开始 6=J (14) 表1综合减摇系统主要参数 设定初始参数 Table 1 Parameters of integrated stabilization system 随机产生N个个体 船长/m 195.3 航速V/(m·s) 9.972 计算系统适应值 船宽/m 25.6 水舱底部通道高度h/m0.520 计算控制指标 吃水/m 3.090 水舱边舱宽度G,/m 0.527 选择部分较优粒子 更新粒子速度 迭代数加1 排水量/m3 1574 鳍面A/m2 3.000 更新粒子位置 鰭力矩至船舶横摇 无因阻尼系数 0.070 5.600 组成新的粒子群 中心的距离l/m 周期T/s 7.243 边舱高H,/m 4.930 计算指标 重力加速度 两个边舱中心之间 N 9.81 8.074 g/(m·s2) 的水平距离L/m Y 水舱布置度H./m 4.930 水舱后稳性高h/m0.9835 结束 水舱底部到船舶重心 升力系数C, 0.055 -1.5 图1改进粒子群算法流程 距离d/m Fig.1 The flow chart of improved PSO algorithm 2.2改进粒子群算法的综合减摇系统PID神经网 3 仿真分析 络解耦控制 为了验证本文提出的改进粒子群算法的可行性 选取式(2)为综合减摇系统模型进行分析,相 应的系统参数如表1所示,并对式(2)进行变换得 以及优劣性,分别采用标准粒子群算法和改进粒子 b+2u中+o中-B版-a,2= Dh'aosin wt 群算法对式(14)中的适应度函数进行仿真,并从收 11+J,+C(10) 敛速度、最优适应度值的变化情况以及搜索精度3 e+2,z+wz-b,中-Rwb=0 方面进行比较。选取相应的参数为:初始关系权重 对式(10)进行Laplace变换并整理可得 W(s)=中(s)/a(s)= ωm=0.9,终惯性权重wn=0.1,最大速度量Vm= o8(s2+2,s+u)/Dm 0.03,最小速度量Vn=-0.03。 (s2+2s+o)(s2+2,3+w)+(6,s2+R@)(-B2-a,) 选取种群规模为m=100,迭代次数为40进行 (11) 仿真,结果如图2~6所示
时变加速度系数的粒子群算法,定义加速度系数公 式如下: c1 = (c1i - c1f) × exp[ - (4t / Tmax) 2 ] + c1f (7) c2 = (c2i - c2f) × exp[ - (4t / Tmax) 2 ] + c2f (8) 式中:c1i和 c2i分别是加速度系数 c1 和 c2 的初始值。 c1f和 c2f分别是加速度系数 c1 和 c2 的最终值。 则改 变加速度系数后,粒子群算法更新方程如下: Vi(t + 1) = ω × Vi(t) + ((c1i - c1f) × exp[ - (4t / Tmax) 2 ] + c1f) × r1 × (pbest i(t) - Xi(t)) + (9) ((c1f - c2f) × exp[ - (4t / Tmax) 2 ] + c2f) × r2 × (gbest i(t) - Xi(t)) 改进粒子群算法流程如图 1 所示。 图 1 改进粒子群算法流程 Fig.1 The flow chart of improved PSO algorithm 2.2 改进粒子群算法的综合减摇系统 PID 神经网 络解耦控制 选取式(2)为综合减摇系统模型进行分析,相 应的系统参数如表 1 所示,并对式(2)进行变换得 ϕ ¨ + 2vϕϕ · + ω 2 ϕϕ - βz ¨ - at z = Dh′a0 sin ωt I1 + Jt + C z ¨ + 2vt z . + ω 2 t z - btϕ ¨ - Rω 2 t ϕ = 0 ì î í ï ï ï ï (10) 对式(10)进行 Laplace 变换并整理可得 Wϕ(s) = ϕ(s) / a(s) = ω 2 ϕ(s 2 + 2vt s + ω 2 t ) / Dh′ (s 2 + 2vϕ s + ω 2 ϕ)(s 2 + 2vt s + ω 2 t ) + (bt s 2 + Rω 2 t )( - βs 2 - αt) (11) 根据表 1 中的数据可以得到该减摇系统具体表 达式为 Wϕ(s) = (0.886 6s 3 + 0.274 6s 2 + 0.586 3s) / (5.06 × 10 -6 s 5 + 4.829 × 10 -4 s 4 + 0.027 67s 3 + 0.407 5s 2 + 4.77 2s + 2) (12) 本文选取综合减摇控制系统性能指标函数为 J = 1 2 ∑ n i = 1 Ei = 1 2 ∑ n i = 1 [φr(t) - φo(t)] 2 (13) 式中:Ei 为输出横摇角的误差平方和,φr( t)为预测 输出横摇角,φo( t)为实际输出横摇角,n 为训练样 本数。 粒子群中个体的适应度函数选为 f i = J (14) 表 1 综合减摇系统主要参数 Table 1 Parameters of integrated stabilization system 船长/ m 195.3 航速 V/ (m·s -1 ) 9.972 船宽/ m 25.6 水舱底部通道高度hd / m 0.520 吃水/ m 3.090 水舱边舱宽度 wr / m 0.527 排水量/ m 3 1 574 鳍面 Af / m 2 3.000 无因阻尼系数 0.070 鳍力矩至船舶横摇 中心的距离 l f / m 5.600 周期 T0 / s 7.243 边舱高 Ht / m 4.930 重力加速度 g / (m·s -2 ) 9.81 两个边舱中心之间 的水平距离 L / m 8.074 水舱布置度Hz / m 4.930 水舱后稳性高 h / m 0.983 5 升力系数 Cy 0.055 水舱底部到船舶重心 距离dt / m -1.5 3 仿真分析 为了验证本文提出的改进粒子群算法的可行性 以及优劣性,分别采用标准粒子群算法和改进粒子 群算法对式(14)中的适应度函数进行仿真,并从收 敛速度、最优适应度值的变化情况以及搜索精度 3 方面进行比较。 选取相应的参数为:初始关系权重 ωmax = 0.9,终惯性权重 ωmin = 0.1,最大速度量 Vmax = 0.03,最小速度量 Vmin = -0.03。 选取种群规模为 m = 100,迭代次数为 40 进行 仿真,结果如图 2~6 所示。 第 5 期 于立君,等:改进粒子群算法的 PID 神经网络解耦控制 ·701·
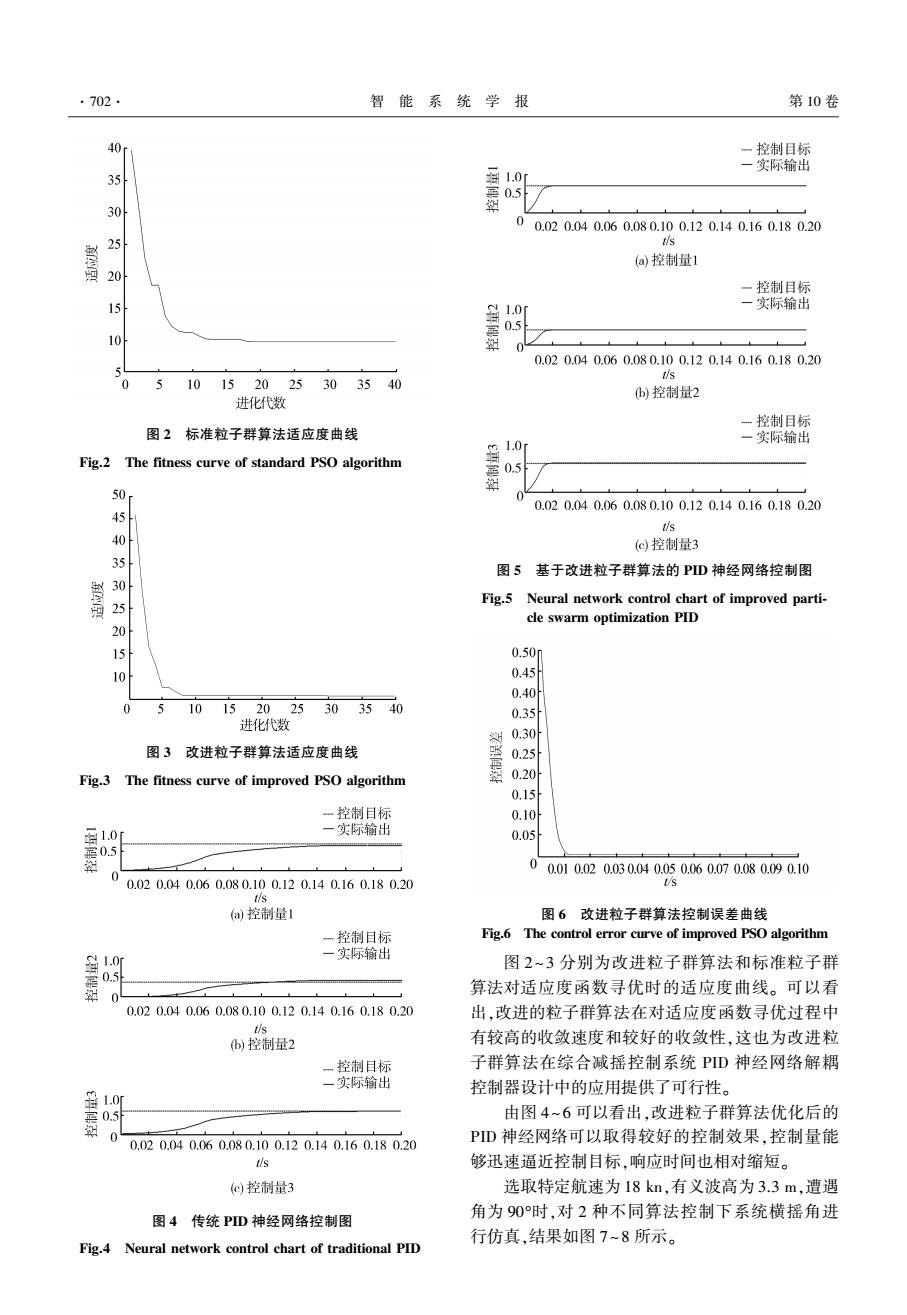
·702 智能系统学报 第10卷 40r 控制目标 一实际输出 35 0.5 30 0 0.020.040.060.080.100.120.140.160.180.20 s (a)控制量1 20 一控制目标 一实际输出 0.5 10 0.020.040.060.080.100.120.140.160.180.20 tis 0 510152025303540 )控制量2 进化代数 一控制目标 图2标准粒子群算法适应度曲线 1.0r 一实际输出 Fig.2 The fitness curve of standard PSO algorithm 0.5 50 0 0.020.040.060.080.100.120.140.160.180.20 tis 40 (c)控制量3 5 图5基于改进粒子群算法的PD神经网络控制图 0万 Fig.5 Neural network control chart of improved parti- cle swarm optimization PID 0.50m 0.45 0.40 0 10 152025 303540 0.35 进化代数 0.30 图3改进粒子群算法适应度曲线 0.25 Fig.3 The fitness curve of improved PSO algorithm 0.20 0.15 一控制目标 0.10 日1.01 一实际输出 0.05 00.010.020.030.040.050.060.070.080.090.10 0.020.040.060.080.100.120.140.160.180.20 s tis (a,控制量1 图6改进粒子群算法控制误差曲线 控制目标 Fig.6 The control error curve of improved PSO algorithm 一实际输出 图2~3分别为改进粒子群算法和标准粒子群 0.5 0 算法对适应度函数寻优时的适应度曲线。可以看 0.020.040.060.080.100.120.140.160.180.20 出,改进的粒子群算法在对适应度函数寻优过程中 tis b)控制量2 有较高的收敛速度和较好的收敛性,这也为改进粒 控制目标 子群算法在综合减摇控制系统PD神经网络解耦 一实际输出 控制器设计中的应用提供了可行性。 1.0 0.5 由图4~6可以看出,改进粒子群算法优化后的 PD神经网络可以取得较好的控制效果,控制量能 0.020.040.060.080.100.120.140.160.180.20 你 够迅速逼近控制目标,响应时间也相对缩短。 (@)控制量3 选取特定航速为18kn,有义波高为3.3m,遭遇 角为90时,对2种不同算法控制下系统横摇角进 图4传统PD神经网络控制图 行仿真,结果如图7~8所示。 Fig.4 Neural network control chart of traditional PID
图 2 标准粒子群算法适应度曲线 Fig.2 The fitness curve of standard PSO algorithm 图 3 改进粒子群算法适应度曲线 Fig.3 The fitness curve of improved PSO algorithm 图 4 传统 PID 神经网络控制图 Fig.4 Neural network control chart of traditional PID 图 5 基于改进粒子群算法的 PID 神经网络控制图 Fig.5 Neural network control chart of improved parti⁃ cle swarm optimization PID 图 6 改进粒子群算法控制误差曲线 Fig.6 The control error curve of improved PSO algorithm 图 2~3 分别为改进粒子群算法和标准粒子群 算法对适应度函数寻优时的适应度曲线。 可以看 出,改进的粒子群算法在对适应度函数寻优过程中 有较高的收敛速度和较好的收敛性,这也为改进粒 子群算法在综合减摇控制系统 PID 神经网络解耦 控制器设计中的应用提供了可行性。 由图 4~6 可以看出,改进粒子群算法优化后的 PID 神经网络可以取得较好的控制效果,控制量能 够迅速逼近控制目标,响应时间也相对缩短。 选取特定航速为 18 kn,有义波高为 3.3 m,遭遇 角为 90°时,对 2 种不同算法控制下系统横摇角进 行仿真,结果如图 7~8 所示。 ·702· 智 能 系 统 学 报 第 10 卷
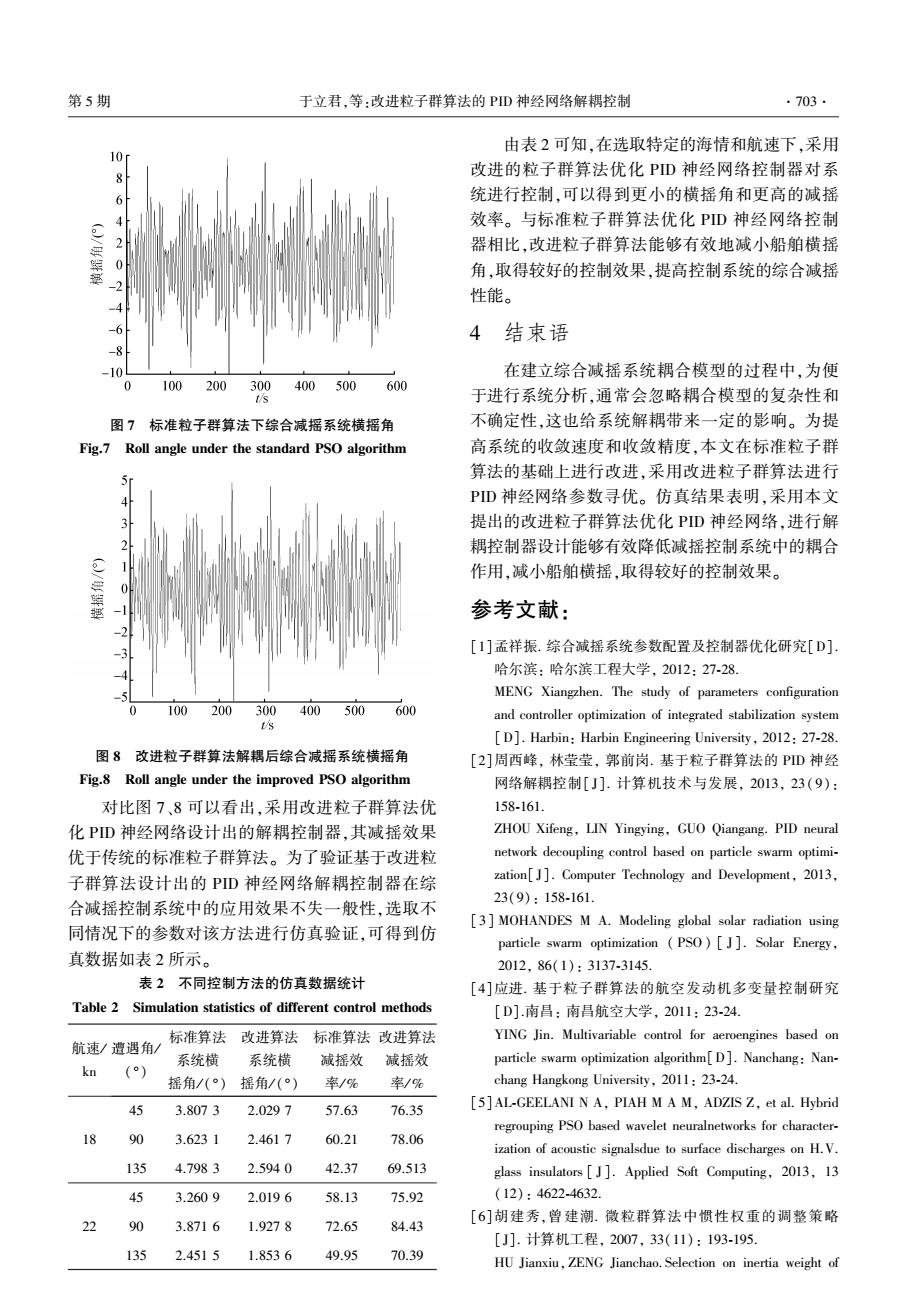
第5期 于立君,等:改进粒子群算法的PD神经网络解耦控制 ·703· 由表2可知,在选取特定的海情和航速下,采用 10 8 改进的粒子群算法优化PD神经网络控制器对系 6 统进行控制,可以得到更小的横摇角和更高的减摇 效率。与标准粒子群算法优化PD神经网络控制 2 器相比,改进粒子群算法能够有效地减小船舶横摇 角,取得较好的控制效果,提高控制系统的综合减摇 性能。 4结束语 -10 在建立综合减摇系统耦合模型的过程中,为便 100200300400500 600 于进行系统分析,通常会忽略耦合模型的复杂性和 图7标准粒子群算法下综合减摇系统横摇角 不确定性,这也给系统解耦带来一定的影响。为提 Fig.7 Roll angle under the standard PSO algorithm 高系统的收敛速度和收敛精度,本文在标准粒子群 算法的基础上进行改进,采用改进粒子群算法进行 PD神经网络参数寻优。仿真结果表明,采用本文 提出的改进粒子群算法优化PID神经网络,进行解 耦控制器设计能够有效降低减摇控制系统中的耦合 作用,减小船舶横摇,取得较好的控制效果。 参考文献: [1]孟祥振.综合减摇系统参数配置及控制器优化研究[D]. 哈尔滨:哈尔滨工程大学,2012:27-28 MENG Xiangzhen.The study of parameters configuration 100200300 400 500 600 and controller optimization of integrated stabilization system t/s [D].Harbin:Harbin Engineering University,2012:27-28. 图8改进粒子群算法解耦后综合减摇系统横摇角 [2]周西峰,林莹莹,郭前岗.基于粒子群算法的PD神经 Fig.8 Roll angle under the improved PSO algorithm 网络解耦控制[J].计算机技术与发展,2013,23(9): 对比图7、8可以看出,采用改进粒子群算法优 158-161 化PD神经网络设计出的解耦控制器,其减摇效果 ZHOU Xifeng,LIN Yingying,GUO Qiangang.PID neural 优于传统的标准粒子群算法。为了验证基于改进粒 network decoupling control based on particle swarm optimi- 子群算法设计出的PD神经网络解耦控制器在综 zation[J].Computer Technology and Development,2013, 23(9):158-161. 合减摇控制系统中的应用效果不失一般性,选取不 [3]MOHANDES M A.Modeling global solar radiation using 同情况下的参数对该方法进行仿真验证,可得到仿 particle swarm optimization (PSO)[J].Solar Energy, 真数据如表2所示。 2012,86(1):3137-3145. 表2不同控制方法的仿真数据统计 [4]应进.基于粒子群算法的航空发动机多变量控制研究 Table 2 Simulation statistics of different control methods [D].南昌:南昌航空大学,2011:23-24. 标准算法改进算法标准算法改进算法 YING Jin.Multivariable control for aeroengines based on 航速/遭遇角/ 系统横 系统横 减摇效 减摇效 particle swarm optimization algorithm[D].Nanchang:Nan- kn (°) 摇角/()摇角/(。) 率/% 率/% chang Hangkong University,2011:23-24. 45 3.8073 2.0297 57.63 76.35 [5]AL-GEELANI N A,PIAH M A M,ADZIS Z,et al.Hybrid regrouping PSO based wavelet neuralnetworks for character- 18 90 3.6231 2.4617 60.21 78.06 ization of acoustic signalsdue to surface discharges on H.V. 135 4.7983 2.5940 42.37 69.513 glass insulators J].Applied Soft Computing,2013,13 45 3.2609 2.0196 58.13 75.92 (12):4622-4632. 22 90 [6]胡建秀,曾建潮.微粒群算法中惯性权重的调整策略 3.8716 1.9278 72.65 84.43 [J].计算机工程,2007,33(11):193-195. 135 2.4515 1.8536 49.95 70.39 HU Jianxiu,ZENG Jianchao.Selection on inertia weight of
图 7 标准粒子群算法下综合减摇系统横摇角 Fig.7 Roll angle under the standard PSO algorithm 图 8 改进粒子群算法解耦后综合减摇系统横摇角 Fig.8 Roll angle under the improved PSO algorithm 对比图 7、8 可以看出,采用改进粒子群算法优 化 PID 神经网络设计出的解耦控制器,其减摇效果 优于传统的标准粒子群算法。 为了验证基于改进粒 子群算法设计出的 PID 神经网络解耦控制器在综 合减摇控制系统中的应用效果不失一般性,选取不 同情况下的参数对该方法进行仿真验证,可得到仿 真数据如表 2 所示。 表 2 不同控制方法的仿真数据统计 Table 2 Simulation statistics of different control methods 航速/ kn 遭遇角/ (°) 标准算法 系统横 摇角/ (°) 改进算法 系统横 摇角/ (°) 标准算法 减摇效 率/ % 改进算法 减摇效 率/ % 18 45 3.807 3 2.029 7 57.63 76.35 90 3.623 1 2.461 7 60.21 78.06 135 4.798 3 2.594 0 42.37 69.513 22 45 3.260 9 2.019 6 58.13 75.92 90 3.871 6 1.927 8 72.65 84.43 135 2.451 5 1.853 6 49.95 70.39 由表 2 可知,在选取特定的海情和航速下,采用 改进的粒子群算法优化 PID 神经网络控制器对系 统进行控制,可以得到更小的横摇角和更高的减摇 效率。 与标准粒子群算法优化 PID 神经网络控制 器相比,改进粒子群算法能够有效地减小船舶横摇 角,取得较好的控制效果,提高控制系统的综合减摇 性能。 4 结束语 在建立综合减摇系统耦合模型的过程中,为便 于进行系统分析,通常会忽略耦合模型的复杂性和 不确定性,这也给系统解耦带来一定的影响。 为提 高系统的收敛速度和收敛精度,本文在标准粒子群 算法的基础上进行改进,采用改进粒子群算法进行 PID 神经网络参数寻优。 仿真结果表明,采用本文 提出的改进粒子群算法优化 PID 神经网络,进行解 耦控制器设计能够有效降低减摇控制系统中的耦合 作用,减小船舶横摇,取得较好的控制效果。 参考文献: [1]孟祥振. 综合减摇系统参数配置及控制器优化研究[D]. 哈尔滨: 哈尔滨工程大学, 2012: 27⁃28. MENG Xiangzhen. The study of parameters configuration and controller optimization of integrated stabilization system [D]. Harbin: Harbin Engineering University, 2012: 27⁃28. [2]周西峰, 林莹莹, 郭前岗. 基于粒子群算法的 PID 神经 网络解耦控制[ J]. 计算机技术与发展, 2013, 23( 9): 158⁃161. ZHOU Xifeng, LIN Yingying, GUO Qiangang. PID neural network decoupling control based on particle swarm optimi⁃ zation[ J]. Computer Technology and Development, 2013, 23(9): 158⁃161. [3] MOHANDES M A. Modeling global solar radiation using particle swarm optimization ( PSO) [ J ]. Solar Energy, 2012, 86(1): 3137⁃3145. [4]应进. 基于粒子群算法的航空发动机多变量控制研究 [D].南昌: 南昌航空大学, 2011: 23⁃24. YING Jin. Multivariable control for aeroengines based on particle swarm optimization algorithm[D]. Nanchang: Nan⁃ chang Hangkong University, 2011: 23⁃24. [5]AL⁃GEELANI N A, PIAH M A M, ADZIS Z, et al. Hybrid regrouping PSO based wavelet neuralnetworks for character⁃ ization of acoustic signalsdue to surface discharges on H.V. glass insulators [ J ]. Applied Soft Computing, 2013, 13 (12): 4622⁃4632. [6]胡建秀,曾建潮. 微粒群算法中惯性权重的调整策略 [J]. 计算机工程, 2007, 33(11): 193⁃195. HU Jianxiu,ZENG Jianchao. Selection on inertia weight of 第 5 期 于立君,等:改进粒子群算法的 PID 神经网络解耦控制 ·703·

·704· 智能系统学报 第10卷 particle swarm optimization[J].Computer Engineering, [14]RATNAWEERA A.HAIGAMUGE S K.WATSON H C. 2007.33(11):193-195. Self-organizing hierarchical particle swarm optimizer with [7]陈水利,蔡国榕.PS0算法加速因子的非线性策略研究 time-varying acceleration coefficients[J].IEEE Transac. [J].长江大学学报(自然版):理工卷,2007,4(4):1-4. tions on Evolutionary Compution,2004,8(3):240-255. CHEN Shuili,CAI Guorong.Nonlinear strategy of PSO algo- [15]乔俊飞,逢泽芳,韩红桂.基于改进粒子群算法的污水 rithm acceleration factor[].Journal of Yangtze University 处理过程神经网络优化控制[J].智能系统学报,2012, Nat Sci Edit):Sci Eng V,2007,4(4):1-4. 7(5):429.436. [8]ALIREZA A.PSO with adaptive mutation and inertia weight QIAO Junfei,PANG Zefang,HAN Honggui.Neural net- and its application in parameter estimation of dynamic sys- work optimal control for wastewater treatment process based tems[J].Acta Automatica Sinica,2011,37(5):541-549. on APSO[J].CAAI Transactions on Intelligent Systems, [9]于立君,孟祥振,金宏章,等.综合减摇系统参数配置 2012,7(5):429.436 研究[J].中国造船,2012,53(4):13-21. 作者简介: YU Lijun,MENG Xiangzhen,JIN Hongzhang,et al.Study 于立君,男,1975年生,副教授,博 of configuration parameters of integrated stabilization system 士,主要研究方向为船舶运动控制、先 [J].Shipbuilding of China,2012,53(4):13-21. 进控制理论及应用。主持并完成博士 [10]于立君,孙经广,刘繁明,等.广义预测算法在综合减 后基金1项、横向项目1项、中央高校 摇系统控制器设计中的应用[J].船舶工程,2013,35 自由探索计划5项,获得黑龙江省科技 (6):76-79.83. 进步二等奖1项。 YU Lijun,SUN Jingguang,LIU Fanming,et al.Applica- tion of generalized prediction algorithm in designing inte- grated stabilization system controller[J].Ship Engineer- 陈佳,女,1989年生,硕士研究生, ing,2013,35(6):76-79,83. 主要研究方向为船舶智能控制理论方 [11]CHIOU J S,TSAI S H,LIU Mingtang.A PSO-based a- 法与应用。 daptive fuzzy PID-controllers [J].Simulation Modelling Practice and Theory,2012,26:49-59. [12]沈锡.基于粒子群优化算法的船舶航向PD控制[D]: 大连:大连海事大学,2011:6-7. SHEN Xi.PID control for ship steering based on particle 刘繁明,男,1963年生,教授,博士 swarm optimization[D].Dalian:Dalian Maritime Universi- 生导师,主要研究方向为水下潜器定位 ty,2011:6-7. 技术、弱信号测量与处理技术、被动导 [13]BOUALLEGUE S.HAGGEGE J.AYADI M,et al.PID- 航与定位技术、工业装置测控技术。承 type fuzzy logic controller tuning based on particle swarm 担“十二五”预先研究项目2项,国家自 optimization[J].Engineering Applications of Artificial In- 然科学基金重点项目1项,设备研制项 elligence,2012,25(3):484-493. 目多项
particle swarm optimization [ J ]. Computer Engineering, 2007, 33(11): 193⁃195. [7]陈水利, 蔡国榕. PSO 算法加速因子的非线性策略研究 [ J]. 长江大学学报(自然版): 理工卷, 2007, 4(4):1⁃4. CHEN Shuili, CAI Guorong. Nonlinear strategy of PSO algo⁃ rithm acceleration factor[ J]. Journal of Yangtze University (Nat Sci Edit): Sci & Eng V, 2007, 4(4): 1⁃4. [8]ALIREZA A. PSO with adaptive mutation and inertia weight and its application in parameter estimation of dynamic sys⁃ tems[J]. Acta Automatica Sinica, 2011, 37(5): 541⁃549. [9]于立君, 孟祥振, 金宏章, 等. 综合减摇系统参数配置 研究[J]. 中国造船, 2012, 53(4): 13⁃21. YU Lijun, MENG Xiangzhen, JIN Hongzhang, et al. Study of configuration parameters of integrated stabilization system [J]. Shipbuilding of China, 2012, 53(4): 13⁃21. [10]于立君, 孙经广, 刘繁明, 等. 广义预测算法在综合减 摇系统控制器设计中的应用[ J]. 船舶工程, 2013, 35 (6): 76⁃79, 83. YU Lijun, SUN Jingguang, LIU Fanming, et al. Applica⁃ tion of generalized prediction algorithm in designing inte⁃ grated stabilization system controller [ J]. Ship Engineer⁃ ing, 2013, 35(6):76⁃79, 83. [11]CHIOU J S, TSAI S H, LIU Mingtang. A PSO⁃based a⁃ daptive fuzzy PID⁃controllers [ J ]. Simulation Modelling Practice and Theory, 2012, 26: 49⁃59. [12]沈锡.基于粒子群优化算法的船舶航向 PID 控制[D]. 大连: 大连海事大学, 2011: 6⁃7. SHEN Xi. PID control for ship steering based on particle swarm optimization[D]. Dalian: Dalian Maritime Universi⁃ ty, 2011: 6⁃7. [13]BOUALLÈGUE S, HAGGÈGE J, AYADI M, et al. PID- type fuzzy logic controller tuning based on particle swarm optimization[ J]. Engineering Applications of Artificial In⁃ telligence, 2012, 25(3): 484⁃493. [14] RATNAWEERA A, HAIGAMUGE S K, WATSON H C. Self⁃organizing hierarchical particle swarm optimizer with time⁃varying acceleration coefficients [ J]. IEEE Transac⁃ tions on Evolutionary Compution, 2004, 8(3): 240⁃255. [15]乔俊飞, 逄泽芳, 韩红桂. 基于改进粒子群算法的污水 处理过程神经网络优化控制[J]. 智能系统学报, 2012, 7(5): 429⁃436. QIAO Junfei, PANG Zefang, HAN Honggui. Neural net⁃ work optimal control for wastewater treatment process based on APSO[ J]. CAAI Transactions on Intelligent Systems, 2012,7(5): 429⁃436. 作者简介: 于立君,男,1975 年生,副教授,博 士,主要研究方向为船舶运动控制、先 进控制理论及应用。 主持并完成博士 后基金 1 项、横向项目 1 项、中央高校 自由探索计划 5 项,获得黑龙江省科技 进步二等奖 1 项。 陈佳,女,1989 年生,硕士研究生, 主要研究方向为船舶智能控制理论方 法与应用。 刘繁明,男,1963 年生,教授,博士 生导师,主要研究方向为水下潜器定位 技术、弱信号测量与处理技术、被动导 航与定位技术、工业装置测控技术。 承 担“十二五”预先研究项目 2 项,国家自 然科学基金重点项目 1 项,设备研制项 目多项。 ·704· 智 能 系 统 学 报 第 10 卷