
第10卷第5期 智能系统学报 Vol.10 No.5 2015年10月 CAAI Transactions on Intelligent Systems 0ct.2015 D0I:10.11992/is.201410036 网s络出版地址:htp:/www.cmki.net/kcms/detail/23.1538.TP.20150827.1030.012.html 参数自适应粒子群算法的给水管网优化研究 王超12,乔俊飞12 (1.北京工业大学电子信息与控制工程学院,北京100124:2.北京工业大学计算智能与智能系统北京市重点实验 室,北京100124) 摘要:针对粒子群算法在解决给水管网优化问题时存在容易陷入局部最优的缺点,通过分析粒子的运动轨迹和相 似程度,提出一种参数自适应粒子群算法。该算法利用种群粒子与期望粒子之间相似度的大小,动态调整算法参 数,平衡算法全局和局部搜索能力,利用分期变异策略增加种群多样性,保证算法收敛于全局最优值。将改进算法 用于优化汉诺塔管网和纽约管网2个经典的管网案例,证明算法可以有效应用于给水管网这类组合优化问题。将 该算法优化实际的管网改扩建案例,结果表明,所提出的算法具有更好的寻优性能和收敛性能。 关键词:给水管网系统:粒子轨迹:相似度:参数调整:自适应粒子群 中图分类号:TP18文献标志码:A文章编号:1673-4785(2015)05-0722-07 中文引用格式:王超,乔俊飞.参数自适应粒子群算法的给水管网优化研究[J].智能系统学报,2015,10(5):722-728. 英文引用格式:WANG Chao,QIAO Junfei..An parameter adaptive particle swarm optimization for optimal design of water supply systems[J].CAAI Transactions on Intelligent Systems,2015,10(5):722-728. An parameter adaptive particle swarm optimization for optimal design of water supply systems WANG Chao2,QIAO Junfei (1.College of Electronic Information and Control Engineering,Beijing University of Technology,Beijing 100124,China;2.Beijing Key Laboratory of Computational Intelligence and Intelligence System,Beijing University of Technology,Beijing 100124,China) Abstract:Particle swarm optimization easily falls into a local optimum when solving water supply optimization prob- lems.In order to solve this weakness,by analyzing particle trajectories and the similarity of particles,this paper proposes a parameter adaptive particle swarm optimization(PAPSO).By estimating the degree of similarity between particles and expected particles,the algorithm dynamically adjusts parameters and balances the global and local search ability.The algorithm uses the variation strategy of staging to increase the population diversity and ensure that it converges to the global optimum.The tower of Hanoi network and New York network have been optimized by the improved algorithm,and the result shows that the PAPSO algorithm can be effectively applied to the combinato- rial optimization of water supply pipeline networks.The proposed algorithm has been applied to optimize an actual pipe network reconstruction case and the result shows that the algorithm has better optimization and convergence performance. Keywords:water supply system;particle trajectories;similarity;parameter adjustment;adaptive particle swarm op- timization 给水管网是城市给水系统的重要组成部分,其80%,而且运行期间还需投入庞大的运行动力费及 投资往往占整个给水系统工程总投资的60%~ 管理维修费)。当前我国各城市给水管网都已达 到一定规模,原有管网出现外壁腐蚀、爆管漏损率高 收稿日期:2014-10-27.网络出版日期:2015-08-27. 基金项目:国家自然科学基金重点资助项目(61034008):国家自然科 等问题:随着城市的快速发展,部分管道无法满足供 学基金杰出青年资助项目(61225016):北京市自然科学基 水需求:城市街道拓宽、其他管线的施工使现有管道 金资助项目(4122006). 通信作者:乔俊飞.E-mail:isibox@sina.com 需做相应调整。针对这些问题,需对给水管网进行
第 10 卷第 5 期 智 能 系 统 学 报 Vol.10 №.5 2015 年 10 月 CAAI Transactions on Intelligent Systems Oct. 2015 DOI:10.11992 / tis.201410036 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.TP.20150827.1030.012.html 参数自适应粒子群算法的给水管网优化研究 王超1,2 ,乔俊飞1,2 (1. 北京工业大学 电子信息与控制工程学院, 北京 100124; 2. 北京工业大学 计算智能与智能系统北京市重点实验 室, 北京 100124) 摘 要:针对粒子群算法在解决给水管网优化问题时存在容易陷入局部最优的缺点,通过分析粒子的运动轨迹和相 似程度,提出一种参数自适应粒子群算法。 该算法利用种群粒子与期望粒子之间相似度的大小,动态调整算法参 数,平衡算法全局和局部搜索能力,利用分期变异策略增加种群多样性,保证算法收敛于全局最优值。 将改进算法 用于优化汉诺塔管网和纽约管网 2 个经典的管网案例,证明算法可以有效应用于给水管网这类组合优化问题。 将 该算法优化实际的管网改扩建案例,结果表明,所提出的算法具有更好的寻优性能和收敛性能。 关键词:给水管网系统;粒子轨迹;相似度;参数调整;自适应粒子群 中图分类号:TP18 文献标志码:A 文章编号:1673⁃4785(2015)05⁃0722⁃07 中文引用格式:王超,乔俊飞. 参数自适应粒子群算法的给水管网优化研究[J]. 智能系统学报, 2015, 10(5): 722⁃728. 英文引用格式:WANG Chao, QIAO Junfei. An parameter adaptive particle swarm optimization for optimal design of water supply systems[J]. CAAI Transactions on Intelligent Systems, 2015, 10(5): 722⁃728. An parameter adaptive particle swarm optimization for optimal design of water supply systems WANG Chao 1,2 , QIAO Junfei 1,2 (1. College of Electronic Information and Control Engineering, Beijing University of Technology, Beijing 100124, China; 2. Beijing Key Laboratory of Computational Intelligence and Intelligence System, Beijing University of Technology, Beijing 100124, China) Abstract:Particle swarm optimization easily falls into a local optimum when solving water supply optimization prob⁃ lems. In order to solve this weakness, by analyzing particle trajectories and the similarity of particles, this paper proposes a parameter adaptive particle swarm optimization (PAPSO). By estimating the degree of similarity between particles and expected particles, the algorithm dynamically adjusts parameters and balances the global and local search ability. The algorithm uses the variation strategy of staging to increase the population diversity and ensure that it converges to the global optimum. The tower of Hanoi network and New York network have been optimized by the improved algorithm, and the result shows that the PAPSO algorithm can be effectively applied to the combinato⁃ rial optimization of water supply pipeline networks. The proposed algorithm has been applied to optimize an actual pipe network reconstruction case and the result shows that the algorithm has better optimization and convergence performance. Keywords:water supply system; particle trajectories; similarity; parameter adjustment; adaptive particle swarm op⁃ timization 收稿日期:2014⁃10⁃27. 网络出版日期:2015⁃08⁃27. 基金项目:国家自然科学基金重点资助项目(61034008);国家自然科 学基金杰出青年资助项目(61225016);北京市自然科学基 金资助项目(4122006). 通信作者:乔俊飞. E⁃mail: isibox@ sina.com. 给水管网是城市给水系统的重要组成部分,其 投资往往占整个给水系统工程总投资的 60% ~ 80%,而且运行期间还需投入庞大的运行动力费及 管理维修费[1] 。 当前我国各城市给水管网都已达 到一定规模,原有管网出现外壁腐蚀、爆管漏损率高 等问题;随着城市的快速发展,部分管道无法满足供 水需求;城市街道拓宽、其他管线的施工使现有管道 需做相应调整。 针对这些问题,需对给水管网进行

第5期 王超,等:参数自适应粒子群算法的给水管网优化研究 ·723· 改扩建优化设计。 的步长,加速系数©,可以调节粒子向群体最优位置 为了优化给水管网,许多方法被广泛应用,如遗 的飞行步长。因此,本文将继续研究这3个参数的 传算法[2】、蚁群算法[、启发式算法[)、差分算 调整策略,并根据以上3个参数的调整思想,为动态 法[o和足球联赛竞争算法[)。其中粒子群(particle 评估种群中各粒子分布状态,实现算法自适应性,对 swarm optimization,PSO)算法因其可调参数少及具 种群粒子进行收敛性分析,定义种群粒子相似度的 有本质的并行性、全局搜索能力强、整体收敛速度快 概念,提出一种参数自适应粒子群算法(parameter 等优点,展现了较大的解决多种优化问题的潜力和 adaptive particle swarm optimization,PAPSO), 发展空间,同时PS0算法在解决给水管网这类组合 进的算法用于优化实际的管网改扩建案例,取得较 优化问题时也存在以下缺点:容易陷入局部极值、局 好的效果。 部搜索能力差导致的搜索精度不高。 1给水管网改扩建描述 针对PS0算法在优化给水管网系统时容易陷 入局部极值的问题,文献[8]提出在PS0算法中加 给水管网系统改扩建优化设计是在改造现有旧 入遗传算法的交叉和变异操作,对新产生的位置进 管网、发挥旧管网输水能力的基础上,决定如何经济 行随机变异,避免算法陷入局部极值,并通过优化实 合理的增敷新管。使新旧管网满足水量、水压 际管网案例表明改进算法的有效性,同时算法在搜 水质的要求,并使管网建造和运行年折算费用最低。 索后期收敛速度变慢:文献[9]提出在PS0算法的 1.1目标函数 速度公式中加入一个收缩因子,实现算法的离散优 给水管网改扩建优化的目的就是建立一个全 化,删除种群中重合的点并随机产生相应的新个体, 面、统一的给水管网改扩建优化设计模型,运用现代 有效增加了种群多样性,避免算法陷入局优,同时算 智能算法,寻求经济合理的改扩建方案),目标函 法的局部搜索能力有待加强:文献[10]通过判断2 数是方案优劣的评价标准,如式(1)所示: 个粒子的空间距离提出聚集度的概念,并根据聚集 度大小对粒子进行变异,避免算法陷入局优,以上随 W=[ +)-+0∑a+bg)1%+ io (1 +io)T 机增加种群多样性的机制在一定程度确实能避免算 T, 法陷入局优,提高全局搜索能力。针对PS0算法在 优化给水管网系统时由于局部搜索能力差导致的搜 (1) 索精度不高的问题,许多学者通过改进参数的调整 式中:i。为基金收益率,m为大修理基金提取率,k 机制,平衡了算法的全局和局部搜索能力,或在算法 为铺设管道数目,a、b、α为管段造价系数,E为电费 中加入局部搜索机制增强算法的局部搜索能力。文 价格,n为泵站效率,D,为第i管段的直径,L:为第i 献[11]通过对自动学习机的研究,提出自动学习调 管段长度,x:为新建或改扩建管段,T为投资回收 整权重和加速系数的方法,对比冒险和保守2个调 期,T1、T2为供水时间和传输时间,Q、H、Q'、H'为 整策略,仿真结果表明具有学习自动调整的冒险策 第泵站高峰用水和最大传输时的流量及扬程,Y,、 略能更高效地平衡算法的全局和局部搜索能力,提 Y2为供水能量变化系数。 高算法的搜索精度,但算法收敛速度变慢:文献 1.2约束条件 [12]提出在PS0算法中加入差分进化算法的变异 给水管网的优化方案需满足一定的约束条件,依 和选择操作,对种群中的个体极值进行变异操作,相 据给水工程的规范要求,目标函数的约束条件如下: 当于对个体极值的周围进行局部搜索操作,增强了 1)节点流量连续性约束 算法的搜索精度:文献[13]提出根据每个粒子与全 (2) 局最优粒子的不同,评估种群粒子的相似度,利用相 ∑(±9g)+Q.=0 似度大小对惯性权重进行动态调整,根据种群分布 2)能量平衡约束 状态,在搜索后期增强算法的局部搜索能力,提高搜 4-0 (3) 索精度。根据以上分析可知,当前改进的PSO算法 3)节点水压约束 在优化给水管网问题时的性能得到一定程度的提 Hmin≤H:≤Hm 升,同时仍存在待提高的研究方向。 4)最小管径及标准管径约束 PS0算法的3个参数w、c、c,对其寻优效果有 d:≥dmin,d:∈D={D1,D2,…,D} (5) 重要影响,惯性权重ω平衡算法的全局和局部搜索 5)水流流速约束 能力,加速系数c,可以调节粒子飞向自身最好位置 Umin≤v:≤ima (6)
改扩建优化设计。 为了优化给水管网,许多方法被广泛应用,如遗 传算法[2⁃3] 、 蚁群算法[4] 、 启发式算法[5] 、 差分算 法[6]和足球联赛竞争算法[7] 。 其中粒子群( particle swarm optimization,PSO)算法因其可调参数少及具 有本质的并行性、全局搜索能力强、整体收敛速度快 等优点,展现了较大的解决多种优化问题的潜力和 发展空间,同时 PSO 算法在解决给水管网这类组合 优化问题时也存在以下缺点:容易陷入局部极值、局 部搜索能力差导致的搜索精度不高。 针对 PSO 算法在优化给水管网系统时容易陷 入局部极值的问题,文献[8]提出在 PSO 算法中加 入遗传算法的交叉和变异操作,对新产生的位置进 行随机变异,避免算法陷入局部极值,并通过优化实 际管网案例表明改进算法的有效性,同时算法在搜 索后期收敛速度变慢;文献[9]提出在 PSO 算法的 速度公式中加入一个收缩因子,实现算法的离散优 化,删除种群中重合的点并随机产生相应的新个体, 有效增加了种群多样性,避免算法陷入局优,同时算 法的局部搜索能力有待加强;文献[10]通过判断 2 个粒子的空间距离提出聚集度的概念,并根据聚集 度大小对粒子进行变异,避免算法陷入局优,以上随 机增加种群多样性的机制在一定程度确实能避免算 法陷入局优,提高全局搜索能力。 针对 PSO 算法在 优化给水管网系统时由于局部搜索能力差导致的搜 索精度不高的问题,许多学者通过改进参数的调整 机制,平衡了算法的全局和局部搜索能力,或在算法 中加入局部搜索机制增强算法的局部搜索能力。 文 献[11]通过对自动学习机的研究,提出自动学习调 整权重和加速系数的方法,对比冒险和保守 2 个调 整策略,仿真结果表明具有学习自动调整的冒险策 略能更高效地平衡算法的全局和局部搜索能力,提 高算法的搜索精度, 但算法收敛速度变慢; 文献 [12]提出在 PSO 算法中加入差分进化算法的变异 和选择操作,对种群中的个体极值进行变异操作,相 当于对个体极值的周围进行局部搜索操作,增强了 算法的搜索精度;文献[13] 提出根据每个粒子与全 局最优粒子的不同,评估种群粒子的相似度,利用相 似度大小对惯性权重进行动态调整,根据种群分布 状态,在搜索后期增强算法的局部搜索能力,提高搜 索精度。 根据以上分析可知,当前改进的 PSO 算法 在优化给水管网问题时的性能得到一定程度的提 升,同时仍存在待提高的研究方向。 PSO 算法的 3 个参数 ω、c1 、c2对其寻优效果有 重要影响,惯性权重 ω 平衡算法的全局和局部搜索 能力,加速系数c1可以调节粒子飞向自身最好位置 的步长,加速系数c2可以调节粒子向群体最优位置 的飞行步长。 因此,本文将继续研究这 3 个参数的 调整策略,并根据以上 3 个参数的调整思想,为动态 评估种群中各粒子分布状态,实现算法自适应性,对 种群粒子进行收敛性分析,定义种群粒子相似度的 概念,提出一种参数自适应粒子群算法( parameter adaptive particle swarm optimization, PAPSO),将改 进的算法用于优化实际的管网改扩建案例,取得较 好的效果。 1 给水管网改扩建描述 给水管网系统改扩建优化设计是在改造现有旧 管网、发挥旧管网输水能力的基础上,决定如何经济 合理的增敷新管[14] 。 使新旧管网满足水量、水压、 水质的要求,并使管网建造和运行年折算费用最低。 1.1 目标函数 给水管网改扩建优化的目的就是建立一个全 面、统一的给水管网改扩建优化设计模型,运用现代 智能算法,寻求经济合理的改扩建方案[15] ,目标函 数是方案优劣的评价标准,如式(1)所示: W = [ iO (1 + iO) T (1 + iO) T - 1 + m 100 ]∑ k i = 1 (a + bD α i )Li xi + 86E η ( T1 T γ1∑ n j = 1 QjHj + T2 T γ2∑ n j = 1 Q′jH′j) (1) 式中:i 0 为基金收益率,m 为大修理基金提取率,k 为铺设管道数目,a、b、α 为管段造价系数,E 为电费 价格,η 为泵站效率,Di 为第 i 管段的直径,Li 为第 i 管段长度,xi 为新建或改扩建管段,T 为投资回收 期,T1 、T2为供水时间和传输时间,Qj、Hj、Qj ′、Hj ′为 第 j 泵站高峰用水和最大传输时的流量及扬程,γ1 、 γ2 为供水能量变化系数。 1.2 约束条件 给水管网的优化方案需满足一定的约束条件,依 据给水工程的规范要求,目标函数的约束条件如下: 1)节点流量连续性约束 ∑( ± qij) + Qi = 0 (2) 2)能量平衡约束 ∑ ni j = 1 hij = 0 (3) 3)节点水压约束 Himin ≤ Hi ≤ Himax (4) 4)最小管径及标准管径约束 di ≥ dmin ,di ∈ D = D1 ,D2 ,…,Dz { } (5) 5)水流流速约束 vimin ≤ vi ≤ vimax (6) 第 5 期 王超,等:参数自适应粒子群算法的给水管网优化研究 ·723·

·724· 智能系统学报 第10卷 6)旧管约束 该线性系统稳定的充分必要条件是特征方程各 d,e[d] (7) 项系数均为正值,因此可得到粒子的位置变化过程 2PS0算法及其改进 稳定条件为 1-w>0 PS0算法结合了生命科学和优化计算的优点, (17) 2+2w>p1+P2 群体中的个体代表问题的一个潜在解,若优化问题的 在算法迭代过程中,使算法参数始终满足式 搜索空间是n维的,则第i粒子的位置和速度可分别 (17),则由Z变换的终值定理可得 表示X=(xa,x2,…,xm)、V=(1,2,…,n)。粒子 根据速度和位置公式迭代如公式(8)和(9)所示。 ()=lim(e-1)x(e)=9,业+,当 (18) p1+P2 X':=X:+V (8) 粒子群在寻优过程中Y将逐步趋向Y,因此在 V':=w':+c(Y:-X)+c22(Y.-X)(9) 无限的搜索时间内,所有粒子的位置将逐步靠近并 式中:ω决定先前速度对现在的影响程度:Y,为个体 极值;Y为全局极值;C1、c2为粒子受到个体认知和社 停止在+9,兰=y,处。通过大量实验研究四发 会认知的影响程度;1、2为0~1的随机数。 P1+92 2.1粒子运动轨迹分析 现,粒子轨迹收敛到固定点的概率与参数选择密切 粒子位置和速度变化过程的分析在本质上是一 相关,若满足式(17),则绝大多数粒子轨迹会收敛 样的,为了描述粒子运动轨迹,本文只分析粒子的位 到固定点,各类问题函数值的分布都有一定规律,即 置变化过程。为便于分析和表达,首先将问题空间 当满足稳定条件时,多数粒子能收敛到固定点,并能 简化为一维的,仅研究某一个粒子的运动轨迹,并暂 为找到最优位置提供一定的线索。 时先假设Y:、Y不变,用p1、P2表示式(9)中的c11和 2.2参数调整机制 c22,且为常数,于是得到粒子i的状态方程组(10)、 粒子适应度值能分辨位置的好坏,为充分利用 (11)61。 粒子适应度分布情况动态调整算法参数,进行上述 x(t+1)=x:(t)+:(t+1) (10) 的粒子轨迹分析,可知所有粒子的位置最终停止在 :(t+1)=w,(t)+9[Y:-x(t)]+92[Y.-x(t)] Y处,但在种群迭代过程中的绝大部分时间里粒子 (11) 是向+P,靠找的,故将其定义为期望粒子位置 将式(11)代入式(10)可得 91+P2 x,(t+1)=x,(t)+wu:(t)+ x.。其中Y对应的适应度值为f,,Y对应的适应度 p[Y-x:(t)]+2[Yg-x(t)] (12) 值为f,故定义期望适应度值f如下: 将式(10)中的时间后推一步,代入式(12),并 pBea e 将该式中的时间前推一步可得一个二阶差分方程, f。= (19) P1+P2 如式(13)所示。 惯性权重的调整很大程度上决定了PS0算法 x:(t+2)=(1+ω-91-P2)x(t+1)- 的优化性能,其大小的调节具有一定规律,且与种群 wx:(t)+9,Y:+P2Y (13) 分布和单个粒子位置密切相关,粒子在迭代过程中 多个粒子位置的发散将使整个种群发散,粒子 相似程度越来越大,通过种群分布状态,利用粒子相 位置变化过程的稳定性对种群的行为将产生重要影 似程度来调节惯性权重,进而分析和改进PS0算 响,故对粒子位置变化过程的稳定性进行分析,将式 法,提出粒子相似度s(i,e)如式(20)所示: (13)取Z变换得 X(2)=(2x(0)+z2(x(1)+(J-1)x,(0)+z(9,Y+ (1,lf -f.I<Dn V-f. 9Y。-Jx:(0)-x(1)/(2+z+w)(z-1) s(i,e)=1- -,Dn≤lf-f|<Dms (14) funa -fgueat 式中:J=9,+92-1-ω。式(14)是一个线性系统,对 0,lf-f|≥Dms 应的特征方程为 (20) (z2+z(91+92-1-ω)+ω)(z-1)=0(15) 式中:s(i,e)表示第i粒子与期望粒子的相似度,f 将:代人式(15).对其进行双性套换得 为第i粒子的适应度值,Dnm、Dn是固定正常数。 文献[13]中基于空间距离提出相似度的概念,表示 (91+92)u2+(2-2ω)u+(2+2m-91-92)=0 的是每个粒子和当前的全局最优粒子的相似程度。 (16) 本文分析了粒子运动轨迹,提出相似度的概念来表
6)旧管约束 dj ∈ [di] (7) 2 PSO 算法及其改进 PSO 算法结合了生命科学和优化计算的优点, 群体中的个体代表问题的一个潜在解,若优化问题的 搜索空间是 n 维的,则第 i 粒子的位置和速度可分别 表示 Xi = xi1 ,xi2 ,…,xin ( ) 、Vi = vi1 ,vi2 ,…,vin ( ) 。 粒子 根据速度和位置公式迭代如公式(8)和(9)所示。 X′i = Xi + V′i (8) V′i = ωVi + c1 r1(Yi - Xi) + c2 r2(Yg - Xi) (9) 式中:ω 决定先前速度对现在的影响程度;Yi为个体 极值;Yg为全局极值;c1 、c2为粒子受到个体认知和社 会认知的影响程度;r1 、r2为 0~1 的随机数。 2.1 粒子运动轨迹分析 粒子位置和速度变化过程的分析在本质上是一 样的,为了描述粒子运动轨迹,本文只分析粒子的位 置变化过程。 为便于分析和表达,首先将问题空间 简化为一维的,仅研究某一个粒子的运动轨迹,并暂 时先假设Yi、Yg不变,用φ1 、φ2表示式(9)中的c1 r1和 c2 r2 ,且为常数,于是得到粒子 i 的状态方程组(10)、 (11) [16] 。 xi(t + 1) = xi(t) + vi(t + 1) (10) vi(t + 1) = ωvi(t) + φ1[Yi - xi(t)] + φ2[Yg - xi(t)] (11) 将式(11)代入式(10)可得 xi(t + 1) = xi(t) + ωvi(t) + φ1 [Yi - xi(t)] + φ2 [Yg - xi(t)] (12) 将式(10)中的时间后推一步,代入式(12),并 将该式中的时间前推一步可得一个二阶差分方程, 如式(13)所示。 xi(t + 2) = (1 + ω - φ1 - φ2 )xi(t + 1) - ωxi(t) + φ1Yi + φ2Yg (13) 多个粒子位置的发散将使整个种群发散,粒子 位置变化过程的稳定性对种群的行为将产生重要影 响,故对粒子位置变化过程的稳定性进行分析,将式 (13)取 Z 变换得 Xi(z)= (z 3 xi(0) + z 2 (xi(1) + (J - 1)xi(0)) + z(φ1Yi + φ2Yg - Jxi(0) - xi(1)))/ ((z 2 + Jz + ω)(z - 1)) (14) 式中:J = φ1 +φ2 -1-ω。 式(14)是一个线性系统,对 应的特征方程为 (z 2 + z(φ1 + φ2 - 1 - ω) + ω)(z - 1) = 0 (15) 将 z = u+1 u-1 代入式(15),对其进行双性变换得 (φ1 + φ2)u 2 + (2 - 2ω)u + (2 + 2ω - φ1 - φ2) = 0 (16) 该线性系统稳定的充分必要条件是特征方程各 项系数均为正值,因此可得到粒子的位置变化过程 稳定条件为 1 - ω > 0 2 + 2ω > φ1 + φ2 { (17) 在算法迭代过程中,使算法参数始终满足式 (17),则由 Z 变换的终值定理可得 xi(t) = lim((z - 1)Xi(z)) = φ1Yi + φ2Yg φ1 + φ2 (18) 粒子群在寻优过程中Yi将逐步趋向Yg ,因此在 无限的搜索时间内,所有粒子的位置将逐步靠近并 停止在 φ1Yi +φ2Yg φ1 +φ2 = Yg处。 通过大量实验研究[17] 发 现,粒子轨迹收敛到固定点的概率与参数选择密切 相关,若满足式(17),则绝大多数粒子轨迹会收敛 到固定点,各类问题函数值的分布都有一定规律,即 当满足稳定条件时,多数粒子能收敛到固定点,并能 为找到最优位置提供一定的线索。 2.2 参数调整机制 粒子适应度值能分辨位置的好坏,为充分利用 粒子适应度分布情况动态调整算法参数,进行上述 的粒子轨迹分析,可知所有粒子的位置最终停止在 Yg处,但在种群迭代过程中的绝大部分时间里粒子 是向 φ1Yi +φ2Yg φ1 +φ2 靠拢的,故将其定义为期望粒子位置 xe。 其中Yi对应的适应度值为f pBest,Yg对应的适应度 值为f gBest,故定义期望适应度值f e如下: f e = φ1 f pBest + φ2 f gBest φ1 + φ2 (19) 惯性权重的调整很大程度上决定了 PSO 算法 的优化性能,其大小的调节具有一定规律,且与种群 分布和单个粒子位置密切相关,粒子在迭代过程中 相似程度越来越大,通过种群分布状态,利用粒子相 似程度来调节惯性权重,进而分析和改进 PSO 算 法,提出粒子相似度 s(i,e)如式(20)所示: s(i,e) = 1, f i - f e < Dmin 1 - f i - f e fmax - f gBest ,Dmin ≤ f i - f e < Dmax 0, f i - f e ≥ Dmax ì î í ï ïï ï ïï (20) 式中:s(i,e)表示第 i 粒子与期望粒子的相似度,f i 为第 i 粒子的适应度值,Dmax、Dmin 是固定正常数。 文献[13]中基于空间距离提出相似度的概念,表示 的是每个粒子和当前的全局最优粒子的相似程度。 本文分析了粒子运动轨迹,提出相似度的概念来表 ·724· 智 能 系 统 学 报 第 10 卷

第5期 王超,等:参数自适应粒子群算法的给水管网优化研究 ·725· 示粒子与期望粒子的相似程度,并自适应调整惯性 就是对原有粒子位置产生一个服从Gaussian分布的 权重和2个加速系数,同时实现变异的自适应性,有 随机扰动项,其中δ为Gaussian分布的标准差,4为 效平衡了粒子群算法的全局搜索能力和收敛速度。 期望,δ越小分布会越集中在x=μ的位置,反之会越 PS0算法搜索前期选择较大权重值,加强粒子 分散。 探索能力,后期选择较小权重值,保持算法收敛速 变异的位置为x物,公式为 度,这种思想被广泛采用。但所有粒子的权重被统 xn(t)=xin+入(x加s一xmin) (28) 一调整,忽略了粒子之间的差异性,若早期就有粒子 变异后粒子的新位置为该粒子上一代位置与变 找到全局最优点,却因其权重过大而跳出,则会降低 异位置连线的中点,公式为 算法搜索效率。为此,本文设计出一种根据各粒子 x'(t)=0.5(xg(t)+xm(t)) (29) 与期望粒子相似度不同而动态调整权重的PS0算 分期变异机制的主要特点:通过评估整个种群 法,公式为 的分布情况,通过该粒子与期望粒子相似程度大小 w*1=wx-(ωmx-wmn)×s(i,e)(21) 来决定是否对其变异:2种变异方法分期交叉进行, 与期望粒子相似度较小的粒子,权重应较大,加 很好地平衡了种群多样性和算法的收敛能力,在前 快粒子探索整个解空间:反之,其权重应较小,这样 期避免算法陷入局优,后期可以使算法快速找到全 可使该粒子在期望最优位置领域内进行微小探索, 局最优值。 加强粒子的开发能力。 2.4算法流程及性能测试 加速系数c,是个体认知,c,是社会认知,算法搜 设微粒数为N,问题的维数为D,最大迭代步数 索初期,c1应较大,增加种群多样性,2应较小,避免 为Tm,本文算法描述如下: 种群陷入局部最优:搜索后期,逐渐找到最优区域, 1)初始化,包括各参数:N、x、v、T,随机产生 c,应较小,加快收敛速度,c2应较大,领导种群趋向 N个粒子及其初始速度,并计算适应度; 全局最优位置。结合以上c1,c,的调整思想,提出其 2)更新粒子的位置和速度: 迭代公式如下: 3)评价种群中各粒子的适应度; c=c1as-(c1s-c1mn)×s'(i,e) (22)》 4)根据适应度值更新粒子的个体极值Y:; c1=c1mim+(c2mx-c2min)×s'(i,e)(23) 5)根据适应度更新种群的全局极值Y; 2.3 分期变异机制 6)计算粒子之间的相似度s(i,e),并根据式 PS0算法在迭代过程中会因种群多样性的缺失 (21)更新惯性权重; 而陷入局部最优,为增加种群多样性,对种群粒子进 7)根据式(24)计算变异概率,并判断是否满足 行变异,当粒子与期望粒子相似度越大时,对应粒子 变异条件,若满足变异条件,则根据式(26)~(29) 变异的概率应越小,反之亦然。定义变异概率p和 进行分期交叉变异,重新计算粒子适应度,并更新 变异条件分别如下: Y、Y.; T p.=cos(2(i,e)) (24) 8)判断算法的终止条件,若满足则停止,输出 相关结果:否则转2)。 rand()<Pim (25) 为了验证算法的有效性,将PAPS0算法用于优 为有效平衡算法的全局搜索能力和收敛速度, 化汉诺塔管网和纽约管网,2个经典管网的布局图、 将混沌变异和Gaussian变异分期交叉进行,整个迭 节点水压和管段长度等详细数据参照文献[18]。 代过程分为4个阶段,每个阶段的前20%的迭代步 根据汉诺塔管网实际问题,进行参数敏感性分 数进行混沌变异,后5%的迭代步数进行Gaussian 析后,PAPSO算法在整个搜索过程中,各参数设置 变异。利用混沌的遍历性,充分增大种群多样性,如 如下:wm=0.9,wmm=0.4,C1=2.05,c2=1.45,V= 式(26)所示;利用Gaussian变异的局部搜索能力, 300,T=100。图1为汉诺塔管网造价收敛曲线, 加快算法的收敛速度,如式(27)所示。 改进的PAPSO算法在第31步就找到了全局最优 Ag=u×A写'(1-A) (26) 值,具有较快的收敛速度。 x expl-(-u) A(x)=1 (27) 对于汉诺塔问题,通过EPANET2.0(w= 282 10.667)水力模拟计算验证,目前最优的解决方案造 式(26)中:A)表示第t步混合演变后的值,当u= 价是6.081×10美元。表1列出了遗传算法、混合 4,A∈(0,1),且0{0.25,0.5,0.75}时,将产 粒子群差分算法、自适应粒子群算法、差分算法和本 生混沌现象,A,(t)在(0,1)内遍历。Gaussian变异 文提出的PAPSO算法优化汉诺塔问题的结果对比
示粒子与期望粒子的相似程度,并自适应调整惯性 权重和 2 个加速系数,同时实现变异的自适应性,有 效平衡了粒子群算法的全局搜索能力和收敛速度。 PSO 算法搜索前期选择较大权重值,加强粒子 探索能力,后期选择较小权重值,保持算法收敛速 度,这种思想被广泛采用。 但所有粒子的权重被统 一调整,忽略了粒子之间的差异性,若早期就有粒子 找到全局最优点,却因其权重过大而跳出,则会降低 算法搜索效率。 为此,本文设计出一种根据各粒子 与期望粒子相似度不同而动态调整权重的 PSO 算 法,公式为 ω t+1 i = ωmax - (ωmax - ωmin ) × s t (i,e) (21) 与期望粒子相似度较小的粒子,权重应较大,加 快粒子探索整个解空间;反之,其权重应较小,这样 可使该粒子在期望最优位置领域内进行微小探索, 加强粒子的开发能力。 加速系数c1是个体认知,c2是社会认知,算法搜 索初期,c1应较大,增加种群多样性,c2应较小,避免 种群陷入局部最优;搜索后期,逐渐找到最优区域, c1应较小,加快收敛速度,c2应较大,领导种群趋向 全局最优位置。 结合以上c1 ,c2的调整思想,提出其 迭代公式如下: c t+1 1i = c1max - (c1max - c1min ) × s t (i,e) (22) c t+1 2i = c1min + (c2max - c2min ) × s t (i,e) (23) 2.3 分期变异机制 PSO 算法在迭代过程中会因种群多样性的缺失 而陷入局部最优,为增加种群多样性,对种群粒子进 行变异,当粒子与期望粒子相似度越大时,对应粒子 变异的概率应越小,反之亦然。 定义变异概率pim和 变异条件分别如下: pim = cos ( π 2 s(i,e)) (24) rand() < pim (25) 为有效平衡算法的全局搜索能力和收敛速度, 将混沌变异和 Gaussian 变异分期交叉进行,整个迭 代过程分为 4 个阶段,每个阶段的前 20%的迭代步 数进行混沌变异,后 5%的迭代步数进行 Gaussian 变异。 利用混沌的遍历性,充分增大种群多样性,如 式(26) 所示;利用 Gaussian 变异的局部搜索能力, 加快算法的收敛速度,如式(27)所示。 λ t ij = u × λ t-1 ij (1 - λ t-1 ij ) (26) λ t ij(x) = 1 δ 2π × exp[ - (x - μ) 2 2δ 2 ] (27) 式(26)中:λ (t) ij 表示第 t 步混合演变后的值,当 u = 4,λ (t) ij ∈( 0,1),且 λ (t) ij ∉{0.25,0.5,0.75} 时,将产 生混沌现象,λij(t)在(0, 1)内遍历。 Gaussian 变异 就是对原有粒子位置产生一个服从 Gaussian 分布的 随机扰动项,其中 δ 为 Gaussian 分布的标准差,μ 为 期望,δ 越小分布会越集中在 x = μ 的位置,反之会越 分散。 变异的位置为xijm ,公式为 xijm(t) = xijmin + λ t ij(xijmax - xijmin ) (28) 变异后粒子的新位置为该粒子上一代位置与变 异位置连线的中点,公式为 x′ij(t) = 0.5(xij(t) + xijm(t)) (29) 分期变异机制的主要特点:通过评估整个种群 的分布情况,通过该粒子与期望粒子相似程度大小 来决定是否对其变异;2 种变异方法分期交叉进行, 很好地平衡了种群多样性和算法的收敛能力,在前 期避免算法陷入局优,后期可以使算法快速找到全 局最优值。 2.4 算法流程及性能测试 设微粒数为 N,问题的维数为 D,最大迭代步数 为Tmax,本文算法描述如下: 1)初始化,包括各参数:N、x、v、Tmax,随机产生 N 个粒子及其初始速度,并计算适应度; 2)更新粒子的位置和速度; 3)评价种群中各粒子的适应度; 4)根据适应度值更新粒子的个体极值Yi; 5)根据适应度更新种群的全局极值Yg ; 6)计算粒子之间的相似度 s ( i,e),并根据式 (21)更新惯性权重; 7)根据式(24)计算变异概率,并判断是否满足 变异条件,若满足变异条件,则根据式(26) ~ (29) 进行分期交叉变异,重新计算粒子适应度,并更新 Yi、Yg ; 8)判断算法的终止条件,若满足则停止,输出 相关结果;否则转 2)。 为了验证算法的有效性,将 PAPSO 算法用于优 化汉诺塔管网和纽约管网,2 个经典管网的布局图、 节点水压和管段长度等详细数据参照文献[18]。 根据汉诺塔管网实际问题,进行参数敏感性分 析后,PAPSO 算法在整个搜索过程中,各参数设置 如下:ωmax = 0. 9,ωmin = 0. 4,c1 = 2. 05,c2 = 1. 45,N = 300,Tmax = 100。 图 1 为汉诺塔管网造价收敛曲线, 改进的 PAPSO 算法在第 31 步就找到了全局最优 值,具有较快的收敛速度。 对 于 汉 诺 塔 问 题, 通 过 EPANET2. 0 ( ω = 10.667)水力模拟计算验证,目前最优的解决方案造 价是 6.081×10 6 美元。 表 1 列出了遗传算法、混合 粒子群差分算法、自适应粒子群算法、差分算法和本 文提出的 PAPSO 算法优化汉诺塔问题的结果对比, 第 5 期 王超,等:参数自适应粒子群算法的给水管网优化研究 ·725·
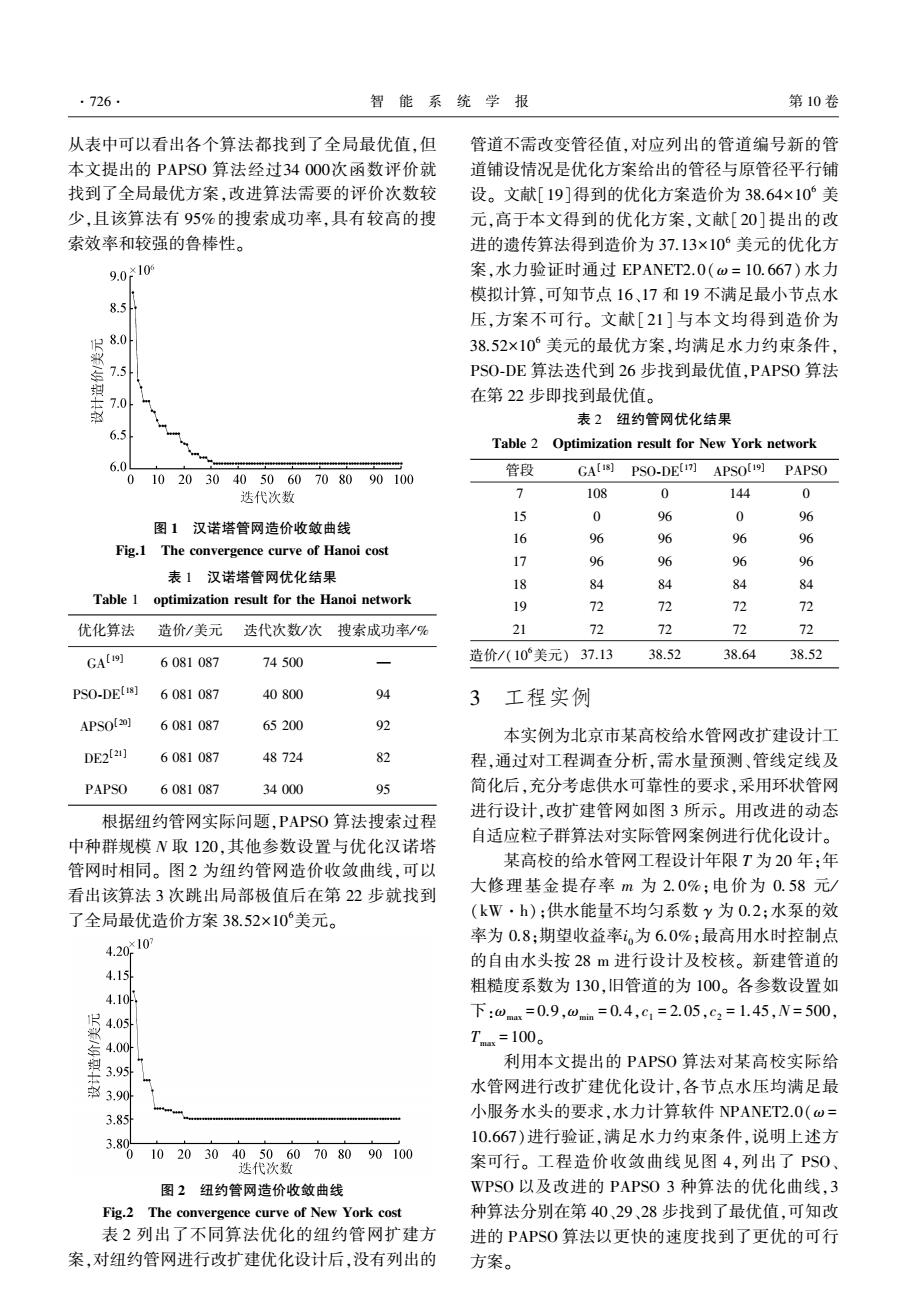
·726 智能系统学报 第10卷 从表中可以看出各个算法都找到了全局最优值,但 管道不需改变管径值,对应列出的管道编号新的管 本文提出的PAPS0算法经过34000次函数评价就 道铺设情况是优化方案给出的管径与原管径平行铺 找到了全局最优方案,改进算法需要的评价次数较 设。文献[19]得到的优化方案造价为38.64×10美 少,且该算法有95%的搜索成功率,具有较高的搜 元,高于本文得到的优化方案,文献[20]提出的改 索效率和较强的鲁棒性。 进的遗传算法得到造价为37.13×10°美元的优化方 9.0x109 案,水力验证时通过EPANET2.0(w=10.667)水力 模拟计算,可知节点16、17和19不满足最小节点水 8.5 压,方案不可行。文献[21]与本文均得到造价为 18.0 38.52×10°美元的最优方案,均满足水力约束条件, 7.5 PSO-DE算法迭代到26步找到最优值,PAPS0算法 7.0 在第22步即找到最优值。 表2纽约管网优化结果 6.5 Table 2 Optimization result for New York network 6.0 01020304050607080 90100 管段 GAUI8]PSO-DEC7]APSO019]PAPSO 迭代次数 个 108 0 144 0 15 0 96 0 96 图1汉诺塔管网造价收敛曲线 16 96 96 96 96 Fig.1 The convergence curve of Hanoi cost 17 96 96 96 96 表1汉诺塔管网优化结果 18 84 84 84 84 Table 1 optimization result for the Hanoi network 19 72 72 72 72 优化算法 造价/美元 迭代次数/次搜索成功率/% 21 72 72 72 72 GAL9] 6081087 74500 造价/(10美元)37.13 38.52 38.64 38.52 PSO-DEU18] 6081087 40800 94 J3 工程实例 APSOI20] 6081087 65200 92 本实例为北京市某高校给水管网改扩建设计工 DE221] 6081087 48724 82 程,通过对工程调查分析,需水量预测、管线定线及 PAPSO 6081087 34000 95 简化后,充分考虑供水可靠性的要求,采用环状管网 进行设计,改扩建管网如图3所示。用改进的动态 根据纽约管网实际问题,PAPSO算法搜索过程 中种群规模V取120,其他参数设置与优化汉诺塔 自适应粒子群算法对实际管网案例进行优化设计。 管网时相同。图2为纽约管网造价收敛曲线,可以 某高校的给水管网工程设计年限T为20年:年 看出该算法3次跳出局部极值后在第22步就找到 大修理基金提存率m为2.0%;电价为0.58元/ 了全局最优造价方案38.52×10美元。 (kW·h):供水能量不均匀系数y为0.2:水泵的效 420*10 率为0.8:期望收益率i。为6.0%;最高用水时控制点 的自由水头按28m进行设计及校核。新建管道的 4.15 粗糙度系数为130,旧管道的为100。各参数设置如 4.10 下:wmm=0.9,wm=0.4,c1=2.05,c2=1.45,N=500, 4.00 Tx=100。 3.95 利用本文提出的PAPSO算法对某高校实际给 3.90 水管网进行改扩建优化设计,各节点水压均满足最 3.85 小服务水头的要求,水力计算软件NPANET2.0(w= 3 10.667)进行验证,满足水力约束条件,说明上述方 102030 405060708090100 迭代次数 案可行。工程造价收敛曲线见图4,列出了PS0、 图2纽约管网造价收敛曲线 WPSO以及改进的PAPSO3种算法的优化曲线,3 Fig.2 The convergence curve of New York cost 种算法分别在第40、29、28步找到了最优值,可知改 表2列出了不同算法优化的纽约管网扩建方 进的PAPSO算法以更快的速度找到了更优的可行 案,对纽约管网进行改扩建优化设计后,没有列出的 方案
从表中可以看出各个算法都找到了全局最优值,但 本文提出的 PAPSO 算法经过34 000次函数评价就 找到了全局最优方案,改进算法需要的评价次数较 少,且该算法有 95%的搜索成功率,具有较高的搜 索效率和较强的鲁棒性。 图 1 汉诺塔管网造价收敛曲线 Fig.1 The convergence curve of Hanoi cost 表 1 汉诺塔管网优化结果 Table 1 optimization result for the Hanoi network 优化算法 造价/ 美元 迭代次数/ 次 搜索成功率/ % GA [19] 6 081 087 74 500 — PSO⁃DE [18] 6 081 087 40 800 94 APSO [20] 6 081 087 65 200 92 DE2 [21] 6 081 087 48 724 82 PAPSO 6 081 087 34 000 95 根据纽约管网实际问题,PAPSO 算法搜索过程 中种群规模 N 取 120,其他参数设置与优化汉诺塔 管网时相同。 图 2 为纽约管网造价收敛曲线,可以 看出该算法 3 次跳出局部极值后在第 22 步就找到 了全局最优造价方案 38.52×10 6美元。 图 2 纽约管网造价收敛曲线 Fig.2 The convergence curve of New York cost 表 2 列出了不同算法优化的纽约管网扩建方 案,对纽约管网进行改扩建优化设计后,没有列出的 管道不需改变管径值,对应列出的管道编号新的管 道铺设情况是优化方案给出的管径与原管径平行铺 设。 文献[19]得到的优化方案造价为 38.64×10 6 美 元,高于本文得到的优化方案,文献[20] 提出的改 进的遗传算法得到造价为 37.13×10 6 美元的优化方 案,水力验证时通过 EPANET2.0(ω = 10.667) 水力 模拟计算,可知节点 16、17 和 19 不满足最小节点水 压,方案不可行。 文献[21] 与本文均得到造价为 38.52×10 6 美元的最优方案,均满足水力约束条件, PSO⁃DE 算法迭代到 26 步找到最优值,PAPSO 算法 在第 22 步即找到最优值。 表 2 纽约管网优化结果 Table 2 Optimization result for New York network 管段 GA [18] PSO⁃DE [17] APSO [19] PAPSO 7 108 0 144 0 15 0 96 0 96 16 96 96 96 96 17 96 96 96 96 18 84 84 84 84 19 72 72 72 72 21 72 72 72 72 造价/ (10 6美元) 37.13 38.52 38.64 38.52 3 工程实例 本实例为北京市某高校给水管网改扩建设计工 程,通过对工程调查分析,需水量预测、管线定线及 简化后,充分考虑供水可靠性的要求,采用环状管网 进行设计,改扩建管网如图 3 所示。 用改进的动态 自适应粒子群算法对实际管网案例进行优化设计。 某高校的给水管网工程设计年限 T 为 20 年;年 大修理基金提存率 m 为 2. 0%;电价为 0. 58 元/ (kW·h);供水能量不均匀系数 γ 为 0.2;水泵的效 率为 0.8;期望收益率i 0为 6.0%;最高用水时控制点 的自由水头按 28 m 进行设计及校核。 新建管道的 粗糙度系数为 130,旧管道的为 100。 各参数设置如 下:ωmax = 0.9,ωmin = 0.4,c1 = 2.05,c2 = 1.45,N = 500, Tmax = 100。 利用本文提出的 PAPSO 算法对某高校实际给 水管网进行改扩建优化设计,各节点水压均满足最 小服务水头的要求,水力计算软件 NPANET2.0(ω = 10.667)进行验证,满足水力约束条件,说明上述方 案可行。 工程造价收敛曲线见图 4,列出了 PSO、 WPSO 以及改进的 PAPSO 3 种算法的优化曲线,3 种算法分别在第 40、29、28 步找到了最优值,可知改 进的 PAPSO 算法以更快的速度找到了更优的可行 方案。 ·726· 智 能 系 统 学 报 第 10 卷
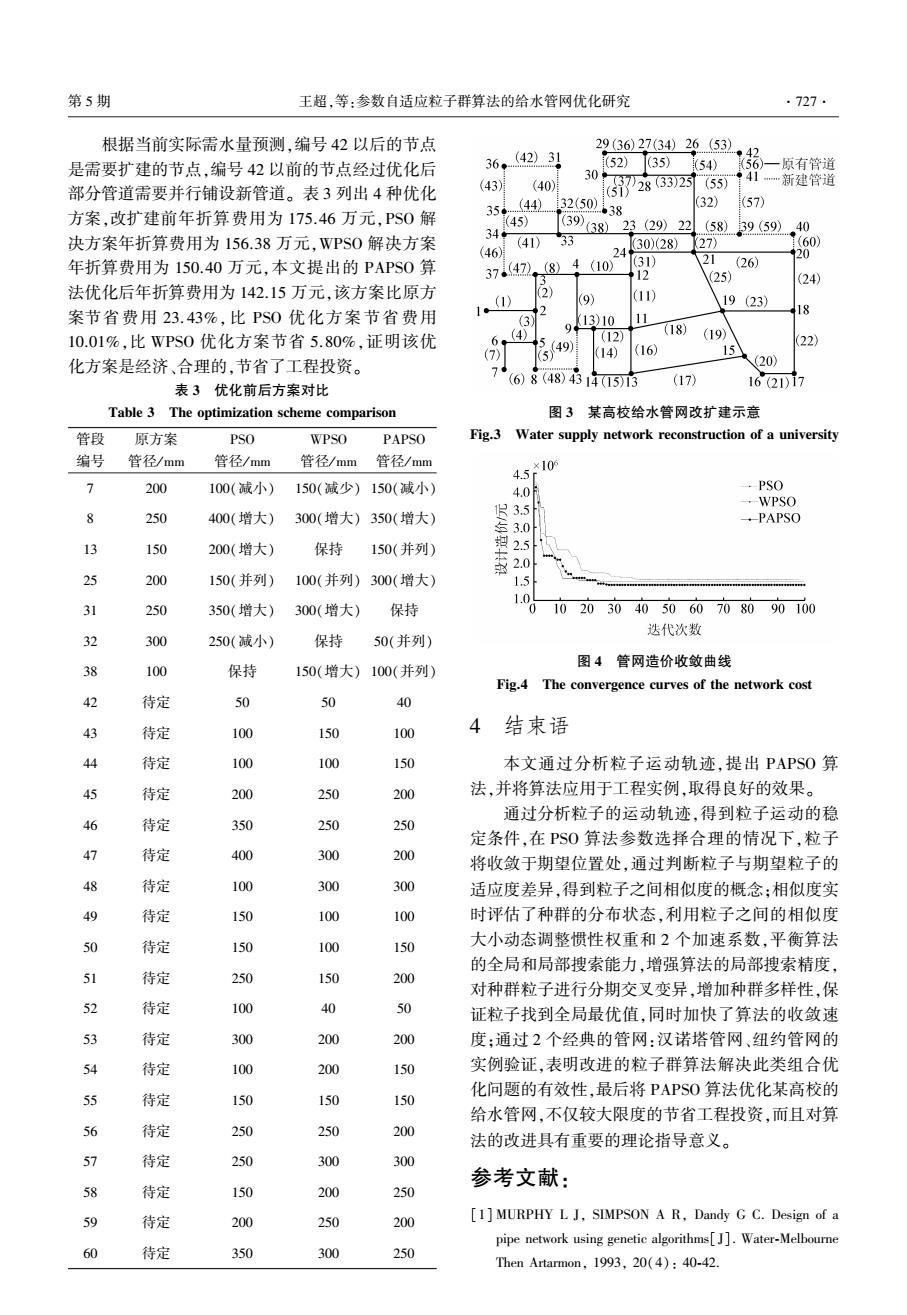
第5期 王超,等:参数自适应粒子群算法的给水管网优化研究 ·727· 根据当前实际需水量预测,编号42以后的节点 29(36)27(34)26(532 (42)31 ·42 是需要扩建的节点,编号42以前的节点经过优化后 36◆ 52)(35) 54) 56) 一原有管道 41 部分管道需要并行铺设新管道。表3列出4种优化 (43) (40) 30G286西 …新建管道 35.(44) 32(50)138 32) (57) 方案,改扩建前年折算费用为175.46万元,PS0解 (45) 39)38123(29)2258)39(592 40 决方案年折算费用为156.38万元,WPS0解决方案 34 (41) 33 (46) 30)(28)27) (60) 4 20 年折算费用为150.40万元,本文提出的PAPS0算 3747) (8)4(10) 31) 21 (26) 12 (25) (24) 法优化后年折算费用为142.15万元,该方案比原方 2) (1) (9) (11) 19(23) 案节省费用23.43%,比PS0优化方案节省费用 18 13)10 (18) 10.01%,比WPS0优化方案节省5.80%,证明该优 4 (12) (19) 49 (22 7 (16) 5】 14) 5 化方案是经济、合理的,节省了工程投资。 (20) 7 (6)8(48)4314(15i3 (17) 表3优化前后方案对比 16(21)17 Table 3 The optimization scheme comparison 图3 某高校给水管网改扩建示意 管段 原方案 PSO WPSO PAPSO Fig.3 Water supply network reconstruction of a university 编号 管径/mm 管径/mm 管径/mm 管径/mm 4.5 ×10 7 200 100(减小) 150(减少) 150(减小) 4.0 -PSO -WPSO 8 250 400(增大) 300(增大)350(增大) 尽3.5 .PAPSO 13 150 200(增大) 保持 150(并列) 2.0 25 200 150(并列) 100(并列)300(增大) 1.0 31 250 350(增大) 300(增大) 保持 102030405060708090100 迭代次数 32 300 250(减小) 保持 50(并列) 图4管网造价收敛曲线 38 100 保持 150(增大)100(并列) Fig.4 The convergence curves of the network cost 42 待定 50 50 40 43 待定 100 150 100 结束语 44 待定 100 100 150 本文通过分析粒子运动轨迹,提出PAPS0算 45 待定 200 250 200 法,并将算法应用于工程实例,取得良好的效果。 46 通过分析粒子的运动轨迹,得到粒子运动的稳 待定 350 250 250 定条件,在PS0算法参数选择合理的情况下,粒子 47 待定 400 300 200 将收敛于期望位置处,通过判断粒子与期望粒子的 48 待定 100 300 300 适应度差异,得到粒子之间相似度的概念:相似度实 49 待定 150 100 100 时评估了种群的分布状态,利用粒子之间的相似度 50 待定 150 100 150 大小动态调整惯性权重和2个加速系数,平衡算法 的全局和局部搜索能力,增强算法的局部搜索精度 51 待定 250 150 200 对种群粒子进行分期交叉变异,增加种群多样性,保 52 待定 100 40 50 证粒子找到全局最优值,同时加快了算法的收敛速 53 待定 300 200 200 度:通过2个经典的管网:汉诺塔管网、纽约管网的 54 待定 100 200 150 实例验证,表明改进的粒子群算法解决此类组合优 化问题的有效性,最后将PAPS0算法优化某高校的 55 待定 150 150 150 给水管网,不仅较大限度的节省工程投资,而且对算 56 待定 250 250 200 法的改进具有重要的理论指导意义。 57 待定 250 300 300 参考文献: 58 待定 150 200 250 59 待定 200 250 200 [1]MURPHY L J,SIMPSON A R,Dandy G C.Design of a pipe network using genetic algorithms[J].Water-Melbourne 60 待定 350 300 250 Then Artarmon.1993.20(4):40-42
根据当前实际需水量预测,编号 42 以后的节点 是需要扩建的节点,编号 42 以前的节点经过优化后 部分管道需要并行铺设新管道。 表 3 列出 4 种优化 方案,改扩建前年折算费用为 175.46 万元,PSO 解 决方案年折算费用为 156.38 万元,WPSO 解决方案 年折算费用为 150.40 万元,本文提出的 PAPSO 算 法优化后年折算费用为 142.15 万元,该方案比原方 案节省费用 23. 43%,比 PSO 优化方案节省费用 10.01%,比 WPSO 优化方案节省 5.80%,证明该优 化方案是经济、合理的,节省了工程投资。 表 3 优化前后方案对比 Table 3 The optimization scheme comparison 管段 编号 原方案 管径/ mm PSO 管径/ mm WPSO 管径/ mm PAPSO 管径/ mm 7 200 100(减小) 150(减少) 150(减小) 8 250 400(增大) 300(增大) 350(增大) 13 150 200(增大) 保持 150(并列) 25 200 150(并列) 100(并列) 300(增大) 31 250 350(增大) 300(增大) 保持 32 300 250(减小) 保持 50(并列) 38 100 保持 150(增大) 100(并列) 42 待定 50 50 40 43 待定 100 150 100 44 待定 100 100 150 45 待定 200 250 200 46 待定 350 250 250 47 待定 400 300 200 48 待定 100 300 300 49 待定 150 100 100 50 待定 150 100 150 51 待定 250 150 200 52 待定 100 40 50 53 待定 300 200 200 54 待定 100 200 150 55 待定 150 150 150 56 待定 250 250 200 57 待定 250 300 300 58 待定 150 200 250 59 待定 200 250 200 60 待定 350 300 250 图 3 某高校给水管网改扩建示意 Fig.3 Water supply network reconstruction of a university 图 4 管网造价收敛曲线 Fig.4 The convergence curves of the network cost 4 结束语 本文通过分析粒子运动轨迹,提出 PAPSO 算 法,并将算法应用于工程实例,取得良好的效果。 通过分析粒子的运动轨迹,得到粒子运动的稳 定条件,在 PSO 算法参数选择合理的情况下,粒子 将收敛于期望位置处,通过判断粒子与期望粒子的 适应度差异,得到粒子之间相似度的概念;相似度实 时评估了种群的分布状态,利用粒子之间的相似度 大小动态调整惯性权重和 2 个加速系数,平衡算法 的全局和局部搜索能力,增强算法的局部搜索精度, 对种群粒子进行分期交叉变异,增加种群多样性,保 证粒子找到全局最优值,同时加快了算法的收敛速 度;通过 2 个经典的管网:汉诺塔管网、纽约管网的 实例验证,表明改进的粒子群算法解决此类组合优 化问题的有效性,最后将 PAPSO 算法优化某高校的 给水管网,不仅较大限度的节省工程投资,而且对算 法的改进具有重要的理论指导意义。 参考文献: [1] MURPHY L J, SIMPSON A R, Dandy G C. Design of a pipe network using genetic algorithms[J]. Water⁃Melbourne Then Artarmon, 1993, 20(4): 40⁃42. 第 5 期 王超,等:参数自适应粒子群算法的给水管网优化研究 ·727·

·728 智能系统学报 第10卷 [2]ABKENAR S M S,CHASE D V,STANLEY S D,et al. [14]COELHO B.ANDRADE-CAMPOS A.Efficiency achieve- Optimizing pumping system for sustainable water distribution ment in water supply systems-a review[J].Renewable network by using genetic algorithm[C]//2013 International and Sustainable Energy Reviews,2014,30:59-84. Green Computing Conference.Arlington,USA,2013:1-6. [15]ANNELIES D C,KENNETH S.Optimisation of gravity-fed [3]BLINCO L J,SIMPSON A R,LAMBERT M F,et al.Ge- water distribution network design:a critical review [J]. netic algorithm optimization of operational costs and green- European Journal of Operational Research,2013,228 house gas emissions for water distribution systems[J].Pro- (1):1-10. cedia Engineering,2014,89:509-516. [16]李宁,孙德宝,邹彤,等.基于差分方程的PS0算法粒 [4]DINARDO A.DINATALE M,GRECO R,et al.Ant algo- 子运动轨迹分析[J].计算机学报,2006,29(11): rithm for smart water network partitioning[J].Procedia En- 2052-2061. gineering,2014,70:525-534. LI Ning,SUN Debao,ZOU Tong,et al.An analysis for a [5]MOOSAVIAN N,ROODSARI B K.Soccer league competi- particle's trajectory of PSO based on difference equation tion algorithm:a novel meta-heuristic algorithm for optimal [J].Chinese Journal of Computers,2006,29(11):2052- design of water distribution networks[J.Swarm and Evolu- 2061. tionary Computation,2014,17:14-24. [17]VANDEN BERGH F.An analysis of particle swarm optimi- [6]LIU Boning,RECKHOW D A,LI Yun.A two-site chlorine zers[D].Pretoria,South Africa:University of Pretoria, decay model for the combined effects of pH,water distribu- 2002:81-83. tion temperature and in-home heating profilesusing differen- [18]SEDKI A,OUAZAR D.Hybrid particle swarm optimiza- tial evolution[J].Water Research,2014,53:47-57. tion and differential evolution for optimal design of water [7]NASER M,ROODSARIB K.Soccer league competition al- distribution systems[J].Advanced Engineering Informat- gorithm:A novel meta-heuristic algorithm for optimal design ic8,2012,26(3):582-591. of water distribution networks[J].Swarm and Evolutionary [19]SAVIC D A,WALTERS G A.Genetic algorithms for least Computation,2014,17:14-24. cost design of water distribution networks[J].Joumal of [8]WANG Hongxiang,GUO Wenxian.Calibrating chlorine wall Water Resources Planning and Management,1997,123 decay coefficients of water distribution systems based on hy- (2):67-77. brid PSO C//Sixth International Conference on Natural [20]IDEL M,JOAQUIN I,RAFAEL P G,et al.Improved per- Computation (ICNC).Yantai,China,2010:3856-3860. formance of PSO with self-adaptive parameters for compu- [9]MONTALVO I M,IZQUIERDO J,PEREZ R,et al.A di- ting the optimal design of water supply systems[].Engi- versity-enriched variant of discrete PSO applied to the de- neering Applications of Artificial Intelligence,2010,23 sign of water distribution networks[].Engineering Optimi- (5):727-735. zation,2008,40(7):655-668. [21]SURIBABU C R.Differential evolution algorithm for opti- [10 ZARGHAMIM,HAJYKAZEMIAN H.Urban water re- mal design of water distribution networks[J].Journal of sources planning by using a modified particle swarm optimi- Hydroinformatics,2010.12(1):66-82. zation algorithm [J].Resources,Conservation and Recy- 作者简介: cling,.2013,70:1-8. 王超,男,1987年生,硕士研究生, [11]HASHEMI A B,MEYBODI M R.A note on the learning 主要研究方向为智能计算和智能优化 automata based algorithms for adaptive parameter selection 算法。 in PSO[J].Applied Soft Computing,2011,11(1):689- 705. [12]DE FATIMA ARAUJO T,UTURBEY W.Performance as- sessment of PSO,DE and hybrid PSO-DE algorithms when applied to the dispatch of generation and demand[].Inter- 乔俊飞,男,1968年生,教授,博士 national Journal of Electrical Power Energy Systems, 主要研究方向为复杂过程建模、优化与 2013,47:205-217. 控制和智能优化控制。主持国家自然 [13]刘建华,樊晓平,瞿志华.一种基于相似度的新型粒子 科学基金项目2项、国家“863”计划项 群算法[J].控制与决策,2007,22(10):1155-1159. 目2项,发表学术论文100余篇,出版 LIU Jianhua,FAN Xiaoping,QU Zhihua.A new particle 专著2部,获国家发明专利授权15项。 swarm optimization algorithm based on similarity[J].Con- trol and Decision,2007,22(10):1155-1159
[2] ABKENAR S M S, CHASE D V, STANLEY S D, et al. Optimizing pumping system for sustainable water distribution network by using genetic algorithm[C] / / 2013 International Green Computing Conference. Arlington, USA, 2013: 1⁃6. [3]BLINCO L J, SIMPSON A R, LAMBERT M F, et al. Ge⁃ netic algorithm optimization of operational costs and green⁃ house gas emissions for water distribution systems[J]. Pro⁃ cedia Engineering, 2014, 89: 509⁃516. [4] DINARDO A, DINATALE M, GRECO R, et al. Ant algo⁃ rithm for smart water network partitioning[J]. Procedia En⁃ gineering, 2014, 70: 525⁃534. [5]MOOSAVIAN N, ROODSARI B K. Soccer league competi⁃ tion algorithm: a novel meta⁃heuristic algorithm for optimal design of water distribution networks[J]. Swarm and Evolu⁃ tionary Computation, 2014, 17: 14⁃24. [6] LIU Boning, RECKHOW D A, LI Yun. A two⁃site chlorine decay model for the combined effects of pH, water distribu⁃ tion temperature and in⁃home heating profilesusing differen⁃ tial evolution[J]. Water Research, 2014, 53: 47⁃57. [7] NASER M, ROODSARIB K. Soccer league competition al⁃ gorithm: A novel meta⁃heuristic algorithm for optimal design of water distribution networks[ J]. Swarm and Evolutionary Computation, 2014, 17: 14⁃24. [8]WANG Hongxiang, GUO Wenxian. Calibrating chlorine wall decay coefficients of water distribution systems based on hy⁃ brid PSO [ C] / / Sixth International Conference on Natural Computation (ICNC). Yantai, China, 2010: 3856⁃3860. [9] MONTALVO I M, IZQUIERDO J, PÉREZ R, et al. A di⁃ versity⁃enriched variant of discrete PSO applied to the de⁃ sign of water distribution networks[J]. Engineering Optimi⁃ zation, 2008, 40(7): 655⁃668. [ 10 ] ZARGHAMIM, HAJYKAZEMIAN H. Urban water re⁃ sources planning by using a modified particle swarm optimi⁃ zation algorithm [ J]. Resources, Conservation and Recy⁃ cling, 2013, 70: 1⁃8. [11] HASHEMI A B, MEYBODI M R. A note on the learning automata based algorithms for adaptive parameter selection in PSO[J]. Applied Soft Computing, 2011, 11(1): 689⁃ 705. [12] DE FÁTIMA ARAU ' JO T, UTURBEY W. Performance as⁃ sessment of PSO, DE and hybrid PSO⁃DE algorithms when applied to the dispatch of generation and demand[J]. Inter⁃ national Journal of Electrical Power & Energy Systems, 2013, 47: 205⁃217. [13]刘建华, 樊晓平, 瞿志华. 一种基于相似度的新型粒子 群算法[J]. 控制与决策, 2007, 22(10): 1155⁃1159. LIU Jianhua, FAN Xiaoping, QU Zhihua. A new particle swarm optimization algorithm based on similarity[ J]. Con⁃ trol and Decision, 2007, 22(10): 1155⁃1159. [14]COELHO B, ANDRADE⁃CAMPOS A. Efficiency achieve⁃ ment in water supply systems—a review [ J]. Renewable and Sustainable Energy Reviews, 2014, 30: 59⁃84. [15]ANNELIES D C, KENNETH S. Optimisation of gravity⁃fed water distribution network design: a critical review [ J]. European Journal of Operational Research, 2013, 228 (1): 1⁃10. [16]李宁, 孙德宝, 邹彤, 等. 基于差分方程的 PSO 算法粒 子运动轨迹分析[ J]. 计算机学报, 2006, 29 ( 11): 2052⁃2061. LI Ning, SUN Debao, ZOU Tong, et al. An analysis for a particles trajectory of PSO based on difference equation [J]. Chinese Journal of Computers, 2006, 29(11): 2052⁃ 2061. [17]VANDEN BERGH F. An analysis of particle swarm optimi⁃ zers [ D]. Pretoria, South Africa:University of Pretoria, 2002: 81⁃83. [18] SEDKI A, OUAZAR D. Hybrid particle swarm optimiza⁃ tion and differential evolution for optimal design of water distribution systems [ J]. Advanced Engineering Informat⁃ ics, 2012, 26(3): 582⁃591. [19] SAVIC D A, WALTERS G A. Genetic algorithms for least cost design of water distribution networks [ J]. Journal of Water Resources Planning and Management, 1997, 123 (2): 67⁃77. [ 20]IDEL M, JOAQUIN I, RAFAEL P G, et al. Improved per⁃ formance of PSO with self⁃adaptive parameters for compu⁃ ting the optimal design of water supply systems[ J]. Engi⁃ neering Applications of Artificial Intelligence, 2010, 23 (5): 727⁃735. [21] SURIBABU C R. Differential evolution algorithm for opti⁃ mal design of water distribution networks [ J]. Journal of Hydroinformatics, 2010, 12(1): 66⁃82. 作者简介: 王超,男,1987 年生,硕士研究生, 主要研究方向为智能计算和智能优化 算法。 乔俊飞,男,1968 年生,教授,博士, 主要研究方向为复杂过程建模、优化与 控制和智能优化控制。 主持国家自然 科学基金项目 2 项、国家“863”计划项 目 2 项,发表学术论文 100 余篇,出版 专著 2 部,获国家发明专利授权 15 项。 ·728· 智 能 系 统 学 报 第 10 卷