
第10卷第6期 智能系统学报 Vol.10 No.6 2015年12月 CAAI Transactions on Intelligent Systems Dec.2015 D0:10.11992/is.201507032 网络出版地址:http://www.cnki.net/kcms/detail/23.1538.tp.20151110.1354.020.html 混沌搜索策略的改进人工蜂群算法 彭晓华1,刘利强 (1.辽宁工程技术大学基础教学部,辽宁葫芦岛125105;2.辽宁工程技术大学电气与控制工程学院,辽宁葫芦岛 125105) 摘要:针对人工蜂群算法的蜂群缺乏多样性、全局和局部搜索能力差及收敛速度较慢,提出一种基于混沌搜索策 略的改进人工蜂群算法。该算法通过载波映射,由混沌-决策变量的变换,产生新的邻域点,为采蜜蜂和被招募的观 察蜂提供了更广阔的搜索空间和更优质的位置蜜源,增强蜂群多样性:同时,引进侦查蜂局部蜜源搜索较好地解决 了算法易陷入局部极小的问题,改善了人工蜂群算法的收敛性能。最后由6个标准测试函数的仿真验证,得到基于 混沌搜索策略的人工蜂群算法性能明显优于标准人工蜂群算法。 关键词:人工蜂群算法:混沌搜索策略:载波映射:局部蜜源搜索:蜂群多样性;混沌-决策变量:收敛性能:仿真实验 中图分类号:TP301.6文献标志码:A文章编号:1673-4785(2015)06-0927-07 中文引用格式:彭晓华,刘利强.混沌搜索策略的改进人工蜂群算法[J].智能系统学报,2015,10(6):927-933. 英文引用格式:PENG Xiaohua,LIU Liqiang.mproved artificial bee colony algorithm based on chaos searching strategy[J].CAAL Transactions on Intelligent Systems,2015,10(6):927-933. Improved artificial bee colony algorithm based on chaos searching strategy PENG Xiaohua',LIU Liqiang (1.Ministry of basic education,Liaoning University of engineering and Technology,Huludao 125105,China;2.College of electrical and control engineering,Liaoning University of engineering and Technology,Huludao 125105,China) Abstract:The current artificial bee colony algorithm results in the swarm lacking diversity,and the global and local search abilities and convergence speed are slow.We propose an improved artificial bee colony algorithm based on a chaotic search strategy.We map the algorithm with the carrier using a chaos decision variable transformation,gen- erating new neighborhood points,and recruiting bees within a broader search space and from better source loca- tions,while enhancing swarm diversity.In addition,the investigation of a local honey bee search better solved the algorithm problem of the local minimum and improved the convergence property of the artificial bee colony algo- rithm.The most recent six simulation validations of the standard test functions using the proposed artificial bee colo- ny algorithm,based on the chaotic search strategy,are significantly better than the performance results of the cur- rent artificial bee colony algorithm. Keywords:artificial bee colony algorithm;chaotic search strategy;carrier mapping;local search nectar;the swarm diversity;chaos-decision variable;convergence performance;simulation experiment 人工蜂群算法(artificial bee colony algorithm,ABCA)是一种模拟自然界中蜜蜂按照不同分工而 共同寻找优质蜜源的智能方法。l995年Seeley首 收稿日期:2015-4-30.网络出版日期:2015-11-10. 次阐述了有关蜜蜂群体行为的自组织模型。2005 基金项目:国家自然科学基金资助项目(51274118):辽宁省教育厅基金 年D.Karaboga建立了具有完整协同动作的人工蜂 资助项目(L2012119). 通信作者:刘利强.E-mail:2965131477@qq.com 群算法模型,而且通过非线性的函数优化实验验证
第 10 卷第 6 期 智 能 系 统 学 报 Vol.10 №.6 2015 年 12 月 CAAI Transactions on Intelligent Systems Dec. 2015 DOI:10.11992 / tis.201507032 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20151110.1354.020.html 混沌搜索策略的改进人工蜂群算法 彭晓华1 , 刘利强2 (1.辽宁工程技术大学 基础教学部,辽宁 葫芦岛 125105; 2.辽宁工程技术大学 电气与控制工程学院,辽宁 葫芦岛 125105) 摘 要:针对人工蜂群算法的蜂群缺乏多样性、全局和局部搜索能力差及收敛速度较慢,提出一种基于混沌搜索策 略的改进人工蜂群算法。 该算法通过载波映射,由混沌-决策变量的变换,产生新的邻域点,为采蜜蜂和被招募的观 察蜂提供了更广阔的搜索空间和更优质的位置蜜源,增强蜂群多样性;同时,引进侦查蜂局部蜜源搜索较好地解决 了算法易陷入局部极小的问题,改善了人工蜂群算法的收敛性能。 最后由 6 个标准测试函数的仿真验证,得到基于 混沌搜索策略的人工蜂群算法性能明显优于标准人工蜂群算法。 关键词:人工蜂群算法;混沌搜索策略;载波映射;局部蜜源搜索;蜂群多样性;混沌-决策变量;收敛性能;仿真实验 中图分类号: TP301.6 文献标志码:A 文章编号:1673⁃4785(2015)06⁃0927⁃07 中文引用格式:彭晓华, 刘利强. 混沌搜索策略的改进人工蜂群算法[J]. 智能系统学报, 2015, 10(6): 927⁃933. 英文引用格式:PENG Xiaohua, LIU Liqiang. Improved artificial bee colony algorithm based on chaos searching strategy[J]. CAAI Transactions on Intelligent Systems, 2015, 10(6): 927⁃933. Improved artificial bee colony algorithm based on chaos searching strategy PENG Xiaohua 1 , LIU Liqiang 2 (1.Ministry of basic education, Liaoning University of engineering and Technology, Huludao 125105,China;2.College of electrical and control engineering, Liaoning University of engineering and Technology, Huludao 125105,China) Abstract:The current artificial bee colony algorithm results in the swarm lacking diversity, and the global and local search abilities and convergence speed are slow. We propose an improved artificial bee colony algorithm based on a chaotic search strategy. We map the algorithm with the carrier using a chaos decision variable transformation, gen⁃ erating new neighborhood points, and recruiting bees within a broader search space and from better source loca⁃ tions, while enhancing swarm diversity. In addition, the investigation of a local honey bee search better solved the algorithm problem of the local minimum and improved the convergence property of the artificial bee colony algo⁃ rithm. The most recent six simulation validations of the standard test functions using the proposed artificial bee colo⁃ ny algorithm, based on the chaotic search strategy, are significantly better than the performance results of the cur⁃ rent artificial bee colony algorithm. Keywords:artificial bee colony algorithm; chaotic search strategy; carrier mapping; local search nectar; the swarm diversity; chaos⁃decision variable; convergence performance; simulation experiment 收稿日期:2015⁃4⁃30. 网络出版日期:2015⁃11⁃10. 基金项目:国家自然科学基金资助项目(51274118);辽宁省教育厅基金 资助项目(L2012119). 通信作者:刘利强.E⁃mail:2965131477@ qq.com. 人工蜂群算法( artificial bee colony algorithm, ABCA)是一种模拟自然界中蜜蜂按照不同分工而 共同寻找优质蜜源的智能方法。 1995 年 Seeley 首 次阐述了有关蜜蜂群体行为的自组织模型。 2005 年 D.Karaboga 建立了具有完整协同动作的人工蜂 群算法模型,而且通过非线性的函数优化实验验证

928 智能系统学报 第10卷 了人工蜂群算法比一般启发式优化算法具有更强的 通过不断探索,保持最优质蜜源,观察蜂及时补充优 稳定性和可靠性。2006年D.Karaboga等又将ABC 质蜜源对应蜜蜂的数目,侦察蜂在蜂群邻域寻找新 理论应用到限制性数值优化问题、神经网络训练、数 蜜源。整个蜂群搜索过程并不是单一地各司其职地 字滤波器设计等,并取得了较好的测试效果。在文 进行,而是3种蜂种在密切的相互联系及转化中完 献[1-2]中,Dervis Karaboga等通过对多种智能优化 成的,并且各个蜂种之间通过蜜蜂独特的交流方式, 算法的定量对比验证,得出在迭代误差曲线对比中, 即找到蜜源的蜂种依靠在指定区域跳摇摆舞向别的 人工蜂群算法要比其他智能优化算法在曲线大部分 蜂种发送自己携带蜜源的信息,同时,通过所携带蜜 阶段上具有更好的优化性能,至少有着相似的性能。 源量的多少决定该蜂种跳摇摆舞的时间长短,蜜源 人工蜂群算法和其他智能优化算法类似,算法本身 花蜜量的多少可以看成是适应度的大小,所以观察 也存在自身的优化缺陷,从全局搜索能力表现出的 蜂看到别的蜂种所跳摇摆舞的时间越长,说明该蜂 搜索速度缓慢或搜索暂时性的停滞现象,在局部搜 种的适应度值越大,所带蜜源花蜜量就越多,反之亦 索能力存在易陷入局部极小值问题,特别是对于人 然。当观察蜂被招募后转化为采蜜蜂,便开始执行 工蜂群算法,存在一个对于该算法优化性能特别重 采蜜蜂的行为,当采蜜蜂放弃原来蜜源而转化为侦 要的影响因素,即蜂群的多样性。多样性降低,会使 查蜂后,便开始在蜂群邻域寻找新蜜源。不断地估 蜜蜂行为中漏掉一定的搜索区域,直接导致算法陷 算比较适应值的大小而进行不同蜂种之间的转化合 入局部最优,进而会影响全局搜索能力,收敛速度会 作,蜂群才能在邻域范围不断地刷新蜂蜜含量较高 受到极大影响。同时,蜂群群体的具体行为也会存 的新蜜源,即找到最优解。 在一些问题,比如:蜂群的不同选择方式和进化策略 为了更好地展示蜜蜂觅食的行为特征,用图1 都会使得算法在处理一些具体优化问题时存在易陷 来展示整个算法搜索过程2],其中观察蜂行为 入早熟收敛或收敛速度慢等问题。文献[6]结合了 (UF),被招募为采蜜蜂采蜜行为(EF1),原采蜜蜂 Markov的性质和随机搜索算法的收敛准则,证明了 采蜜行为(EF2),S线为侦察蜂寻找蜂巢附近的蜜 ABC算法具备全局收敛的性质,并提出一种搜索效 源行为,R线为被招募的观察蜂寻找蜜源行为。 率更高的局部搜索代替原来的随机解的设想:文献 未知蜜源 蜜源B [7]分别从蜂群初始化、邻域搜索及跟随蜂行为这3 EF S线 EF UF EF 个角度对人工蜂群算法进行了改进优化,有效地平 S线 衡了全局搜索和局部搜索,算法的性能也得到了提 潜在觅食 U陶载花货 R线 高:文献[8]充分考虑以粒子群算法为代表的智能 跳舞区B EF R线 优化算法普遍存在的算法局限性的问题,针对不同 跳舞区A 的缺陷提出改进策略,通过将多种改进策略进行融 EF, S线 合,通过自适应学习机制选出恰当的策略来解决不 蜂房 UF从御载花蜜 同形态的复杂问题。 S线 UF EF 人工蜂群算法是依赖位置信息最终搜索到最优 未知密源 EF 蜜源A 蜜源,所以邻域搜索就显得格外重要。目前人工蜂 群算法的改进方法大多是从收敛速度的角度出发, 图1人工蜂群算法的基本原理 从全局搜索角度来看,极有可能漏掉一部分的邻域 Fig.1 The basic principle of artificial swarm algorithm 搜索范围,而这种邻域搜索的局限性会直接导致蜂 图1完整地描述了3种蜂种协同合作、共同寻 群多样性降低,容易陷入局部极值,针对特殊优化问 找最优蜜源的原理,人工蜂群算法的基本步骤如 题时,有可能得不出全局最优解。所以,提出一种基 下34: 于混沌搜索策略的改进人工蜂群算法,引入混沌搜 1)初始化参数。设置蜂群规模N。,采蜜蜂 索的思想,通过载波方式将混沌变量的值映射到优 N。,观察蜂N,蜜源个数N/2,蜜源维数D,邻域 化变量的取值范围内,产生局部最优解的新增邻域 搜索空间S,迭代次数K,蜜蜂停留阈值Limit,采蜜 点5.),从而增强种群的多样性,提高全局搜索能 蜂种群记为X=[X,X2…Xx],其中X:∈ 力,使其免于陷人局部最优而获得全局最优解。 S(i≤N)是N。个个体,X(O)代表初始采蜜蜂种 群,X(n)代表第n代采蜜蜂种群。 1 人工蜂群算法 2)对于n=0时刻,随机生成N,个可行解(X1, 人工蜂群算法搜索蜜源过程中,蜜蜂按照不同 X2,…,X),具体随机产生的可行解X为 的分工可分为采蜜蜂、观察蜂和侦查蜂3种,采蜜蜂 =im+rand(0,I)(nx-a) (1)
了人工蜂群算法比一般启发式优化算法具有更强的 稳定性和可靠性。 2006 年 D.Karaboga 等又将 ABC 理论应用到限制性数值优化问题、神经网络训练、数 字滤波器设计等,并取得了较好的测试效果。 在文 献[1⁃2]中,Dervis Karaboga 等通过对多种智能优化 算法的定量对比验证,得出在迭代误差曲线对比中, 人工蜂群算法要比其他智能优化算法在曲线大部分 阶段上具有更好的优化性能,至少有着相似的性能。 人工蜂群算法和其他智能优化算法类似,算法本身 也存在自身的优化缺陷,从全局搜索能力表现出的 搜索速度缓慢或搜索暂时性的停滞现象,在局部搜 索能力存在易陷入局部极小值问题,特别是对于人 工蜂群算法,存在一个对于该算法优化性能特别重 要的影响因素,即蜂群的多样性。 多样性降低,会使 蜜蜂行为中漏掉一定的搜索区域,直接导致算法陷 入局部最优,进而会影响全局搜索能力,收敛速度会 受到极大影响。 同时,蜂群群体的具体行为也会存 在一些问题,比如:蜂群的不同选择方式和进化策略 都会使得算法在处理一些具体优化问题时存在易陷 入早熟收敛或收敛速度慢等问题。 文献[6]结合了 Markov 的性质和随机搜索算法的收敛准则,证明了 ABC 算法具备全局收敛的性质,并提出一种搜索效 率更高的局部搜索代替原来的随机解的设想;文献 [7]分别从蜂群初始化、邻域搜索及跟随蜂行为这 3 个角度对人工蜂群算法进行了改进优化,有效地平 衡了全局搜索和局部搜索,算法的性能也得到了提 高;文献[8]充分考虑以粒子群算法为代表的智能 优化算法普遍存在的算法局限性的问题,针对不同 的缺陷提出改进策略,通过将多种改进策略进行融 合,通过自适应学习机制选出恰当的策略来解决不 同形态的复杂问题。 人工蜂群算法是依赖位置信息最终搜索到最优 蜜源,所以邻域搜索就显得格外重要。 目前人工蜂 群算法的改进方法大多是从收敛速度的角度出发, 从全局搜索角度来看,极有可能漏掉一部分的邻域 搜索范围,而这种邻域搜索的局限性会直接导致蜂 群多样性降低,容易陷入局部极值,针对特殊优化问 题时,有可能得不出全局最优解。 所以,提出一种基 于混沌搜索策略的改进人工蜂群算法,引入混沌搜 索的思想,通过载波方式将混沌变量的值映射到优 化变量的取值范围内,产生局部最优解的新增邻域 点[5,9] ,从而增强种群的多样性,提高全局搜索能 力,使其免于陷人局部最优而获得全局最优解。 1 人工蜂群算法 人工蜂群算法搜索蜜源过程中,蜜蜂按照不同 的分工可分为采蜜蜂、观察蜂和侦查蜂 3 种,采蜜蜂 通过不断探索,保持最优质蜜源,观察蜂及时补充优 质蜜源对应蜜蜂的数目,侦察蜂在蜂群邻域寻找新 蜜源。 整个蜂群搜索过程并不是单一地各司其职地 进行,而是 3 种蜂种在密切的相互联系及转化中完 成的,并且各个蜂种之间通过蜜蜂独特的交流方式, 即找到蜜源的蜂种依靠在指定区域跳摇摆舞向别的 蜂种发送自己携带蜜源的信息,同时,通过所携带蜜 源量的多少决定该蜂种跳摇摆舞的时间长短,蜜源 花蜜量的多少可以看成是适应度的大小,所以观察 蜂看到别的蜂种所跳摇摆舞的时间越长,说明该蜂 种的适应度值越大,所带蜜源花蜜量就越多,反之亦 然。 当观察蜂被招募后转化为采蜜蜂,便开始执行 采蜜蜂的行为,当采蜜蜂放弃原来蜜源而转化为侦 查蜂后,便开始在蜂群邻域寻找新蜜源。 不断地估 算比较适应值的大小而进行不同蜂种之间的转化合 作,蜂群才能在邻域范围不断地刷新蜂蜜含量较高 的新蜜源,即找到最优解。 为了更好地展示蜜蜂觅食的行为特征,用图 1 来展示整个算法搜索过程[1⁃2] , 其中观察蜂行为 (UF),被招募为采蜜蜂采蜜行为(EF1),原采蜜蜂 采蜜行为(EF2), S 线为侦察蜂寻找蜂巢附近的蜜 源行为, R 线为被招募的观察蜂寻找蜜源行为。 图 1 人工蜂群算法的基本原理 Fig.1 The basic principle of artificial swarm algorithm 图 1 完整地描述了 3 种蜂种协同合作、共同寻 找最优蜜源的原理,人工蜂群算法的基本步骤如 下[3⁃4] : 1) 初始化参数。 设置蜂群规模 NP ,采蜜蜂 Ne ,观察蜂 Nu ,蜜源个数 NP / 2,蜜源维数 D ,邻域 搜索空间 S ,迭代次数 K ,蜜蜂停留阈值 Limit,采蜜 蜂种群记为 X = [X1 X2 … XNe ] ,其中 Xi ∈ S(i ≤Ne) 是 Ne 个个体, X(0) 代表初始采蜜蜂种 群, X(n) 代表第 n 代采蜜蜂种群。 2)对于 n = 0 时刻,随机生成 Ns 个可行解 (X1 , X2 ,…,XNe ) ,具体随机产生的可行解 Xi 为 X j i = X j min + rand(0,1)(X j max - X j min ) (1) ·928· 智 能 系 统 学 报 第 10 卷

第6期 彭晓华,等:混沌搜索策略的改进人工蜂群算法 ·929· 式中:j取值于{1,2,…,D},为D维解向量的某个 基于混沌搜索策略的改进人工蜂群 分量。分别计算各向量的适应度值,并将排名前一 算法 半的作为初始的采蜜蜂种群X(0),初始标志向量 针对人工蜂群算法(ABC)寻优过程中缺乏多 ail(i)=0,记录采蜜蜂停留同一蜜源的搜索次数。 样性,收敛速度较慢,易陷入局部最优等缺陷,引入 3)设置初始迭代次数iter=0,对于第n步的采 混沌搜索策略的改进人工蜂群算法(improved artifi- 蜜蜂X,(n),在当前位置向量附近邻域进行搜索新 cial bee colony algorithm of chaos searching strategy, 的位置,搜索公式为 CSABCA),采用混沌搜索策略细化人工蜂群算法中 new_=+(X-X) (2) 采蜜蜂和观察蜂的搜索空间,在迭代进化中产生局 式中:j取值于{1,2,…,D},k取值于{1,2,…, 部最优解的新增邻域点,从而加速了侦查蜂的搜索, N},且k≠i。k,j均为[-1,1]的随机数。 使得蜂群以最快速度找到最优蜜源。 4)根据最优适应度选择原则,既要保留最优位 混沌搜索的基本思想)是根据式(6) 置蜜源,又要使蜂群搜索方向向着蜜源含量高升的 Yyn+i.4=uy.d(1-ynd) (6) 方向迭代。故当采蜜蜂在蜂巢邻域范围第2次找到 新蜜源时,记此时位置向量为new_X:,而上一次所 产生混沌序列,然后通过载波方式将混沌变量的值 映射到优化变量的取值范围。式(6)中,n∈[1, 找到的蜜源位置向量为X,,则记2次蜜源搜索中, 适应度值较大的位置蜜源为T,,其概率分布为 N],d∈[1,D],u是混沌状态的控制参数,当 PT(X,new_X)=new_X= u=4时,Logistic方程为完全混沌状态。它的数学 描述过程为:当有采蜜蜂转变为侦查蜂时,产生一个 1,f(new_X,)≥f(x,) (3) D维随机向量%=[yo.1o.2…]yo∈[0,1], 0,f(newX;)Limit且不满足式(3)时,即说明该邻域范 的N。个互异D维向量y。,通过式(7)的载波方式将 围位置蜜源含蜜量整体偏低,若再在此地搜索蜜源, y。映射到原解空间邻域范围内,产生决策变量。 会严重影响蜜源质量及搜索速度,故须将此类采蜜 3)将混沌变量y'.,d和yn,线性组合得到新的决 蜂重新规定初始蜜源位置。即 策变量y”nd【o: X(n+1)= y”m,d=(1-7)y'a,d+ya.d (8) Xmin+rand(O,l(Xax-Xma),trail(i)≥Limit 式中:7为动态调整系数,7的表达式为7=1- (n),trail(i)<Limit (5) K,)”,σ由目标函数而定。 K 8)如果满足停止准则,则停止计算并输出最优 4)按照操作2)~6)进行。 适应度值Best_Fitness,迭代次数iter=iter+1,相应的 5)通过计算适应度函数值Fitness(y'。,d),取 参数(x1,2,…,x),否则转向第3)步。 适应度值大的前/2个向量作为蜜源位置,对
式中: j 取值于 {1,2,…,D} ,为 D 维解向量的某个 分量。 分别计算各向量的适应度值,并将排名前一 半的作为初始的采蜜蜂种群 X(0) ,初始标志向量 trail(i)= 0,记录采蜜蜂停留同一蜜源的搜索次数。 3) 设置初始迭代次数 iter = 0,对于第 n 步的采 蜜蜂 Xi(n) ,在当前位置向量附近邻域进行搜索新 的位置,搜索公式为 new_X j i = X j i + φ j i(X j i - X j k) (2) 式中: j 取值于 {1,2,…,D} , k 取值于 {1,2,…, Ne} ,且 k ≠ i 。 k , j 均为 [ - 1,1] 的随机数。 4)根据最优适应度选择原则,既要保留最优位 置蜜源,又要使蜂群搜索方向向着蜜源含量高升的 方向迭代。 故当采蜜蜂在蜂巢邻域范围第 2 次找到 新蜜源时,记此时位置向量为 new_Xi ,而上一次所 找到的蜜源位置向量为 Xi ,则记 2 次蜜源搜索中, 适应度值较大的位置蜜源为 Ts ,其概率分布为 P{Ts(Xi,new_Xi) = new_Xi} = 1 , f(new_Xi) ≥ f(Xi) {0 , f(new_Xi) < f(Xi) (3) 5)当许多个采蜜蜂将所采蜜源信息带到舞蹈 区共享给观察蜂时,观察蜂将会做出 2 个动作行为: 首先,观察蜂根据概率式(4)选择符合自身条件的 采蜜蜂,转化为采蜜蜂;其次,通过式(4) 中适应度 值公式在蜂群邻域进行初次蜜源的搜索。 不同观察 蜂被招募为对应采蜜蜂的概率为 P{Ts1(X) = Xi} = f(Xi) ∑ Ne m = 1 f(Xm ) (4) 式中: Ts1 表示随机映射。 6)对比多次搜索到的新蜜源位置,生成最优蜜 源位置向量集 (x1 ,x2 ,…,xd ) , d 为现有采蜜蜂个 数,同时得出,到目前为止更新的最优适应度 Best_ Fitness。 7)在蜜源搜索中,不断地用标志向量 trail( i) 记录着同一采蜜蜂对同一蜜源位置的搜索次数,当 trail(i)>Limit 且不满足式(3)时,即说明该邻域范 围位置蜜源含蜜量整体偏低,若再在此地搜索蜜源, 会严重影响蜜源质量及搜索速度,故须将此类采蜜 蜂重新规定初始蜜源位置。 即 Xi(n + 1) = Xmin + rand(0,1)(Xmax - Xmin ),trail(i) ≥ Limit {Xi(n),trail(i) < Limit (5) 8)如果满足停止准则,则停止计算并输出最优 适应度值 Best_Fitness,迭代次数 iter = iter+1,相应的 参数 (x1 ,x2 ,…,xD) ,否则转向第 3)步。 2 基于混沌搜索策略的改进人工蜂群 算法 针对人工蜂群算法(ABC) 寻优过程中缺乏多 样性,收敛速度较慢,易陷入局部最优等缺陷,引入 混沌搜索策略的改进人工蜂群算法(improved artifi⁃ cial bee colony algorithm of chaos searching strategy, CSABCA),采用混沌搜索策略细化人工蜂群算法中 采蜜蜂和观察蜂的搜索空间,在迭代进化中产生局 部最优解的新增邻域点,从而加速了侦查蜂的搜索, 使得蜂群以最快速度找到最优蜜源。 混沌搜索的基本思想[5]是根据式(6) yn+1,d = μ·yn,d(1 - yn,d ) (6) 产生混沌序列,然后通过载波方式将混沌变量的值 映射到优化变量的取值范围。 式(6) 中, n ∈ [1, Nmax] , d ∈ [1,D] , μ 是混沌状态的控制参数,当 μ =4 时,Logistic 方程为完全混沌状态。 它的数学 描述过程为:当有采蜜蜂转变为侦查蜂时,产生一个 D 维随机向量 y0 = [y0,1 y0,2 … ],y0 ∈ [0,1] , y0 为迭代初始值,通过 Logistic 方程开始迭代,得到 序列 yn,d 。 同时,根据式(6) 产生的局部最优解的 新增邻域点,按照载波方式将混沌变量放大后应用 在待进行蜜源搜索的单个变量 f i,d 上,可得新个体 y′n,d = f i,d + Ri,d(2yn,d - 1) (7) 将混沌变量 yn,d 映射到了决策变量 y′n,d ,其中 y′n,d 是以转化为侦查蜂的采蜜蜂所在蜜源 f i,d 为中心,以 Ri,d 为半径的区域内。 最后,计算蜜源收益度 Fit⁃ ness (y′n,d ) ,同时计算在混沌迭代过程中的最优收 益度 Best _ Fitness (y′n,d ) ,若优于 Fitness (y′n,d ) , 替换原蜜源。 对于 目 标 函 数 minf(x) , 目 标 变 量 为 X = [x1 x2 … xd ] T ,完整的基于混沌搜索策略的人 工蜂群算法(CSABC)实现步骤如下: 1) 按照操作 1) 进行,记最大混沌迭代次数为 Cmax 。 2)利用混沌序列初始蜂群生成数值都在 (0,1) 的 NP 个互异 D 维向量 y0 ,通过式(7)的载波方式将 y0 映射到原解空间邻域范围内,产生决策变量。 3)将混沌变量 y′n,d 和 yn,d 线性组合得到新的决 策变量 y″n,d [19] : y″n,d = (1 - η)y′n,d + ηyn,d (8) 式中: η 为动态调整系数, η 的表达式为 η = 1 - ( K - 1 K ) σ , σ 由目标函数而定。 4)按照操作 2) ~6)进行。 5)通过计算适应度函数值 Fitness( y′ n,d ) ,取 适应度值大的前 NP / 2 个向量作为蜜源位置,对 第 6 期 彭晓华,等:混沌搜索策略的改进人工蜂群算法 ·929·

.930. 智能系统学报 第10卷 应N。/2个采蜜蜂。通过式(2)更新蜂群位置, N。/2个采蜜蜂在邻域附近按照式(7)寻找新解 3 CSABC算法仿真 y”.,d,再次计算适应度值Best_Fitness(y'n,d),若 3.1标准测试函数 Best-Fitness(y”a.d)>Fitness(y'.d),y'nd= 为验证基于混沌搜索策略的人工蜂群算法的性 y”,d,trail(i)=0;否则y',d不变,trail(i)= 能,选用6个标准测试函数Sphere、Rosenbrock、Ras trail(i)+1,并计算观察蜂转化为采蜜蜂的个数。 6)若trail(i)>Limit时,进行7),然后第i个 trigrin、Griewank、Ackley和Schwefel进行性能测 采蜜蜂舍弃蜜源转变为侦查蜂,侦查蜂在混沌区域 试s.i川。Sphere是一个基本单峰优化函数,只有全 范围内搜索邻域蜜源y”.,d。 局极值,用于测试算法寻优精度和收敛速度;Rosen- 7)记录到目前为止的所有蜜蜂寻找的最优蜜 bock是非凸、病态单峰函数,有局部极小值,用于测 源,更新iter=iter+l,判断是否达到最大混沌迭代次 试算法的收敛速度和执行效率;Rastrigrin、Grie 数,如果是,结束混沌搜索,找到最优解,否则,返回 wank、Ackley和Schwefel都是复杂的非线性多峰函 到2)。CSABC算法的基本流程图14如图2。 数,有许多局部极值点,用于测试算法的全局搜索能 采蜜驿按(7)、(8)寻找新解,计 力、跳出局部极值并避免早熟的能力5,0,20.6个标 算适应度函数值,更新蜜源位 置令trial(i)=0,否则trial(i)= 准测试函数的表达式、搜索空间及最优解见表1。 trial(i)+l 3.2实验仿真分析 初始化蜂群各参数采用 观察蜂转化为采蜜蜂进行邻域 混沌序列初始化蜂群,户 生互异随机向量 瘦索计算适应度函数值,判断 采用CSABC与ABC2种算法的对比仿真实验 是否保留蜜源更新标志向量 rial 进行性能测试。在ABC算法中,设定初始参数:蜂 通过载波方式将混沌变 N 量的值映射到决策变量 LimiD 群规模Np=100,蜜源个数为50,D=100,N。=20, 的邻域范围 V。=10,N,=40,搜索次数极限Limit=100,最大迭 通过线性组合生成动态 第i个采蜜蜂放弃当前蜜源 代次数为2O00:在CSABC算法中,混沌状态的控制 可调的决策变量邻域范 成为侦查蜂,在解空间随机 周 产生新蜜源 参数μ=4,为混沌映射半径Rd为函数自变量定义 计算适应度函数值♪ites 记录当前所有蜜蜂找到的最 域的3/10,调节系数σ=0.25,其余参数均与ABC 用标志向量trial()标记 优值,即全局最优解 采蜜蜂在同一蜜源的连 Best Fitness,.更新iter=ter+H 相同。图3~图8是为标准人工蜂群算法(ABC)与 续停留次数 N 本文提出的基于混沌搜索策略的改进人工蜂群算法 iter Y (CSABCA)对6个标准测试函数的优化过程中,蜂 终止搜索 群寻优对比曲线。 图2 CSABC算法流程图 Fig.2 CSABC algorithm flow chart 表1标准测试函数 Table 1 Standard test functions 函数 测试函数表达式 搜索范围 最优值 f ()=∑2 [-100,100] f(0,0,…,0)=0 f 6x)=2[100(-2)2+(4-1)] [-30,30] f5(1,1,…,1)=0 m1 5 5()=∑(2-10eos(2m,)+10) [-5.12,5.12] f53(0,0,…,0)=0 )2-Πcs()+1 [-600,600] f(0,0.…,0)=0 =-(-a22) [-32,32] f5(0,0.…,0)=0 f6(420.9687,…)= f6(x)=- ∑,(sin(v) [-500,500] 418.9829
应 NP / 2 个采蜜蜂。 通过式( 2) 更新蜂群位置, NP / 2 个采蜜蜂在邻域附近按照式( 7) 寻找新解 y″ n,d ,再次计算适应度值 Best_Fitness ( y′ n,d ) ,若 Best _ Fitness ( y″ n,d ) > Fitness( y′ n,d ) , y′ n,d = y″ n,d , trail ( i) = 0; 否 则 y′ n,d 不 变, trail ( i) = trail( i) + 1,并计算观察蜂转化为采蜜蜂的个数。 6)若 trail (i) > Limit 时,进行 7),然后第 i 个 采蜜蜂舍弃蜜源转变为侦查蜂,侦查蜂在混沌区域 范围内搜索邻域蜜源 y″n,d 。 7)记录到目前为止的所有蜜蜂寻找的最优蜜 源,更新 iter = iter+1,判断是否达到最大混沌迭代次 数,如果是,结束混沌搜索,找到最优解,否则,返回 到 2)。 CSABC 算法的基本流程图[14]如图 2。 图 2 CSABC 算法流程图 Fig.2 CSABC algorithm flow chart 3 CSABC 算法仿真 3.1 标准测试函数 为验证基于混沌搜索策略的人工蜂群算法的性 能,选用 6 个标准测试函数 Sphere、Rosenbrock、Ras⁃ trigrin、 Griewank、 Ackley 和 Schwefel 进 行 性 能 测 试[15⁃17] 。 Sphere 是一个基本单峰优化函数,只有全 局极值,用于测试算法寻优精度和收敛速度;Rosen⁃ brock 是非凸、病态单峰函数,有局部极小值,用于测 试算 法 的 收 敛 速 度 和 执 行 效 率; Rastrigrin、 Grie⁃ wank、Ackley 和 Schwefel 都是复杂的非线性多峰函 数,有许多局部极值点,用于测试算法的全局搜索能 力、跳出局部极值并避免早熟的能力[5,10,20] 。 6 个标 准测试函数的表达式、搜索空间及最优解见表 1。 3.2 实验仿真分析 采用 CSABC 与 ABC 2 种算法的对比仿真实验 进行性能测试。 在 ABC 算法中,设定初始参数:蜂 群规模 NP = 100,蜜源个数为 50, D = 100, Ne = 20, Nu = 10, Ns = 40,搜索次数极限 Limit = 100,最大迭 代次数为 2 000;在 CSABC 算法中,混沌状态的控制 参数 μ = 4,为混沌映射半径 Ri,d 为函数自变量定义 域的 3 / 10,调节系数 σ = 0.25,其余参数均与 ABC 相同。 图 3~图 8 是为标准人工蜂群算法(ABC)与 本文提出的基于混沌搜索策略的改进人工蜂群算法 (CSABCA)对 6 个标准测试函数的优化过程中,蜂 群寻优对比曲线。 表 1 标准测试函数 Table 1 Standard test functions 函数 测试函数表达式 搜索范围 最优值 f 1 f 1(x) = ∑ n i = 1 xi2 [ - 100,100] f 1(0,0,…,0) = 0 f 2 f 2(x) = ∑ n i = 1 [100 (xi+1 - xi2) 2 + (xi - 1) 2 ] [ - 30,30] f 2(1,1,…,1) = 0 f 3 f 3(x) = ∑ n i = 1 (xi2 - 10cos (2πxi) + 10) [ - 5.12,5.12] f 3(0,0,…,0) = 0 f 4 f 4(x) = 1 400∑ n i = 1 xi2 - ∏ n i = 1 cos( xi i ) + 1 [ - 600,600] f 4(0,0,…,0) = 0 f 5 f 5(x) = - 20exp( - 0.2 1 n ∑ n i = 1 xi2 ) - exp( 1 n ∑ n i = 1 cos 2πxi) + 20 + e [ - 32,32] f 5(0,0,…,0) = 0 f 6 f 6(x) = - ∑ n i = 1 (xi sin( xi )) [ - 500,500] f 6(420.968 7,…) = 418.982 9 ·930· 智 能 系 统 学 报 第 10 卷
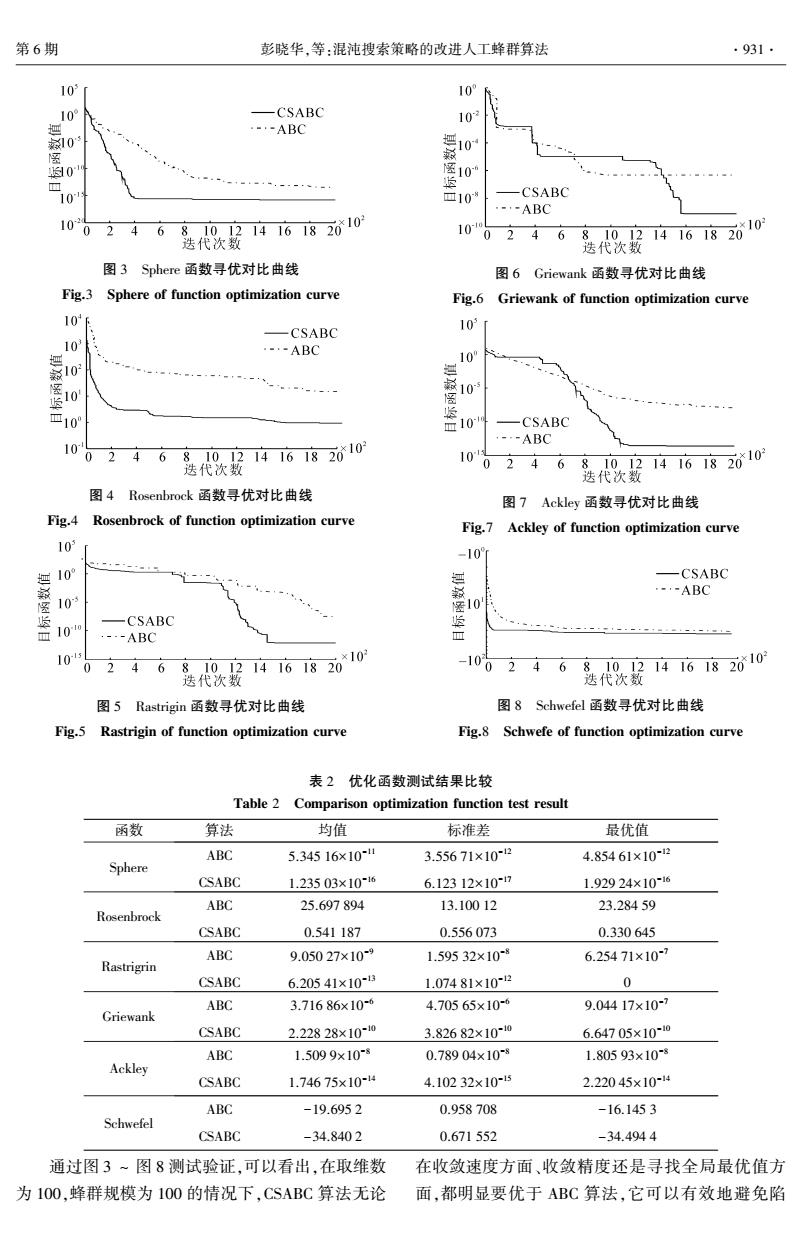
第6期 彭晓华,等:混沌搜索策略的改进人工蜂群算法 ·931· 10 10 10° -CSABC 10 ·--ABC 10 0 106 国 10 m10% -CSABC --ABC 102 024 6 8法9号416182010 10 0 24 迭代次数 6 91416182010 迭代次数 图3 Sphere函数寻优对比曲线 图6 Griewank函数寻优对比曲线 Fig.3 Sphere of function optimization curve Fig.6 Griewank of function optimization curve 10 103 -CSABC 10 --ABC 10 --- 10 立10 -CSABC -·-ABC 10 02 46 母铁92146182010 10 迭代次数 0 2 46 8921416182010 迭代次数 图4 Rosenbrock函数寻优对比曲线 图7 Ackley函数寻优对比曲线 Fig.4 Rosenbrock of function optimization curve Fig.7 Ackley of function optimization curve 103 -10 原 10° -CSABC 医发 --ABC 10 -CSABO 1010 ---ABC 10 024 6 8爱14161820*10 -100 246 89.21416182010 迭代次数 迭代次数 图5 Rastrigin函数寻优对比曲线 图8 Schwefel函数寻优对比曲线 Fig.5 Rastrigin of function optimization curve Fig.8 Schwefe of function optimization curve 表2优化函数测试结果比较 Table 2 Comparison optimization function test result 函数 算法 均值 标准差 最优值 ABC 5.34516×10- 3.55671×102 4.85461×102 Sphere CSABC 1.23503×1016 6.12312×10-7 1.92924×10-16 ABC 25.697894 13.10012 23.28459 Rosenbrock CSABC 0.541187 0.556073 0.330645 ABC 9.05027×109 1.59532×10- 6.25471×10-7 Rastrigrin CSABC 6.20541×10-18 1.07481×10~2 0 ABC 3.71686×10-6 4.70565×10-6 9.04417×10-7 Griewank CSABC 2.22828×10-10 3.82682×10-10 6.64705×10~10 ABC 1.5099×10-8 0.78904×10-8 1.80593×10-8 Ackley CSABC 1.74675×10-4 4.10232×10-5 2.22045×10-4 ABC -19.6952 0.958708 -16.1453 Schwefel CSABC -34.8402 0.671552 -34.4944 通过图3~图8测试验证,可以看出,在取维数 在收敛速度方面、收敛精度还是寻找全局最优值方 为100,蜂群规模为100的情况下,CSABC算法无论 面,都明显要优于ABC算法,它可以有效地避免陷
图 3 Sphere 函数寻优对比曲线 Fig.3 Sphere of function optimization curve 图 4 Rosenbrock 函数寻优对比曲线 Fig.4 Rosenbrock of function optimization curve 图 5 Rastrigin 函数寻优对比曲线 Fig.5 Rastrigin of function optimization curve 图 6 Griewank 函数寻优对比曲线 Fig.6 Griewank of function optimization curve 图 7 Ackley 函数寻优对比曲线 Fig.7 Ackley of function optimization curve 图 8 Schwefel 函数寻优对比曲线 Fig.8 Schwefe of function optimization curve 表 2 优化函数测试结果比较 Table 2 Comparison optimization function test result 函数 算法 均值 标准差 最优值 Sphere ABC 5.345 16×10 -11 3.556 71×10 -12 4.854 61×10 -12 CSABC 1.235 03×10 -16 6.123 12×10 -17 1.929 24×10 -16 Rosenbrock ABC 25.697 894 13.100 12 23.284 59 CSABC 0.541 187 0.556 073 0.330 645 Rastrigrin ABC 9.050 27×10 -9 1.595 32×10 -8 6.254 71×10 -7 CSABC 6.205 41×10 -13 1.074 81×10 -12 0 Griewank ABC 3.716 86×10 -6 4.705 65×10 -6 9.044 17×10 -7 CSABC 2.228 28×10 -10 3.826 82×10 -10 6.647 05×10 -10 Ackley ABC 1.509 9×10 -8 0.789 04×10 -8 1.805 93×10 -8 CSABC 1.746 75×10 -14 4.102 32×10 -15 2.220 45×10 -14 Schwefel ABC -19.695 2 0.958 708 -16.145 3 CSABC -34.840 2 0.671 552 -34.494 4 通过图 3 ~ 图 8 测试验证,可以看出,在取维数 为 100,蜂群规模为 100 的情况下,CSABC 算法无论 在收敛速度方面、收敛精度还是寻找全局最优值方 面,都明显要优于 ABC 算法,它可以有效地避免陷 第 6 期 彭晓华,等:混沌搜索策略的改进人工蜂群算法 ·931·
.932· 智能系统学报 第10卷 入局部极值而加速收敛。测试结果参数见表2。 由表2可以看出,6个测试函数中,CSABC算法 参考文献: 的最优值,均值及标准差均优于ABC算法。将本文 [1]KARABOGA D,AKAY B.A comparative study of artificial CSABC算法与根据文献[11]中的改进算法IABC, bee colony algorithm[J].Applied Mathematics and Compu- 文献[12]中的算法SFABC,文献[13]中的算法 tation,2009,214(1):108-132. LRABC,再次进行寻优测试进而验证本文算法的有 [2]KARABOGA D,OZTURK C.A novel clustering approach: 效性,取最大混沌搜索次数Cs=40,取标准测试函 artificial bee colony (ABC)algorithm [J].Applied Soft Computing,2011,11(1):652-657. 数Rosenbrock和Griewank分别测试运行40次,设 [3]ZHU Guopu,KWONG S.Gbest-guided artificial bee colony 算法精度为10-5,进行对比验证,见表3。 algorithm for numerical function optimization[J].Applied 表3不同改进人工蜂群算法优化结果 Mathematics and Computation,2010,217(7):3166-3173. Table 3 Different improved artificial colony algorithms op- [4]SZETO W Y,WU Yongzhong,HO S C.An artificial bee timization results colony algorithm for the capacitated vehicle routing problem 函数 算法 均值 标准差 平均时间 [J].European Journal of Operational Research,2011,215 LABC4.95867×10-17.66847×10-1 25.1755 (1):126-135. Rosen-SFABC 6.471200 3.852700 26.6514 [5]罗钧,李研.具有混沌搜索策略的蜂群优化算法[J].控 brock LRABC1.35918×10~8.74717×102 制与决策,2010,25(12):1913-1916. 24.1843 CSABC5.2657×10-26.38326×10317.5548 LUO Jun,LI Yan.Artificial bee colony algorithm with chaot- ic-search strategy [J].Control and Decision,2010,25 IABC 0 0 31.0128 (12):1913-1916, Gie.SFABC2.5457×1057.78426×10622.8748 [6]宁爱平,张雪英.人工蜂群算法的收敛性分析[J].控制 wank LRABC 0 0 27.8934 与决策,2013,28(10):1554-1558 CSABC 0 0 18.2354 NING Aiping,ZHANG Xueying.Convergence analysis of ar- 由表3中多种改进人工蜂群算法的对比测试可 tificial bee colony algorithm[J].Control and Decision, 得到,对测试函数Griewank、IABC、SFABC和CSABC 2013,28(10):1554-1558. [7]王冰.基于局部最优解的改进人工蜂群算法[J].计算机 算法均达到最优值,而对Rosenbrock测试函数中, 应用研究,2014,31(4):1024-1026. CSABC算法在均值、标准差及平均运行时间上均优 WANG Bing.Improved artificial bee colony algorithm based 于IABC、SFABC和LRABC算法,从而进一步验证了 on local best solution[J.Application Research of Comput- CSABC算法的优越性。 es,2014,31(4):1024-1026. 5结束语 [8]伍大清,郑建国.基于混合策略自适应学习的并行粒子 群优化算法[J].控制与决策,2013,28(7):1087-1093. 本文主要针对人工蜂群算法,蜂群搜索速度慢 WU Daqing,ZHENG Jianguo.Improved parallel particle 甚至停滞,多样性降低,容易陷入局部极值等诸多不 swarm optimization algorithm with hybrid strategy and self-a- 足,提出了一种基于混沌搜索策略的改进人工蜂群 daptive learning[J].Control and Decision,2013,28(7): 算法。该算法引入了混沌搜索策略,通过载波方式 1087-1093. [9]胥小波,郑康锋,李丹,等.新的混沌粒子群优化算法 将混沌变量的值映射到优化变量的取值范围内,产 [J].通信学报,2012,33(1):24-30,37. 生局部最优解的新增邻域点,从而加快了全局搜索 XU Xiaobo,ZHENG Kangfeng,LI Dan,et al.New chaos- 能力和局部搜索能力,增强了蜂群多样性,跳出了局 particle swarm optimization algorithm[J].Journal on Com- 部极值,提高了算法收敛速度。通过6个标准测试 munications,2012,33(1):24-30,37. 函数的对比寻优验证,CSABC算法具有收敛速度 [l0]匡芳君,徐蔚鸿,金忠.自适应Tent混沌搜索的人工蜂 快,收敛精度高和较强的全局搜索能力。同时,对比 群算法[J].控制理论与应用,2014,31(11):1502 了多种改进人工蜂群算法,充分验证本文算法的有 1509 效性和优越性。 KUANG Fangjun,XU Weihong,JIN Zhong.Artificial bee colony algorithm based on self-adaptive tent chaos search [J ]Control Theory Applications,2014,31 (11):
入局部极值而加速收敛。 测试结果参数见表 2。 由表 2 可以看出,6 个测试函数中,CSABC 算法 的最优值,均值及标准差均优于 ABC 算法。 将本文 CSABC 算法与根据文献[11] 中的改进算法 IABC, 文献 [12] 中的算法 SFABC,文献 [13] 中的算法 LRABC,再次进行寻优测试进而验证本文算法的有 效性,取最大混沌搜索次数 Cmax = 40,取标准测试函 数 Rosenbrock 和 Griewank 分别测试运行 40 次,设 算法精度为 10 -25 ,进行对比验证,见表 3。 表 3 不同改进人工蜂群算法优化结果 Table 3 Different improved artificial colony algorithms op⁃ timization results 函数 算法 均值 标准差 平均时间 Rosen⁃ brock IABC 4.958 67×10 -1 7.668 47×10 -1 25.175 5 SFABC 6.471 200 3.852 700 26.651 4 LRABC 1.359 18×10 -1 8.747 17×10 -2 24.184 3 CSABC 5.265 7×10 -2 6.383 26×10 -3 17.554 8 Grie⁃ wank IABC 0 0 31.0128 SFABC 2.545 7×10 -15 7.784 26×10 -16 22.874 8 LRABC 0 0 27.893 4 CSABC 0 0 18.235 4 由表 3 中多种改进人工蜂群算法的对比测试可 得到,对测试函数 Griewank、IABC、SFABC 和 CSABC 算法均达到最优值,而对 Rosenbrock 测试函数中, CSABC 算法在均值、标准差及平均运行时间上均优 于 IABC、SFABC 和 LRABC 算法,从而进一步验证了 CSABC 算法的优越性。 5 结束语 本文主要针对人工蜂群算法,蜂群搜索速度慢 甚至停滞,多样性降低,容易陷入局部极值等诸多不 足,提出了一种基于混沌搜索策略的改进人工蜂群 算法。 该算法引入了混沌搜索策略,通过载波方式 将混沌变量的值映射到优化变量的取值范围内,产 生局部最优解的新增邻域点,从而加快了全局搜索 能力和局部搜索能力,增强了蜂群多样性,跳出了局 部极值,提高了算法收敛速度。 通过 6 个标准测试 函数的对比寻优验证,CSABC 算法具有收敛速度 快,收敛精度高和较强的全局搜索能力。 同时,对比 了多种改进人工蜂群算法,充分验证本文算法的有 效性和优越性。 参考文献: [1]KARABOGA D, AKAY B. A comparative study of artificial bee colony algorithm[ J]. Applied Mathematics and Compu⁃ tation, 2009, 214(1): 108⁃132. [2]KARABOGA D, OZTURK C. A novel clustering approach: artificial bee colony ( ABC) algorithm [ J ]. Applied Soft Computing, 2011, 11(1): 652⁃657. [3]ZHU Guopu, KWONG S. Gbest⁃guided artificial bee colony algorithm for numerical function optimization [ J]. Applied Mathematics and Computation, 2010, 217(7): 3166⁃3173. [4]SZETO W Y, WU Yongzhong, HO S C. An artificial bee colony algorithm for the capacitated vehicle routing problem [J]. European Journal of Operational Research, 2011, 215 (1): 126⁃135. [5]罗钧, 李研. 具有混沌搜索策略的蜂群优化算法[ J]. 控 制与决策, 2010, 25(12): 1913⁃1916. LUO Jun, LI Yan. Artificial bee colony algorithm with chaot⁃ ic⁃search strategy [ J ]. Control and Decision, 2010, 25 (12): 1913⁃1916. [6]宁爱平, 张雪英. 人工蜂群算法的收敛性分析[ J]. 控制 与决策, 2013, 28(10): 1554⁃1558. NING Aiping, ZHANG Xueying. Convergence analysis of ar⁃ tificial bee colony algorithm [ J ]. Control and Decision, 2013, 28(10): 1554⁃1558. [7]王冰. 基于局部最优解的改进人工蜂群算法[ J]. 计算机 应用研究, 2014, 31(4): 1024⁃1026. WANG Bing. Improved artificial bee colony algorithm based on local best solution[ J]. Application Research of Comput⁃ ers, 2014, 31(4): 1024⁃1026. [8]伍大清, 郑建国. 基于混合策略自适应学习的并行粒子 群优化算法[J]. 控制与决策, 2013, 28(7): 1087⁃1093. WU Daqing, ZHENG Jianguo. Improved parallel particle swarm optimization algorithm with hybrid strategy and self⁃a⁃ daptive learning[ J]. Control and Decision, 2013, 28( 7): 1087⁃1093. [9]胥小波, 郑康锋, 李丹, 等. 新的混沌粒子群优化算法 [J]. 通信学报, 2012, 33(1): 24⁃30, 37. XU Xiaobo, ZHENG Kangfeng, LI Dan, et al. New chaos⁃ particle swarm optimization algorithm[ J]. Journal on Com⁃ munications, 2012, 33(1): 24⁃30, 37. [10]匡芳君, 徐蔚鸿, 金忠. 自适应 Tent 混沌搜索的人工蜂 群算法[ J]. 控制理论与应用, 2014, 31 ( 11): 1502⁃ 1509. KUANG Fangjun, XU Weihong, JIN Zhong. Artificial bee colony algorithm based on self⁃adaptive tent chaos search [ J ]. Control Theory & Applications, 2014, 31 ( 11 ): ·932· 智 能 系 统 学 报 第 10 卷

第6期 彭晓华,等,混沌搜索策略的改进人工蜂群算法 .933. 1502-1509 [18]KARABOGA N.A new design method based on artificial [11]王辉.改进的蜂群算法[J].计算机工程与设计,2011, bee colony algorithm for digital IIR filters[J].Journal of 32(11):3869-3872. the Franklin Institute,2009,346(4):328-348. WANG Hui.Improved artificial bee colony algorithm[J]. [19]王瑞琪,李珂,张承慧.基于混沌多目标遗传算法的微 Computer Engineering and Design,2011,32(11):3869- 网系统容量优化[J].电力系统保护与控制,2011,39 3872 (22):16-22 [12]王辉.一种带共享因子的人工蜂群算法[J].计算机工 WANG Ruiqi,LI Ke,ZHANG Chenghui.Optimization al- 程,2011,37(22):139-142. location of microgrid capacity based on chaotic multi-objec- WANG Hui.Artificial bee colony algorithm with sharing tive genetic algorithm[J].Power System Protection and factor[J].Computer Engineering,2011,37(22):139- Control,2011,39(22):16-22. 142. [20]暴励,曾建潮.一种双种群差分蜂群算法[J].控制理论 [13]刘三阳,张平,朱明敏.基于局部搜索的人工蜂群算法 与应用,2011,28(2):266-272. [J].控制与决策,2014,29(1):123-128. BAO Li,ZENG Jianchao.A bi-group differential artificial LIU Sanyang,ZHANG Ping,ZHU Mingmin.Artificial bee bee colony algorithm[J].Control Theory Applications, colony algorithm based on local search[]].Control and De- 2011,28(2):266-272. cision,2014,29(1):123-128 作者简介: [14]彭泓,丁玉成.基于遗传交叉因子的蝙蝠算法的改进 彭晓华,女,1963年生,教授,博士, [J].激光杂志,2015,36(2):23-26. 主要研究方向为煤层瓦斯渗流理论研 PENG Hong,DING Yucheng.Improved bats algorithm op- 究、智能控制理论方法与应用研究。参 timization based on genetic hybrid genes[J].Laser Jour- 加国家自然基金项目2项,主持和参加 nal.2015,36(2):23-26. 省教育厅科学研究基金项目各一项,主 [15]GAO Weifeng,LIU Sanyang.A modified artificial bee colo- 持或参加其他科研项目10余项。通过 ny algorithm [J].Computers Operations Research, 省市和学校鉴定的科研课题多项,获科研成果10余项。发 2012,39(3):687-697. 表学术论文20余篇。 [16]OMKAR S N,SENTHILNATH J,RAHUL K,et al.Arti- ficial bee colony (ABC)for multi-objective design optimi- zation of composite structures[].Applied Soft Compu- 刘利强,男,1988年生,硕士研究 ting,2011,11(1):489-499. 生,主要研究方向为智能检测与故障诊 [17]KARABOGA D,AKAY B.Artificial bee colony (ABC)al- 断。 gorithm on training artificial neural networks [C]//Pro- ceedings of IEEE 15th Signal Processing and Communica- tions Applications.Eskisehir:IEEE,2007:1-4
1502⁃1509. [11]王辉. 改进的蜂群算法[ J]. 计算机工程与设计, 2011, 32(11): 3869⁃3872. WANG Hui. Improved artificial bee colony algorithm[ J]. Computer Engineering and Design, 2011, 32(11): 3869⁃ 3872. [12]王辉. 一种带共享因子的人工蜂群算法[ J]. 计算机工 程, 2011, 37(22): 139⁃142. WANG Hui. Artificial bee colony algorithm with sharing factor[ J]. Computer Engineering, 2011, 37 ( 22): 139⁃ 142. [13]刘三阳, 张平, 朱明敏. 基于局部搜索的人工蜂群算法 [J]. 控制与决策, 2014, 29(1): 123⁃128. LIU Sanyang, ZHANG Ping, ZHU Mingmin. Artificial bee colony algorithm based on local search[J]. Control and De⁃ cision, 2014, 29(1): 123⁃128. [14]彭泓, 丁玉成. 基于遗传交叉因子的蝙蝠算法的改进 [J]. 激光杂志, 2015, 36(2): 23⁃26. PENG Hong, DING Yucheng. Improved bats algorithm op⁃ timization based on genetic hybrid genes [ J]. Laser Jour⁃ nal, 2015, 36(2): 23⁃26. [15]GAO Weifeng, LIU Sanyang. A modified artificial bee colo⁃ ny algorithm [ J ]. Computers & Operations Research, 2012, 39(3): 687⁃697. [16] OMKAR S N, SENTHILNATH J, RAHUL K, et al. Arti⁃ ficial bee colony (ABC) for multi⁃objective design optimi⁃ zation of composite structures [ J]. Applied Soft Compu⁃ ting, 2011, 11(1): 489⁃499. [17]KARABOGA D, AKAY B. Artificial bee colony (ABC) al⁃ gorithm on training artificial neural networks [ C] / / Pro⁃ ceedings of IEEE 15th Signal Processing and Communica⁃ tions Applications. Eskisehir: IEEE, 2007: 1⁃4. [18]KARABOGA N. A new design method based on artificial bee colony algorithm for digital IIR filters [ J]. Journal of the Franklin Institute, 2009, 346(4): 328⁃348. [19]王瑞琪, 李珂, 张承慧. 基于混沌多目标遗传算法的微 网系统容量优化[ J]. 电力系统保护与控制, 2011, 39 (22): 16⁃22. WANG Ruiqi, LI Ke, ZHANG Chenghui. Optimization al⁃ location of microgrid capacity based on chaotic multi⁃objec⁃ tive genetic algorithm [ J]. Power System Protection and Control, 2011, 39(22): 16⁃22. [20]暴励, 曾建潮. 一种双种群差分蜂群算法[J]. 控制理论 与应用, 2011, 28(2): 266⁃272. BAO Li, ZENG Jianchao. A bi⁃group differential artificial bee colony algorithm[ J]. Control Theory & Applications, 2011, 28(2): 266⁃272. 作者简介: 彭晓华,女,1963 年生,教授,博士, 主要研究方向为煤层瓦斯渗流理论研 究、智能控制理论方法与应用研究。 参 加国家自然基金项目 2 项,主持和参加 省教育厅科学研究基金项目各一项,主 持或参加其他科研项目 10 余项。 通过 省市和学校鉴定的科研课题多项,获科研成果 10 余项。 发 表学术论文 20 余篇。 刘利强,男, 1988 年生,硕士研究 生,主要研究方向为智能检测与故障诊 断。 第 6 期 彭晓华,等:混沌搜索策略的改进人工蜂群算法 ·933·