
第10卷第5期 智能系统学报 Vol.10 No.5 2015年10月 CAAI Transactions on Intelligent Systems 0ct.2015 D0I:10.11992/is.201407003 网s络出版t地址:htp:/ww.cmki.net/kcms/detail/23.1538.tp.20151008.1000.004.html 一种生物地理学移动机器人路径规划算法 莫宏伟,马靖雯 (哈尔滨工程大学自动化学院,黑龙江哈尔滨150001) 摘要:目前,虽然有多种智能计算方法用于移动机器人路径规划问题,但在复杂环境下,多数智能计算方法表现出 效率低下,结果较差的问题。提出一种结合基于有效顶点的栅格编码法和改进的生物地理学优化算法的移动机器 人路径规划方法,以解决该类问题。结合已知的环境信息,从精英策略、降维机制和基于惯性算子的迁移操作3方面 改进了生物地理学优化算法。改进算法用于机器人移动路径,与人工蜂群算法、粒子群算法和人工鱼群算法等智能 算法进行比较,实验的结果证实改进算法能够更有效地解决复杂环境下机器人路径规划问题。 关键词:移动机器人:路径规划:生物地理优化算法:有效顶点:栅格编码法 中图分类号:TP301文献标志码:A文章编号:1673-4785(2015)05-0705-07 中文引用格式:莫宏伟,马靖要.一种生物地理学移动机器人路径规划算法[J].智能系统学报,2015,10(5):705-711. 英文引用格式:MO Hongwei,MA Jingwen..A biogeography-based mobile robot path planning algorithm[J】.CAAI Transactions on Intelligent Systems,2015,10(5):705-711. A biogeography-based mobile robot path planning algorithm MO Hongwei,MA Jingwen College of Automation,Harbin Engineering University,Harbin 150001,China) Abstract:At present,there are many intelligent computing methods used in mobile robot path planning;however, in complex environments,most of them have low efficiency and poor results.In order to solve such problems,this paper proposes a new method for mobile robot path planning,which combines the grid coding method based on the effective vertex with the improved biogeography-based optimization (BBO).On the basis of the environmental infor- mation that has been learned,the BBO is improved in three aspects:elite strategies,dimension reduction mecha- nisms and migration based on inertial operator.The improved BBO is applied in path planning.The method is com- pared with artificial bee colony (ABC),particle swarm optimization (PSO)and artificial fish algorithm (AFA). Experiment results show that the improved method can solve the problem of mobile robot path planning in a complex environment more efficiently. Keywords:mobile robot;path planning;biogeography-based optimization (BBO);effective vertex;grid coding method 移动机器人路径规划主要解决3个问题:1)使 概括为以下4类:模版匹配路径规划技术、人工 机器人能从初始点运动到目标点:2)用一定的算法 势场路径规划技术、地图构建路径规划技术和人工 使机器人能绕开障碍物,并且经过某些必须经过的 智能路径规划技术。 点完成相应的作业任务;3)在完成以上任务的前提 模版匹配技术在环境确定情况下,有较好的应 下,尽量优化机器人运行轨迹。移动机器人路径规 用效果2。人工势场路径规划将机器人在环境中 划技术从移动机器人路径规划的具体算法与策略可 的运动视为一种机器人在虚拟的人工受力场中的运 动。障碍物对机器人产生斥力,目标点对机器人产 收稿日期:2014-07-01.网络出版日期:201410-08 生引力,引力和斥力的合力作为机器人的控制力,从 基金项目:中央高校基本科研业务经费资助项目(HEUCFX041306) 通信作者:莫宏伟.E-mail:honwei.2004@126.com. 而控制机器人避开障碍物而到达目标位置6-2)。地 图构建分为路标法和栅格法,路标法是构造一幅由
中央高校基本科研业务经费资助项目 收稿日期: 第 10 卷第 5 期 智 能 系 统 学 报 Vol.10 №.5 2015 年 10 月 CAAI Transactions on Intelligent Systems Oct. 201 基金项目 2014⁃07⁃01. 网络出版日期: 通信作者:莫宏伟. E⁃mail:honwei2004@ 126.com. 2014⁃10⁃08. 5 DOI:10.11992 / tis.201407003 网络出版地址:http: / / www.cnki.net / kcms/ detail / 23.1538.tp.20151008.1000.004.html 一种生物地理学移动机器人路径规划算法 莫宏伟,马靖雯 (哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001) 摘 要:目前,虽然有多种智能计算方法用于移动机器人路径规划问题,但在复杂环境下,多数智能计算方法表现出 效率低下,结果较差的问题。 提出一种结合基于有效顶点的栅格编码法和改进的生物地理学优化算法的移动机器 人路径规划方法,以解决该类问题。 结合已知的环境信息,从精英策略、降维机制和基于惯性算子的迁移操作 3 方面 改进了生物地理学优化算法。 改进算法用于机器人移动路径,与人工蜂群算法、粒子群算法和人工鱼群算法等智能 算法进行比较,实验的结果证实改进算法能够更有效地解决复杂环境下机器人路径规划问题。 关键词:移动机器人;路径规划;生物地理优化算法;有效顶点;栅格编码法 中图分类号:TP301 文献标志码:A 文章编号:1673⁃4785(2015)05⁃0705⁃07 中文引用格式:莫宏伟,马靖雯. 一种生物地理学移动机器人路径规划算法[J]. 智能系统学报, 2015,10(5): 705⁃711. 英文引用格式:MO Hongwei, MA Jingwen. A biogeography⁃based mobile robot path planning algorithm[ J]. CAAI Transactions on Intelligent Systems, 2015,10(5): 705⁃711. A biogeography⁃based mobile robot path planning algorithm MO Hongwei, MA Jingwen (College of Automation, Harbin Engineering University, Harbin 150001, China) Abstract:At present, there are many intelligent computing methods used in mobile robot path planning; however, in complex environments, most of them have low efficiency and poor results. In order to solve such problems, this paper proposes a new method for mobile robot path planning, which combines the grid coding method based on the effective vertex with the improved biogeography⁃based optimization (BBO). On the basis of the environmental infor⁃ mation that has been learned, the BBO is improved in three aspects: elite strategies, dimension reduction mecha⁃ nisms and migration based on inertial operator. The improved BBO is applied in path planning. The method is com⁃ pared with artificial bee colony (ABC), particle swarm optimization (PSO) and artificial fish algorithm (AFA). Experiment results show that the improved method can solve the problem of mobile robot path planning in a complex environment more efficiently. Keywords:mobile robot; path planning; biogeography⁃based optimization (BBO); effective vertex; grid coding method 移动机器人路径规划主要解决 3 个问题:1)使 机器人能从初始点运动到目标点;2)用一定的算法 使机器人能绕开障碍物,并且经过某些必须经过的 点完成相应的作业任务;3)在完成以上任务的前 (HEUCFX041306). 提 下,尽量优化机器人运行轨迹。 移动机器人路径规 划技术从移动机器人路径规划的具体算法与策略可 概括为以下 4 类[1] :模版匹配路径规划技术、人工 势场路径规划技术、地图构建路径规划技术和人工 智能路径规划技术。 模版匹配技术在环境确定情况下,有较好的应 用效果[2⁃5] 。 人工势场路径规划将机器人在环境中 的运动视为一种机器人在虚拟的人工受力场中的运 动。 障碍物对机器人产生斥力,目标点对机器人产 生引力,引力和斥力的合力作为机器人的控制力,从 而控制机器人避开障碍物而到达目标位置[6-12] 。 地 图构建分为路标法和栅格法,路标法是构造一幅由 :

·706 智能系统学报 第10卷 标志点和连接边线组成的机器人可行路径图,如可 y,≠yb (2) 视线方法、切线图方法、Voronoi图方法和概率图展 以图1为例,按照有效顶点法将产生31个有效 开法等13]。计算智能路径规划将生物启发的计算 顶点加入到有效顶点列表S,遍历这31个有效顶点 方法应用于移动机器人的路径规划中,如人工神经 并删除重复的顶点,最后如图1所示10×10的栅格 网络、进化计算、蚁群算法生物地理优化算法等。 地图描述为27个有效顶点。在路径规划之前,需要 但上述方法尤其是计算智能方法在复杂环境下都缺 将起始顶点和目的顶点加入到有效顶点列表。 乏效率,结果也不够准确。本文针对一类复杂环境 定义Available,=☑表示,顶点s:∈S的直线可 下的机器人路径规划问题,提出基于改进的生物地 达顶点集合。对于每个顶点s∈S且i≠若直线可 理学优化方法(biogeography--based optimization, 达检测通过,则向Available:添加s,并记录d=da= BB0),以期更有效地解决该类问题。 √s:-s‖。 1有效顶点栅格环境 栅格法是将环境离散化为二维(或三维)的基 本单元栅格,栅格大小决定了离散化环境的分辨率, 通过对这些栅格的标示来完成对机器人环境的建 模,若为了节约存储空间可采用四叉树等方法进行 B 建模,也可以从方便访问的角度出发建立逐点扫描 的二维环境,最后利用搜索算法得到规划路径。这 种方法因离散化的建模思想极其符合计算机的存储 运算特点而得到了广泛的应用。基本栅格法包括4 个步骤:1)栅格化二维平面:2)障碍物膨胀:3)标记 9 10 障碍物:4)自由栅格之间的连接信息。这种方法存 在以下缺点: 图1基于有效顶点的栅格示意图 1)栅格在被选入路径后需要加入禁忌表,即该 Fig.1 Schematic diagram of grids based on effective vertex 栅格不能再次被选入路径中,这样当遇到一些U型 2 BBO 槽等复杂环境会迅速生成有效的路径: 2)自由栅格大部分都不是有效栅格,路径规划 生物地理学是一门研究物种生存的自然学科, 结果的信息仅包含障碍物顶点附近的部分栅格: 物种种群分布的地域(栖息地)各不相同。每个栖 3)分辨率大小难以确定。分辨率过高,增加搜 息地的生活环境各不相同,而且每个物种根据自身 索算法的运算量:分辨率过小会导致路径规划结果 的生活条件也各不相同,所以对每个栖息地的适应 粗糙,在极端情况下会造成本来分开的障碍物连通, 程度也不相同,因此就有了物种的各式各样的分布、 最终得不到有效的路径。 迁移和灭绝等现象。每个栖息地的适应度指数 本文针对基本栅格法的以上3方面缺点,引入 (habitat suitability index,HSI)的高低根据该栖息地 了一种更为有效的方法一基于有效定点的栅格编 的多种因素称为适应度指数变量(suitability index 码法。该方法充分借鉴了可视图法和基本栅格法的 variable,SIV)相关,如种群类别、降雨量、地质状况、 特点而提出的方法,有效地解决了基本栅格法因分 植被和气候等。如果该栖息地的适应度指数较高, 辨率而增加额外运算规模,搜索规模只与有效顶点 那么有以下结果:物种必然呈现多样性,即物种数量 个数,即障碍物个数及其轮廓复杂度有关系。该方 大,但每个栖息地容纳物种的数量是有限度的,栖息 法从模型上解决了U型槽等障碍物模型机器人路 地会因为物种众多而导致资源匮乏,适应度下降导 径规划导致的算法陷入局部收敛问题。 致了物种选择离开栖息地:进入该栖息地的物种数 在mxn的栅格环境中,定义g(i,j)为{g(i,j)li∈ 量小于迁出该栖息地的物种数量:若栖息地的适应 [1,m-1],je[1,n-1],ieN,jeN}。若栅格g(i, 度指数较低,那么物种多样性减少,即物种数量稀 ),g(i,+1),g(i+1,),g(i+1,j+1)4个栅格中有 少,但是由于物种较少,导致物种选择迁入到该栖息 且只有一个障碍物栅格g(xb,yb),那么这个4个 地的数量高于迁出该栖息地的物种。任何一个栖息 栅格中必存在一个有效顶点g(x,y.),8与g.同 地的环境状况都有一定概率发生变异,导致HS发 时满足以下2个条件: 生改变。本文提出了基于生物地理优化的旅行商问 x。≠xb (1) 题求解算法[]
标志点和连接边线组成的机器人可行路径图,如可 视线方法、切线图方法、Voronoi 图方法和概率图展 开法等[ 1 3 ] 。 计算智能路径规划将生物启发的计算 方法应用于移动机器人的路径规划中,如人工神经 网络、进化计算、蚁群算法生物地理优化算法等[14] 。 但上述方法尤其是计算智能方法在复杂环境下都缺 乏效率,结果也不够准确。 本文针对一类复杂环境 下的机器人路径规划问题,提出基于改进的生物地 理 学 优 化 方 法 ( biogeography⁃based optimization, BBO),以期更有效地解决该类问题。 1 有效顶点栅格环境 栅格法是将环境离散化为二维(或三维) 的基 本单元栅格,栅格大小决定了离散化环境的分辨率, 通过对这些栅格的标示来完成对机器人环境的建 模,若为了节约存储空间可采用四叉树等方法进行 建模,也可以从方便访问的角度出发建立逐点扫描 的二维环境,最后利用搜索算法得到规划路径。 这 种方法因离散化的建模思想极其符合计算机的存储 运算特点而得到了广泛的应用。 基本栅格法包括 4 个步骤:1)栅格化二维平面;2)障碍物膨胀;3)标记 障碍物;4)自由栅格之间的连接信息。 这种方法存 在以下缺点: 1) 栅格在被选入路径后需要加入禁忌表,即该 栅格不能再次被选入路径中,这样当遇到一些 U 型 槽等复杂环境会迅速生成有效的路径; 2) 自由栅格大部分都不是有效栅格,路径规划 结果的信息仅包含障碍物顶点附近的部分栅格; 3) 分辨率大小难以确定。 分辨率过高,增加搜 索算法的运算量;分辨率过小会导致路径规划结果 粗糙,在极端情况下会造成本来分开的障碍物连通, 最终得不到有效的路径。 本文针对基本栅格法的以上 3 方面缺点,引入 了一种更为有效的方法———基于有效定点的栅格编 码法。 该方法充分借鉴了可视图法和基本栅格法的 特点而提出的方法,有效地解决了基本栅格法因分 辨率而增加额外运算规模,搜索规模只与有效顶点 个数,即障碍物个数及其轮廓复杂度有关系。 该方 法从模型上解决了 U 型槽等障碍物模型机器人路 径规划导致的算法陷入局部收敛问题。 在 m×n 的栅格环境中,定义 g(i,j)为{g(i,j) |i∈ [1,m-1],j∈[1,n-1],i∈N,j∈N}。 若栅格 g( i, j),g(i,i+1),g(i+1,j),g( i+1,j+1) 4 个栅格中有 且只有一个障碍物栅格 gob( xob,yob),那么这个 4 个 栅格中必存在一个有效顶点 gv( xv,yv ),gob与 gv 同 时满足以下 2 个条件: xv ≠ xob (1) yv ≠ yob (2) 以图 1 为例,按照有效顶点法将产生 31 个有效 顶点加入到有效顶点列表 S,遍历这 31 个有效顶点 并删除重复的顶点,最后如图 1 所示 10×10 的栅格 地图描述为 27 个有效顶点。 在路径规划之前,需要 将起始顶点和目的顶点加入到有效顶点列表。 定义 Availablei = ∅表示,顶点 si ∈S 的直线可 达顶点集合。 对于每个顶点 sj∈S 且 i≠j 若直线可 达检测通过,则向Availablei 添加 sj,并记录 dij = dji = ‖si -sj‖。 图 1 基于有效顶点的栅格示意图 Fig.1 Schematic diagram of grids based on effective vertex 2 BBO 生物地理学是一门研究物种生存的自然学科, 物种种群分布的地域(栖息地) 各不相同。 每个栖 息地的生活环境各不相同,而且每个物种根据自身 的生活条件也各不相同,所以对每个栖息地的适应 程度也不相同,因此就有了物种的各式各样的分布、 迁移和灭绝等现象。 每个栖息地的适应度指数 (habitat suitability index,HSI)的高低根据该栖息地 的多种因素称为适应度指数变量( suitability index variable,SIV)相关,如种群类别、降雨量、地质状况、 植被和气候等。 如果该栖息地的适应度指数较高, 那么有以下结果:物种必然呈现多样性,即物种数量 大,但每个栖息地容纳物种的数量是有限度的,栖息 地会因为物种众多而导致资源匮乏,适应度下降导 致了物种选择离开栖息地;进入该栖息地的物种数 量小于迁出该栖息地的物种数量;若栖息地的适应 度指数较低,那么物种多样性减少,即物种数量稀 少,但是由于物种较少,导致物种选择迁入到该栖息 地的数量高于迁出该栖息地的物种。 任何一个栖息 地的环境状况都有一定概率发生变异,导致 HIS 发 生改变。 本文提出了基于生物地理优化的旅行商问 题求解算法[15] 。 ·706· 智 能 系 统 学 报 第 10 卷

第5期 莫宏伟,等:一种生物地理学移动机器人路径规划算法 ·707. 2.1适应度指数变量SIV与机器人路径的关系 以及P、;保存最小路径信息和最小路径值到Dm; 设有m个岛屿,那么第i个岛屿的SV:= 3)初始化迭代次数nc=0: (SIV,SIV,…,SIV),对于每一个SIV有 4)执行迁移操作: SIV=SIV,()∈(0,1) (3) 5)是否执行变异操作,若不执行则跳过: 另外,生成第i个岛屿所代表的路径列表Path,=☑, 6)计算每个岛屿的路径D,并根据D:确定S, 令V,加入到Path:中,设当前路径顶点列表Path:有 以及P;计算当前代数最小路径D,若D“0 1)初始化最大循环次数N:初始化BBO的各个 (11)) 参数:岛屿数M,最大变异率mmx;最大物种数Sms= 式中:a为降维因子,a≥1,b为常数。 M-1,最大迁出率E=1,最大嵌入率1=1:初始化每 个岛屿i的SV,SV=rand(0,l): 3仿真与分析 2)计算每个岛屿的路径D,并根据D:确定S, 实验加载30×30环境模型路径起始点坐标为
2.1 适应度指数变量 SIV 与机器人路径的关系 设有 m 个 岛 屿, 那 么 第 i 个 岛 屿 的 SIVi = (SIV 1 i ,SIV 2 i ,…,SIV n i ),对于每一个 SIV j i 有 SIV j i = SIVi(j) ∈ (0,1) (3) 另外,生成第i 个岛屿所代表的路径列表Pathi =∅, 令 Vs 加入到 Pathi 中,设当前路径顶点列表 Pathi 有 j 个顶点,那么第 j 个顶点 sj 的可直线到达列表 Availablei,定义集合 Mi =Availablei -Pathi,定义 n 为 Mi 的个数,那么添加顶点 sj+1到 Pathi 的队尾直到目 的地顶点 Vt 添加到 Pathi。 sj+1选取方法如式(4)所 示。 sj+1 = Mi(n × SIV j i) (4) SIVi 需要包含的变量个数需要达到 N-1(N 为 有效顶点列表 S 的个数)才能够保证机器人路径生 成的绝对安全。 2.2 BBO 的迁移操作 对于每一个 SIV j i,表示岛屿 i 的第 j 个适应度指 数变量是否被从其他岛屿的 SIV j k 迁入所取代的判 定:随机数 rand(0,1) <λi 是否成立,若成立则 SIV j i 将被迁入变量所取代;不成立则不执行迁入操作。 迁入操作描述如下,根据每个岛屿的迁出率 μi 进行贪婪算法选择岛屿 k,迁出操作将 SIV j k 迁入到 SIV j i,如式(5)所示。 SIV j i = SIV j k (5) 2.3 BBO 的变异操作 设有 M 个岛屿,根据 2.1 描述的如何将 SIV 转 换为路径列表 Path,计算每个岛屿的所代表的路径 的长度 D= {D1 ,D2 ,…,Dm-1 ,Dm },Di 越小的代表越 高的 HIS,所以按照 Di 的大小由小到大将集合 D 排 序,排序索引可以表示为 Index = { I1 , I2 ,…, IM-1 , IM },Ii 表示 M 个 Di 由小到大排序的岛屿 i 在排序 的中的位置。 那么岛屿 i 的物种数 Si 可表示为 Si = M - Index(i) (6) 生物地理学认为栖息地的物种数量过大和过小 都将导致栖息地的 SIV 变异率较高。 定义岛屿 i 的 变异率 mi: mi = mmax 1 - PSi Pmax æ è ç ö ø ÷ (7) 式中:mmax为算法需要人工设定的最大变异率。 2.4 算法流程 基于生物地理学的路径规划算法流程下: 1)初始化最大循环次数 N;初始化 BBO 的各个 参数:岛屿数 M,最大变异率 mmax;最大物种数 Smax = M-1,最大迁出率 E = 1,最大嵌入率 I = 1;初始化每 个岛屿 i 的 SIV,SIV j i = rand(0,1); 2)计算每个岛屿的路径 D,并根据 Di 确定 Si, 以及 PSi ;保存最小路径信息和最小路径值到 Dmin ; 3)初始化迭代次数 nc = 0; 4)执行迁移操作; 5)是否执行变异操作,若不执行则跳过; 6)计算每个岛屿的路径 D,并根据 Di 确定 Si, 以及 PSi ;计算当前代数最小路径 D nc min ,若 D nc min<Dmin , 则 D nc min =Dmin ,保存最小路径信息; 7)nc<N 是否成立,若成立,则 nc = nc+1,跳到 4);若不成立,则跳到 7); 8)输出最短路径值和最短路径信息。 2.5 算法的改进 2.5.1 精英策略 由 2.3 可知,mi 为岛屿 i 的变异率,那么当 i = Index(1)时,将得到最大的变异率,也就是说:路径 最短的岛屿具有很高的变异率。 这一结果将可能导 致算法的进化出现退化。 因此,精英岛屿具有变异 率为 0 的特性。 设算法有 n 个精英岛屿,那么设置 方法如下: mIndex(i) = 0,(i = 1,2,…,n) (8) 在算法步骤上,只需要将算法流程中所述的算 法步骤的 2)和 6)分别在最末加入式(8)。 2.5.2 降维 根据 2.1 描述可以看出,SIVi 需要包含的变量个 数需要达到 N-1(N 为有效顶点列表 S 的个数),即岛 屿的变量需要达到和有效顶点数相同(或在单项搜索 的时候少 1 个变量,双向搜索的时候少 2 个变量)才 能够保证机器人路径生成的绝对稳定。 但一般情况 下,路径规划的结果只包含整个有效顶点结合中少数 个顶点。 这说明,若不改进算法,算法将会是一个维 数巨大的计算,而且是不必要的大维度计算。 本文尝试提出了一种降维机制描述如下: 对于在 t = 0 时,有效顶点集合 S 内共有 X 个顶 点,那么所有岛屿的 SIV 0 的维数 Y = X-2;按照 2.1 方法生成完整的路径,记录第 i 个岛屿的正向有效 的 SIV 个数 xi,和反向有效的 SIV 个数 yi。 在 t 时 刻,定义 ω(t) = min{x1(t) + y1(t),x2(t) + y2(t),…,xM(t) + yM(t)} (9) ωmin = min{ω(0),ω(1),…,ω(t - 1)} (10) t 时刻所有岛屿的 SIV 的维数: Y(t) = X - 2,t = 0 {α·max{ωmin ,ω(t)} + b, t > 0 (11) 式中:α 为降维因子,α≥1,b 为常数。 3 仿真与分析 实验加载 30×30 环境模型路径起始点坐标为 第 5 期 莫宏伟,等:一种生物地理学移动机器人路径规划算法 ·707·
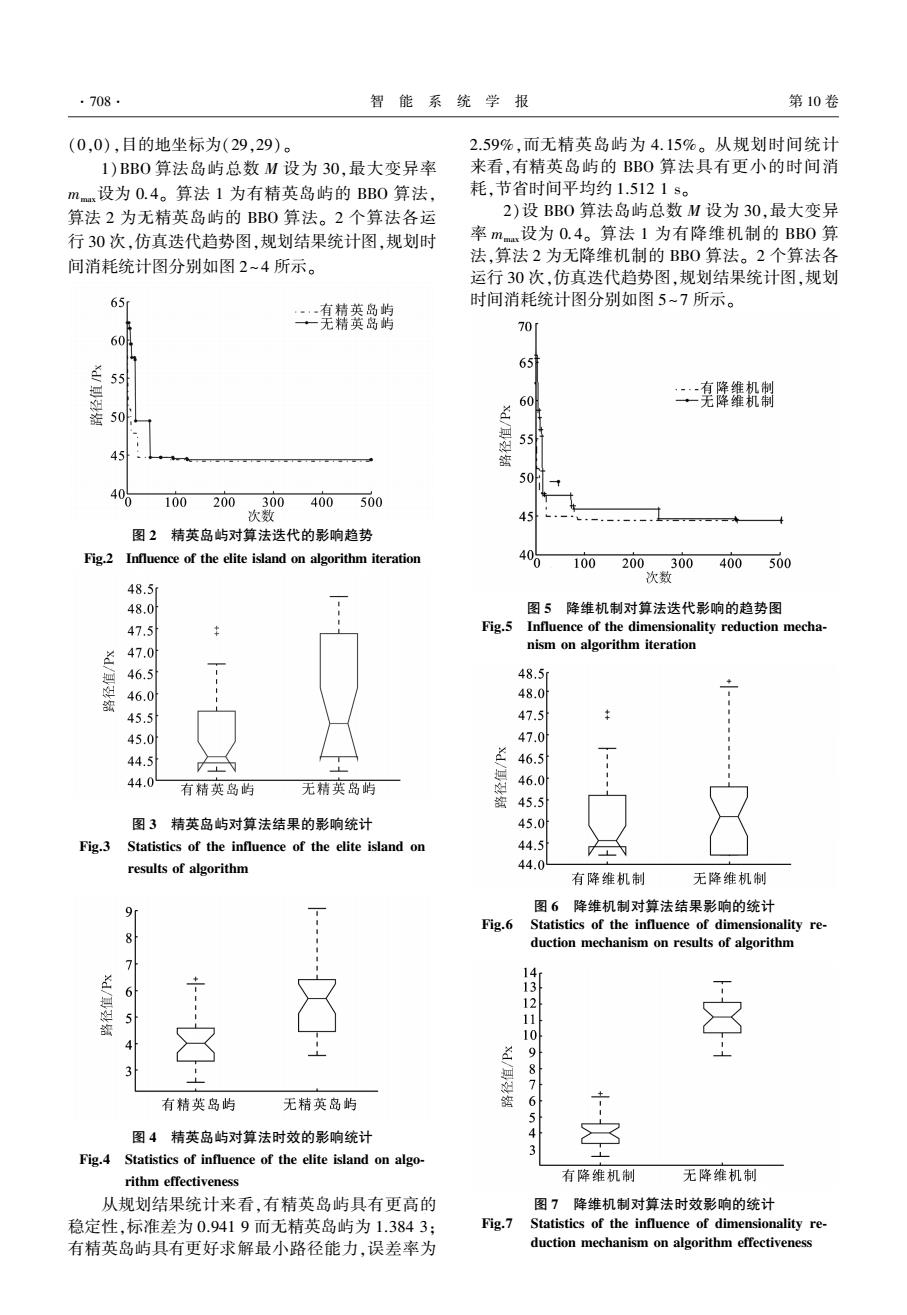
·708 智能系统学报 第10卷 (0,0),目的地坐标为(29,29)。 2.59%,而无精英岛屿为4.15%。从规划时间统计 1)BB0算法岛屿总数M设为30,最大变异率 来看,有精英岛屿的BBO算法具有更小的时间消 mm设为0.4。算法1为有精英岛屿的BB0算法, 耗,节省时间平均约1.5121s。 算法2为无精英岛屿的BB0算法。2个算法各运 2)设BB0算法岛屿总数M设为30,最大变异 行30次,仿真迭代趋势图,规划结果统计图,规划时 率m设为0.4。算法1为有降维机制的BB0算 间消耗统计图分别如图2~4所示。 法,算法2为无降维机制的BB0算法。2个算法各 运行30次,仿真迭代趋势图,规划结果统计图,规划 65 时间消耗统计图分别如图5~7所示。 70 60 651 55 一有降维机制 60 ·一无降维机制 55 45- 50 100 200300 400500 次数 图2精英岛屿对算法迭代的影响趋势 Fig.2 Influence of the elite island on algorithm iteration 00 100 200300400500 次数 48.5 48.0 图5降维机制对算法迭代影响的趋势图 47.5 Fig.5 Influence of the dimensionality reduction mecha- 47.0 nism on algorithm iteration 46.5 48.5 46.0 48.0 45.5 47.5 45.0 47.0 44.5 兰 46.5 44.0 无精英岛屿 46.0 有精英岛屿 45.5 图3精英岛屿对算法结果的影响统计 45.0 Fig.3 Statistics of the influence of the elite island on 44.5 results of algorithm 44.0 有降维机制 无降维机制 9 图6降维机制对算法结果影响的统计 Fig.6 Statistics of the influence of dimensionality re- duction mechanism on results of algorithm 14 6 5 10 9 如 8 有精英岛屿 无精英岛屿 6 图4精英岛屿对算法时效的影响统计 4 Fig.4 Statistics of influence of the elite island on algo- rithm effectiveness 有降维机制 无降维机制 从规划结果统计来看,有精英岛屿具有更高的 图7降维机制对算法时效影响的统计 稳定性,标准差为0.9419而无精英岛屿为1.3843: Fig.7 Statistics of the influence of dimensionality re- 有精英岛屿具有更好求解最小路径能力,误差率为 duction mechanism on algorithm effectiveness
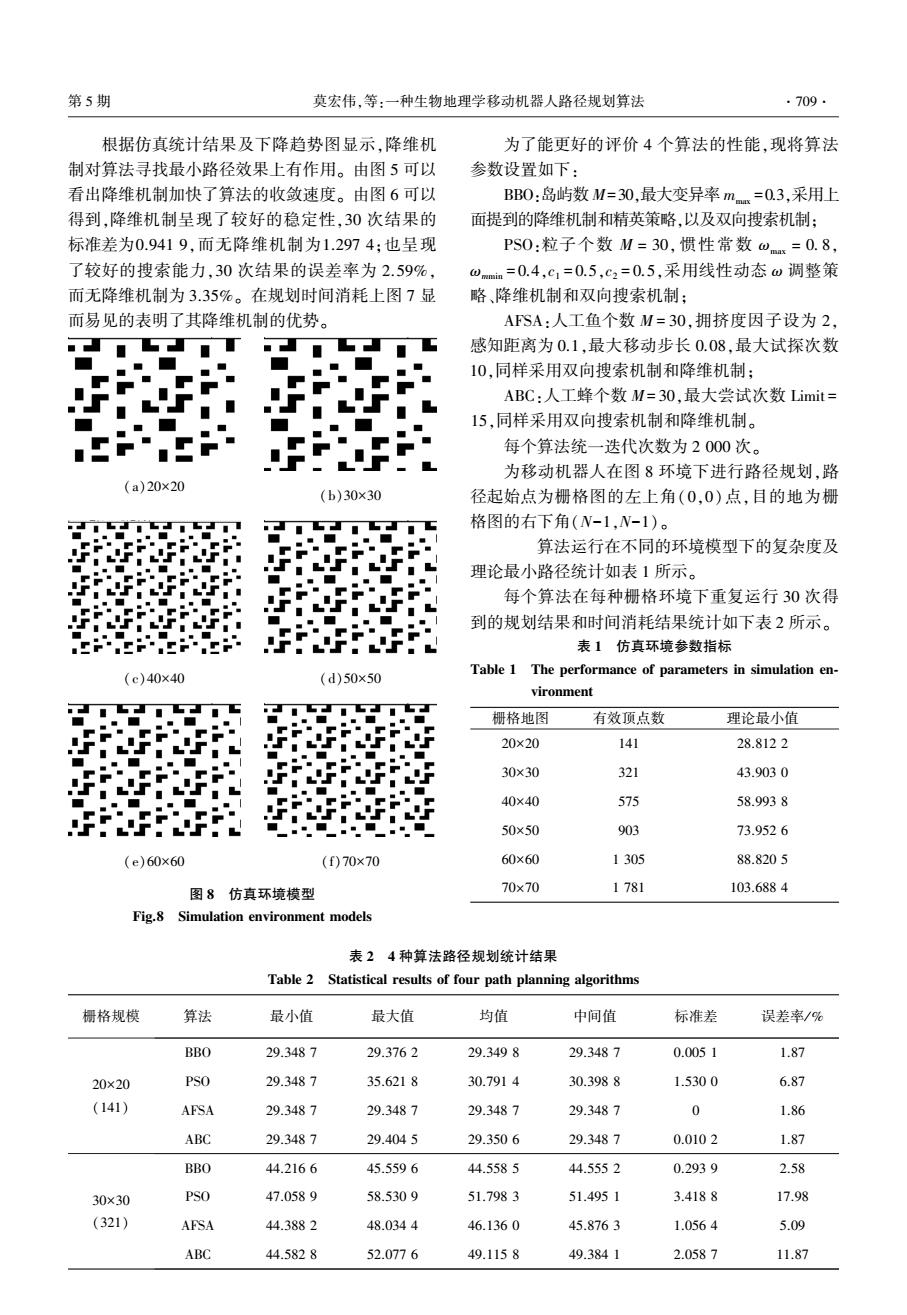
(0,0),目的地坐标为(29,29)。 1)BBO 算法岛屿总数 M 设为 30,最大变异率 mmax设为 0.4。 算法 1 为有精英岛屿的 BBO 算法, 算法 2 为无精英岛屿的 BBO 算法。 2 个算法各运 行 30 次,仿真迭代趋势图,规划结果统计图,规划时 间消耗统计图分别如图 2~4 所示。 图 2 精英岛屿对算法迭代的影响趋势 Fig.2 Influence of the elite island on algorithm iteration 图 3 精英岛屿对算法结果的影响统计 Fig.3 Statistics of the influence of the elite island on results of algorithm 图 4 精英岛屿对算法时效的影响统计 Fig.4 Statistics of influence of the elite island on algo⁃ rithm effectiveness 从规划结果统计来看,有精英岛屿具有更高的 稳定性,标准差为 0.941 9 而无精英岛屿为 1.384 3; 有精英岛屿具有更好求解最小路径能力,误差率为 2.59%,而无精英岛屿为 4.15%。 从规划时间统计 来看,有精英岛屿的 BBO 算法具有更小的时间消 耗,节省时间平均约 1.512 1 s。 2)设 BBO 算法岛屿总数 M 设为 30,最大变异 率 mmax设为 0.4。 算法 1 为有降维机制的 BBO 算 法,算法 2 为无降维机制的 BBO 算法。 2 个算法各 运行 30 次,仿真迭代趋势图,规划结果统计图,规划 时间消耗统计图分别如图 5~7 所示。 图 5 降维机制对算法迭代影响的趋势图 Fig.5 Influence of the dimensionality reduction mecha⁃ nism on algorithm iteration 图 6 降维机制对算法结果影响的统计 Fig.6 Statistics of the influence of dimensionality re⁃ duction mechanism on results of algorithm 图 7 降维机制对算法时效影响的统计 Fig.7 Statistics of the influence of dimensionality re⁃ duction mechanism on algorithm effectiveness ·708· 智 能 系 统 学 报 第 10 卷
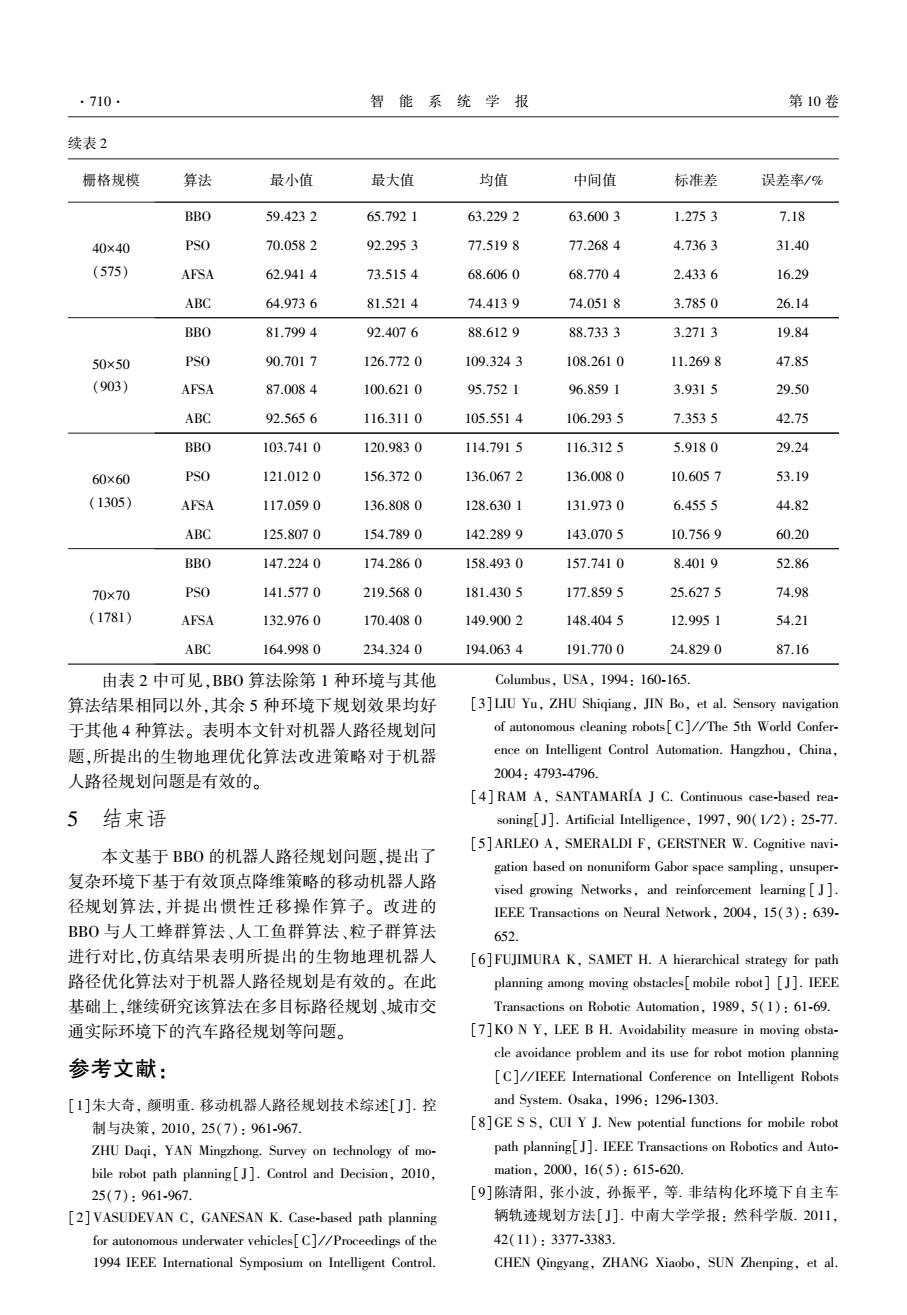
第5期 莫宏伟,等:一种生物地理学移动机器人路径规划算法 ·709. 根据仿真统计结果及下降趋势图显示,降维机 为了能更好的评价4个算法的性能,现将算法 制对算法寻找最小路径效果上有作用。由图5可以 参数设置如下: 看出降维机制加快了算法的收敛速度。由图6可以 BB0:岛屿数M=30,最大变异率mm=0.3,采用上 得到,降维机制呈现了较好的稳定性,30次结果的 面提到的降维机制和精英策略,以及双向搜索机制: 标准差为0.9419,而无降维机制为1.2974:也呈现 PS0:粒子个数M=30,惯性常数ωms=0.8, 了较好的搜索能力,30次结果的误差率为2.59%, min=0.4,C1=0.5,c2=0.5,采用线性动态w调整策 而无降维机制为3.35%。在规划时间消耗上图7显 略、降维机制和双向搜索机制; 而易见的表明了其降维机制的优势 AFSA:人工鱼个数M=30,拥挤度因子设为2, 感知距离为0.1,最大移动步长0.08,最大试探次数 ■ ■ 10,同样采用双向搜索机制和降维机制: ■ ■ ABC:人工蜂个数M=30,最大尝试次数Limit= 15,同样采用双向搜索机制和降维机制。 ■ 每个算法统一迭代次数为2000次。 为移动机器人在图8环境下进行路径规划,路 (a)20x20 (b)30×30 径起始点为栅格图的左上角(0,0)点,目的地为栅 格图的右下角(N-1,N-1)。 算法运行在不同的环境模型下的复杂度及 ◆ ” 理论最小路径统计如表1所示。 t ◆ ◆ 每个算法在每种栅格环境下重复运行30次得 到的规划结果和时间消耗结果统计如下表2所示。 ■ ■ 表1仿真环境参数指标 (c)40x40 Table 1 The performance of parameters in simulation en- (d)50x50 vironment 栅格地图 有效顶点数 理论最小值 20×20 141 28.8122 30×30 321 43.9030 40×40 575 58.9938 ■ 50x50 903 73.9526 (e)60x60 (f)70×70 60X60 1305 88.8205 图8仿真环境模型 70×70 1781 103.6884 Fig.8 Simulation environment models 表24种算法路径规划统计结果 Table 2 Statistical results of four path planning algorithms 栅格规模 算法 最小值 最大值 均值 中间值 标准差 误差率/% BBO 29.3487 29.3762 29.3498 29.3487 0.0051 1.87 20×20 PSO 29.3487 35.6218 30.7914 30.3988 1.5300 6.87 (141) AFSA 29.3487 29.3487 29.3487 29.3487 0 1.86 ABC 29.3487 29.4045 29.3506 29.3487 0.0102 1.87 BBO 44.2166 45.5596 44.5585 44.5552 0.2939 2.58 30×30 PSO 47.0589 58.5309 51.7983 51.4951 3.4188 17.98 (321) AFSA 44.3882 48.0344 46.1360 45.8763 1.0564 5.09 ABC 44.5828 52.0776 49.1158 49.3841 2.0587 11.87
根据仿真统计结果及下降趋势图显示,降维机 制对算法寻找最小路径效果上有作用。 由图 5 可以 看出降维机制加快了算法的收敛速度。 由图 6 可以 得到,降维机制呈现了较好的稳定性,30 次结果的 标准差为0.941 9,而无降维机制为1.297 4;也呈现 了较好的搜索能力,30 次结果的误差率为 2.59%, 而无降维机制为 3.35%。 在规划时间消耗上图 7 显 而易见的表明了其降维机制的优势。 (a)20×20 (b)30×30 (c)40×40 (d)50×50 (e)60×60 (f)70×70 图 8 仿真环境模型 Fig.8 Simulation environment models 为了能更好的评价 4 个算法的性能,现将算法 参数设置如下: BBO:岛屿数 M=30,最大变异率 mmax =0.3,采用上 面提到的降维机制和精英策略,以及双向搜索机制; PSO:粒子个数 M = 30,惯性常数 ωmax = 0. 8, ωmmin = 0.4,c1 = 0.5,c2 = 0.5,采用线性动态 ω 调整策 略、降维机制和双向搜索机制; AFSA:人工鱼个数 M = 30,拥挤度因子设为 2, 感知距离为 0.1,最大移动步长 0.08,最大试探次数 10,同样采用双向搜索机制和降维机制; ABC:人工蜂个数 M= 30,最大尝试次数 Limit = 15,同样采用双向搜索机制和降维机制。 每个算法统一迭代次数为 2 000 次。 为移动机器人在图 8 环境下进行路径规划,路 径起始点为栅格图的左上角(0,0)点,目的地为栅 格图的右下角(N-1,N-1)。 算法运行在不同的环境模型下的复杂度及 理论最小路径统计如表 1 所示。 每个算法在每种栅格环境下重复运行 30 次得 到的规划结果和时间消耗结果统计如下表 2 所示。 表 1 仿真环境参数指标 Table 1 The performance of parameters in simulation en⁃ vironment 栅格地图 有效顶点数 理论最小值 20×20 141 28.812 2 30×30 321 43.903 0 40×40 575 58.993 8 50×50 903 73.952 6 60×60 1 305 88.820 5 70×70 1 781 103.688 4 表 2 4 种算法路径规划统计结果 Table 2 Statistical results of four path planning algorithms 栅格规模 算法 最小值 最大值 均值 中间值 标准差 误差率/ % 20×20 (141) BBO 29.348 7 29.376 2 29.349 8 29.348 7 0.005 1 1.87 PSO 29.348 7 35.621 8 30.791 4 30.398 8 1.530 0 6.87 AFSA 29.348 7 29.348 7 29.348 7 29.348 7 0 1.86 ABC 29.348 7 29.404 5 29.350 6 29.348 7 0.010 2 1.87 30×30 (321) BBO 44.216 6 45.559 6 44.558 5 44.555 2 0.293 9 2.58 PSO 47.058 9 58.530 9 51.798 3 51.495 1 3.418 8 17.98 AFSA 44.388 2 48.034 4 46.136 0 45.876 3 1.056 4 5.09 ABC 44.582 8 52.077 6 49.115 8 49.384 1 2.058 7 11.87 第 5 期 莫宏伟,等:一种生物地理学移动机器人路径规划算法 ·709·
·710 智能系统学报 第10卷 续表2 栅格规模 算法 最小值 最大值 均值 中间值 标准差 误差率/% BBO 59.4232 65.7921 63.2292 63.6003 1.2753 7.18 40×40 PSO 70.0582 92.2953 77.5198 77.2684 4.7363 31.40 (575) AFSA 62.9414 73.5154 68.6060 68.7704 2.4336 16.29 ABC 64.9736 81.5214 74.4139 74.0518 3.7850 26.14 BBO 81.7994 92.4076 88.6129 88.7333 3.2713 19.84 50×50 PSO 90.7017 126.7720 109.3243 108.2610 11.2698 47.85 (903) AFSA 87.0084 100.6210 95.7521 96.8591 3.9315 29.50 ABC 92.5656 116.3110 105.5514 106.2935 7.3535 42.75 BBO 103.7410 120.9830 114.7915 116.3125 5.9180 29.24 60×60 PSO 121.0120 156.3720 136.0672 136.0080 10.6057 53.19 (1305) AFSA 117.0590 136.8080 128.6301 131.9730 6.4555 44.82 ABC 125.8070 154.7890 142.2899 143.0705 10.7569 60.20 BBO 147.2240 174.2860 158.4930 157.7410 8.4019 52.86 70×70 PSO 141.5770 219.5680 181.4305 177.8595 25.6275 74.98 (1781) AFSA 132.9760 170.4080 149.9002 148.4045 12.9951 54.21 ABC 164.9980 234.3240 194.0634 191.7700 24.8290 87.16 由表2中可见,BB0算法除第1种环境与其他 Columbus,USA,1994:160-165 算法结果相同以外,其余5种环境下规划效果均好 [3]LIU Yu,ZHU Shiqiang,JIN Bo,et al.Sensory navigation 于其他4种算法。表明本文针对机器人路径规划问 of autonomous cleaning robots[C]//The 5th World Confer- 题,所提出的生物地理优化算法改进策略对于机器 ence on Intelligent Control Automation.Hangzhou,China, 人路径规划问题是有效的。 2004:4793-4796. [4]RAM A,SANTAMARIA J C.Continuous case-based rea- 5结束语 soning[]]Artificial Intelligence,1997,90(1/2):25-77. [5]ARLEO A,SMERALDI F,GERSTNER W.Cognitive navi- 本文基于BBO的机器人路径规划问题,提出了 gation based on nonuniform Gabor space sampling,unsuper- 复杂环境下基于有效顶点降维策略的移动机器人路 vised growing Networks,and reinforcement learning[]. 径规划算法,并提出惯性迁移操作算子。改进的 IEEE Transactions on Neural Network,2004,15(3):639- BBO与人工蜂群算法、人工鱼群算法、粒子群算法 652. 进行对比,仿真结果表明所提出的生物地理机器人 [6]FUJIMURA K,SAMET H.A hierarchical strategy for path 路径优化算法对于机器人路径规划是有效的。在此 planning among moving obstacles[mobile robot][J].IEEE 基础上,继续研究该算法在多目标路径规划、城市交 Transactions on Robotic Automation,1989,5(1):61-69. 通实际环境下的汽车路径规划等问题。 [7]KO N Y,LEE B H.Avoidability measure in moving obsta- cle avoidance problem and its use for robot motion planning 参考文献: [C]//IEEE International Conference on Intelligent Robots [1]朱大奇,颜明重.移动机器人路径规划技术综述[J].控 and System.Osaka,1996:1296-1303. 制与决策.2010,25(7):961-967. [8]GE S S,CUI Y J.New potential functions for mobile robot ZHU Daqi,YAN Mingzhong.Survey on technology of mo- path planning[J].IEEE Transactions on Robotics and Auto- bile robot path planning[J].Control and Decision,2010, mation,.2000,16(5):615-620. 25(7):961-967. [9]陈清阳,张小波,孙振平,等.非结构化环境下自主车 [2]VASUDEVAN C,GANESAN K.Case-based path planning 辆轨迹规划方法[J].中南大学学报:然科学版.2011, for autonomous underwater vehicles[C]//Proceedings of the 42(11):3377-3383. 1994 IEEE International Symposium on Intelligent Control. CHEN Qingyang,ZHANG Xiaobo,SUN Zhenping,et al
续表 2 栅格规模 算法 最小值 最大值 均值 中间值 标准差 误差率/ % 40×40 (575) BBO 59.423 2 65.792 1 63.229 2 63.600 3 1.275 3 7.18 PSO 70.058 2 92.295 3 77.519 8 77.268 4 4.736 3 31.40 AFSA 62.941 4 73.515 4 68.606 0 68.770 4 2.433 6 16.29 ABC 64.973 6 81.521 4 74.413 9 74.051 8 3.785 0 26.14 50×50 (903) BBO 81.799 4 92.407 6 88.612 9 88.733 3 3.271 3 19.84 PSO 90.701 7 126.772 0 109.324 3 108.261 0 11.269 8 47.85 AFSA 87.008 4 100.621 0 95.752 1 96.859 1 3.931 5 29.50 ABC 92.565 6 116.311 0 105.551 4 106.293 5 7.353 5 42.75 60×60 (1305) BBO 103.741 0 120.983 0 114.791 5 116.312 5 5.918 0 29.24 PSO 121.012 0 156.372 0 136.067 2 136.008 0 10.605 7 53.19 AFSA 117.059 0 136.808 0 128.630 1 131.973 0 6.455 5 44.82 ABC 125.807 0 154.789 0 142.289 9 143.070 5 10.756 9 60.20 70×70 (1781) BBO 147.224 0 174.286 0 158.493 0 157.741 0 8.401 9 52.86 PSO 141.577 0 219.568 0 181.430 5 177.859 5 25.627 5 74.98 AFSA 132.976 0 170.408 0 149.900 2 148.404 5 12.995 1 54.21 ABC 164.998 0 234.324 0 194.063 4 191.770 0 24.829 0 87.16 由表 2 中可见,BBO 算法除第 1 种环境与其他 算法结果相同以外,其余 5 种环境下规划效果均好 于其他 4 种算法。 表明本文针对机器人路径规划问 题,所提出的生物地理优化算法改进策略对于机器 人路径规划问题是有效的。 5 结束语 本文基于 BBO 的机器人路径规划问题,提出了 复杂环境下基于有效顶点降维策略的移动机器人路 径规划算法,并提出惯性迁移操作算子。 改进的 BBO 与人工蜂群算法、人工鱼群算法、粒子群算法 进行对比,仿真结果表明所提出的生物地理机器人 路径优化算法对于机器人路径规划是有效的。 在此 基础上,继续研究该算法在多目标路径规划、城市交 通实际环境下的汽车路径规划等问题。 参考文献: [1]朱大奇, 颜明重. 移动机器人路径规划技术综述[ J]. 控 制与决策, 2010, 25(7): 961⁃967. ZHU Daqi, YAN Mingzhong. Survey on technology of mo⁃ bile robot path planning[ J]. Control and Decision, 2010, 25(7): 961⁃967. [2]VASUDEVAN C, GANESAN K. Case⁃based path planning for autonomous underwater vehicles[C] / / Proceedings of the 1994 IEEE International Symposium on Intelligent Control. Columbus, USA, 1994: 160⁃165. [3]LIU Yu, ZHU Shiqiang, JIN Bo, et al. Sensory navigation of autonomous cleaning robots[C] / / The 5th World Confer⁃ ence on Intelligent Control Automation. Hangzhou, China, 2004: 4793⁃4796. [4] RAM A, SANTAMARÍA J C. Continuous case⁃based rea⁃ soning[J]. Artificial Intelligence, 1997, 90(1 / 2): 25⁃77. [5]ARLEO A, SMERALDI F, GERSTNER W. Cognitive navi⁃ gation based on nonuniform Gabor space sampling, unsuper⁃ vised growing Networks, and reinforcement learning [ J ]. IEEE Transactions on Neural Network, 2004, 15(3): 639⁃ 652. [6]FUJIMURA K, SAMET H. A hierarchical strategy for path planning among moving obstacles[mobile robot] [J]. IEEE Transactions on Robotic Automation, 1989, 5(1): 61⁃69. [7]KO N Y, LEE B H. Avoidability measure in moving obsta⁃ cle avoidance problem and its use for robot motion planning [C] / / IEEE International Conference on Intelligent Robots and System. Osaka, 1996: 1296⁃1303. [8]GE S S, CUI Y J. New potential functions for mobile robot path planning[J]. IEEE Transactions on Robotics and Auto⁃ mation, 2000, 16(5): 615⁃620. [9]陈清阳, 张小波, 孙振平, 等. 非结构化环境下自主车 辆轨迹规划方法[ J]. 中南大学学报: 然科学版. 2011, 42(11): 3377⁃3383. CHEN Qingyang, ZHANG Xiaobo, SUN Zhenping, et al. ·710· 智 能 系 统 学 报 第 10 卷

第5期 莫宏伟,等:一种生物地理学移动机器人路径规划算法 ·711. Trajectory planning for autonomous driving in unstructured [14]MO Hongwei,MENG Longlong.Robot path planning based environments[J].Journal of Central South University:atu- on differential evolution in static environment[J.Interna ral and Technology,2011,42(11):3377-3383. tional Journal of Digital Content Technology and its Appli- [10]王鸿鹏,杨云,刘景泰.高速移动机器人的研究现状与 cations,2012,6(20):122-129. 发展趋势[J].自动化与仪表,2011,26(12):1-4. [15]MO Hongwei,XU Lifang.Biogeography migration algo- WANG Hongpeng,YANG Yun,LIU Jingtai.Research and rithm for traveling salesman problem[J].International development trend of high-speed mobile robot[].Automa- Journal of Intelligent Computing and Cybernetics,2011,4 tion and Instrumentation,2011,26(12):1-4. (3):311-330. [11]谭民,王硕.机器人技术研究进展[J].自动化学报, 作者简介: 2013,39(7):963-972 莫宏伟,男,1973年生,教授,主要 TAN Min,WANG Shuo.Research progress on robotics 研究方向为自然计算理论与应用、机器 [J].Acta Automatica Sinica,2013,39(7):963-972. 人、机器学习与数据挖掘。主持完成国 [12]JARADAT M A K,GARIBEH M H,FEILAT E A.Dy- 家自然科学基金等国家、省部级及横向 namic motion planning for autonomous mobile robot using 课题16项,获得省科技进步奖2项,发 fuzzy potential field [C]//Proceeding of the 6th Interna- 表学术论文60余篇,其中被SCI检索 tional Symposium on Mechatronics and its Applications. 11篇,EI检索40篇。 Sharjah,UAE,2009:24-26. [13]LINGELBACH F.Path planning using probabilistic cell de- 马靖雯,女,1988年生,硕士研究 composition[C]//IEEE International Conference on Ro- 生,主要研究方向为自然计算及其 botics and Automation.New Orleans,USA,2004:467- 应用。 472. 2016年第21届亚洲和南太平洋设计自动化大会 2016 21st Asia and South Pacific Design Automation Conference (ASP-DAC) ASP-DAC 2016 is the twenty-first annual international conference on VLSI design automation in Asia and South Pacific region, one of the most active regions of design and fabrication of silicon chips in the world.The conference aims at providing the Asian and South Pacific CAD/DA and Design community with opportunities of presenting recent advances and with forums for future directions in technologies related to Electronic Design Automation (EDA).The format of the meeting intends to cultivate and promote an instructive and productive interchange of ideas among EDA researchers/developers and system/circuit/device designers.All scientists,engineers, and students who are interested in theoretical and practical aspects of VISI design and design automation are welcomed to ASP-DAC. Areas of Interest: Original papers in,but not limited to,the following areas are invited. 1)System-Level Modeling and Design Methodology; 2)Embedded System Architecture and Design; 3)On-chip Communication and Networks-on-Chip: 4)Embedded Software: 5)Device/Circuit-Level Modeling,Simulation and Verification; 6)Analog,RF and Mixed Signal; 7)System-Level Power and Thermal Management; 8)Device/Circuit/Gate-Level Low Power Design: 9)Logic/Behavioral/High-Level Synthesis and Optimization; 10)Physical Design; 11)Design for Manufacturability and Reliability; 12)Timing and Signal/Power Integrity; 13)Test and Design for Testability; 14)Security and Fault-Tolerant System; 15)Emerging Technology; 16)Emerging Application. Website:http://www.amsv.umac.mo/aspdac2016/
Trajectory planning for autonomous driving in unstructured environments[J]. Journal of Central South University: atu⁃ ral and Technology, 2011, 42(11): 3377⁃3383. [10]王鸿鹏, 杨云, 刘景泰. 高速移动机器人的研究现状与 发展趋势[J]. 自动化与仪表, 2011, 26(12): 1⁃4. WANG Hongpeng, YANG Yun, LIU Jingtai. Research and development trend of high⁃speed mobile robot[J]. Automa⁃ tion and Instrumentation, 2011, 26(12): 1⁃4. [11]谭民, 王硕. 机器人技术研究进展[ J]. 自动化学报, 2013, 39(7): 963⁃972. TAN Min, WANG Shuo. Research progress on robotics [J]. Acta Automatica Sinica, 2013, 39(7): 963⁃972. [12] JARADAT M A K, GARIBEH M H, FEILAT E A. Dy⁃ namic motion planning for autonomous mobile robot using fuzzy potential field [ C] / / Proceeding of the 6th Interna⁃ tional Symposium on Mechatronics and its Applications. Sharjah, UAE, 2009: 24⁃26. [13]LINGELBACH F. Path planning using probabilistic cell de⁃ composition [ C] / / IEEE International Conference on Ro⁃ botics and Automation. New Orleans, USA, 2004: 467⁃ 472. [14]MO Hongwei, MENG Longlong. Robot path planning based on differential evolution in static environment[ J]. Interna⁃ tional Journal of Digital Content Technology and its Appli⁃ cations, 2012, 6(20): 122⁃129. [15] MO Hongwei, XU Lifang. Biogeography migration algo⁃ rithm for traveling salesman problem [ J ]. International Journal of Intelligent Computing and Cybernetics, 2011, 4 (3): 311⁃330. 作者简介: 莫宏伟,男,1973 年生,教授,主要 研究方向为自然计算理论与应用、机器 人、机器学习与数据挖掘。 主持完成国 家自然科学基金等国家、省部级及横向 课题 16 项,获得省科技进步奖 2 项,发 表学术论文 60 余篇,其中被 SCI 检索 11 篇,EI 检索 40 篇。 马靖雯,女,1988 年生,硕士研究 生, 主 要 研 究 方 向 为 自 然 计 算 及 其 应用。 2016 年第 21 届亚洲和南太平洋设计自动化大会 2016 21st Asia and South Pacific Design Automation Conference (ASP⁃DAC) ASP⁃DAC 2016 is the twenty⁃first annual international conference on VLSI design automation in Asia and South Pacific region, one of the most active regions of design and fabrication of silicon chips in the world. The conference aims at providing the Asian and South Pacific CAD/ DA and Design community with opportunities of presenting recent advances and with forums for future directions in technologies related to Electronic Design Automation (EDA). The format of the meeting intends to cultivate and promote an instructive and productive interchange of ideas among EDA researchers/ developers and system/ circuit / device designers. All scientists, engineers, and students who are interested in theoretical and practical aspects of VLSI design and design automation are welcomed to ASP⁃DAC. Areas of Interest: Original papers in, but not limited to, the following areas are invited. 1) System⁃Level Modeling and Design Methodology; 2) Embedded System Architecture and Design; 3) On⁃chip Communication and Networks⁃on⁃Chip; 4) Embedded Software; 5) Device / Circuit⁃Level Modeling, Simulation and Verification; 6) Analog, RF and Mixed Signal; 7) System⁃Level Power and Thermal Management; 8) Device / Circuit / Gate⁃Level Low Power Design; 9) Logic / Behavioral / High⁃Level Synthesis and Optimization; 10) Physical Design; 11) Design for Manufacturability and Reliability; 12) Timing and Signal / Power Integrity; 13) Test and Design for Testability; 14) Security and Fault⁃Tolerant System; 15) Emerging Technology; 16) Emerging Application. Website: http: / / www.amsv.umac.mo / aspdac2016 / 第 5 期 莫宏伟,等:一种生物地理学移动机器人路径规划算法 ·711·