智能系统：基于特征选择聚类方法的稀疏TSK模糊系统编辑部

第10卷第4期 智能系统学报 Vol.10 No.4 2015年8月 CAAI Transactions on Intelligent Systems Aug.2015 D0:10.3969/j.issn.1673-4785.201412001 网络出版地址：http://www.cnki.net/kcms/detail/23.1538.tp.20150716.0934.004.html 基于特征选择聚类方法的稀疏TSK模糊系统 张佳骕，蒋亦樟，王士同 (江南大学数字媒体学院，江苏无锡214122) 摘要：为避免模糊系统建模和估计领域的"维数灾难"，将TSK(Takagi-Sugeno-Kang)模糊系统建模转换为一个分块 稀疏表示问题，提出FCA稀疏TSK模糊系统(FCA-sparse TSK)。首先运用模糊聚类算法(FCA)对样本特征进行化 简，并产生模糊系统字典：再利用存在于TSK模糊系统中的分块结构信息，选取重要的模糊规则并对所选模糊规则 的后件参数进行估计。该系统同时对模糊规则及模糊规则数进行化简，在合成数据集和真实数据集上都表现出较 好的性能。 关键词：TS模糊系统：模糊系统字典：模糊聚类：特征选择；分块结构：稀疏表示：规则约减：参数估计 中图分类号：TP391文献标志码：A文章编号：1673-4785(2015)04-0583-09 中文引用格式：张佳骕，蒋亦樟，王士同.基于特征聚类方法的稀疏TSK模糊系统[J].智能系统学报，2015,10(4)：583-591. 英文引用格式：ZHANG Jiasu,JIANG Yizhang,WANG Shitong.Sparse TSK fuzzy system based on feature clustering method[J]. CAAI Transactions on Intelligent Systems,2015,10(4):583-591. Sparse TSK fuzzy system based on feature selection clustering method ZHANG Jiasu,JIANG Yizhang,WANG Shitong (School of Digital Media,Jiangnan University,Wuxi 214122,China) Abstract:In order to solve the curse of dimensionality existing in fuzzy system identification and approximation,this paper proposes the FCA-sparseTSK fuzzy system by casting the Takagi-Sugeno-Kang(TSK )fuzzy system identifica- tion into a block sparse representation problem.First,FCA-sparseTSK fuzzy system uses the fuzzy clustering algo- rithm (FCA)to simplify sample features and generate fuzzy system dictionary.Then selects main important fuzzy rules and estimate the fuzzy rule's consequent parameter vector by taking into account the block-structured informa- tion that exists in the TSK fuzzy model.The FCA-sparseTSK fuzzy system simplifies the fuzzy rules and the number of fuzzy rules at the same time and shows good performance in artificial datasets and real-world datasets. Keywords:TSK fuzzy system;fuzzy system dictionary;fuzzy clustering;feature selection;block structure;sparse representation;rules reduction;parameter estimation 在各种不同的模糊推理系统之中，Takagi--Suge 模糊控制方法和各种控制策略（随机控制、滑模变 no-Kang(TSK)模糊系统提供了一个合理的框架，将 结构控制等)相结合，成为目前控制线性系统控制 一个非线性系统分解成若干局部线性模型。因为传 领域的一个研究热点。但是，基于数据驱动的TSK 统的数学模型无法描述复杂非线性系统的行为，所 模糊系统建模并不简单，并且可能会产生一个非线 以T-$模糊系统的潜在应用范围很广。近年来，在 性规划问题。在模糊系统模型中，模糊规则包括前 进行复杂非线性系统的控制器设计过程中，将TSK 件隶属度函数以及相应的后件参数，寻找到最优的 模糊规则是模糊系统建模过程中较为重要的工作。 收稿日期：2014-12-01.网络出版日期：2015-07-16 一些数值优化算法，例如通过梯度下降优化技 基金项目：国家自然科学基金资助项目(61272210)：江苏省自然科学基 术[2]的模糊神经网络技术、均衡模型复杂度和精 金资助项目(BK2011417,BK20130155). 通信作者：张佳绑.E-mail:jiasu0306@163.com. 确度的遗传算法[)，Levenberg-Marquardt算法[s)等

第 １０ 卷第 ４ 期 智 能 系 统 学 报 Ｖｏｌ．１０ №．４ ２０１５ 年 ８ 月 ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ Ａｕｇ． ２０１５ ＤＯＩ：１０．３９６９ ／ ｊ．ｉｓｓｎ．１６７３⁃４７８５．２０１４１２００１ 网络出版地址：ｈｔｔｐ： ／ ／ ｗｗｗ．ｃｎｋｉ．ｎｅｔ ／ ｋｃｍｓ／ ｄｅｔａｉｌ ／ ２３．１５３８．ｔｐ．２０１５０７１６．０９３４．００４．ｈｔｍｌ 基于特征选择聚类方法的稀疏 ＴＳＫ 模糊系统 张佳骕，蒋亦樟，王士同 （江南大学 数字媒体学院，江苏 无锡 ２１４１２２） 摘 要：为避免模糊系统建模和估计领域的＂维数灾难＂ ，将 ＴＳＫ（Ｔａｋａｇｉ⁃Ｓｕｇｅｎｏ⁃Ｋａｎｇ）模糊系统建模转换为一个分块 稀疏表示问题，提出 ＦＣＡ 稀疏 ＴＳＫ 模糊系统（ＦＣＡ－ｓｐａｒｓｅ ＴＳＫ）。 首先运用模糊聚类算法（ＦＣＡ）对样本特征进行化 简，并产生模糊系统字典；再利用存在于 ＴＳＫ 模糊系统中的分块结构信息，选取重要的模糊规则并对所选模糊规则 的后件参数进行估计。 该系统同时对模糊规则及模糊规则数进行化简，在合成数据集和真实数据集上都表现出较 好的性能。 关键词：Ｔ⁃Ｓ 模糊系统；模糊系统字典；模糊聚类；特征选择；分块结构；稀疏表示；规则约减；参数估计 中图分类号： ＴＰ３９１ 文献标志码：Ａ 文章编号：１６７３⁃４７８５（２０１５）０４⁃０５８３⁃０９ 中文引用格式：张佳骕，蒋亦樟，王士同． 基于特征聚类方法的稀疏 ＴＳＫ 模糊系统［Ｊ］． 智能系统学报， ２０１５， １０（４）： ５８３⁃５９１． 英文引用格式：ＺＨＡＮＧ Ｊｉａｓｕ， ＪＩＡＮＧ Ｙｉｚｈａｎｇ， ＷＡＮＧ Ｓｈｉｔｏｎｇ． Ｓｐａｒｓｅ ＴＳＫ ｆｕｚｚｙ ｓｙｓｔｅｍ ｂａｓｅｄ ｏｎ ｆｅａｔｕｒｅ ｃｌｕｓｔｅｒｉｎｇ ｍｅｔｈｏｄ［Ｊ］． ＣＡＡＩ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｔｅｌｌｉｇｅｎｔ Ｓｙｓｔｅｍｓ， ２０１５， １０（４）： ５８３⁃５９１． Ｓｐａｒｓｅ ＴＳＫ ｆｕｚｚｙ ｓｙｓｔｅｍ ｂａｓｅｄ ｏｎ ｆｅａｔｕｒｅ ｓｅｌｅｃｔｉｏｎ ｃｌｕｓｔｅｒｉｎｇ ｍｅｔｈｏｄ ＺＨＡＮＧ Ｊｉａｓｕ， ＪＩＡＮＧ Ｙｉｚｈａｎｇ， ＷＡＮＧ Ｓｈｉｔｏｎｇ （Ｓｃｈｏｏｌ ｏｆ Ｄｉｇｉｔａｌ Ｍｅｄｉａ， Ｊｉａｎｇｎａｎ Ｕｎｉｖｅｒｓｉｔｙ， Ｗｕｘｉ ２１４１２２， Ｃｈｉｎａ） Ａｂｓｔｒａｃｔ：Ｉｎ ｏｒｄｅｒ ｔｏ ｓｏｌｖｅ ｔｈｅ ｃｕｒｓｅ ｏｆ ｄｉｍｅｎｓｉｏｎａｌｉｔｙ ｅｘｉｓｔｉｎｇ ｉｎ ｆｕｚｚｙ ｓｙｓｔｅｍ ｉｄｅｎｔｉｆｉｃａｔｉｏｎ ａｎｄ ａｐｐｒｏｘｉｍａｔｉｏｎ， ｔｈｉｓ ｐａｐｅｒ ｐｒｏｐｏｓｅｓ ｔｈｅ ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ ｆｕｚｚｙ ｓｙｓｔｅｍ ｂｙ ｃａｓｔｉｎｇ ｔｈｅ Ｔａｋａｇｉ⁃Ｓｕｇｅｎｏ⁃Ｋａｎｇ（ＴＳＫ ） ｆｕｚｚｙ ｓｙｓｔｅｍ ｉｄｅｎｔｉｆｉｃａ⁃ ｔｉｏｎ ｉｎｔｏ ａ ｂｌｏｃｋ ｓｐａｒｓｅ ｒｅｐｒｅｓｅｎｔａｔｉｏｎ ｐｒｏｂｌｅｍ． Ｆｉｒｓｔ， ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ ｆｕｚｚｙ ｓｙｓｔｅｍ ｕｓｅｓ ｔｈｅ ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏ⁃ ｒｉｔｈｍ （ＦＣＡ） ｔｏ ｓｉｍｐｌｉｆｙ ｓａｍｐｌｅ ｆｅａｔｕｒｅｓ ａｎｄ ｇｅｎｅｒａｔｅ ｆｕｚｚｙ ｓｙｓｔｅｍ ｄｉｃｔｉｏｎａｒｙ． Ｔｈｅｎ ｓｅｌｅｃｔｓ ｍａｉｎ ｉｍｐｏｒｔａｎｔ ｆｕｚｚｙ ｒｕｌｅｓ ａｎｄ ｅｓｔｉｍａｔｅ ｔｈｅ ｆｕｚｚｙ ｒｕｌｅ＇ｓ ｃｏｎｓｅｑｕｅｎｔ ｐａｒａｍｅｔｅｒ ｖｅｃｔｏｒ ｂｙ ｔａｋｉｎｇ ｉｎｔｏ ａｃｃｏｕｎｔ ｔｈｅ ｂｌｏｃｋ⁃ｓｔｒｕｃｔｕｒｅｄ ｉｎｆｏｒｍａ⁃ ｔｉｏｎ ｔｈａｔ ｅｘｉｓｔｓ ｉｎ ｔｈｅ ＴＳＫ ｆｕｚｚｙ ｍｏｄｅｌ． Ｔｈｅ ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ ｆｕｚｚｙ ｓｙｓｔｅｍ ｓｉｍｐｌｉｆｉｅｓ ｔｈｅ ｆｕｚｚｙ ｒｕｌｅｓ ａｎｄ ｔｈｅ ｎｕｍｂｅｒ ｏｆ ｆｕｚｚｙ ｒｕｌｅｓ ａｔ ｔｈｅ ｓａｍｅ ｔｉｍｅ ａｎｄ ｓｈｏｗｓ ｇｏｏｄ ｐｅｒｆｏｒｍａｎｃｅ ｉｎ ａｒｔｉｆｉｃｉａｌ ｄａｔａｓｅｔｓ ａｎｄ ｒｅａｌ⁃ｗｏｒｌｄ ｄａｔａｓｅｔｓ． Ｋｅｙｗｏｒｄｓ：ＴＳＫ ｆｕｚｚｙ ｓｙｓｔｅｍ； ｆｕｚｚｙ ｓｙｓｔｅｍ ｄｉｃｔｉｏｎａｒｙ； ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ； ｆｅａｔｕｒｅ ｓｅｌｅｃｔｉｏｎ； ｂｌｏｃｋ ｓｔｒｕｃｔｕｒｅ； ｓｐａｒｓｅ ｒｅｐｒｅｓｅｎｔａｔｉｏｎ； ｒｕｌｅｓ ｒｅｄｕｃｔｉｏｎ； ｐａｒａｍｅｔｅｒ ｅｓｔｉｍａｔｉｏｎ 收稿日期：２０１４⁃１２⁃０１． 网络出版日期：２０１５⁃０７⁃１６． 基金项目：国家自然科学基金资助项目（６１２７２２１０）；江苏省自然科学基 金资助项目（ＢＫ２０１１４１７，ＢＫ２０１３０１５５）． 通信作者：张佳骕． Ｅ⁃ｍａｉｌ：ｊｉａｓｕ０３０６＠ １６３．ｃｏｍ． 在各种不同的模糊推理系统之中，Ｔａｋａｇｉ⁃Ｓｕｇｅ⁃ ｎｏ⁃Ｋａｎｇ（ＴＳＫ）模糊系统提供了一个合理的框架，将 一个非线性系统分解成若干局部线性模型。 因为传 统的数学模型无法描述复杂非线性系统的行为，所 以 Ｔ⁃Ｓ 模糊系统的潜在应用范围很广。 近年来，在 进行复杂非线性系统的控制器设计过程中，将 ＴＳＫ 模糊控制方法和各种控制策略（随机控制、滑模变 结构控制等） 相结合，成为目前控制线性系统控制 领域的一个研究热点。 但是，基于数据驱动的 ＴＳＫ 模糊系统建模并不简单，并且可能会产生一个非线 性规划问题。 在模糊系统模型中，模糊规则包括前 件隶属度函数以及相应的后件参数，寻找到最优的 模糊规则是模糊系统建模过程中较为重要的工作。 一些数值优化算法，例如通过梯度下降优化技 术［２⁃３］的模糊神经网络技术、均衡模型复杂度和精 确度的遗传算法［４］ 、Ｌｅｖｅｎｂｅｒｇ⁃Ｍａｒｑｕａｒｄｔ 算法［５］ 等

·584· 智能系统学报 第10卷 已经被广泛应用于模糊系统建模领域。基于数据驱 模糊语言命题Aa(x4)进行描述： 动的TSK模糊系统建模过程中有2个步骤非常关 键：一是确定模糊规则前件，在这一步中将输入空间 (x)=exp 划分成一定数量的模糊域：二是估计模糊规则后件 式中：k=1,2,…,n,:和o.分别表示相应的钟形 参数向量，在这一步中在每一个用于建立模糊系统 隶属函数的均值和方差。TSK模糊系统的输出函数 的模糊域中对系统的行为进行描述。我们常常利用 可以表示为 聚类技术划分输入空间并且确定模糊规则前件的隶 属度函数，例如K均值算法[6)，模糊c均值算法及其 =∑，(x)(x) (2) i1 扩展I]减法聚类算法[8]、Gath-Geva聚类算法[ 式中9，(x)表示输入变量x:对于第j条规则的触 Gustafson-Kessel聚类算法[o)、向量量化(VQ)算 发强度： 法门等。 (x:) (x)= 在模糊规则前件确定之后，对后件参数的估计 可以看作是在输入输出数据的积空间的一个线性回 A() (3) 归问题。传统的回归算法将所有的后件参数视为回 ,(x)=Π(xa) 归系数并且将它们单独处理。但一方面，这些方法 k=1 忽视了存在于TSK模糊模型中的分块结构信息：另 而l(x:)=0n+01xa+02x2+…+0nxn=[1,x]'w 一方面，冗余的模糊规则不可避免地导致模糊模型 是输入变量x:对于第j条规则的输出结果，其中州，= 的复杂度变高以及过拟合的问题。 [00,0a,02,…,0n]T表示第j条规则后件的参数。 为了解决当前TSK模糊系统建模问题中的模 接下来介绍一下TSK模糊系统建模在数据驱 糊规则复杂及规则冗余的问题。LoM等提出了 动方面的一些概念。先来看一下输入输出数据集 H-sparseFIS算法a1,这是一种层次结构稀疏表示方 D=(xy)x=[xa.x2,…,xn],i=1,2,…,N 法，能有效地降低模糊规则的冗余度。本文对TSK 式中x:和y:分别表示第i个n维输入和输出变量。 模糊系统的建模过程做了进一步的优化：在前件学 为了简洁，用M。表示有r条规则的TSK模糊系统， 习时采用一种具备特征选择功能的聚类方法FCA 且这个系统是从数据集D进行学习的。将TSK模 算法来获取更为精简有效的特征组合，从而降低模 糊系统M,的输出表示成y=[y1y2,…,y]T: 糊规则的复杂度：在估计模糊规则后件参数过程中， y=∑更w,=重w (4) 利用存在于TSK模糊模型中的分块结构信息，将分 块结构稀疏表示引入T$K模糊系统建模的框架中， 式中：更∈Ra)是由r个块结构更，∈Ra+w构 利用块匹配追踪算法[]选择出较为重要的模糊规 成，也就是说，=[，④2，…，④]。 则，同时减少了非零后件参数的数目，进一步减少模 ④=diag(p(x1),9(x2),…,9(xw))X。(5) 糊规则的条数，有效地降低了规则的冗余度。 式中：j=1,2,…,r,X=[1,X],其中X=[x1,x2, …,x]。相应的，w=[w,w5,…,w]∈Ra”。根 1TSK模糊系统概况 据定义，重∈Ra+)叫做TSK模糊系统M的字典， 在这一部分，首先对TSK模糊系统的一些基本 成分更，∈R(a是对应于第j条规则的子字典。很 概念进行回顾，然后对模糊系统字典和模糊系统子 明显，这个TSK模糊系统字典是一个分块结构。在 字典的概念进行介绍。这些子字典构成了一个有意 这个意义上讲，模糊模型输出y可以用模糊规则子 义的分块结构TSK模糊系统字典。 字典的一个线性组合表示。 TSK模糊系统是由前件和后件形式为“IF- THEN”的模糊规则组成的，模糊规则的后件被定义 2FCA稀疏TSK模糊系统 为一个仿射函数。对于一个n维输入变量x:= 在模糊规则前件提取中，使用FCA聚类算法对 (x1,x2,…,xn)「∈R”,第j条规则可以表示成下面 样本输入空间进行划分并确定模糊规则前件的隶属 这种形式： 度函数。在这个过程中，F℃A算法能够对噪声特征 R:If xa is An and x2 is An..and xi is Am,then 和不重要的特征进行约减。之后，对模糊系统字典 y:=10n+101x1+102x2+…+0nxn 的分块结构信息进行阐述，并将TSK模糊系统建模 式中j=1,2,…,「。在文中使用钟形隶属度函数对 过程转化为一个分块结构稀疏恢复问题。在模糊规

已经被广泛应用于模糊系统建模领域。 基于数据驱 动的 ＴＳＫ 模糊系统建模过程中有 ２ 个步骤非常关 键：一是确定模糊规则前件，在这一步中将输入空间 划分成一定数量的模糊域；二是估计模糊规则后件 参数向量，在这一歩中在每一个用于建立模糊系统 的模糊域中对系统的行为进行描述。 我们常常利用 聚类技术划分输入空间并且确定模糊规则前件的隶 属度函数，例如 Ｋ 均值算法［６］ 、模糊 ｃ 均值算法及其 扩展［７］ 、减法聚类算法［８］ 、Ｇａｔｈ⁃Ｇｅｖａ 聚类算法［９］ 、 Ｇｕｓｔａｆｓｏｎ⁃Ｋｅｓｓｅｌ 聚类算法［１０］ 、 向量量化 （ ＶＱ） 算 法［１１］等。 在模糊规则前件确定之后，对后件参数的估计 可以看作是在输入输出数据的积空间的一个线性回 归问题。 传统的回归算法将所有的后件参数视为回 归系数并且将它们单独处理。 但一方面，这些方法 忽视了存在于 ＴＳＫ 模糊模型中的分块结构信息；另 一方面，冗余的模糊规则不可避免地导致模糊模型 的复杂度变高以及过拟合的问题。 为了解决当前 ＴＳＫ 模糊系统建模问题中的模 糊规则复杂及规则冗余的问题。 Ｌｕｏ Ｍ 等提出了 Ｈ⁃ｓｐａｒｓｅＦＩＳ 算法［１２］ ，这是一种层次结构稀疏表示方 法，能有效地降低模糊规则的冗余度。 本文对 ＴＳＫ 模糊系统的建模过程做了进一步的优化：在前件学 习时采用一种具备特征选择功能的聚类方法 ＦＣＡ 算法来获取更为精简有效的特征组合，从而降低模 糊规则的复杂度；在估计模糊规则后件参数过程中， 利用存在于 ＴＳＫ 模糊模型中的分块结构信息，将分 块结构稀疏表示引入 ＴＳＫ 模糊系统建模的框架中， 利用块匹配追踪算法［１２］ 选择出较为重要的模糊规 则，同时减少了非零后件参数的数目，进一步减少模 糊规则的条数，有效地降低了规则的冗余度。 １ ＴＳＫ 模糊系统概况 在这一部分，首先对 ＴＳＫ 模糊系统的一些基本 概念进行回顾，然后对模糊系统字典和模糊系统子 字典的概念进行介绍。 这些子字典构成了一个有意 义的分块结构 ＴＳＫ 模糊系统字典。 ＴＳＫ 模糊系统是由前件和后件形式为 “ ＩＦ⁃ ＴＨＥＮ”的模糊规则组成的，模糊规则的后件被定义 为一个仿射函数。 对于一个 ｎ 维输入变量 ｘｉ ＝ （ｘｉ１ ，ｘｉ２ ，…，ｘｉｎ ） Ｔ∈Ｒ ｎ ，第 ｊ 条规则可以表示成下面 这种形式： Ｒ ｊ ：Ｉｆ ｘｉ１ ｉｓ Ａｊ１ ａｎｄ ｘｉ２ ｉｓ Ａｊ２… ａｎｄ ｘｉｎ ｉｓ Ａｊｎ ， ｔｈｅｎ ｙｉ ＝ ｗｊ０ ＋ ｗｊ１ ｘｉ１ ＋ ｗｊ２ ｘｉ２ ＋ … ＋ ｗｊｎ ｘｉｎ 式中 ｊ ＝ １，２，…，ｒ 。 在文中使用钟形隶属度函数对 模糊语言命题 Ａｊｋ（ｘｉｋ） 进行描述： μＡｊｋ （ｘｉｋ） ＝ ｅｘｐ － ｘｉｋ － ｃｊｋ σｊｋ æ è ç ö ø ÷ ２ é ë ê ê ù û ú ú （１） 式中： ｋ ＝ １，２，…，ｎ ， ｃｊｋ 和 σｊｋ 分别表示相应的钟形 隶属函数的均值和方差。 ＴＳＫ 模糊系统的输出函数 可以表示为 ｙ ＾ ｉ ＝ ∑ ｒ ｊ ＝ １ φｊ（ｘｉ）ｌ ｊ（ｘｉ） （２） 式中 φｊ （ｘｉ）表示输入变量 ｘｉ 对于第 ｊ 条规则的触 发强度： φｊ（ｘｉ） ＝ μｊ（ｘｉ） ∑ ｒ ｔ ＝ １ μｔ（ｘｉ） μｊ（ｘｉ） ＝ ∏ ｎ ｋ ＝ １ μＡｊｋ （ｘｉｋ） ì î í ï ï ï ï ï ï （３） 而 ｌ ｊ （ｘｉ） ＝ ｗｊ０ ＋ｗｊ１ ｘｉ１ ＋ｗｊ２ ｘｉ２ ＋…＋ｗｊｎ ｘｉｎ ＝ ［１，ｘ Ｔ ｉ ］ Ｔｗｊ 是输入变量 ｘｉ 对于第 ｊ 条规则的输出结果，其中 ｗｊ ＝ ［ｗｊ０ ，ｗｊ１ ，ｗｊ２ ，…，ｗｊｎ ］ Ｔ 表示第 ｊ 条规则后件的参数。 接下来介绍一下 ＴＳＫ 模糊系统建模在数据驱 动方面的一些概念。 先来看一下输入输出数据集 Ｄ ＝ ｛（ｘ Ｔ ｉ ，ｙｉ） Ｔ ：ｘｉ ＝ ［ｘｉ１， ｘｉ２，…，ｘｉｎ ］ Ｔ ，ｉ ＝ １，２，…，Ｎ｝ 式中 ｘｉ 和 ｙｉ 分别表示第 ｉ 个 ｎ 维输入和输出变量。 为了简洁，用 Ｍ ｒ Ｄ 表示有 ｒ 条规则的 ＴＳＫ 模糊系统， 且这个系统是从数据集 Ｄ 进行学习的。 将 ＴＳＫ 模 糊系统 Ｍ ｒ Ｄ 的输出表示成 ｙ ＾ ＝ ［ｙ ＾ １ ，ｙ ＾ ２ ，…，ｙ ＾ Ｎ］ Ｔ ： ｙ ＾ ＝ ∑ ｒ ｊ ＝ １ Φｊｗｊ ＝ Φｗ （４） 式中：Φ∈Ｒ Ｎ×ｒ（ｎ＋１） 是由 ｒ 个块结构 Φｊ ∈Ｒ Ｎ×（ｎ＋１） 构 成，也就是说，Φ＝ ［Φ１ ，Φ２ ，…，Φｒ］。 Φｊ ＝ ｄｉａｇ（φｊ（ｘ１ ），φｊ（ｘ２ ），…，φｊ（ｘＮ））Ｘｅ （５） 式中： ｊ ＝ １，２，…，ｒ ，Ｘｅ ＝ ［１，Ｘ Ｔ ］，其中 Ｘ ＝ ［ ｘ１ ，ｘ２ ， …，ｘＮ］。 相应的，ｗ＝ ［ｗ Ｔ １ ，ｗ Ｔ ２ ，…，ｗ Ｔ ｒ ］∈Ｒ ｒ（ｎ＋１） 。 根 据定义，Φ∈Ｒ Ｎ×ｒ（ｎ＋１）叫做 ＴＳＫ 模糊系统 Ｍ ｒ Ｄ 的字典， 成分 Φｊ∈Ｒ Ｎ×（ｎ＋１）是对应于第 ｊ 条规则的子字典。 很 明显，这个 ＴＳＫ 模糊系统字典是一个分块结构。 在 这个意义上讲，模糊模型输出 ｙ ＾ 可以用模糊规则子 字典的一个线性组合表示。 ２ ＦＣＡ 稀疏 ＴＳＫ 模糊系统 在模糊规则前件提取中，使用 ＦＣＡ 聚类算法对 样本输入空间进行划分并确定模糊规则前件的隶属 度函数。 在这个过程中，ＦＣＡ 算法能够对噪声特征 和不重要的特征进行约减。 之后，对模糊系统字典 的分块结构信息进行阐述，并将 ＴＳＫ 模糊系统建模 过程转化为一个分块结构稀疏恢复问题。 在模糊规 ·５８４· 智 能 系 统 学 报 第 １０ 卷

第4期 张佳啸，等：基于特征聚类方法的稀硫TSK模糊系统 .585. 则选取的过程之中，我们使用块正交匹配追踪算法， 这样，就能减少模糊系统的规则数目。 ∑kg=1,m>1。 2.1模糊规则前件提取 在FCA算法中，U、V、W和B在y和a满足一 在很多特定的情况下，专家可以根据先验知识 定条件的时候能够使得J(U,V,W,B)达到局部最 提供一些模糊规则。但在大多数情况下，对于划分 优，下面分别给出U、V、W和B的迭代更新表达式： 输入空间和确定模糊规则前件的隶属度函数，通常 1 10= (7) 使用统计学方法或聚类技术。本文使用FCA算法 D 从数据集D提取模糊规则前件。 通过FCA算法)，每个类均与一条模糊规则 相联系。通过类在每个变量上的投影产生模糊规则 式中D= 前件的钟形隶属度函数A,也就是说，在每一维上 的类中心和方差被视为钟形隶属度函数A:的均值 F B= (8) c和方差0t,这里，j=1,2,…,r,k=1,2,…,n。 一旦模糊规则前件确定下来，模糊字典Φ以及 三响 所包含的模糊规则子字典重(=1,2，…，r)也可以 式中F:= 通过式(5)获得。一般来说，通过对模糊规则回归 1 模型的后件参数估计的方法来对TSK模糊系统进 八= (9) 行建立。基于FCA算法的TSK模糊系统的建模流 程图如图1所示。 输人-输出 数据集 式中f= FCA 模糊划分以 模糊规 d(xg)。 及特征优化 则前件 模糊规 则数目r 模糊规 LS 模糊系 (10) 则后件 统字典 图1基于FCA聚类算法的TSK模糊系统模型流程图 滑 Fig.1 Flowchart of TSK fuzzy system modeling on the 根据上述更新规则，在有限次迭代后，J(U,V, basis of FCA clustering W,B)将会收敛到局部极小值或鞍点。具体FCA算 FCA算法是一种加权模糊聚类算法，该算法在 法（算法1）如下。 实现对数据进行聚类的同时，可以按样本特征对聚 1)输入：输入输出数据集的输入部分X=[x1, 类的贡献进行排序。因此，本文先使用FCA算法实 x2,…,xw],聚类数r,初始聚类中心V以及误差控 现模糊划分并挑选出对聚类贡献较大的若干特征生 制量8>0（其中可不设定）。 成模糊规则前件，从而化简了模糊规则的复杂度。 2)初始化：根据数据集信息随机初始化°，随 依据上文，样本集的输入部分可以表示为X= 机产生满足条件的WB°，若未输入初始聚类中心， [x1,x2…x],x=[xa,x2,…,xn]TeR”,C为聚 则通过公式(10)计算初始聚类中心。 类数目，集合V=[,2,…,c],:= 3)步骤： ["a,"2,…,ym]TeR"表示聚类中心，g表示样本x FORn=1,2,… 隶属于第j类的隶属度，W=[w1,02,…,w.]是样本 使用式(7)迭代产生W 特征的权重，此处w>0且a为其参数，B=[B,B2, 使用式(8)迭代产生B+ …,B、]是样本的权重，此处B>0且Y为其参数，建 使用式(9)迭代产生Um+1 立目标函数如下： 使用式(10)迭代产生Vm J(U.V.W.B)= IF |J(U+1,V+1,W+1,B1)-J(U,V,W,B)|<ε (6) break ELSE n =n 1 4)输出：Umt1、Vm1、Wm1和Ba*1

则选取的过程之中，我们使用块正交匹配追踪算法， 这样，就能减少模糊系统的规则数目。 ２．１ 模糊规则前件提取 在很多特定的情况下，专家可以根据先验知识 提供一些模糊规则。 但在大多数情况下，对于划分 输入空间和确定模糊规则前件的隶属度函数，通常 使用统计学方法或聚类技术。 本文使用 ＦＣＡ 算法 从数据集 Ｄ 提取模糊规则前件。 通过 ＦＣＡ 算法［１３］ ，每个类均与一条模糊规则 相联系。 通过类在每个变量上的投影产生模糊规则 前件的钟形隶属度函数 Ａｊｋ ，也就是说，在每一维上 的类中心和方差被视为钟形隶属度函数 Ａｊｋ 的均值 ｃｊｋ 和方差 σｊｋ ，这里， ｊ ＝ １，２，…，ｒ ， ｋ ＝ １，２，…，ｎ 。 一旦模糊规则前件确定下来，模糊字典 Φ 以及 所包含的模糊规则子字典 Φｊ（ｊ ＝ １，２，…，ｒ）也可以 通过式（５）获得。 一般来说，通过对模糊规则回归 模型的后件参数估计的方法来对 ＴＳＫ 模糊系统进 行建立。 基于 ＦＣＡ 算法的 ＴＳＫ 模糊系统的建模流 程图如图 １ 所示。 图 １ 基于 ＦＣＡ 聚类算法的 ＴＳＫ 模糊系统模型流程图 Ｆｉｇ．１ Ｆｌｏｗｃｈａｒｔ ｏｆ ＴＳＫ ｆｕｚｚｙ ｓｙｓｔｅｍ ｍｏｄｅｌｉｎｇ ｏｎ ｔｈｅ ｂａｓｉｓ ｏｆ ＦＣＡ ｃｌｕｓｔｅｒｉｎｇ ＦＣＡ 算法是一种加权模糊聚类算法，该算法在 实现对数据进行聚类的同时，可以按样本特征对聚 类的贡献进行排序。 因此，本文先使用 ＦＣＡ 算法实 现模糊划分并挑选出对聚类贡献较大的若干特征生 成模糊规则前件，从而化简了模糊规则的复杂度。 依据上文，样本集的输入部分可以表示为 Ｘ ＝ ［ｘ１ ，ｘ２ ，…，ｘＮ］，∀ｘｉ ＝ ［ｘｉ１， ｘｉ２ ，…，ｘｉｎ ］ Ｔ∈Ｒ ｎ ，Ｃ 为聚 类 数 目， 集 合 Ｖ ＝ ［ ｖ１ ， ｖ２ ， …， ｖＣ ］， ∀ｖｉ ＝ ［ｖｉ１， ｖｉ２ ，…，ｖｉｎ ］ Ｔ∈Ｒ ｎ 表示聚类中心，μｉｊ表示样本 ｘｉ 隶属于第 ｊ 类的隶属度，Ｗ ＝ ［ｗ１ ，ｗ２ ，…，ｗｎ ］是样本 特征的权重，此处 ｗｋ ＞ ０ 且 α 为其参数，β ＝ ［β１ ，β２ ， …，βＮ］是样本的权重，此处 βｉ ＞０ 且 γ 为其参数，建 立目标函数如下： Ｊ（Ｕ，Ｖ，Ｗ，β） ＝ ∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μ ｍ ｉｊ β γ ｉ ∑ ｎ ｋ ＝ １ ｗ α ｋ ｄ（ｘｉｋ，ｖ ( ｊｋ）) （６） 式中： ｄ（ｘｉｋ，ｖｊｋ） ＝ （ｘｉｋ － ｖｊｋ） ２ ，∑ ｎ ｋ ＝ １ ｗｋ ＝ １，∑ Ｎ ｉ ＝ １ βｉ ＝ １ ，∑ Ｃ ｊ ＝ １ μｉｊ ＝ １， ｍ ＞ １。 在 ＦＣＡ 算法中，Ｕ、Ｖ、Ｗ 和 β 在 γ 和 α 满足一 定条件的时候能够使得 Ｊ （Ｕ，Ｖ，Ｗ，β）达到局部最 优，下面分别给出 Ｕ、Ｖ、Ｗ 和 β 的迭代更新表达式： ｗｋ ＝ １ ∑ ｎ ｐ ＝ １ Ｄ １ α－１ ｋ Ｄ １ α－１ ｐ （７） 式中 Ｄｋ ＝ ∑ Ｎ ｉ ＝ １ ∑ Ｃ ｊ ＝ １ μ ｍ ｉｊ β γ ｉ ｄ（ｘｉｋ，ｖｊｋ） 。 βｉ ＝ Ｆ １ γ＋１ ｉ ∑ Ｎ ｓ ＝ １ Ｆ １ γ＋１ ｓ （８） 式中 Ｆｉ ＝ ∑ Ｃ ｊ ＝ １ μ ｍ ｉｊ ∑ ｄ ｋ ＝ １ ｗ α ｋ ｄ（ｘｉｋ，ｖ ( ｊｋ） ) 。 μｉｊ ＝ １ ∑ Ｃ ｑ ＝ １ ｆ １ ｍ－１ ｉｊ ｆ １ ｍ－１ ｉｑ （９） 式中 ｆ ｉｊ ＝ ∑ ｄ ｋ ＝ １ ｗ α ｋ ｄ（ｘｉｋ，ｖｊｋ） 。 ｖｊｋ ＝ ∑ Ｎ ｉ ＝ １ μ ｍ ｉｊ β γ ｉ ｘｉｋ ∑ Ｎ ｉ ＝ １ μ ｍ ｉｊ β γ ｉ （１０） 根据上述更新规则，在有限次迭代后， Ｊ （Ｕ，Ｖ， Ｗ，β）将会收敛到局部极小值或鞍点。 具体 ＦＣＡ 算 法（算法 １）如下。 １）输入：输入输出数据集的输入部分 Ｘ ＝ ［ ｘ１ ， ｘ２ ，…，ｘＮ］，聚类数 ｒ，初始聚类中心 Ｖ ０ 以及误差控 制量 ε ＞ ０（其中 Ｖ ０ 可不设定）。 ２）初始化：根据数据集信息随机初始化 Ｕ ０ ，随 机产生满足条件的 Ｗ ０ 、β ０ ，若未输入初始聚类中心， 则通过公式（１０）计算初始聚类中心。 ３）步骤： ＦＯＲ ｎ ＝ １，２，… 使用式（７）迭代产生 Ｗ ｎ＋１ 使用式（８）迭代产生 β ｎ＋１ 使用式（９）迭代产生 Ｕ ｎ＋１ 使用式（１０）迭代产生 Ｖ ｎ＋１ ＩＦ Ｊ（Ｕ ｎ＋１ ，Ｖ ｎ＋１ ，Ｗ ｎ＋１ ，β ｎ＋１ ） － Ｊ（Ｕ ｎ ，Ｖ ｎ ，Ｗ ｎ ，β ｎ ） ＜ ε ｂｒｅａｋ ＥＬＳＥ ｎ ＝ ｎ ＋ １ ４）输出：Ｕ ｎ＋１ 、Ｖ ｎ＋１ 、Ｗ ｎ＋１和 β ｎ＋１ 。 第 ４ 期 张佳骕，等：基于特征聚类方法的稀疏 ＴＳＫ 模糊系统 ·５８５·

·586· 智能系统学报 第10卷 2.2模糊规则选取的分块结构稀疏表示 式中：Iwl2o=I(Iw,l2,‖w2l2,…,w,lz)‖o 通常，使用LS算法对模糊规则后件参数向量 实际上反映的是模糊规则的数目，并且￡表示模型 w:估计的方式有2种，一种是通过求解LS问题的 精度的上限。优化问题(11)的目的是使得结果参 w=[w1,w2,…,w,]全局学习，另外一种是通过求解 数向量w尽可能的块稀疏并均衡模型的精度和复 r个独立的加权LS问题w:(i=1,2,…,r)的局部学 杂度。通过图2来说明这种块结构稀疏回归。 习。然而，全局学习在估计过程中将后件参数独立 2.3块正交匹配追踪算法应用于TSK模糊系统建模 对待，忽略了存在于模糊系统字典Φ中的分块结 在过去的研究中，优化问题(11)已被证明是 构。局部学习是对每一条模糊规则分别估计后件参 NP难问题；然而，通常有2种方法求近似解：1)松 数，其实质是一种结构化学习：然而所有的结果参数 弛方法，例如‖·21范数凸优化近似求解的一般 w:(i=1,2,…,r)都未经选择就进行估计了，这就导 方法：2)分块（分组）贪婪选择算法，例如块正交匹 致了所有的模糊规则都参与了模糊系统的建模。事 配追踪算法(block OMP算法)、块匹配追踪算法 实上，一些模糊规则是不必要的，删去它们并没有很 (OMP算法)等。在本文中，使用块正交匹配追踪算 显著的影响一个模型的效果。更为严重的是，过多 法去解决优化问题(11)，因为该算法在计算代价方 的模糊规则难免会导致过拟合问题，并使得泛化效 面有优势。 果变差。 作为OMP算法的一个继承，在稀疏回归时，分 为了克服上述问题，利用分块结构的优势，并利 块OMP算法进行的是块变量的选择而不是对单个 用一个LS算法对分块结构稀疏表示的TSK模糊系 变量的选择。它以一种非常直观的方式运作。在每 统进行建模，作为对传统稀疏表示的继承，分块结构 一步迭代中，根据减少的残差选择最优块。一旦块 稀疏表示首次在组LASSO14中进行介绍和研究。 被选定，在已经选定的块上执行S最小化获得对 它介绍了一种回归模型，在这种回归模型中，很多贡 相应系数的估计。每次迭代结束，算法检查停止条 献小的分块的回归系数能够在保证模型精度较高的 件是否已经达到。这个停止条件通常是残差的最小 条件下削减接近于零。 范围或者是迭代的最大次数。在TSK模糊系统建 功 模的框架中，因为块变量w:是与第i条模糊规则的 后件参数向量相联系的，故对块变量的选择，实际上 就是对模糊规则的选择。 使用分块OMP算法（算法2）对模糊规则进行 选取的过程如下。 1)输入：依据数据集D生成的TSK模糊系统字 典Φ=[，Φ2，…，重]。 2)初始化：初始化标签集=☑，后件参数向 图2分块结构稀疏表示 量wo)=0,残差ro=y。 Fig.2 Block-structured sparse representation 3)步骤： 在TSK模糊系统的建模过程中，模糊规则的数 FORK=1,2,… 目越多，模型的精度一般更高：但是，太多的模糊规 令j=arg max(r-)更（更更）1更r) 则也会不可避免地将模糊系统变得复杂，甚至会导 IF终止条件为真，break 致过拟合问题。所以，模糊规则的选取变成了一个 设定=1U 很关键的问题，要选取一个合理的参数化问题既要 通过w名=arg min‖重w-y‖，计算当前 能控制规则数目也能够控制训练误差。利用TSK 的后件参数向量w并且设置w倪)=0 模糊模型的块结构的优势，找到了一种TSK模糊规 更新当前残差r()=y-w() 则选择的块结构回归方法。在系统建模过程中，这 4)输出：中选定的模糊规则子字典，以及模 种方法将许多贡献小的块的后件参数w,(i=1,2, 糊规则后件参数向量w。 …,)缩减至零。它们可以表示成如下优化问题 在第k次迭代，C{1,2,…,r表示已选模 minimize‖w‖z.o 糊子字典的标签集：w)∈Ra+)表示模糊规则后件 参数向量：r)=y-重w表示相应的残差。初始化 后件参数向量为wo)=0,残差为r=y。更心表示

２．２ 模糊规则选取的分块结构稀疏表示 通常，使用 ＬＳ 算法对模糊规则后件参数向量 ｗｉ 估计的方式有 ２ 种，一种是通过求解 ＬＳ 问题的 ｗ＝ ［ｗ１ ，ｗ２ ，…，ｗｒ］全局学习，另外一种是通过求解 ｒ 个独立的加权 ＬＳ 问题 ｗｉ（ ｉ ＝ １，２，…，ｒ）的局部学 习。 然而，全局学习在估计过程中将后件参数独立 对待，忽略了存在于模糊系统字典 Φ 中的分块结 构。 局部学习是对每一条模糊规则分别估计后件参 数，其实质是一种结构化学习；然而所有的结果参数 ｗｉ（ｉ ＝ １，２，…，ｒ）都未经选择就进行估计了，这就导 致了所有的模糊规则都参与了模糊系统的建模。 事 实上，一些模糊规则是不必要的，删去它们并没有很 显著的影响一个模型的效果。 更为严重的是，过多 的模糊规则难免会导致过拟合问题，并使得泛化效 果变差。 为了克服上述问题，利用分块结构的优势，并利 用一个 ＬＳ 算法对分块结构稀疏表示的 ＴＳＫ 模糊系 统进行建模，作为对传统稀疏表示的继承，分块结构 稀疏表示首次在组 ＬＡＳＳＯ ［１４］ 中进行介绍和研究。 它介绍了一种回归模型，在这种回归模型中，很多贡 献小的分块的回归系数能够在保证模型精度较高的 条件下削减接近于零。 图 ２ 分块结构稀疏表示 Ｆｉｇ．２ Ｂｌｏｃｋ⁃ｓｔｒｕｃｔｕｒｅｄ ｓｐａｒｓｅ ｒｅｐｒｅｓｅｎｔａｔｉｏｎ 在 ＴＳＫ 模糊系统的建模过程中，模糊规则的数 目越多，模型的精度一般更高；但是，太多的模糊规 则也会不可避免地将模糊系统变得复杂，甚至会导 致过拟合问题。 所以，模糊规则的选取变成了一个 很关键的问题，要选取一个合理的参数化问题既要 能控制规则数目也能够控制训练误差。 利用 ＴＳＫ 模糊模型的块结构的优势，找到了一种 ＴＳＫ 模糊规 则选择的块结构回归方法。 在系统建模过程中，这 种方法将许多贡献小的块的后件参数 ｗｉ（ ｉ ＝ １，２， …，ｒ）缩减至零。 它们可以表示成如下优化问题 ｍｉｎｉｍｉｚｅ ‖ｗ‖２，０ ｓｕｂｊｅｃｔ ｔｏ １ ２ ‖ｙ － ∑ ｒ ｉ ＝ １ Φｉｗｉ‖ ２ ２ ≤ ε （１１） 式中：‖ｗ‖２，０ ＝ ‖（‖ｗ１‖２，‖ｗ２‖２，…，‖ｗｒ‖２）‖０ 实际上反映的是模糊规则的数目，并且 ε 表示模型 精度的上限。 优化问题（１１） 的目的是使得结果参 数向量 ｗ 尽可能的块稀疏并均衡模型的精度和复 杂度。 通过图 ２ 来说明这种块结构稀疏回归。 ２．３ 块正交匹配追踪算法应用于 ＴＳＫ 模糊系统建模 在过去的研究中，优化问题（ １１） 已被证明是 ＮＰ 难问题；然而，通常有 ２ 种方法求近似解：１） 松 弛方法，例如 ‖·‖２，１ 范数凸优化近似求解的一般 方法；２）分块（分组）贪婪选择算法，例如块正交匹 配追踪算法（ ｂｌｏｃｋ ＯＭＰ 算法）、块匹配追踪算法 （ＯＭＰ 算法）等。 在本文中，使用块正交匹配追踪算 法去解决优化问题（１１），因为该算法在计算代价方 面有优势。 作为 ＯＭＰ 算法的一个继承，在稀疏回归时，分 块 ＯＭＰ 算法进行的是块变量的选择而不是对单个 变量的选择。 它以一种非常直观的方式运作。 在每 一步迭代中，根据减少的残差选择最优块。 一旦块 被选定，在已经选定的块上执行 ＬＳ 最小化获得对 相应系数的估计。 每次迭代结束，算法检查停止条 件是否已经达到。 这个停止条件通常是残差的最小 范围或者是迭代的最大次数。 在 ＴＳＫ 模糊系统建 模的框架中，因为块变量 ｗｉ 是与第 ｉ 条模糊规则的 后件参数向量相联系的，故对块变量的选择，实际上 就是对模糊规则的选择。 使用分块 ＯＭＰ 算法（算法 ２）对模糊规则进行 选取的过程如下。 １）输入：依据数据集 Ｄ 生成的 ＴＳＫ 模糊系统字 典 Φ＝ ［Φ１ ，Φ２ ，…，Φｒ］。 ２）初始化：初始化标签集 Ｉ （０） ＝ ∅ ，后件参数向 量 ｗ （０）＝ ０，残差 ｒ （０）＝ ｙ。 ３）步骤： ＦＯＲ Ｋ ＝ １，２，… 令 ｊ （ｋ） ＝ ａｒｇ ｍａｘ ｊ （ｒ （ｋ－１） ） ＴΦｊ（Φ Ｔ ｊ Φｊ） －１Φ Ｔ ｊ ｒ （ｋ－１） ＩＦ 终止条件为真，ｂｒｅａｋ 设定 Ｉ （ｋ） ＝ Ｉ （ｋ） ∪ ｊ （ｋ） 通过 ｗ （ｋ） Ｉ （ｋ） ＝ ａｒｇ ｍｉｎ ｗＩ （ｋ） ‖ΦＩ （ｋ）ｗＩ （ｋ） －ｙ‖２ 计算当前 的后件参数向量 ｗ （ｋ）并且设置 ｗ （ｋ） （Ｉ （ｋ）） ｃ ＝ ０ 更新当前残差 ｒ （ｋ）＝ ｙ－Φｗ （ｋ） ４）输出： Ｉ （ｋ） 中选定的模糊规则子字典，以及模 糊规则后件参数向量 ｗ ｋ 。 在第 ｋ 次迭代， Ｉ （ｋ） ⊂ ｛１，２，…，ｒ｝ 表示已选模 糊子字典的标签集；ｗ （ｋ）∈Ｒ ｒ（ｎ＋１）表示模糊规则后件 参数向量；ｒ （ｋ） ＝ ｙ－Φｗ （ｋ） 表示相应的残差。 初始化 后件参数向量为 ｗ （０）＝ ０，残差为 ｒ （０） ＝ ｙ。 ΦＩ （ｋ）表示 ·５８６· 智 能 系 统 学 报 第 １０ 卷

第4期 张佳骕，等：基于特征聚类方法的稀疏TSK模糊系统 ·587. 对④进行限制的变量集是{④：i∈}。 上述优化问题在信号和图像处理领域有广泛和 在第k次迭代中选取的最好的规则要使残差减 深入的研究，跟经典的飞，范数支持向量回归一样。 少得越多越好，事实上，在第k次迭代中第j条模糊 有几种较为成熟的算法去解决上述问题，比如迭代 规则子字典产生的误差为 重加权最小二乘算法、最小角回归算法以及迭代收 G)=‖电w,-r-wI (12) 缩算法，本文采用L1范式最小二乘方法[]对上述 为了将其最小化，则w=(更更)更rD,此处， 问题进行求解。 j=1,2,…,r,将w°带入()得 2.5FCA-sparseTSK应用于TSK模糊系统建模 s0)F0,19,-r》= 在这一部分中，将算法1与块算法2相结合，提 川电w-r-”3= 出了一种有效的TSK模糊系统建模的方法，称之为 I重（电，）r-”--wI子= FCA-sparseTSK(算法3)。该模型在划分输入空间 ‖r-”I-(r-”)更（更更，）更r-” 过程中采用了FCA聚类算法，对权重较小的特征进 行去除，从而化简了模糊规则：在选择模糊规则过程 (13) 中采用了Block OMP算法，挑选出较为重要的若干 为了保证误差尽可能多地减少，在第k次迭代 规则，去除了冗余规则，并利用稀疏表示的方法对后 过程中，选择出的模糊规则子字典中要满足 件参数进行估计。所以，通过FCA-sparseTSK建立 =arg max(r-)r更（电）更r- 的模糊系统的模糊规则数及非零后件参数的数目均 (14) 得到了约减。 在)中已经选定的模糊规则子字典将不会再 FCA-稀疏TSK(FCA-sparseTSK)算法如下： 被选取，假设在k次迭代之后选取的模糊规则为 1)输入：输入输出数据集D。 心，那么通过式(15)估计后件参数向量： 2)特征优化：通过F℃A聚类算法进行模糊划分 w8=arg min‖电w-yI2w倪e=0 并挑选出权重较大的特征生成TSK模糊系统字典。 w》 (15) 3)块结构稀疏：运行Block OMP算法选择出k 在算法2中(1)表示1)的补集。w品的最 条重要的模糊规则子字典并得到相应的类中心。 优值是通过将下面的二次导数置零获得： 4)优化学习：将上一步得到的类中心最为初始 D(Dw-y）=-Φ=0(16) 类中心，再次运行FCA聚类算法，并产生一个新的 所以，所有在标签集中选择过的模糊规则 模糊系统字典。 子字典将不会再被式(14)选取。 5)稀疏表示：根据稀疏表示对相应的模糊规则 2.4已选模糊规则后件的稀疏正则化 后件参数进行估计。 本文提出了一个分块结构的稀疏回归模型来挑 6)输出：优化的TSK模糊系统。 选一个T$K模糊模型最重要的模糊规则。在这一 3 实验 部分，稀疏表示进一步被应用于减少TSK模糊规则 最小非零后件参数。通过块OMP算法选择出最重 用数值实验证明所提出FCA-sparseTSK模型的 要的k条规则之后，可以用矿表示模糊系统字典。 有效性并与相关算法比较。在本实验中，将初始的 最普通的用于寻找后件参数的方法是 模糊规则条数设置为30。设输入输出数据集的形 mim3y-l+AIw。(17) 式如下所示： D={[x,y:]Tx=[xax2,…xn]T,i=1,2,…,N 这里的参数入是用于平衡模型的误差以及后 根据相关实验的具体情况选择不同的评价指 件中非零参数的数目。不过已经证明了带有 标，例如均方误差MSE=∑( (y:-)2和平均绝 ‖·‖。范数的稀疏正则项的补偿函数是NP难的。 一般情况下，会用平滑补偿函数的松弛算法对上述 问题进行近似求解。在多种估计方法中，一种较为 对误差MAE=N三~l。这里，表示TSK模 常用的方法就是将‖·I。范数改成‖·‖1范数。 糊系统对应变量x,(i=1,2,…,N)的输出。 这样，优化问题(17)被改写成 本文所有实验均对数据进行标准化处理，并采用 min2Iy-wwl经+入lwl,(18) 五折交叉验证的方法对FCA-sparseTSK算法中所涉 及到的参数进行寻优。算法中，m和α的寻优范围设

对 Φ 进行限制的变量集是｛Φｉ：ｉ∈Ｉ （ｋ） ｝。 在第 ｋ 次迭代中选取的最好的规则要使残差减 少得越多越好，事实上，在第 ｋ 次迭代中第 ｊ 条模糊 规则子字典产生的误差为 ε（ｊ） ＝ ‖Φｊｗｊ － ｒ （ｋ－１）‖２ ２ （１２） 为了将其最小化，则 ｗ ∗ ｊ ＝ （Φ Ｔ ｊ Φｊ） －１ Φ Ｔ ｊ ｒ （ｋ－１） ，此处， ｊ ＝１，２，…，ｒ ，将 ｗ ∗ ｊ 带入 ε（ｊ）得 ε（ｊ） ＝ ｍｉｎ ｗｊ∈ℝ ｎ＋１ ‖Φｊｗｊ － ｒ （ｋ－１）‖２ ２ ＝ ‖Φｊｗ ∗ ｊ － ｒ （ｋ－１）‖２ ２ ＝ ‖Φｊ （Φ Ｔ ｊ Φｊ） －１Φ Ｔ ｊ ｒ （ｋ－１） － ｒ （ｋ－１）‖２ ２ ＝ ‖ｒ （ｋ－１）‖２ ２ － （ｒ （ｋ－１） ） ＴΦｊ（Φ Ｔ ｊ Φｊ） －１Φ Ｔ ｊ ｒ （ｋ－１） （１３） 为了保证误差尽可能多地减少，在第 ｋ 次迭代 过程中，选择出的模糊规则子字典 Φｊ （ｋ）要满足 ｊ （ｋ） ＝ ａｒｇ ｍａｘ ｊ （ｒ （ｋ－１） ） ＴΦｊ （Φ Ｔ ｊ Φｊ） －１Φ Ｔ ｊ ｒ （ｋ－１） （１４） 在 Ｉ （ｋ） 中已经选定的模糊规则子字典将不会再 被选取，假设在 ｋ 次迭代之后选取的模糊规则为 Ｒ ｊ （ｋ） ，那么通过式（１５）估计后件参数向量 ｗ （ｋ） ： ｗ （ｋ） Ｉ （ｋ） ＝ ａｒｇ ｍｉｎ ｗＩ （ｋ） ‖ΦＩ （ｋ）ｗＩ （ｋ） － ｙ‖２ ｗ （ｋ） （Ｉ （ｋ）） ｃ ＝ ０ （１５） 在算法 ２ 中 （Ｉ （ｋ） ） ｃ 表示 Ｉ （ｋ） 的补集。 ｗ （ｋ） Ｉ （ｋ）的最 优值是通过将下面的二次导数置零获得： Φ Ｔ Ｉ （ｋ）（ΦＩ （ｋ）ｗＩ （ｋ） － ｙ） ＝－ Φ Ｔ Ｉ （ｋ） ｒ （ｋ） ＝ ０ （１６） 所以，所有在标签集 Ｉ （ｋ） 中选择过的模糊规则 子字典将不会再被式（１４）选取。 ２．４ 已选模糊规则后件的稀疏正则化 本文提出了一个分块结构的稀疏回归模型来挑 选一个 ＴＳＫ 模糊模型最重要的模糊规则。 在这一 部分，稀疏表示进一步被应用于减少 ＴＳＫ 模糊规则 最小非零后件参数。 通过块 ＯＭＰ 算法选择出最重 要的 ｋ 条规则之后，可以用 Φ ｋ 表示模糊系统字典。 最普通的用于寻找后件参数的方法是 ｍｉｎ １ ２ ‖ｙ － Φ ｋｗ‖２ ２ ＋ λ ‖ｗ‖０ （１７） 这里的参数 λ 是用于平衡模型的误差以及后 件中 非 零 参 数 的 数 目。 不 过 已 经 证 明 了 带 有 ‖·‖０ 范数的稀疏正则项的补偿函数是 ＮＰ 难的。 一般情况下，会用平滑补偿函数的松弛算法对上述 问题进行近似求解。 在多种估计方法中，一种较为 常用的方法就是将‖·‖０ 范数改成‖·‖１ 范数。 这样，优化问题（１７）被改写成 ｍｉｎ １ ２ ‖ｙ － Φ ｋｗ‖２ ２ ＋ λ ‖ｗ‖１ （１８） 上述优化问题在信号和图像处理领域有广泛和 深入的研究，跟经典的 ｌ １ 范数支持向量回归一样。 有几种较为成熟的算法去解决上述问题，比如迭代 重加权最小二乘算法、最小角回归算法以及迭代收 缩算法，本文采用 Ｌ１ 范式最小二乘方法［１５］ 对上述 问题进行求解。 ２．５ ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 应用于 ＴＳＫ 模糊系统建模 在这一部分中，将算法 １ 与块算法 ２ 相结合，提 出了一种有效的 ＴＳＫ 模糊系统建模的方法，称之为 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ（算法 ３）。 该模型在划分输入空间 过程中采用了 ＦＣＡ 聚类算法，对权重较小的特征进 行去除，从而化简了模糊规则；在选择模糊规则过程 中采用了 Ｂｌｏｃｋ ＯＭＰ 算法，挑选出较为重要的若干 规则，去除了冗余规则，并利用稀疏表示的方法对后 件参数进行估计。 所以，通过 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 建立 的模糊系统的模糊规则数及非零后件参数的数目均 得到了约减。 ＦＣＡ⁃稀疏 ＴＳＫ（ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ）算法如下： １）输入：输入输出数据集 Ｄ。 ２）特征优化：通过 ＦＣＡ 聚类算法进行模糊划分 并挑选出权重较大的特征生成 ＴＳＫ 模糊系统字典。 ３）块结构稀疏：运行 Ｂｌｏｃｋ ＯＭＰ 算法选择出 ｋ 条重要的模糊规则子字典并得到相应的类中心。 ４）优化学习：将上一步得到的类中心最为初始 类中心，再次运行 ＦＣＡ 聚类算法，并产生一个新的 模糊系统字典。 ５）稀疏表示：根据稀疏表示对相应的模糊规则 后件参数进行估计。 ６）输出：优化的 ＴＳＫ 模糊系统。 ３ 实验 用数值实验证明所提出 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 模型的 有效性并与相关算法比较。 在本实验中，将初始的 模糊规则条数设置为 ３０。 设输入输出数据集的形 式如下所示： Ｄ ＝ ｘ Ｔ ｉ ，ｙｉ [ ] Ｔ ：ｘｉ ＝ ｘｉ１，ｘｉ２，…，ｘｉｎ [ ] Ｔ { ，ｉ ＝ １，２，…，Ｎ} 根据相关实验的具体情况选择不同的评价指 标，例如均方误差 ＭＳＥ ＝ １ Ｎ∑ Ｎ ｉ ＝ １ ｙｉ － ｙ ＾ ｉ ( ) ２ 和平均绝 对误差 ＭＡＥ ＝ １ Ｎ∑ Ｎ ｉ ＝ １ ｙｉ － ｙ ＾ ｉ 。 这里 ｙ ＾ ｉ 表示 ＴＳＫ 模 糊系统对应变量 ｘｉ（ｉ ＝ １，２，…，Ｎ）的输出。 本文所有实验均对数据进行标准化处理，并采用 五折交叉验证的方法对 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 算法中所涉 及到的参数进行寻优。 算法中， ｍ 和 α 的寻优范围设 第 ４ 期 张佳骕，等：基于特征聚类方法的稀疏 ＴＳＫ 模糊系统 ·５８７·

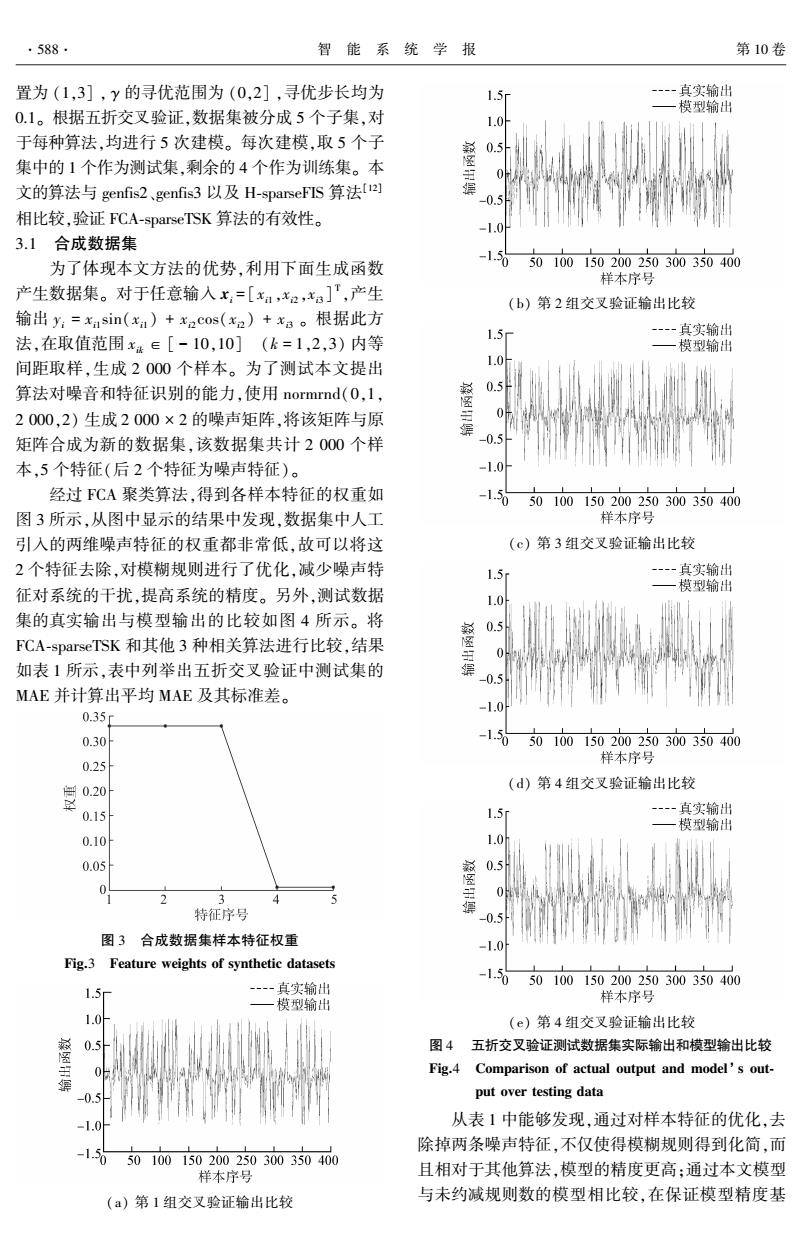
·588· 智能系统学报 第10卷 置为(1,3]，y的寻优范围为(0,2]，寻优步长均为 1.5 --真实输出 0.1。根据五折交叉验证，数据集被分成5个子集，对 模型输出 1.0 于每种算法，均进行5次建模。每次建模，取5个子 0.5 集中的1个作为测试集，剩余的4个作为训练集。本 文的算法与genfis2.、genfis3.以及H-sparseFIS算法[12] 0.5 相比较，验证FCA-sparseTSK算法的有效性。 -1.0 3.1合成数据集 为了体现本文方法的优势，利用下面生成函数 -1.30 50100150200250300350400 样本序号 产生数据集。对于任意输人x=[x1x2xa],产生 (b)第2组交叉验证输出比较 输出y:=x1sin(x1)+x2cos(x2)+x3。根据此方 1.5 ---真实输出 法，在取值范围x4∈[-10,10](k=1,2,3)内等 模型输出 间距取样，生成2000个样本。为了测试本文提出 1.0 算法对噪音和特征识别的能力，使用normrnd(0,1, 0.5 2000,2)生成2000×2的噪声矩阵，将该矩阵与原 矩阵合成为新的数据集，该数据集共计2000个样 05 本，5个特征（后2个特征为噪声特征）。 -1.0 经过FCA聚类算法，得到各样本特征的权重如 1.50 50100150200250300350400 图3所示，从图中显示的结果中发现，数据集中人工 样本序号 引入的两维噪声特征的权重都非常低，故可以将这 (c)第3组交叉验证输出比较 2个特征去除，对模糊规则进行了优化，减少噪声特 1.5 -真实输出 模型输出 征对系统的干扰，提高系统的精度。另外，测试数据 1.0 集的真实输出与模型输出的比较如图4所示。将 0.5 FCA-sparseTSK和其他3种相关算法进行比较，结果 如表1所示，表中列举出五折交叉验证中测试集的 -0.5 MAE并计算出平均MAE及其标准差。 -1.0 0.35 0.30 150 50100150200250300350400 0.25 样本序号 (d)第4组交叉验证输出比较 0.20 0.15 1.5r --真实输出 模型输出 0.10 1.0 0.05 0.5 0 特征序号 0.5 图3合成数据集样本特征权重 -1.0 Fig.3 Feature weights of synthetic datasets -150 50100150200250300350400 --真实输出 —模型输出 样本序号 1.0h (e)第4组交叉验证输出比较 0.5 图4五折交叉验证测试数据集实际输出和模型输出比较 Fig.4 Comparison of actual output and model's out- put over testing data 从表1中能够发现，通过对样本特征的优化，去 150 除掉两条噪声特征，不仅使得模糊规则得到化简，而 50100150200250300350400 样本序号 且相对于其他算法，模型的精度更高：通过本文模型 (a)第1组交叉验证输出比较 与未约减规则数的模型相比较，在保证模型精度基

置为 （１，３］ ， γ 的寻优范围为 （０，２］ ，寻优步长均为 ０．１。 根据五折交叉验证，数据集被分成 ５ 个子集，对 于每种算法，均进行 ５ 次建模。 每次建模，取 ５ 个子 集中的 １ 个作为测试集，剩余的 ４ 个作为训练集。 本 文的算法与 ｇｅｎｆｉｓ２、ｇｅｎｆｉｓ３ 以及 Ｈ⁃ｓｐａｒｓｅＦＩＳ 算法［１２］ 相比较，验证 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 算法的有效性。 ３．１ 合成数据集 为了体现本文方法的优势，利用下面生成函数 产生数据集。 对于任意输入 ｘｉ ＝ ［ｘｉ１ ，ｘｉ２ ，ｘｉ３ ］ Ｔ ，产生 输出 ｙｉ ＝ ｘｉ１ ｓｉｎ（ｘｉ１ ） ＋ ｘｉ２ ｃｏｓ（ｘｉ２ ） ＋ ｘｉ３ 。 根据此方 法，在取值范围 ｘｉｋ ∈ ［ － １０，１０］ （ｋ ＝ １，２，３） 内等 间距取样，生成 ２ ０００ 个样本。 为了测试本文提出 算法对噪音和特征识别的能力，使用 ｎｏｒｍｒｎｄ（０，１， ２ ０００，２） 生成 ２ ０００ × ２ 的噪声矩阵，将该矩阵与原 矩阵合成为新的数据集，该数据集共计 ２ ０００ 个样 本，５ 个特征（后 ２ 个特征为噪声特征）。 经过 ＦＣＡ 聚类算法，得到各样本特征的权重如 图 ３ 所示，从图中显示的结果中发现，数据集中人工 引入的两维噪声特征的权重都非常低，故可以将这 ２ 个特征去除，对模糊规则进行了优化，减少噪声特 征对系统的干扰，提高系统的精度。 另外，测试数据 集的真实输出与模型输出的比较如图 ４ 所示。 将 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 和其他 ３ 种相关算法进行比较，结果 如表 １ 所示，表中列举出五折交叉验证中测试集的 ＭＡＥ 并计算出平均 ＭＡＥ 及其标准差。 图 ３ 合成数据集样本特征权重 Ｆｉｇ．３ Ｆｅａｔｕｒｅ ｗｅｉｇｈｔｓ ｏｆ ｓｙｎｔｈｅｔｉｃ ｄａｔａｓｅｔｓ （ａ） 第 １ 组交叉验证输出比较 （ｂ） 第 ２ 组交叉验证输出比较 （ｃ） 第 ３ 组交叉验证输出比较 （ｄ） 第 ４ 组交叉验证输出比较 （ｅ） 第 ４ 组交叉验证输出比较 图 ４ 五折交叉验证测试数据集实际输出和模型输出比较 Ｆｉｇ．４ Ｃｏｍｐａｒｉｓｏｎ ｏｆ ａｃｔｕａｌ ｏｕｔｐｕｔ ａｎｄ ｍｏｄｅｌ’ ｓ ｏｕｔ⁃ ｐｕｔ ｏｖｅｒ ｔｅｓｔｉｎｇ ｄａｔａ 从表 １ 中能够发现，通过对样本特征的优化，去 除掉两条噪声特征，不仅使得模糊规则得到化简，而 且相对于其他算法，模型的精度更高；通过本文模型 与未约减规则数的模型相比较，在保证模型精度基 ·５８８· 智 能 系 统 学 报 第 １０ 卷

第4期 张佳骕，等：基于特征聚类方法的稀疏TSK模糊系统 .589· 本一致的前提下，本文算法平均约减规则13.2条， 故对冗余规则的去除是有效的。 表1合成数据集各模型性能比较 Table 1 The performance of each model on synthetic datasets 算法 特征数 性能指标 1 2 3 4 5 均值 MAE 0.04840.04560.06710.06180.0448 0.0535±0.0102 genfis2 5 规则数 21 18 20 21 19 19.8 MAE 0.27730.26640.28520.30230.2789 0.2820±0.0132 genfis3 5 规则数 20 20 20 20 20 20 MAE 0.04470.04850.07580.08840.0824 0.0680±0.0200 H-sparseFIS 5 规则数 25 25 16 15 19 20 MAE 0.01120.0107 0.01080.01170.0116 0.0112±0.0005 规则数 30 30 30 30 30 30 FCA-sparseTSK MAE 0.01430.01270.01590.01860.0162 0.0155±0.0022 规则数 13 18 16 16 17 16.8 3.2真实数据集 表2结果显示，对于airfoil self-noise数据集，使 3.2.1 Airfoil Self-.Noise数据集 用FCA-sparseTSK构建出的模型性能最好。本文所 该数据集从UCI machine learning repository获 提出的模型相比于genfis2、genfis.3和H-sparseFIS性 取，记录了不同尺寸的NACA O012机翼在不同风动 能有所提升，并且FCA-sparseTSK去除掉2条不重 速度和攻角下的性能，共计1503个样本，5条特征。 要的特征，化简了模糊规则的复杂程度，使模糊系统 输入分别为频率、攻角、弦长、自由流速度以及吸力 变得简洁：通过与未约减规则数的实验相比较，本文 面位移厚度，输出为声压等级。各算法在五折交叉 算法平均约规则19.2条，且误差与未约减规则时基 验证中测试集的MSE及规则数目如表2所示。 本一致，故对冗余规则的去除是有效的。 表2 Airfoil self-noise数据集各模型性能比较 Table 2 The performance of each model on airfoil self-noise datasets 算法 特征数 性能指标 1 2 4 均值 MSE 0.05030.05470.05230.05650.0458 0.0519±0.0042 genfis2 5 规则数 11 10 11 10 11 10.6 MSE 0.05790.06750.06400.07460.0643 0.0657±0.0061 genfis3 5 规则数 15 15 15 15 15 15 MSE 0.04230.04880.04550.0593 0.0482 0.0488±0.0064 H-sparseFIS 规则数 12 13 11 12 13 12.2 MSE 0.04530.04740.03940.05160.0424 0.0452±0.0047 规则数 30 30 30 30 30 30 FCA-sparseTSK 3 MSE 0.04040.04970.03540.05320.0395 0.0436±0.0075 规则数 12 10 10 11 10.8 3.2.2 Machine CPU performance数据集 表3结果显示，对于machine CPU performance 该数据集从knowledge extraction based on evolus- 数据集，使用FCA-sparseTSK构建出的模型性能最 tionary learning(KEEL)获取，记录了相对CPU性能 好。本文所提出的模型相比于genfis2、genfis.3和H- 数据，共计209个样本，6条特征。数据输入分别为 sparseFIS性能有所提升，并且FCA-sparseTSK去除 机器周期时间(MYCT)、最小内存(MMIN)、最大内 掉1条不重要的特征，化简了模糊规则的复杂程度； 存(MMAX)、快速存储器(CACH)、最小通道 通过与未约减规则数的实验相比较，本文算法平均 (CHMIN)、最大通道(CHMAX),输出为CPU的相 约规则25.4条，且精度与未约减规则的模型相比略 对性能(PRP)。各算法在五折交叉验证中测试集 有提升，故对冗余规则的去除是有效的。 的MAE及规则数目如表3所示

本一致的前提下，本文算法平均约减规则 １３．２ 条， 故对冗余规则的去除是有效的。 表 １ 合成数据集各模型性能比较 Ｔａｂｌｅ １ Ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｅａｃｈ ｍｏｄｅｌ ｏｎ ｓｙｎｔｈｅｔｉｃ ｄａｔａｓｅｔｓ 算法 特征数 性能指标 １ ２ ３ ４ ５ 均值 ｇｅｎｆｉｓ２ ５ ＭＡＥ 规则数 ０．０４８ ４ ２１ ０．０４５ ６ １８ ０．０６７ １ ２０ ０．０６１ ８ ２１ ０．０４４ ８ １９ ０．０５３ ５±０．０１０ ２ １９．８ ｇｅｎｆｉｓ３ ５ ＭＡＥ 规则数 ０．２７７ ３ ２０ ０．２６６ ４ ２０ ０．２８５ ２ ２０ ０．３０２ ３ ２０ ０．２７８ ９ ２０ ０．２８２ ０±０．０１３ ２ ２０ Ｈ⁃ｓｐａｒｓｅＦＩＳ ５ ＭＡＥ 规则数 ０．０４４ ７ ２５ ０．０４８ ５ ２５ ０．０７５ ８ １６ ０．０８８ ４ １５ ０．０８２ ４ １９ ０．０６８ ０±０．０２０ ０ ２０ ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ ３ ＭＡＥ 规则数 ＭＡＥ 规则数 ０．０１１ ２ ３０ ０．０１４ ３ １３ ０．０１０ ７ ３０ ０．０１２ ７ １８ ０．０１０ ８ ３０ ０．０１５ ９ １６ ０．０１１ ７ ３０ ０．０１８ ６ １６ ０．０１１ ６ ３０ ０．０１６ ２ １７ ０．０１１ ２ ± ０．０００ ５ ３０ ０．０１５ ５±０．００２ ２ １６．８ ３．２ 真实数据集 ３．２．１ Ａｉｒｆｏｉｌ Ｓｅｌｆ⁃Ｎｏｉｓｅ 数据集 该数据集从 ＵＣＩ ｍａｃｈｉｎｅ ｌｅａｒｎｉｎｇ ｒｅｐｏｓｉｔｏｒｙ 获 取，记录了不同尺寸的 ＮＡＣＡ ００１２ 机翼在不同风动 速度和攻角下的性能，共计 １ ５０３ 个样本，５ 条特征。 输入分别为频率、攻角、弦长、自由流速度以及吸力 面位移厚度，输出为声压等级。 各算法在五折交叉 验证中测试集的 ＭＳＥ 及规则数目如表 ２ 所示。 表 ２ 结果显示，对于 ａｉｒｆｏｉｌ ｓｅｌｆ⁃ｎｏｉｓｅ 数据集，使 用 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 构建出的模型性能最好。 本文所 提出的模型相比于 ｇｅｎｆｉｓ２、ｇｅｎｆｉｓ３ 和 Ｈ⁃ｓｐａｒｓｅＦＩＳ 性 能有所提升，并且 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 去除掉 ２ 条不重 要的特征，化简了模糊规则的复杂程度，使模糊系统 变得简洁；通过与未约减规则数的实验相比较，本文 算法平均约规则 １９．２ 条，且误差与未约减规则时基 本一致，故对冗余规则的去除是有效的。 表 ２ Ａｉｒｆｏｉｌ ｓｅｌｆ⁃ｎｏｉｓｅ 数据集各模型性能比较 Ｔａｂｌｅ ２ Ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｅａｃｈ ｍｏｄｅｌ ｏｎ ａｉｒｆｏｉｌ ｓｅｌｆ⁃ｎｏｉｓｅ ｄａｔａｓｅｔｓ 算法 特征数 性能指标 １ ２ ３ ４ ５ 均值 ｇｅｎｆｉｓ２ ５ ＭＳＥ 规则数 ０．０５０ ３ １１ ０．０５４ ７ １０ ０．０５２ ３ １１ ０．０５６ ５ １０ ０．０４５ ８ １１ ０．０５１ ９±０．００４ ２ １０．６ ｇｅｎｆｉｓ３ ５ ＭＳＥ 规则数 ０．０５７ ９ １５ ０．０６７ ５ １５ ０．０６４ ０ １５ ０．０７４ ６ １５ ０．０６４ ３ １５ ０．０６５ ７±０．００６ １ １５ Ｈ⁃ｓｐａｒｓｅＦＩＳ ５ ＭＳＥ 规则数 ０．０４２ ３ １２ ０．０４８ ８ １３ ０．０４５ ５ １１ ０．０５９ ３ １２ ０．０４８ ２ １３ ０．０４８ ８±０．００６ ４ １２．２ ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ ３ ＭＳＥ 规则数 ＭＳＥ 规则数 ０．０４５ ３ ３０ ０．０４０ ４ １２ ０．０４７ ４ ３０ ０．０４９ ７ １１ ０．０３９ ４ ３０ ０．０３５ ４ １０ ０．０５１ ６ ３０ ０．０５３ ２ １０ ０．０４２ ４ ３０ ０．０３９ ５ １１ ０．０４５ ２ ± ０．００４ ７ ３０ ０．０４３ ６±０．００７ ５ １０．８ ３．２．２ Ｍａｃｈｉｎｅ ＣＰＵ ｐｅｒｆｏｒｍａｎｃｅ 数据集 该数据集从 ｋｎｏｗｌｅｄｇｅ ｅｘｔｒａｃｔｉｏｎ ｂａｓｅｄ ｏｎ ｅｖｏｌｕ⁃ ｔｉｏｎａｒｙ ｌｅａｒｎｉｎｇ（ＫＥＥＬ）获取，记录了相对 ＣＰＵ 性能 数据，共计 ２０９ 个样本，６ 条特征。 数据输入分别为 机器周期时间（ＭＹＣＴ）、最小内存（ＭＭＩＮ）、最大内 存 （ ＭＭＡＸ）、 快 速 存 储 器 （ ＣＡＣＨ ）、 最 小 通 道 （ＣＨＭＩＮ）、最大通道（ＣＨＭＡＸ），输出为 ＣＰＵ 的相 对性能（ ＰＲＰ）。 各算法在五折交叉验证中测试集 的 ＭＡＥ 及规则数目如表 ３ 所示。 表 ３ 结果显示，对于 ｍａｃｈｉｎｅ ＣＰＵ ｐｅｒｆｏｒｍａｎｃｅ 数据集，使用 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 构建出的模型性能最 好。 本文所提出的模型相比于 ｇｅｎｆｉｓ２、ｇｅｎｆｉｓ３ 和 Ｈ⁃ ｓｐａｒｓｅＦＩＳ 性能有所提升，并且 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 去除 掉 １ 条不重要的特征，化简了模糊规则的复杂程度； 通过与未约减规则数的实验相比较，本文算法平均 约规则 ２５．４ 条，且精度与未约减规则的模型相比略 有提升，故对冗余规则的去除是有效的。 第 ４ 期 张佳骕，等：基于特征聚类方法的稀疏 ＴＳＫ 模糊系统 ·５８９·

.590. 智能系统学报 第10卷 表3 Machine CPU performance数据集各模型性能比较 Table 3 The performance of each model on machine CPU performance datasets 算法 特征数性能指标 1 3 4 5 均值 MAE 0.0569 0.04690.07070.05690.0748 0.0612±0.0114 genfis2 6 规则数 6 6 5 4 5.2 MAE 0.07460.05830.07680.06910.0910 0.0740±0.0119 genfis3 6 规则数 5 MAE 0.05690.03570.04890.05270.0600 0.0508±0.0094 H-sparseFIS 6 规则数 6 4 5 4 7 5.2 MAE 0.05320.0367 0.0628 0.04860.0559 0.0514±0.0097 规则数 30 30 30 30 30 30 FCA-sparseTSK MAE 0.04390.04000.04780.04070.0586 0.0462±0.0076 规则数 4 4 4.6 3.2.3 Stock prices数据集 格作为输入，对第10个公司的股票价格进行估计。 该数据集从KEEL获取，由I0个航空航天公司 各算法在五折交叉验证中测试集的MAE集规则数 从1988年1月到1991年10月的日常股票价格，共 目如表4所示。 计950个样本，9条特征。用前9个公司的股票价 表4 Stock prices数据集各模型性能比较 Table 4 The performance of each model on stock prices datasets 算法 特征数 性能指标 1 2 3 4 5 均值 MAE 0.04100.0395 0.04390.04110.0431 0.0417±0.0018 genfis2 9 规则数 21 22 21 21 24 21.8 MAE 0.13230.1309 0.12980.1300 0.1337 0.1313±0.0016 genfis3 9 规则数 20 20 20 20 20 20 MAE 0.03860.04470.04940.04690.0425 0.0444±0.0041 H-sparseFIS 9 规则数 22 17 20 22 22 20.6 MAE 0.04740.04440.0496 0.04670.04550.0467±0.0020 规则数 30 30 30 30 30 30 FCA-sparseTSK 6 MAE 0.04730.04760.04710.04720.0472 0.0476±0.0007 规则数 17 17 18 17 17 17.6 表4结果显示，对于stock数据集，genfis.2构建 以及真实数据集上的实验证明，FCA-sparseTSK模 出的模型性能最好。本文所提出的模型与genfis2 型能够在保证系统性能的前提下，同时化简模糊规 和H-sparseFIS相比性能大体一致，但FCA-spar 则并消减冗余模糊规则。 seTSK去除掉3条不重要的特征，大大化简了模糊 规则的复杂程度，使模糊系统变得简洁：通过与不约 参考文献： 减规则数的实验相比较，本文算法平均约减掉12.4 [1]DING B.Dynamic output feedback predictive control for 条规则，且误差与未约减规则时基本持平，故对冗余 nonlinear systems represented by a Takagi-Sugeno model 规则的去除是有效的。 [J].IEEE Transactions on Fuzzy Systems,2011,19(5): 831-843. 4结束语 [2]JANG J S R.ANFIS:adaptive-network-based fuzzy infer- ence system[J].IEEE Transactions on Systems,Man and 本文提取出存在于TSK模糊系统中的分块结 Cybernetics,1993,23(3):665-685. 构信息，将模糊系统建模问题转化为一个结构化的 [3]QIN Hao,YANG S X.Adaptive neuro-fuzzy inference sys- 稀疏恢复问题。FCA-sparseTSK算法在构建模糊系 tems based approach to nonlinear noise cancellation for ima- 统的过程中，对样本特征进行优化，选取重要的模糊 ges[J].Fuzzy Sets and Systems,2007,158(10):1036- 规则并对规则的后件参数进行估计。在合成数据集 1063

表 ３ Ｍａｃｈｉｎｅ ＣＰＵ ｐｅｒｆｏｒｍａｎｃｅ 数据集各模型性能比较 Ｔａｂｌｅ ３ Ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｅａｃｈ ｍｏｄｅｌ ｏｎ ｍａｃｈｉｎｅ ＣＰＵ ｐｅｒｆｏｒｍａｎｃｅ ｄａｔａｓｅｔｓ 算法 特征数 性能指标 １ ２ ３ ４ ５ 均值 ｇｅｎｆｉｓ２ ６ ＭＡＥ 规则数 ０．０５６ ９ ６ ０．０４６ ９ ５ ０．０７０ ７ ６ ０．０５６ ９ ５ ０．０７４ ８ ４ ０．０６１ ２±０．０１１ ４ ５．２ ｇｅｎｆｉｓ３ ６ ＭＡＥ 规则数 ０．０７４ ６ ５ ０．０５８ ３ ５ ０．０７６ ８ ５ ０．０６９ １ ５ ０．０９１ ０ ５ ０．０７４ ０±０．０１１ ９ ５ Ｈ⁃ｓｐａｒｓｅＦＩＳ ６ ＭＡＥ 规则数 ０．０５６ ９ ６ ０．０３５ ７ ４ ０．０４８ ９ ５ ０．０５２ ７ ４ ０．０６０ ０ ７ ０．０５０ ８±０．００９ ４ ５．２ ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ ５ ＭＡＥ 规则数 ＭＡＥ 规则数 ０．０５３ ２ ３０ ０．０４３ ９ ４ ０．０３６ ７ ３０ ０．０４０ ０ ４ ０．０６２ ８ ３０ ０．０４７ ８ ５ ０．０４８ ６ ３０ ０．０４０ ７ ４ ０．０５５ ９ ３０ ０．０５８ ６ ６ ０．０５１ ４ ± ０．００９ ７ ３０ ０．０４６ ２±０．００７ ６ ４．６ ３．２．３ Ｓｔｏｃｋ ｐｒｉｃｅｓ 数据集 该数据集从 ＫＥＥＬ 获取，由 １０ 个航空航天公司 从 １９８８ 年 １ 月到 １９９１ 年 １０ 月的日常股票价格，共 计 ９５０ 个样本，９ 条特征。 用前 ９ 个公司的股票价 格作为输入，对第 １０ 个公司的股票价格进行估计。 各算法在五折交叉验证中测试集的 ＭＡＥ 集规则数 目如表 ４ 所示。 表 ４ Ｓｔｏｃｋ ｐｒｉｃｅｓ 数据集各模型性能比较 Ｔａｂｌｅ ４ Ｔｈｅ ｐｅｒｆｏｒｍａｎｃｅ ｏｆ ｅａｃｈ ｍｏｄｅｌ ｏｎ ｓｔｏｃｋ ｐｒｉｃｅｓ ｄａｔａｓｅｔｓ 算法 特征数 性能指标 １ ２ ３ ４ ５ 均值 ｇｅｎｆｉｓ２ ９ ＭＡＥ 规则数 ０．０４１ ０ ２１ ０．０３９ ５ ２２ ０．０４３ ９ ２１ ０．０４１ １ ２１ ０．０４３ １ ２４ ０．０４１ ７±０．００１ ８ ２１．８ ｇｅｎｆｉｓ３ ９ ＭＡＥ 规则数 ０．１３２ ３ ２０ ０．１３０ ９ ２０ ０．１２９ ８ ２０ ０．１３０ ０ ２０ ０．１３３ ７ ２０ ０．１３１ ３±０．００１ ６ ２０ Ｈ⁃ｓｐａｒｓｅＦＩＳ ９ ＭＡＥ 规则数 ０．０３８ ６ ２２ ０．０４４ ７ １７ ０．０４９ ４ ２０ ０．０４６ ９ ２２ ０．０４２ ５ ２２ ０．０４４ ４±０．００４ １ ２０．６ ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ ６ ＭＡＥ 规则数 ＭＡＥ 规则数 ０．０４７ ４ ３０ ０．０４７ ３ １７ ０．０４４ ４ ３０ ０．０４７ ６ １７ ０．０４９ ６ ３０ ０．０４７ １ １８ ０．０４６ ７ ３０ ０．０４７ ２ １７ ０．０４５ ５ ３０ ０．０４７ ２ １７ ０．０４６ ７ ± ０．００２ ０ ３０ ０．０４７ ６±０．０００ ７ １７．６ 表 ４ 结果显示，对于 ｓｔｏｃｋ 数据集，ｇｅｎｆｉｓ２ 构建 出的模型性能最好。 本文所提出的模型与 ｇｅｎｆｉｓ２ 和 Ｈ⁃ｓｐａｒｓｅＦＩＳ 相 比 性 能 大 体 一 致， 但 ＦＣＡ⁃ｓｐａｒ⁃ ｓｅＴＳＫ 去除掉 ３ 条不重要的特征，大大化简了模糊 规则的复杂程度，使模糊系统变得简洁；通过与不约 减规则数的实验相比较，本文算法平均约减掉 １２．４ 条规则，且误差与未约减规则时基本持平，故对冗余 规则的去除是有效的。 ４ 结束语 本文提取出存在于 ＴＳＫ 模糊系统中的分块结 构信息，将模糊系统建模问题转化为一个结构化的 稀疏恢复问题。 ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 算法在构建模糊系 统的过程中，对样本特征进行优化，选取重要的模糊 规则并对规则的后件参数进行估计。 在合成数据集 以及真实数据集上的实验证明，ＦＣＡ⁃ｓｐａｒｓｅＴＳＫ 模 型能够在保证系统性能的前提下，同时化简模糊规 则并消减冗余模糊规则。 参考文献： ［１］ ＤＩＮＧ Ｂ． Ｄｙｎａｍｉｃ ｏｕｔｐｕｔ ｆｅｅｄｂａｃｋ ｐｒｅｄｉｃｔｉｖｅ ｃｏｎｔｒｏｌ ｆｏｒ ｎｏｎｌｉｎｅａｒ ｓｙｓｔｅｍｓ ｒｅｐｒｅｓｅｎｔｅｄ ｂｙ ａ Ｔａｋａｇｉ⁃Ｓｕｇｅｎｏ ｍｏｄｅｌ ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｆｕｚｚｙ Ｓｙｓｔｅｍｓ， ２０１１， １９（５）： ８３１⁃８４３． ［２］ ＪＡＮＧ Ｊ Ｓ Ｒ． ＡＮＦＩＳ： ａｄａｐｔｉｖｅ⁃ｎｅｔｗｏｒｋ⁃ｂａｓｅｄ ｆｕｚｚｙ ｉｎｆｅｒ⁃ ｅｎｃｅ ｓｙｓｔｅｍ［ Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｓｙｓｔｅｍｓ， Ｍａｎ ａｎｄ Ｃｙｂｅｒｎｅｔｉｃｓ， １９９３， ２３（３）： ６６５⁃６８５． ［３］ＱＩＮ Ｈａｏ， ＹＡＮＧ Ｓ Ｘ． Ａｄａｐｔｉｖｅ ｎｅｕｒｏ⁃ｆｕｚｚｙ ｉｎｆｅｒｅｎｃｅ ｓｙｓ⁃ ｔｅｍｓ ｂａｓｅｄ ａｐｐｒｏａｃｈ ｔｏ ｎｏｎｌｉｎｅａｒ ｎｏｉｓｅ ｃａｎｃｅｌｌａｔｉｏｎ ｆｏｒ ｉｍａ⁃ ｇｅｓ［Ｊ］． Ｆｕｚｚｙ Ｓｅｔｓ ａｎｄ Ｓｙｓｔｅｍｓ， ２００７， １５８（ １０）： １０３６⁃ １０６３． ·５９０· 智 能 系 统 学 报 第 １０ 卷

第4期 张佳骕，等：基于特征聚类方法的稀疏TSK模糊系统 ·591. [4]WANG Di,ZENG Xiaojun,KEANE J A.An evolving-con- ranking features and identifying noise simultaneously[J]. struction scheme for fuzzy systems[J].IEEE Transactions Acta Automatica Sinica,2009,35(2):145-153.[14] on Fuzzy Systems,2010,18(4):755-770. YUAN Ming,LIN Yi.Model selection and estimation in regres- [5]LUGHOFER E.Evolving fuzzy systems-methodologies,ad- sion with grouped variables[J].Journal of the Royal Statistical vanced concepts and applications[M].Heidelberg:Spring- Society:Series B(Statistical Methodology),2006,68(1):49- er,2011:81-85. 67. [6]JAIN A K.Data clustering:50 years beyond K-means[J]. [15]KIM S J,KOH K,LUSTIG M,et al.A interior-point Pattern recognition letters,2010,31(8):651-666. method for large-scale (,-regularized least squares [J]. [7]TSEKOURAS G E.On the use of the weighted fuzzy c-means IEEE Journal on Selected Topics in Signal Processing, in fuzzy modeling[J].Advances in Engineering Software, 2007,1(4):606-617. 2005,36(5):287-300. 作者简介： [8]YAGER RR,FILEV D P.Generation of fuzzy rules by 张佳骕，男，1990年生，硕士研究 mountain clustering J].Journal of Intelligent and Fuzzy 生，主要研究方向为人工智能与模式识 Systems,1994,2(3):209-219. 别、模糊系统。 [9]GATH I,GEVA A B.Unsupervised optimal fuzzy clustering [J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(7):773-780. [10]GUSTAFSON D E,KESSEL W C.Fuzzy clustering with a fuzzy covariance matrix [C]//IEEE Conference on Deci- 蒋亦樟，男，1988年生，博士研究 生，主要研究方向为人工智能与模式识 sion and Control including the 17th Symposium on Adaptive 别、模糊系统。 Processes.San Diego,USA,1978:761-766. [11]LUGHOFER E.Extensions of vector quantization for incre- mental clustering[J].Pattern Recognition,2008,41(3): 995-1011. 王士同，男，1964年生，教授，博士 [12]LUO Minnan,SUN Fuchun,LIU Huaping.Hierarchical 生导师，主要研究方向为人工智能、模 structured sparse representation for T-S fuzzy systems iden- tification[J].IEEE Transactions on Fuzzy Systems,2013, 式识别和生物信息。 21(6):1032-1043. [13]皋军，王士同.具有特征排序功能的鲁棒性模糊聚类方 法[J].自动化学报，2009,35(2)：145-153. [责任编辑：刘畅] GAO Jun,WANG Shitong.Fuzzy clustering algorithm with

［４］ＷＡＮＧ Ｄｉ， ＺＥＮＧ Ｘｉａｏｊｕｎ， ＫＥＡＮＥ Ｊ Ａ． Ａｎ ｅｖｏｌｖｉｎｇ⁃ｃｏｎ⁃ ｓｔｒｕｃｔｉｏｎ ｓｃｈｅｍｅ ｆｏｒ ｆｕｚｚｙ ｓｙｓｔｅｍｓ ［ Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｆｕｚｚｙ Ｓｙｓｔｅｍｓ， ２０１０， １８（４）： ７５５⁃７７０． ［５］ ＬＵＧＨＯＦＥＲ Ｅ． Ｅｖｏｌｖｉｎｇ ｆｕｚｚｙ ｓｙｓｔｅｍｓ⁃ｍｅｔｈｏｄｏｌｏｇｉｅｓ， ａｄ⁃ ｖａｎｃｅｄ ｃｏｎｃｅｐｔｓ ａｎｄ ａｐｐｌｉｃａｔｉｏｎｓ［Ｍ］． Ｈｅｉｄｅｌｂｅｒｇ： Ｓｐｒｉｎｇ⁃ ｅｒ， ２０１１： ８１⁃８５． ［６］ＪＡＩＮ Ａ Ｋ． Ｄａｔａ ｃｌｕｓｔｅｒｉｎｇ： ５０ ｙｅａｒｓ ｂｅｙｏｎｄ Ｋ⁃ｍｅａｎｓ［ Ｊ］． Ｐａｔｔｅｒｎ ｒｅｃｏｇｎｉｔｉｏｎ ｌｅｔｔｅｒｓ， ２０１０， ３１（８）： ６５１⁃６６６． ［７］ＴＳＥＫＯＵＲＡＳ Ｇ Ｅ． Ｏｎ ｔｈｅ ｕｓｅ ｏｆ ｔｈｅ ｗｅｉｇｈｔｅｄ ｆｕｚｚｙ ｃ⁃ｍｅａｎｓ ｉｎ ｆｕｚｚｙ ｍｏｄｅｌｉｎｇ ［ Ｊ］． Ａｄｖａｎｃｅｓ ｉｎ Ｅｎｇｉｎｅｅｒｉｎｇ Ｓｏｆｔｗａｒｅ， ２００５， ３６（５）： ２８７⁃３００． ［８］ ＹＡＧＥＲ Ｒ Ｒ， ＦＩＬＥＶ Ｄ Ｐ． Ｇｅｎｅｒａｔｉｏｎ ｏｆ ｆｕｚｚｙ ｒｕｌｅｓ ｂｙ ｍｏｕｎｔａｉｎ ｃｌｕｓｔｅｒｉｎｇ ［ Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ｉｎｔｅｌｌｉｇｅｎｔ ａｎｄ Ｆｕｚｚｙ Ｓｙｓｔｅｍｓ， １９９４， ２（３）： ２０９⁃２１９． ［９］ＧＡＴＨ Ｉ， ＧＥＶＡ Ａ Ｂ． Ｕｎｓｕｐｅｒｖｉｓｅｄ ｏｐｔｉｍａｌ ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｐａｔｔｅｒｎ Ａｎａｌｙｓｉｓ ａｎｄ Ｍａｃｈｉｎｅ Ｉｎｔｅｌｌｉｇｅｎｃｅ， １９８９， １１（７）： ７７３⁃７８０． ［１０］ＧＵＳＴＡＦＳＯＮ Ｄ Ｅ， ＫＥＳＳＥＬ Ｗ Ｃ． Ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ｗｉｔｈ ａ ｆｕｚｚｙ ｃｏｖａｒｉａｎｃｅ ｍａｔｒｉｘ ［ Ｃ］ ／ ／ ＩＥＥＥ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ｄｅｃｉ⁃ ｓｉｏｎ ａｎｄ Ｃｏｎｔｒｏｌ ｉｎｃｌｕｄｉｎｇ ｔｈｅ １７ｔｈ Ｓｙｍｐｏｓｉｕｍ ｏｎ Ａｄａｐｔｉｖｅ Ｐｒｏｃｅｓｓｅｓ． Ｓａｎ Ｄｉｅｇｏ， ＵＳＡ， １９７８： ７６１⁃７６６． ［１１］ＬＵＧＨＯＦＥＲ Ｅ． Ｅｘｔｅｎｓｉｏｎｓ ｏｆ ｖｅｃｔｏｒ ｑｕａｎｔｉｚａｔｉｏｎ ｆｏｒ ｉｎｃｒｅ⁃ ｍｅｎｔａｌ ｃｌｕｓｔｅｒｉｎｇ［Ｊ］． Ｐａｔｔｅｒｎ Ｒｅｃｏｇｎｉｔｉｏｎ， ２００８， ４１（３）： ９９５⁃１０１１． ［１２］ ＬＵＯ Ｍｉｎｎａｎ， ＳＵＮ Ｆｕｃｈｕｎ， ＬＩＵ Ｈｕａｐｉｎｇ． Ｈｉｅｒａｒｃｈｉｃａｌ ｓｔｒｕｃｔｕｒｅｄ ｓｐａｒｓｅ ｒｅｐｒｅｓｅｎｔａｔｉｏｎ ｆｏｒ Ｔ⁃Ｓ ｆｕｚｚｙ ｓｙｓｔｅｍｓ ｉｄｅｎ⁃ ｔｉｆｉｃａｔｉｏｎ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｆｕｚｚｙ Ｓｙｓｔｅｍｓ， ２０１３， ２１（６）： １０３２⁃１０４３． ［１３］皋军， 王士同． 具有特征排序功能的鲁棒性模糊聚类方 法［Ｊ］． 自动化学报， ２００９， ３５（２）： １４５⁃１５３． ＧＡＯ Ｊｕｎ， ＷＡＮＧ Ｓｈｉｔｏｎｇ． Ｆｕｚｚｙ ｃｌｕｓｔｅｒｉｎｇ ａｌｇｏｒｉｔｈｍ ｗｉｔｈ ｒａｎｋｉｎｇ ｆｅａｔｕｒｅｓ ａｎｄ ｉｄｅｎｔｉｆｙｉｎｇ ｎｏｉｓｅ ｓｉｍｕｌｔａｎｅｏｕｓｌｙ［ Ｊ］． Ａｃｔａ Ａｕｔｏｍａｔｉｃａ Ｓｉｎｉｃａ， ２００９， ３５ （ ２）： １４５⁃１５３． ［ １４］ ＹＵＡＮ Ｍｉｎｇ， ＬＩＮ Ｙｉ． Ｍｏｄｅｌ ｓｅｌｅｃｔｉｏｎ ａｎｄ ｅｓｔｉｍａｔｉｏｎ ｉｎ ｒｅｇｒｅｓ⁃ ｓｉｏｎ ｗｉｔｈ ｇｒｏｕｐｅｄ ｖａｒｉａｂｌｅｓ［ Ｊ］． Ｊｏｕｒｎａｌ ｏｆ ｔｈｅ Ｒｏｙａｌ Ｓｔａｔｉｓｔｉｃａｌ Ｓｏｃｉｅｔｙ： Ｓｅｒｉｅｓ Ｂ （Ｓｔａｔｉｓｔｉｃａｌ Ｍｅｔｈｏｄｏｌｏｇｙ）， ２００６， ６８（１）： ４９⁃ ６７． ［１５］ ＫＩＭ Ｓ Ｊ， ＫＯＨ Ｋ， ＬＵＳＴＩＧ Ｍ， ｅｔ ａｌ． Ａ ｉｎｔｅｒｉｏｒ⁃ｐｏｉｎｔ ｍｅｔｈｏｄ ｆｏｒ ｌａｒｇｅ⁃ｓｃａｌｅ ℓ１ ⁃ｒｅｇｕｌａｒｉｚｅｄ ｌｅａｓｔ ｓｑｕａｒｅｓ ［ Ｊ ］． ＩＥＥＥ Ｊｏｕｒｎａｌ ｏｎ Ｓｅｌｅｃｔｅｄ Ｔｏｐｉｃｓ ｉｎ Ｓｉｇｎａｌ Ｐｒｏｃｅｓｓｉｎｇ， ２００７， １（４）： ６０６⁃６１７． 作者简介： 张佳骕，男，１９９０ 年生，硕士研究 生，主要研究方向为人工智能与模式识 别、模糊系统。 蒋亦樟，男，１９８８ 年生，博士研究 生，主要研究方向为人工智能与模式识 别、模糊系统。 王士同，男，１９６４ 年生，教授，博士 生导师，主要研究方向为人工智能、模 式识别和生物信息。 ［责任编辑：刘畅］ 第 ４ 期 张佳骕，等：基于特征聚类方法的稀疏 ＴＳＫ 模糊系统 ·５９１·