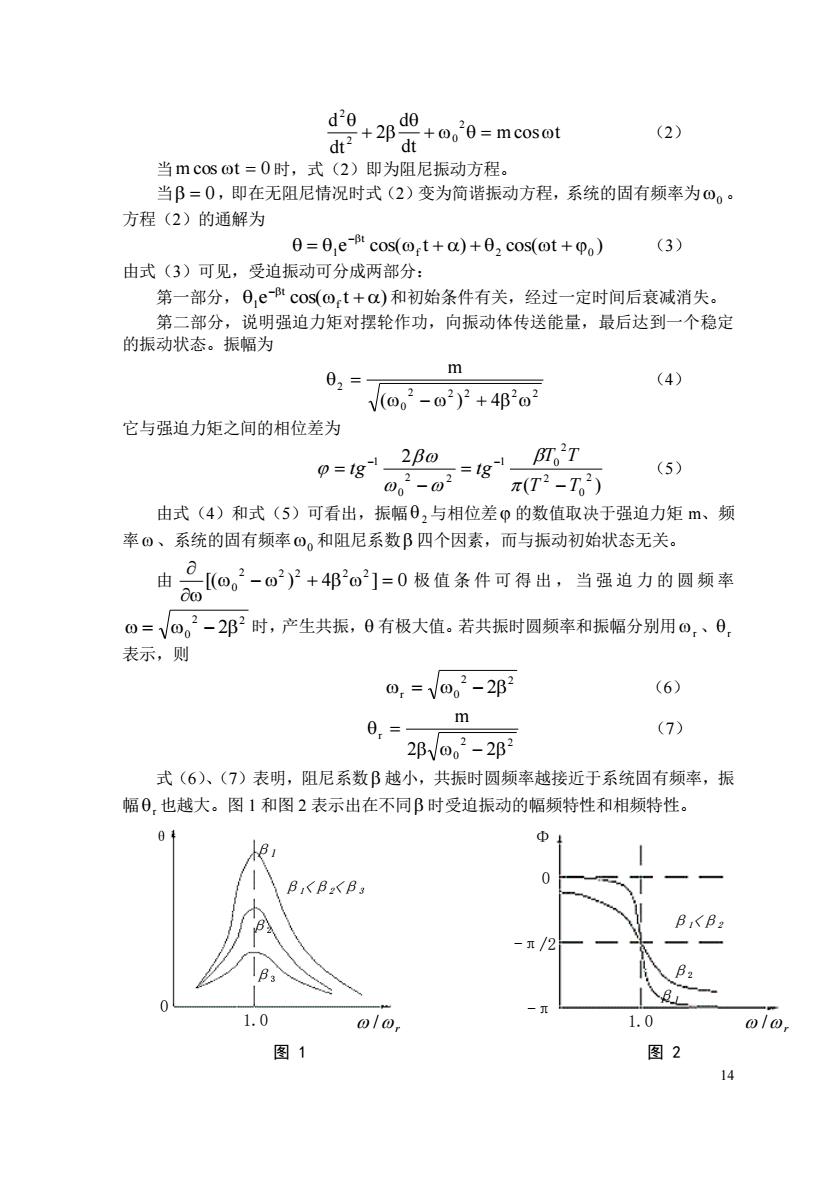
(2) dt 当m cos ot=0时，式(2)即为阻尼振动方程。 当B=0,即在无阻尼情况时式(2)变为简谐振动方程，系统的固有频率为O0· 方程(2)的通解为 日=日，ecos(ot+a)+02cos(ot+po) (3) 由式(3)可见，受迫振动可分成两部分： 第一部分，0，ecos(ot+a)和初始条件有关，经过一定时间后衰减消失。 第二部分，说明强迫力矩对摆轮作功，向振动体传送能量，最后达到一个稳定 的振动状态。振幅为 m 02 (4) V@,2-02y2+4B20 它与强迫力矩之间的相位差为 0,2-02*gm7 0=g12B@ (5) π(T2-T。2) 由式(4)和式(5)可看出，振幅0，与相位差p的数值取决于强迫力矩m、频 率0、系统的固有频率⊙。和阻尼系数B四个因素，而与振动初始状态无关。 品a-+邦0-0极监条件可得出，当强边力的圆频车 由 0=√@。2-2邛2时，产生共振，0有极大值。若共振时圆频率和振幅分别用0，、0， 表示，则 0,=V0,2-2p1 (6) m 0.=- (7) 2邓V02-2B 式(6)、(7)表明，阻尼系数β越小，共振时圆频率越接近于系统固有频率，振 幅0，也越大。图1和图2表示出在不同B时受迫振动的幅频特性和相频特性。 Φ BB2B3 8<B 9 1.0 1.0 图1 图2 1414 mcos t dt d 2 dt d 2 2 0 2 +   =   +   （2） 当 mcos t = 0 时，式（2）即为阻尼振动方程。 当  = 0 ，即在无阻尼情况时式（2）变为简谐振动方程，系统的固有频率为 0 。 方程（2）的通解为 e cos( t ) cos( t ) f 2 0 t  = 1  +  +   +  − （3） 由式（3）可见，受迫振动可分成两部分： 第一部分， e cos( t ) f t 1  +  − 和初始条件有关，经过一定时间后衰减消失。 第二部分，说明强迫力矩对摆轮作功，向振动体传送能量，最后达到一个稳定 的振动状态。振幅为 2 2 2 2 2 0 2 ( ) 4 m  −  +    = （4） 它与强迫力矩之间的相位差为 ( ) 2 2 0 2 2 1 0 2 2 0 1 T T T T tg tg − = − = − −        （5） 由式（4）和式（5）可看出，振幅 2 与相位差  的数值取决于强迫力矩 m、频 率  、系统的固有频率 0 和阻尼系数  四个因素，而与振动初始状态无关。 由 [( ) 4 ] 0 2 2 2 2 2 0 − +   =   极 值 条 件 可 得 出 ， 当 强 迫 力 的 圆 频 率 2 2  = 0 − 2 时，产生共振，  有极大值。若共振时圆频率和振幅分别用 r 、r 表示，则 2 2 r = 0 − 2 （6） 2 2 0 r 2 2 m   −   = （7） 式（6）、（7）表明，阻尼系数  越小，共振时圆频率越接近于系统固有频率，振 幅 r 也越大。图 1 和图 2 表示出在不同  时受迫振动的幅频特性和相频特性。 图 1 图 2   r / β1 β2 β1<β2 -π -π/2 0 Φ 1.0 β1 β2 β3 β1<β2<β3   r 1.0 / θ 0