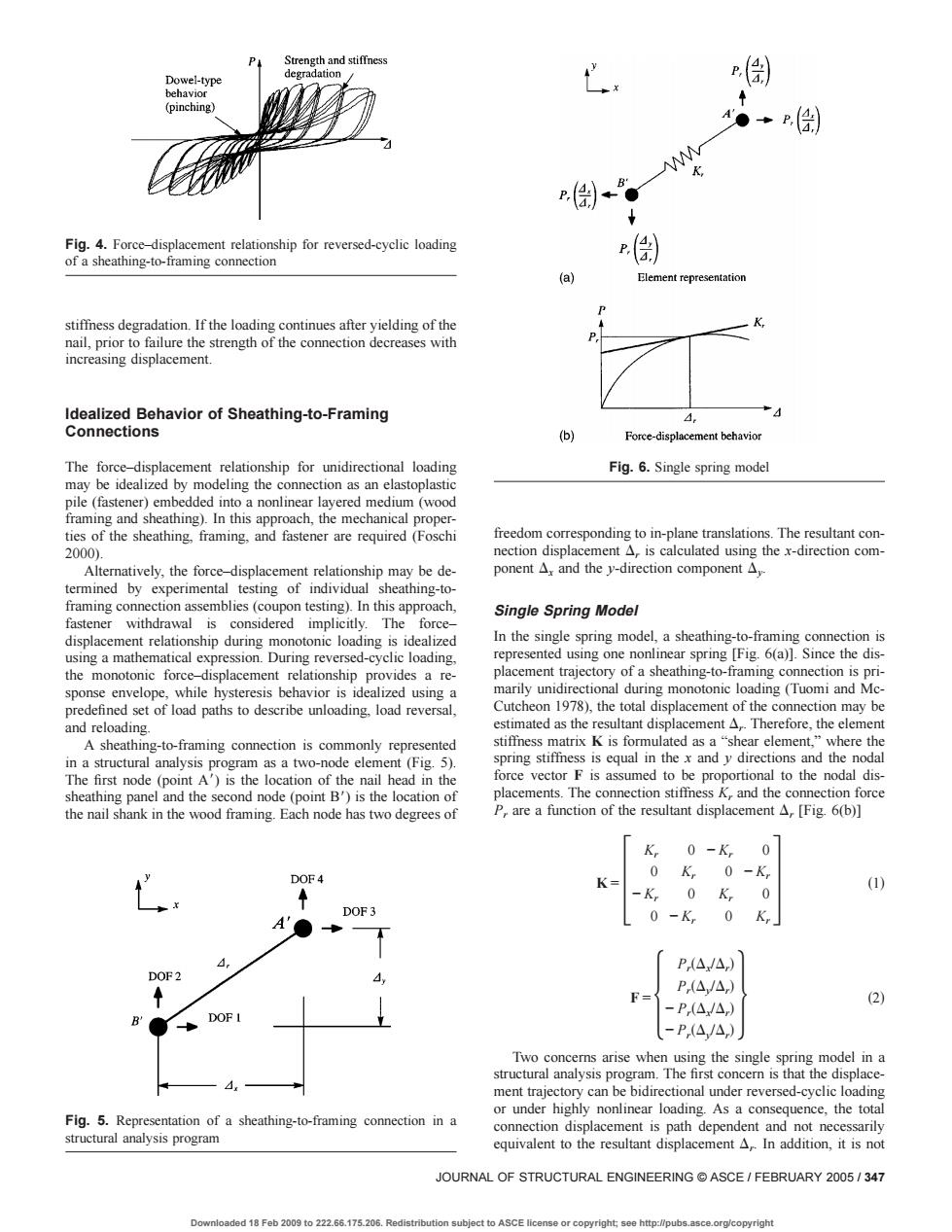
r" a stiftess degradation.If the loading continues after yielding of the &saeioeavorotsheahngofamng (b) Force-displacement behavior The for Fig.6.Single spring model freedom corresponding to in-plane translations.The resultant con 2000) de. framing con considered Single Spring Model .The In the single spring model,a sheathing-to-framing connection is (a)Since the dis hile hy onship provides a re marily unidire and hcathin mattKi5fomulatcdas in a structural analysis d t on the nail shank in the wood framing Each node has two degrees of 、 1 A'● d. [P△△) PIA/A 2) DOF .( -P(/A,) Two concemns arise when structural analysi Fig.5.Representation of a sheathing-to-framing connection in a structural analysis program JOURNAL OF STRUCTURAL ENGINEERINGASCE/FEBRUARY 2005/347 1F62009to22266,17520 ASCEstiffness degradation. If the loading continues after yielding of the nail, prior to failure the strength of the connection decreases with increasing displacement. Idealized Behavior of Sheathing-to-Framing Connections The force–displacement relationship for unidirectional loading may be idealized by modeling the connection as an elastoplastic pile (fastener) embedded into a nonlinear layered medium (wood framing and sheathing). In this approach, the mechanical proper￾ties of the sheathing, framing, and fastener are required (Foschi 2000). Alternatively, the force–displacement relationship may be de￾termined by experimental testing of individual sheathing-to￾framing connection assemblies (coupon testing). In this approach, fastener withdrawal is considered implicitly. The force– displacement relationship during monotonic loading is idealized using a mathematical expression. During reversed-cyclic loading, the monotonic force–displacement relationship provides a re￾sponse envelope, while hysteresis behavior is idealized using a predefined set of load paths to describe unloading, load reversal, and reloading. A sheathing-to-framing connection is commonly represented in a structural analysis program as a two-node element (Fig. 5). The first node (point A8) is the location of the nail head in the sheathing panel and the second node (point B8) is the location of the nail shank in the wood framing. Each node has two degrees of freedom corresponding to in-plane translations. The resultant con￾nection displacement Dr is calculated using the x-direction com￾ponent Dx and the y-direction component Dy. Single Spring Model In the single spring model, a sheathing-to-framing connection is represented using one nonlinear spring [Fig. 6(a)]. Since the dis￾placement trajectory of a sheathing-to-framing connection is pri￾marily unidirectional during monotonic loading (Tuomi and Mc￾Cutcheon 1978), the total displacement of the connection may be estimated as the resultant displacement Dr. Therefore, the element stiffness matrix K is formulated as a “shear element,” where the spring stiffness is equal in the x and y directions and the nodal force vector F is assumed to be proportional to the nodal dis￾placements. The connection stiffness Kr and the connection force Pr are a function of the resultant displacement Dr [Fig. 6(b)] K = 3 Kr 0 − Kr 0 0 Kr 0 − Kr − Kr 0 Kr 0 0 − Kr 0 Kr 4 s1d F = 5 PrsDx/Drd PrsDy/Drd − PrsDx/Drd − PrsDy/Drd 6 s2d Two concerns arise when using the single spring model in a structural analysis program. The first concern is that the displace￾ment trajectory can be bidirectional under reversed-cyclic loading or under highly nonlinear loading. As a consequence, the total connection displacement is path dependent and not necessarily equivalent to the resultant displacement Dr. In addition, it is not Fig. 4. Force–displacement relationship for reversed-cyclic loading of a sheathing-to-framing connection Fig. 5. Representation of a sheathing-to-framing connection in a structural analysis program Fig. 6. Single spring model JOURNAL OF STRUCTURAL ENGINEERING © ASCE / FEBRUARY 2005 / 347 Downloaded 18 Feb 2009 to 222.66.175.206. Redistribution subject to ASCE license or copyright; see http://pubs.asce.org/copyright