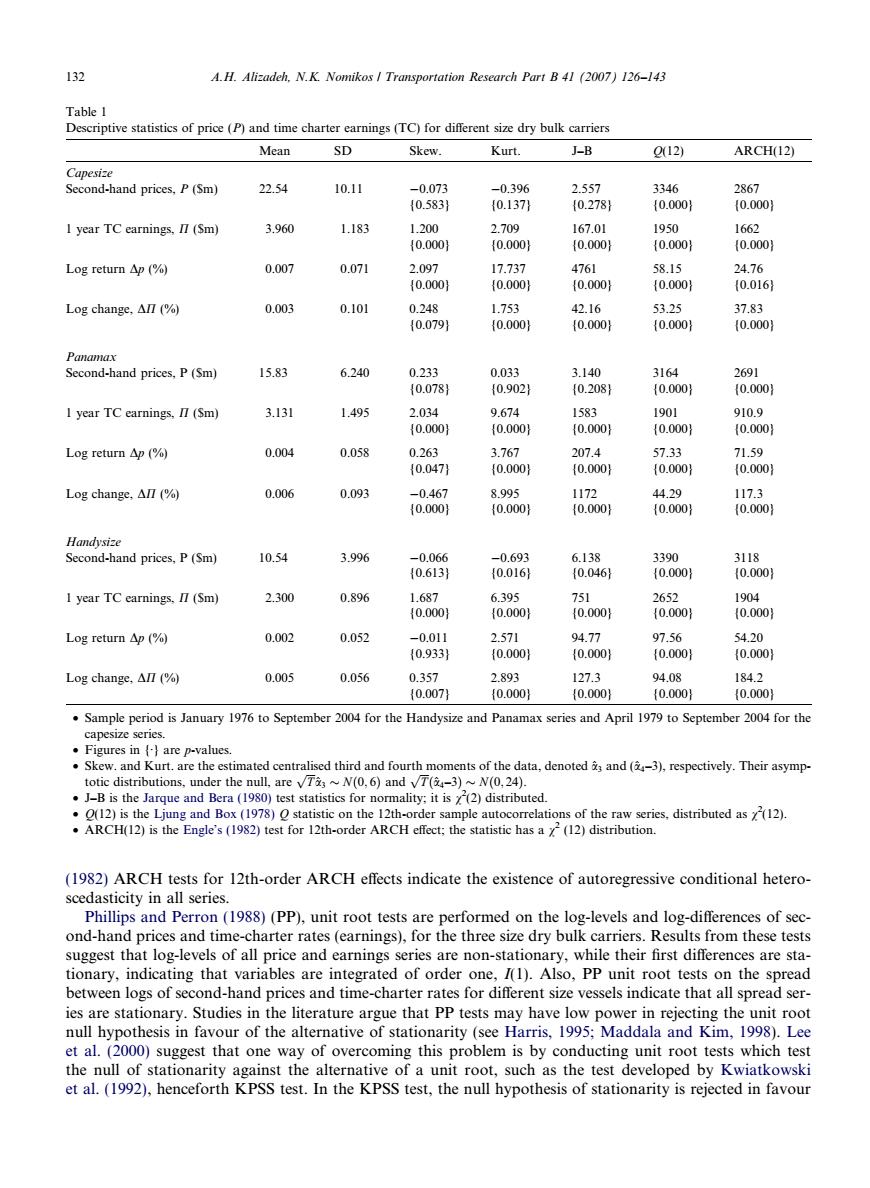
132 A.H.Alizadeh.N.K.Nomikos Transportation Research Part B 41 (2007)126-143 Table1 Descriptive statistics of price (P)and time charter earnings(TC)for different size dry bulk carriers Mean SD Skew Kurt. J-B Q12) ARCH(12) Capesize Second-hand prices,P(Sm) 22.54 10.11 -0.073 -0.396 2.557 3346 2867 {0.583} {0.137} {0.278} {0.0001 {0.0001 I year TC earnings,I(Sm) 3.960 1.183 1.200 2.709 167.01 1950 1662 {0.000 {0.0001 {0.000} {0.0001 (0.0001 Log return△p(o) 0.007 0.071 2.097 17.737 4761 58.15 24.76 {0.000} {0.000} {0.0001 {0.0001 {0.016} Log change,△Π(% 0.003 0.101 0.248 1.753 42.16 53.25 37.83 {0.0791 {0.000} {0.000} {0.0001 {0.000} Panamax Second-hand prices,P(Sm) 15.83 6.240 0.233 0.033 3.140 3164 2691 {0.078} {0.902} {0.208} {0.0001 (0.0001 I year TC earnings.II(Sm) 3.131 1.495 2.034 9.674 1583 1901 910.9 {0.0001 {0.000} {0.000} {0.000} {0.0001 Log return△p(% 0.004 0.058 0.263 3.767 207.4 57.33 71.59 {0.047} {0.000} {0.000} {0.000} {0.0001 Log change,△Ⅱ(y% 0.006 0.093 -0.467 8.995 1172 44.29 117.3 {0.0001 {0.0001 {0.000} {0.000} (0.0001 Handysize Second-hand prices,P(Sm) 10.54 3.996 -0.066 -0.693 6.138 3390 3118 {0.613} {0.016} {0.046} {0.000} (0.0001 1 year TC earnings,I(Sm) 2.300 0.896 1.687 6.395 751 2652 1904 {0.000} {0.0001 {0.000} {0.000} (0.0001 Log return△p(o 0.002 0.052 -0.011 2.571 94.77 97.56 54.20 {0.933} {0.000} {0.000} {0.000} {0.000} Log change,△Ⅱ(yo 0.005 0.056 0.357 2.893 127.3 94.08 184.2 {0.007} {0.0001 {0.0001 {0.0001 {0.0001 Sample period is January 1976 to September 2004 for the Handysize and Panamax series and April 1979 to September 2004 for the capesize series. Figures in are p-values. Skew.and Kurt.are the estimated centralised third and fourth moments of the data,denoted and (-3),respectively.Their asymp- totic distributions,under the null,are vT~N(0,6)and vT(3)~N(0,24). .J-B is the Jarque and Bera(1980)test statistics for normality:it is (2)distributed. .(12)is the Ljung and Box(1978)O statistic on the 12th-order sample autocorrelations of the raw series.distributed as (12). .ARCH(12)is the Engle's(1982)test for 12th-order ARCH effect:the statistic has a(12)distribution. (1982)ARCH tests for 12th-order ARCH effects indicate the existence of autoregressive conditional hetero- scedasticity in all series. Phillips and Perron(1988)(PP),unit root tests are performed on the log-levels and log-differences of sec- ond-hand prices and time-charter rates(earnings),for the three size dry bulk carriers.Results from these tests suggest that log-levels of all price and earnings series are non-stationary,while their first differences are sta- tionary,indicating that variables are integrated of order one,I(1).Also,PP unit root tests on the spread between logs of second-hand prices and time-charter rates for different size vessels indicate that all spread ser- ies are stationary.Studies in the literature argue that PP tests may have low power in rejecting the unit root null hypothesis in favour of the alternative of stationarity (see Harris,1995;Maddala and Kim,1998).Lee et al.(2000)suggest that one way of overcoming this problem is by conducting unit root tests which test the null of stationarity against the alternative of a unit root,such as the test developed by Kwiatkowski et al.(1992),henceforth KPSS test.In the KPSS test,the null hypothesis of stationarity is rejected in favour(1982) ARCH tests for 12th-order ARCH effects indicate the existence of autoregressive conditional hetero￾scedasticity in all series. Phillips and Perron (1988) (PP), unit root tests are performed on the log-levels and log-differences of sec￾ond-hand prices and time-charter rates (earnings), for the three size dry bulk carriers. Results from these tests suggest that log-levels of all price and earnings series are non-stationary, while their first differences are sta￾tionary, indicating that variables are integrated of order one, I(1). Also, PP unit root tests on the spread between logs of second-hand prices and time-charter rates for different size vessels indicate that all spread ser￾ies are stationary. Studies in the literature argue that PP tests may have low power in rejecting the unit root null hypothesis in favour of the alternative of stationarity (see Harris, 1995; Maddala and Kim, 1998). Lee et al. (2000) suggest that one way of overcoming this problem is by conducting unit root tests which test the null of stationarity against the alternative of a unit root, such as the test developed by Kwiatkowski et al. (1992), henceforth KPSS test. In the KPSS test, the null hypothesis of stationarity is rejected in favour Table 1 Descriptive statistics of price (P) and time charter earnings (TC) for different size dry bulk carriers Mean SD Skew. Kurt. J–B Q(12) ARCH(12) Capesize Second-hand prices, P ($m) 22.54 10.11 0.073 0.396 2.557 3346 2867 {0.583} {0.137} {0.278} {0.000} {0.000} 1 year TC earnings, P ($m) 3.960 1.183 1.200 2.709 167.01 1950 1662 {0.000} {0.000} {0.000} {0.000} {0.000} Log return Dp (%) 0.007 0.071 2.097 17.737 4761 58.15 24.76 {0.000} {0.000} {0.000} {0.000} {0.016} Log change, DP (%) 0.003 0.101 0.248 1.753 42.16 53.25 37.83 {0.079} {0.000} {0.000} {0.000} {0.000} Panamax Second-hand prices, P ($m) 15.83 6.240 0.233 0.033 3.140 3164 2691 {0.078} {0.902} {0.208} {0.000} {0.000} 1 year TC earnings, P ($m) 3.131 1.495 2.034 9.674 1583 1901 910.9 {0.000} {0.000} {0.000} {0.000} {0.000} Log return Dp (%) 0.004 0.058 0.263 3.767 207.4 57.33 71.59 {0.047} {0.000} {0.000} {0.000} {0.000} Log change, DP (%) 0.006 0.093 0.467 8.995 1172 44.29 117.3 {0.000} {0.000} {0.000} {0.000} {0.000} Handysize Second-hand prices, P ($m) 10.54 3.996 0.066 0.693 6.138 3390 3118 {0.613} {0.016} {0.046} {0.000} {0.000} 1 year TC earnings, P ($m) 2.300 0.896 1.687 6.395 751 2652 1904 {0.000} {0.000} {0.000} {0.000} {0.000} Log return Dp (%) 0.002 0.052 0.011 2.571 94.77 97.56 54.20 {0.933} {0.000} {0.000} {0.000} {0.000} Log change, DP (%) 0.005 0.056 0.357 2.893 127.3 94.08 184.2 {0.007} {0.000} {0.000} {0.000} {0.000} • Sample period is January 1976 to September 2004 for the Handysize and Panamax series and April 1979 to September 2004 for the capesize series. • Figures in {Æ} are p-values. • Skew. and Kurt. are the estimated centralised third and fourth moments of the data, denoted ^a3 and (^a4–3), respectively. Their asymp￾totic distributions, under the null, are ffiffiffi T p ^a3 Nð0; 6Þ and ffiffiffi T p ð^a4–3Þ Nð0; 24Þ. • J–B is the Jarque and Bera (1980) test statistics for normality; it is v2 (2) distributed. • Q(12) is the Ljung and Box (1978) Q statistic on the 12th-order sample autocorrelations of the raw series, distributed as v2 (12). • ARCH(12) is the Engle’s (1982) test for 12th-order ARCH effect; the statistic has a v2 (12) distribution. 132 A.H. Alizadeh, N.K. Nomikos / Transportation Research Part B 41 (2007) 126–143