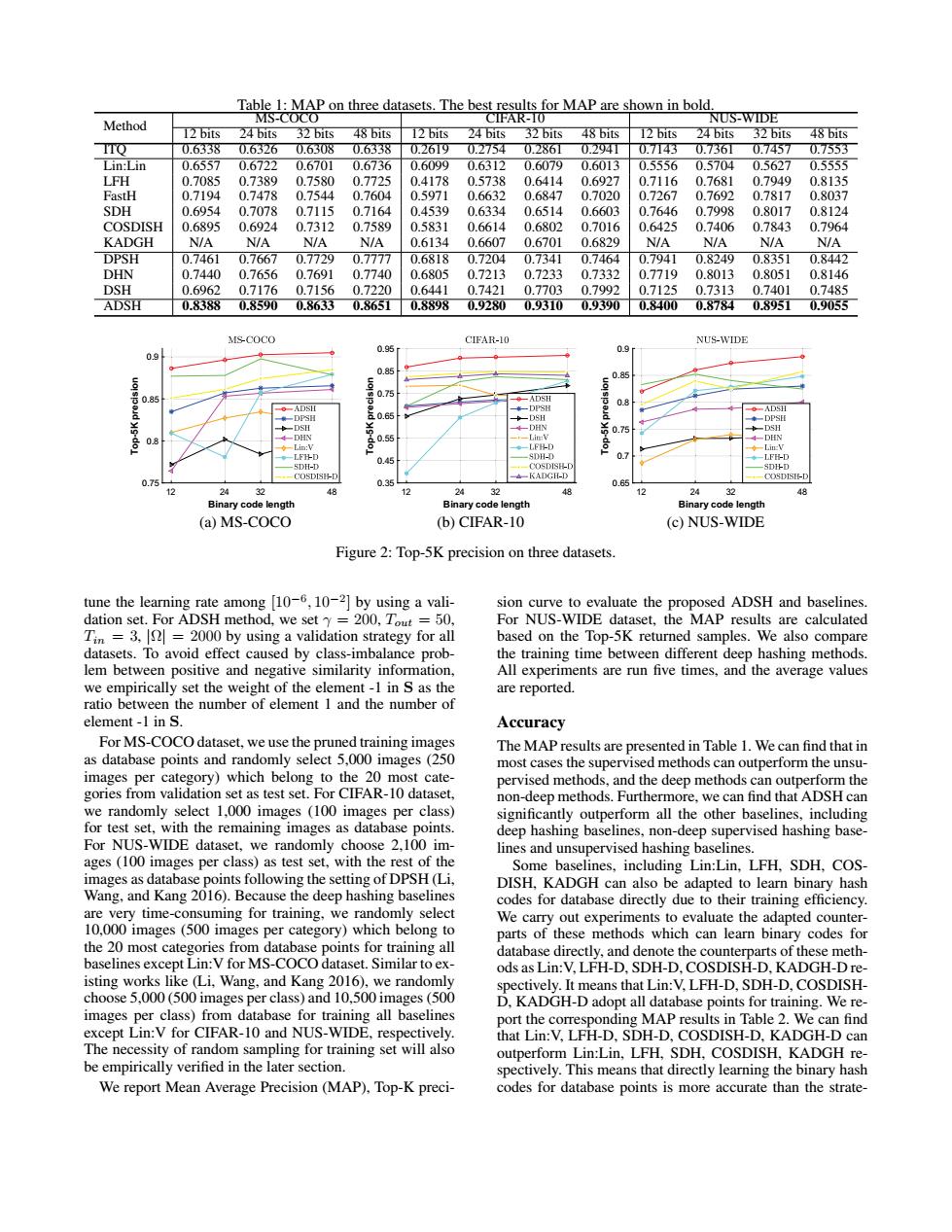
Table 1:MAP on three datasets.The best results for MAP are shown in bold MS-COCO CIFAR-10 NUS-WIDE Method 12 bits 24 bits 32 bits 48 bits 12 bits 24 bits 32bits 48 bits 12 bits 24 bits 32bits 48 bits TTo 0.6338 0.63260.6308 0.6338 0.26I9 0.2754 0.286T 0.294T 0.71430.73610.7457 0.7553 Lin:Lin 0.6557 0.6722 0.6701 0.6736 0.6099 0.6312 0.6079 0.6013 0.5556 0.5704 0.5627 0.5555 LFH 0.7085 0.7389 0.7580 0.7725 0.4178 0.5738 0.6414 0.6927 0.7116 0.7681 0.7949 0.8135 FastH 0.7194 0.7478 0.7544 0.7604 0.5971 0.6632 0.6847 0.7020 0.7267 0.7692 0.7817 0.8037 SDH 0.6954 0.7078 0.7115 0.7164 0.4539 0.6334 0.6514 0.6603 0.7646 0.7998 0.8017 0.8124 COSDISH 0.6895 0.6924 0.7312 0.7589 0.5831 0.6614 0.6802 0.7016 0.6425 0.7406 0.7843 0.7964 KADGH N/A N/A N/A N/A 0.6134 0.6607 0.6701 0.6829 N/A N/A N/A N/A DPSH 0.7461 0.7667 0.7729 0.7777 0.6818 0.7204 0.7341 0.7464 0.7941 0.8249 0.8351 0.8442 DHN 0.7440 0.7656 0.7691 0.7740 0.6805 0.7213 0.7233 0.7332 0.7719 0.8013 0.8051 0.8146 DSH 0.6962 0.7176 0.7156 0.7220 0.6441 0.7421 0.7703 0.7992 0.7125 0.7313 0.7401 0.7485 ADSH 0.8388 0.8590 0.8633 0.8651 0.8898 0.9280 0.9310 0.9390 0.8400 0.8784 0.8951 0.9055 MSCOCO CIFAR-10 NUS-WIDE 0.95 0.9 0.9 0.85 0.85 08 A1 +-DPSI -DHN 0.75 DHN DHN 08 Lin:V ◆。Li 0.45 5H- 0.7 ◆-LFED SDH-I -●05DSFD --KADGH-D -●0SDSF-D 0.75 0.35 0.65 12 24 48 24 A 12 24 32 48 Binary code length Binary code length Binary code length (a)MS-COCO (b)CIFAR-10 (c)NUS-WIDE Figure 2:Top-5K precision on three datasets. tune the learning rate among [10-6,10-2]by using a vali- sion curve to evaluate the proposed ADSH and baselines dation set.For ADSH method,we set y 200,Tout =50, For NUS-WIDE dataset,the MAP results are calculated Tin =3,=2000 by using a validation strategy for all based on the Top-5K returned samples.We also compare datasets.To avoid effect caused by class-imbalance prob- the training time between different deep hashing methods lem between positive and negative similarity information, All experiments are run five times,and the average values we empirically set the weight of the element-1 in S as the are reported. ratio between the number of element 1 and the number of element-1 in S. Accuracy For MS-COCO dataset,we use the pruned training images The MAP results are presented in Table 1.We can find that in as database points and randomly select 5,000 images (250 most cases the supervised methods can outperform the unsu- images per category)which belong to the 20 most cate- pervised methods,and the deep methods can outperform the gories from validation set as test set.For CIFAR-10 dataset, non-deep methods.Furthermore,we can find that ADSH can we randomly select 1,000 images (100 images per class) significantly outperform all the other baselines,including for test set,with the remaining images as database points deep hashing baselines,non-deep supervised hashing base- For NUS-WIDE dataset,we randomly choose 2,100 im- lines and unsupervised hashing baselines. ages(100 images per class)as test set,with the rest of the Some baselines,including Lin:Lin,LFH,SDH,COS- images as database points following the setting of DPSH(Li, DISH.KADGH can also be adapted to learn binary hash Wang,and Kang 2016).Because the deep hashing baselines codes for database directly due to their training efficiency are very time-consuming for training,we randomly select We carry out experiments to evaluate the adapted counter- 10,000 images(500 images per category)which belong to parts of these methods which can learn binary codes for the 20 most categories from database points for training all database directly,and denote the counterparts of these meth- baselines except Lin:V for MS-COCO dataset.Similar to ex- ods as Lin:V,LFH-D,SDH-D,COSDISH-D,KADGH-Dre- isting works like (Li,Wang,and Kang 2016),we randomly spectively.It means that Lin:V,LFH-D,SDH-D,COSDISH- choose 5,000(500 images per class)and 10,500 images(500 D.KADGH-D adopt all database points for training.We re- images per class)from database for training all baselines port the corresponding MAP results in Table 2.We can find except Lin:V for CIFAR-10 and NUS-WIDE,respectively. that Lin:V,LFH-D,SDH-D,COSDISH-D,KADGH-D can The necessity of random sampling for training set will also outperform Lin:Lin,LFH,SDH,COSDISH,KADGH re- be empirically verified in the later section. spectively.This means that directly learning the binary hash We report Mean Average Precision(MAP),Top-K preci- codes for database points is more accurate than the strate-Table 1: MAP on three datasets. The best results for MAP are shown in bold. Method MS-COCO CIFAR-10 NUS-WIDE 12 bits 24 bits 32 bits 48 bits 12 bits 24 bits 32 bits 48 bits 12 bits 24 bits 32 bits 48 bits ITQ 0.6338 0.6326 0.6308 0.6338 0.2619 0.2754 0.2861 0.2941 0.7143 0.7361 0.7457 0.7553 Lin:Lin 0.6557 0.6722 0.6701 0.6736 0.6099 0.6312 0.6079 0.6013 0.5556 0.5704 0.5627 0.5555 LFH 0.7085 0.7389 0.7580 0.7725 0.4178 0.5738 0.6414 0.6927 0.7116 0.7681 0.7949 0.8135 FastH 0.7194 0.7478 0.7544 0.7604 0.5971 0.6632 0.6847 0.7020 0.7267 0.7692 0.7817 0.8037 SDH 0.6954 0.7078 0.7115 0.7164 0.4539 0.6334 0.6514 0.6603 0.7646 0.7998 0.8017 0.8124 COSDISH 0.6895 0.6924 0.7312 0.7589 0.5831 0.6614 0.6802 0.7016 0.6425 0.7406 0.7843 0.7964 KADGH N/A N/A N/A N/A 0.6134 0.6607 0.6701 0.6829 N/A N/A N/A N/A DPSH 0.7461 0.7667 0.7729 0.7777 0.6818 0.7204 0.7341 0.7464 0.7941 0.8249 0.8351 0.8442 DHN 0.7440 0.7656 0.7691 0.7740 0.6805 0.7213 0.7233 0.7332 0.7719 0.8013 0.8051 0.8146 DSH 0.6962 0.7176 0.7156 0.7220 0.6441 0.7421 0.7703 0.7992 0.7125 0.7313 0.7401 0.7485 ADSH 0.8388 0.8590 0.8633 0.8651 0.8898 0.9280 0.9310 0.9390 0.8400 0.8784 0.8951 0.9055 Binary code length 12 24 32 48 Top-5K precision 0.75 0.8 0.85 0.9 (a) MS-COCO Binary code length 12 24 32 48 Top-5K precision 0.35 0.45 0.55 0.65 0.75 0.85 0.95 (b) CIFAR-10 Binary code length 12 24 32 48 Top-5K precision 0.65 0.7 0.75 0.8 0.85 0.9 (c) NUS-WIDE Figure 2: Top-5K precision on three datasets. tune the learning rate among [10−6 , 10−2 ] by using a vali￾dation set. For ADSH method, we set γ = 200, Tout = 50, Tin = 3, |Ω| = 2000 by using a validation strategy for all datasets. To avoid effect caused by class-imbalance prob￾lem between positive and negative similarity information, we empirically set the weight of the element -1 in S as the ratio between the number of element 1 and the number of element -1 in S. For MS-COCO dataset, we use the pruned training images as database points and randomly select 5,000 images (250 images per category) which belong to the 20 most cate￾gories from validation set as test set. For CIFAR-10 dataset, we randomly select 1,000 images (100 images per class) for test set, with the remaining images as database points. For NUS-WIDE dataset, we randomly choose 2,100 im￾ages (100 images per class) as test set, with the rest of the images as database points following the setting of DPSH (Li, Wang, and Kang 2016). Because the deep hashing baselines are very time-consuming for training, we randomly select 10,000 images (500 images per category) which belong to the 20 most categories from database points for training all baselines except Lin:V for MS-COCO dataset. Similar to ex￾isting works like (Li, Wang, and Kang 2016), we randomly choose 5,000 (500 images per class) and 10,500 images (500 images per class) from database for training all baselines except Lin:V for CIFAR-10 and NUS-WIDE, respectively. The necessity of random sampling for training set will also be empirically verified in the later section. We report Mean Average Precision (MAP), Top-K preci￾sion curve to evaluate the proposed ADSH and baselines. For NUS-WIDE dataset, the MAP results are calculated based on the Top-5K returned samples. We also compare the training time between different deep hashing methods. All experiments are run five times, and the average values are reported. Accuracy The MAP results are presented in Table 1. We can find that in most cases the supervised methods can outperform the unsu￾pervised methods, and the deep methods can outperform the non-deep methods. Furthermore, we can find that ADSH can significantly outperform all the other baselines, including deep hashing baselines, non-deep supervised hashing base￾lines and unsupervised hashing baselines. Some baselines, including Lin:Lin, LFH, SDH, COS￾DISH, KADGH can also be adapted to learn binary hash codes for database directly due to their training efficiency. We carry out experiments to evaluate the adapted counter￾parts of these methods which can learn binary codes for database directly, and denote the counterparts of these meth￾ods as Lin:V, LFH-D, SDH-D, COSDISH-D, KADGH-D re￾spectively. It means that Lin:V, LFH-D, SDH-D, COSDISH￾D, KADGH-D adopt all database points for training. We re￾port the corresponding MAP results in Table 2. We can find that Lin:V, LFH-D, SDH-D, COSDISH-D, KADGH-D can outperform Lin:Lin, LFH, SDH, COSDISH, KADGH re￾spectively. This means that directly learning the binary hash codes for database points is more accurate than the strate-