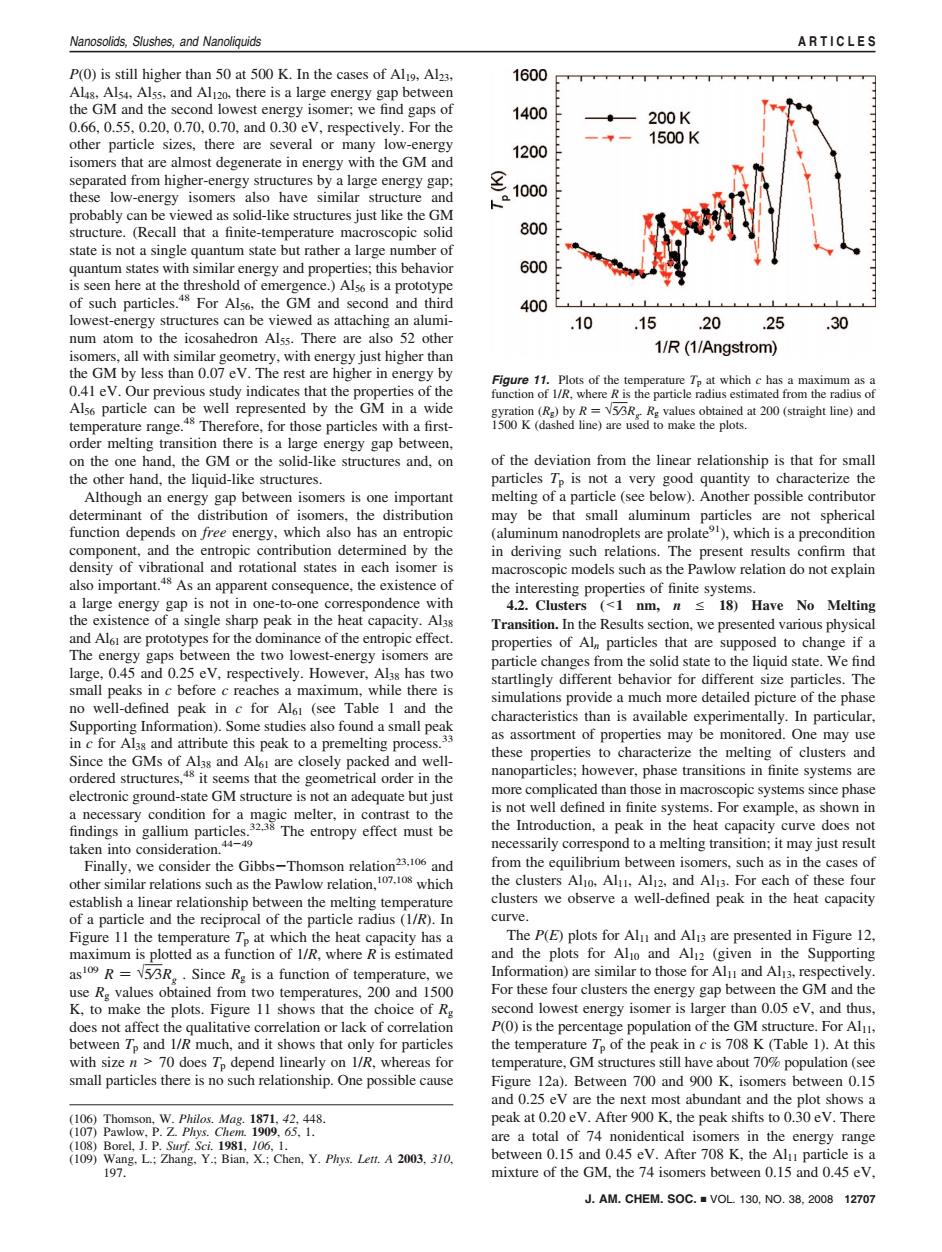
Nanosolids,Slushes,and Nanoliquids ARTICLES P(0)is still higher than 50 at 500 K.In the cases of Al9,Al23. 1600 Alis.Als4.Alss,and Al120.there is a large energy gap between the GM and the second lowest energy isomer;we find gaps of 1400 0.66,0.55,0.20,0.70,0.70,and 0.30 eV,respectively.For the 200K other particle sizes,there are several or many low-energy 1500K 1200 isomers that are almost degenerate in energy with the GM and separated from higher-energy structures by a large energy gap: these low-energy isomers also have similar structure and 1000 人。】 probably can be viewed as solid-like structures just like the GM structure.(Recall that a finite-temperature macroscopic solid 800 state is not a single quantum state but rather a large number of quantum states with similar energy and properties;this behavior 600 is seen here at the threshold of emergence.)Als6 is a prototype of such particles.48 For Als6.the GM and second and third 400 lowest-energy structures can be viewed as attaching an alumi- 10 .15 .20 .25 .30 num atom to the icosahedron Alss.There are also 52 other isomers,all with similar geometry,with energy just higher than 1/R(1/Angstrom) the GM by less than 0.07 eV.The rest are higher in energy by Figure 11.Plots of the temperature Tp at which c has a maximum as a 0.41 eV.Our previous study indicates that the properties of the function of 1/R,where R is the particle radius estimated from the radius of Als6 particle can be well represented by the GM in a wide gyration(Rg)by R=V53R Rg values obtained at 200(straight line)and temperature range.Therefore,for those particles with a first- 1500 K (dashed line)are used to make the plots. order melting transition there is a large energy gap between, on the one hand,the GM or the solid-like structures and,on of the deviation from the linear relationship is that for small the other hand,the liquid-like structures. particles Tp is not a very good quantity to characterize the Although an energy gap between isomers is one important melting of a particle (see below).Another possible contributor determinant of the distribution of isomers,the distribution may be that small aluminum particles are not spherical function depends on free energy,which also has an entropic (aluminum nanodroplets are prolate),which is a precondition component,and the entropic contribution determined by the in deriving such relations.The present results confirm that density of vibrational and rotational states in each isomer is macroscopic models such as the Pawlow relation do not explain also important.48 As an apparent consequence,the existence of the interesting properties of finite systems. a large energy gap is not in one-to-one correspondence with 4.2.Clusters (<1 nm,n s 18)Have No Melting the existence of a single sharp peak in the heat capacity.Al3s Transition.In the Results section,we presented various physical and Al61 are prototypes for the dominance of the entropic effect. properties of Alm particles that are supposed to change if a The energy gaps between the two lowest-energy isomers are particle changes from the solid state to the liquid state.We find large,0.45 and 0.25 eV,respectively.However,Al3s has two startlingly different behavior for different size particles.The small peaks in c before c reaches a maximum,while there is simulations provide a much more detailed picture of the phase no well-defined peak in c for Al1 (see Table 1 and the characteristics than is available experimentally.In particular. Supporting Information).Some studies also found a small peak in c for Alss and attribute this peak to a premelting process.33 as assortment of properties may be monitored.One may use Since the GMs of Al3s and Al61 are closely packed and well- these properties to characterize the melting of clusters and ordered structures,48 it seems that the geometrical order in the nanoparticles;however,phase transitions in finite systems are electronic ground-state GM structure is not an adequate but just more complicated than those in macroscopic systems since phase a necessary condition for a magic melter,in contrast to the is not well defined in finite systems.For example,as shown in findings in gallium particles.32 The entropy effect must be the Introduction,a peak in the heat capacity curve does not taken into consideration.44-49 necessarily correspond to a melting transition:it may just result Finally,we consider the Gibbs-Thomson relation23.106 and from the equilibrium between isomers,such as in the cases of other similar relations such as the Pawlow relation,1070 which the clusters Aljo,Alu,Alj2,and Al13.For each of these four establish a linear relationship between the melting temperature clusters we observe a well-defined peak in the heat capacity of a particle and the reciprocal of the particle radius (1/R).In curve. Figure 11 the temperature Tp at which the heat capacity has a The P(E)plots for Alu and Alj3 are presented in Figure 12, maximum is plotted as a function of 1/R,where R is estimated and the plots for Alo and Al2 (given in the Supporting as109 R=153R.Since Re is a function of temperature,we Information)are similar to those for Alu and Al13,respectively. use Rg values obtained from two temperatures,200 and 1500 For these four clusters the energy gap between the GM and the K,to make the plots.Figure 11 shows that the choice of Rg second lowest energy isomer is larger than 0.05 eV,and thus, does not affect the qualitative correlation or lack of correlation P(0)is the percentage population of the GM structure.For Al, between Tp and 1/R much,and it shows that only for particles the temperature Tp of the peak in c is 708 K (Table 1).At this with size n >70 does Tp depend linearly on I/R,whereas for temperature,GM structures still have about 70%population(see small particles there is no such relationship.One possible cause Figure 12a).Between 700 and 900 K,isomers between 0.15 and 0.25 eV are the next most abundant and the plot shows a (106)Thomson,W.Philos.Mag.1871,42,448 peak at 0.20 eV.After 900 K,the peak shifts to 0.30 eV.There (107)Pawlow.P.Z.Phys.Chem.1909.65.1. (108)Borel,J.P.Suf.Sci.1981,106,1. are a total of 74 nonidentical isomers in the energy range (109)Wang,L.;Zhang,Y.;Bian,X.:Chen,Y.Phys.Lett.A 2003,310, between 0.15 and 0.45 eV.After 708 K,the Alu particle is a 197. mixture of the GM,the 74 isomers between 0.15 and 0.45 eV, J.AM.CHEM.SOC.VOL 130,NO.38,2008 12707P(0) is still higher than 50 at 500 K. In the cases of Al19, Al23, Al48, Al54, Al55, and Al120, there is a large energy gap between the GM and the second lowest energy isomer; we find gaps of 0.66, 0.55, 0.20, 0.70, 0.70, and 0.30 eV, respectively. For the other particle sizes, there are several or many low-energy isomers that are almost degenerate in energy with the GM and separated from higher-energy structures by a large energy gap; these low-energy isomers also have similar structure and probably can be viewed as solid-like structures just like the GM structure. (Recall that a finite-temperature macroscopic solid state is not a single quantum state but rather a large number of quantum states with similar energy and properties; this behavior is seen here at the threshold of emergence.) Al56 is a prototype of such particles.48 For Al56, the GM and second and third lowest-energy structures can be viewed as attaching an alumi￾num atom to the icosahedron Al55. There are also 52 other isomers, all with similar geometry, with energy just higher than the GM by less than 0.07 eV. The rest are higher in energy by 0.41 eV. Our previous study indicates that the properties of the Al56 particle can be well represented by the GM in a wide temperature range.48 Therefore, for those particles with a first￾order melting transition there is a large energy gap between, on the one hand, the GM or the solid-like structures and, on the other hand, the liquid-like structures. Although an energy gap between isomers is one important determinant of the distribution of isomers, the distribution function depends on free energy, which also has an entropic component, and the entropic contribution determined by the density of vibrational and rotational states in each isomer is also important.48 As an apparent consequence, the existence of a large energy gap is not in one-to-one correspondence with the existence of a single sharp peak in the heat capacity. Al38 and Al61 are prototypes for the dominance of the entropic effect. The energy gaps between the two lowest-energy isomers are large, 0.45 and 0.25 eV, respectively. However, Al38 has two small peaks in c before c reaches a maximum, while there is no well-defined peak in c for Al61 (see Table 1 and the Supporting Information). Some studies also found a small peak in c for Al38 and attribute this peak to a premelting process.33 Since the GMs of Al38 and Al61 are closely packed and well￾ordered structures,48 it seems that the geometrical order in the electronic ground-state GM structure is not an adequate but just a necessary condition for a magic melter, in contrast to the findings in gallium particles.32,38 The entropy effect must be taken into consideration.44-49 Finally, we consider the Gibbs-Thomson relation23,106 and other similar relations such as the Pawlow relation,107,108 which establish a linear relationship between the melting temperature of a particle and the reciprocal of the particle radius (1/R). In Figure 11 the temperature Tp at which the heat capacity has a maximum is plotted as a function of 1/R, where R is estimated as109 R ) √5⁄3Rg . Since Rg is a function of temperature, we use Rg values obtained from two temperatures, 200 and 1500 K, to make the plots. Figure 11 shows that the choice of Rg does not affect the qualitative correlation or lack of correlation between Tp and 1/R much, and it shows that only for particles with size n > 70 does Tp depend linearly on 1/R, whereas for small particles there is no such relationship. One possible cause of the deviation from the linear relationship is that for small particles Tp is not a very good quantity to characterize the melting of a particle (see below). Another possible contributor may be that small aluminum particles are not spherical (aluminum nanodroplets are prolate91), which is a precondition in deriving such relations. The present results confirm that macroscopic models such as the Pawlow relation do not explain the interesting properties of finite systems. 4.2. Clusters (<1 nm, n e 18) Have No Melting Transition. In the Results section, we presented various physical properties of Aln particles that are supposed to change if a particle changes from the solid state to the liquid state. We find startlingly different behavior for different size particles. The simulations provide a much more detailed picture of the phase characteristics than is available experimentally. In particular, as assortment of properties may be monitored. One may use these properties to characterize the melting of clusters and nanoparticles; however, phase transitions in finite systems are more complicated than those in macroscopic systems since phase is not well defined in finite systems. For example, as shown in the Introduction, a peak in the heat capacity curve does not necessarily correspond to a melting transition; it may just result from the equilibrium between isomers, such as in the cases of the clusters Al10, Al11, Al12, and Al13. For each of these four clusters we observe a well-defined peak in the heat capacity curve. The P(E) plots for Al11 and Al13 are presented in Figure 12, and the plots for Al10 and Al12 (given in the Supporting Information) are similar to those for Al11 and Al13, respectively. For these four clusters the energy gap between the GM and the second lowest energy isomer is larger than 0.05 eV, and thus, P(0) is the percentage population of the GM structure. For Al11, the temperature Tp of the peak in c is 708 K (Table 1). At this temperature, GM structures still have about 70% population (see Figure 12a). Between 700 and 900 K, isomers between 0.15 and 0.25 eV are the next most abundant and the plot shows a peak at 0.20 eV. After 900 K, the peak shifts to 0.30 eV. There are a total of 74 nonidentical isomers in the energy range between 0.15 and 0.45 eV. After 708 K, the Al11 particle is a mixture of the GM, the 74 isomers between 0.15 and 0.45 eV, (106) Thomson, W. Philos. Mag. 1871, 42, 448. (107) Pawlow, P. Z. Phys. Chem. 1909, 65, 1. (108) Borel, J. P. Surf. Sci. 1981, 106, 1. (109) Wang, L.; Zhang, Y.; Bian, X.; Chen, Y. Phys. Lett. A 2003, 310, 197. Figure 11. Plots of the temperature Tp at which c has a maximum as a function of 1/R, where R is the particle radius estimated from the radius of gyration (Rg) by R ) √5⁄3Rg. Rg values obtained at 200 (straight line) and 1500 K (dashed line) are used to make the plots. J. AM. CHEM. SOC. 9 VOL. 130, NO. 38, 2008 12707 Nanosolids, Slushes, and Nanoliquids ARTICLES