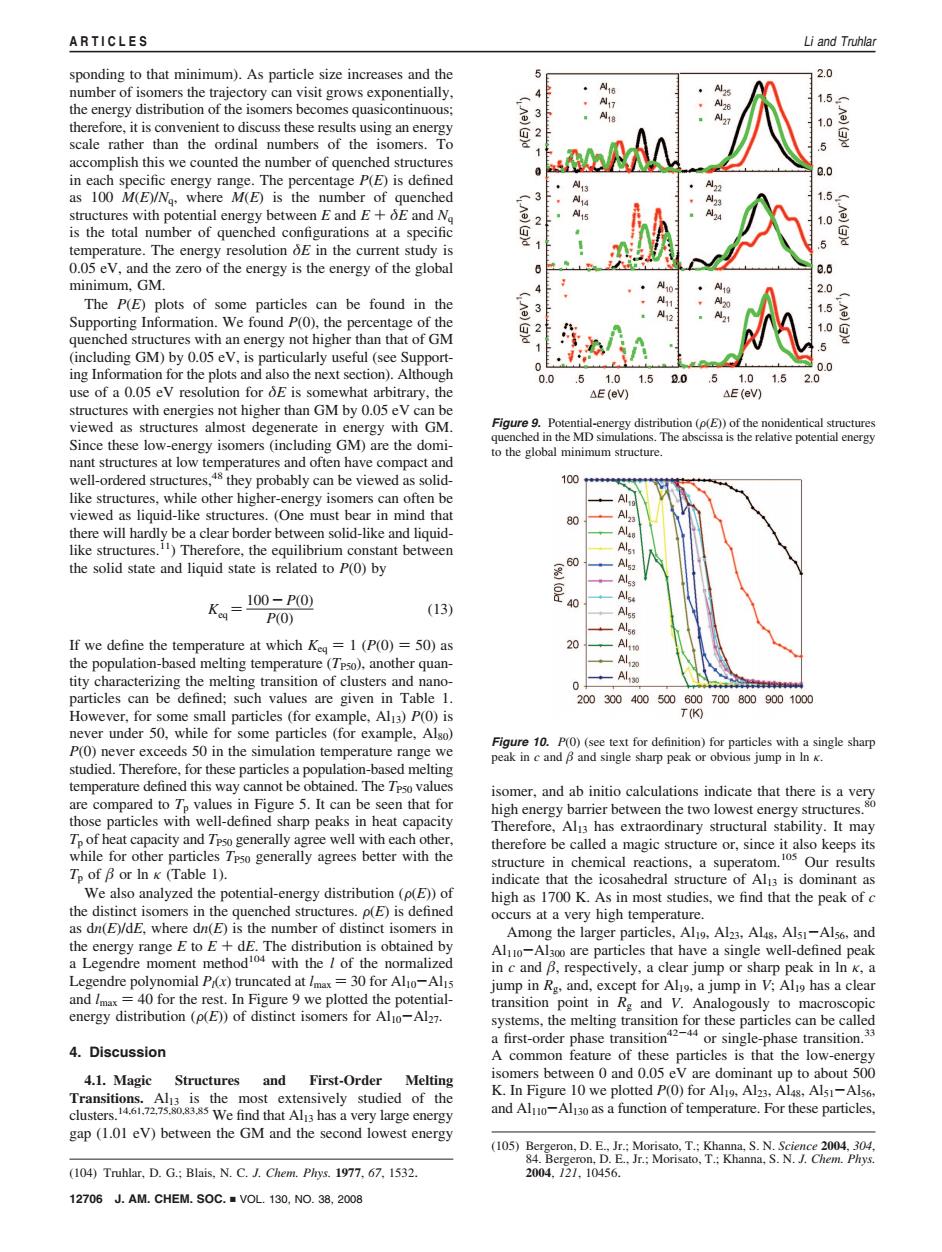
ARTICLES Li and Truhlar sponding to that minimum).As particle size increases and the 2.0 number of isomers the trajectory can visit grows exponentially, A 1.5 the energy distribution of the isomers becomes quasicontinuous; therefore,it is convenient to discuss these results using an energy A27 (Ae)(3)d scale rather than the ordinal numbers of the isomers.To 5 accomplish this we counted the number of quenched structures 0,0 in each specific energy range.The percentage P(E)is defined as 100 M(E)/Ng.where M(E)is the number of quenched 1.5 structures with potential energy between E and E+OE and Na 1.0 is the total number of quenched configurations at a specific g temperature.The energy resolution oE in the current study is 0.05 ev,and the zero of the energy is the energy of the global 0.6 minimum,GM. 2.0 The P(E)plots of some particles can be found in the 1.5 Supporting Information.We found P(0),the percentage of the 1.0 quenched structures with an energy not higher than that of GM 5 (including GM)by 0.05 eV,is particularly useful(see Support- 0.0 ing Information for the plots and also the next section).Although 0.0 5 1.0 1.5 0 .5 1,0 1.5 2.0 use of a 0.05 eV resolution for E is somewhat arbitrary,the △E(eV) AE(ev) structures with energies not higher than GM by 0.05 eV can be viewed as structures almost degenerate in energy with GM. Figure 9.Potential-energy distribution (p(E))of the nonidentical structures Since these low-energy isomers(including GM)are the domi- quenched in the MD simulations.The abscissa is the relative potential energy to the global minimum structure. nant structures at low temperatures and often have compact and well-ordered structures,48 they probably can be viewed as solid- 100 like structures,while other higher-energy isomers can often be viewed as liquid-like structures.(One must bear in mind that there will hardly be a clear border between solid-like and liquid- Al like structures.)Therefore,the equilibrium constant between Alst the solid state and liquid state is related to P(0)by Als K=100-P0 Alsa (13) P(O) Alss Alsn If we define the temperature at which Keg =1 (P(0)=50)as 20 Alto the population-based melting temperature (Tpso),another quan- Al2 tity characterizing the melting transition of clusters and nano- 0 。444 particles can be defined;such values are given in Table 1. 2003004005006007008009001000 However,for some small particles (for example,Alj3)P(O)is T(9 never under 50,while for some particles (for example,Also) P(0)never exceeds 50 in the simulation temperature range we Figure 10.P(O)(see text for definition)for particles with a single sharp peak in c and B and single sharp peak or obvious jump inIn K. studied.Therefore,for these particles a population-based melting temperature defined this way cannot be obtained.The Tpso values isomer,and ab initio calculations indicate that there is a very are compared to Tp values in Figure 5.It can be seen that for high energy barrier between the two lowest energy structures. those particles with well-defined sharp peaks in heat capacity Therefore,Al3 has extraordinary structural stability.It may Tp of heat capacity and Tpso generally agree well with each other, therefore be called a magic structure or,since it also keeps its while for other particles Tpso generally agrees better with the structure in chemical reactions,a superatom.s Our results Tp of B or In k (Table 1). indicate that the icosahedral structure of Al 3 is dominant as We also analyzed the potential-energy distribution (p(E))of high as 1700 K.As in most studies,we find that the peak of c the distinct isomers in the quenched structures.p(E)is defined occurs at a very high temperature. as dn(E)/dE.where dn(E)is the number of distinct isomers in Among the larger particles,Al19.Al23.Al48,Alsi-Als6,and the energy range E to E+dE.The distribution is obtained by Aluo-Al300 are particles that have a single well-defined peak a Legendre moment method'04 with the of the normalized in c and B,respectively,a clear jump or sharp peak in In k,a Legendre polynomial Px)truncated at /max=30 for Alo-Alis jump in Rg,and,except for Al9,a jump in V:Al9 has a clear and /max=40 for the rest.In Figure 9 we plotted the potential- transition point in Rg and V.Analogously to macroscopic energy distribution(p(E))of distinct isomers for Alo-Al27. systems,the melting transition for these particles can be called a first-order phase transition4 or single-phase transition.3 4.Discussion A common feature of these particles is that the low-energy 4.1.Magic Structures and First-Order Melting isomers between 0 and 0.05 eV are dominant up to about 500 Transitions.Al13 is the most extensively studied of the K.In Figure 10 we plotted P(0)for Al9,Al23,Al48,Als1-Al56, clusters.14.61.72.75.80.83.85 We find that Al3 has a very large energy and Aluo-Al13o as a function of temperature.For these particles, gap(1.01 ev)between the GM and the second lowest energy (105)Bergeron,D.E..Jr.;Morisato,T.:Khanna,S.N.Science 2004,304, 84.Bergeron,D.E..Jr.;Morisato,T.:Khanna,S.N.J.Chem.Phys. (104)Truhlar,D.G.;Blais,N.C.J.Chem.Plrys.1977,67,1532. 2004,121,10456. 12706J.AM.CHEM.S0C.■VOL.130,NO.38,2008sponding to that minimum). As particle size increases and the number of isomers the trajectory can visit grows exponentially, the energy distribution of the isomers becomes quasicontinuous; therefore, it is convenient to discuss these results using an energy scale rather than the ordinal numbers of the isomers. To accomplish this we counted the number of quenched structures in each specific energy range. The percentage P(E) is defined as 100 M(E)/Nq, where M(E) is the number of quenched structures with potential energy between E and E + δE and Nq is the total number of quenched configurations at a specific temperature. The energy resolution δE in the current study is 0.05 eV, and the zero of the energy is the energy of the global minimum, GM. The P(E) plots of some particles can be found in the Supporting Information. We found P(0), the percentage of the quenched structures with an energy not higher than that of GM (including GM) by 0.05 eV, is particularly useful (see Support￾ing Information for the plots and also the next section). Although use of a 0.05 eV resolution for δE is somewhat arbitrary, the structures with energies not higher than GM by 0.05 eV can be viewed as structures almost degenerate in energy with GM. Since these low-energy isomers (including GM) are the domi￾nant structures at low temperatures and often have compact and well-ordered structures,48 they probably can be viewed as solid￾like structures, while other higher-energy isomers can often be viewed as liquid-like structures. (One must bear in mind that there will hardly be a clear border between solid-like and liquid￾like structures.11) Therefore, the equilibrium constant between the solid state and liquid state is related to P(0) by Keq ) 100 - P(0) P(0) (13) If we define the temperature at which Keq ) 1 (P(0) ) 50) as the population-based melting temperature (TP50), another quan￾tity characterizing the melting transition of clusters and nano￾particles can be defined; such values are given in Table 1. However, for some small particles (for example, Al13) P(0) is never under 50, while for some particles (for example, Al80) P(0) never exceeds 50 in the simulation temperature range we studied. Therefore, for these particles a population-based melting temperature defined this way cannot be obtained. The TP50 values are compared to Tp values in Figure 5. It can be seen that for those particles with well-defined sharp peaks in heat capacity Tp of heat capacity and TP50 generally agree well with each other, while for other particles TP50 generally agrees better with the Tp of
or ln κ (Table 1). We also analyzed the potential-energy distribution (F(E)) of the distinct isomers in the quenched structures. F(E) is defined as dn(E)/dE, where dn(E) is the number of distinct isomers in the energy range E to E + dE. The distribution is obtained by a Legendre moment method104 with the l of the normalized Legendre polynomial Pl(x) truncated at lmax ) 30 for Al10-Al15 and lmax ) 40 for the rest. In Figure 9 we plotted the potential￾energy distribution (F(E)) of distinct isomers for Al10-Al27. 4. Discussion 4.1. Magic Structures and First-Order Melting Transitions. Al13 is the most extensively studied of the clusters.14,61,72,75,80,83,85 We find that Al13 has a very large energy gap (1.01 eV) between the GM and the second lowest energy isomer, and ab initio calculations indicate that there is a very high energy barrier between the two lowest energy structures.80 Therefore, Al13 has extraordinary structural stability. It may therefore be called a magic structure or, since it also keeps its structure in chemical reactions, a superatom.105 Our results indicate that the icosahedral structure of Al13 is dominant as high as 1700 K. As in most studies, we find that the peak of c occurs at a very high temperature. Among the larger particles, Al19, Al23, Al48, Al51-Al56, and Al110-Al300 are particles that have a single well-defined peak in c and
, respectively, a clear jump or sharp peak in ln κ, a jump in Rg, and, except for Al19, a jump in V; Al19 has a clear transition point in Rg and V. Analogously to macroscopic systems, the melting transition for these particles can be called a first-order phase transition42-44 or single-phase transition.33 A common feature of these particles is that the low-energy isomers between 0 and 0.05 eV are dominant up to about 500 K. In Figure 10 we plotted P(0) for Al19, Al23, Al48, Al51-Al56, and Al110-Al130 as a function of temperature. For these particles, (104) Truhlar, D. G.; Blais, N. C. J. Chem. Phys. 1977, 67, 1532. (105) Bergeron, D. E., Jr.; Morisato, T.; Khanna, S. N. Science 2004, 304, 84. Bergeron, D. E., Jr.; Morisato, T.; Khanna, S. N. J. Chem. Phys. 2004, 121, 10456. Figure 9. Potential-energy distribution (F(E)) of the nonidentical structures quenched in the MD simulations. The abscissa is the relative potential energy to the global minimum structure. Figure 10. P(0) (see text for definition) for particles with a single sharp peak in c and
and single sharp peak or obvious jump in ln κ. 12706 J. AM. CHEM. SOC. 9 VOL. 130, NO. 38, 2008 ARTICLES Li and Truhlar