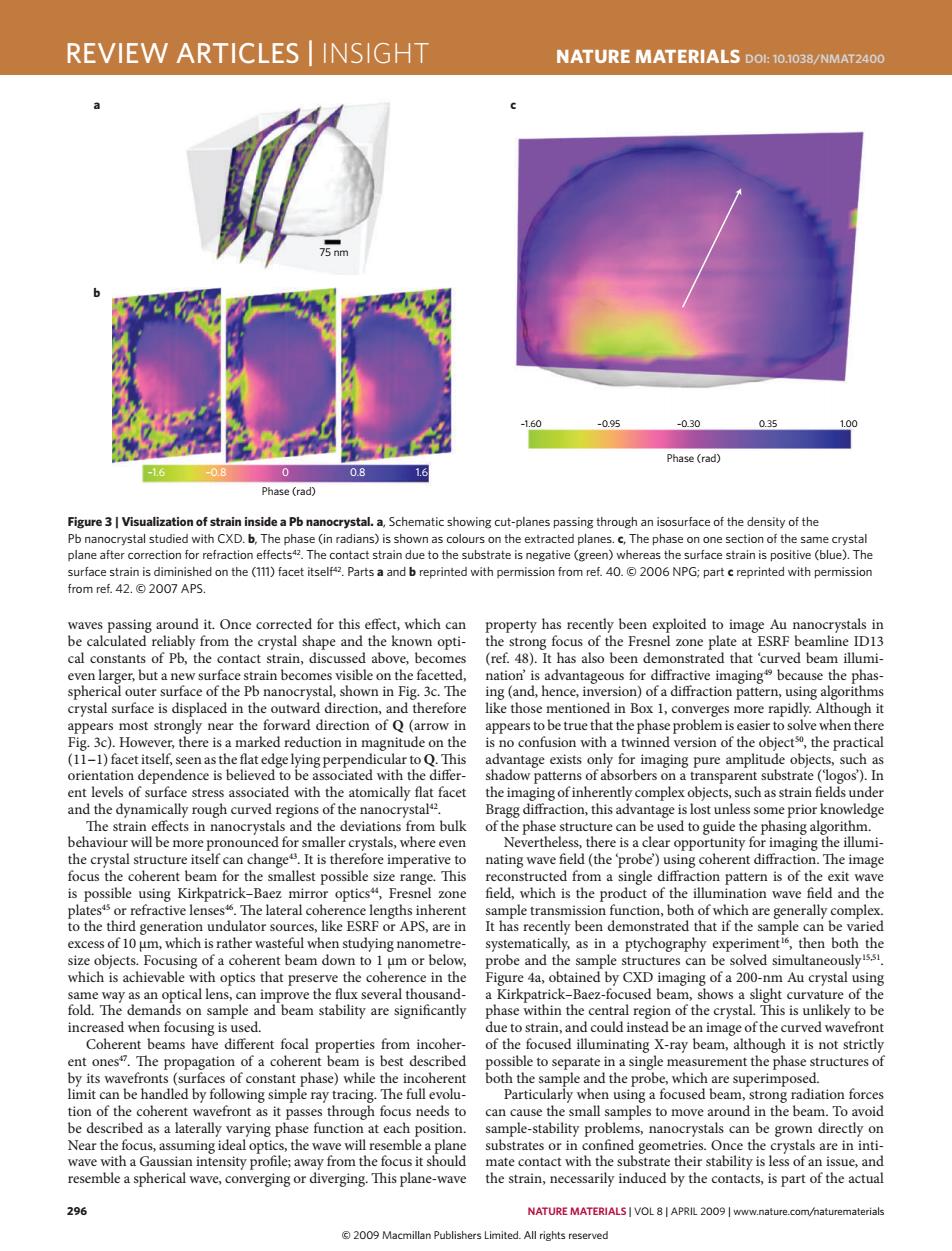
REVIEW ARTICLES INSIGHT NATURE MATERIALS DOL:10.1038/NMAT2400 nm -1.60 -0.95 -0.30 0.35 .00 Phase (rad) 0 0.8 16 Phase(rad) Figure 3 Visualization of strain inside a Pb nanocrystal.a,Schematic showing cut-planes passing through an isosurface of the density of the Pb nanocrystal studied with CXD.b,The phase(in radians)is shown as colours on the extracted planes.c,The phase on one section of the same crystal plane after correction for refraction effects42.The contact strain due to the substrate is negative (green)whereas the surface strain is positive (blue).The surface strain is diminished on the (11)facet itself42.Parts a and b reprinted with permission from ref.40.@2006 NPG;part c reprinted with permission from ref.42.©2007APS. waves passing around it.Once corrected for this effect,which can property has recently been exploited to image Au nanocrystals in be calculated reliably from the crystal shape and the known opti- the strong focus of the Fresnel zone plate at ESRF beamline ID13 cal constants of Pb,the contact strain,discussed above,becomes (ref.48).It has also been demonstrated that 'curved beam illumi- even larger,but a new surface strain becomes visible on the facetted, nation'is advantageous for diffractive imaging because the phas- spherical outer surface of the Pb nanocrystal,shown in Fig.3c.The ing(and,hence,inversion)of a diffraction pattern,using algorithms crystal surface is displaced in the outward direction,and therefore like those mentioned in Box 1,converges more rapidly.Although it appears most strongly near the forward direction of Q(arrow in appears to be true that the phase problem is easier to solve when there Fig.3c).However,there is a marked reduction in magnitude on the is no confusion with a twinned version of the objects,the practical (11-1)facet itself,seen as the flat edge lying perpendicular to Q.This advantage exists only for imaging pure amplitude objects,such as orientation dependence is believed to be associated with the differ- shadow patterns of absorbers on a transparent substrate ('logos').In ent levels of surface stress associated with the atomically flat facet the imaging of inherently complex objects,such as strain fields under and the dynamically rough curved regions of the nanocrystal. Bragg diffraction,this advantage is lost unless some prior knowledge The strain effects in nanocrystals and the deviations from bulk of the phase structure can be used to guide the phasing algorithm. behaviour will be more pronounced for smaller crystals,where even Nevertheless,there is a clear opportunity for imaging the illumi- the crystal structure itself can change.It is therefore imperative to nating wave field(the 'probe)using coherent diffraction.The image focus the coherent beam for the smallest possible size range.This reconstructed from a single diffraction pattern is of the exit wave is possible using Kirkpatrick-Baez mirror optics",Fresnel zone field,which is the product of the illumination wave field and the platests or refractive lenses46.The lateral coherence lengths inherent sample transmission function,both of which are generally complex. to the third generation undulator sources,like ESRF or APS,are in It has recently been demonstrated that if the sample can be varied excess of 10 um,which is rather wasteful when studying nanometre- systematically,as in a ptychography experiment',then both the size objects.Focusing of a coherent beam down to 1 um or below, probe and the sample structures can be solved simultaneouslyss which is achievable with optics that preserve the coherence in the Figure 4a,obtained by CXD imaging of a 200-nm Au crystal using same way as an optical lens,can improve the flux several thousand- a Kirkpatrick-Baez-focused beam,shows a slight curvature of the fold.The demands on sample and beam stability are significantly phase within the central region of the crystal.This is unlikely to be increased when focusing is used. due to strain,and could instead be an image of the curved wavefront Coherent beams have different focal properties from incoher- of the focused illuminating X-ray beam,although it is not strictly ent onest.The propagation of a coherent beam is best described possible to separate in a single measurement the phase structures of by its wavefronts (surfaces of constant phase)while the incoherent both the sample and the probe,which are superimposed. limit can be handled by following simple ray tracing.The full evolu- Particularly when using a focused beam,strong radiation forces tion of the coherent wavefront as it passes through focus needs to can cause the small samples to move around in the beam.To avoid be described as a laterally varying phase function at each position. sample-stability problems,nanocrystals can be grown directly on Near the focus,assuming ideal optics,the wave will resemble a plane substrates or in confined geometries.Once the crystals are in inti- wave with a Gaussian intensity profile;away from the focus it should mate contact with the substrate their stability is less of an issue,and resemble a spherical wave,converging or diverging.This plane-wave the strain,necessarily induced by the contacts,is part of the actual 296 NATURE MATERIALS VOL 8|APRIL 2009 www.nature.com/naturematerials 2009 Macmillan Publishers Limited.All rights reserved296 nature materials | VOL 8 | APRIL 2009 | www.nature.com/naturematerials review articles | insight NaTure maTerials doi: 10.1038/nmat2400 waves passing around it. Once corrected for this effect, which can be calculated reliably from the crystal shape and the known opti￾cal constants of Pb, the contact strain, discussed above, becomes even larger, but a new surface strain becomes visible on the facetted, spherical outer surface of the Pb nanocrystal, shown in Fig. 3c. The crystal surface is displaced in the outward direction, and therefore appears most strongly near the forward direction of Q (arrow in Fig. 3c). However, there is a marked reduction in magnitude on the (11−1) facet itself, seen as the flat edge lying perpendicular to Q. This orientation dependence is believed to be associated with the differ￾ent levels of surface stress associated with the atomically flat facet and the dynamically rough curved regions of the nanocrystal42. The strain effects in nanocrystals and the deviations from bulk behaviour will be more pronounced for smaller crystals, where even the crystal structure itself can change43. It is therefore imperative to focus the coherent beam for the smallest possible size range. This is possible using Kirkpatrick–Baez mirror optics44, Fresnel zone plates45 or refractive lenses46. The lateral coherence lengths inherent to the third generation undulator sources, like ESRF or APS, are in excess of 10 μm, which is rather wasteful when studying nanometre￾size objects. Focusing of a coherent beam down to 1 μm or below, which is achievable with optics that preserve the coherence in the same way as an optical lens, can improve the flux several thousand￾fold. The demands on sample and beam stability are significantly increased when focusing is used. Coherent beams have different focal properties from incoher￾ent ones47. The propagation of a coherent beam is best described by its wavefronts (surfaces of constant phase) while the incoherent limit can be handled by following simple ray tracing. The full evolu￾tion of the coherent wavefront as it passes through focus needs to be described as a laterally varying phase function at each position. Near the focus, assuming ideal optics, the wave will resemble a plane wave with a Gaussian intensity profile; away from the focus it should resemble a spherical wave, converging or diverging. This plane-wave property has recently been exploited to image Au nanocrystals in the strong focus of the Fresnel zone plate at ESRF beamline ID13 (ref. 48). It has also been demonstrated that ‘curved beam illumi￾nation’ is advantageous for diffractive imaging49 because the phas￾ing (and, hence, inversion) of a diffraction pattern, using algorithms like those mentioned in Box 1, converges more rapidly. Although it appears to be true that the phase problem is easier to solve when there is no confusion with a twinned version of the object50, the practical advantage exists only for imaging pure amplitude objects, such as shadow patterns of absorbers on a transparent substrate (‘logos’). In the imaging of inherently complex objects, such as strain fields under Bragg diffraction, this advantage is lost unless some prior knowledge of the phase structure can be used to guide the phasing algorithm. Nevertheless, there is a clear opportunity for imaging the illumi￾nating wave field (the ‘probe’) using coherent diffraction. The image reconstructed from a single diffraction pattern is of the exit wave field, which is the product of the illumination wave field and the sample transmission function, both of which are generally complex. It has recently been demonstrated that if the sample can be varied systematically, as in a ptychography experiment16, then both the probe and the sample structures can be solved simultaneously15,51. Figure 4a, obtained by CXD imaging of a 200-nm Au crystal using a Kirkpatrick–Baez-focused beam, shows a slight curvature of the phase within the central region of the crystal. This is unlikely to be due to strain, and could instead be an image of the curved wavefront of the focused illuminating X-ray beam, although it is not strictly possible to separate in a single measurement the phase structures of both the sample and the probe, which are superimposed. Particularly when using a focused beam, strong radiation forces can cause the small samples to move around in the beam. To avoid sample-stability problems, nanocrystals can be grown directly on substrates or in confined geometries. Once the crystals are in inti￾mate contact with the substrate their stability is less of an issue, and the strain, necessarily induced by the contacts, is part of the actual –1.60 –0.95 –0.30 0.35 1.00 –1.6 –0.8 0.8 1.6 75 nm 0 Phase (rad) Phase (rad) a b c Figure 3 | Visualization of strain inside a Pb nanocrystal. a, Schematic showing cut-planes passing through an isosurface of the density of the Pb nanocrystal studied with CXD. b, The phase (in radians) is shown as colours on the extracted planes. c, The phase on one section of the same crystal plane after correction for refraction effects42. The contact strain due to the substrate is negative (green) whereas the surface strain is positive (blue). The surface strain is diminished on the (111) facet itself42. Parts a and b reprinted with permission from ref. 40. © 2006 NPG; part c reprinted with permission from ref. 42. © 2007 APS. nmat_2400_APR09.indd 296 13/3/09 12:04:32 © 2009 Macmillan Publishers Limited. All rights reserved