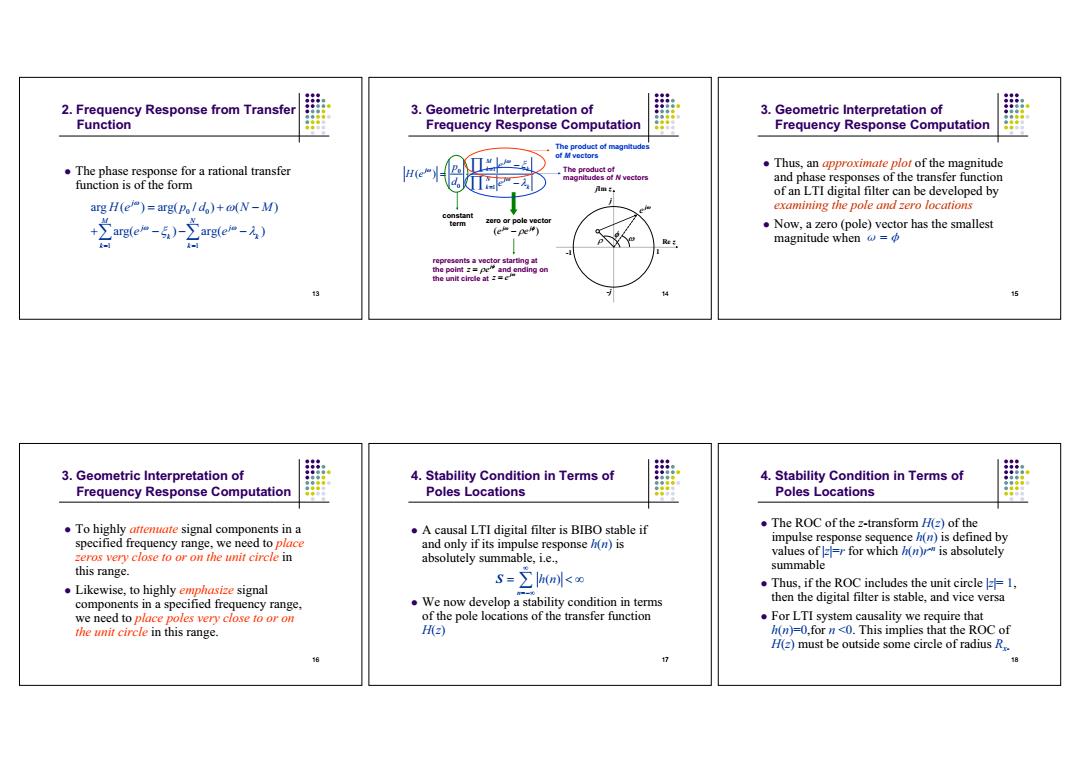
2.Frequency Response from Transfer 3.Geometric Interpretation of 3.Geometric Interpretation of Function Frequency Response Computation Frequency Response Computation The product omgnude of M voctors .The phase response for a rational transfer .Thus,an approximate plot of the magnitude H(e The product of d magnitudes of N vectors and phase responses of the transfer function function is of the form of an LTI digital filter can be developed by arg H(e)=arg(po/do)+(N-M) examining the pole and zero locations 之arg(em-5)-之arg(em-A) term zero or pole vector (e-pe) Now,a zero (pole)vector has the smallest magnitude when w=中 represents a vector starting at the point ==pe and ending on the unit circle at=e 13 15 3.Geometric Interpretation of 4.Stability Condition in Terms of 4.Stability Condition in Terms of Frequency Response Computation Poles Locations Poles Locations .To highly attenuate signal components in a .A causal LTI digital filter is BIBO stable if .The ROC of the z-transform (z)of the specified frequency range,we need to place and only if its impulse response h(n)is impulse response sequence h(n)is defined by zeros very close to or on the unit circle in absolutely summable,i.e., values of =r for which h()is absolutely this range. summable Likewise,to highly emphasize signal s=Σnlk .Thus,if the ROC includes the unit circle1, components in a specified frequency range, We now develop a stability condition in terms then the digital filter is stable,and vice versa we need to place poles very close to or on of the pole locations of the transfer function For LTI system causality we require that the unit circle in this range. H() h(n)=0,for n<0.This implies that the ROC of H(z)must be outside some circle of radius R. 多 1813 2. Frequency Response from Transfer Function The phase response for a rational transfer function is of the form 0 0 1 1 arg ( ) arg( / ) ( ) arg( ) arg( ) j M N j j k k k k He p d N M e e          14 3. Geometric Interpretation of Frequency Response Computation 1 0 0 1 ( ) M j k k j N j k k p e H e d e           constant term zero or pole vector ( ) j j e e    represents a vector starting at the point and ending on the unit circle at j z e    j z e  -1 1 Re z jIm z j -j   The product of magnitudes of M vectors The product of magnitudes of N vectors j e 15 3. Geometric Interpretation of Frequency Response Computation Thus, an approximate plot of the magnitude and phase responses of the transfer function of an LTI digital filter can be developed by examining the pole and zero locations Now, a zero (pole) vector has the smallest magnitude when ¹ =¶ 16 3. Geometric Interpretation of Frequency Response Computation To highly attenuate signal components in a specified frequency range, we need to place zeros very close to or on the unit circle in this range. Likewise, to highly emphasize signal components in a specified frequency range, we need to place poles very close to or on the unit circle in this range. 17 4. Stability Condition in Terms of Poles Locations A causal LTI digital filter is BIBO stable if and only if its impulse response h(n) is absolutely summable, i.e., We now develop a stability condition in terms of the pole locations of the transfer function H(z) ( ) n h n  S   18 4. Stability Condition in Terms of Poles Locations The ROC of the z-transform H(z) of the impulse response sequence h(n) is defined by values of |z|=r for which h(n)r-n is absolutely summable Thus, if the ROC includes the unit circle |z|= 1, then the digital filter is stable, and vice versa For LTI system causality we require that h(n)=0,for n <0. This implies that the ROC of H(z) must be outside some circle of radius Rx-