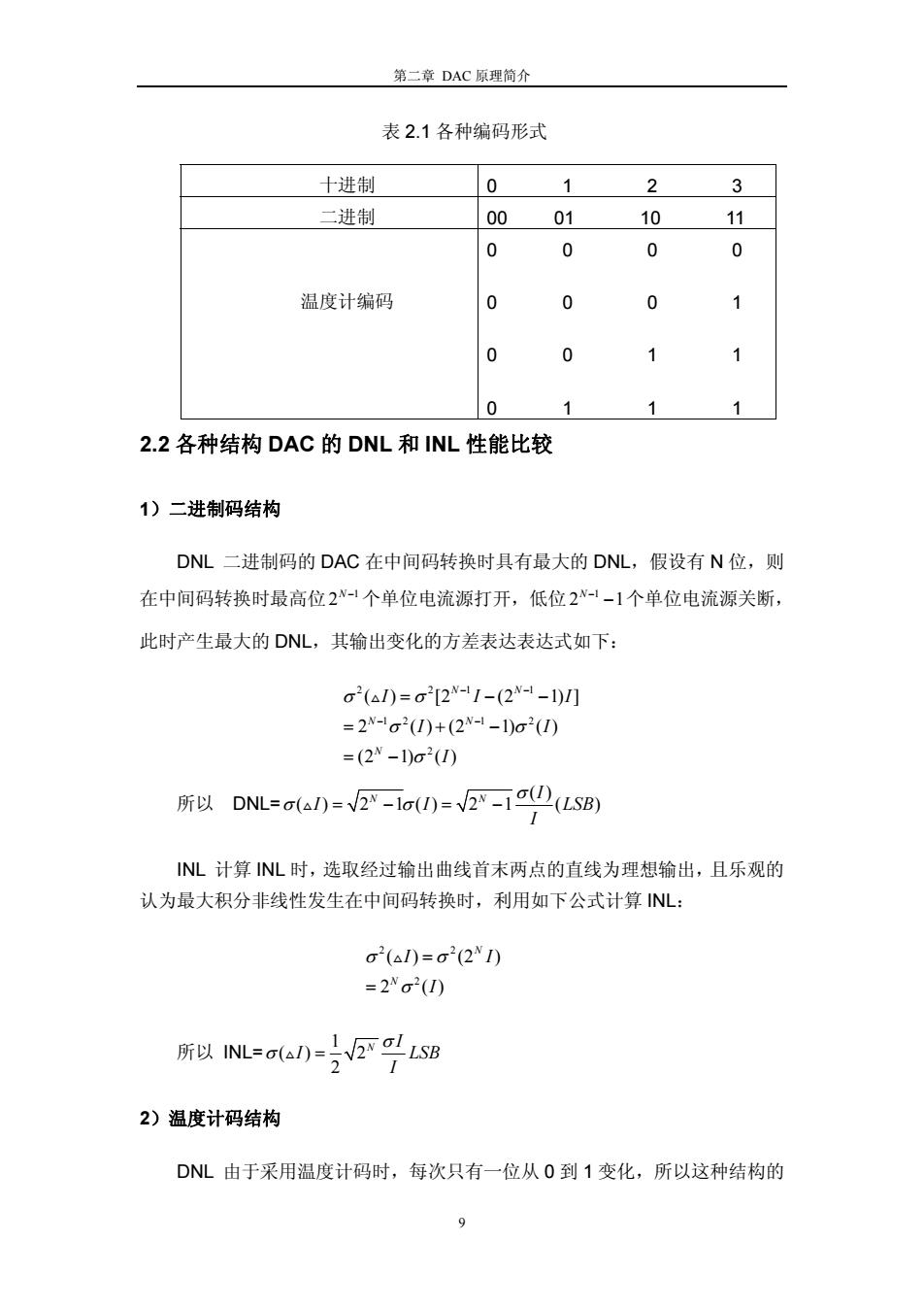
第二章DAC原理简介 表2.1各种编码形式 十进制 0 2 3 二进制 00 01 10 11 0 0 0 0 温度计编码 0 0 0 1 0 0 1 1 0 1 2.2各种结构DAC的DNL和INL性能比较 1)二进制码结构 DNL二进制码的DAC在中间码转换时具有最大的DNL,假设有N位，则 在中间码转换时最高位2-1个单位电流源打开，低位21-1个单位电流源关断， 此时产生最大的DNL,其输出变化的方差表达表达式如下： σ2(a1)=σ2[2-1-(2--1)] =2-σ2(I)+(2--10o2(I0 =(2-1)o2(I) 所以DNL=a(A)=√2-i()=V2-i0(LSB) INL计算NL时，选取经过输出曲线首末两点的直线为理想输出，且乐观的 认为最大积分非线性发生在中间码转换时，利用如下公式计算NL: o2(△0=σ2(21) =2σ2(I) 所以INL=a(a)=}V2oLSB 2)温度计码结构 DNL由于采用温度计码时，每次只有一位从0到1变化，所以这种结构的 9第二章 DAC 原理简介 9 表 2.1 各种编码形式 十进制 0 1 2 3 二进制 00 01 10 11 温度计编码 0 0 0 0 0 0 0 1 0 0 1 1 0 1 1 1 2.2 各种结构 DAC 的 DNL 和 INL 性能比较 1）二进制码结构 DNL 二进制码的 DAC 在中间码转换时具有最大的 DNL，假设有 N 位，则 在中间码转换时最高位 1 2N − 个单位电流源打开，低位 1 2 1 N− − 个单位电流源关断， 此时产生最大的 DNL，其输出变化的方差表达表达式如下： 所以 DNL= ( ) ( ) 2 1() 2 1 ( ) N N I I I LSB I σ σ σ + =− =− INL 计算 INL 时，选取经过输出曲线首末两点的直线为理想输出，且乐观的 认为最大积分非线性发生在中间码转换时，利用如下公式计算 INL： 2 2 2 ( ) (2 ) 2 () N N I I I σ σ σ = = + 所以 INL= 1 () 2 2 N I I LSB I σ σ + = 2）温度计码结构 DNL 由于采用温度计码时，每次只有一位从 0 到 1 变化，所以这种结构的 2 21 1 12 1 2 2 ( ) [2 (2 1) ] 2 ( ) (2 1) ( ) (2 1) ( ) N N N N N I I I I I I σ σ σ σ σ − − − − = −− = +− = − +