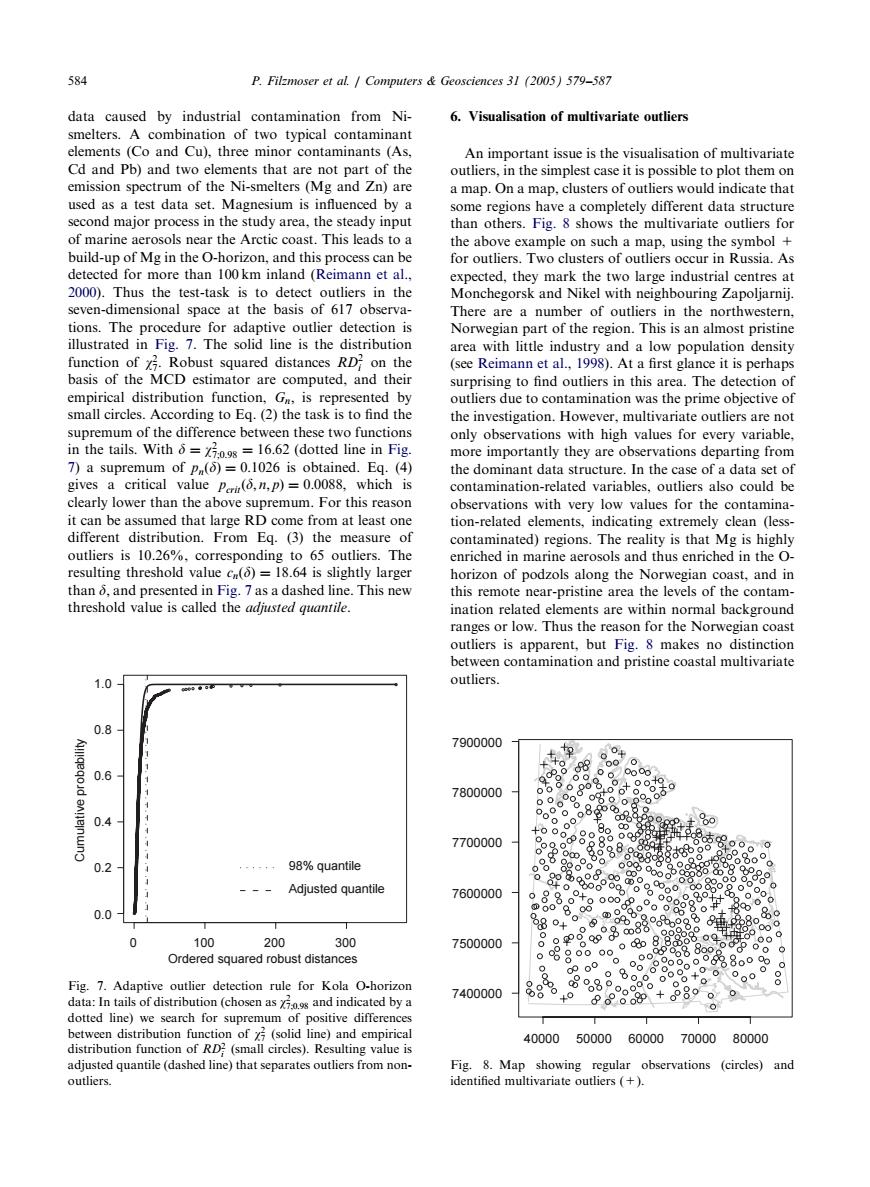
584 P.Filzmoser et al.Computers Geosciences 31 (2005)579-587 data caused by industrial contamination from Ni- 6.Visualisation of multivariate outliers smelters.A combination of two typical contaminant elements (Co and Cu).three minor contaminants (As. An important issue is the visualisation of multivariate Cd and Pb)and two elements that are not part of the outliers,in the simplest case it is possible to plot them on emission spectrum of the Ni-smelters (Mg and Zn)are a map.On a map,clusters of outliers would indicate that used as a test data set.Magnesium is influenced by a some regions have a completely different data structure second major process in the study area,the steady input than others.Fig.8 shows the multivariate outliers for of marine aerosols near the Arctic coast.This leads to a the above example on such a map,using the symbol build-up of Mg in the O-horizon,and this process can be for outliers.Two clusters of outliers occur in Russia.As detected for more than 100 km inland (Reimann et al., expected,they mark the two large industrial centres at 2000).Thus the test-task is to detect outliers in the Monchegorsk and Nikel with neighbouring Zapoljarnij. seven-dimensional space at the basis of 617 observa- There are a number of outliers in the northwestern, tions.The procedure for adaptive outlier detection is Norwegian part of the region.This is an almost pristine illustrated in Fig.7.The solid line is the distribution area with little industry and a low population density function of Robust squared distances RD on the (see Reimann et al.,1998).At a first glance it is perhaps basis of the MCD estimator are computed,and their surprising to find outliers in this area.The detection of empirical distribution function,G,is represented by outliers due to contamination was the prime objective of small circles.According to Eq.(2)the task is to find the the investigation.However.multivariate outliers are not supremum of the difference between these two functions only observations with high values for every variable. in the tails.With==16.62(dotted line in Fig. more importantly they are observations departing from 7)a supremum of p(5)=0.1026 is obtained.Eq.(4) the dominant data structure.In the case of a data set of gives a critical value per(,n,p)=0.0088,which is contamination-related variables,outliers also could be clearly lower than the above supremum.For this reason observations with very low values for the contamina- it can be assumed that large RD come from at least one tion-related elements,indicating extremely clean (less- different distribution.From Eq.(3)the measure of contaminated)regions.The reality is that Mg is highly outliers is 10.26%.corresponding to 65 outliers.The enriched in marine aerosols and thus enriched in the O- resulting threshold value cn()=18.64 is slightly larger horizon of podzols along the Norwegian coast,and in than 6,and presented in Fig.7 as a dashed line.This new this remote near-pristine area the levels of the contam- threshold value is called the adjusted quantile ination related elements are within normal background ranges or low.Thus the reason for the Norwegian coast outliers is apparent,but Fig.8 makes no distinction between contamination and pristine coastal multivariate 1.0 outliers 0.8 7900000 8o 0.6 00 7800000 anneinwno 0.4 0 88.9 7700000 88 0.2 98%quantile 8g88 点58890。 %80°。 88088 88 Adjusted quantile 7600000 0 0 0.0 839t8wg 86 %g+ 89 0 100 200 300 7500000 。多之色会一 0 o8 09 8o88o0 Ordered squared robust distances 00 888898 06 Fig.7.Adaptive outlier detection rule for Kola O-horizon 7400000 data:In tails of distribution(chosen asand indicated by a 88 88°006e +0 0 dotted line)we search for supremum of positive differences between distribution function ofy(solid line)and empirical 40000 5000060000 70000 80000 distribution function of RD?(small circles).Resulting value is adjusted quantile(dashed line)that separates outliers from non- Fig.8.Map showing regular observations (circles)and outliers. identified multivariate outliers (+)data caused by industrial contamination from Ni￾smelters. A combination of two typical contaminant elements (Co and Cu), three minor contaminants (As, Cd and Pb) and two elements that are not part of the emission spectrum of the Ni-smelters (Mgand Zn) are used as a test data set. Magnesium is influenced by a second major process in the study area, the steady input of marine aerosols near the Arctic coast. This leads to a build-up of Mgin the O-horizon, and this process can be detected for more than 100 km inland (Reimann et al., 2000). Thus the test-task is to detect outliers in the seven-dimensional space at the basis of 617 observa￾tions. The procedure for adaptive outlier detection is illustrated in Fig. 7. The solid line is the distribution function of w2 7: Robust squared distances RD2 i on the basis of the MCD estimator are computed, and their empirical distribution function, Gn; is represented by small circles. Accordingto Eq. (2) the task is to find the supremum of the difference between these two functions in the tails. With d ¼ w2 7;0:98 ¼ 16:62 (dotted line in Fig. 7) a supremum of pnðdÞ ¼ 0:1026 is obtained. Eq. (4) gives a critical value pcritð Þ¼ d; n; p 0:0088; which is clearly lower than the above supremum. For this reason it can be assumed that large RD come from at least one different distribution. From Eq. (3) the measure of outliers is 10.26%, correspondingto 65 outliers. The resultingthreshold value cnð Þ d ¼ 18:64 is slightly larger than d; and presented in Fig. 7 as a dashed line. This new threshold value is called the adjusted quantile. 6. Visualisation of multivariate outliers An important issue is the visualisation of multivariate outliers, in the simplest case it is possible to plot them on a map. On a map, clusters of outliers would indicate that some regions have a completely different data structure than others. Fig. 8 shows the multivariate outliers for the above example on such a map, usingthe symbol + for outliers. Two clusters of outliers occur in Russia. As expected, they mark the two large industrial centres at Monchegorsk and Nikel with neighbouring Zapoljarnij. There are a number of outliers in the northwestern, Norwegian part of the region. This is an almost pristine area with little industry and a low population density (see Reimann et al., 1998). At a first glance it is perhaps surprisingto find outliers in this area. The detection of outliers due to contamination was the prime objective of the investigation. However, multivariate outliers are not only observations with high values for every variable, more importantly they are observations departingfrom the dominant data structure. In the case of a data set of contamination-related variables, outliers also could be observations with very low values for the contamina￾tion-related elements, indicatingextremely clean (less￾contaminated) regions. The reality is that Mg is highly enriched in marine aerosols and thus enriched in the O￾horizon of podzols alongthe Norwegian coast, and in this remote near-pristine area the levels of the contam￾ination related elements are within normal background ranges or low. Thus the reason for the Norwegian coast outliers is apparent, but Fig. 8 makes no distinction between contamination and pristine coastal multivariate outliers. ARTICLE IN PRESS 0 100 200 300 0.0 0.2 0.4 0.6 0.8 1.0 Ordered squared robust distances Cumulative probability 98% quantile Adjusted quantile Fig. 7. Adaptive outlier detection rule for Kola O-horizon data: In tails of distribution (chosen as w2 7;0:98 and indicated by a dotted line) we search for supremum of positive differences between distribution function of w2 7 (solid line) and empirical distribution function of RD2 i (small circles). Resultingvalue is adjusted quantile (dashed line) that separates outliers from non￾outliers. 7400000 7500000 7600000 7700000 7800000 7900000 40000 50000 60000 70000 80000 Fig. 8. Map showing regular observations (circles) and identified multivariate outliers (+). 584 P. Filzmoser et al. / Computers & Geosciences 31 (2005) 579–587