正在加载图片...
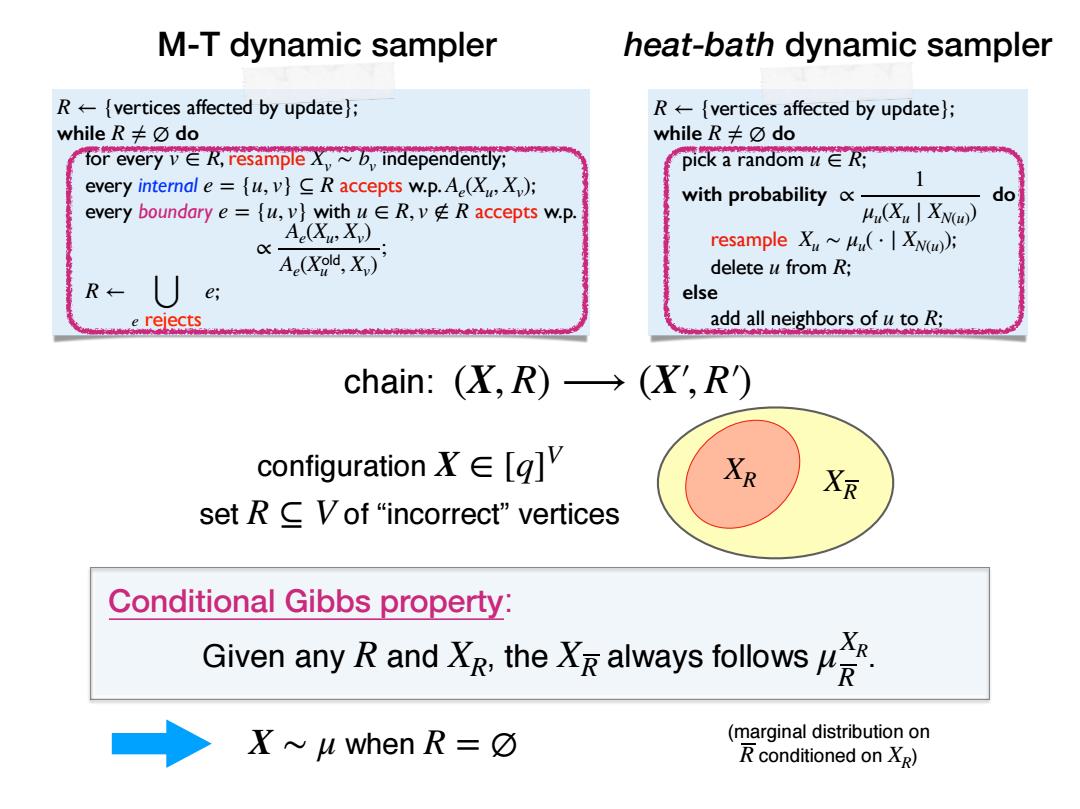
M-T dynamic sampler heat-bath dynamic sampler R[vertices affected by update); R[vertices affected by update); while R≠odo while R≠odo for every R,resampleb,independently; pick a random u ER; every internal e={u,v}C R accepts w.p.A(XX); 1 with probability o- do every boundary e=u,v}with u ER,vR accepts w.p. Hu(Xu IXN() Ae(Xe X) resample X.~h(·|Xwog A(Xold,X.) delete u from R; R- e, else e rejects add all neighbors of u to R; chain:(X,R)→(X',R) configuration Xe [g] XR XR set R C Vof“incorrect'”vertices Conditional Gibbs property: Given anyRandtealways follows X~u when R=☑ (marginal distribution on R conditioned on Xg); while do for every , resample independently; every internal accepts w.p. ; every boundary with accepts w.p. ; R ← {vertices affected by update} R ≠ ∅ v ∈ R Xv ∼ bv e = {u, v} ⊆ R Ae(Xu, Xv) e = {u, v} u ∈ R, v ∉ R ∝ Ae(Xu, Xv) Ae(X��� u , Xv) ; R ← ⋃ e rejects e ; while do pick a random ; with probability do resample ; delete from ; else add all neighbors of to ; R ← {vertices affected by update} R ≠ ∅ u ∈ R ∝ 1 μu(Xu ∣ XN(u)) Xu ∼ μu( ⋅ ∣ XN(u) ) u R u R M-T dynamic sampler heat-bath dynamic sampler configuration set of “incorrect” vertices X ∈ [q] V R ⊆ V Given any R and X , the always follows . R XR μ XR R Conditional Gibbs property: (marginal distribution on R conditioned on X ) R XR XR X ∼ μ when R = ∅ chain: (X, R) ⟶ (X′ , R′)