
第4章:超声波的传播特性
第4章:超声波的传播特性
医学超声中的介质
医学超声中的介质
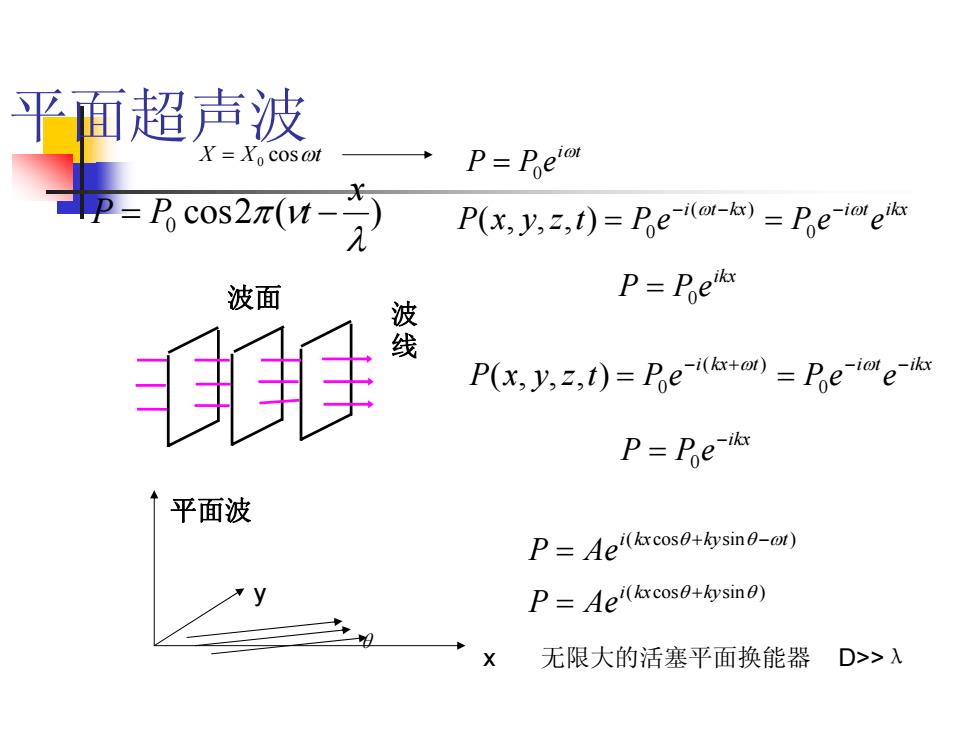
平面超声波X = X,cosotP= PeiotIP= P cos2元(vP(x, y, z, t) = Pe-i(or-a) = Pe-ioleikr元P= Peikr波面波线P(x, y,z,t) = Pe-i(k+l) = Pe-iale-ikxP= Pe-ikr↑平面波P= Aei(kxcosO+hysin0-o1)P= Aei(kxcos0+kysin0)无限大的活塞平面换能器D>> 入
平面超声波 平面波 波 线 波面 )(2cos 0 λ νπ x = tPP − kxti ikxti eePePtzyxP ω −− − ω = = 0 )( 0 ),( tkxi ikxti eePePtzyxP +− −− = = ω ω 0 )( 0 ),( x y θ )sincos( )sincos( θθ ωθθ kykxi tkykxi AeP AeP + −+ = = ikx = 0ePP ikx ePP − = 0 tXX 无限大的活塞平面换能器 D>>λ = 0 cosω ti ePP ω = 0

球面超声波P exp(ikr)Or = /(x-x)2 +(y- yo) +(z-z0)2对于发射声波的换能器,只要它的孔径远小于波长.它们产生的声场就可球面波以看成向外发散的球面波,一个完成的球壳声源会向球心发射会聚的球面波Pe-krP_
球面超声波 ( ) 1P exp ikr P r = 2 0 2 0 2 0 −+−+−= zzyyxxr )()()( 球面波 对于发射声波的换能器,只要它的孔 径远小于波长,它们产生的声场就可 以看成向外发散的球面波, 一个完 成的球壳声源会向球心发射会聚的 球面波 r eP P −kr = 0

边界条件1表征介质分界面两侧的声学参量之间的关系的函数为声学边界条件,传播介质的边界形式有两种给定方式:■1)、给定分界面一边的声学参数值■2)给定分界面两边的声学参数的关系
边界条件 表征介质分界面两侧的声学参量之间的 关系的函数趁为声学边界条件. 传播介质的边界形式有两种给定方式: 1)、给定分界面一边的声学参数值 2)给定分界面两边的声学参数的关系

第一类、第一种边界条件给定边界上的力,绝对软边界条件:易变形介质PA
第一类、第一种边界条件 给定边界上的力,绝对软边界条件: 易变形介质 P Σ = 0 ∑ p

第一类、第二种边界条件绝对硬边界条件不能变形介质-Vn
第一类、第二种边界条件 绝对硬边界条件 不能变形介质 v n Σ = 0 n v

第一类、第三种边界条件给定声压和质点法线速度的关系(阻抗边界条件)VnpA
第一类、第三种边界条件 给定声压和质点法线速度的关系(阻抗边界 条件) v n Σ p ∑ = ∑)( n n v p Z

连接边界条件■在不同声阻抗的介质交界面上的声波满足的条件。= P2lp.Vinlz = V2nl2VinV2np1P2Z
连接边界条件 在不同声阻抗的介质交界面上的声波满足的条 件。 ∑ ∑ ∑ ∑ = = n n vv pp 1 2 1 2 v1n Σ p1 v 2 n p 2
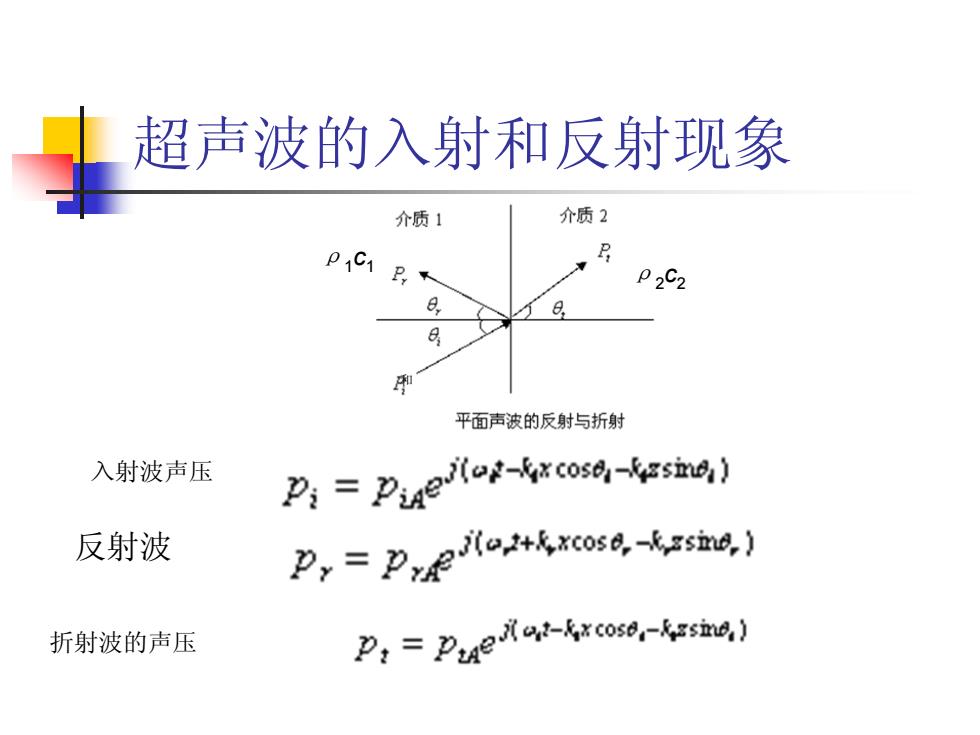
超声波的入射和反射现象介质2介质1PpaC PP2C28.e8P和平面声波的反射与折射入射波声压tat-kxcosej-kasime,!P;gstat+kxcose,-kgsime,反射波P,=PxAP, = Praellot-krcoso,-kssne)折射波的声压
超声波的入射和反射现象 入射波声压 反射波 和 ρ1c1 ρ 2 c 2 折射波的声压