
Computational Neuroscience The mathematical theory of our brain Lecture 1 神经元的整合发放(IF)模型 2020年计算神经科. 号:983068756 ▣动 Daqing Guo/郭大庆 dqguo@uestc.edu.cn Department of Biomedical Engineering, School of Life Science and Technology, University of Electronic Science and Technology of China Before the course 讲授内容: Neuronal >神经元:电特性、数学模型、动力学分析方法 Dynamics >突触:数学模型、突触可塑性(与学习有关) >神经噪声:噪声源、神经元的随机动力学 >神经元网络:拓扑结构、神经计算、神经元编解码基础 http://neuronaldynamics.epfl.ch/online/index.html 考核方式: >课程设计:50% 神经网络模型的构建 >平时成绩:50%,出勤率、作业 程序语言 Matlab/Python 先行课:神经科学基础知识、数值计算、非线性动力学、微分方程

Content 0 Simple Introduction 1.1 Neurons and Synapses: 1.2 The Passive Membrane(被动膜) -Linear circuit Dirac delta-function 1.3 Leaky Integrate-and-Fire Model 1.4 Generalized Integrate-and-Fire Model 整合发放模型 1.5.Quality of Integrate-and-Fire Models Introduction 《埃德温·史密斯纸草文稿》 古埃及:人类最早关于脑的文献记录 埃及医师伊姆霍特普(Imhotep)一公元 前2600年 纸莎草纸(Papyrus)一公元前3000年 --- 盒N 脑:brain (古埃及象形文字) 于公元前1600-1700完成的纸草文稿,手稿第一位已知持有者埃德温·史密斯(1822-1906)

Introduction 古罗马:神经输送脑脊液至身体外围 盖伦认为: ●脑的深处是一个由相互连通的腔组成 的迷宫,内含无色的液体,即脑脊液。 神经(nerves)输送脑脊液至神经的外围 部分。最早描述了脑萎缩。 ●灵气学说:脑中的精气决定运动、感 知和感觉。心的活气控制体内的血液 古罗马医生盖伦Galen 和体温。肝的动气控制营养和新陈代 (公元129-199) 谢。 √对灵气说的否定:意大利维萨留斯,发现不同动物的脑没有本质差别,不足以说 明动物之间在智力水平上的悬殊差异;英国威廉哈维,建立了血液循环理论等。 Introduction 加伐尼与伏特:神经电,挑战生物神圣的概念 加伐尼 (Luigi Galvani, 1737-1798别 伏打 Alessandro Volta (1745-1827) 修正观点:电流油不 提出神经中有电流,认 同金属,在青蛙体液 为电建立了活力和生命 中产生的金属电位差 之的密切联系,电是生 所导致。建立了伏打 命之力。 电堆,证明电可以代 替人的灵气使肌肉收 加伐尼时代的电生理实验室 缩
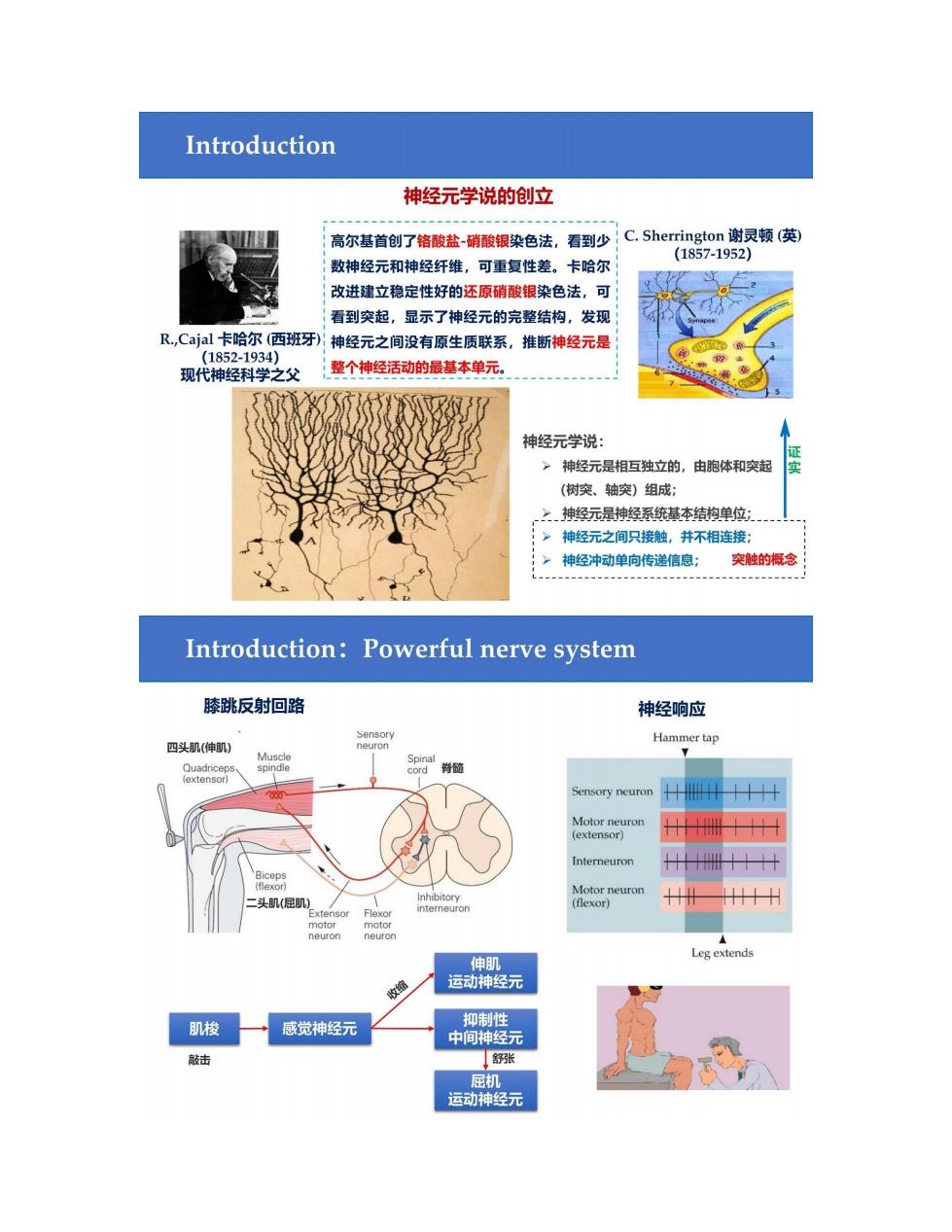
Introduction 神经元学说的创立 高尔基首创了铬酸盐-硝酸银染色法,看到少 C.Sherrington谢灵顿(英) (1857-1952) 数神经元和神经纤维,可重复性差。卡哈尔 改进建立稳定性好的还原硝酸银染色法,可 看到突起,显示了神经元的完整结构,发现 R,Cajal卡哈尔(西班牙)神经元之间没有原生质联系,推断神经元是 (1852-1934) 现代神经科学之父 整个神经活动的最基本单元。 神经元学说: 证 >神经元是相互独立的, 由胞体和突起 (树突、轴突)组成: 之.神经元是神经系统基本结构单位: 神经元之间只接触,并不相连接 神经冲动单向传递信息: 突触的概念 Introduction:Powerful nerve system 膝跳反射回路 神经响应 Sensory 四头肌(伸肌) Hammer tap neuron Muscle 里 Quadriceps spindle (extensor) Sensory neuron Motor neuron (extensor) Interneuron flexor】 Motor neuron 二头肌(屈肌)】 Inhibitory (flexor) Extensor F月lexor interneuron motor motor neuron neuron Leg extends 伸肌 收缩 运动神经元 肌梭 感觉神经元 抑制性 中间神经元 敲击 1舒张 屈机 运动神经元
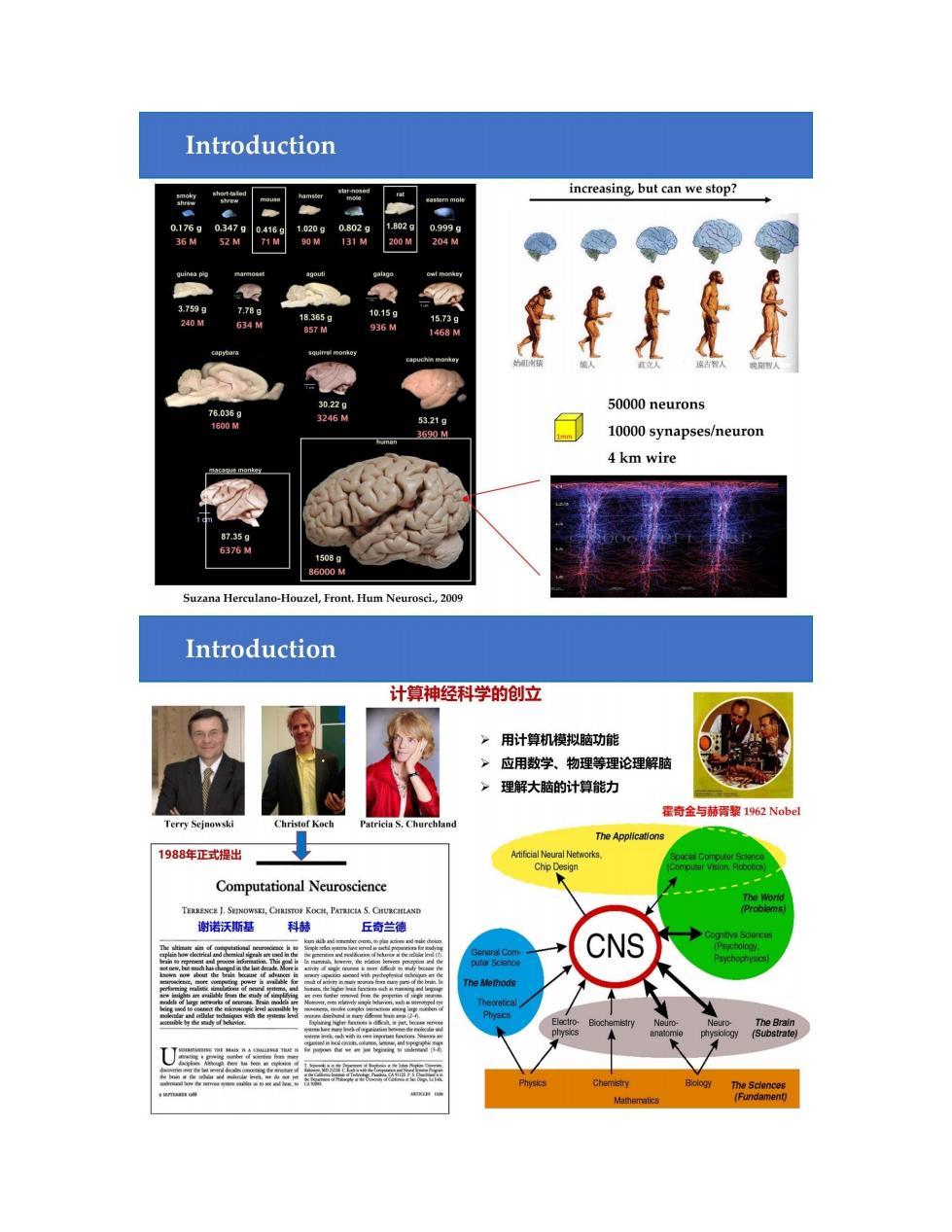
Introduction a购 hamster increasing,but can we stop? 0.176g0.347g 0,418g 1.020g 0.802g 1.802g 0.999g 36M 52M 7 90M 131M 200M 204M guineap 3759g 7.78g 240M 18,.365g 10.15a 634M 1573g 857M 936M 1468M 30.22g 50000 neurons 76.036g 3246M 53.21g 1600M 3590M 10000 synapses/neuron 4 km wire 87.35g 6376M 1508g 86000M Suzana Herculano-Houzel,Front.Hum Neurosci.,2009 Introduction 计算神经科学的创立 用计算机模拟脑功能 应用数学、物理等理论理解脑 理解大脑的计算能力 霍奇金与赫胥黎1962 Nobel Terry Sejnowski Christof Koch Patricia S.Churchla The Appllcations 1988年正式提出 Artificial Neural Networks. Chip Design (Computer Viion,Robotics) Computational Neuroscience The World TERKENCE J.SEINOWSKI,CHRISTO KOCH,PATRICIA S.CHURCILAND (Problems) 谢诺沃斯基 科赫 丘奇兰德 CNS Comnitive Scionces The Methods Electro.Biochemistry Neuro The Brain (Substrate Physics Chemistry Biology d (Fundament)

2019第一届中国计算与认知神经科学会议 The 1st Chinese Computational and Cognitive Neuroscience(C'N)Conference. (第三轮通知)“ 计算神经科学是脑科学中最前沿的跨领域交叉学科之一,它综合了信息科学、神经科 学、认知科学、物理学、数学和生物学等众多领域的方法,以建模和仿真为首选工具,研 究和揭示生物大脑复杂行为(如注意、学习、记亿、情感、意识等)的工作机制。计算神 经科学是信息科学与现代认知神经科学真正实现结合的关健桥梁,在帮助揭示脑机理、发 展类脑计草和人工智能方面起着至关重要的作用。, 本届C、会议是海内外华人计算神经科学协会与中国神经科学学会计算神经料学和神 经工程分会联合主办的第一次活动,由电子科技大学生命科学与技术学院、神经信息教育部 重点实验室承办。CN以后将每年在国内不同地方举办。本次会议将邀请计算神经料学、认 知神经科学及相关领域的4位keynote speaker和25位Invitedspeaker做专题报告。本次会 议不安排征文,但将设置墙报展示环节,为参会者提供一个充分交流最新研究成果的机会。 欢迎计算神经科学、认知神经科学、人工智能及相关领城的学者、专家及研究生踊跃参会。 现将相关事项通知如下:· 组织委员会 主席:汪小京(知约大学、上海脑中心)廿 成员:吴思(北京大学) 毕国强(中国料技大学) 周林逆(上海交通大学) 陈爱华(华东师范大学)· 李永杰(电子科技大学) 都大庆(电子科技大学) Introduction:Big names and courses op H-Index for Computational Neuroscience: u5m103.5138 David Cai SiWu 2622 84.799 119 Xiaojing Wang Jianfeng Feng NYU Shanghai 上海交大(已故) 复旦大学 北京大学 1094 45,90090 21611 27,45号78 342 t时m7076 Xiaogin Wang Zhaoping Li Yuguo Yu 清华大学 北京师范大学 清料买学 复旦大学 576375 4933.s9461 64629 t有GER5TER Many courses and summer schools 6897 Austna14,70758 78350 Luted states 28,448 55 3,6154 ohnK,Tot 121350 47
Introduction:Software and Books 编程语言和软件: .Matlab,C/C++,Python,Fortran NERUON/Parallel NERUON:http://www.neuron.yale.edu/neuron/ NEST:http://www.nest-initiative.org/index.php/Software:About NEST 。BRAIN Simulator 参考书籍: "Dayan and Abbott,"Theoretical Neuroscience:Computational and Mathematical Modeling ofNeural Systems"(MIT Press,2001) Gerstner and Kistler,"Spiking Neuron Models"(Cambridge U.Press,2002) Izhikevich,"Dynamical Systems in Neuroscience:The Geometry of Excitability and Bursting"(MIT Press,2007) .Koch,"Biophysics of Computation:Information Processing in Single Neurons"(Oxford U.Press,1999) 1.1 Neuron and Synapse 神经元基本结构 膜电位:Vm=Va-Vout 细 “5 5一离子通道。 离子泵 Na+ 膜外 膜 树突(dendrites) 压控 :非压控 膜内 Neuron Microelectrode 当电驱动化学驱动时,处于resting potential(静息电位) membrane 跑体(s0ma) potential 100mV 轴突(axon) nt 树突:接收信号 胞体:整合信号 多输入,单输出? 轴突:传出信号 Subthreshold regime 神经元基本电属性

1.1 Neuron and Synapse 神经元不应期(Refractory periods) 突触后电位(Postsynaptic potential) Absolute refractory period Rolative refractory period ●化学突触: >兴奋性: >抑制性: 30 ·电突触 action Post-S oEat EPSP 2 3 4 5 Time(ms) Exitatory Po-Syeptic Poteial 极化过程:去极化(De)→复极化(Re)→After-hyper(后超极化) Spike train 绝对不应期:threshold→resting potential 相对不应期:resting potential→resting potential regular or irregular? 思考以下几个问题 A cortical neuron sends out signals The dendrite is a part of the neuron which are called: where synapses are located [action potentials which collects signals from other [spikes neurons [postsynaptic potential [along which spikes are sent to other neurons In vivo,a typical cortical neuron exhibits rare output spikes [regular firing activity [a fluctuating membrane potential Multiple answers possible!
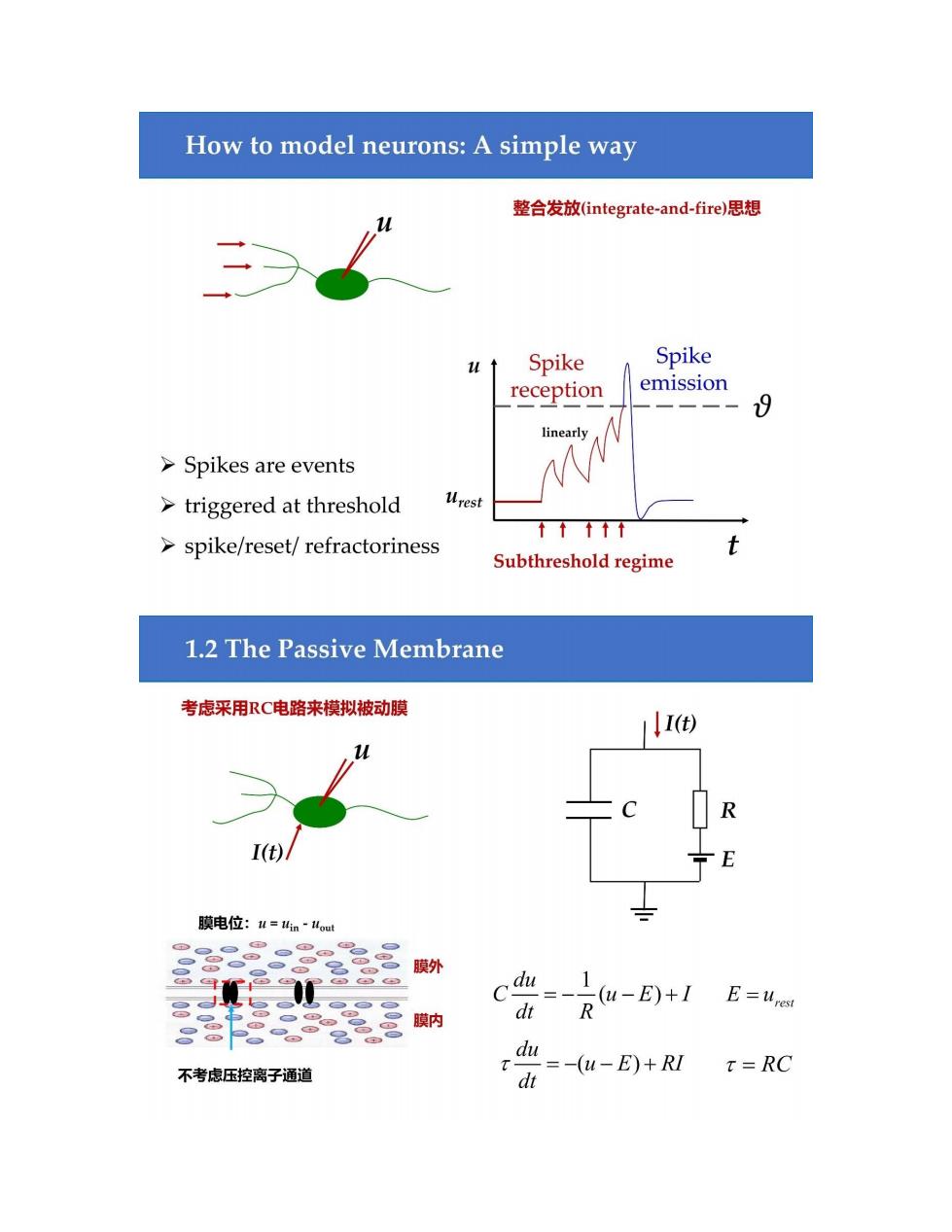
How to model neurons:A simple way 整合发放(integrate-and-fire)思想 Spike Spike reception emission 一一一 9 linearly >Spikes are events >triggered at threshold Urest ↑↑↑↑1 spike/reset/refractoriness t Subthreshold regime 1.2 The Passive Membrane 考虑采用RC电路来模拟被动膜 () I(t). E 膜电位:=4n~out 22 膜外 膜内 dt u-E)+IE=re R du 不考虑压控离子通道 =-(u-E)+RI dt

1.2 The Passive Membrane 考虑第1种情况: I() 若初始条件满足u(O)=4st+u和()=0,试分析u随时间的变化 R 数学分析过程: 令V=u-urest 则业 d(u-ure)_-V+Rl dt dt T 因为It)=0,所以:V=Cer=u-ue d=-(u-we)+R d 考虑初始条件u(0)=uet+lo,可得到:C=4o 1u↑ 解为:u=4e+uer 以指数形式达到稳态4est >膜时间常数控制达稳态速度 1.2 The Passive Membrane (step response) 考虑第2种情况(step current input): I(t)为下图所示的阶跃函数,初始条件满足u(t)=4est(t冬t), I(t) 试分析u随时间的变化 以指数相关的形式达到稳态lest+R R 达到稳态后所有电流都从电阻走 =-(u-uet)+Rl dt w+I-Ce学→C=-,→u=w+M,a-e台)