
第二节 第六章 定积分在儿何学上的立用 平面图形的面积 二、 平面曲线的弧长 三、 已知平行截面面积函数的 立体体积 四、 旋转体的侧面积补充) HIGH EDUCATION PRESS 机动目录上页下页返回结束
四、 旋转体的侧面积 (补充) 三、已知平行截面面积函数的 立体体积 第二节 一、 平面图形的面积 二、 平面曲线的弧长 机动 目录 上页 下页 返回 结束 定积分在几何学上的应用 第六章
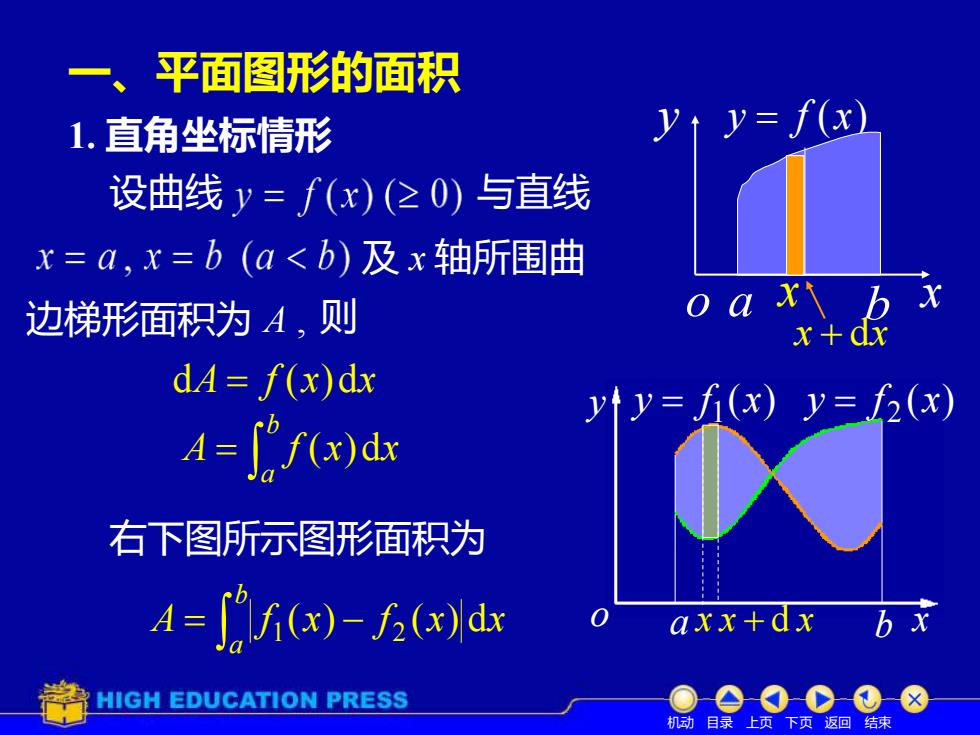
一、平面图形的面积 1.直角坐标情形 yt y=f(x) 设曲线y=f(x)(20)与直线 x=a,x=b(a<b)及x轴所围曲 边梯形面积为A,则 oax\b x+dx dA=f(x)dx 4-CG)dx y=(x)y=f2(x) 右下图所示图形面积为 4=[f(x)-()dx axx+dx HIGH EDUCATION PRESS 机动目录上页下页返回结束
一、平面图形的面积 1. 直角坐标情形 设曲线 与直线 及 x 轴所围曲 则 dA = f (x)dx o a b x y y = f (x) x x + dx A f x x b a ( )d = 机动 目录 上页 下页 返回 结束 边梯形面积为 A , 右下图所示图形面积为 y o a b x ( ) 2 ( ) y = f x 1 y = f x A f x f x x b a ( ) ( ) d = 1 − 2 x x + d x
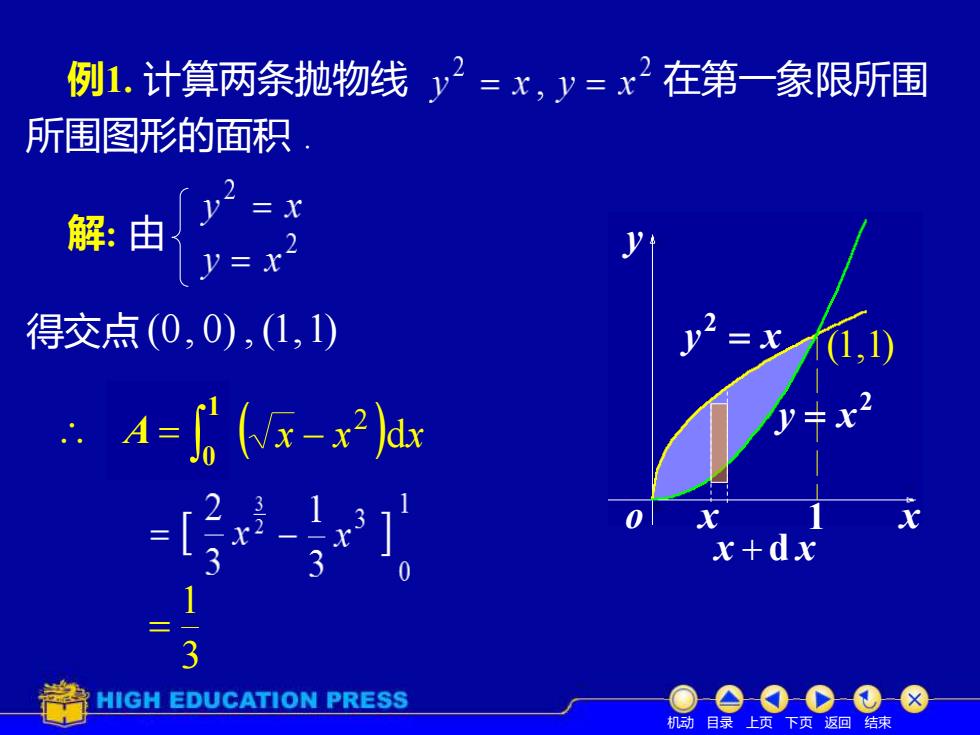
例1.计算两条抛物线y2=x,y=x2在第一象限所围 所围图形的面积 解:由 y=x y=x 得交点(0,0),1,1) .A=-x2)dx -6 x+dx HIGH EDUCATION PRESS 机动目录上页下页返回结束
例1. 计算两条抛物线 在第一象限所围 所围图形的面积 . x y = x 2 o y 2 y = x x x + d x 解: 由 得交点 (0, 0) , (1,1) (1,1) 1 d A ( x x )dx 2 = − 3 1 = = 1 0 A 机动 目录 上页 下页 返回 结束

例2.计算抛物线y2=2x与直线y=x-4所围图形 的面积 解:由 y2=2x 得交点 J y=X-4 1y2=2x (8,4) v+d (2,-2),(8,4) 为简便计算,选取y作积分变量, =X- 则有 A=2(y+4-y2)d [y2+4y-y3]2=18 HIGH EDUCATION PRESS 机动目录上页下页返回结束
x y 2x 2 = o y y = x − 4 例2. 计算抛物线 y 2x 2 = 与直线 的面积 . 解: 由 得交点 (2, − 2) , (8, 4) (8,4) d A ( y 4 y )dy 2 2 1 = + − =18 y = x − 4 所围图形 (2,− 2) 为简便计算, 选取 y 作积分变量, 则有 y y + d y − = 4 2 A 机动 目录 上页 下页 返回 结束

x2 例3.求椭圆 =1所围图形的面积 解:利用对称性,有dA=ydx 1=4a 利用椭圆的参数方程 oxx+dxa x x acost y=bsint (0≤t≤2π) 应用定积分换元法得 A=4 bsint.(-asint)dt =4ab =πab 当a=b时得圆面积公式 HIGH EDUCATION PRESS @-0C08 机动目录上页下页返回结束
a b o x y x 例3. 求椭圆 解: 利用对称性 , d A = y dx 所围图形的面积 . 有 = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos = = t y b t x a t 应用定积分换元法得 = 2 0 2 4 sin d ab t t = 4ab 2 1 2 = ab 当 a = b 时得圆面积公式 机动 目录 上页 下页 返回 结束 x + d x

一般地,当曲边梯形的曲边由参数方程 9 给出时,按顺时针方向规定起点和终点的参数值1,2 1y1 0 00 (G1对应x=a》 (t对应x=b) 则曲边梯形面积 A=∫0'0d HIGH EDUCATION PRESS 动目录上页下页返回结束
一般地 , 当曲边梯形的曲边由参数方程 给出时, 按顺时针方向规定起点和终点的参数值 则曲边梯形面积 机动 目录 上页 下页 返回 结束

例4.求由摆线x=a(t-sint),y=a(I-cost)(a>0) 的一拱与x轴所围平面图形的面积 解:A=a0-cos)-al-cos)d/ -a"(1-cost)2di 2πa =a2 si'udu(令a=) -16asin udu =16a2.3.1.z =3πa2 422 HIGH EDUCATION PRESS 机动目录上页下页返回结束
例4. 求由摆线 的一拱与 x 轴所围平面图形的面积 . 解: dA = a (1− cost) a (1− cost)d t a (1 cost) d t 2 0 2 2 = − t t a d 2 4 sin 2 0 2 4 = ) 2 ( t 8a sin u d u 令u = 0 2 4 = 16a sin u d u 2 0 2 4 = 2 = 3 a = 2 0 A 机动 目录 上页 下页 返回 结束 x y o 2 a

2.极坐标情形 设p(0)eC[a,B],p(0)≥0,求由曲线r=p(0)及 射线0=α,0=B围成的曲边扇形的面积 在区间a,B]上任取小区间[0,0+d0] 则对应该小区间上曲边扇形面积的近似值为 所求曲边扇形的面积为 A-3O)d0 HIGH EDUCATION PRESS 机动目录上页下页返回结束
2. 极坐标情形 求由曲线 及 围成的曲边扇形的面积 . r =( ) x d 在区间 上任取小区间 则对应该小区间上曲边扇形面积的近似值为 ( ) d 2 1 d 2 A = 所求曲边扇形的面积为 ( )d 2 1 2 A = 机动 目录 上页 下页 返回 结束

例5.计算阿基米德螺线r=a0(a>0)对应0从0变 到2π所围图形面积 2π4 3x32 点击图片任意处 播放开始或暂停 HIGH EDUCATION PRESS ©-◆OC①8 机动目录上页下页返回结束
例5. 计算阿基米德螺线 对应 从 0 变 解: x 2 a o d ( ) d 2 1 2 a = 2 0 A 2 2 a = 3 3 1 0 2 3 2 3 4 = a 点击图片任意处 播放开始或暂停 机动 目录 上页 下页 返回 结束 到 2 所围图形面积

例6.计算心形线r=a1+cos0)(a>0)所围图形的 面积 解A=2月2a21+2d0 (利用对称性) de 令1=g -8a2cos*rdr =8a2.3.1.3 4222 HIGH EDUCATION PRESS 心形线目录上页下页返回结束
8a cos t dt 2 0 2 4 = 例6. 计算心形线 所围图形的 面积 . 解: o 2a x d (1 cos ) d 2 1 2 2 a + = 0 2 a d 2 4cos4 (利用对称性) 2 令t = = 2 8a 4 3 2 1 2 2 2 3 = a 心形线 目录 上页 下页 返回 结束