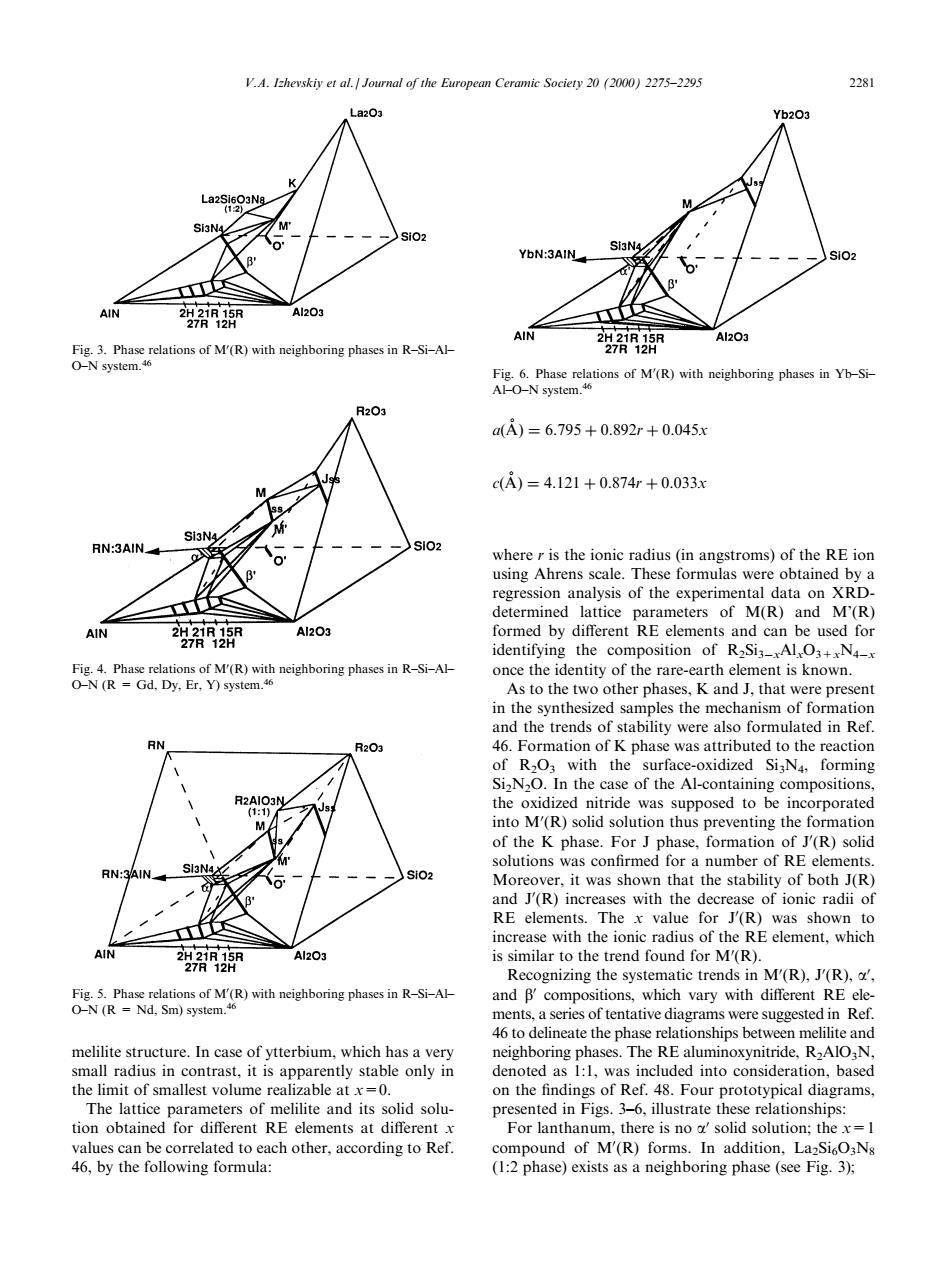
V.A.Izhevskiy et al. al of the European Ceramic Society 20(20)2275-229 -28 DN:3AIN AIN Al203 ns of M(R) oring pha 2 是o ofM(R) oring phases in Yb-s a=6.795+0.892r+0.045x c)=4.121+0.874r+0.033 3AIN regression analysis of the experimenand M(R) identifving the composition of RSiN once the identity of the rare-earth element is known. 二欧 .K and that were presen of the M(ovnthe omation of the K phase.For J phase,formation of J'(R)solid numbe crease of ionic radii of RE elements.The x value for J(R)was shown to increase with the ionic radius o the RE element,which rends in M(R).(R). and Bcompositions.which vary with different RE ele an melilite structure In case of vtterhi which has denoted as :1 was included into consideration.basco the limit of smallest volume realizable at0. on the findings of Ref.48.Four prototypical diagrams. ips ted Io of M'(R)fo 46,by the following formula: (1:2 phase)exists as a neighboring phase (seeFig3) melilite structure. In case of ytterbium, which has a very small radius in contrast, it is apparently stable only in the limit of smallest volume realizable at x=0. The lattice parameters of melilite and its solid solu￾tion obtained for di€erent RE elements at di€erent x values can be correlated to each other, according to Ref. 46, by the following formula: a…A  † ˆ 6:795 ‡ 0:892r ‡ 0:045x c…A  † ˆ 4:121 ‡ 0:874r ‡ 0:033x where r is the ionic radius (in angstroms) of the RE ion using Ahrens scale. These formulas were obtained by a regression analysis of the experimental data on XRD￾determined lattice parameters of M(R) and M'(R) formed by di€erent RE elements and can be used for identifying the composition of R2Si3ÿxAlxO3+xN4ÿx once the identity of the rare-earth element is known. As to the two other phases, K and J, that were present in the synthesized samples the mechanism of formation and the trends of stability were also formulated in Ref. 46. Formation of K phase was attributed to the reaction of R2O3 with the surface-oxidized Si3N4, forming Si2N2O. In the case of the Al-containing compositions, the oxidized nitride was supposed to be incorporated into M0 (R) solid solution thus preventing the formation of the K phase. For J phase, formation of J0 (R) solid solutions was con®rmed for a number of RE elements. Moreover, it was shown that the stability of both J(R) and J0 (R) increases with the decrease of ionic radii of RE elements. The x value for J0 (R) was shown to increase with the ionic radius of the RE element, which is similar to the trend found for M0 (R). Recognizing the systematic trends in M0 (R), J0 (R), a0 , and b0 compositions, which vary with di€erent RE ele￾ments, a series of tentative diagrams were suggested in Ref. 46 to delineate the phase relationships between melilite and neighboring phases. The RE aluminoxynitride, R2AlO3N, denoted as 1:1, was included into consideration, based on the ®ndings of Ref. 48. Four prototypical diagrams, presented in Figs. 3±6, illustrate these relationships: For lanthanum, there is no a0 solid solution; the x=1 compound of M0 (R) forms. In addition, La2Si6O3N8 (1:2 phase) exists as a neighboring phase (see Fig. 3); Fig. 3. Phase relations of M0 (R) with neighboring phases in R±Si±Al± O±N system.46 Fig. 4. Phase relations of M0 (R) with neighboring phases in R±Si±Al± O±N (R = Gd, Dy, Er, Y) system.46 Fig. 5. Phase relations of M0 (R) with neighboring phases in R±Si±Al± O±N (R = Nd, Sm) system.46 Fig. 6. Phase relations of M0 (R) with neighboring phases in Yb±Si± Al±O±N system.46 V.A. Izhevskiy et al. / Journal of the European Ceramic Society 20 (2000) 2275±2295 2281