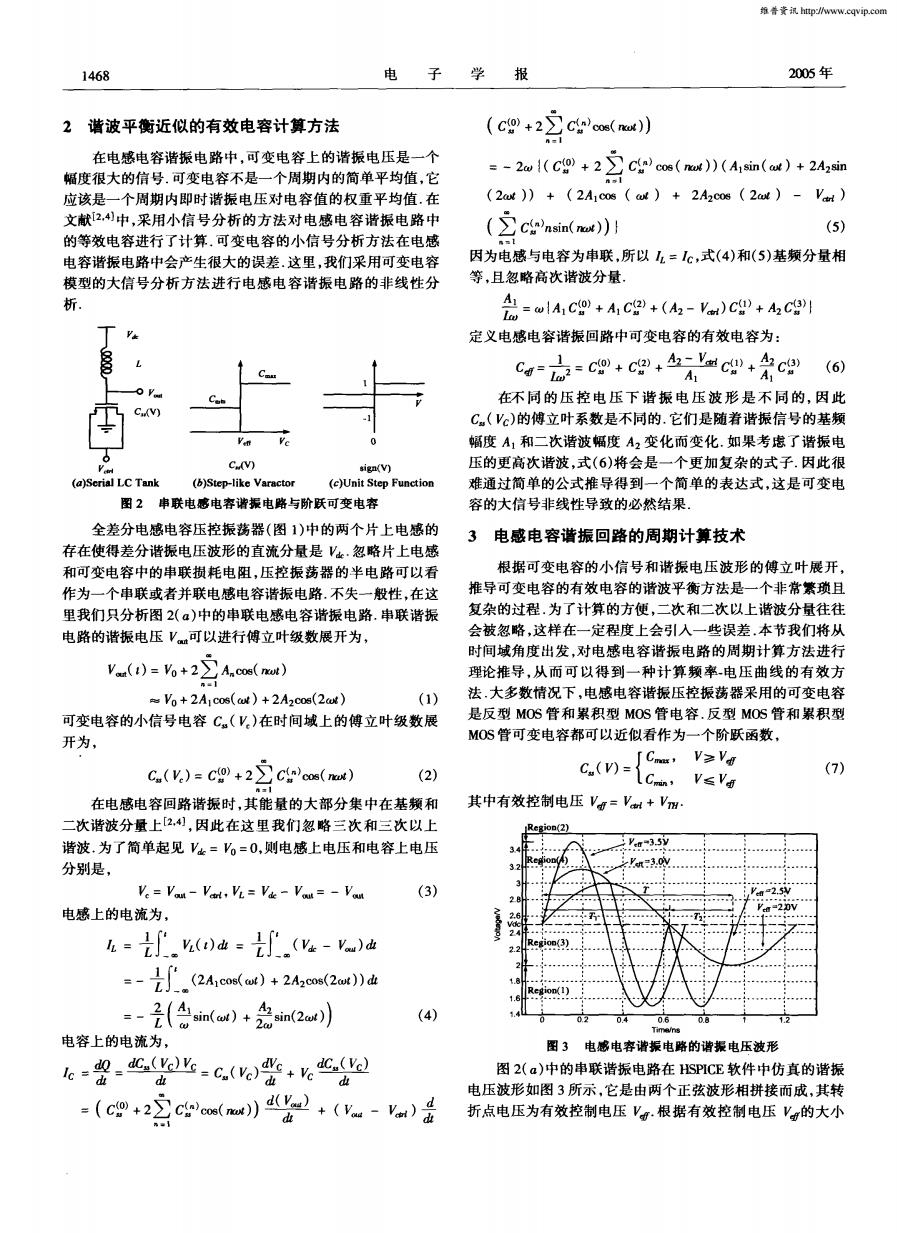
维誉章讯http://www.cqvip..com 1468 电 学 报 2005年 2谐波平衡近似的有效电容计算方法 (c9+22cnos(a）】 -1 在电感电容谐振电路中，可变电容上的谐振电压是一个 =-2(+2c coe (n))(Aisin(ot )+2Azsin 幅度很大的信号.可变电容不是一个周期内的简单平均值，它 nI 应该是一个周期内即时谐振电压对电容值的权重平均值.在 (2ad)）+（2A1co6(a)+2A2cos(2at）-Ve） 文献24)中，采用小信号分析的方法对电感电容谐振电路中 (5) 的等效电容进行了计算.可变电容的小信号分析方法在电感 ((m) 电容谐振电路中会产生很大的误差.这里，我们采用可变电容 因为电感与电容为串联，所以2=1c,式(4)和(5)基频分量相 模型的大信号分析方法进行电感电容谐振电路的非线性分 等，且忽略高次谐波分量. 析. AA C+AC+(A2-V)C+AzC 定义电感电容谐振回路中可变电容的有效电容为： C==c四+cg+mc0+cg A (6) 在不同的压控电压下谐振电压波形是不同的，因此 C(Vc)的傅立叶系数是不同的.它们是随着谐振信号的基频 幅度A1和二次谐波幅度A2变化而变化.如果考虑了谐振电 C(V) sign(V) 压的更高次谐波，式(6)将会是一个更加复杂的式子.因此很 (a)Serial LC Tank (b)Step-like Varactor (c)Unit Step Function 难通过简单的公式推导得到一个简单的表达式，这是可变电 图2串联电感电容谐振电路与阶跃可变电容 容的大信号非线性导致的必然结果. 全差分电感电容压控振荡器（图1）中的两个片上电感的 3电感电容谐振回路的周期计算技术 存在使得差分谐振电压波形的直流分量是V.忽略片上电感 和可变电容中的串联损耗电阻，压控振荡器的半电路可以看 根据可变电容的小信号和谐振电压波形的傅立叶展开， 作为一个申联或者并联电感电容谐振电路.不失一般性，在这 推导可变电容的有效电容的谐波平衡方法是一个非常紫琐且 里我们只分析图2（α）中的串联电感电容谐振电路.串联谐振 复杂的过程.为了计算的方便，二次和二次以上谐波分量往往 电路的谐振电压V可以进行傅立叶级数展开为， 会被忽略，这样在一定程度上会引入一些误差.本节我们将从 Vl)=o+22Aos(m） 时间域角度出发，对电感电容谐振电路的周期计算方法进行 理论推导，从而可以得到一种计算频率电压曲线的有效方 序=1 Vo+2A1cos(aN)+2A2cos(2c) (1) 法，大多数情况下，电感电容谐振压控振荡器采用的可变电容 可变电容的小信号电容C.(V)在时间域上的傅立叶级数展 是反型MOS管和累积型MOS管电容.反型MOS管和累积型 开为， MOS管可变电容都可以近似看作为一个阶跃函数， C.(V)=c+2Ccos(mw) JCm,V≥V (2) (7) n=l c(={cn.v≤v 在电感电容回路谐振时，其能量的大部分集中在基频和 其中有效控制电压V=Vr+Vm: 二次谐波分量上2，！，因此在这里我们忽略三次和三次以上 Region(2) 谐波，为了简单起见Vk=V=0,则电感上电压和电容上电压 35型 分别是， V3.0v Ve Vou-Vart VL=Vie Vau =-Vou (3) 2.5V 电感上的电流为， 20V 么=.)=.（-)恤 io(3) --(2A(w)+2Ao(2wu))d =-是（名in(ow)+2急in2or) (4) 0 0.6 17 Time/ns 电容上的电流为， 图3电感电容谐振电路的谐报电压波形 6-盟.c-g2业=c(些+%C 图2(a)中的串联谐振电路在SPCE软件中仿真的谐振 d d山 d山 电压波形如图3所示，它是由两个正弦波形相拼接而成，其转 =(c0+22ces(w)0+(-a去 折点电压为有效控制电压V.根据有效控制电压V的大小电 子 学 报 2OO5钲 2 谐波平衡近似的有效电容计算方法 在电感电容谐振 电路中 ，可变 电容 上的谐振 电压是 一个 幅度 很大的信号 ．可变 电容 不是一个周期内 的简单平均值 ，它 应该 是一 个周期内即时 谐振 电压 对 电容 值 的权重平 均值 ．在 文献【 】中，采用小信号分析的方法对电感电容谐振电路 中 的等效 电容进行 了计算 ．可变 电容 的小信号 分析方 法在 电感 电容 谐振 电路 中会 产生很大 的误差 ．这里 ，我们采用 可变 电容 模型的大信号分 析方 法进 行 电感 电容谐 振 电路 的非 线性 分 析． C V) O sign(v) (a)S~rialLCTank (b)Step-likeVaractor (c)UnitStepFunction 图 2 串联 电感 电容谐振 电路与阶跃可变 电容 全差分 电感 电容压 控振荡器 (图 1)中的两 个片 上电感 的 存在使得差分谐振 电压 波形 的直流分量是 。忽略 片上电感 和可变电容 中的串联损 耗 电阻 ，压 控振 荡器 的半 电路 可 以看 作为一个 串联或者并联 电感 电容谐振 电路 ．不失一 般性 ，在这 里我们只分析 图 2(o)中的串联 电感 电容谐振 电路 ．串联谐振 电路 的谐振 电压 可以进行傅立 叶级数展 开为 ， (1)：Vo+2∑ ACOS(trot) 一 Vo+2A1COS(cot)+2A2eos(2cvt) (1) 可变电容的小信号 电容 ( )在时 间域上 的傅 立叶级数 展 开为 ， ( )：c +2∑ c c0s( ) (2) 在电感电容回路谐振 时 ，其 能量 的大部 分集 中在基频 和 二次谐波分量上[．4]，因此 在这 里 我们 忽略 三次 和三 次 以上 谐波 ．为 了简单起 见 ：Vo：0，则 电感上 电压 和电容上电压 分别是 ， ： Volt一 ，VL= 一 ：一 (3) 电感 上的电流为 ， ： 』’ (t)dL：』’(一 ) ： 一 _{Il (2A1cos(cot)+2A2cos(2oot))dt ： 一 (sjn(t)+A2sin(2cot)) (4) 电容上的电流为 ， ，c= ： ：()警+ = (c+2客c)cos()) +(一 )d (G +2∑^=I c cos( )) ：一2c￡J{(c +2∑ c cOS( ))(A1sin(“)+2A2sin (2“ )) + (2A1c0s(“ ) (∑n = 1 c nsin(trot))} + 2A212OS(2c,~t) 一 ) (5) 因为 电感与 电容 为串联 ，所 以 =，c，式(4)和(5)基频分量相 等 ，且 忽略高次谐波分量 ． ： c￡J{A1c +A1c +(A2一 )c +A2c } 定义 电感 电容谐振 回路 中可变电容 的有效 电容为 ： = ： c c c A2 。 (3 (6) 在不 同 的 压 控 电压 下 谐 振 电 压 波 形 是 不 同 的，因此 ( )的傅立叶系数是不同的．它们是随着谐振信号的基频 幅度 A 和二次谐波幅度 A2变 化而 变化 ．如果 考虑 了谐振 电 压的更高次谐波 ，式 (6)将 会是 一个更 加复杂 的式 子．因此很 难通 过简单的公式推 导得到一 个简 单的表 达式 ，这是 可变 电 容的大信号非线性导致 的必 然结果 ． 3 电感电容谐振回路的周期计算技术 根据可变电容的小信号和谐振电压波形 的傅立叶展开， 推导可变 电容 的有效 电容 的谐波平衡 方法是一个非常繁琐且 复杂 的过程 ．为 了计算 的方便 ，二次 和二次 以上谐波分量往往 会被忽 略 ，这样在一定程度 上会 引入一些误差 ．本节我们将从 时间域 角度出发 ，对 电感 电容 谐振 电路 的周期计 算方 法进行 理论推导 ，从 而 可 以得 到一 种计 算 频 率．电压 曲线 的有效 方 法 ．大多数情况下 ，电感 电容谐振压控振荡 器采用的可变电容 是反 型 MOS管 和累积型 MOS管 电容 ．反型 MOS管和 累积型 MOS管可变 电容都可 以近似 看作 为一个阶跃 函数 ， ，乏 其 中有效 控制电压 = + ． 11m n8 图 3 电感 电容谐振 电路 的谐振 电压波 形 图 2(a)中的串联谐振电路在 HSPICE软件 中仿真 的谐振 电压波形如 图 3所示 ，它是由两个正弦波形相拼接而 成 ，其转 折点电压为有效控制电压 ．根据有效控制 电压 的大小 甲∽ 维普资讯 http://www.cqvip.com