
维誉黄讯htp:www.cqvip.com 第8期 电子学报 Val.33 No.8 2005年8月 ACTA ELECTRONICA SINICA Ag,2005 电感电容压控振荡器调谐曲线的时域分析 唐长文,何捷,营洪彦,张海青,闵吴 (复旦大学专用集成电路与系统国家重点实验室,上海200433) 摘要:本文提出了一种基于周期计算技术的压控振荡器频率电压调谐曲线的分析方法.在传统的谐波平衡 近似方法中,通过大信号非线性分析方法可以计算出一个周期内可变电容的有效电容值.然而通过有效电容推导的调 谐曲线并不准确,况且如果高阶谐波分量不可以忽略的话,谐波平衡近似分析方法将会变得很复杂,本文提出的周期 计算方法所得到的振荡调谐曲线比传统谐波平衡近似分析方法更加精确.在0.35m2P4 M CMOS工艺上实现的电感电 容压控振荡器的实验测试证明了该理论分析的正确性. 关键词:MOS管可变电容;电感电容回路;压控振荡器;累积型MOS管;振荡调谐曲线 中图分类号:TN4 文献标识码:A 文章编号:0372-2112(2005)08-1467-06 Time-Domain Analysis of LC-VCOs'Tuning Curves TANG Zhang-wen,HE Jie,JIAN Hong-yan,ZHANG Hai-qing,MIN Hao ASIC System Stnte Key Laboratory,Fudan University,Shanghai 200433,China) Abstract:This paper describes a new analytical method of tuning curves of a LC-tank voltage-controlled oscillator (VCO)with period calculation technique.In traditional analysis method,the hammonic approximation is employed,and an effective capacitance of varactors during one period is calculated by the large-signal nonlinear analysis.However,the oscillator tuning curve derived from the effective capacitance is inaccurate,and complex if higher order harmonics could not be neglected.In this paper a novel convenient method of calculating oscillating period is proposed.With this period calculation technique,the prediction of oscillator tuning curves is more accurate compared with the traditional harmonic approximation.The theoretical analyses are experimentally validated with a CMOS complementary LC-tank VCO implemented in 0.35um 2P4M CMOS process. Key words:MOS varactor;LC tank;voltage-controlled oscillator (VCO);accumulation MOS;oscillator tuning curve (OTC) 1引言 本文的工作8]就是:在第二节对采用非线性可变电容的 压控振荡器电路进行了理论分 互补、交叉耦合型负阻结构的电感电容压控振荡器如图 析,给出了谐波平衡近似计算 1所示,交叉耦合的PMOS管对和NMOS管对产生一个负阻用 有效电容的方法;第三节从时 来抵消片上电感和可变电容中的串联电阻,从而使得电感电 间域角度对电感电容谐振电路 容谐振电路能够持续振荡起来.目前有许多发表的文章1,2】 的周期进行了理论推导,得到 中的电感电容压控振荡器电路采用了这种结构,但是它们的 了一种频率电压调谐曲线的 频率-电压(F.V)调谐曲线都是采用SICE仿真或者是侧试得 计算方法:在第四节中我们提 到的,很少是通过理论分析计算得到的.在文献[2]中,S.Lev- 出的周期计算方法与其他文献 antino等人提出了一种频率-电压调谐曲线分析方法,并且采 中的方法进行了详细比较:在 用数值计算的方法得到了FV调谐曲线,我们知道数值计算 最后两节中我们采用HSPICE 是一个复杂而且费时的方法,特别当改变偏置电流的情况下, 软件对串联电感电容谐振电路 整个数值计算结果需要重新进行计算.在文献[3]中,E Hegazi 和压控振荡器电路进行仿真验 等人通过可变电容小信号模型和非线性分析得到了一个精简 证,并且压控振荡器电路进行 的有效电容的计算公式,从而计算得到FV调谐曲线,然而 了流片测试验证,仿真和测试图1CMOS互补、交又糯合型 负阻结构压控振荡器 该方法是基于电容的小信号模型且忽略了高次谐波分量得到 验证结果表明理论公式计算的 的,在一定程度上存在误差。 FV调谐曲线与仿真和测试结果非常吻合. 收稿日期:2004-08-19:缘回日期:2005-01-05 基金项目:上海市科学技术委员2003年度集成电路设计科技专项(No.037062019):上海-应用材料研究与发展基金(No.0425)
第 8期 2005年 8月 电 子 学 报 ACTA EIECI1R0M CA sIM CA V01.33 No.8 Aug. 2005 电感 电容 压 控 振 荡器 调 谐 曲线 的 时域 分析 唐长文,何 捷,菅洪彦 ,张海青,闵 昊 (复旦大学专用集成电路与系统国家重点实验室 ,上海 200433) 摘 要: 本文提出了一种基于周期计算技术的压控振荡器频率一电压调谐 曲线的分析方法 .在传统的谐波平衡 近似方法 中 ,通过大信号非线性 分析 方法可以计算 出一个周期 内可变电容的有效 电容值 .然而通过有效 电容推导 的调 谐 曲线并不准确 ,况且如果高 阶谐 波分量不可 以忽略 的话 ,谐波平 衡近似 分析方法将 会变得 很复杂 .本文提 出的周期 计算方法所得 到的振 荡调谐 曲线 比传统谐波 平衡 近似分析方法更加精确 .在 0.35tan 2P4MCMOS工艺上实现 的电感 电 容压控振荡器 的实验 测试 证明 了该理论分析 的正确性 . 关键词 : MOS管可变 电容 ;电感 电容 回路 ;压 控振荡器 ;累积型 MOS管 ;振荡调谐 曲线 中图分 类号 : TN4 文献标识码 : A 文章 编号 : 0372—2112(2oo5)08-1467—06 Time-DomainAnalysisofLC-VCOs’Tuning Curves TANG Zhang-wen,HEJie,JIAN Hong—yan,ZHANG Hai—qing,MIN Hao (ASIC&5如 StateKeyLak~atory,FudanUniversity,Shanghai200433,Ch/na) Abstract= ThispaperdescribesallewanalyticalmethodoftuningcurvesofaLC—tankvoltage-controlledoscillator(vco)with period calculationtechnique.In traditionalanalysisme thod ,theharmonicapproximation isemployed,and allefec tivecapacitanceof varactorsduring ollepe riod iscalculatedbythe large-signalnonlinearanalysis.However,the oscillatortuning eurvederived from the efectivecapacitanceisinaccurate,andcomplexifhigheroMerharmonicscouldnotbeneOected.In thispaperanovelconvenient me thod of calculating oscillating pe riod ispmpesed.W ith thisperiod calculationtec hniqu e,thepredictionof oscillatortuning curvesis IIioreaccurate compared wi th the traditionalharmonic approximation.The theoreticalanalysesare expe rimentally validated wi th a CMOScompleme ntaryLC—tankVCOimpleme ntedin0.35tma2P4MCMOSprocess. Key、『IIonds: MOSvaractor;I|Ctank;voltage-controlledoscillator(vco);accumulationMOS;oscillatortuning curve(om ) 1 引言 互补 、交叉耦合 型负阻结 构 的电感 电容压控 振荡 器如 图 1所示 ,交叉耦合的 PMOS管对 和 NMOS管对 产生一 个负阻用 来抵消片上电感和可变 电容 中的 串联 电阻 ,从 而使得 电感 电 容谐振 电路 能够 持续 振荡 起来 .目前 有许 多发 表 的文 章 lI2J 中的电感电容压控振荡 器 电路 采用 了这种结 构 ,但是 它们 的 频率 一电压(F-V)调谐 曲线 都是 采用 SPICE仿 真或者是 测试得 到的 ,很少是通 过理论分析计算得 到 的.在文 献 [2]中 ,S.Lev— antino 等人提出 了一 种频率 一电压 调谐 曲线 分析 方法 ,并 且采 用数值 计算的方法得到 了 调谐 曲线 .我们 知道数值 计算 是一个复杂而且费时 的方法 ,特别当改变偏置 电流 的情 况下 , 整个数值计 算结果需要重新进行计算 .在文献 [3]中 ,EHegazi 等人通过可变电容小信号模型 和非线性 分析得到 了一个精简 的有效 电容 的计算 公 式 ,从 而计算 得 到 调谐 曲线 .然 而 该 方法是基于电容的小信号模型且 忽略了高次谐波分量得 到 的 ,在一定程度上存 在误 差 . 本文 的工作 [8]就是 :在第二节 对采用非 线性可 变电容 的 压控振荡器 电路 进行 了理论 分 析 ,给 出 了谐波 平 衡 近似 计 算 有 效电容 的方 法 ;第 三节 从 时 Mpl 问域角度对 电感电容谐振 电路 的周期进 行 了理论 推 导 ,得 到 了一种 频 率一电压 调 谐 曲线 的 计 算方法 ;在第 四节 中我 们 提 出的周期计算 方法与其他文 献 中的方法 进 行 了详 细 比较 ;在 - 最后 两节 中 我 们 采 用 HSPICE 软件对 串联 电感电容谐振 电路 和压控振荡器 电路 进行仿 真验 证 ,并且 压 控振 荡 器 电路 进 行 了流片测 试验 证 ,仿 真和 测试 团 验 证结果表 明理论公式计算 的 ] < [ / ’ L I, L — 厂 ^ 2 CMOS互补、交叉耦合型 负阻结构压控振 荡器 调谐 曲线 与仿真和测试结果非 常吻合 . 收稿 日期 :2OO4-O6.19;修 回 日期 :2005-01—05 基金项 目:上海市科学技术委 员 2003年度集成电路设 计科技 专项(No.037062019);上海 应用材料研究 与发展 基金(No.0425) 维普资讯 http://www.cqvip.com
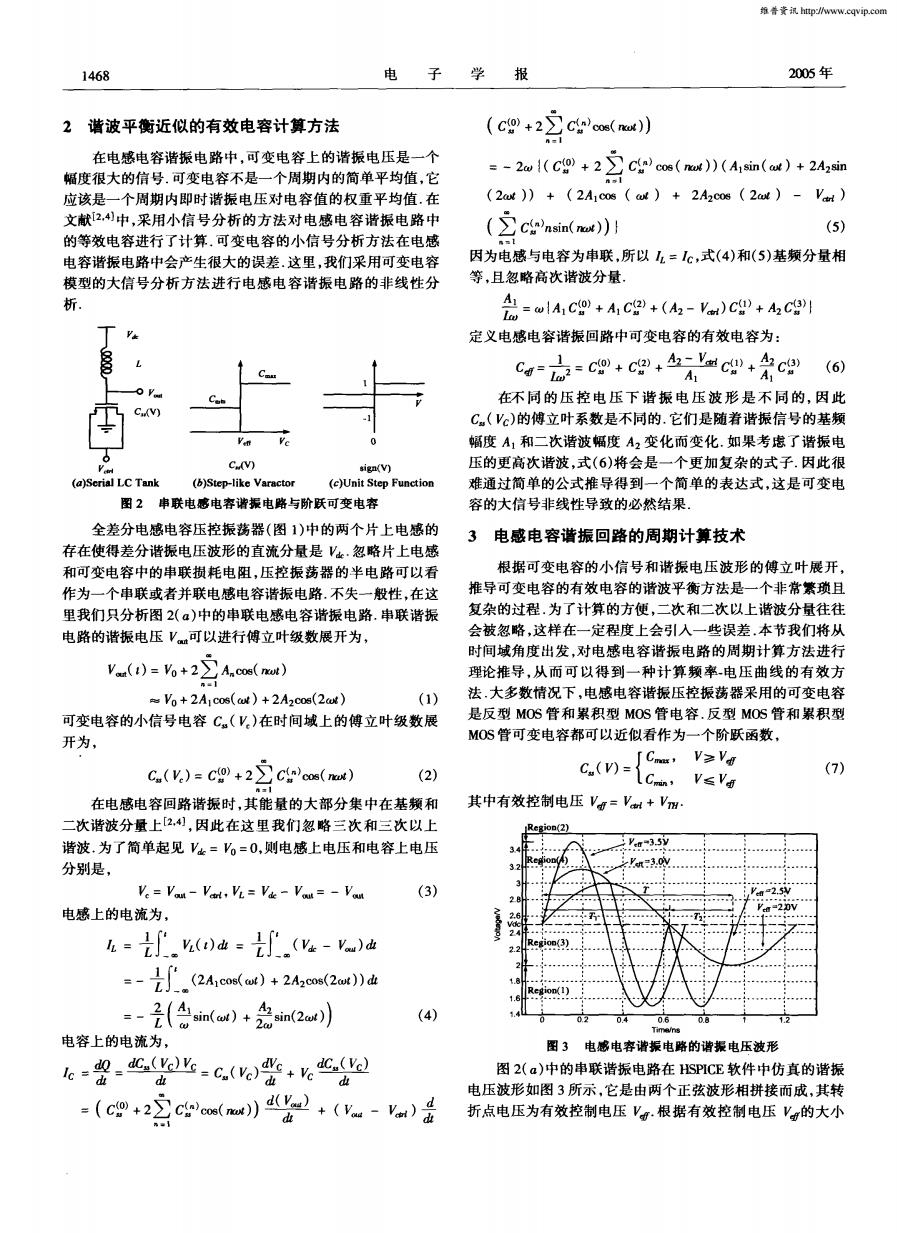
维誉章讯http://www.cqvip..com 1468 电 学 报 2005年 2谐波平衡近似的有效电容计算方法 (c9+22cnos(a)】 -1 在电感电容谐振电路中,可变电容上的谐振电压是一个 =-2(+2c coe (n))(Aisin(ot )+2Azsin 幅度很大的信号.可变电容不是一个周期内的简单平均值,它 nI 应该是一个周期内即时谐振电压对电容值的权重平均值.在 (2ad))+(2A1co6(a)+2A2cos(2at)-Ve) 文献24)中,采用小信号分析的方法对电感电容谐振电路中 (5) 的等效电容进行了计算.可变电容的小信号分析方法在电感 ((m) 电容谐振电路中会产生很大的误差.这里,我们采用可变电容 因为电感与电容为串联,所以2=1c,式(4)和(5)基频分量相 模型的大信号分析方法进行电感电容谐振电路的非线性分 等,且忽略高次谐波分量. 析. AA C+AC+(A2-V)C+AzC 定义电感电容谐振回路中可变电容的有效电容为: C==c四+cg+mc0+cg A (6) 在不同的压控电压下谐振电压波形是不同的,因此 C(Vc)的傅立叶系数是不同的.它们是随着谐振信号的基频 幅度A1和二次谐波幅度A2变化而变化.如果考虑了谐振电 C(V) sign(V) 压的更高次谐波,式(6)将会是一个更加复杂的式子.因此很 (a)Serial LC Tank (b)Step-like Varactor (c)Unit Step Function 难通过简单的公式推导得到一个简单的表达式,这是可变电 图2串联电感电容谐振电路与阶跃可变电容 容的大信号非线性导致的必然结果. 全差分电感电容压控振荡器(图1)中的两个片上电感的 3电感电容谐振回路的周期计算技术 存在使得差分谐振电压波形的直流分量是V.忽略片上电感 和可变电容中的串联损耗电阻,压控振荡器的半电路可以看 根据可变电容的小信号和谐振电压波形的傅立叶展开, 作为一个申联或者并联电感电容谐振电路.不失一般性,在这 推导可变电容的有效电容的谐波平衡方法是一个非常紫琐且 里我们只分析图2(α)中的串联电感电容谐振电路.串联谐振 复杂的过程.为了计算的方便,二次和二次以上谐波分量往往 电路的谐振电压V可以进行傅立叶级数展开为, 会被忽略,这样在一定程度上会引入一些误差.本节我们将从 Vl)=o+22Aos(m) 时间域角度出发,对电感电容谐振电路的周期计算方法进行 理论推导,从而可以得到一种计算频率电压曲线的有效方 序=1 Vo+2A1cos(aN)+2A2cos(2c) (1) 法,大多数情况下,电感电容谐振压控振荡器采用的可变电容 可变电容的小信号电容C.(V)在时间域上的傅立叶级数展 是反型MOS管和累积型MOS管电容.反型MOS管和累积型 开为, MOS管可变电容都可以近似看作为一个阶跃函数, C.(V)=c+2Ccos(mw) JCm,V≥V (2) (7) n=l c(={cn.v≤v 在电感电容回路谐振时,其能量的大部分集中在基频和 其中有效控制电压V=Vr+Vm: 二次谐波分量上2,!,因此在这里我们忽略三次和三次以上 Region(2) 谐波,为了简单起见Vk=V=0,则电感上电压和电容上电压 35型 分别是, V3.0v Ve Vou-Vart VL=Vie Vau =-Vou (3) 2.5V 电感上的电流为, 20V 么=.)=.(-)恤 io(3) --(2A(w)+2Ao(2wu))d =-是(名in(ow)+2急in2or) (4) 0 0.6 17 Time/ns 电容上的电流为, 图3电感电容谐振电路的谐报电压波形 6-盟.c-g2业=c(些+%C 图2(a)中的串联谐振电路在SPCE软件中仿真的谐振 d d山 d山 电压波形如图3所示,它是由两个正弦波形相拼接而成,其转 =(c0+22ces(w)0+(-a去 折点电压为有效控制电压V.根据有效控制电压V的大小
电 子 学 报 2OO5钲 2 谐波平衡近似的有效电容计算方法 在电感电容谐振 电路中 ,可变 电容 上的谐振 电压是 一个 幅度 很大的信号 .可变 电容 不是一个周期内 的简单平均值 ,它 应该 是一 个周期内即时 谐振 电压 对 电容 值 的权重平 均值 .在 文献【 】中,采用小信号分析的方法对电感电容谐振电路 中 的等效 电容进行 了计算 .可变 电容 的小信号 分析方 法在 电感 电容 谐振 电路 中会 产生很大 的误差 .这里 ,我们采用 可变 电容 模型的大信号分 析方 法进 行 电感 电容谐 振 电路 的非 线性 分 析. C V) O sign(v) (a)S~rialLCTank (b)Step-likeVaractor (c)UnitStepFunction 图 2 串联 电感 电容谐振 电路与阶跃可变 电容 全差分 电感 电容压 控振荡器 (图 1)中的两 个片 上电感 的 存在使得差分谐振 电压 波形 的直流分量是 。忽略 片上电感 和可变电容 中的串联损 耗 电阻 ,压 控振 荡器 的半 电路 可 以看 作为一个 串联或者并联 电感 电容谐振 电路 .不失一 般性 ,在这 里我们只分析 图 2(o)中的串联 电感 电容谐振 电路 .串联谐振 电路 的谐振 电压 可以进行傅立 叶级数展 开为 , (1):Vo+2∑ ACOS(trot) 一 Vo+2A1COS(cot)+2A2eos(2cvt) (1) 可变电容的小信号 电容 ( )在时 间域上 的傅 立叶级数 展 开为 , ( ):c +2∑ c c0s( ) (2) 在电感电容回路谐振 时 ,其 能量 的大部 分集 中在基频 和 二次谐波分量上[.4],因此 在这 里 我们 忽略 三次 和三 次 以上 谐波 .为 了简单起 见 :Vo:0,则 电感上 电压 和电容上电压 分别是 , : Volt一 ,VL= 一 :一 (3) 电感 上的电流为 , : 』’ (t)dL:』’(一 ) : 一 _{Il (2A1cos(cot)+2A2cos(2oot))dt : 一 (sjn(t)+A2sin(2cot)) (4) 电容上的电流为 , ,c= : :()警+ = (c+2客c)cos()) +(一 )d (G +2∑^=I c cos( )) :一2c£J{(c +2∑ c cOS( ))(A1sin(“)+2A2sin (2“ )) + (2A1c0s(“ ) (∑n = 1 c nsin(trot))} + 2A212OS(2c,~t) 一 ) (5) 因为 电感与 电容 为串联 ,所 以 =,c,式(4)和(5)基频分量相 等 ,且 忽略高次谐波分量 . : c£J{A1c +A1c +(A2一 )c +A2c } 定义 电感 电容谐振 回路 中可变电容 的有效 电容为 : = : c c c A2 。 (3 (6) 在不 同 的 压 控 电压 下 谐 振 电 压 波 形 是 不 同 的,因此 ( )的傅立叶系数是不同的.它们是随着谐振信号的基频 幅度 A 和二次谐波幅度 A2变 化而 变化 .如果 考虑 了谐振 电 压的更高次谐波 ,式 (6)将 会是 一个更 加复杂 的式 子.因此很 难通 过简单的公式推 导得到一 个简 单的表 达式 ,这是 可变 电 容的大信号非线性导致 的必 然结果 . 3 电感电容谐振回路的周期计算技术 根据可变电容的小信号和谐振电压波形 的傅立叶展开, 推导可变 电容 的有效 电容 的谐波平衡 方法是一个非常繁琐且 复杂 的过程 .为 了计算 的方便 ,二次 和二次 以上谐波分量往往 会被忽 略 ,这样在一定程度 上会 引入一些误差 .本节我们将从 时间域 角度出发 ,对 电感 电容 谐振 电路 的周期计 算方 法进行 理论推导 ,从 而 可 以得 到一 种计 算 频 率.电压 曲线 的有效 方 法 .大多数情况下 ,电感 电容谐振压控振荡 器采用的可变电容 是反 型 MOS管 和累积型 MOS管 电容 .反型 MOS管和 累积型 MOS管可变 电容都可 以近似 看作 为一个阶跃 函数 , ,乏 其 中有效 控制电压 = + . 11m n8 图 3 电感 电容谐振 电路 的谐振 电压波 形 图 2(a)中的串联谐振电路在 HSPICE软件 中仿真 的谐振 电压波形如 图 3所示 ,它是由两个正弦波形相拼接而 成 ,其转 折点电压为有效控制电压 .根据有效控制 电压 的大小 甲∽ 维普资讯 http://www.cqvip.com

维誉膏讯http://www,cqvip..com 第8期 唐长文:电感电容压控振荡器调谐曲线的时域分析 1469 可以将压控过程划分为以下四种情况: (4)当Vk≤V≤Vk+Am时,可变电容的LV轨迹满足 (1)当V≤Vk-An时,谐振波形是一个最小幅值A 两个椭圆方程: 的正弦波,最小频率w· =2,V≥Vw (2)当V≥Vk+Am时,谐振波形是一个最大幅值Am 的正弦波,最大频率wx (3)当Vk-A≤Vg≤V时,在电压Vg以上的谐振波 椭圆相似系数日满足1≤9≤A二 A四 形是最小幅值A的正弦波的一部分,最小频率w: =1,V<Va (12) 电压V以下是幅值为Am(0为椭圆相似系数)的正 弦波的一部分,频率为w 在上述四个情况下,谐振电路的谐振周期分别为: (4)当Va≤V面≤Vk+Amm时,在电压Vg以上的波形是 (1)当V≤Vk-Am时,谐振周期 幅值为A(0为椭圆相似系数)的正弦波形的一部 T=Tna=2πV√LCmx (13) 分,频率为Wma;电压Vr以下是最大幅值A的正弦 (2)当Vr≥Vk+Anm时,谐振周期 波形的一部分,最大频率wm T=Tm=2r√/LC (14) (3)当Vk-Am≤V≤V时,谐振周期为谐振电压波形 在两个椭圆上的时间之和T=T1+T2.T1为在幅值A的椭 圆上的时间,T2为在幅值A=的椭圆上的时间. 如图4所示,在交接点处可变电容上电压和电流分别是 Vg和1.求解式(10)的两个方程,可以得到椭圆相似系数日. 2.00V 由式(10)的第一个椭圆方程可以得到:I=±Wnin Cn A =3)V m-2.50V 275V m3.25V √1-(),代入第二个椭圆方程得, =3.50V -(+(8-(i 1.6 1,8 22242628 32 由式(11)有 图4谐振电路中可变电容的V轨迹图 有效控制电压V控制的四种情况也可以分别用可变电 名√8 (15) 容的1V轨迹图来表示.图4说明了阶跃可变电容的【V轨迹 是由两个椭圆拼接而成.随者有效压控电压的变化,两个椭圆 -' (16) 分别满足两个不同的椭圆方程. 可以计算出在两个椭圆上的时间分别为 (1)当Vg≤Vk-An时,可变电容的LV轨迹满足椭圆 方程: T1= + 元 (8) IV-V4l (2)当V≥Vk+A时,可变电容的V轨迹满足椭圆 T2= 方程: 则谐振电压波形的周期为, (0'+(d (9) T=T+T (3)当V-Amn≤时≤Vk时,可变电容的1V轨迹满足 受+a(】 Amin 两个椭圆方程: (10) ) (17) 椭圆相似系数0满足 (4)当Vk≤V≤Vk+A时,与式(3)相同的方法,求解式 A≤0∈】 (12)的两个方程可以得到:椭圆相似系数和谐振周期 A.gas 特别地,当有效控制电压V=Vk,椭圆相似系数0=1时, --('到 (18) Immx=min C u A min=mr Cmin A mar (11) 其中I是电感和可变电容中的最大电流值。 T=支T+rm+(-am(')r
第 8 期 唐长文 :电感电容压控振荡器调谐 曲线 的时域分析 1469 可以将压控过程划分为 以下 四种情况 : (1)当 ≤ 一A 时 ,谐振 波形 是一个 最 小幅值 A 的正弦波 ,最小 频率 . (2)当 ≥ +A一 时 ,谐振 波形是 一个 最大 幅值 A一 的正弦波 ,最 大频率 一 . (3)当 一A ≤ ≤ 时 ,在 电压 以上 的谐 振波 形是最小幅值A 的正弦波的一部分,最小频率 面; 电压 以下是幅值 为 一 (0为椭 圆相似系数 )的正 弦波的一部分 ,频率为 一 . (4)当 ≤ ≤ +A一 时 ,在 电压 以上的波 形是 幅值 为 似 (0为椭 圆相 似 系数 )的正 弦波 形的 一部 分 ,频率为 ~omin;电压 以下 是最大 幅值 A一 的正 弦 波形的一部分 ,最大频率 ∞一 . 圈 4 谐振 电路 中可变 电容 的 轨迹 图 有效控制电压 艘 制的四种情况也可以分别用可变电 容的 ,- 轨迹 图来表 示.图 4说 明了阶跃可变 电容的 /-V轨迹 是 由两个椭 圆拼接而成 .随着有效压控 电压 的变化 ,两个椭 圆 分别满 足两个 不同的椭 圆方程 . (1)当 ≤ 一A 时 ,可变 电容的 /-V轨迹 满 足椭 圆 方程 : ( )2+( I )=- (8) (2)当 ≥ +A一 时 ,可变 电容 的 ,- 轨迹满 足椭 圆 方程 : ( )2+( I )=· (9) (3)当 一A ≤ ≤ 时 ,可变 电容的 /-V轨迹满 足 两个椭 圆方程 : ( )2+( )2 ≥ ( )2+( I J2: (·。) 椭 圆相似系数 0满 足 ≤ 0≤ 1 特别 地 ,当有效控制 电压 : ,椭 圆相似系数 0:1时 , ,眦 :叫 C— A :叫一 C A一 (11) 其 中 ,一是 电感和 可变 电容 中的最大 电流值 . (4)当 ≤ ≤ +A一 时 ,可变 电容 的 /-V轨 迹满 足 两个椭 圆方程 : ( )2+( ) ≥ , 椭 圆相 似系数 满 足 1≤ ≤ . ( )2+( I ) < (12) 在 上述 四个 情况下 ,谐振 电路 的谐振周期分别为 : (1)当 ≤ 一A面时 ,谐振周期 : :27tv厂瓦_叫 (13) (2)当 ≥ +A一时 ,谐振 周期 = :2丌~/LCm (14) (3)当 一A ≤ ≤ 时 ,谐 振周 期为谐振 电压 波形 在 两个 椭圆上的时 间之和 T:T1+ . 1为 在幅值 A面的椭 圆上的时间, 为在幅值 一的椭圆上的时间. 如图 4所示 ,在交接 点处可变 电容上 电压 和 电流分别 是 和 .求 解式 (10)的两个方 程 ,可以得到椭 圆相似 系数 0. 由式 (10)的第 一个 椭 圆方程 可 以得 到 : = ± 面 c— A √1一( ),代人第二个椭圆方程得, : ( )2+(糍 )(·一( )) 由式(11)有 A=一√毛c : √·一( )+( ) 可 以计算 出在两个椭 圆 E的时间分别 为 耻 2 +asin Am : 则谐振 电压 波形 的周期为 , T : T1+ m , :号——+—。—s—ir.—(=————一)1m 4-专——一—。———(=————一 )1Ⅱtn : 1( + )+(。( ) … in( ) ) (4)当 ≤ ≤ +A一 时 ,与 式 (3)相 同的方 法 ,求 解 式 (12)的两个方 程可以得到 :椭 圆相 似系数和谐振周期 . : : 吉c + +{(一 ( ) (18) 维普资讯 http://www.cqvip.com
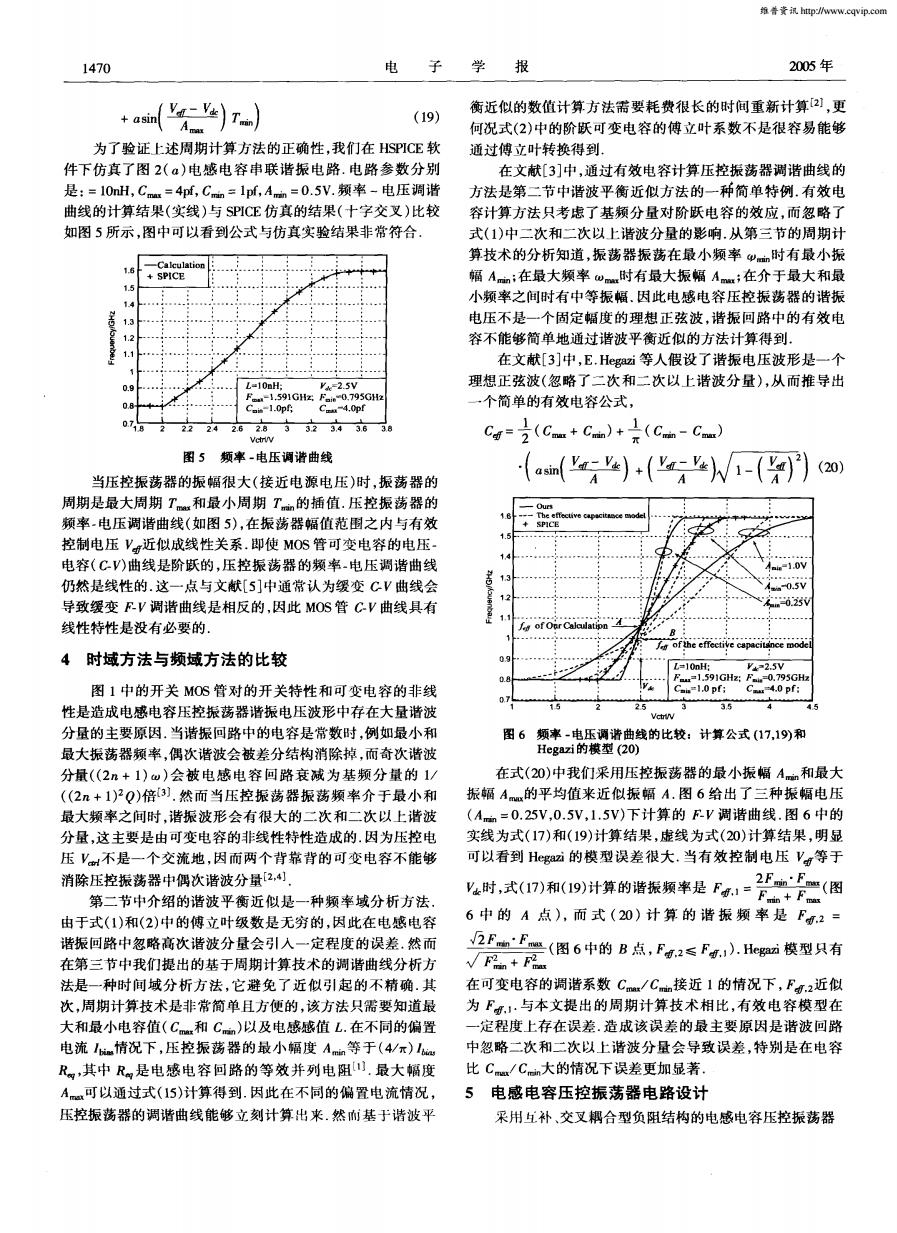
维告黄讯http://www,cqvip..com 1470 电 子 学 报 2005年 +)r 衡近似的数值计算方法需要耗费很长的时间重新计算2!,更 (19) 何况式(2)中的阶跃可变电容的傅立叶系数不是很容易能够 为了验证上述周期计算方法的正确性,我们在HSPICE软 通过傅立叶转换得到. 件下仿真了图2(α)电感电容串联谐振电路.电路参数分别 在文献[3]中,通过有效电容计算压控振荡器调谐曲线的 是:=10mH,Cmu=4pf,Cmn=1pf,Am=0.5V.频率-电压调谐 方法是第二节中谐波平衡近似方法的一种简单特例.有效电 曲线的计算结果(实线)与SPICE仿真的结果(十字交叉)比较 容计算方法只考虑了基频分量对阶跃电容的效应,而忽略了 如图5所示,图中可以看到公式与仿真实验结果非常符合 式(1)中二次和二次以上谐波分量的影响.从第三节的周期计 算技术的分析知道,振荡器振荡在最小频率wm时有最小振 1.6 SPICE 幅A:在最大频率wm时有最大振幅Am;在介于最大和最 1.4 小频率之间时有中等振幅.因此电感电容压控振荡器的谐振 1.3 电压不是一个固定幅度的理想正弦波,谐振回路中的有效电 1.2 容不能够简单地通过谐波平衡近似的方法计算得到. 1.1 在文献[3]中,E.Hegazi等人假设了谐振电压波形是一个 0.9 L=10nH; k-2.5V 理想正弦波(忽略了二次和二次以上谐波分量),从而推导出 F.-1.591GHx:F0.795GH2 0.8时 Csis-1.0pf C-4.0p 一个简单的有效电容公式, 0718 22 24 2.62.83 32343638 cg=2(cam+ca)+(ca-C) 图5频率-电压调谐曲线 (20 当压控振荡器的振幅很大(接近电源电压)时,振荡器的 asm')+('W1-( 周期是最大周期T和最小周期T的插值.压控振荡器的 颍率.电压调谐曲线(如图5),在振荡器幅值范围之内与有效 SPICE 控制电压V近似成线性关系.即使MOS管可变电容的电压 电容(CV)曲线是阶跃的,压控振荡器的频率-电压调谐曲线 -1.0V 仍然是线性的.这一点与文献[5]中通常认为缓变CV曲线会 0.5V 导致缓变FV调谐曲线是相反的,因此MOS管CV曲线具有 线性特性是没有必要的」 of the effective capacitance mode 4时域方法与频域方法的比较 L=10nH: -2.5V F=1.591GHz:Fm=0.795GH 图1中的开关MOS管对的开关特性和可变电容的非线 Cai=1.0 pf: C4.0D: 性是造成电感电容压控振荡器谐振电压波形中存在大量谐波 25 3.5 Vctry 分量的主要原因.当谐振回路中的电容是常数时,例如最小和 图6频率-电压调谐曲线的比较:计算公式(17,19)和 最大振荡器频率,偶次谐波会被差分结构消除掉,而奇次谐波 Hegazi的模型(20) 分量(2n+1)w)会被电感电容回路衰减为基频分量的1/ 在式(20)中我们采用压控振荡器的最小振幅Am和最大 (2n+1)2Q)倍3).然而当压控振荡器振荡频率介于最小和 振幅Am的平均值来近似振幅A.图6给出了三种振幅电压 最大频率之间时,谐振波形会有很大的二次和二次以上谐波 (A=0.25V,0.5V,1.5V)下计算的E-V调谐曲线.图6中的 分量,这主要是由可变电容的非线性特性造成的.因为压控电 实线为式(17)和(19)计算结果,虚线为式(20)计算结果,明显 压V不是一个交流地,因而两个背靠背的可变电容不能够 可以看到Hegazi的模型误差很大.当有效控制电压Vg等于 消除压控振荡器中偶次谐波分量[2,, 2FnF(图 第二节中介绍的谐波平衡近似是一种频率域分析方法, y时,式(17)和(19)计算的谐振频率是F1=FF二 由于式(1)和(2)中的傅立叶级数是无穷的,因此在电感电容 6中的A点),而式(20)计算的谐振频率是F.2= 谐振回路中忽略高次谐波分量会引入一定程度的误差.然而 2FF(图6中的B点,F2≤F,.Heg模型只有 在第三节中我们提出的基于周期计算技术的调谐曲线分析方 √F2n+F 法是一种时间域分析方法,它避免了近似引起的不精确.其 在可变电容的调谐系数Cm/Cm接近1的情况下,F.2近似 次,周期计算技术是非常简单且方便的,该方法只需要知道最 为F,1·与本文提出的周期计算技术相比,有效电容模型在 大和最小电容值(C和C)以及电感感值L.在不同的偏置 一定程度上存在误差.造成该误差的最主要原因是谐波回路 电流情况下,压控振荡器的最小幅度Am等于(4/r)lb 中忽略二次和二次以上谐波分量会导致误差,特别是在电容 R,其中R是电感电容回路的等效并列电阻.最大幅度 比Cmx/Cmn大的情况下误差更加显著。 A可以通过式(15)计算得到.因此在不同的偏置电流情况, 5电感电容压控振荡器电路设计 压控振荡器的调谐曲线能够立刻计算出来.然而基于谐波平 采用互补、交叉耦合型负阻结构的电感电容压控振荡器
1470 电 子 学 报 2OO5矩 … in( ) ) (19) 为 了验证上述周期计算 方法的正确性 ,我们 在 HSPICE软 件下仿真 了图 2(a)电感 电容 串联 谐 振 电路 .电路参 数 分别 是 :=10nil,c~ =4pf,C =lpf,A,m =0.5V.频率 一电压 调谐 曲线 的计算结果 (实线 )与 SPICE仿真 的结果 (十字交叉 )比较 如图 5所示 ,图中可 以看到公式 与仿 真实 验结果非常符合 . - CalculationI SPICE I L=10nH; _2 V . 1.591GHz;F I。 795GHz _·_●一 Cml。=1.op C .Opf V etrl/V 图 5 频率 .电压调谐 曲线 当压控振荡器 的振 幅很大 (接 近电 源电压 )时 ,振荡 器的 周期是最大周期 7I眦 和最 小周 期 7 的插 值 .压控 振荡 器的 频率 .电压 调谐 曲线 (如 图 5),在振荡器 幅值范 围之 内与有 效 控制电压 近似成线性关 系.即使 MOS管可变 电容的 电压 一 电容 (C-V)曲线是阶跃 的,压控 振荡器 的频率 一电压调谐 曲线 仍 然是 线性 的 .这一点 与文 献[5]中通常认为缓变 C-V曲线会 导致缓变 F-V调谐 曲线 是相反的 ,因此 MOS管 C-V曲线具有 线 性特性是没有必要的 . 4 时域方法与频域方法的比较 图 1中的开关 MOS管对 的开关特性 和 可变 电容 的非线 性是造成电感电容压控振荡器谐振电压波形中存在大量谐波 分量 的主要原因.当谐振 回路 中的电容是 常数 时 ,例如最小 和 最大振荡器频率 ,偶次谐波会被差分结构 消除掉 ,而奇次谐波 fitjr((2n+1) )会被 电感 电容 回路 衰减 为 基频 分 量 的 1/ ((2n+1)0p)倍[31.然 而 当压 控振 荡器 振 荡频率 介 于最 小和 最大频率之 间时 ,谐振 波形 会有 很大的 二次 和二次 以上谐波 分量 ,这 主要 是由可变 电容的非线性特性造成 的.因为压控 电 压 不 是一个 交流地 ,因而两 个背靠 背的 可变 电容 不能够 消除压控振荡器 中偶 次谐 波分 量Ll4J. 第二节 中介绍 的谐 波平衡近 似是 一种频 率域分 析方 法 . 由于式 (1)和(2)中的傅 立叶级数 是无穷 的 ,因此在 电感 电容 谐振回路中忽略高次谐 波分量会 引入 一定程 度的误 差 .然而 在第三节 中我们提 出的基 于周期计算技 术的调谐曲线分析方 法是一种 时 间域 分 析方 法 ,它避 免 了近似 引起 的不精 确 .其 次 ,周期计算技术是非 常简单且 方便 的 ,该方 法只需要知道最 大和最小电容值(c~和 c )以及电感感值 .在不同的偏置 电流 Jbi膻情况下 ,压 控 振荡 器 的最小 幅度 A 等 于 (4/ ) R棚,其中 R 是电感电容 回路的等效并列电阻_lj.最大幅度 A一可 以通过式(15)计算得 到.因此在 不同 的偏 置 电流情况 , 压控振荡器 的调谐 曲线能够 立刻计 算 出来 .然 mi基 于谐波 平 衡近似的数值计算方法需要耗费很长的时问重新计算 J,更 何况式 (2)中的阶跃可变 电容 的傅 立叶系数 不是很 容易能 够 通过傅 立叶转换得 到 . 在文 献[3]中 ,通过有效 电容计算 压控振荡器调谐 曲线 的 方法是第二节中谐波平衡近似方法的一种简单特例.有效电 容计算方法 只考虑 了基频分 量对 阶跃 电容 的效应 ,而忽略 了 式 (1)中二 次和二次以上谐波分量的影响 .从 第三节的周期计 算技术 的分析知道 ,振荡 器振 荡在最 小频 率 时有最 小振 幅 A ;在最 大频率 ct,一时有最大振幅 A~ ;在介于 最大和最 小频 率之间时有 中等振 幅 .因此 电感 电容 压控振 荡器 的谐振 电压 不是一个 固定幅度 的理想 正弦 波 ,谐 振 回路中 的有 效 电 容不能够简单地通过谐 波平 衡近似的方法计算得到 . 在文献 [3]中,E.Hegazi等人假设 了谐振 电压波形 是一个 理想正弦波(忽 略了二次 和二次 以上谐波 分量 ),从 而推 导 出 一 个简单的有效 电容公式 , c =号(c~+c ) _=,It-(c 一c~) 。 (锄( )+( )√一())c加 图 6 频率 一电压调 谐 曲线的 比较 :计算公式 (17,19)和 Hegazi的模 型 (2O) 在式 (20)中我们采用压控振荡器 的最 小振 幅 A 和最大 振 幅 A 的平均值来 近似振 幅 A.图 6给出 了三种 振幅 电压 (A =0.25V,0.5V,1.5V)下 计算 的 F-V调谐 曲线 .图 6中的 实线 为式 (17)和(19)计算结 果 ,虚线 为式 (20)计算 结果 ,明显 可以看到 Hegazi的模 型误差 很 大.当有 效控 制 电压 等于 ,)F .F 时 ,式(17)和 (19)计算 的谐振 频率是 .。= (图 6中 的 A 点 ),而 式 (20)计 算 的 谐 振 频 率 是 .2= "~ / F . F .I"min = I'max(图 6中的 B点 , , 2≤ ,1).Hegazi模 型 只有 V , + ,_眦 在可变 电容 的调谐 系数 /C 接 近 1的情 况下 , .2近似 为 .,.与本文提 出的周 期计 算技 术相 比,有 效 电容模 型 在 一 定程度上存在误差 .造 成该误 差 的最 主要 原因是谐 波 回路 中忽略二次和二次 以上谐波 分量 会导致 误差 ,特别 是在 电容 比 c一/c 大 的情况下误差 更加 显著 . 5 电感 电容压 控振 荡器 电路设计 采用互补 、交叉耦 合型负阻结构 的电感 电容压控振 荡器 N工0『^3u∞ 正 维普资讯 http://www.cqvip.com

维普黄讯http://www.cqvip.com 第8期 唐长文:电感电容压控振荡器调谐曲线的时域分析 1471 电路(图7)在IsMC0.35m1P4M3.3V逻辑工艺上实 现,该电路的芯片照片如图8所示,大多数工艺厂 SUE 商,尤其是数字工艺,不提供累积型MOS管模型,为 R(5.280hm) Lg(2.05nH) 了解决SPICE瞬态仿真的问题,我们采用BSM3V3 D+ 0 W 000 ● 模型的子电路来等效累积型MOS可变电容6)(图 n-well p-8u的 9).因为累积型NMOS是实现在N阱中,其电容工作 Cpm(85.2F) Cpm(84.2 在累积区和耗尽区两个区域.普通的NMOS不能够 R R-b1(0.7510hm) 实现电容值在累积区和耗尽区两个区域之间变化, SUB R(1.I5Ohm) 因此选用一个PMOS管作为可变电的主体,橱极与村 SUBO 底电容C作为可变电容值. 因为累积型MOS管可变电容不会形成反型沟 图9累积型MOS可变电容子电路模型 图10片上螺旋电感等效π模型 道,为了使普通的PMOS管具有与累积型NMOS管相 修改PMOS管的BSM3V3模型来解决这个问题,另外一方面 由于BSM3V3模型的仿真收敛性要求交叠电容不能为零,实 10nH L2 际上我们将PMOS管的参数CGD0和CGSO减小到一个可以 20pf 忽略的值.(譬如如诚小为1/10倍). p 累积型NMOS管品质因数Q反比于2,所以采用最小沟 00/0.35 4000.35 L0-2L 道长度(0.35m),其宽长比为1200m/0.35m.可变电容版图 50/03 0Q020 500.33 实现采用全差分叉指结构布局,两边可变电容的栅极交叉排 12000.35 1200/0.35 Mn6 列,不形成源漏内插结构,这样可以进一步降低交叠寄生电 容,谐振电感0是采用片上对称差分结构螺旋电感.我们采 C0-C CO-C 1600.35 1600.35 用M2-M3-M4三层金属并联来降低串联电阻.而使用M1金 Mn2 属连接分段的N阱形成电场地隔离屏蔽层来提高电感在2~ 3GHz频率范围的Q值,在2.8CHz频率工作点上,Q值最大 C3 20pf 为5.片上电感的等效π模型(图10)参数在ASTC软件中 提取得到. 交叉耦合的PMOS对管和NMOS对管的跨导选择使得谐 C310p 振波形的直流电平位于Va2.一方面这样可以使得谐振电压 图7互补、交叉耦合型负阻结构的电感电容压控振荡器 有尽量大的振幅;另一方面可以保证压控电压范围很大,从而 域小压控增益系数,提高振酱器的相位噪声性能.为了使 得交叉耦合MOS管产生的负阻更大一些,Mnl-Mn2,柳l- 柳2管的栅长都选择最小尺寸0.35m.我们采用了开稀输出 的缓冲器作为输出级,在片外使用Bias-T电路进行电流偏置. 开漏输出的缓冲器MOS管Mn5-Mn6的宽度选择一个比较小 的值(50m),以降低寄生电容.Mn3-Mn4是镜像电流源,其栅 长取得大一些(0.8m),降低沟道调制效应. 片上电感L1和电容C1组成的电感电容谐振回路用来 抑制交叉耦合NMOS对管的共模二次谐波分量;片上电感L2 和电容C2组成的电感电容谐振回路用来抑制交叉耦合 PMOS对管的共模二次谐波分量.电容C3用来抑制Mn4-Mn3 管的1/f噪声和M3管的沟道调制引起的AM-FM效应 6仿真和测试验证 细 图7的电感电容压控振荡器电路在HSPICE软件上进行 图8振荡器芯片照片 仿真,通过改变压控电压,测量振荡器的基次谐波的频率,我 同的特性,在普通PMOS管的源漏与地之间接一个非常大的 们得到如图11所示的频率-电压(FV)调谐曲线.电感电容谐 电阻(譬如10CD的电阻).另外普通的PMOS管的源漏与栅之 振回路的电感是一个差分电感,对于单端而言电感感值为 间的存在很大的交叠电容,而在累积型NMOS管中,由于源漏 1.025nlH.最大和最小振荡频率分别是f=3.04CHz和f= 区的注入类型与衬底的相同,交叠电容不存在.我们可以通过 2.53GHz,可变电容的最大和最小值分别是Cmm=3.866pf和
第 8 期 唐 长文 :电感 电容压控振 荡器调谐曲线的时域分析 1471 电路 (图 7)在 TSMC0.35pro 1P4M3.3V逻辑 工艺 上实 现 ,该 电路 的 芯 片照 片 如 图 8所 示 .大 多 数 工 艺 厂 商 ,尤其是数字工 艺 ,不提供 累积 型 MOS管 模型 .为 了解决 SPICE瞬 态仿 真 的问 题 ,我 们 采 用 BSIM3V3 模型的 子 电路 来 等效 累积 型 MOS可 变 电容 _6j(图 9).因为累积型 NMOS是实现在 N阱 中,其 电容 工作 在 累积 区和 耗尽 区 两个 区域 .普通 的 NMOS不 能 够 实现 电容值在 累积 区和 耗尽 区两 个 区域 之间 变化 , 因此选用一个 PMOS管作 为可变电的主体 ,栅极 与衬 底 电容 Ccz作为可变 电容值 . 因为累积型 NMOS管 可变 电容不会 形成反 型沟 道 ,为了使普通 的 PMOS管 具有与 累积 型 NMOS管 相 10nH 凄£ L2 . 35 CO=C CO=C 图 7 互补、 ] Mp2;i羞!; LI C320pf 上 L王 G 5.28Ohm) 工 2.05nil) 图 9 累积型 MOS可变 电容子 电路模型 图 lO 片上螺旋 电感等效 石模型 交叉耦合 型负阻结构 的电感 电容 压控振荡器 图 8 振荡 器芯片照片 同的特性 ,在普通 PMOS管的源漏与地之间接一个非常大的 电阻(譬如 lOCAl的电阻).另外普通 的 PMOS管 的源漏 与栅 之 间的存在很 大的交叠电容 ,而在 累积型 NMOS管 中,由于源漏 区的注入类 型与衬底的相 同,交叠 电容不存 在 .我们 可以通过 修 改 PMOS管 的 BSIK3V3模 型来解 决这个 问题 ,另外 一方 面 由于 BSIM3V3模型 的仿真 收敛性 要求交 叠电容 不能 为零 ,实 际上我 们将 PMOS管 的参数 CGDO和 CGSO减 小到一 个可 以 忽略 的值 .(譬如如减小 为 1/10倍 ). 累积 型 NMOS管 品质 因数 Q反 比于 ,所 以采用 最小沟 道长度 (0.35,ttm),其宽 长 比为 1200tm~0.35,ttm.可变 电容版 图 实现采 用全差分叉指结 构布局 ,两边可变 电容 的栅极 交叉排 列 ,不形成源 漏 内插结 构 ,这样 可 以进 一步 降低 交叠 寄 生 电 容.谐振电感 加 是采用片上对称差分结构螺旋电感.我们采 用 M2.M3.M4三层 金属并联来 降低 串联 电阻 .而使用 M1金 属连 接分段 的 N阱形成 电场地隔离屏蔽层 来提 高电感在 2~ 3GHz频率范围的 Q值,在 2.8GHz频率工作点上,Q值最大 为 5.片上 电感 的等效 7c模 型 (图 10)参数 在 ASITIC[]软件 中 提取得 到 . 交叉耦合 的 PMOS对管和 NMOS对管 的跨导选 择使得 谐 振 波形 的直流电平位于 /2.一方 面这样 可以使 得谐振 电压 有尽量大 的振 幅 ;另一方面 可以保证压控 电压范围很大 ,从 而 减小压控增益 系数 ,提高振 荡器 的相 位 噪声性 能 .为 了使 得交 叉 耦 合 MOS管产 生 的负 阻更 大 一 些 ,Mn1.Mn2,Mp1. Mp2管的栅长都选择最小 尺寸 0.35tan.我们采 用 了开漏输 出 的缓 冲器作 为输 出级 ,在片外使用 Bia.s-T电路进行 电流偏置 . 开漏输 出的缓 冲器 MOS管 Mn5.Mn6的宽度选 择一个 比较小 的值 ( 朋),以降低 寄生电容 .Mn3一Mn4是镜像 电流源 ,其栅 长取得大一些 (0.8tma),降低沟道调制效应 . 片上 电感 ,J1和 电容 C1组成 的 电感 电容 谐振 回路 用来 抑制交叉耦合 NMOS对管 的共模 二次谐 波分量 ;片上 电感 2 和电容 c2组 成 的 电感 电 容 谐 振 回路 用 来 抑 制 交 叉 耦 合 PMOS对 管的共 模二次谐波分量 .电容 c3用来 抑制 Mn4一Mn3 管 的 1/f噪声和 Mn3管 的沟道调制引起 的 AM-FM 效应 . 6 仿 真和 测试 验证 图 7的电感 电容压控 振荡器 电路在 HSPICE软 件上进 行 仿 真 .通过改变压控 电压 ,测量振 荡器 的基次谐 波 的频率 ,我 们得 到如 图 11所示 的频 率一电压(r-v)调 谐曲线 .电感 电容谐 振 回路 的电感 是 一 个差 分 电感 ,对 于 单端 而 言 电感 感 值 为 1.025nH.最大 和最 小振荡频率分别是 /.咄 =3.04GHz和 / : 2.53GHz,可变 电容 的最 大 和最小 值分 别 是 C =3.866pf和 一 一 田 2 5‰ T● 工 ll 维普资讯 http://www.cqvip.com

维告黄讯http://www,cqvip..com 1472 电 学 2005年 Can=2.678pf.谐振电压的直流电平Vk= Caculation -Caculation 1.842V,振幅最小值为Am=0.977V,振幅 SPICE +SPICE 最大值根据公式(15)计算为Am=1.174V. 2.9 444 因此根据式(17)和(19)可以得到FV调谐 28 曲线如图11实线所示,十字交叉为HSPICE 27 仿真结果,可以看到仿真结果与计算结果 La1.025n -1&42V L-1.0250H: V-1.837V 非常吻合,FV调谐曲线的测试结果与公 R-3.04GHz "2.53GHz =3.03GHz:F-2.48GH2 Cnn-2.678pf:Cma-3.866pf 2 Cm-2.694pfCm-4.036p 式计算结果比较结果如图12所示,由于电 Anin-0.977V;Ame-1.174V 4-0.958V:Am=1.172V 16 2 2.4 25 3 3.5 0.5 2.5 3 35 路版图设计中会引人一些寄生电容,使得 Vctrl/Vottage VervVoltage 测试结果的最小频率比SPICE仿真的要小 图11F-V调谐曲线的仿真与计算结果比较图12F-V调谐曲线的测试与计算结果比较 一些.然而FV调谐曲线的测试结果与公式计算结果还是非 [5 F Svelto,P Erratico,et al.A Metal-Oxide-Semiconductor varactor[J] 常的接近的 IEEE Electron Device Letters,1999,20(4):164-166. [6]K Molnar,G Rappitsch,et al.MOS varactor modeling with a subcircuit 7结论 utilizing the BSIM3v3 model [J].IEEE Trans on Electron Devices, 电感电容压控振荡器的谐振电压不再是一个小信号了, 2002,49(7):1206-1211. 传统的小信号分析方法将会产生很大的误差.以往通过电感 [7 ASTTIC Website:http://rfic.eecs.berkeley.edu/~niknejad/asitic. 电容谐振回路的非线性分析方法是一个非常复杂的、精度不 html. 高的等效电容计算方法.本文从时间域角度对电感电容谐振 [8]唐长文.电感电容压控振荡器[D].上海:复旦大学,2004 电路的周期进行了理论上推导,得到了一种计算频率一电压 调谐曲线的方法.最后,我们采用HSPICE软件对电感电容串 作者简介: 联谐振电路和电感电容压控振荡器电路进行仿真验证,并且 压控振荡器电路进行了流片测试验证.仿真和测试验证结果 唐长文男,197年出生于江西临川,1999 表明我们提出的周期计算技术得到的FV调谐曲线与仿真 年毕业于复且大学电子工程系,获电路与系统专 和测试结果非常吻合. 业学士学位:204年获得复旦大学微电子学系电 路与系统专业理学博士学位,现在复旦专用集成 参考文献: 电路与系统国家重点实验室工作,研究方向为单 [1 A Hajimiri,T H Lee.Design issues in CMOS differential LC oecillators 片多制式数字桃频编码器系统研究、CMO6运算 [J].IEEE J.Solid-State Circuits,1999,34:717-724. 放大器的设计与优化、射频集成电路分析与设 [2]S Levantino,C Samori,et al.Frequency dependence on bias current in 计、CMOS单片集成数字电视调谐器.E-mail:zwtang@fudan.c.cn. 5-GHz CMOS VCOs:Impact on tuning range and flicker noise upcon- version[J].IEEE J.Solid-State Circuits,2002,37:1003-1011. 何捷男,1978年出生于江苏省丹阳市, [3]E Hegazi.A Abidi.Varactor characteristics,oscillator tuning curves, 2000年毕业于复且大学电子工程系,获理学学士 and AM-FM conversion[J].IEEE J Solid-State Circuits,2003.38(6): 学位,现在是复旦大学微电子系博士研究生,研 1033-1043. 究方向为混合信号集成电路设计、集成频率综合 [4 S Levantino,C Samori,et al.AM-to-PM conversion in varactor-tuned 器 cecillator[J].IEEE Trans on Circuits ad System-II,Analog and Digi- tal Signal Procesaing,2002,49(7):509-513
1472 电 子 学 报 2OO5证 C =2.678pf.谐振电压的直流电平 = 1.842V,振幅最 小 值 为 面 =0.977V,振 幅 最大值根据公式(15)计算为 一 :1.174V 因此根据式 (17)和 (19)可 以得到 F-V调谐 曲线如 图 11实线所示 ,十字交叉为 HSPICE 仿真结果 ,可 以看 到仿 真 结果 与计 算 结果 非常吻合 ,F-V调 谐 曲线 的测 试 结果 与公 式计算结果比较结果如图 12所示 .由于电 路版图设计 中会 引 入一 些 寄生 电容 ,使 得 测试结果 的最 小频率 比 SPICE仿 真 的要 小 · — — Caculation + SPlCE - - IL=1.025nil; ;1.842V l Ⅱ=304GHz;Fm 2.53GII: 。 。 Ic =2.678pf;G =3.866pf f…=-0977V; 一 =1.I74V · — + C S a P ~ lC llI E ation , _d ● . . . £=1.025nH; =I.83W . . f.址 =3.03GHz;f 一2.48GHz 2.694pf; :4.036pf =0.958V; _l=1.172V 图 l1 调谐 曲线 的仿真与计算结果 比较 图 l2 调谐 曲线 的测 试与计算结果 比较 一 些 .然 而 F-V调谐 曲线的测试结 果与公 式计算 结果还 是非 常的接近 的. 7 结 论 电感电容压控振荡器的谐振 电压不再是一个小信号了, 传统的小信号分析方法 将会产 生很大 的误差 .以往通过 电感 电容谐 振回路的非线性 分析方法 是一 个非常 复杂 的 、精 度不 高的等效电容计算方法 .本 文从 时 间域角度 对 电感电容 谐振 电路的周期进行了理论上 推导 ,得 到了一种计 算频 率 一电压 调谐曲线的方法 .最 后 ,我们采用 HSPICE软 件对 电感 电容 串 联谐振 电路 和电感电容压 控振荡 器 电路 进行仿 真验 证 ,并且 压控振 荡器 电路进行 了流片测试 验证 .仿真 和测试 验证结 果 表明我们提出的周期 计 算技 术得 到 的 F-V调谐 曲线 与仿 真 和测试结果 非常吻合 . 参考文献 : 【1] Amjimiri,THLee.DesignissuesinCMOSdiferentialLCoscillators [J].—IEE—EJSolld-StateCircuits,1999,34:717—724. [2] SLevantino,CSamori,eta1.Frequencydependence(311biascurrentin 5一GHzCMOS VCOs:III (311tuning range and flickernoise up(~3/l— version[J].mEEJSolid.StateCircuits,2002,37:1003—1011. [3] EHegn~,A Abidi.Varactorcharacteristics,oscillatort,mmsCUrVes, andAM-FM conversion[J].—IEE—EJSolid-StateCircuits,20O3,38(6): 1033— 1043. [4] SLevantino,CSamori,eta1.AM-to-PM (;onversion invaractor-tuned oscillator[J].—IEE—ETram (311CircuitsandSystems-II,AnalogandDisi— talSi Pr0c ,2002,49(7):509—513. [5] [6] [7] [8] FSvelto,PEIT~CO,eta1.AMetal-Oxide-Semiconductorvar,~ [Jj IEEEElectronDeviceLetters,1999,2O(4):164—166 K Molnar.G Rappitsch.eta1 .M0S va -ct0r,r~ eling with asubciwuit utilizingtheBSIM3v3model[J].—1EE—I~Tram OilElectronDevious, 20O2,49(7):1206—1211 AS1TICWebsite:http://rficee .berkeley.edu/~niknejad/asitlc htm1 唐长文 电感电容压控振荡器 [D]上海 :复旦大学 ,20O4 作者简介 : Nz0舌 cg 拈 ” Nz0~uc∞3寸鬯 一璧 维普资讯 http://www.cqvip.com