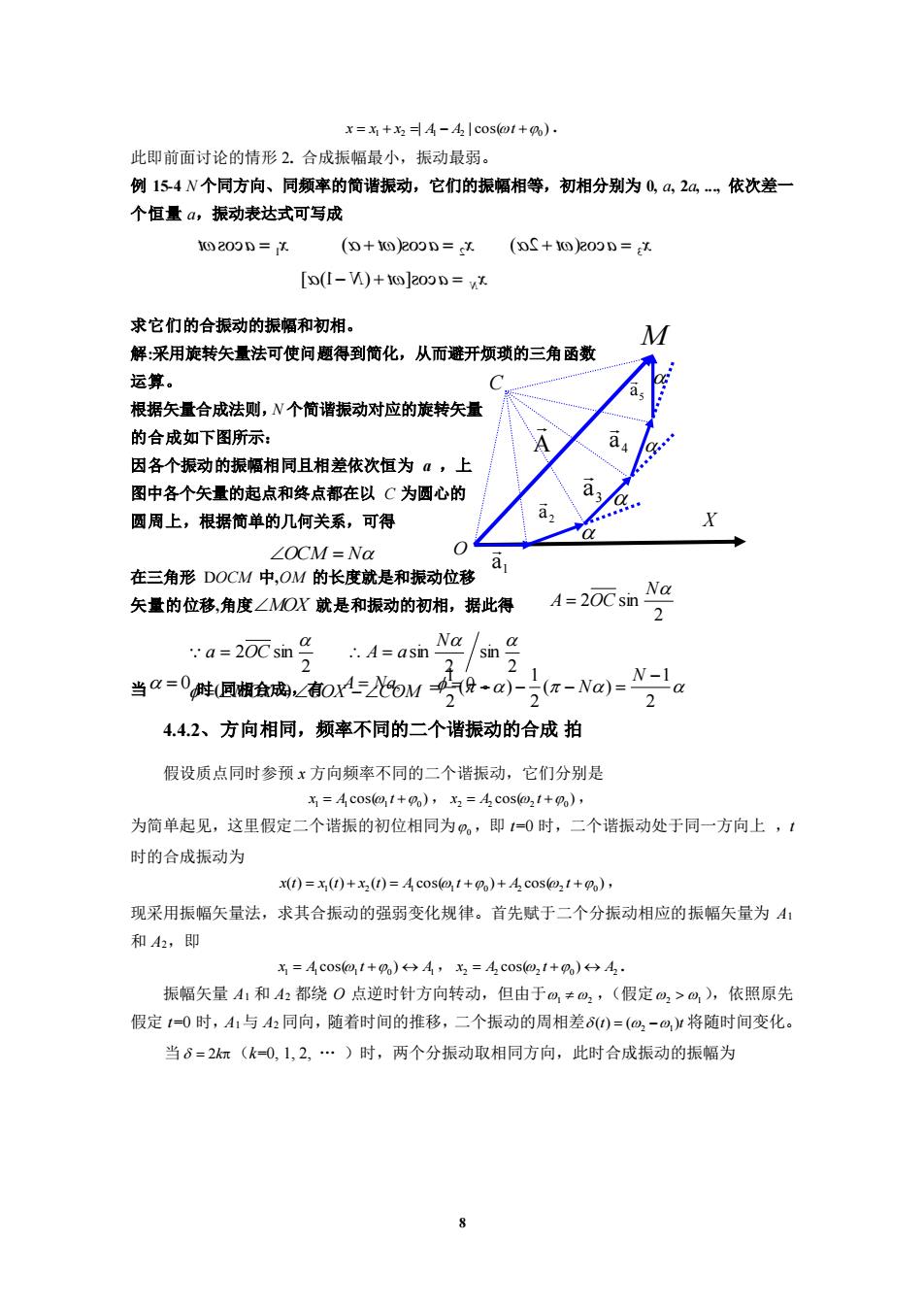
x=+4-c0s1+%): 此即前面讨论的情形2.合成振幅最小，振动最弱。 例154N个同方向、同颜率的简谐振动，它们的振幅相等，初相分别为0，a,2a,依次差一 个恒量a,振动表达式可写成 0200D=X (0+0)200n=x(oS+003n=x [D(1-M)+@]20n=wx 求它们的合振动的振幅和初相。 M 解：采用旋转矢量法可使问题得到简化，从而避开烦琐的三角函数 坛算。 根据矢量合成法则，N个简谐振动对应的旋转矢量 的合成如下图所示： A 因各个振动的振幅相同且相差依次恒为a,上 图中各个矢量的起点和终点都在以C为圆心的 圆周上，根据简单的几何关系，可得 ∠OCM=Na 在三角形DOCM中，0OM的长度就是和振动位移司， 矢量的位移，角度∠MOX就是和振动的初相，据此得 A=20Csin Na :a=2元mgA=asn/sm 2 当a=0阵（圆撰盒魂0r52bM受-a-之（a-Na)-Na 2 4.42、方向相同，频率不同的二个谐振动的合成拍 假设质点同时参预x方向频率不同的二个谐振动，它们分别是 x=AC0s1+0),x2=4c0s21+0), 为简单起见，这里假定二个谐振的初位相同为风，即0时，二个谐振动处于同一方向上，【 时的合成振动为 M)=x)+x2()=4C0s41+P%)+4C0s31+go), 现采用振幅矢量法，求其合振动的强弱变化规律。首先赋于二个分振动相应的振幅矢量为A: 和A2,即 x=4 coso1+0)←A,x,=AC0s@,1+2←→A,. 振幅矢量A1和A都绕O点逆时针方向转动，但由于似≠仙，（假定仙，>），依照原先 假定1一0时，A1与A2同向，随者时间的推移，二个振动的周相差)=(a,-将随时间变化。 当6=2(k-0,1,2,.)时，两个分振动取相同方向，此时合成振动的振幅为8 O X 1 a  2 a  3 a  4 a  5 a      C A  M | | cos( ) = 1 + 2 = 1 − 2  +0 x x x A A t . 此即前面讨论的情形 2. 合成振幅最小，振动最弱。 例 15-4 N 个同方向、同频率的简谐振动，它们的振幅相等，初相分别为 0, a, 2a, ., 依次差一 个恒量 a，振动表达式可写成 求它们的合振动的振幅和初相。 解:采用旋转矢量法可使问题得到简化，从而避开烦琐的三角函数 运算。 根据矢量合成法则，N 个简谐振动对应的旋转矢量 的合成如下图所示： 因各个振动的振幅相同且相差依次恒为 a ，上 图中各个矢量的起点和终点都在以 C 为圆心的 圆周上，根据简单的几何关系，可得 在三角形 DOCM 中,OM 的长度就是和振动位移 矢量的位移,角度 就是和振动的初相，据此得 当 时(同相合成)，有 4.4.2、方向相同，频率不同的二个谐振动的合成 拍 假设质点同时参预 x 方向频率不同的二个谐振动，它们分别是 cos( ) 1 = 1 1 +0 x A t ， cos( ) 2 = 2 2 +0 x A t ， 为简单起见，这里假定二个谐振的初位相同为 0 ，即 t=0 时，二个谐振动处于同一方向上 ，t 时的合成振动为 ( ) ( ) ( ) cos( ) cos( ) = 1 + 2 = 1 1 +0 + 2 2 +0 x t x t x t A t A t ， 现采用振幅矢量法，求其合振动的强弱变化规律。首先赋于二个分振动相应的振幅矢量为 A1 和 A2，即 1 1 1 0 1 x = A cos( t + )  A ， 2 2 2 0 2 x = A cos( t + )  A . 振幅矢量 A1 和 A2 都绕 O 点逆时针方向转动，但由于 1  2 ，（假定 2  1 ），依照原先 假定 t=0 时，A1与 A2 同向，随着时间的推移，二个振动的周相差 (t) ( )t  = 2 −1 将随时间变化。 当  = 2k （k=0, 1, 2, . ）时，两个分振动取相同方向，此时合成振动的振幅为 t  cos a x =1 ) cos( +  =2 t a x ) 2 cos(  +  =3 t a x ] )1− N( +t  cos[ a = xN OCM = N MOX 2 2 sin N A = OC 2 2 sin  a = OC 2 sin 2 sin N   A = a  = MOX = COX −COM      2 1 ( ) 2 1 ( ) 2 1 − = − − − = N  = 0 A = Na,  = 0 。 N