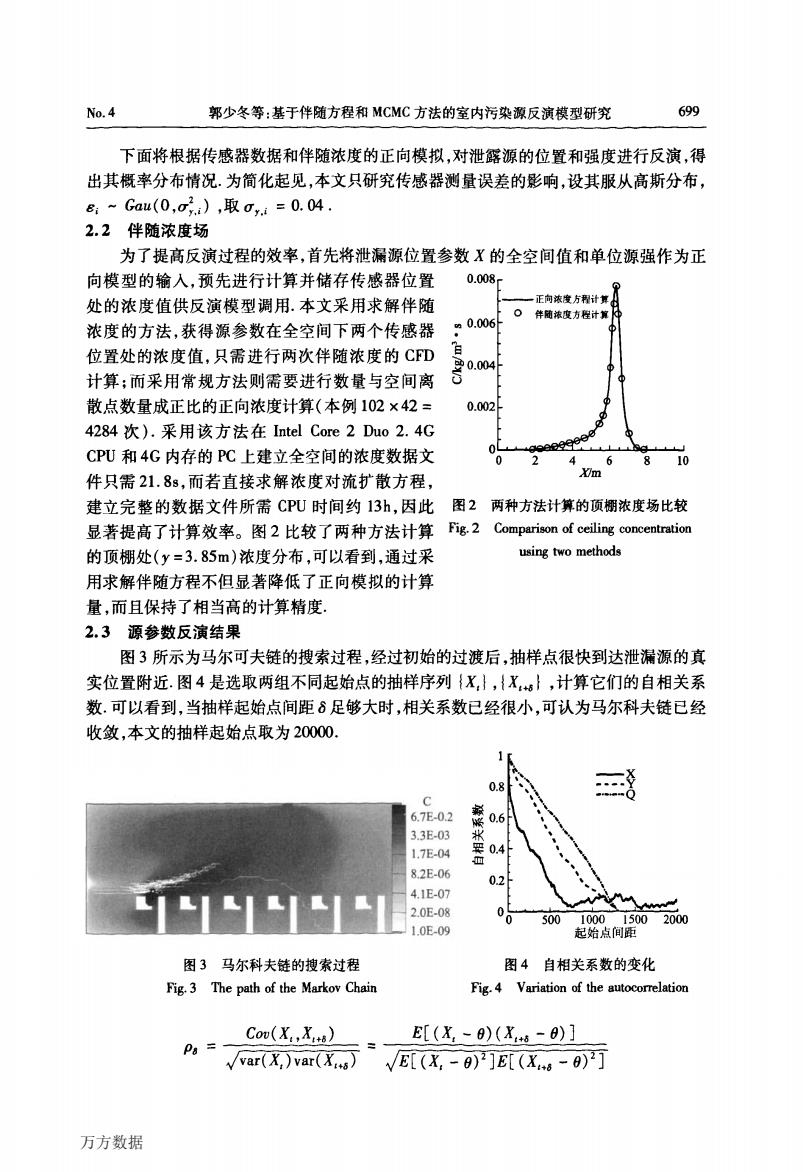
No.4 郭少冬等：基于伴随方程和MCMC方法的室内污染源反演模型研究 699 下面将根据传感器数据和伴随浓度的正向模拟，对泄露源的位置和强度进行反演，得 出其概率分布情况.为简化起见，本文只研究传感器测量误差的影响，设其服从高斯分布， &:~Gau(0,oi),取oi=0.04. 2.2伴随浓度场 为了提高反演过程的效率，首先将泄漏源位置参数X的全空间值和单位源强作为正 向模型的输入，预先进行计算并储存传感器位置 0.008 处的浓度值供反演模型调用.本文采用求解伴随 一正向浓发方程计算 n0.006 口伴随浓度方程计算 浓度的方法，获得源参数在全空间下两个传感器 位置处的浓度值，只需进行两次伴随浓度的CFD 计算：而采用常规方法则需要进行数量与空间离 散点数量成正比的正向浓度计算（本例102×42= 0.002 4284次).采用该方法在Intel Core2Duo2.4G CPU和4G内存的P℃上建立全空间的浓度数据文 e9e9 4 6 810 件只需21.8s,而若直接求解浓度对流扩散方程， m 建立完整的数据文件所需CPU时间约13h,因此图2两种方法计算的顶棚浓度场比较 显著提高了计算效率。图2比较了两种方法计算Fig2 Comparison of ceiing concentration 的顶棚处(y=3.85m)浓度分布，可以看到，通过采 using two methods 用求解伴随方程不但显著降低了正向模拟的计算 量，而且保持了相当高的计算精度. 2.3源参数反演结果 图3所示为马尔可夫链的搜索过程，经过初始的过渡后，抽样点很快到达泄漏源的真 实位置附近.图4是选取两组不同起始点的抽样序列{X,},{X,s},计算它们的自相关系 数.可以看到，当抽样起始点间距8足够大时，相关系数已经很小，可认为马尔科夫链已经 收敛，本文的抽样起始点取为20000 0.8 6.7E-0.2 0.6 3.3E-03 1.7E-04 0.4 ◇ 82E-06 02 4.1E-07 2.0E-08 00 500100015002000 1.0E-09 起始点间距 图3马尔科夫链的搜索过程 图4自相关系数的变化 Fig.3 The path of the Markov Chain Fig.4 Variation of the autocorrelation Cov(X.,X) E[(X,-8)(X6-8)] Pa= √ar(X,)var(X6)√E[(X,-9)]E[(X-)] 万方数据No．4 郭少冬等：基于伴随方程和MCMC方法的室内污染源反演模型研究 699 下面将根据传感器数据和伴随浓度的正向模拟，对泄露源的位置和强度进行反演，得 出其概率分布情况．为简化起见，本文只研究传感器测量误差的影响，设其服从高斯分布， 毋一Gau(O，盯y2．i)，取盯y，f=0．04． 2．2伴随浓度场 为了提高反演过程的效率，首先将泄漏源位置参数x的全空间值和单位源强作为正 向模型的输入，预先进行计算并储存传感器位置 处的浓度值供反演模型调用．本文采用求解伴随 浓度的方法，获得源参数在全空间下两个传感器 位置处的浓度值，只需进行两次伴随浓度的CFD 计算；而采用常规方法则需要进行数量与空间离 O．008 。0．006 目 章o．004 U 散点数量成正比的正向浓度计算(本例102×42=0．002 4284次)．采用该方法在Intel Core 2 Duo 2．4G 图3马尔科夫链的搜索过程 Fig．3 The path of the Markov Chin 图4自相关系数的变化 Fig．4 Variation of the autocorrelation Coy(X。，XⅢ) E[(置～0)(xm—o)] 几2蕊乖而示i 2万雨i丽丽ii两 万方数据