
第18卷4期 应用基础与工程科学学报 Vol.18,No.4 2010年8月 JOURNAL OF BASIC SCIENCE AND ENGINEERING August 2010 文章编号:10050930(2010)040695-10 中图分类号:X830.2 文献标识码:A doi:10.3969/5.isn.1005-0930.2010.04.017 基于伴随方程和MCMC方法的 室内污染源反演模型研究 郭少冬12,杨锐,苏国锋,张辉 (1.清华大学工程物理系,公共安全研究中心,北京100084;2.北京应用物理与计算数学研究所,北京100094) 摘要:研究了室内污染彻扩散后的源反演方法.通过数值求解浓度场的伴随方 程,并结合传感器测量信息,构造似然函数;利用基于贝叶斯推断理论的Markov Chain Monte Carlo(MCMC)抽样方法,对污染源的位置、强度的后验概率进行计 算,反演结果与污染源的真实参数吻合.该方法与传统的室内污染物反演方法相 比,极大地降低了计算量.此外,还讨论了传感器性能对结果的影响,研究表明传 感器误差概率分布越平坦,污染源反演信息的不确定度越大;而过低的测量灵敏 度,则会导致反演结果呈现多个局部极值点的特性 关键词:室内污染源反演;贝叶斯推断:伴随方程:计算流体力学 公用建筑内相对密闭,人员密集,一旦出现有毒气体泄漏或遭受生化袭击,有毒气体 会在通风气流等作用下迅速扩散,带来巨大威胁.而能否迅速准确地掌握释放源的相关信 息,对于应急疏散和处置策略的制定十分重要. 源项反演目前主要有直接求解、优化方法和概率方法等.直接求解方法通过构造控制 微分方程的反问题,利用正则变换,将其转化为适定的问题,进行解析或数值求解.解析解 的研究主要集中在热传导领域)和大气污染问题).随着C℉D算法的成熟,反演的数值 方法也开始得到发展.Skaggs[)采用拟可逆(Quasi-Reveraibility)方法在一维对流扩散方程 中引人了四阶耗散项抑制振荡,解决了稳定性问题;Bagtzoglou),Zhang's)分别将此方法 用于地下水污染源、室内污染源的定位研究.另一类重要的反演方法是优化方法, Skaggst6)和Alapati1分别采用正则优化方法和最小二乘法对地下水污染源进行参数反演 研究 贝叶斯概率方法因其可直接引入测量误差和数值模型误差的影响,受到了研究者广 泛的关注.在城区有害气体扩散和水污染的源参数反演方面,Kats⑧]、朱嵩]等采用 Markov Chain Monte Carlo(MCMC)抽样方法取得了一系列的研究成果.根据伴随算子的线 性性质,刘峰等o)发展了一种针对任意污染源的风险函数计算方法.Liu和Zhai1山将伴 收稿日期:2008-1009:修订日期:2009-05-19 基金项目:国家自然科学基金(50804027) 作者简介:郭少冬(1982一),男,博士,助理研究员. 通迅作者:杨锐(1976一),男,博士,副教授.E-mail:yang@tsinghua.cdu.cn 万方数据
第18卷4期 2010年8月 应用基础与工程科学学报 JOURNAL OF BASIC SCIENCE AND ENGINEERING V01.18.No.4 August 2010 文章编号:1005-0930(2010)04-0695-10 中图分类号:X830.2 文献标识码:A doi:10.3969/j.i啪.1005-0930.2010.04.017 基于伴随方程和MCMC方法的 室内污染源反演模型研究 郭少冬1’2, 杨 锐1, 苏国锋1, 张辉1 (1.清华大学工程物理系,公共安全研究中心,北京100084;2.北京应用物理与计算数学研究所,北京100094) 摘要:研究了室内污染物扩散后的源反演方法.通过数值求解浓度场的伴随方 程,并结合传感器测量信息,构造似然函数;利用基于贝叶斯推断理论的Markov Chain Monte Carlo(MCMC)抽样方法,对污染源的位置、强度的后验概率进行计 算,反演结果与污染源的真实参数吻合.该方法与传统的室内污染物反演方法相 比,极大地降低了计算量.此外,还讨论了传感器性能对结果的影响,研究表明传 感器误差概率分布越平坦,污染源反演信息的不确定度越大;而过低的测量灵敏 度,则会导致反演结果呈现多个局部极值点的特性. 关键词:室内污染源反演;贝叶斯推断;伴随方程;计算流体力学 公用建筑内相对密闭,人员密集,一旦出现有毒气体泄漏或遭受生化袭击,有毒气体 会在通风气流等作用下迅速扩散,带来巨大威胁.而能否迅速准确地掌握释放源的相关信 息,对于应急疏散和处置策略的制定十分重要. 源项反演目前主要有直接求解、优化方法和概率方法等.直接求解方法通过构造控制 微分方程的反问题,利用正则变换,将其转化为适定的问题,进行解析或数值求解.解析解 的研究主要集中在热传导领域¨1和大气污染问题【2 J.随着CFD算法的成熟,反演的数值 方法也开始得到发展.Skaggs”1采用拟可逆(Quasi-Reversibility)方法在一维对流扩散方程 中引入了四阶耗散项抑制振荡,解决了稳定性问题;BagtzoglOUl4J,Zhang【5 o分别将此方法 用于地下水污染源、室内污染源的定位研究.另一类重要的反演方法是优化方法, Skaggs∞1和Alapati【7j分别采用正则优化方法和最小二乘法对地下水污染源进行参数反演 研究. 贝叶斯概率方法因其可直接引入测量误差和数值模型误差的影响,受到了研究者广 泛的关注.在城区有害气体扩散和水污染的源参数反演方面,Keats【8 J、朱嵩一。等采用 Markov Chain Monte Carlo(MCMC)抽样方法取得了一系列的研究成果.根据伴随算子的线 性性质,刘峰等¨叫发展了一种针对任意污染源的风险函数计算方法.uu和Zhai 011]将伴 收稿日期:2008.10-09;修订日期:2009-05—19 基金项目:国家自然科学基金(50804027) 作者简介:郭少冬(1982一),男,博士,助理研究员. 通迅作者:杨锐(1976一),男,博士,副教授.E-mail:ryang@tsinghua.edu.Cll 万方数据

696 应用基础与工程科学学报 Vol.18 随方法应用于室内空气污染源的定位,数值求解后向概率密度输运方程,并通过在全参数 空间内积分,直接计算源位置的后验概率.该研究是在释放源强已知的情况下,对释放源 位置进行反演,因此可采用全参数空间的积分获得后验分布,计算量并不大,但当释放源 强度也未知时,若直接计算后验概率会涉及高维的积分,计算效率会显著降低, 本文采用MCMC抽样算法,产生一组收敛于后验分布的抽样点,并对其进行统计分 析,获得室内污染源位置和强度的概率信息.同时,通过构造浓度场的伴随方程,解决 MCMC方法需要大量正向计算的困难.此外,本文还对传感器测量误差分布和测量范围对 反演结果的影响进行了分析讨论 1模型描述 1.1贝叶斯推断 根据贝叶斯理论 p(x)=(YI(p(1x).p(x) P() (1) 其中X为污染源的相关参数,是需要进行反演的随机变量:Y为传感器的测量信息或其它 观测信息;(X)为源项参数X的先验分布,可以根据事先对源项的已知信息和判断给 定;p(Y1)为给定源项参数X下,数据Y的条件概率,称为似然概率,它的确定通常需 要综合考虑传感器的相关特性和正向数值模拟的误差;(XIY)指在获取有关信息Y后, 源参数X的概率分布.当得到源参数X的后验分布后,就可以对该参数进行估计,从而实 现对污染源空间位置的定位和强度反演. 1.2测量误差与模型误差 传统的直接反演方法,通常假设传感器的测量结果和数值模型的预测是精确的.即使 考虑误差因素,也只是在求出源参数后,对结果进行扰动分析;而基于贝叶斯推断的概率 方法可以在反演模型本身引人传感器和数值模型的误差,对反演结果的不确定性进行分 析,进而给出一定置信概率下的置信区间. 设观测点的测量值为Y={Y,Y2,…,Y:,…,Y},数值正向模型在测量点的预测值为 F={F,F2,…,F,…,F},而实际理论值为T={T,T2,…,T,…,T},引人传感器测量值 与理论值的误差e:,Y:=T:+8:;正向数值模型预测值与理论值的误差e,F:(X)=T:() +e.通常这两种误差可近似认为服从高斯分布8)e~Gau(0,ci)和e:~Gau(0,c). 从而得到 ()p 2 (2) pTix,F)xep-(T)二FX)1 (3) 2o 假设两种误差相互独立,则 D-I0zi,Pne-g (4) 假设每个测量点相互独立,则得到似然概率 万方数据
应用基础与工程科学学报 V01.18 随方法应用于室内空气污染源的定位,数值求解后向概率密度输运方程,并通过在全参数 空间内积分,直接计算源位置的后验概率.该研究是在释放源强已知的情况下,对释放源 位置进行反演,因此可采用全参数空间的积分获得后验分布,计算量并不大,但当释放源 强度也未知时,若直接计算后验概率会涉及高维的积分,计算效率会显著降低. 本文采用MCMC抽样算法,产生一组收敛于后验分布的抽样点,并对其进行统计分 析,获得室内污染源位置和强度的概率信息.同时,通过构造浓度场的伴随方程,解决 MCMC方法需要大量正向计算的困难.此外,本文还对传感器测量误差分布和测量范围对 反演结果的影响进行了分析讨论. 1模型描述 1.1 贝叶斯推断 根据贝叶斯理论 p(x t玢:趔等弹,盟芘p(Yt x),p(x) (1) P~1, 其中x为污染源的相关参数,是需要进行反演的随机变量;Y为传感器的测量信息或其它 观测信息;p(X)为源项参数x的先验分布,可以根据事先对源项的已知信息和判断给 定;P(YI x)为给定源项参数x下,数据y的条件概率,称为似然概率,它的确定通常需 要综合考虑传感器的相关特性和正向数值模拟的误差;p(xI l,)指在获取有关信息y后, 源参数x的概率分布.当得到源参数x的后验分布后,就可以对该参数进行估计,从而实 现对污染源空间位置的定位和强度反演. 1.2 测量误差与模型误差 传统的直接反演方法,通常假设传感器的测量结果和数值模型的预测是精确的.即使 考虑误差因素,也只是在求出源参数后,对结果进行扰动分析;而基于贝叶斯推断的概率 方法可以在反演模型本身引入传感器和数值模型的误差,对反演结果的不确定性进行分 析,进而给出一定置信概率下的置信区间. 设观测点的测量值为Y={L,y2,…,yi,…,K},数值正向模型在测量点的预测值为 F={F。,R,…,E,…,凡},而实际理论值为T={L,疋,…,正,…,瓦},引入传感器测量值 与理论值的误差反,K=t+岛;正向数值模型预测值与理论值的误差e;,Fi(x)=正(X) +e;.通常这两种误差可近似认为服从高斯分布哺1B—Gau(O,盯,2.i)和e‘~C,au(O,%2i). 从而得到 p(yi I正,x)茁exp{一掣 p(t Ix,F)。c exp{一生堡垒铲) 假设两种误差相互独立,则 则㈨=如(m剐驰胂…p{-端) 假设每个测量点相互独立,则得到似然概率 (2) (3) (4) 万方数据

No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 697 p(1=ip(g10e-含2+ (F(x)-Y) (5) 1.3伴随方程与正问题数值方法 计算后验概率时,需要考虑全参数空间或该空间的许多抽样点,传统的方法经常需要 对所有可能的源参数进行正向数值模拟,求解稳态N-S方程和组分扩散方程(6),得到测 量点处的浓度值F(X)· r.VC-V·(D7C)=Sxen l6.c.7C.n=0 (6) XEan 计算量是非常巨大的.考虑到传感器的数量通常较少,而每一次的正向模拟也只是为得到 有限传感器位置的浓度值,因此可利用伴随算子的性质,求解与原浓度场对应的伴随浓 度场) r-7·7G-7·(D7G)=(X-X') X∈n 1b.c.CV.i+DVG.n=0 (7) Xean 根据 C(X)={C(x)8(X-X')d (8) 将式(7)代入,并根据场论和不可压缩条件有 c(X)=[C(-v.Vc-V.(DVC))dx =-A[-cC+Gv·(DvC)+7·(CGW+7·(cDVG) -V·(DGVC)]dX (9) 代人方程(6),有 C(x')=[GS-V·(CG-7·(cD7G)+V·(DGVC)]d (10) 根据高斯定理,有 C(X)=[csax-ccv.idr-cDvc.idr+Dcvc.idr (11) 代入边界条件VC·元=0,G·元+DVG·n=0(Xen),可得到 C(X)=[G(X,X')S(X)dx (12) 传统方法中,当需要求解在n个不同位置(X,Xa,…,X.,…,Xm)污染源,扩散到某个传 感器位置X'处的浓度值时,需要进行次正向数值模拟,得到同一个点处的浓度值.而利 用上述关系,只需将污染源放置在该空间点X′处,强度取一个单位,求解一次伴随方程 (方程(7)是点源连续泄漏问题),得到伴随浓度场G(X,X),进而利用方程(12),即可得 到同一空间点处在不同源条件下的浓度值. 当污染源为点源时,S=Q·8(X-X,),可进一步得到 c(X)[Q.G(X,X')8(X-x,)dx Q.c(X.X) (13) 因此利用求解一次伴随方程获得的浓度场,即可获得个不同源参数下在同一传感器位 万方数据
No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 697 p(yI x)=lkIp(y:l x)。c exp{一毫嬲) (5) 1.3伴随方程与正问题数值方法 计算后验概率时,需要考虑全参数空间或该空间的许多抽样点,传统的方法经常需要 对所有可能的源参数进行正向数值模拟,求解稳态N·S方程和组分扩散方程(6),得到测 量点处的浓度值F(X’). ∥Vc一∑。(DVc)=s x∈Q (6) 1 b.c.VC.元=0 X∈aQ ¨7 计算量是非常巨大的.考虑到传感器的数量通常较少,而每一次的正向模拟也只是为得到 有限传感器位置的浓度值,因此可利用伴随算子的性质,求解与原浓度场对应的伴随浓 度场”1 f一矿·VG—V·(DVG)=6(X—X’) Z∈Q ,,、 1 b.c.G『矿.五+DvG·矗=0 x E aQ 、。7 根据 c(x’)=f c(x)6(X—X’)栅 (8) 将式(7)代入,并根据场论和不可压缩条件有 c(石’)=I.C(一矿·VG—V·(DVG))dx =一f.[一G矿Vc+GV·(DVc)+V·(cG矿)+V·(CDVG) 一V·(DGVC)]dX (9) 代入方程(6),有 C(X’)=f.[船一V·(COP)一V·(CDVG)+V·(DGVC)]dX (10) 根据高斯定理,有 C(X’)=f GSdX—f cG矿·元d厂一f.CDVG·矗d,+f DGVC·矗d厂 (11) Jn Jan Jdn J#O 代入边界条件VC·元=0,西·完+DVG·高=o(x∈aQ),可得到 c(X’)=J G(x,x’)s(x)锻 (12) 传统方法中,当需要求解在n个不同位置(L,Xa,…,如,…,五。)污染源,扩散到某个传 感器位置x’处的浓度值时,需要进行n次正向数值模拟,得到同一个点处的浓度值.而利 用上述关系,只需将污染源放置在该空间点X’处,强度取一个单位,求解一次伴随方程 (方程(7)是点源连续泄漏问题),得到伴随浓度场G(x,x7),进而利用方程(12),即可得 到同一空间点处在不同源条件下的浓度值. 当污染源为点源时,S=Q·8(x一置),可进一步得到 C(X’)=J。Q。a(X,X’)艿(x一置)dX=Q‘c(墨,X’) (13) 因此利用求解一次伴随方程获得的浓度场,即可获得n个不同源参数下在同一传感器位 万方数据

698 应用基础与工程科学学报 Vol.18 置处的浓度值 (QG(XX'),02G(X2,X).QG(Xx),.0G(XX')) 正问题的计算需要求解不可压缩Navier-Stokes方程组和伴随方程(7).由于组分源 对环境流场的影响较小,因此本文假定处于相同位置而不同的泄漏源强度,其速度场保持 不变.计算中将连续方程、动量方程与浓度扩散方程分离求解,即先求解速度和压力场,在 其收敛后,将速度场和湍流粘性系数代入伴随方程(7),求解浓度场。数值格式采用基于 有限体积交错网格的SIMPLE算法,湍流模型采用标准k-ε模型. 1.4MCMC算法 公式(1)确定了后验概率密度的计算方法,其中分母为 n=jr1x(x0en-言0+品 、(F(X)-Y)21 (14) 该积分在整个参数空间上进行,对于参数空间维数较低时,其计算量尚可接受,但实际中 通常需要估计的源参数都是多维向量,即使采用传统的Monte Carlo积分方法,计算这种 多维积分效率也很低 注意到后验概率正比于似然概率(5)和先验分布的乘积,因此可采用MCMC方法,通 过合理的构造转移概率,直接产生一组分布概率为后验概率的随机抽样点,这些抽样点构 成一条马尔可夫链,该马氏链收敛后的静态分布即为所需的后验分布.满足上述要求的转 移概率和MCMC抽样方法主要有Gibbs算法,Metropolis算法、Metropolis--Hasting算法等. 本文采用结合Metropolis-Hasting算法的MCMC抽样,具体步骤见文献[I2]. 2室内污染源反演问题研究 2.1场景描述 Liu和Zhai研究了室内污染源的二维定位问题,本文选取类似的场景,如图1所 示,一个4m高,10m长的房间内有6个人和6台计算机及办公桌,左侧1.5一1.8m高处 有一空调送风口,以1m/s的速度水平送风,房间顶棚有一通风口,与外界进行质量交换. 在房间顶部通风口两侧对称地安装有两个传感器.污染源位于人头部的前方,位置坐标 (1.95m,1.25m),坐标原点取在房间的左下角.污染源强度为0.8kg/m3·8. 出口 传感器十传感器 6.7E-0.2 3.3E-03 1.7E-04 送风▣ 8.2E-06 4.1E-07 2.0E-08 1.0E-09 图1房间简化图与稳态浓度场 Fig.1 simplified diagram of the room and steady concentration field 万方数据
应用基础与工程科学学报 VDl.18 置处的浓度值 (Q,。G(置。,X7),Q也G(X,2,X’),…,Q,IG(置。,X’),…,Q,。G(置。,X’)) 正问题的计算需要求解不可压缩Navier—Stokes方程组和伴随方程(7).由于组分源 对环境流场的影响较小,因此本文假定处于相同位置而不同的泄漏源强度,其速度场保持 不变.计算中将连续方程、动量方程与浓度扩散方程分离求解,即先求解速度和压力场,在 其收敛后,将速度场和湍流粘性系数代入伴随方程(7),求解浓度场。数值格式采用基于 有限体积交错网格的SIMPLE算法,湍流模型采用标准k-8模型. 1.4 MCMC算法 公式(1)确定了后验概率密度的计算方法,其中分母为 p(1,)=』p(1,I x)p(x)d.Y。c-f exp{一圭i=1{粼)p(x)dx(14) 该积分在整个参数空间上进行,对于参数空间维数较低时,其计算量尚可接受,但实际中 通常需要估计的源参数都是多维向量,即使采用传统的Monte Carlo积分方法,计算这种 多维积分效率也很低. 注意到后验概率正比于似然概率(5)和先验分布的乘积,因此可采用MCMC方法,通 过合理的构造转移概率,直接产生一组分布概率为后验概率的随机抽样点,这些抽样点构 成一条马尔可夫链,该马氏链收敛后的静态分布即为所需的后验分布.满足上述要求的转 移概率和MCMC抽样方法主要有Gibbs算法,Metropolis算法、Metropolis—Hasting算法等. 本文采用结合Metropolis—Hasting算法的MCMC抽样,具体步骤见文献[12]. 2室内污染源反演问题研究 2.1场景描述 Ⅱu和Zhai[I¨研究了室内污染源的二维定位问题,本文选取类似的场景,如图1所 示,一个4m高,10m长的房间内有6个人和6台计算机及办公桌,左侧1.5一1.8m高处 有一空调送风口,以lm/s的速度水平送风,房间顶棚有一通风口,与外界进行质量交换. 在房间顶部通风13两侧对称地安装有两个传感器.污染源位于人头部的前方,位置坐标 (1.95m,1.25m),坐标原点取在房间的左下角.污染源强度为0.8kg/m3·8. 图1 房间简化图与稳态浓度场 Fig.1 simplified diagram of the loom and steady concentration field 万方数据
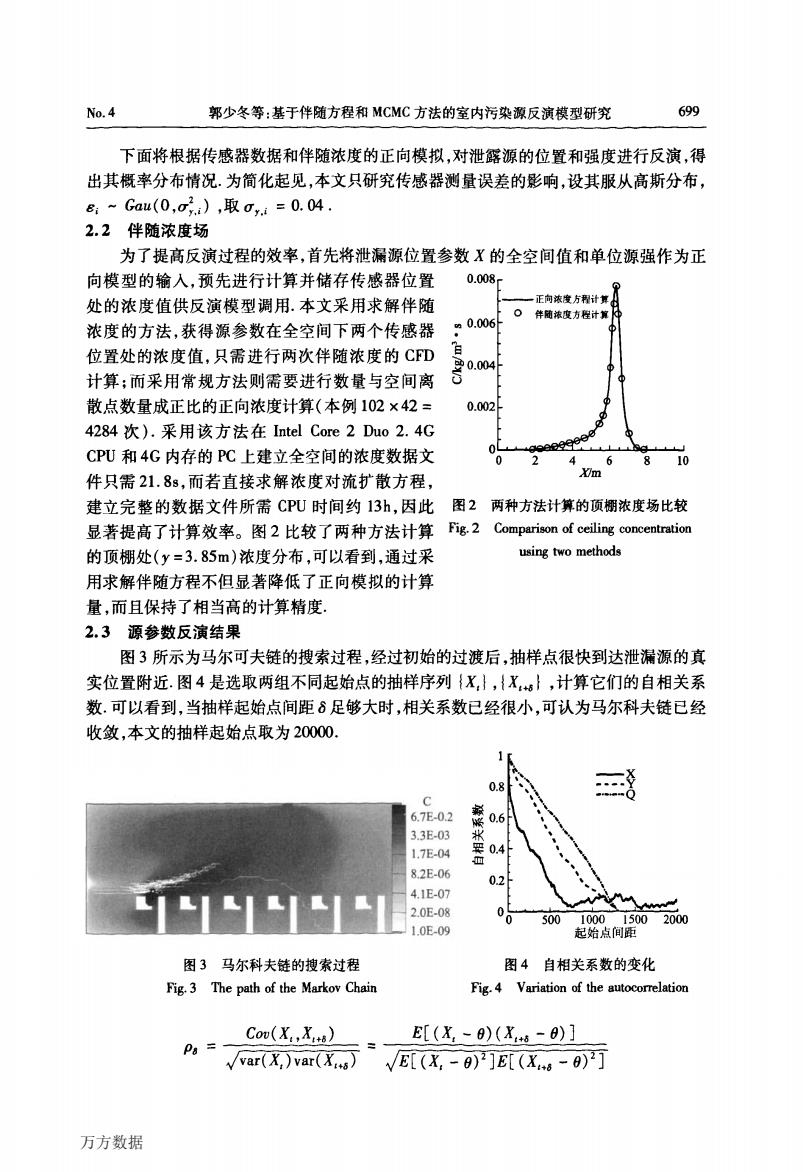
No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 699 下面将根据传感器数据和伴随浓度的正向模拟,对泄露源的位置和强度进行反演,得 出其概率分布情况.为简化起见,本文只研究传感器测量误差的影响,设其服从高斯分布, &:~Gau(0,oi),取oi=0.04. 2.2伴随浓度场 为了提高反演过程的效率,首先将泄漏源位置参数X的全空间值和单位源强作为正 向模型的输入,预先进行计算并储存传感器位置 0.008 处的浓度值供反演模型调用.本文采用求解伴随 一正向浓发方程计算 n0.006 口伴随浓度方程计算 浓度的方法,获得源参数在全空间下两个传感器 位置处的浓度值,只需进行两次伴随浓度的CFD 计算:而采用常规方法则需要进行数量与空间离 散点数量成正比的正向浓度计算(本例102×42= 0.002 4284次).采用该方法在Intel Core2Duo2.4G CPU和4G内存的P℃上建立全空间的浓度数据文 e9e9 4 6 810 件只需21.8s,而若直接求解浓度对流扩散方程, m 建立完整的数据文件所需CPU时间约13h,因此图2两种方法计算的顶棚浓度场比较 显著提高了计算效率。图2比较了两种方法计算Fig2 Comparison of ceiing concentration 的顶棚处(y=3.85m)浓度分布,可以看到,通过采 using two methods 用求解伴随方程不但显著降低了正向模拟的计算 量,而且保持了相当高的计算精度. 2.3源参数反演结果 图3所示为马尔可夫链的搜索过程,经过初始的过渡后,抽样点很快到达泄漏源的真 实位置附近.图4是选取两组不同起始点的抽样序列{X,},{X,s},计算它们的自相关系 数.可以看到,当抽样起始点间距8足够大时,相关系数已经很小,可认为马尔科夫链已经 收敛,本文的抽样起始点取为20000 0.8 6.7E-0.2 0.6 3.3E-03 1.7E-04 0.4 ◇ 82E-06 02 4.1E-07 2.0E-08 00 500100015002000 1.0E-09 起始点间距 图3马尔科夫链的搜索过程 图4自相关系数的变化 Fig.3 The path of the Markov Chain Fig.4 Variation of the autocorrelation Cov(X.,X) E[(X,-8)(X6-8)] Pa= √ar(X,)var(X6)√E[(X,-9)]E[(X-)] 万方数据
No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 699 下面将根据传感器数据和伴随浓度的正向模拟,对泄露源的位置和强度进行反演,得 出其概率分布情况.为简化起见,本文只研究传感器测量误差的影响,设其服从高斯分布, 毋一Gau(O,盯y2.i),取盯y,f=0.04. 2.2伴随浓度场 为了提高反演过程的效率,首先将泄漏源位置参数x的全空间值和单位源强作为正 向模型的输入,预先进行计算并储存传感器位置 处的浓度值供反演模型调用.本文采用求解伴随 浓度的方法,获得源参数在全空间下两个传感器 位置处的浓度值,只需进行两次伴随浓度的CFD 计算;而采用常规方法则需要进行数量与空间离 O.008 。0.006 目 章o.004 U 散点数量成正比的正向浓度计算(本例102×42=0.002 4284次).采用该方法在Intel Core 2 Duo 2.4G 图3马尔科夫链的搜索过程 Fig.3 The path of the Markov Chin 图4自相关系数的变化 Fig.4 Variation of the autocorrelation Coy(X。,XⅢ) E[(置~0)(xm—o)] 几2蕊乖而示i 2万雨i丽丽ii两 万方数据
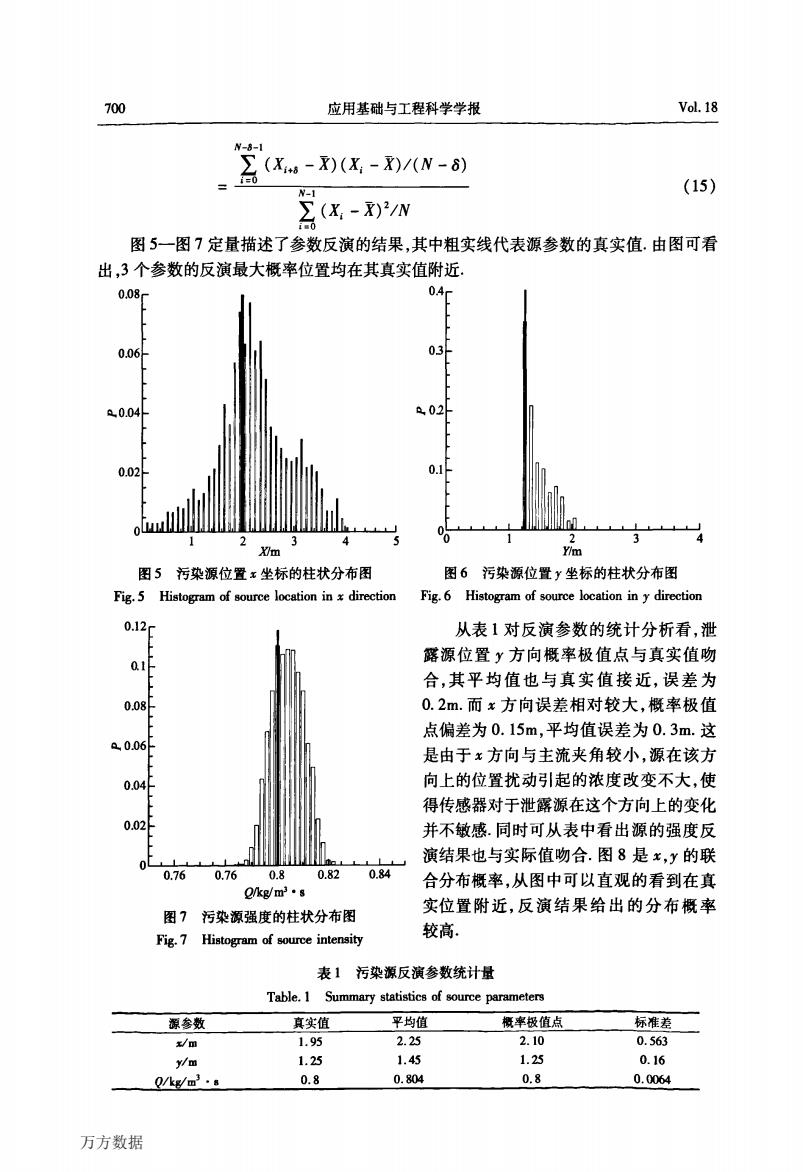
700 应用基础与工程科学学报 Vol.18 N-8-1 (X-)(X-)/(N-6) N-1 (15) X-w 图5一图7定量描述了参数反演的结果,其中粗实线代表源参数的真实值.由图可看 出,3个参数的反演最大概率位置均在其真实值附近, 0.08 0.4 0.06 03 0.04 &02外 0.02 01 o 2 3 2 4 3 m m 图5污染源位置x坐标的柱状分布图 图6污染源位置y坐标的柱状分布图 Fig.5 Histogram of source location in x direction Fig.6 Histogram of source location in y direction 0.12c 从表1对反演参数的统计分析看,泄 露源位置y方向概率极值点与真实值吻 合,其平均值也与真实值接近,误差为 0.08 0.2m.而x方向误差相对较大,概率极值 点偏差为0.15m,平均值误差为0.3m.这 a0.06 是由于x方向与主流夹角较小,源在该方 0.04 向上的位置扰动引起的浓度改变不大,使 得传感器对于泄露源在这个方向上的变化 0.02 并不敏感.同时可从表中看出源的强度反 演结果也与实际值吻合.图8是x,y的联 0.76 0.76 0.80.82 0.84 合分布概率,从图中可以直观的看到在真 2/kg/m3·8 图7污染源强度的柱状分布图 实位置附近,反演结果给出的分布概率 Fig.7 Histogram of source intensity 较高。 表1污染源反演参数统计量 Table.1 Summary statistics of source parameters 源参数 真实值 平均值 概率极值点 标准差 利m 1.95 2.25 2.10 0.563 y/m 1.25 1.45 1.25 0.16 Qgm3·s 0.8 0.804 0.8 0.0064- 万方数据
700 应用基础与工程科学学报 V01.18 Jv一占一l ∑(置+。一叉)(Xi—X)/(N一鳓 i=0 2—————1£广—————一 ∑(置一元)2/N i=0 (15) 图5一图7定量描述了参数反演的结果,其中粗实线代表源参数的真实值.由图可看 出,3个参数的反演最大概率位置均在其真实值附近. O.12 Ql O.08 钆O.06 0.04 O.02 O Q/kg/m3·s 图7污染源强度的柱状分布图 Fig.7 Histogram of 80UIP弛intensity 胁‰……… Y/m 图6污染源位置Y坐标的柱状分布图 Fig.6 Histogram of source location in,,direction 从表l对反演参数的统计分析看,泄 露源位置Y方向概率极值点与真实值吻 合,其平均值也与真实值接近,误差为 0.2m.而茗方向误差相对较大,概率极值 点偏差为0.15m,平均值误差为0.3m.这 是由于戈方向与主流夹角较小,源在该方 向上的位置扰动引起的浓度改变不大,使 得传感器对于泄露源在这个方向上的变化 并不敏感.同时可从表中看出源的强度反 演结果也与实际值吻合.图8是茗,Y的联 合分布概率,从图中可以直观的看到在真 实位置附近,反演结果给出的分布概率 较高. 表l污染源反演参数统计量 7r址de.1 Summary statistic8 of source parameters 源参数 真实值 平均值 概率极值点 标准差 x/m 1.95 2.25 2.10 0.563 v/m 1.25 1.45 1.25 0.16 ∥ks/Ⅲ3-s 0.8 0.804 0.8 0.0064 万方数据

No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 701 利用上述方法,可以在对源位置和强 P:0.1020.110.1180.1260.1340.142 度有关参数完全未知的情况下,仅根据空 间结构、通风状况和有限测量值,实现泄露 物质的浓度场重建,给出在一定置信度(本 文中取为0.9)下整个房间浓度分布的上 限和下限,如图9所示.即在所给定传感器 信息的情况下,空间各点浓度低于图9(a) 图8污染源位置的概率分布 所示浓度的可能性为90%(同样,空间各 Fig.8 The two dimensional joint distributions 点浓度高于图9(b)所示浓度的可能性也 of source location 为90%).由于在实际处置过程中,各种信 息源给出的信息都会带有一定的偏差(传感器、数值模型误差),因此给出一定置信度下 的浓度范围,比给定单点的预测值更有意义, 3.9E02 3.9E-02 2.1E-03 2.1E-03 1.1E-04 1.1E-04 62E-06 62E.06 3.4E-07 3.4E07 1.8E-08 1.8E-08 1.0E-09 1.0E-09 (a)上限分布 (b)下限分布 图9单侧置信度0.9的浓度上下限分布 Fig.9 Extreme concentration distribution with confidence of 0.9 2.4传感器测量误差与测量范围的影响分析 传感器都有测量误差和测量极限,可能会影响反演.下面针对4种不同性能的传感 器,分析误差分布σ,及测量下限对结果的影响. 表2传感器的4种情况 Table.2 Four cases of sensors Case 1 Case 2 Case 3 Case4 0.04 0.04 0.2 0.2 测量下限 0.01 0.1 0.01 0.1 图10为4种情况下污染源位置的概率分布.分别对比case1和case2,以及case3和 cse4,即当测量下限较高(灵敏度较低)时,得到的概率分布会呈现多个局部极值点,主 要原因是较低的灵敏度会造成其中的某个传感器无法提供正确信息,导致多个概率局部 极值的出现;对比case1和case3,当测量误差分布g,增大时,虽没有出现多个局部极值 点,但概率大于0.1的范围明显增大,从而导致反演结果的不确定度增加,置信区间变宽 万方数据
No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 利用上述方法,可以在对源位置和强 度有关参数完全未知的情况下,仅根据空 间结构、通风状况和有限测量值,实现泄露 物质的浓度场重建,给出在一定置信度(本 文中取为0.9)下整个房间浓度分布的上 限和下限,如图9所示.即在所给定传感器 信息的情况下,空间各点浓度低于图9(a) 图8污染源位置的概率分布 所示浓度的可能性为90%(同样,空间各 Fig.8 The two dimensional joint distributions 点浓度高于图9(b)所示浓度的可能性也 of source location 为90%).由于在实际处置过程中,各种信 息源给出的信息都会带有一定的偏差(传感器、数值模型误差),因此给出一定置信度下 的浓度范围,比给定单点的预测值更有意义. 图9单侧置信度0.9的浓度上下限分布 Fig.9 Extreme concentration distribution with confidence of 0.9 2.4传感器测量误差与测量范围的影响分析 传感器都有测量误差和测量极限,可能会影响反演.下面针对4种不同性能的传感 器,分析误差分布盯,及测量下限对结果的影响. 表2传感器的4种情况 T小le.2 Four Cfl,ses of sensors 图10为4种情况下污染源位置的概率分布.分别对比case 1和case 2,以及case 3和 case 4,即当测量下限较高(灵敏度较低)时,得到的概率分布会呈现多个局部极值点,主 要原因是较低的灵敏度会造成其中的某个传感器无法提供正确信息,导致多个概率局部 极值的出现;对比case 1和case 3,当测量误差分布o"r增大时,虽没有出现多个局部极值 点,但概率大于0.1的范围明显增大,从而导致反演结果的不确定度增加,置信区间变宽. 万方数据
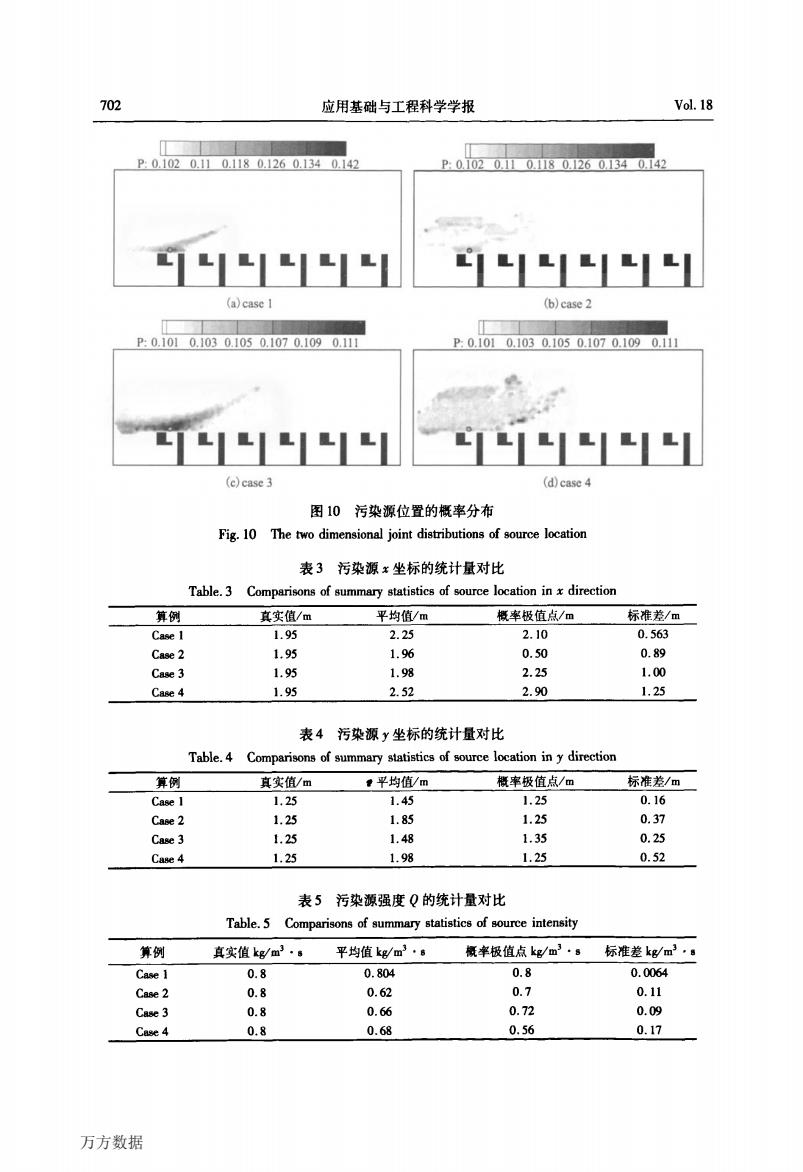
702 应用基础与工程科学学报 Vol.18 P:0.1020.110.1180.1260.1340.142 P:0102011011802601340.142 (a)case I (b)case 2 P:0.1010.1030.1050.1070.1090.111 P.0.1010.1030.1050.1070.1090.111 (c)case 3 (d)case 4 图10污染源位置的概率分布 Fig.10 The two dimensional joint distributions of source location 表3污染源x坐标的统计量对比 Table.3 Comparisons of summary statistics of source location in x direction 算例 其实值/m 平均值/m 概率极值点/m 标准差/m Case1 1.95 2.25 2.10 0.563 Case2 1.95 1.96 0.50 0.89 Case3 1.95 1.98 2.25 1.00 Case4 1.95 2.52 2.90 1.25 表4污染源y坐标的统计量对比 Table.4 Comparisons of summary statistics of source location in y direction 算例 真实值/m 量平均值/m 概率极值点/m 标准差/m Case 1 1.25 1.45 1.25 0.16 Case 2 1.25 1.85 1.25 0.37 Case 3 1.25 1.48 1.35 0.25 Case 4 1.25 1.98 1.25 0.52 表5污染源强度Q的统计量对比 Table.5 Comparisons of summary statistics of source intensity 算例 真实值kgm3·s 平均值kgm3·s 概率极值点gm·s 标准差kg/m3·。 Case 1 0.8 0.804 0.8 0.0064 Case2 0.8 0.62 0.7 0.11 Case 3 0.8 0.66 0.72 0.09 Case 4 0.8 0.68 0.56 0.17 万方数据
702 应用基础与工程科学学报 V01.18 图10污染源位置的概率分布 Fig.10 The two dimensional joint distributions of source location 表3污染源茗坐标的统计量对比 Table.3 Comparisons of summary statistics of source location in髫direction 表4污染源Y坐标的统计量对比 Table.4 Comparisons of aummary staffstics of source location in y direction 算例 真实值/m ●平均值/m 概率极值点/m 标准差/m Case 1 1.25 1.45 1.25 0.16 Case 2 1.25 1.85 1.25 0.37 Case 3 1.25 1.48 1.35 0.25 Case 4 1.25 1.98 1.25 0.52 表5污染源强度Q的统计量对比 T棚e.5 Comparisons of summary statistics of source intensity 算例 真实值ks/m3·s 平均值ks/m3·8 概率极值点ks/m3·8 标准差ks/m3·s Case 1 0.8 0.804 0.8 0.0064 Case 2 0.8 0.62 0.7 0.11 Case 3 0.8 0.66 0.72 0.09 Case4 0.8 0.68 0.56 0.17 万方数据

No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 703 表3一表5分别列出了4种情况下,污染源参数(x,y,Q)反演后的统计量对比.与 图10的结论类似,随误差σ,增大,反演结果的标准差一般也呈增大趋势.同时当传感器 测量下限取较大的值时,在x方向概率极值点的位置与真实位置差别较大,如Cse2在 0.5m处,Case4在2.90m处. 从以上分析可看出,在反演算法中,传感器测量误差分布和测量范围对结果的影响明 显.当泄漏源的信息未知时,传感器数据的可信度及信息量直接反映在反演结果的统计分 布上,较宽的误差概率分布,会显著提高泄漏源反演信息的不确定度,而过低的测量灵敏 度,会导致反演结果呈现多个局部极值点. 3结论 针对室内污染源定位和强度反演问题,本文采用计算流体力学方法求解伴随浓度方 程,利用贝叶斯推断理论的MCMC抽样方法计算污染源参数的后验概率分布,及相关统 计分析,由此得到整个空间区域各点浓度的概率分布及其单侧置信上、下限等相关统计 量.通过与真实值的对比,证实了该算法的有效性.同时采用基于求解伴随方程的算法,避 免了多次的正向模拟,显著提高了计算效率.此外,还对传感器性能(测量误差分布和测 量下限)对反演结果的影响进行了分析和讨论,表明较宽的传感器误差概率分布,会显著 提高泄漏源反演信息的不确定度,而过低的测量灵敏度,会导致反演结果呈现多个局部极 值点的特性.本文研究的是扩散达到稳态后的反演问题,若考虑时间效应,如何利用不同 时刻的传感器数据更新泄漏源反演结果,还需进一步深人研究, 参考文献 [I Alifanov O M.Inverse heat transfer problems[M].Berlin:Springer-Verlag,1994 [2 Enting I.Inverse problems in atmoepheric constituent transport[M].Cambridge:Cambridge University Press,2002 [3 Skaggs T H,Kabala Z J.Recovering the history of a groundwater contaminant plume:method of quasi-reversibility[J]. Water Resources Research.1995.31(11 ):2669-2673 [4 Bagtzoglou A C,Atmadja J.Marching-jury backward beam equation and quasi-reversibility methods for hydrologic inversion:application to contaminant plume spatial distribution recovery[J].Water Resources Research,2003,39 (2):1038 [5 Zhang T F,Chen Q.Identification of contaminant sources in enclosed environments by inverse CFD modeling[J]. ndoor Air,2007,17(3):l67-l7 [6]Skaggs T H,Kabala ZJ.Recovering the release history of a groundwater contaminant[J.Water Resources Research, 1994,30(1):71-79 [7]Alapati S,Kabala Z J.Recovering the release history of a groundwater contaminant via the non-linear least-squares estimation[]]Hydrological Process,2000,14(6):1003-1016 [8]Keats A,Yee E,Lien FS.Bayesian inference for source determination with applications to a complex urban environment [J].Atmospheric Environment,2007,41(3):465-479 [9]朱嵩,毛根海,程伟平,等.基于贝叶斯推理的水环境系统参数识别[J].江苏大学学报(自然科学版),2007,28 (3):237-240 Zhu Song,Mao Genhai.Cheng Weiping,et al.Parameter identification for water environmental system based on Bayesian inference[J].Journal of Jiangsu University(Natural Science Edition),2007,28(3):237-240 [10]刘峰,黄顺样,胡非,等.用伴随方法对毒气泄漏事件进行危害评估[J].中国安全科学学报,2003,13(9): 74-77 Liu Feng,Huang Shunxiang,Hu Fei,et al.Adjoint method for the risk evaluation of poisonous gases leakage [J].China 万方数据
No.4 郭少冬等:基于伴随方程和MCMC方法的室内污染源反演模型研究 703 表3一表5分别列出了4种情况下,污染源参数(髫,Y,Q)反演后的统计量对比.与 图10的结论类似,随误差矿,增大,反演结果的标准差一般也呈增大趋势.同时当传感器 测量下限取较大的值时,在戈方向概率极值点的位置与真实位置差别较大,如Case 2在 0.5m处,Case 4在2.90m处. 从以上分析可看出,在反演算法中,传感器测量误差分布和测量范围对结果的影响明 显.当泄漏源的信息未知时,传感器数据的可信度及信息量直接反映在反演结果的统计分 布上.较宽的误差概率分布,会显著提高泄漏源反演信息的不确定度,而过低的测量灵敏 度,会导致反演结果呈现多个局部极值点. 3 结论 针对室内污染源定位和强度反演问题,本文采用计算流体力学方法求解伴随浓度方 程,利用贝叶斯推断理论的MCMC抽样方法计算污染源参数的后验概率分布,及相关统 计分析,由此得到整个空间区域各点浓度的概率分布及其单侧置信上、下限等相关统计 量.通过与真实值的对比,证实了该算法的有效性.同时采用基于求解伴随方程的算法,避 免了多次的正向模拟,显著提高了计算效率.此外,还对传感器性能(测量误差分布和测 量下限)对反演结果的影响进行了分析和讨论,表明较宽的传感器误差概率分布,会显著 提高泄漏源反演信息的不确定度,而过低的测量灵敏度,会导致反演结果呈现多个局部极 值点的特性.本文研究的是扩散达到稳态后的反演问题,若考虑时间效应,如何利用不同 时刻的传感器数据更新泄漏源反演结果,还需进一步深入研究. 参考文献 [1]Alifanov 0 M.Inverse heat trall舒er problems[M].Berlin:sprillger—Verlag,1994 [2]EInjng I.Inverse problems in atmospheric constituent transport[M].Cambridge:Cambridge University Press,2002 [3]Skaggs T H,Kabala Z J.Recovering the history of a groundwater contaminant plume:method of quasi—reversibility[J]. WaterResourcesResearch,1995,31(11):2669-2673 [4] Bagtzoglou A C,Atmadja J.Marching-jury backward beam equation and quasi—reversibility methods for hydrologic inversion:application to contaminant flume spatial distribution recovery[J].Water Besources Research,2003,39 (2):1038 [5】Zhang T F,Chen Q.Identification of contaminant∞urce8 in enclosed environments by inverse CFD modeling[J]. Indoor Air,2007,17(3):167—177 [6]Skaggs T H,Kabala Z J.Recovering the release history of a groundwater contaminant[J].Water Resources Research, 1994,30(1):71-79 [7] Alapati S,Kabala z J.Recovering the release history of a groundwater contaminant via the non—linear least—squares estimation[J].Hydmlo画cal Process,2000,14(6):1003—1016 [8] Keats A,Yee E,Lien F S.Bayesian inference for$Olllme determination with applications to a complex urban environment [J].Atmospheric Environment,2007。41(3):465-479 [9]朱嵩,毛根海,程伟平,等.基于贝叶斯推理的水环境系统参数识别[J].江苏大学学报(自然科学版),2007,28 (3):237-240 Zhu Song,Mao Genhai,Cheng Weiping,et a1.Parameter identification for water environmental system based on Bayesian inference[J].Journal of Jiangsu University(Natural Science Edition),2007,28(3):237-240 [10]刘峰,黄顺祥,胡非,等.用伴随方法对毒气泄漏事件进行危害评估[J].中国安全科学学报,2003,13(9): 74-77 LiuFeng,Huang Shunxiang,HuFei,et a1.Adjointmethodfortherisk evaluation ofpoiBonona gasesle出ge[J].China 万方数据

704 应用基础与工程科学学报 Vol.18 Safety Science Joumal,2003,13(9):74-77 [11]Liu X.Zhai Z.Location identification for indoor instantaneous point contaminant source by probability-based invere Computational Fluid Dynamics modeling [J].Indoor Air,2008,18(1):2-11 [12] 郭少冬,杨锐,翁文国.基于MCMC方法的城区有毒气体扩散源反演[J].清华大学学报(自然科学版),2009, 49(5):629634 Guo Shaodong,Yang Rui,Weng Wenguo.Source inversion of toxic gas dispersion in urban areas based on the MCMC method []]Journal of Tainghua University(Science and Technology),2009,49(5):629-634 Investigation of the Inversion Modeling for Indoor Contaminant Source Based on the Adjoint Equation and MCMC Method GUO Shaodong'2,YANG Rui',SU Guofeng',ZHANG Hui (1.Centre for Public Safety Research,Department of Engineering Physics,Tsinghua University,Beijing 100084,China; 2.Institute of Applied Physisc and Computational Mathematics,Beijing 100084,China) Abstract Source inversion and identification method of contaminant dispersion in buildings was studied.An adjoint transportation equation was introduced and solved numerically,and a likelihood function was computed using predicted concentration database.Markov Chain Monte Carlo(MCMC)sampling based on Bayesian inference was used to inverse the parameters, including the source location and intensity.The agreement of the predicted results with the actual source location and intensity indicated that the method could be used to estimate indoor source parameters effectively.The studies also showed that the proposed procedure was more efficient when using the adjoint transportation equation with MCMC methods.The effects of the error probability distribution and detection limits of the sensors on the sensitivity and reliability of the method were then discussed.Analyses show that flatter and broader probability distribution of the sensor error leads to inversion results with larger uncertainty,while the lower sensor sensitivity leads to insufficient information and ill-posed characteristics of the inversion results with several clusters of possible source locations. Keywords:indoor contaminant source inversion;Bayesian inference;adjoint equation; computational fluid dynamics 万方数据
704 应用基础与工程科学学报 V01.18 Safety Science Journal,2003,13(9):74j77 [11]Liu X,Zhai z.Location identification for indoor instantaneous point contaminant floulw*by probability.based inverse Computational Fluid Dyllafflic$modeling[J].Indoor Air,2008,18(1):2-1 1 [12]郭少冬,杨锐,翁文国.基于MCMC方法的城区有毒气体扩散源反演[J].清华大学学报(自然科学版),2009, 49(5):629-634 Guo Shaodong,Yang Rui,Weng Wenguo.Source inversion of toxic gas dispersion in urban glma8 based on the MCMC method[J].Journal ofTsinshua Unlvemity(Science and Technology)。2009,49(5):629-634 Investigation of the Inversion Modeling for Indoor Contaminant Source Based on the Adjoint Equation and MCMC Method GUO Shaodon91’。,YANG Ruil,SU Guofen91,ZHANG Huil (1.Centre for Public Safety Research,Department of Ensineering Physics,Tsinghua University,Beijing 100084,China; 2.Institute of Apphed Physisc and Computational Mathematics,Beijing 100084,China) Abstract Source inversion and identification method of contaminant dispersion in buildings was studied.An adjoint transportation equation was introduced and solved numerically,and a likelihood function WflS computed using predicted concentration database.Markov Chin Monte Carlo(MCMC)sampling based on Bayesian inference Was used to inverse the parameters, including the source location and intensity.The agreement of the predicted results with the actual source location and intensity indicated that the method could be used to estimate indoor source parameters effectively.The studies also showed that the proposed procedure Was more efficient when using the adjoint transportation equation with MCMC methods.The effects of the error probability distribution and detection limits of the sensors on the sensitivity and reliability of the method were then discussed.Analyses show that flatter and broader probability distribution of the sensor en'or leads to inversion results with larger uncertainty,while the lower sensor sensitivity leads to insufficient information and ill—posed characteristics of the inversion results with several clusters of possible source locations. Keywords: indoor contaminant source inversion;Bayesian inference;adjoint equation; computational fluid dynamics 万方数据