
第20卷第14期 系统仿真学报© ol.20No.14 2008年7月 Journal of System Simulation Jul..2008 基于MCMC模拟的相关系数平稳序列模型及其应用 李卫国',熊炳忠2 (1.北京航空航天大学数学系,"“数学、信息与行为"教育部垂点实验室,北京100083:2.嘉兴学院,数学与信息工程学院,浙江嘉兴314000) 捕婴:提出了基于MCMC方法来估计相关系数平稳序列模型的参数:给出基于贝叶斯分布的相 关系平稳序列模型敏的算法;在无信总先验分布下,模拟证明了用此方法估计相关系数平稳 序列模型参数的优良效果,最后对实际的广西电网月负荷数据,分别用基于相关系数平稳序列模 型的MCMC方法和极大似然估计法以及基于经典的ARMA模型建模,结采表明采用MCMC方法 得到的模型给出的预测是最好的。 关键词:相关系数平稳序列;MCMC摸拟;贝叶斯估计;Gibbs袖样算法;电网负荷 中图分类号:0212:TP391 文献标识码:A文章编号:1004-731X(2008)143648-04 Correlation Coefficient Stationary Series Model Based on MCMC and ItsApplication LI Wei-guo,XIONG Bing-zhong? (1.Department of Mathematics,Beihang University.LMIB of the ministry of Education,Beijing 100083.China 2.School of Mathematies and Information Engineering.Jiaxing University Jiaxing Zhejiang 314000.China) Abstract:MCMC method was proposed to estimate the parameters of the correlation coefficient stationary series.The algorithm of using Bayesian distribution to estimate the model parameters was given.Extensive simulation experiments have shown that the Bayesian estimation procedure under the non-informative prior distribution works well.The MCMC method and the maximum like hood estimation method on the correlation coefficient stationary series and model on the classical ARMA were applied on the real electric net load monthly data of Guangxi.The results show that the MCMC method provides the most precise prediction. Key words:correlation coefficient stationary series;MCMC simulation;Bayesian estimation;Gibbs sampling algorithms; electric net monthly load. 引言 论在实际中的应用。为使此类模型的参数更容易估计出,本 文提出采用基于MCMC模拟的方法来估计它的参数。 工程实际中遇到的随机过程其均值和方差都是随时间 MCMC方法在统计上的应用是最近(不到二十年)发展起 变化的,因此,我们无法用传统的平稳随机过程来解决。 来的一种行之有效的贝叶斯估计方法,由于它使得统计学家 通过对大量实测数据的分析与研究,文献2]提出一种新的时 们能解决更复杂、更一般化的实际模型,已引起人们对它越 间序列模型,称为相关系数平稳序列。该序列的特征是:序 来越多的关注,更方便的是,由英国的Imperil college和 列均值和方差可随时间变化,相关函数不再是时间间隔的单 MRC Medical Research Council联合开发推出的用MCMC 变量函数,但相关系数函数仍然是时间间隔的单变量函数, 方法进行贝叶斯推断的专用软件包5 WinBUGS(Bayesian 从而使模型更加符合实际。在此基础上,文献3)又进一步提 inference Using Gibbs Sampling)的推广应用,以及现代计算 出了相关系数AR(p)和ARMA(p,q)模型,该棋型既描述了时 机性能的飞速发展,使得非常复杂模型的贝叶斯推断求解变 间序列均值和方差随时间变化的情况又考虑到数据间的相 得非常的容易和便捷。 关性,因此,它能更好地符合实际。然而,纵观已有的关于 1相关系数平稳系列的数学模型 相关系数平稳序列文献[2-4],在估计模型参数上采用的方法 主要是极大似然方法,从实际求解中知道,要得到各个参数 1.1相关系数平稳正态过程 的估计值就得求解一些非常复杂的非线性方程组。此时,一 定义1:设(x),1eT}是随机过程,如果 般采用数值求解法,壁如,拟牛顿迭代法、梯度法或者是收 ①{x),teT}是二阶矩过程: 敛速度更快的非线性方程组的一元化方法。实际计算表明, ②对任意的t,1+,有 即使采用相对简化的条件极大似然方法来估计模型各个参 p(i,I+)=cov(x(1)x+))+ 数仍然还是比较复杂和繁琐,这极大影响了相关系数平稳理 (1) √var(xt)lvar{xt+x》=p(x) 即自相关系数是单变量x的函数,则称{x(),1∈T}为相关系 收精日期:2007-03-22售回日期:2008-04-21 作者简介:李卫国(1955-),男,北京人,刷教授.研究方向为非平稳时间 数平稳过程。 序列分析方法与复杂系统的建模、控制:熊炳忠(11以.江西玉山人,讲 定义2:设{x(),teT)既是相关系数平稳过程,又是正 师,研究方向为时间序列分析、仿真建模、数理金融 ·3648- 万方数据
第20卷第14期 系 统仿真 学报@ V01.20№.14 2008年7月 Journal of System simuIation Jul.,2008 基于MCMC模拟的相关系数平稳序列模型及其应用 李卫国1,熊炳忠2 (1.北京航空航天大学数学系。“数学、信息与行为”教育部重点实验室,北京100083;2.嘉兴学院,数学与信息工程学院.浙江嘉兴314000) 摘要:提出了基于McMc方法来估计相关系数平穗序列模型的参数;给出基于贝叶斯分布的相 关系数平稳序列模型参数的算法;在无信息先验分布下,模拟证明了用此方法估计相关系数平稳 序列模型参数的优良效果.最后对实际的广西电网.月负荷数据,分别用基于相关系数平稳序列模 型的McMc方法和极大似然估计法以及基于经典的ARMA模型建模,结果表明采用McMc方法 得到的模型给出的预测是最好的。 关键词:相关系数平稳序列;McMC模拟;贝叶斯估计;Gibbs抽样算法;电网负荷 中图分类号:0212;11P39l 文献标识码:A 文章编号l 1004—731X(2008)1牛3“8·04 Correlation Coemcient Stationary Series Model Based on MCMC and ItsApplication L,’饱f.g“D1,jⅣD^n3 Bf,zg.z^D,192 (1.Dcpanmcnt of MatIlcmaIics,BeiII卸g UIlive巧i吼L~ⅡB of ttlc IIliIlis时of Education,Bc司ing 100083,ChiⅡa; 2.School of Mathc脚dcs aⅡd IⅡ妇Ⅱ0ⅡEngin∞血g.Ji“iⅡg UIliVersi吼Ji缸iⅡg zhcji孤g 314000.Cbi舱) Kb詈ha出McMc method w∞pmposcd to esttmme the p口rameters o,tk correknion co胡ic证m st口nonaq s盯ies.Tk 口增D—f砌t D,淞咖B口),Ps缸n硪sf一6“fiDn fD已J加懈把f^已mod纠p口加m£把坩'',础gfV已,1.ExtensiVe simu】ation exp硎ments haVe shown nlat the Bayesian estimation Drocedure under t11e non.infonnative prior distribution worlcs well.The MCMC metllOd 柚d tlle maximum like hood estimation method on me corrclation coefficient stationarv series and model on山e classical ARMA were邳Iplied on山e real electric net load monthlV data of Gu柚gxi.The results sbow mat me MCMC metIlod pI.oVides山e most precise prediction. Key words:correlation coef!ficiem s诅tionaDr s舐es;MCMC simulation;Bayesi柚estimation;Gibbs s锄pling algorithms; electric net monmly load. 引 言 工程实际中遇到的随机过程其均值和方差都是随时间 变化的,因此,我们无法用传统的平稳随机过程…来解决。 通过对大量实测数据的分析与研究,文献[2】提出一种新的时 间序列模型,称为相关系数平稳序列。该序列的特征是:序 列均值和方差可随时间变化,相关函数不再是时间间隔的单 变量函数,但相关系数函数仍然是时间间隔的单变量函数, 从而使模型更加符合实际。在此基础上,文献【3】又进一步提 出了相关系数AR(p)和ARMA(p,q)模型,该模型既描述了时 间序列均值和方差随时间变化的情况又考虑到数据间的相 关性,因此,它能更好地符合实际。然而,纵观已有的关于 相关系数平稳序列文献【2卅,在估计模型参数上采用的方法 主要是极大似然方法,从实际求解中知道,要得到各个参数 的估计值就得求解一些非常复杂的非线性方程组。此时,一 般采用数值求解法,譬如,拟牛顿迭代法、梯度法或者是收 敛速度更快的非线性方程组的一元化方法。实际计算表明, 即使采用相对简化的条件极大似然方法来估计模型各个参 数仍然还是比较复杂和繁琐,这极大影响了相关系数平稳理 收藕日期I 2007.03-22 ●回日期l 2008—04—2I 作者简介t李卫田(1955-),男,北京人,副教授,研究方向为非平稳时间 序列分析方法与复杂系统的建模、控制:熊炳患(197l一),江西玉山人。讲 师。研究方向为时间序列分析、仿真建模、数理金融。 论在实际中的应用。为使此类模型的参数更容易估计出,本 文提出采用基于MCMC模拟的方法来估计它的参数。 MCMC方法在统计上的应用是最近(不到二十年)发展起 来的一种行之有效的贝叶斯估计方法,由于它使得统计学家 们能解决更复杂、更一般化的实际模型,已引起人们对它越 来越多的关注,更方便的是,由英国的Imp耐l college和 MRC Medjcal Rese孙ch Council联合开发推出的用MCMC 方法进行贝叶斯推断的专用软件包【5晰nBuGS(Bayesian iIlfcrence using Gibbs s锄pling)的推广应用,以及现代计算 机性能的飞速发展,使得非常复杂模型的贝叶斯推断求解变 得非常的容易和便捷。 1相关系数平稳系列的数学模型 1.1相关系数平稳正态过程 定义l:设f工(f),f∈r}是随机过程,如果 ①{工(f),f∈丁}是二阶矩过程; ②对任意的f,f+t有 p(f,f+f)=cov(工(f),石(f+f))+ √Var(工(f)1var{J(f+彳)l=p(f) ‘。 即自相关系数是单变量f的函数,则称{J(f),f∈丁}为相关系 数平稳过程。 定义2:设{工(f)。,∈r)既是相关系数平稳过程,又是正 ·36牾· 万方数据

第20鞋第14期 6l20No.14 2008年7月 李卫国,等:基于MCMC模拟的相关系数平稳序列模型及其应用 jul,2008 态随机过程,则称{x),reT}为相关系数平稳正态过程。记 从而得到相关系数平稳AR()序列模型的似然函数为: 相关系数平稳正态过程的均值、方差函数分别为: L0=(无,,5x色b,n心) E(x()}=μ(a,) (2) =4o4,∑(-4ai-八TP,)(I1) var(x(t)]=o2(b.t) (3) 式中a=(a,4a,,b=(你,…b,)了均为待定参数。函数 式中的x:a,)表示均值为a,标准差为B的正态分布密 4(,σ()具体形式可用文献4提出的时间序列均值方差 度函数。设模型的各个参数的先验分布相互独立,则有: 函数的确定方法以及结合所研究问题的物理性质、经验公式 p()=p(a)p(b)p(n)p(oi) (12) 等求得。 根据贝叶斯公式便有:参数0的联合后验分布密度函数 12相关系数平稳序列 f(): f(a,b,n,o2,…,x)eL(0)p(0) (13) 定义3:,设{x(),teT}是相关系数平稳过程,记 x=(,,xy为它的一个样本,其中无=,),=6+山, 2.2MCMC方法、Gibbs抽样及Metropolis-Hasting 。,△山分别是采样初始时刻和采样间隔。设y=(%,2,…y,)y 算法 是传统的AR(p以、MA(q)或ARMA(P,q)序列,若 MCMC方法5-刀的基本思想是构造一条具有指定平稳分 y=-4a】 (4) 布π(X)的马尔可夫链,即它的转移分布收敛到的后验分 1(b,4) 布。然后充分长地运行链,到链上取值的分布与其平稳分布 E{x)j=4(a,) (5) 足够接近时,把来自链上的样本作为来自(X)的样本, var(x(t))=l2(b,t) (6) 基于这些样本进行各种统计推断。例如求均值、方差等。不 上式中a=(a,a…a,),b=(,hb,,哈均为待定参 同的MCMC方法主要是构造Markov链的方法不同,常用 数,则称x=(:,,…x了为相关系数平稳ARp)序列、MA(q 来构造链的方法有Gibbs算法和Metropolis-Hasting算法。 序列或ARMA(p,q序列,此时也称(xt),t∈T]为相关系数 Gibbs抽样的思想是利用条件分布族来得到以()为 ARp、MA(q)或(ARMA P,q)过程。这样一般的相关系数 平稳分布的马尔可夫链。 平稳ARMA(p,q)序列模型为: 设π=π(8,…,8.) (14) 本a2-2n西-a】+4-2⑦ 记0=(g,,8"),8四=(g,…,8"): Ib,)台 1(b,-) 再记第1个至第(k-1)个分量固定为2,…,,同时将第 (7式中E{x(4)}=4(a,4),var{x)}=o2(b,), (k+1)至第m个分量固定为,…,的条件下,第k个分 ELELE:]=026x, 量8的条件分布为: 其中当k=i时6=1,当k≠i时,6=0,乃…np,…入为 π(88…,,,…,),定义转移概率: 常数。当q=0时,(⑤)式表示的就是相关系数平稳AR(p)序列 Pagn兰p(0-→g2) 模型,当p-0时,(5)式是相关系数平稳MA(q)序列模型。 下文主要研究相关系数平稳AR(P)序列模型参数的贝叶斯 =1xaa,8m,8.,,8) (15) 估计。 可以证明{P}为一个转移矩阵,π()是它的平稳分 2相关系数平稳AR(1)序列模型的参数估计 布。这里并不需要知道π的具体表达式,只需知道固定其它 一切分量的条件下,余下一个分量的条件分布。 21模型的贝叶斯分析 如果条件分布不是来自一个标准分布族,则估计参数就 湍要用Metropolis-Hasting算法。该算法最早由Metropolis 设,e,是高斯过程,给定样本观测值(0,,,…x,)条 于1953年提出,1970年Hasting对它加以推广。由于分布 件下,记0=(a,b,n02y,a=(a,a…a,)b=(6,…b), 族未知,抽样无法直接从原来分布族进行,此时,从另一个 刀=(,…n,)厂,则相关系数平稳AR(p)序列模型中各个量 被称为建议分布的已知分布开始。假定建议分布为T(x,y), 的关系可表示为: 当前状态为x,其算法为: (xo0)-N(ao,bio2) (8) ①从建议分布T(x,y)产生y: (,,-p,)- (9) ②②由均匀分布U(0,)抽取u: N吃-以ai-Arb.D ③③计算比率(x,y),其中 (a,b,n.o2)-P(a,b,n.o2) (10) r(y)=min(l)T(. (16) π(x)T(xy) 式中x2表示给定元条件下的x,N(μ,o)表示均值为4, ④x+0= [y,if usr(x,y) (17) 方差为σ2的正态分布函数,P(表示关于0的分布函数。 x,other ·3649· 万方数据
第20卷第14期 2008年7月 李卫国,等:基于McMc模拟的相关系数平稳序列模型及其应用 VU.20No.14 Jul.,2008 态随机过程,则称{工(f),f∈r}为相关系数平稳正态过程。记 相关系数平稳正态过程的均值、方差函数分别为: E{工(f)}=∥(a,f) (2) var{工(f)l=仃2(b,f) (3) 式中a=‰,国…珥)7,b=(%,岛…仇)r均为待定参数。函数 ∥(·),仃2(·)具体形式可用文献【4】提出的时间序列均值方差 函数的确定方法以及结合所研究问题的物理性质、经验公式 等求得。 1.2相关系数平稳序列 定义3:.设{工(f),f∈丁)是相关系数平稳过程,记 工=“,死,…而)7为它的一个样本,其中玉=石(‘),^=岛+池, f0,△f分别是采样初始时刻和采样间隔。设y=(为,弛,…儿)r 是传统的AR(p)、MA(q)或ARMA(p,q)序列,若 yj:譬娑掣 一 (4) ,(b,‘) ~ 耳z(f))=∥(a,f) (5) var{工(f)}=研,2(b,f) (6) 上式中a=(嘞,砚…珥)7’b=(%,籼…眈)r,D吾均为待定参 数,则称石=(礼花,…而)7为相关系数平稳AR(p)序列、MA(q) 序列或ARMA(p,q)序列,此时也称{工(f),f∈7’)为相关系数 AR(p)、MA(q)或(ARMA p,q)过程。这样一般的相关系数 平稳ARMA(p,q)序列模型为: 铧:圭吼堕掣+&一窆概。(7) J(b,ft) 智” ,(b,“) ‘智一’ ~ (7)式中E{j【(“)}=∥(a,“), vaf{工(“)}=盯2,2(b,“), E【岛岛】=盯2最, 。 其中当七=f时况=l,当七≠i时,况=o,研…仉,丑…五为 常数。当q.0时,(5)式表示的就是相关系数平稳AR(p)序列 模型,当p=o时,(5)式是相关系数平稳MA(q)序列模型。 下文主要研究相关系数平稳AR(p)序列模型参数的贝叶斯 估计。 2相关系数平稳AR(1)序列模型的参数估计 2.1模型的贝叶斯分析 设而,局是高斯过程,给定样本观测值(知,再,恐,…而)条 件下,记0=(a’b,lI,盯2)7,a=(口o,口1…口,)7,b=(%,岛…阢)’, 玎=(砀,…仉)7,则相关系数平稳A尺(p)序列模型中各个量 的关系可表示为: (知fo)~Ⅳ(珊,蹭cr2) (8) (再I再一I'.一,再一p,o)一 (9) P Ⅳ(∑叩,(再一,一∥(a,f一_『)),盯2,2(b,f) 卢l (a,b,q,仃2)一P(a,b,q,盯2) (10) 从而得到相关系数平稳AR(p)序列模型的似然函数为: 以0)=以知,再,·-j矗khqD2) =奴如;匈,如).n豇玉;∑仿(再叫一“a'l一脚,D2,2(b’f))(11) 式中的纵工;口,∥)表示均值为口,标准差为∥的正态分布密 度函数。设模型的各个参数的先验分布相互独立,则有: p(0)=P(a)p(b)p(11)p(口2) (12) 根据贝叶斯公式便有:参数O的联合后验分布密度函数 ,(·): ,(a,b,'I,cr2 l葡,而…,五。)氍L(o)p(o) (13) 2.2 McMC方法、Gibbs抽样及MetmpoIis.H嬲ting 算法 MCMC方法‘"1的基本思想是构造一条具有指定平稳分 布石(臼Ix)的马尔可夫链,即它的转移分布收敛到的后验分 布。然后充分长地运行链,到链上取值的分布与其平稳分布 足够接近时,把来自链上的样本作为来自石(口Ix)的样本, 基于这些样本进行各种统计推断。例如求均值、方差等。不 同的McMC方法主要是构造Markov链的方法不同,常用 来构造链的方法有Gibbs算法和Me仃opolis.H越ting算法。 Gibbs抽样的思想是利用条件分布族来得到以万(口)为 平稳分布的马尔可夫链。 设石=万(岛,·一,以) (14) 记伊1)=(研”,…,碟’),伊2)=(岛。’,…,簖’); 再记第1个至第(七一1)个分量固定为研舶,…,碰2,,同时将第 (七+1)至第m个分量固定为绣¨l,…,创’的条件下,第k个分 量倪的条件分布为: 万(晚l纠”,…,联二,戗?1’.”,酬’),定义转移概率: p掣‘w2)皇p(伊1’—》目‘2’) =兀万(岛I岛‘孙,…,B一1‘21,皖+1m,…,以‘1’) (15) 可以证明{办咐:,}为一个转移矩阵,石(∞是它的平稳分 布。这里并不需要知道石的具体表达式,只需知道固定其它 一切分量的条件下,余下一个分量的条件分布。 如果条件分布不是来自一个标准分布族,则估计参数就 需要用Me昀polis—Has“g算法。该算法最早由Metmpolis 于1953年提出,1970年Hasting对它加以推广。由于分布 族未知,抽样无法直接从原来分布族进行,此时,从另一个 被称为建议分布的已知分布开始。假定建议分布为r(工,y), 当前状态为石“),其算法为: ①从建议分布丁(五y)产生y; ②②由均匀分布u(o,1)抽取“; ③③计算比率,(工,y),其中 啾朋刊n{1,嬲器); (16) 雾塞£辚黧篡篇茄霈’ ④∥枷镀乞∥∥”∥’ ∽, 方差为仃2的正态分布函数,P(·)表示关于0的分布函数。 【一”, Dt妇r 、’ ·3649· 万方数据
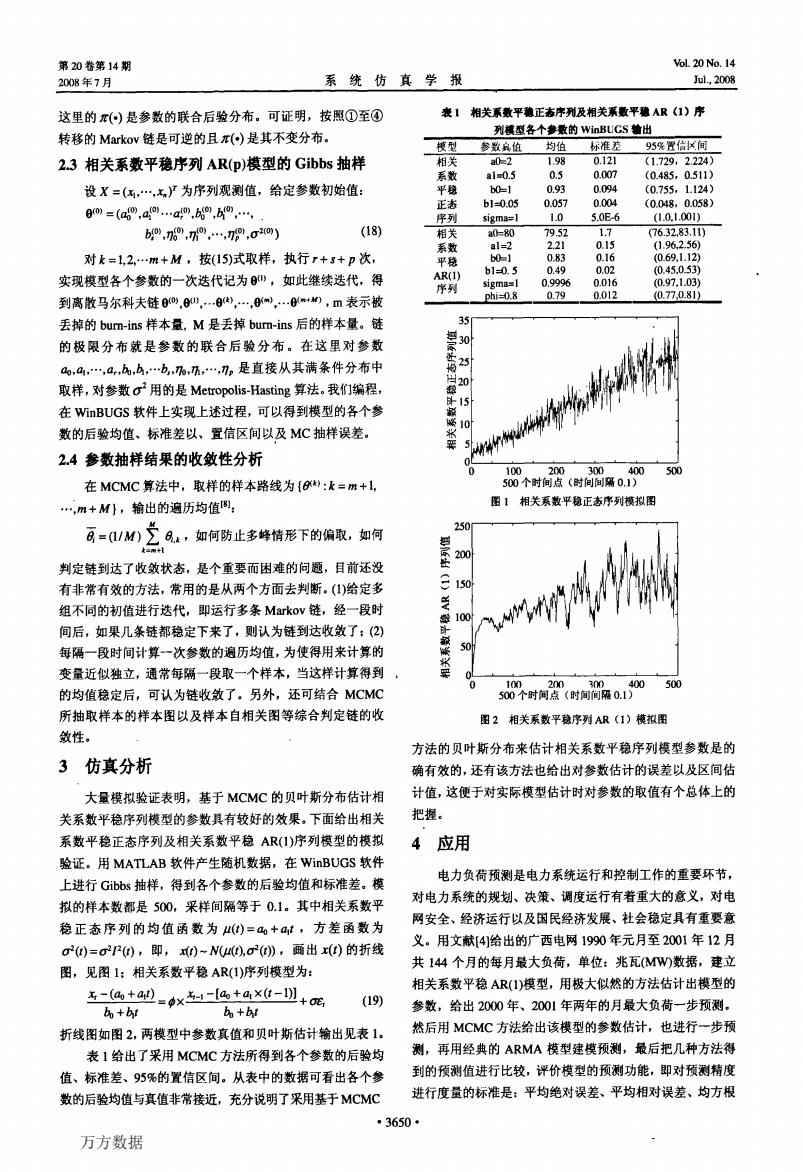
第20卷第14期 Vol.20 No.14 2008年7月 系统仿真学报 Jul,2008 这里的π()是参数的联合后验分布。可证明,按照①至④ 表1相关系数平雅正志序列及相关系数平确AR(1)序 转移的Markov链是可逆的且()是其不变分布。 列该型各个参最的WinBUGS塘出 模型参数值均伯 标准范 95降置信铁间 2.3相关系数平稳序列AR(p)模型的Gibbs抽样 相关 a0=2 198 0.121 (1.729,2224) 系数 a1=0.5 0.5 0.007 (0.485,0.511) 设X=(,…,x了为序列观测值,给定参数初始值: 平稳 b0=1 0.93 0.094 (0.755,1.124) 正志 b1-0.05 0.057 0.004 (0.048,0.058) 0om=(a0,ao…a,h6,0,, 序列 sigma=1 1.0 5.0E6 (1.0.1.001) b0,7%,7,,79,c240) (18) 相关 a0-80 79.52 1.7 (76.32,83.11) 系数 a1=2 2.21 0.15 (1.96.2.56 对k=1,2…m+M,按(15)式取样,执行r+3+p次, 平稳 b0=1 0.83 0.16 (0.691.12) AR(1) b10.5 0.49 0.02 (0.45.0.53) 实现模型各个参数的一次迭代记为,如此继续迭代,得 序列 sigma=1 09996 0.016 (0.97.1.03) 到离散马尔科夫链0,0四,…0,…,0,…0+),m表示被 phi-0.8 0.79 0.012 (0.770.81) 丢掉的burm-ins样本量,M是丢掉bum-ins后的样本量。链 5 的极限分布就是参数的联合后验分布。在这里对参数 30 o,4,,a,,4,…b,,乃,…,1p是直接从其满条件分布中 25 20 取样,对参数C2用的是Metropolis-Hasting算法。我们编程, 15 在WinBUGS软件上实现上述过程,可以得到模型的各个参 数的后验均值、标准差以、置信区间以及MC抽样误差。 2.4参数抽样结果的收敛性分析 10 500 在MCMC算法中,取样的样本路线为{0,:k=m+L, 500个时间点(时间间隔0.1) ,m+M},输出的遍历均值⑧: 图1相关系数平稳正态序列模拟图 A=/M)立a,如何防止多峰情形下的偏取,如何 250 判定链到达了收敛状态,是个重要而困难的问题,目前还没 200 有非常有效的方法,常用的是从两个方面去判断。()给定多 150 组不同的初值进行迭代,即运行多条Markov链,经一段时 间后,如果几条链都稳定下来了,则认为链到达收敛了:(2) 每隔一段时间计算一次参数的遍历均值,为使得用来计算的 变量近似独立,通常每隔一段取一个样本,当这样计算得到 0 100200 300 400500 的均值稳定后,可认为链收敛了。另外,还可结合MCMC 500个时闻点(时间间隔0.) 所抽取样本的样本图以及样本自相关图等综合判定链的收 图2相关系数平稳序列AR(1)模拟图 敛性。 方法的贝叶斯分布来估计相关系数平稳序列模型参数是的 3仿真分析 确有效的,还有该方法也给出对参数估计的误差以及区间估 大量模拟验证表明,基于MCMC的贝叶斯分布估计相 计值,这便于对实际模型估计时对参数的取值有个总体上的 关系数平稳序列模型的参数具有较好的效果。下面给出相关 把握。 系数平稳正态序列及相关系数平稳AR(1)序列模型的模拟 4应用 验证。用MATLAB软件产生随机数据,在WinBUGS软件 上进行Gibbs抽样,得到各个参数的后验均值和标准差。模 电力负荷预测是电力系统运行和控制工作的重要环节, 拟的样本数都是500,采样间隔等于0.1。其中相关系数平 对电力系统的规划、决策、调度运行有者重大的意义,对电 网安全、经济运行以及因民经济发展、杜会稳定具有重要意 稳正态序列的均值函数为)=+at,方差函数为 2)=σ22),即,0-N(4(),o2(),画出x()的折线 义。用文献4]给出的广西电网1990年元月至2001年12月 共144个月的每月最大负荷,单位:兆瓦(MW)数据,建立 图,见图1:相关系数平稳AR(1)序列模型为: 相关系数平稳AR(I)模型,用极大似然的方法估计出模型的 -(a+a型=x4-a+ax-+E (19) bo+b! bo+bt 参数,给出2000年、2001年两年的月最大负荷一步预测。 折线图如图2,两模型中参数真值和贝叶斯估计输出见表1。 然后用MCMC方法给出该模型的参数估计,也进行一步预 表1给出了采用MCMC方法所得到各个参数的后验均 测,再用经典的ARMA模型建模预测,最后把几种方法得 值、标准差、95%的置信区间。从表中的数据可看出各个参 到的预测值进行比较,评价模型的预测功能,即对预测精度 数的后验均值与真值非常接近,充分说明了采用基于MCMC 进行度量的标准是:平均绝对误差、平均相对误差、均方根 ·3650 万方数据
第20卷第】4期 2008年7月 系统仿真学报 、,01.20No.14 Jul.2008 这里的石(·)是参数的联合后验分布。可证明,按照①至④ 转移的Markov链是可逆的且石(·)是其不变分布。 2.3相关系数平稳序列AR(p)模型的Gibbs抽样 设x=(而,…,矗)7为序列观测值,给定参数初始值: o(o)=(毋’,4f0J...口50),蹦们,研们,…,. 辨m,刀50’,硝m,…,,7字’,仃2(o’) (18) 对七=1,2,…m+肘,按(15)式取样,执行,+J+p次, 实现模型各个参数的一次迭代记为0(n,如此继续迭代,得 到离散马尔科夫链0(m,O(”,…0(n,…,O(…,…0(“…,m表示被 丢掉的bum.irIs样本量,M是丢掉bum.ins后的样本量。链 的极限分布就是参数的联合后验分布。在这里对参数 嘞,口I,…,口,,%,岛,…既,枷,哺,…,,7,是直接从其满条件分布中 取样,对参数盯2用的是Me廿opohs.H弱ting算法。我们编程, 在砌nBuGS软件上实现上述过程,可以得到模型的各个参 数的后验均值、标准差以、置信区间以及Mc抽样误差。 2.4参数抽样结果的收敛性分析 在McMC算法中,取样的样本路线为f∥‘’:七=所+l, …,小+Ml,输出的遍历均值【g】= 虿=(1/M)∑岛,。,如何防止多峰情形下的偏取,如何 t;1 判定链到达了收敛状态,是个重要而困难的问题,目前还没 有非常有效的方法,常用的是从两个方面去判断。(1)给定多 组不同的初值进行迭代,即运行多条Markov链,经一段时 间后,如果几条链都稳定下来了,则认为链到达收敛了;(2) 每隔一段时间计算一次参数的遍历均值,为使得用来计算的 变量近似独立,通常每隔一段取一个样本,当这样计算得到 的均值稳定后,可认为链收敛了。另外,还可结合McMC 所抽取样本的样本图以及样本自相关图等综合判定链的收 敛性。 3仿真分析 大量模拟验证表明,基于McMc的贝叶斯分布估计相 关系数平稳序列模型的参数具有较好的效果。下面给出相关 系数平稳正态序列及相关系数平稳AR(1)序列模型的模拟 验证。用MATLAB软件产生随机数据,在winBuGs软件 上进行Gibbs抽样,得到各个参数的后验均值和标准差。模 拟的样本数都是500,采样间隔等于0.1。其中相关系数平 稳正态序列的均值函数为∥(f)=嘞+确f,方差函数为 cr2(f)=矿,z(f),即,m)一JV∽(f),矿(f)),画出工(f)的折线 图,见图1;相关系数平稳AR(1)序列模型为: 生尘趔:痧×生l二堕兰垡』三盟+∞ (19) %+岛f %+岛‘ 折线图如图2,两模型中参数真值和贝叶斯估计输出见表l。 表l给出了采用McMc方法所得到各个参数的后验均 值、标准差、95%的置信区间。从表中的数据可看出各个参 数的后验均值与真值非常接近,充分说明了采用基于MCMc 袭l相关系敷平稳正杏序列及相关系数平穗AR(1)序 列模型各个参致的wiIIBuGs■出 相关 扯80 79.52 1.7 (76 32,83.11) 系数 al=2 2.2l O.15 (1.96,2.56) 平籀b0=l O.83 O.16 (O,69,1.12) 慨,是篙。甄盟 嬲器; :::: P坐兰:! !::: !:!!; 生:::!:!12 趔 承 世 : V 爱 瓣 } 籁 倏 牛K 罂 500个时间点(时『日J捌隔0.1) 图1相关系数平稳正态序列模拟图 图2相关系数平稳序列AR(1)模拟图 方法的贝叶斯分布来估计相关系数平稳序列模型参数是的 确有效的,还有该方法也给出对参数估计的误差以及区间估 计值,这便于对实际模型估计时对参数的取值有个总体上的 把握。 4应用 电力负荷预测是电力系统运行和控制工作的重要环节, 对电力系统的规划、决策、调度运行有着重大的意义,对电 网安全、经济运行以及国民经济发展、社会稳定具有重要意 义。用文献【4】给出的广西电网1990年元月至2001年12月 共144个月的每月最大负荷,单位:兆瓦(M、们数据,建立 相关系数平稳AR(1)模型,用极大似然的方法估计出模型的 参数,给出2000年、2001年两年的月最大负荷一步预测。 然后用MCMC方法给出该模型的参数估计,也进行一步预 测,再用经典的ARMA模型建模预测,最后把几种方法得 到的预测值进行比较,评价模型的预测功能,即对预测精度 进行度量的标准是:平均绝对误差、平均相对误差、均方根 ·3650· 万方数据
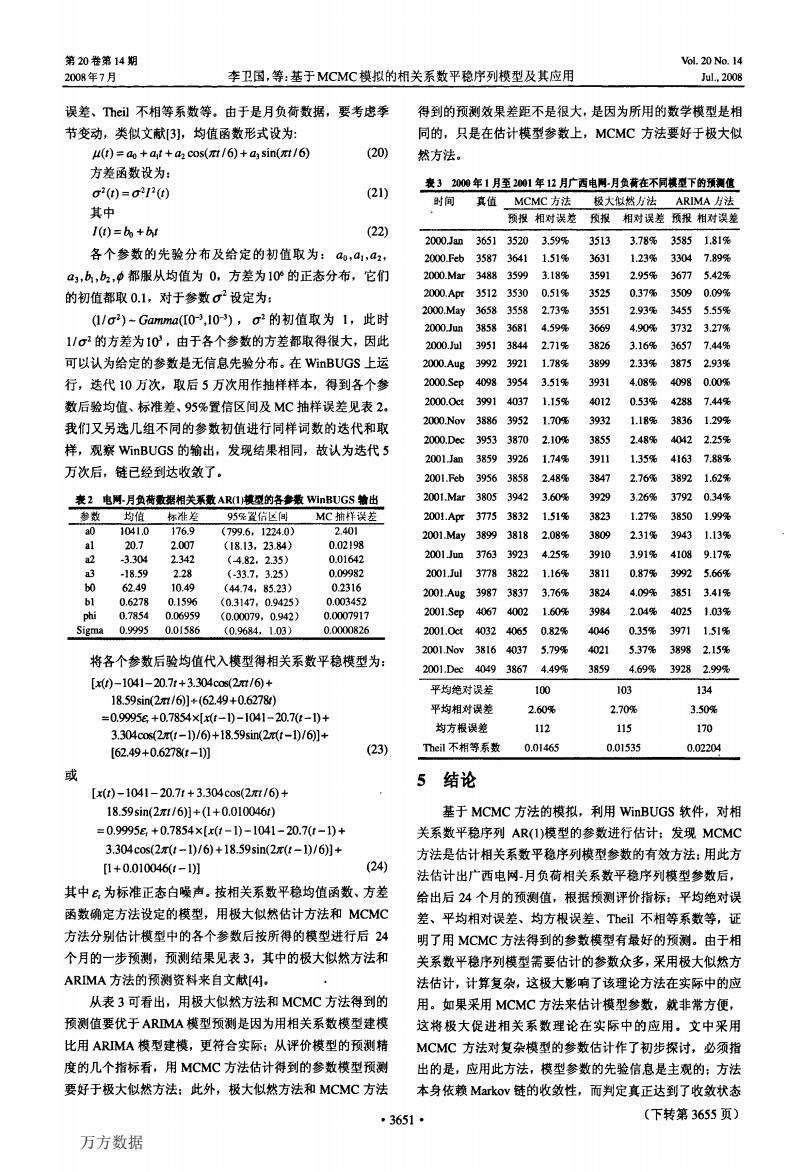
第20卷第14期 Vol.20 No.14 2008年7月 李卫国,等:基于MCMC模拟的相关系数平稳序列模型及其应用 Jul,2008 误差、Theil不相等系数等。由于是月负荷数据,要考虑季 得到的预测效果差距不是很大,是因为所用的数学模型是相 节变动,类似文献3引,均值函数形式设为: 同的,只是在估计模型参数上,MCMC方法要好于极大似 u(t)=ao+at +a cos(/6)+a sin(/6) (20) 然方法。 方差函数设为: (21) 表32000年1月至2001年12月广西电网月负黄在不同模型下的预测值 o2()=0212() 时间真值MCMC方法极大似然方法ARIMA方法 其中 预报相对误差预报相对误差顶报相对误差 I(t)=b+1 (22) 2000.Jam365135203.59% 35133.78%35851,81% 各个参数的先验分布及给定的初值取为:ao,a1,a2, 2000Feb35873641 1.51% 3631 1.23%3304 789% ag,,b2,中都服从均值为0,方差为10的正态分布,它们 2000.Mar348835993.18% 3591 2.95%36775.42% 的初值都取0.1,对于参数σ2设定为: 2000.Apr351235300.51% 3525 0.37%35090.09% (I/o2)-Gamma(I0,10),σ2的初值取为1,此时 2000.May36583558 2.73% 3551 2.93%3455 5.55% 2000Jun385836814.59% 3669 4.90%37323.27% 1/σ2的方差为10,由于各个参数的方差都取得很大,因此 2000.Jm13951 3844 2.71% 3826 3.16% 3657 7.44% 可以认为给定的参数是无信息先验分布。在WinBUGS上运 2000.Aug39923921 1.78% 3899 2.33%3875 2.93% 行,选代10万次,取后5万次用作抽样样本,得到各个参 2000.Scp409839543.51% 3931 4.08%4098 0.00% 数后验均值、标准差、95%置信区间及MC抽样误差见表2, 2000.0ct39914037 1.15% 4012 0.53% 4288 7.44% 2000.Now38863952 170 3932 1.18% 3836 1.29% 我们又另选几组不同的参数初值进行同样词数的迭代和取 2000.Dec39533870 2109 3855 2.48% 4042 2.25% 样,观察WinBUGS的输出,发现结果相同,故认为迭代5 2001Jan38593926 174 3911 1.35% 4163 7.88% 万次后,链已经到达收敛了。 2001.Feb39563858 248 3847 2.76% 3892 1.62% 表2电网-月负荷数据相关系数AR(I模级的各参表WinBUGS物出 2001.Mar38053942 3929 3.26% 3792 0.34% 参数均值杯准差 95%置份区间MC抽样误差 2001.Apr37753832 151% 3823 1.27% 3850 1.99% a0 1041.0 176.9 (799.6,1224.0) 2.401 2001May38993818 2.08% 3809 20.7 2.31% 3943 1.13% al 2.007 (18.13,23.84) 0.02198 a2 -3304 2.342 (4.82.2.35) 0.01642 2001Jum37633923 4.25% 3910 3.91% 4108 9.17% a3 -18.59 2.28 (-33.7.3.25) 0.09982 2001.Jul377838221.16% 3811 0.87%3992 5.66% 0 6249 10.49 (44.74,85.23) 0.2316 2001.Aug398738373.76% 3824 4.09%3851 3.41% b1 0.62780.159% (0.3147,0.9425) 0.003452 phi 0.7854 0.06959 (0.00079,0.942) 0.0007917 2001.Scp406740021.60% 3984 2.04%4025 1.03% Sigma0.99950.01586 (0.96841.03) 0.0000826 2001.0ct403240650.82% 4046 0.35%3971151% 2001.Nov381640375.79% 4021 537%38982.15% 将各个参数后验均值代入模型得相关系数平稳模型为: 2001.Dec404938674.49%38594.69%39282.99% [0)-1041-20.7t+3.304cos(2m/6+ 平均绝对误差 100 103 134 18.59sin(2m/6]+(62.49+0.6278) 平均相对误差 2.60% 2.70% 3.50% =0.9995e+0.7854×[xt-1)-1041-20.7(t-1)+ 3.304cos(2t-1)/6)+18.59sin(2t-10/6+ 均方根误差 112 115 170 [62.49+0.62781-10j (23) Theil不相等系数 0.01465 0.01535 0.02204 或 5结论 [x(t)-1041-20.7t+3.304cos(2t/6)+ 18.59sin(2x1/6)]+(1+0.010046t) 基于MCMC方法的模拟,利用WinBUGS软件,对相 =0.9995E+0.7854×[x(t-1)-1041-20.7t-1)+ 关系数平稳序列AR(I)模型的参数进行估计:发现MCMC 3.304cos(2m(t-1)/6)+18.59sin(2x(t-10/6)]+ 方法是估计相关系数平稳序列模型参数的有效方法:用此方 [1+0.010046(t-1】 (24) 法估计出广西电网-月负荷相关系数平稳序列模型参数后, 其中6为标准正态白噪声。按相关系数平稳均值函数、方差 给出后24个月的预测值,根据预测评价指标:平均绝对误 函数确定方法设定的模型,用极大似然估计方法和MCMC 差、平均相对误差、均方根误差、Theil不相等系数等,证 方法分别估计模型中的各个参数后按所得的模型进行后24 明了用MCMC方法得到的参数模型有最好的预测。由于相 个月的一步预测,预测结果见表3,其中的极大似然方法和 关系数平稳序列模型需要估计的参数众多,采用极大似然方 ARMA方法的预测资料来自文献[4. 法估计,计算复杂,这极大影响了该理论方法在实际中的应 从表3可看出,用极大似然方法和MCMC方法得到的 用。如果采用MCMC方法来估计模型参数,就非常方便, 预测值要优于ARMA模型预测是因为用相关系数模型建模 这将极大促进相关系数理论在实际中的应用。文中采用 比用ARMA模型建模,更符合实际:从评价模型的预测精 MCMC方法对复杂模型的参数估计作了初步探讨,必须指 度的几个指标看,用MCMC方法估计得到的参数模型预测 出的是,应用此方法,模型参数的先验信息是主观的:方法 要好于极大似然方法:此外,极大似然方法和MCMC方法 本身依赖Markov链的收敛性,而判定真正达到了收敛状态 ·3651 (下转第3655页) 万方数据
第加卷第14期 2I)08年7月 李卫国,等:基于McMC模拟的相关系数平稳序列模型及其应用 V01.20№.14 Jul..2008 误差、111cil不相等系数等。由于是月负荷数据,要考虑季 节变动,类似文献【3】,均值函数形式设为: ∥(f)=口o+qf+口2cos(刀彳/6)+口3 sin(册/6) (20) 方差函数设为: 仃2(f)=仃2,2(r) (21) 其中 ,(f)=%+岛f (22) 各个参数的先验分布及给定的初值取为:‰,口,,口:, 口3,岛,坑,≯都服从均值为0,方差为106的正态分布,它们 的初值都取O.1,对于参数cr2设定为: (1/仃2)~G口,,z,M(r0-3,104),盯2的初值取为l,此时 1/盯:的方差为103,由于各个参数的方差都取得很大,因此 可以认为给定的参数是无信息先验分布。在winBuGs上运 行,迭代10万次,取后5万次用作抽样样本,得到各个参 数后验均值、标准差、95%置信区间及MC抽样误差见表2。 我们又另选几组不同的参数初值进行同样词数的迭代和取 样,观察、MnBuGS的输出,发现结果相同,故认为迭代5 万次后,链已经到达收敛了。 衰2电同.月负荷敷据相关系教AR(1)模型的各馘wjnBuGs输出 将各个参数后验均值代入模型得相关系数平稳模型为: [瓤f)一1041—20.7f+3.30400s(勿盯,6,+ 18.59s砥2村/6)】÷(62.49+0.627&) =0.9995£+0.7854×【颤f一1)一1041—20.7(f一1)+ 3.30400s(2万(f一1),6)+1&59sin(2积f一1),6)】+ 【62.49+O.627即一1)】 (23) 或 [J(f)一104l一20.7f+3.304cos(2刀7/6)+ 18.59sin(2肌/6)】+(1+0.010046f) =O.99956+O.7854×【J0—1)一1041—20.7(f一1)+ 3.304cos(2石(f—1),6)+18.59sin(2刀<f一1),6)】+ [1+0.010046(f一1)】 (24) 其中晶为标准正态白噪声。按相关系数平稳均值函数、方差 函数确定方法设定的模型,用极大似然估计方法和MCMC 方法分别估计模型中的各个参数后按所得的模型进行后24 个月的一步预测,预测结果见表3,其中的极大似然方法和 ARIMA方法的预测资料来自文献【4】。 . 从表3可看出,用极大似然方法和MCMC方法得到的 预测值要优于AR珊队模型预测是因为用相关系数模型建模 比用AIuMA模型建模,更符合实际;从评价模型的预测精 度的几个指标看,用MCMC方法估计得到的参数模型预测 要好于极大似然方法;此外,极大似然方法和MCMC方法 得到的预测效果差距不是很大,是因为所用的数学模型是相 同的,只是在估计模型参数上,MCMC方法要好于极大似 然方法。 衰3 20∞年1月至2帅1年12月广西电圈.月负荷在不同模型下的预测值 平均绝对误差 平均相对误差 均方根误差 Theil不相等系数 103 2.70% 115 134 3.50% 170 O.02204 5结论 基于MCMC方法的模拟,利用WinBUGS软件,对相 关系数平稳序列AR(1)模型的参数进行估计:发现MCMC 方法是估计相关系数平稳序列模型参数的有效方法;用此方 法估计出广西电网一月负荷相关系数平稳序列模型参数后, 给出后24个月的预测值,根据预测评价指标:平均绝对误 差、平均相对误差、均方根误差、Theil不相等系数等,证 明了用MCMC方法得到的参数模型有最好的预测。由于相 关系数平稳序列模型需要估计的参数众多,采用极大似然方 法估计,计算复杂,这极大影响了该理论方法在实际中的应 用。如果采用MCMC方法来估计模型参数,就非常方便, 这将极大促进相关系数理论在实际中的应用。文中采用 MCMc方法对复杂模型的参数估计作了初步探讨,必须指 出的是,应用此方法,模型参数的先验信息是主观的;方法 本身依赖Markov链的收敛性,而判定真正达到了收敛状态 ·365l· (下转第3655页) =m一 万方数据

第20卷第14期 ol.20No.14 2008年7月 陆秀令,等:电力谐波滑窗迭代DFT检测算法的研究与仿真 Jul,2008 小、灵活性高、易于工程实现的特点。 参考文献: 50 0050.1015 02 025 03 0.35 0.4 [】王兆安,杨君,刘进军.谐被神制与无功功率补偿M.北京:机 城工业出版杜,1998. AAAAMAMAA 2) 陆秀令,周腊吾.基于爵时无功功率的谐波电压检测法仞.高电 压技术,2006.32(18890, 3 李红,杨善水。傅立叶电力系统谐波检测方法综述们.现代电力 00050.10150.20250.3035 0.4 2004,21(4分:3944. [41 李圣清,朱英浩,周有庆,等.电网谐波检测方法的棕述们高电 0料 压技术,2004.30(3):3942. [5)叶德云,罗欢,刘开培.基于Fy心功率定义的三相系统广义无功 00.05010.150.20250.30350.4 实时检测方法U.电气应用,2005,24(10以142-147. [6】张国荣,丁明,架海涛。等.一种应用于单相DVR的检剩算法与 图3滑篚选代DFT检测算法仿真波形图 仿真0.系统仿真学报,200m,19(4:732-734.(ZHANG Gu0-rog, (a)检测信号b)检测得到的负载基被信号(C)检测得到的谐波信号 DING Ming.LIANG Hai-tao,et al Algorithm and simulation to Detect Voltage for Single-phase Dynamic Voltage Restorer U). Joural of System Simulation,2007.19 (4):732-734.) W [刀潘文,钱愈海,周列.基于加窗插值FFT的电力谐被测量理论窗函 数研究门.电工技术学报,1994,9(1上50-54. 0050.10150.20.250.30.35 04 8) 陈长兴,高晓光,刘昌云.基于傅立叶变换的积分算法研究功 系统仿真学报.2004.16(4)817-819.(CHEN Chang-xing,GA0 Xiao-guang.LIU Chang-yun.Study on Integral Algorithm Basedon Fourier Transform []Joural of System Simulation,2004,16(4): 817-819.) 0.050.1015020250,30.3504 高大威。孙孝瑞,卢青春.基于神经网络电流检测的有源电力沈 被器研究).电力电子技术,2002,36(54849. ywMw4解*mw [10马野。王老遵,戴腰.基于模制神经网络的自适应滤波方法仿真 研究0.系统仿真学报,2005,17(10:2447-2449.0MaYe,Wg 00050.101502025030.3504 Xiao-tong,Dai Yao.Research on Adaptive Filtering Based on Fuzzy Neural Networks []Joumal of System Simulation,2005,17(10): 图4,检测算法仿真波形图 2447-2449.) (a)检测信号)检测得到的负载基波信号(©)检测得到的谐波信号 [】吴言风.吴正国,夏立.一种基于自适应涉波的三相有源电力器 的检测算法).海军工程大学学报.2002,14(1少5457. 4结论 [12]Wang Qun,Wu Ning.Wang Zhaoan.A neuron adaptive detecting approach of harmonic cuent for APF and its realization of analog 针对AP℉谐波检测技术实时性、准确性的需求,本文 circuit [J].IEEE Trans.on Instrumentation and Measurement 提出了一种滑窗迭代DT算法,能实时、有效地检测出谐 (S730B0001-TM0),2001,50177-84. 波参考指令电流,通过对该算法进行扩展,还能应用于单次 [13引罗安.电网谱波治理和无功补偿技术及装备M,北京:中国电力 出版社,2006. 谐波的检测,从而可以有效地提高参考谐波电流信号的运算 速度与跟踪精度。仿真与实验结果都表明该算法能有效地提 高系统的实时性、目标跟随特性和抗干扰性,并具有计算量 (上接第3651页) [4]刘成瑞。相关系数平稳序列分析方法及其应用D.北京:北京航 以及采用MCMC方法对一些更复杂模型的参数估计还需进 空航天大学图书馆,2006:96-98. 一步探讨和研究。 [5]茆诗松,王静龙,璞晓龙.高等数理统计M)第2版.北京:高 等教育出版社.2006:440452 参考文献: [6]林静,韩玉启,朱慧明.等.基于MCMC稳态模拟的Webu回归 [山田饰,吴雅琴,王红军,等.非线性时间序列建模的混合GARCH 模型机器可靠性应用[).系统仿真学报,2006,18(5):1161-1163. 方法).系统仿真学报,2005.17(81867-1871. 7 龚光鲁,钱敏平应用随机过程教程及在智能计算中的陆机模型 2)傅惠民。相关系数平稳过程方法刀.机械强度,2002,243): M.北京:清华大学出版杜.2004:186201. 400404. [8]Tiemey,L.Markov chains for exploring posterior distributions (with [3)傅惠民,刘成瑞.相关系数ARMA(p,q)序列分析方法机.航空动 discussion)].The Analysis of Statistics,22,1701-1762. 力学报.2003,183:161-166. 3655· 万方数据
第20卷第14期 2008年7月 陆秀令,等:电力谐波滑窗迭代DFT检测算法的研究与仿真 、7b1.20No.14 JuI.2008 ≤ 楚 孽 5 O -5 O 005 O.1 O.'5 02 025 03 O.35 0.4 5 0栅删岫帅㈣黼帅蝴 枷怖脚忡 m脚岬洲 } ; 4 小、灵活性高、易于工程实现的特点。 参考文献: 【l】 王兆安,杨君,刘进军.谐波抑制与无功功率补偿【M】.北京:机 械工业出版杜.1998. 【2】 陆秀令,周腊吾.基于瞬时无功功率的谐波电压检测法们.高电 压技术。2006。32(1):88.90. 【3】 李红,杨普水.傅立叶电力系统谐波检测方法综述【J】.现代电力, 2004.21“):39掣. 【41 李圣清,朱英浩,周有庆,等.电网谐波检测方法的综述【力.高电 压技术,2004,30(3):39_42. t『s Ncural NetwofI(s【J】.Joumal of Sy啦m Simulati咀2005,17(10): 图4分‘检测算法仿真波形图2447—2449.) (a)检测信号(b)检测得到的负载基波信号(c)检测得到的谐波信号 【ll】吴言凤.吴正国,夏立.一种基于自适应滤波的三相有源电力器 的检测算法【刀.海军工程大学学报,2002,14(1):54—57. 4 结论 [121 w觚g Q吣wu N吨t wang zhaD趾·A枷姗a血pdVe d咖廿ng aplP∞∞h of ll乏盯nonic cll玎ent fbr Af'F柚d i协删i盈tioⅡof删og 针对APF谐波检测技术实时性、准确性的需求,本文cifclIit【力.删阻T哪s.∞Ins仇lm朗伽∞and Me∞llre姗nt 提出了一种滑窗迭代DFT算法,能实时、有效地检测出谐 (s73∞000l-T蹦)·2001t 50(1):77—84· 波参考指令怵通过对该算法进行扩展,还能应用于单次 n31詈差嚣波治理和无功补偿技术及装备嗍·北煎中国电力 谐波的检测,从而可以有效地提高参考谐波电流信号的运算 速度与跟踪精度。仿真与实验结果都表明该算法能有效地提 高系统的实时性、目标跟随特性和抗干扰性,并具有计算量 一-■-川■-…■-…■_…■一川■-川■-…■_…■-Ⅲ一·…一·…■-一 (上接第365 l页) [4】 刘成瑞.相关系数平稳序列分析方法及其应用【D】.北京:北京航 以及采用MCMc方法对一些更复杂模型的参数估计还需进 一步探讨和研究。 参考文献: 【1】 田铮。吴雅琴,王红军,等.非线性时间序列建模的混合Gm圮H 方法Ⅲ.系统仿真学报,2005,17(8):1867.1871. 【2】 傅惠民,相关系数平稳过程方法叨.机械强度,2002,24(3): 41)岫04. 【3】 傅惠民,刘成瑞.相关系数Almn(p,q)序列分析方法【J】.航空动 力学报,2003。18(3):16l-166. 空航天大学图书馆,2006:96.98. 【5】 茆诗松,王静龙。璞晓龙.高等数理统计【M】.第2版.北京:高 等教育出版社,2006:440_452. 【6】 林静,韩玉启,朱慧明,等.基于McMc稳态模拟的wbibull回归 模型机器可靠性应用【J】.系统仿真学报.2006,18(5):1161—1163. [7】 龚光鲁.钱敏平.应用随机过程教程及在智能计算中的随机模型 D川.北京:清华大学出版社,2004:186-201. 【8】 nemey.L.Markov chains fbr既ploring post耐or dis砸butio璐(’vith di虻ussi叽)【J】.11圮Analysis ofStanstics。22,170l—1762. ·3655· 万方数据