
第27卷第7期 统计研究 Vol.27,No.7 2010年7月 Statistical Research Jal.2010 基于MCMC稳态模拟的异质性 经济增长模型研究 朱慧明曾惠芳 虞克明 内容提要:针对同质性增长模型无法描述各个经济体经济增长存在的异质性现象,提出了一类基于MCMC稳 态模拟的异质性经济增长模型,它可以用来描述经济增长的异质性以及政策变量的差异影响。由于模型参数的后 验条件分布没有确定的分布形式,通过数据扩充得到参数的完全条件分布从而实现模型参数的贝叶斯估计。对改 革开放以来我国各省市区经济增长收敛性进行分析发现大规模股份制改革前经济增长具有问质性而大规模股份 制改革后经济增长只有异质性,且可以用新古典经济增长理论来解释各地区经济的发展状况。 关键词:经济增长:分位数回归:MCMC模拟:异质性 中图分类号:0212 文献标识码:A文章编号:1002-4565(2010)07-0052-08 Modeling the Heterogeneity of Economic Growth via MCMC Simulation Zhu Huiming Zeng Huifang Yu Keming Abstract:The homogeneous growth theory does not support the possibility that economies follow the different growth paths.This paper proposed the heterogeneous growth models which can eapture systematic infuenesof policy variables on the location,scale and shape of the conditional distribution of the CDP growth rates.The models were estimated via Gibbs sampler with data augmentation by a mixture of standard exponential distribution and standard normal distribution to represent the asymmetric Laplace distribution.Bayesian inference revealed effective in our application to the GDP growth rates of every province in China after the reform and opening-up.the results show that there exist homogeneity of growth before the shareholding system reform on an enlarged scale but not after that.The findings support that the underlying growth model for cross-provinces is of neoclassical growth type. Key words:Economic growth;Quantile regression;MCMC simulation;Heterogeneity 一、引言 同质性假设意味着物质资本,人力资本投资以及人 区域经济增长收敛问题是近年来区域经济学界 口增长率等政策因素对不同经济体经济增长的影响 研究的一个热点,其中主要以新古典经济增长理论 相同,这与实际不符。Quah(1996)指出不同的经济 体具有内在不同的特质,因此其对政策变量的反应 为研究基础。然而,在新古典模型中,稳态人均资本 有所差异。Durlauf,Kourtellos和Minkin(2001)利用 水平和稳态人均产出水平取决于储蓄倾向,人口增 非线性函数描述了各个国家经济增长的异质性,并 长率以及生产函数等特征,而这些特征在不同的经 指出经济增长异质性可以很好地解释各个国家经济 济体之间会发生变化,那么收敛仅在条件意义上 发展的不平衡。Kourtellos(2002)也发现参数异质 成立。 性的存在,且发现参数的异质性不仅依赖于初始人 新古典经济增长理论的先驱工作是由Bamo和 力资本,也依赖于种族多样性(ethnic diversity)。对 Sala-i-Martin(1992)以及Mankiw等(1992)做出的, 随后得到迅速的发展,但是他们提出的增长模型有 一个共同的不足,即参数同质性假设。Durlauf和 *因家自然科学基金项目(70771038):救育部人文杜科规划项 Johnson(1995)对参数同质性假设提出了批评,参数 日(06JA9100001)。 万方数据
第27卷第7期 2010年7月 统计研究 S妇tisticai Research VOI.27。No.7 Jul.2010 基于MCMC稳态模拟的异质性 经济增长模型研究’ 朱慧明 曾惠芳 虞克明 内容提要:针对同质性增长模型无法描述各个经济体经济增长存在的异质性现象,提出了一类基于MCMC稳 态模拟的异质性经济增长模型,它可以用来描述经济增长的异质性以及政策变量的差异影响。由于模型参数的后 验条件分布没有确定的分布形式,通过数据扩充得到参数的完全条件分布从而实现模型参数的贝叶斯估计。对改 革开放以来我周各省市区经济增长收敛性进行分析发现大规模股份制改革前经济增长具有同质性而大规模股份 制改革后经济增长具有异质性,且可以用新古典经济增长理论来解释各地区经济的发展状况。 关键词:经济增长;分位数回归;MCMC模拟;异质性 中图分类号:0212 文献标识码:A 文章编号:1002—4565(2010)07—0052一08 Modeling the Heterogeneity of Economic Growth via MCMC Simulation Zhu Huiming Zeng Huifang Yu Keming Abstract:The homogeneous growth theory does not support the possibility that economies follow the different growth paths.This paper proposed the heterogeneous growth models which can capture systematic influences of policy variables on the location,scale and shape of the conditional distribution of the GDP growth rates.The models were estimated via Gibbs sampler with data augmentation·by a mixture of standard exponential distribution and standard normal distribution to represent the asymmetric Laplace distribution.Bayesian inference revealed effective in our application to the GDP growth rates of every province in China after the reform and opening—up,the results show that there exist homogeneity of growth before the shareholding system reform on an enlarged scale but not after that.The findings support that the underlying growth model for cross—provinces is of neoclassical growth type. Key words:Economic growth;Quantile regression;MCMC simulation;Heterogeneity 一、引言 区域经济增长收敛问题是近年来区域经济学界 研究的一个热点,其中主要以新古典经济增长理论 为研究基础。然而,在新古典模型中,稳态人均资本 水平和稳态人均产出水平取决于储蓄倾向,人口增 长率以及生产函数等特征,而这些特征在不同的经 济体之间会发生变化,那么收敛仅在条件意义上 成立。 、、 新古典经济增长理论的先驱工作是由Barro和 Sala.i.Matin(1992)以及Mankiw等(1992)做出的, 随后得到迅速的发展,但是他们提出的增长模型有 一个共同的不足,即参数同质性假设。Durlauf和 Johnson(1995)对参数同质性假设提出了批评,参数 同质性假设意味着物质资本,人力资本投资以及人 口增长率等政策因素对不同经济体经济增长的影响 相同,这与实际不符。Quah(1996)指出不同的经济 体具有内在不同的特质,因此其对政策变量的反应 有所差异。Durlauf,Kourtellos和Minkin(2001)利用 非线性函数描述了各个国家经济增长的异质性,并 指出经济增长异质性可以很好地解释各个国家经济 发展的不平衡。Kourtellos(2002)也发现参数异质 性的存在,且发现参数的异质性不仅依赖于初始人 力资本,也依赖于种族多样性(ethnic diversity)。对 ·国家自然科学基金项目(70771038);教育部人文社科规划项 目(06JA9100001)。 万方数据

第27卷第7期 朱慧明等:基于MCMC稳态顿拟的异质性经济增长模型研究 ·53· 异质性经济增长理论做出突出贡献的还有Eicher 称Laplace分布对分位数回归模型进行贝叶斯分 和Leukert(2006),Phillips和Sul(2007)以及 析。随后,Tsionas(2003),Yu等(2005)对贝叶斯分 Hineline(2008)。 位数回归模型进行了进-一步的研究。月前,对分位 对经济增长模型的估计.Bernard和Durlauf 数回归增长模型的估计仅限于频率统计方法,应用 (1996)指出应用最小二乘法估计经济增长模型存 频率统计方法对各个国家(或地区)的经济增长进 在不足,因为最小二乘估计只能描述经济增长的中 行分析时存在一些缺陷,比如样本茧过少难以满足 心趋势,而不能描述经济增长的尾部特征。分位数 估计量的大样本性质,以及假设参数固定不变很难 回归方法是由Koenker和Bassett(I978)提出的,它 描述各个国家(或地区)经济结构的复杂性、政策效 是最小二乘估计方法(OLS)的一种推广,考虑了在 应和区域经济发展的差异性。 不同分位水平下因变量对自变量的回归,因此它可 本文提出了一类异质性经济增长模型,并应用 以描述解释变量对因变量条件分布位置、尺度以及 MCMC模拟实现了异质性经济增长模型贝叶斯分 形状的影响,它弥补了最小二乘估计只能描述解释 析,最后应用异质性经济增长模型对中国各省市区 变量对因变量条件均值影响的缺陷。特别当经济变 的经济增长收敛性进行了实证研究。 量的分布是非常态分布时,不同分位数水平下经济 二、模型的结构分析 变量之间可能会表现出不同的相关性和显著性,因 如果分析各个经济体经济增长时使用相同的 此分位数回归方法可以为经济增长异质性提供一种 全新的解释角度,并且可以全面地解释政策变量对 Cobb-Douglas函数,这意味着物质资本,人力资本投 资以及人口增长率等政策内素对不同经济体经济增 经济增长的差异影响。Mello和PereⅢi(20O3)利用 长的影响相同,这与实际不符。实际上,不同的经济 分位数回归方法研究100个国家1960-1985年经 体具有内在不同的特质,从而导致各个经济体具有 济增长收敛性时发现,经济发展快的国家存在绝对 不同的经济增长速度,不同的经济增长路径以及不 收敛而经济发展慢的国家不存在绝对收敛,由此说 同的稳态。首先,考虑初始资本存敏对各个经济体 明,分位数回归方法不分割样本也可以描述经济增 经济增长的差异影响,提出异质性绝对收敛模型 长的异质性。Canarella和Pollard(2004)利用分位 数回归方法分析了86个国家1960-2000年的横截 gi =a(T)+b(T)In(y..o)+ui. (1) 面数据,结果发现增长模型的参数存在异质性,即不 其中g4=ln(y,/yo),y.,表示第i个经济体t期人 同的地区物质资本和人力资本投资对经济增长的影 均GDP,yo表示初期人均GDP,g:表示经济增长 响程度不同。周业安,章泉(2008)应用分位数回归 率,a,b是区间[0,1]上的未知实函数,0<T<1。若 方法研究了中国城市间经济增长的趋同性,发现不 随机变量,表示由其他经济条件所产生的扰动项, 同城市的经济增长方式存在差异。 且其分位数都为0,那么8,的T条件分位函数为 在经济系统中,许多经济变量的分布参数不是 Q(rlyo)=a(r)+b(r)ln(yo) (2) 固定不变,而是逐步变化的,参数的各种波动具有随 由式(2)可知,经济增长变量在不同分位点的收敛 机性的特征与经典统计的基本观点“总体分布参数 性由b(:)决定。随着T不同,b(r)可以取不同的 是固定的常数”是不相符的。贝叶斯方法为解决以 值,若b(?)在所有的分位点处都为负,说明各个经 上问题提供了一种便利的分析框架,因为在贝叶斯 济体经济增长存在全局绝对收敛性。若b(?)在不 理论框架中参数是一个随机变量,可以用于解决小 同的分位点处有止有负,说明各个经济体经济增长 样本条件下参数估计与假设检验问题。同时,在分 存在局部绝对收敛性。若b(?)在不同的分位点处 位数回归估计理论中,参数估计基的方差依赖于残 都为正,说明各个经济体经济增长存在全局发散性。 差项的分布,因此难以得到参数的置信区间以及进 绝对收敛内含一个严格的假设条件,即假定各 行相应的假设检验,但是参数的贝叶斯估计量的后 个经济体(国家或地区)有完全相同的储蓄率、人口 验方差不依赖于残差项的分布,因此贝叶斯方法更 增长率、资本折旧率和生产函数等基本经济特征。 容易得到参数的贝叶斯区间估计以及进行相应的假 但现实中,各个经济体之间并不完全问质,其平衡增 设检验。Yu和Moyeed(2001)首先提出了应用非对 长路径会受各个地区或国家的经济体制、市场结构、 万方数据
第27卷第7期 朱慧明等:基于MCMC稳态模拟的异质性经济增长模型研究 ·53· 异质性经济增长理论做出突出贡献的还有Eicher 和Leukert(2006),Phillips和Sul(2007)以及 Hineline(2008)。 对经济增长模型的估计,Bernard和Durlauf (1996)指出应用最小二乘法估计经济增长模型存 在不足,因为最/b--乘估计只能描述经济增长的中 心趋势,而不能描述经济增长的尾部特征。分位数 回归方法是由Koenker和Bassett(1978)提出的,它 是最小二乘估计方法(OLS)的一种推广,考虑了在 不同分位水平下因变量对自变量的回归,因此它可 以描述解释变量对因变量条件分布位置、尺度以及 形状的影响,它弥补了最小二乘估计只能描述解释 变量对因变量条件均值影响的缺陷。特别当经济变 量的分布是非常态分布时,不同分位数水平下经济 变量之间可能会表现出不同的相关性和显著性,因 此分位数回归方法可以为经济增长异质性提供一种 全新的解释角度,并且可以全面地解释政策变量对 经济增长的差异影响。Mello和Perrelli(2003)利用 分位数回归方法研究100个国家1960—1985年经 济增长收敛性时发现,经济发展快的国家存在绝对 收敛而经济发展慢的国家不存在绝对收敛,由此说 明,分位数回归方法不分割样本也可以描述经济增 长的异质性。Canarella和Pollard(2004)利用分位 数回归方法分析了86个国家1960—2000年的横截 面数据,结果发现增长模型的参数存在异质性,即不 同的地区物质资本和人力资本投资对经济增长的影 响程度不同。周业安,章泉(2008)应用分位数回归 方法研究了中国城市间经济增长的趋同性,发现不 同城市的经济增长方式存在差异。 在经济系统中,许多经济变量的分布参数不是 固定不变,而是逐步变化的,参数的各种波动具有随 机性的特征与经典统计的基本观点“总体分布参数 是固定的常数”是不相符的。贝叶斯方法为解决以 上问题提供了一种便利的分析框架,因为在贝叶斯 理论框架中参数是一个随机变量,可以用于解决小 样本条件下参数估计与假设检验问题。同时,在分 位数回归估计理论中,参数估计量的方差依赖于残 差项的分布,因此难以得到参数的置信区间以及进 行相应的假设检验,但是参数的贝叶斯估计量的后 验方差不依赖于残差项的分布,因此贝叶斯方法更 容易得到参数的贝叶斯区间估计以及进行相应的假 设检验。Yu和Moyeed(2001)首先提出了应用非对 称Laplace分布对分位数回归模型进行贝叶斯分 析。随后,Tsionas(2003),Yu等(2005)对贝叶斯分 位数回归模型进行了进一步的研究。目前,对分位 数回归增长模型的估计仅限于频率统汁方法,应用 频率统计方法对各个国家(或地区)的经济增长进 行分析时存在一些缺陷,比如样本量过少难以满足 估计量的大样本性质,以及假设参数固定不变很难 描述各个国家(或地区)经济结构的复杂性、政策效 应和区域经济发展的差异性。 本文提出了一类异质性经济增长模型,并应用 MCMC模拟实现了异质性经济增长模型贝叶斯分 析,最后应用异质性经济增长模型对中国各省市区 的经济增长收敛性进行了实证研究。 二、模型的结构分析 如果分析各个经济体经济增长时使用相同的 Cobb.Douglas函数,这意味着物质资本,人力资本投 资以及人口增长率等政策因素对不同经济体经济增 长的影晌栩同,这与实际不符。实际上,不同的经济 体具有内在不同的特质,从而导致各个经济体具有 不同的经济增长速度,不同的经济增长路径以及不 同的稳态。首先,考虑初始资本存量对各个经济体 经济增长的差异影响,提出异质性绝对收敛模型 g“=g(下)+b(丁)In(YI.0)+//,“ (1) 其中g“=In(Yi 油), Yi,t 表示第个经济体期人.t/y i t 均GDP,Y油表示初期人均GDP,g。表示经济增长 率,a,b是区间[0,1]上的未知实函数,0<丁<l。若 随机变量M“表示由其他经济条件所产生的扰动项, 且其分位数都为0,那么g。的r条件分位函数为 Q。(r I Y油)=口(_r)+b(丁)In(Y油) (2) 由式(2)可知,经济增长变量在不同分位点的收敛 性由b(Jr)决定。随着f不同,b(r)可以取不同的 值,若b(r)在所有的分位点处都为负,说明各个经 济体经济增长存在全局绝对收敛性。若b(r)在不 同的分位点处有止有负,说明各个经济体经济增长 存在局部绝对收敛性。若b(t)在不同的分位点处 都为正,说明各个经济体经济增长存在全局发散性。 绝对收敛内含一个严格的假设条件,即假定各 个经济体(国家或地区)有完全相同的储蓄率、人口 增长率、资本折旧率和生产函数等基本经济特征。 但现实中,各个经济体之间并不完全同质,其平衡增 长路径会受各个地区或囤家的经济体制、市场结构、 万方数据

·54 统计研究 2010年7月 政府政策等因素的影响。加人这些因素后,不同的 √n((r)-(r))→N(0,r(1-r)D'DD)(6) 经济体将具有不同的经济增长速度以及不同的稳 其中D。=E(X,X',)=limn4∑X,X:,D, 态,模型可以表示为 g:=a(r)+b(r)ln(y.o)+Y(r)X+4,(3) =limn f()]f(())< 那么g的T条件分位函数为 是4密度函数。 Q(r1y.o,X,)=a(r)+b(r)ln(y.o)+Ψ'(r)X: 由于参数估计量的方差与残差项的分布有关, (4) 因此频率统计方法很雅实现参数估计量方差的估 其中X表示控制稳态产出水平的一系列政策变量。 计,从而难以得到参数的置信区间以及进行相应的 记=(1,ln(y.o),X)',0(r)=(a(r),b(r),Ψ 假设检验。然而,参数的贝叶斯估计量的后验方差 (x)',那么式(4)的向敏乘积形式可以表示为Q。 不依赖于残差项的分布,因此贝叶斯方法更容易得 (rlyo,X:)=X'(r)。Q(rly.o,X:)表示经济增 到参数的贝叶斯区间估计并进行相应的假设检验。 长分布的不同分位点,b()表示初始资本存量影响 三、模型的MCMC模拟 各个地区经济增长的弹性系数,业(τ)表示政策变 在经济系统中,许多经济变量的分布参数不是 量影响各个地区经济增长的弹性系数,随着分位水 固定不变,而是逐步变化的,参数的各种波动具有随 平?的不同,解释变量对不同地区经济增长的影响 机性的特征与经典统计的基本观点“总体分布参数 程度不同,因此可以描述各个经济体经济增长的异 是固定的常数”是不相符的。贝叶斯方法为解决以 质性。由式(4)可知,经济增长变量在不同分位点 上问题提供了一种便利的分析框架,因为在贝叶斯 处的收敛性由b()决定。随着?不同,b(r)可以取 理论框架中参数是一个随机变量,可以用于解决小 不同的值,若b(τ)在所有的分位点处都为负,说明 样本条件下参数估计与假设检验问题。若随机变量 各个经济体经济增长存在全局条件收敛性。若b “:.服从非对称Laplace分布,它的密度函数可以表 ()在不同的分位点处有正有负,说明各个经济体 示为 经济增长存在局部条件收敛性。也就是说,在某一 分位点附近的经济体,落后地区的人均收人增长速 f4)=1-exp-p,( (7) 度快于发达地区;而另一分位点附近的经济体,落后 此时,增长模型的分位回归估计可以通过贝叶斯方 地区的人均收人增长速度并未快于发达地区。若b 法来实现。利用非对称Laplace分布对增长模型进 ()在不同的分位点处都为正,说明各个经济体经 行贝叶斯分析,模型的似然函数为 济增长不存在条件收敛性。另外,若b()在不同的 L(yl 0,;X)o a"expl-op.(8u-X0) 分位点处取值基本一致,说明经济增长具有同质性; 若(?)在不同的分位点处取值不同,说明经济增长 (8) 具有异质性。传统的经济增长模型只从均值拟合的 其中y=(g1,82…g),X=(X,X2….)。目标 角度考虑经济增长的收敛状况,只能描述经济收敛 函数式(5)的最小化等价于式(8)似然函数的最大 状况的中心趋势且容易受异常点的影响。但是分位 化。假设参数的先验分布为 数回归拟合可以全面地描述经济增长变量的分布特 π(0,)=T(0)r(c) (9) 征,且各个分位点的拟合不受异常点的影响。 其中0~N(,),0-1G(no/2,5o/2),IG(·,·) 根据Koenker和Xiao(2002)对分位回归理论的 表示逆伽玛分布(Inver3 e Gamma distribution)。根据 研究,增长模型的参数估计可以通过解决如下最优 贝叶斯公式,模型参数的联合后验分布为 化问题来实现 (0,c|y,X)xL(yl0,o;X)π(8,o) 0()arg min p.(g.-X0()) (5) g(1/o)…epl-。'(p,(g-K0)+2) 其中p,(u)=u(r-I(u<0),此处I(·)为示性函 (0-)2 (10) 数。基于分位回归估计理论,()估计量服从如下 2E。 渐近过程,且是参数(r)的一致估计 若日为已知,可以得到σ的后验条件分布 万方数据
·54· 统计研究 2010年7月 政府政策等因素的影响。加入这些因素后,不同的 经济体将具有不同的经济增长速度以及不同的稳 态,模型可以表示为 gf.。=口(下)+b(f)In(Yf.o)+缈’(r)Xf+u¨(3) 那么g。。的7-条件分位函数为 Q轧(f Yi.0,X。)=口(7)+b(下)In(Yi.0)+缈’(|r)置 (4) 其中x表示控制稳态产出水平的一系列政策变量。 记置i=(1,In(Yi.o),X;)’,口(丁)=(a(丁),b(f),缈’ (r))’,那么式(4)的向量乘积形式可以表示为Q。 (rIy油,X;)=X’。p(7-)。Q“(下lY啪,X,)表示经济增 长分布的不同分位点,6(.r)表示初始资本存量影响 各个地区经济增长的弹性系数,哕’(r)表示政策变 量影响各个地区经济增长的弹性系数,随着分位水 平7的不同,解释变量对不同地区经济增长的影响 程度不同,因此可以描述各个经济体经济增长的异 质性。由式(4)可知,经济增长变量在不同分位点 处的收敛性由6(f)决定。随着7不同,b(下)可以取 不同的值,若6(r)在所有的分位点处都为负,说明 各个经济体经济增长存在全局条件收敛性。若b (下)在不同的分位点处有正有负,说明各个经济体 经济增长存在局部条件收敛性。也就是说,在某一 分位点附近的经济体,落后地区的人均收入增长速 度快于发达地区;而另一分位点附近的经济体,落后 地区的人均收入增长速度并未快于发达地区。若b (Jr)在不同的分位点处都为正,说明各个经济体经 济增长不存在条件收敛性。另外,若b(r)在不同的 分位点处取值基本一致,说明经济增长具有同质性; 若b(.r)在不同的分位点处取值不同,说明经济增长 具有异质性。传统的经济增长模型只从均值拟合的 角度考虑经济增长的收敛状况,只能描述经济收敛 状况的中心趋势且容易受异常点的影响。但是分位 数回归拟合可以全面地描述经济增长变量的分布特 征,且各个分位点的拟合不受异常点的影响。 根据Koenker和Xiao(2002)对分位回归理论的 研究,增长模型的参数估计可以通过解决如下最优 化问题来实现 n a(r)=a。辱min芝■(gf.1一一口(r)) (5) …‘ i=i 其中P,(u)=扯(r一,(Ⅱ<0)),此处,(·)为示性函 数。基于分位回归估计理论,a(t)估计量服从如下 渐近过程,且是参数口(f)的一致估计 石(台(_r)一口(_r))jⅣ(o,r(1一f)D—DilDil)(6) 其中口。=E(X一;X一’i)=limn“∑元;叉7i,D。 =limn卅∑z[Ⅱ小(r)]夏i叉’;,0<,(M¨(丁))<∞ 是“;。密度函数。 由于参数估计量的方差与残差项的分布有关, 因此频率统计方法很难实现参数估计量方差的估 计,从而难以得到参数的置信区间以及进行相应的 假设检验。然而,参数的贝叶斯估计量的后验方差 不依赖于残差项的分布,因此贝叶斯方法更容易得 到参数的贝叶斯区间估计并进行相应的假设检验。 三、模型的MCMC模拟 在经济系统中,许多经济变量的分布参数不是 固定不变,而是逐步变化的,参数的各种波动具有随 机性的特征与经典统计的基本观点“总体分布参数 是固定的常数”是不相符的。贝叶斯方法为解决以 上问题提供了一种便利的分析框架,因为在贝叶斯 理论框架中参数是一个随机变量,可以用于解决小 样本条件下参数估计与假设检验问题。若随机变量 H“服从非对称Laplace分布,它的密度函数可以表 示为 肌.I)=坐≯exp{Ⅵ(等)} (7) 此时,增长模型的分位回归估计可以通过贝叶斯方 法来实现。利用非对称Laplace分布对增长模型进 行贝叶斯分析,模型的似然函数为 L(y 1日,盯;夏)∞or”exp{一or一∑p,(gi.。一夏’i口)} 再1 (8) 其中Y=(91'I,g:。。…g。.。),叉=(夏。,叉:…叉。)。目标 函数式(5)的最小化等价于式(8)似然函数的最大 化。假设参数的先验分布为 仃(9,or)=仃(口)丌(or) (9) 其中9一Ⅳ(肛口,三。),矿一,G(n。/2,so/2),IG(·,·) 表示逆伽玛分布(Inverse Gamma distribution)。根据 贝叶斯公式,模型参数的联合后验分布为 仃(p,01 Y,X)OC L(Y I p,or;X)仃(p,or) oC(1/矿)孚”“exp{一盯-1(∑p,(既.。一夏’i口)+詈) 一掣} ^F (10) 、 一, 二.‘0 若日为已知,可以得到or的后验条件分布 万方数据

第27卷第7期 朱慧明等:基于MCMC弹态模拟的异质性经济增长模型研究 55· (X)(1/0)exp- () 0,10,oy,-c1c(26.) (17) 其中D=p,(8-0)+宁,显然m(o16y, 其中8=(g,-X:0)2/m2σ,=2/o+中2/m2g,G1G (·)表示广义逆高斯分布(Generalized inverse X)-1G(受+n,D)。在m(0,oy,X)中对。进行积 Gaussian distribution)。参数g的完全条件分布为 分,可以得到日的后验条件分布 a1,-16(号 (18) (01 y,X)(0,1 y.X)do 其中元=m。+3n,;=0+2∑期,+∑(g4-X',0 cexp(-(g-4,)2 22水wo)ep(-do -中iw:)2/n2wo 由以上数据扩张得到参数的完全条件分布,利 ep(-()Dr+ 用Gibbs抽样模拟Markov链,此链的平稳分布是模 2Σ。 型参数的后验条件分布,通过一段预迭代后,产生一 系列Markov链模拟值可以作为来自后验条件分布 的独立样本,从而用这些样本对模型的参数进行估 计。假设给定初始值8=(80,,σ0),第k-1 exp(-( (12) 次送代获得模拟样本为日=(0-”,n-”, 2。 。-”),那么第k次迭代可以描述如下, 参数日的后验条件分布的具体分布形式未知, 6~r(0f0-,c-”;y,) 因此需要通过数据扩充(Data augmentation)来实现 o-r(wlg,c-”y,R) 对g的Gibbs抽样。因为非对称Laplace分布的随 )(BI),w);y,X) 机变量可以表示为指数分布和正态分布的混合分 重复上述过程可以实现模型参数的MCMC模拟。 布,即 四、区域经济增长收敛性的实证分析 u:=中0:+刀√o0 (13) 利用1978-2007年我国各省市自治区的截面 其中0:~exp(-:/o),:~N(0,1),中= 1-2r 数据,其中考虑到西藏的数据不健全以及重庆1996 (1-r) 年以前没有独立的数据而予以剔除,分析我国大陆 2 7=7-7。因此,式(3)可以表示为 29个省市区人均国内生产总值(GDP)的年均增长 率与其期初人均实际国内生产总值的关系。分别以 g4=X'0+中w:+刀√G0, (14) 1978年(改革开放试点初期)、1992年(改革进人以 这样,B:可看作服从均值为X'0+中w:,方差为 大规模股份制改革为标志的新阶段)为初始年份进 7σw:的正态分布,模型似然函数为 行时段划分,对1978-1991年,1978-2007年以及 (y10,o,:)x(o)·exp- 1992-2007年三个时段的真实人均GDP增长率的 横截面数据进行分位数回归分析。所有省份人均 (ga-0-如, (15) GDP数据均来源于《中国统计年鉴》(国家统计 2nc0: 局)。各省份的真实人均GDP在前述数据基础上以 其中0=(01,02,…,0a)'。假设Y,=(61a-01, 各省份同年物价指数进行修正。由于各省份的物价 B2,-中2,…,g4-0。)',参数0的完全条件分 指数难以获得,故采用同年全国的物价数据来进行 布为 处理,其中全国物价指数采用以1950年为基期的 0l0,0y,X~N(,。) (16) “商品零售价格总指数”计量。该指数为定基指数, 其中'=江X+',4,=三,(X红Y, 需做如下修正:第i年真实人均GDP=第i年人均 +4a),£=diag(now1,now2,…,n2ow.)。0: GDP/第i年物价指数。 的完全条件分布为 首先,利用频率统计方法分阶段对1978年以来 万方数据
第27卷第7期 朱慧明等:基于MCMC稳态模拟的异质性经济增长模型研究 ·55· ,r(矿I口;),,Yc)oc(1/矿)竽+n”exp{一旦} (11) 埘。I疗,盯;y,元。GIG(1,吾。,9i) (17) 仃 / 其中D=∑p,(g叫一夏’ip):卜下50,显然仃(盯1日,),, 贾)。,G(要+n,D)。在霄(O,orl,,,夏)dex于盯进行积 分,可以得到0的后验条件分布 or(O r),,夏)oc,z-(0,盯I y,昱)d盯 …p(_掣)n川争川exp(一詈№ oc exp(一!旦I;譬)。一孚+“Jrl(弓÷+n) ×f———望!二(1/矿)挈+n+-exp(一盯一,D)d盯 。,(等+n) 伍exp(_掣)一“ (12) 参数0的后验条件分布的具体分布形式未知, 因此需要通过数据扩充(Data augmentation)来实现 对0的Gibbs抽样。因为非对称Laplace分布的随 机变量可以表示为指数分布和正态分布的混合分 布,即u¨=币埘;+'7厕; (13) 其中”exp(飞纠以一N(O,1),咖=者%, 叩=高。因此,式(3)可以表示为 g。=弘0+4,w。+7/“而。 (14) 这样,g“可看作服从均值为置’i0+咖们i,方差为 田20.Wi的正态分布,模型似然函数为 L(y l p,or,钾;夏)oc(17埘iⅣ2)·expl一∑ 亟毒善±丛} ^ Z (15) ’ ’ 其中钾=(埘l,阳2,…,埘。)’。假设Ye=(g。.:一咖埘l, g:.,一咖伽:,…,g。一4,w。)’,参数0的完全条件分 布为 0 I埘,or;,,,置一Ⅳ(五。,三。) (16) 其中三f1 27.娩。1置’+三i1,五。=毛(砭。1匕 +三i1肛口),三=diag(叩20'tOl,叼20"1,132,…,,720.tO。)。埘‘ 的完全条件分布为 其中鹫=(g“一置’ip)2/叼2盯,9;=2/0"+咖2/'q20r,GIG (·)表示广义逆高斯分布(Generalized inverse Gaussian distribution)。参数or的完全条件分布为 盯I t17,O;y,X—IG(-4“--,-4。-) (18) 厶 厶 ^ n 其中n=no+3n,;=50+2∑埘f+∑(g¨一置’。日 两 甬 一枷i)2/'1/2埘i。 由以上数据扩张得到参数的完全条件分布,利 用Gibbs抽样模拟Markov链,此链的平稳分布是模 型参数的后验条件分布,通过一段预迭代后,产生一 系列Markov链模拟值可以作为来自后验条件分布 的独立样本,从而用这些样本对模型的参数进行估 计。假设给定初始值@=(0∞’,埘∞’,口∞’),第k一1 次迭代获得模拟样本为O=(0¨一’,埘¨。’, 盯¨一’),那么第k次迭代可以描述如下, 0‘¨。仃(0 I埘(‘一¨,盯(‘一¨;Y,X) to‘¨。丌(|t,1 0(¨,盯‘‘一¨;Y,叉) or‘¨一仃(口1 0‘¨,叫‘¨;,,,叉) 重复上述过程可以实现模型参数的MCMC模拟。 四、区域经济增长收敛性的实证分析 利用1978—2007年我国各省市自治区的截面 数据,其中考虑到西藏的数据不健全以及重庆1996 年以前没有独立的数据而予以剔除,分析我国大陆 29个省市区人均国内生产总值(GDP)的年均增长 率与其期初人均实际国内生产总值的关系。分别以 1978年(改革开放试点初期)、1992年(改革进入以 大规模股份制改革为标志的新阶段)为初始年份进 行时段划分,对1978—1991年,1978—2007年以及 1992—2007年三个时段的真实人均GDP增长率的 横截面数据进行分位数回归分析。所有省份人均 GDP数据均来源于《中国统计年鉴》(国家统计 局)。各省份的真实人均GDP在前述数据基础上以 各省份同年物价指数进行修正。由于各省份的物价 指数难以获得,故采用同年全国的物价数据来进行 处理,其中全国物价指数采用以1950年为基期的 “商品零售价格总指数”计量。该指数为定基指数, 需做如下修正:第i年真实人均GDP=第i年人均 GDP/第i年物价指数。 首先,利用频率统计方法分阶段对1978年以来 万方数据
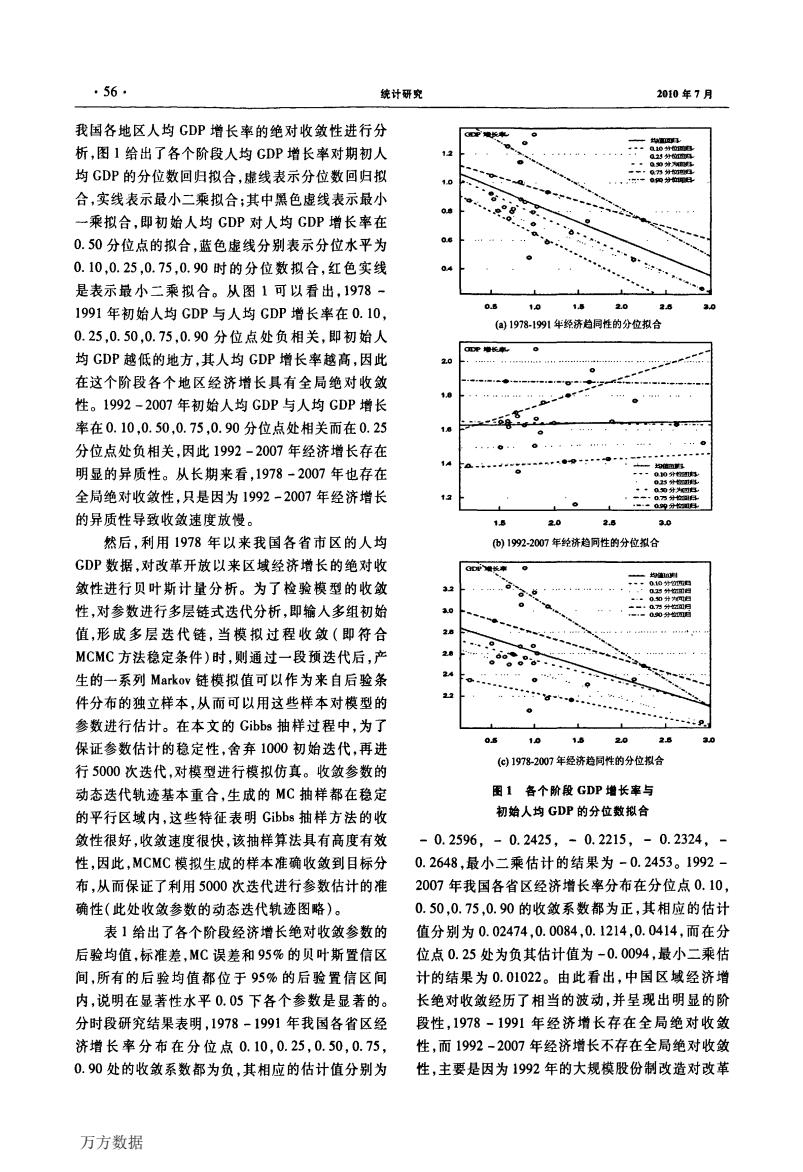
·56· 统计研究 2010年7月 我国各地区人均GDP增长率的绝对收敛性进行分 析,图1给出了各个阶段人均GDP增长率对期初人 12 均GDP的分位数回归拟合,虚线表示分位数回归拟 10 合,实线表示最小二乘拟合;其中黑色虚线表示最小 一乘拟合,即初始人均GDP对人均GDP增长率在 ...g0g 0.50分位点的拟合,蓝色虚线分别表示分位水平为 0 0.10,0.25,0.75,0.90时的分位数拟合,红色实线 04 是表示最小二乘拟合。从图1可以看出,1978- 08 10 1.5 1991年初始人均GDP与人均GDP增长率在0.10, 20 28 (a)1978-1991年经济趋同性的分位拟合 0.25,0.50,0.75,0.90分位点处负相关,即初始人 均GDP越低的地方,其人均GDP增长率越高,因此 20 在这个阶段各个地区经济增长具有全局绝对收敛 18 ● 性。1992-2007年初始人均GDP与人均GDP增长 率在0.10,0.50,0.75,0.90分位点处相关而在0.25 9 10 分位点处负相关,因此1992-2007年经济增长存在 . 14 明显的异质性。从长期来看,1978-2007年也存在 ---00外 全局绝对收敛性,只是因为1992-2007年经济增长 的异质性导致收敛速度放慢。 15 20 24 30 然后,利用1978年以来我国各省市区的人均 (b)1992-2007年经济趋同性的分位拟合 GDP数据,对改革开放以来区域经济增长的绝对收 G睡长率0 敛性进行贝叶斯计量分析。为了检验模型的收敛 性,对参数进行多层链式迭代分析,即输人多组初始 30 值,形成多层迭代链,当模拟过程收敛(即符合 28 4,9 MCMC方法稳定条件)时,则通过一段预迭代后,产 2 生的一系列Markov链模拟值可以作为来自后验条 24 0 g 22 件分布的独立样本,从而可以用这些样本对模型的 参数进行估计。在本文的Gibbs抽样过程中,为了 ......................... 保证参数估计的稳定性,舍弃1000初始迭代,再进 10 15 2025 0 (C)1978-2007年经济趋同性的分位拟合 行5000次迭代,对模型进行模拟仿真。收敛参数的 动态迭代轨迹基本重合,生成的MC抽样都在稳定 图1各个阶段GDP增长率与 的平行区域内,这些特征表明Gibbs抽样方法的收 初始人均GDP的分位数拟合 敛性很好,收敛速度很快,该抽样算法具有高度有效 -0.2596,-0.2425,-0.2215,-0.2324,- 性,因此,MCMC模拟生成的样本准确收敛到目标分 0.2648,最小二乘估计的结果为-0.2453.1992- 布,从而保证了利用5000次迭代进行参数估计的准 2007年我国各省区经济增长率分布在分位点0.10, 确性(此处收敛参数的动态迭代轨迹图略)。 0.50,0.75,0.90的收敛系数都为正,其相应的估计 表】给出了各个阶段经济增长绝对收敛参数的 值分别为0.02474,0.0084,0.1214,0.0414,而在分 后验均值,标准差,MC误差和95%的贝叶斯置信区 位点0.25处为负其估计值为-0.0094,最小二乘估 间,所有的后验均值都位于95%的后验置信区间计的结果为0.01022。由此看出,中国区域经济增 内,说明在显著性水平0.05下各个参数是显著的。 长绝对收敛经历了相当的波动,并呈现出明显的阶 分时段研究结果表明,1978-1991年我国各省区经 段性,1978-1991年经济增长存在全局绝对收敛 济增长率分布在分位点0.10,0.25,0.50,0.75, 性,而1992-2007年经济增长不存在全局绝对收敛 0.90处的收敛系数都为负,其相应的估计值分别为 性,主要是因为1992年的大规模股份制改造对改革 万方数据
·56‘ 统计研究 2010年7月 我国各地区人均GDP增长率的绝对收敛性进行分 析,图1给出了各个阶段人均GDP增长率对期初人 均GDP的分位数回归拟合,虚线表示分位数回归拟 合,实线表示最小二乘拟合;其中黑色虚线表示最小 一乘拟合,即初始人均GDP对人均GDP增长率在 0.50分位点的拟合,蓝色虚线分别表示分位水平为 0.10,0.25,0.75,0.90时的分位数拟合,红色实线 是表示最小二乘拟合。从图1可以看出。1978— 1991年初始人均GDP与人均GDP增长率在0.10, 0.25,0.50,0.75,0.90分位点处负相关,即初始人 均GDP越低的地方,其人均GDP增长率越高,因此 在这个阶段各个地区经济增长具有全局绝对收敛 性。1992—2007年初始人均GDP与人均GDP增长 率在0.10,0.50,0.75,0.90分位点处相关而在0.25 分位点处负相关,因此1992—2007年经济增长存在 明显的异质性。从长期来看,1978—2007年也存在 全局绝对收敛性,只是因为1992—2007年经济增长 的异质性导致收敛速度放慢。 然后,利用1978年以来我国各省市区的人均 GDP数据,对改革开放以来区域经济增长的绝对收 敛性进行贝叶斯计量分析。为了检验模型的收敛 性,对参数进行多层链式迭代分析,即输人多组初始 值,形成多层迭代链,当模拟过程收敛(即符合 MCMC方法稳定条件)时,则通过一段预迭代后,产 生的一系列Markov链模拟值可以作为来自后验条 件分布的独立样本,从而可以用这些样本对模型的 参数进行估计。在本文的Gibbs抽样过程中,为了 保证参数估计的稳定性,舍弃1000初始迭代,再进 行5000次迭代,对模型进行模拟仿真。收敛参数的 动态迭代轨迹基本重合,生成的MC抽样都在稳定 的平行区域内,这些特征表明Gibbs抽样方法的收 敛性很好,收敛速度很快,该抽样算法具有高度有效 性,因此,MCMC模拟生成的样本准确收敛到目标分 布,从而保证了利用5000次迭代进行参数估计的准 确性(此处收敛参数的动态迭代轨迹图略)。 表1给出了各个阶段经济增长绝对收敛参数的 后验均值,标准差,MC误差和95%的贝叶斯置信区 间,所有的后验均值都位于95%的后验置信区间 内,说明在显著性水平0.05下各个参数是显著的。 分时段研究结果表明,1978—1991年我国各省区经 济增长率分布在分位点0.10,0.25,0.50,0.75. 0.90处的收敛系数都为负,其相应的估计值分别为 O.S 1由 1,S 2.0 2.S a.O (a)1978·1991年经济趋同性的分位拟合 'J 乏o 2J (”1992-2007年经济趋同性的分位拟合 oj 1● 1占20 2J 3丑 (c)1978-2007年经济趋同性的分位拟合 图1各个阶段GDP增长率与 初始人均GDP的分位数拟合 一0.2596,一0.2425,一0.2215,一0.2324。一 0.2648,最/b---乘估计的结果为一0.2453。1992— 2007年我国各省区经济增长率分布在分位点0.10, 0.50,0.75,0.90的收敛系数都为正,其相应的估计 值分别为0.02474,0.0084,0.1214,0.0414,而在分 位点0.25处为负其估计值为一0.0094,最/b--乘估 计的结果为0.01022。由此看出,中国区域经济增 长绝对收敛经历了相当的波动,并呈现出明显的阶 段性,1978—1991年经济增长存在全局绝对收敛 性,而1992—2007年经济增长不存在全局绝对收敛 性,主要是因为1992年的大规模股份制改造对改革 万方数据
第27卷第7期 朱慧明等:基于MCMC稳态模拟的异质性经济增长横型研究 ·57. 表1 各个阶段绝对收敛参数的贝叶斯分位回归估计 时段 方法 变唯 均值 标准差 MC误差 下限 中位数 上限 0Ls回」 b(ols) -0.2453 0.0697 6.65E-4 -0.3839 -0.2453 -0.1087 6(0.10) -0.2596 0.0521 4.97E-4 -0.3752 -0.2539 -0.1737 1978 b(0.25) -0.2425 0.0424 4.13E-4 -0.3405 -0.2392 -0.1647 1991 分位问归 6(0.50) -0.2215 0.0680 7.02E-4 -0.3390 -0.2284 -0.0777 6(0.75) -0.2324 0.0952 9.83E-4 -0.4084 -0.2330 -0.0339 b(0.90) -0.2648 0.1162 0.0013 -0.4378 -0.2862 0.0299 0LS回归 b(ols) 0.01022 0.0798 7.94E-4 -0.1441 0.0094 0.1705 6(0.10) 0.02474 0.0648 7.98E-4 -0.1261 0.0314 0.1297 1992 b(0.25) -0.0094 0.0807 0.0011 -0.1879 -0.0027 0.1337 分 2007 回归 b(0.50) 0.0084 0.0686 9.88E-4 -0.1124 0.0020 0.1580 b(0.75) 0.1214 0.1142 0.0025 -0.0986 0.1206 0.3345 b(0.90) 0.0414 0.1258 0.0026 -0.2011 0.0349 0.3018 0LS4归 b(ols) -0.2568 0.1140 0.0010 -0.4790 -0.2569 -0.0304 6(0.10) -0.2063 0.0809 7.79E-4 -0.4067 -0.1919 -0.0815 1978 b(0.25) -0.2578 0.0871 7.85E-4 -0.4514 -0.2525 -0.0899 2007 公格 b(0.50) -0.2138 0.0971 9.73E-4 -0.3987 -0.2162 -0.0240 b(0.75) -0.2639 0.1521 0.0015 -0.5304 -0.2727 0.0743 b(0.90) -0.3827 0.1654 0.0020 -0.6196 -0.4155 0.0327 注:下限和上限分别表示2.5%的分位数和97.5%的分位数。 开放以来区域收敛有重要的影响。特别是,1992年 学在校生占年末总人口的平均比例来度量:变量: 以后是中国经济发展的高峰时期,东、西部经济差距 表示1992-2007年各个地区各年末总人口增长率。 加大,因此我国各省市区经济增长具有明显的异质 图2给出了物质资本,人口增长率以及人力资本对 性。但是,1978-2007年我国各省区经济增长率分 各地区人均GDP增长率的分位数拟合,虚线表示分 布在分位点0.10,0.25,0.50,0.75,0.90处的收敛 位回归拟合,实线表示最小二乘拟合;其中黑色虚线 系数都为负,其相应的估计值分别为-0.2063, 表示最小一乘拟合,即分位数为0.50时变量之间的 -0.2578,-0.2138,-0.2639,-0.3827,最小二乘 拟合,蓝色虚线分别表示分位水平为0.10,0.25, 估计的结果为-0.2568,说明从长期来看中国各省 0.75,0.90时的拟合,红色实线表示最小二乘拟合。 市区经济增长存在全局绝对收敛性。从估计结果还 表2给出了1992-2007年条件收敛参数,物质 可以看出分位估计与最小二乘估计结果具有一致 资本,人口增长率以及人力资本对经济增长的弹性 性,但是分位估计可以更全面地描述我国各地区经 系数的后验均值,标准差,MC误差和95%的贝叶斯 济增长的收敛性。同时,1978-1991年我国各地区 置信区间,所有的后验均值都位于95%的后验置信 经济增长率的各分位点参数的取值基本一致,说明 区间内,说明在显著性水平0.05下各个参数是显著 了从改革开放到大规模股份制改造时期中国各省市 的。1992-2007年我国各省市区的经济增长率在 区的经济增长具有同质性,但是大规模股份制改革 分位点0.10,0.25,0.50,0.75,090处都为负,说明 以来,由于政策因素,地理位置的影响,我国各省市 都存在全局条件收敛,其相应的估计分别为 区的经济增长具有异质性。 -0.3808,-0.1804,-0.0652,-0.0503,-0.0731, 对政策变量如物质资本,人口增长率以及人力 最小二乘估计的结果为-0.1895,对条件收敛性的 资本进行控制,讨论初始收人和经济增长率之间是 判断,分位估计与最小二乘估计结果是一致的,但是 否存在条件收敛,异质性增长模型可以表示为 不同分位点收敛系数取值不同,说明各地区的局部 Q (I yX)=a()+b(T)In(yio)+()In(s:) 条件收敛速度不同,因此分位回归估计可以更全面 +2()In(n+g+8)+()In(s) (19) 地描述各个地区的收敛特征的差异性。(s:)的弹 其中表示物质资本,用1992-2007年各个地区 性系数在分位点0.10,0.25,0.50,0.75,0.90处的 每年固定资产总额占当年GDP的平均比重来度量; 估计值都为正,其相应的估计分别为0.3636, $表示人力资本,用1992-2007年各个地区普通中 0.0454,0.0286,0.1763,0.7277,最小二乘估计的结 万方数据
第27卷第7期 朱慧明等:基于MCMC稳态模拟的异质性经济增长模型研究 ·57· 表1 各个阶段绝对收敛参数的贝叶斯分位回归估计 时段 方法 变鼍 均值 标准差 MC误差 下限 中位数 上限 OLS回¨j b(ols) 一0.2453 0.0697 6.65E一4 —0.3839 —0.2453 一O.1087 6(0.10) 一0.2596 0.052l 4.97E一4 —0.3752 —0.2539 一O.1737 1978 6(0.25) —0.2425 0.0424 4.13E一4 —0.3405 —0.2392 —0.1647 一 1991 分位回归 6(0.50) 一O.2215 0.0680 7.02E一4 —0.3390 —0.2284 —0.0777 6(0.75) —0.2324 O.0952 9.83E一4 —0.4084 —0.2330 —0.0339 6(0.90) 一O.2648 0.1162 O.0013 —0.4378 —0.2862 0.0299 OLS回归 6(ols) O.01022 0.0798 7.94E一4 一O.144l 0.0094 0.1705 6(0.10) 0.02474 0.0648 7.98E一4 —0.126l O.0314 0.1297 1992 b(0.25) 一O.0094 0.0807 0.00ll 一0.1879 一O.0027 0.1337 分位 b(0.50) 0.0084 0.0686 9.88E一4 一O.1124 O.0020 0.1580 2007 回归 6(0.75) 0.1214 O.1142 0.0025 —0.0986 O.1206 0.3345 b(0.90) 0.0414 O.1258 0.0026 —0.201l 0.0349 0.3018 OLS回归 b(ols) 一0.2568 O.1140 0.0010 —0.4790 —0.2569 —0.0304 6(0.10) 一O.2063 O.0809 7.79E一4 —0.4067 一O.1919 一O.0815 1978 6(0.25) —0.2578 0.087l 7.85E一4 —0.4514 —0.2525 —0.0899 分位 6(0.50) 一O.2138 0.0971 9.73E一4 —0.3987 一O.2162 —0.0240 2007 回归 b(O.75) —0.2639 0.1521 O.0015 —0.5304 —0.2727 0.0743 b(0.90) —0.3827 O.1654 0.0020 一O.6196 —0.4155 0.0327 注:F限和上限分别表不2.5%的分位效和97.5%的分位数。 开放以来区域收敛有重要的影响。特别是,1992年 以后是中国经济发展的高峰时期,东、西部经济差距 加大,因此我国各省市区经济增长具有明显的异质 性。但是,1978—2007年我国各省区经济增长率分 布在分位点0.10,0.25,0.50,0.75,0.90处的收敛 系数都为负,其相应的估计值分别为一0.2063, 一0.2578,一0.2138,一0.2639,一0.3827,最,J、二乘 估计的结果为一0.2568,说明从长期来看中国各省 市区经济增长存在全局绝对收敛性。从估计结果还 可以看出分位估计与最小二乘估计结果具有一致 性,但是分位估计可以更全面地描述我国各地区经 济增长的收敛性。同时,1978—1991年我国各地区 经济增长率的各分位点参数的取值基本一致,说明 了从改革开放到大规模股份制改造时期中国各省市 区的经济增长具有同质性,但是大规模股份制改革 以来,由于政策因素,地理位置的影响,我国各省市 区的经济增长具有异质性。 对政策变量如物质资本,人口增长率以及人力 资本进行控制,讨论初始收入和经济增长率之间是 否存在条件收敛,异质性增长模型可以表示为 Q.。(7.1咒'o弼=口(Jr)+6(r)ln(咒p)+9l(r)ln(s:) +妒2(r)In(,lf+g+6)+93(r)In(5:) (19) 其中s:表示物质资本,用1992—2007年各个地区 每年固定资产总额占当年GDP的平均比重来度量; s?表示人力资本,用1992—2007年各个地区普通中 学在校生占年末总人口的平均比例来度量;变量ni 表示1992—2007年各个地区各年末总人口增长率。 图2给出了物质资本,人口增长率以及人力资本对 各地区人均GDP增长率的分位数拟合,虚线表示分 位回归拟合,实线表示最小二乘拟合;其中黑色虚线 表示最小一乘拟合,即分位数为0.50时变量之间的 拟合,蓝色虚线分别表示分位水平为0.10,0.25, 0.75,0.90时的拟合,红色实线表示最小二乘拟合。 表2给出了1992—2007年条件收敛参数,物质 资本,人口增长率以及人力资本对经济增长的弹性 系数的后验均值,标准差,MC误差和95%的贝叶斯 置信区间,所有的后验均值都位于95%的后验置信 区间内,说明在显著性水平0.05下各个参数是显著 的。1992—2007年我国各省市区的经济增长率在 分位点0.10,0.25,0.50,0.75,0.90处都为负,说明 都存在全局条件收敛,其相应的估计分别为 一0.3808,-0.1804,一0.0652,一0.0503,-0.0731, 最小二乘估计的结果为一0.1895,对条件收敛性的 判断,分位估计与最小二乘估计结果是一致的,但是 不同分位点收敛系数取值不同,说明各地区的局部 条件收敛速度不同,因此分位回归估计可以更全面 地描述各个地区的收敛特征的差异性。ln(s:)的弹 性系数在分位点0.10,0.25,0.50,0.75,0.90处的 估计值都为正,其相应的估计分别为0.3636, 0.0454,0.0286,0.1763,0.7277,最小二乘估计的结 万方数据
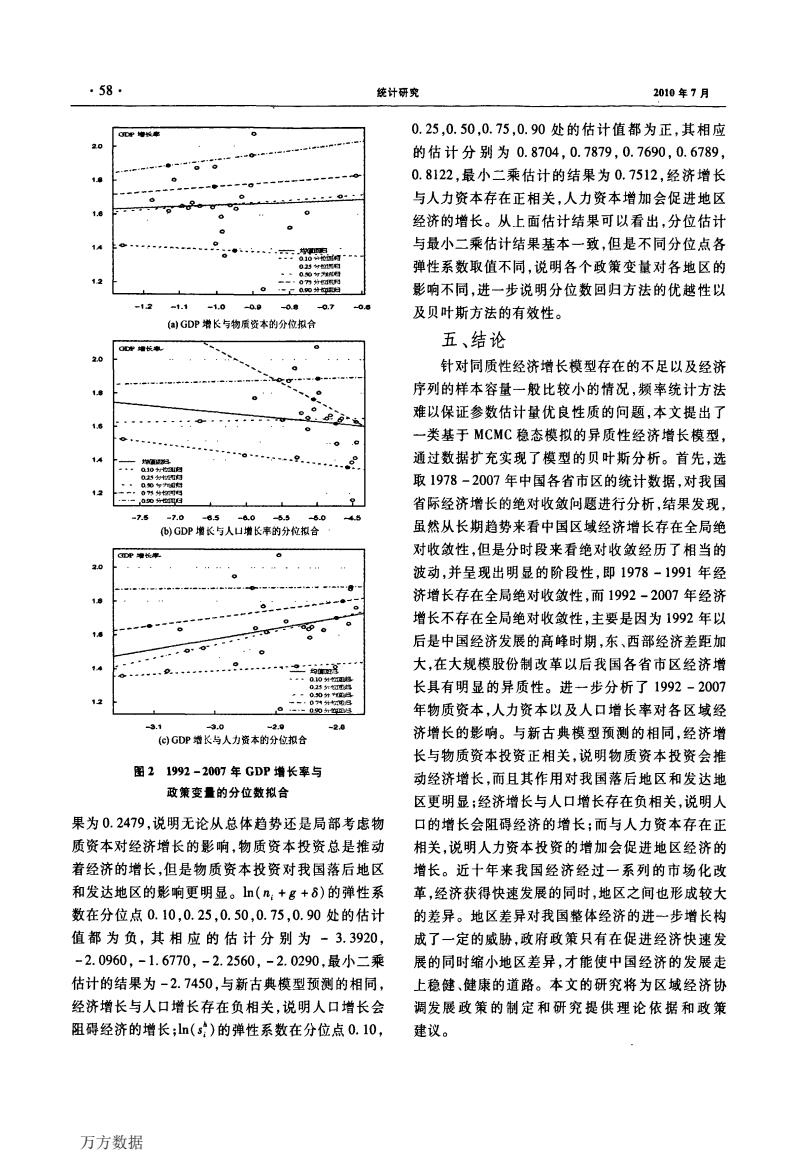
·58 统计研究 2010年7月 0.25,0.50,0.75,0.90处的估计值都为正,其相应 的估计分别为0.8704,0.7879,0.7690,0.6789, 0.8122,最小二乘估计的结果为0.7512,经济增长 与人力资本存在正相关,人力资本增加会促进地区 经济的增长。从上面估计结果可以看出,分位估计 与最小二乘估计结果基本一致,但是不同分位点各 弹性系数取值不同,说明各个政策变量对各地区的 0 影响不同,进一步说明分位数回归方法的优越性以 11 -1.0 -09 0 -0.7 及贝叶斯方法的有效性。 (a)GDP增长与物质资本的分位拟合 五、结论 针对同质性经济增长模型存在的不足以及经济 序列的样本容量一般比较小的情况,频率统计方法 难以保证参数估计量优良性质的问题,本文提出了 一类基于MCMC稳态模拟的异质性经济增长模型, 通过数据扩充实现了模型的贝叶斯分析。首先,选 取1978-2007年中国各省市区的统计数据,对我国 省际经济增长的绝对收敛问题进行分析,结果发现, -7.0 8.0 5.5 -50 )GDP增长与人山增长率的分位拟合 虽然从长期趋势来看中国区域经济增长存在全局绝 对收敛性,但是分时段来看绝对收敛经历了相当的 波动,并呈现出明显的阶段性,即1978-1991年经 济增长存在全局绝对收敛性,而1992-2007年经济 增长不存在全局绝对收敛性,主要是因为1992年以 后是中国经济发展的高峰时期,东、西部经济差距加 大,在大规模股份制改革以后我国各省市区经济增 00外m 长具有明显的异质性。进一步分析了1992-2007 年物质资本,人力资本以及人口增长率对各区域经 -3.1 -3.0 -20 -20 (C)GDP增长与人力资本的分包拟合 济增长的影响。与新古典模型预测的相同,经济增 长与物质资本投资正相关,说明物质资本投资会推 图21992-2007年GDP增长率与 动经济增长,而且其作用对我国落后地区和发达地 政策变量的分位数拟合 区更明显;经济增长与人口增长存在负相关,说明人 果为0.2479,说明无论从总体趋势还是局部考虑物 口的增长会阻碍经济的增长;而与人力资本存在正 质资本对经济增长的影响,物质资本投资总是推动 相关,说明人力资本投资的增加会促进地区经济的 着经济的增长,但是物质资本投资对我国落后地区 增长。近十年来我国经济经过一系列的市场化改 和发达地区的影响更明显。n(n:+g+8)的弹性系 革,经济获得快速发展的同时,地区之间也形成较大 数在分位点0.10,0.25,0.50,0.75,0.90处的估计 的差异。地区差异对我国整体经济的进一步增长构 值都为负,其相应的估计分别为-3.3920, 成了一定的威胁,政府政策只有在促进经济快速发 -2.0960,-1.6770,-2.2560,-2.0290,最小二乘 展的同时缩小地区差异,才能使中国经济的发展走 估计的结果为-2.7450,与新古典模型预测的相同, 上稳健、健康的道路。本文的研究将为区域经济协 经济增长与人口增长存在负相关,说明人口增长会 调发展政策的制定和研究提供理论依据和政策 阻碍经济的增长;ln(s)的弹性系数在分位点0.10, 建议。 万方数据
… ∞一 -2.Q 。24 (C)GDP增长与人力资本的分位拟合 图2 1992—2007年GDP增长率与 政策变量的分位数拟合 苎望o·2479,说明无论从总体趋势还是局部考虑物 零资本对经济增长的影响,物质资本投资总是推荔 着经济的增长,但是物质资本投资对我国落后地区 妻芋达地区的影响更明显。ln(厅;+g+∞的弹性系 鍪套分位点o·10,o.25,o.50,o.75,o.90处的估计 值都为负,其相应的估计分别为一3.3920 _2·0960,一1. ,一2. ,., ,最小二乘,6770 2560 2 0290 竺尊的结果为一2.7450,与新古典模型预测的相同’, 竺鋈增长与人口增长存在负相关,说明人口增长丢 阻碍经济的增长;ln(s?)的弹性系数在分位点j.10一, 万方数据

第27卷第7期 朱意阴等:基于MCMC稳态模拟的异质性经济增长模型研究 ·59· 表2 条件收敛参数的贝叶斯分位回归估计 方法 变量 均值 标荐是 MC误差 下限 中位数 上:限 0L5回的 b(ols) -0.1895 0.1025 0.0053 -0.3901 -0.1907 0.0157 6(0.10) -0.3808 0.0735 0.0034 -0.5117 -0.3866 -0.2180 b(0.25) -0.1804 0.1212 0.0075 -0.4223 -0.1775 0.0455 分位回归 6(0.50) -0.0652 0.1178 0.0078 -0.3407 =0.0532 0.1371 6(0.75) -0.0503 0.1047 0.0049 -0.2704 -0.0478 0.1526 6(0.90) -0.0731 0.1041 0.0029 -0.2758 -0.0766 0.1423 0Is同H p1(o山) 0.2479 0.2842 0.0098 -0.3004 0.2529 0.8107 P,(0.10) 0.3636 0.2177 0.0098 -0.0581 0.3529 0.8291 e1(0.25) 0.0454 0.3537 0.0188 -0.6742 0.0558 0.6931 分位回归 1(0.50) 0.0286 0.2803 0.0126 -0.5078 0.0239 0.6215 0:(0.75) 0.1763 0.2603 0.0123 -0.2918 0.1556 0.7586 :(0.90) 0.7277 0.5250 0.0334 -0.2325 0.7169 1.6610 0Ls回妇 (ols) -2.7450 0.9297 0.0662 -4.513 -2.7750 -0.9159 学2(0.10) -3.3920 0.5451 0.0436 -4.455 -3.4050 -2.4610 9(0.25) -2.0960 1.0310 0.0807 -4.3900 -2.0450 -0.1607 分位回归 P2(0.50) -1.6770 1.1530 0.0910 -4.6250 -1.6400 0.3543 (0.75) -2.2560 0.8383 0.0674 -4.2800 -2.2220 -0.7705 (0.90) -2.0290 0.7735 0.0583 -3.6960 -2.0090 -0.3874 0LS同归 p3(o) 0.7512 0.3332 0.0119 0.0539 0.7520 1.3980 3(0.10) 0.8704 0.3500 0.0264 0.2574 0.8387 1,7540 (0.25) 0.7879 0.3264 0.0199 0.2095 0.7649 1.496041 分位回归 3(0.50) 0.7690 0.2450 0.0129 0.3094 0.7646 1.2810 3(0.75) 0.6789 0.2876 0.0186 0.0943 0.6871 1.2240 93(0.90) 0.8122 0.5886 0.0434 -0.5780 0.8764 1.7460 注:下限和上限分别表示25%的分位数和97.5%的分位数。 参考文献 [11]R Koenker,W Bassett.Regression Quantiles J].Econometrica, [1 Barro,X Sala-i-Martin.Convergence J].Joumal of Political 1978(46):33-50. Economy,1992(100):223-251. [12 M Mello,R Perrelli.Growth equations:a quantile regression 2 ]NG Mankiw,D Romer,D Weil.A contribution to the empiries of exploration[J].The quarterly review of economics and finance, economic growth[J].Quarterly Joumal of Economies,1992(107): 2003(43):643-667 407-437. (13]G Canarella,S Pollard.Parameter heterogeneity in the neoclassical 3 SN Durlauf,PA Johnson.Multiple Regimes and Cross-Country growth model:quantile regression approach[J].Joumal of Growth Behavior[J].Joural of Applied Econometrics,1995(10): economic development,2004,29(1):1 -31. 365-384. [14]周业安,章泉.参数异质胜,经济趋同与中国区线经济发展 4 DT Qush.Twin peaks:Growth and convergence in models of [J].经济研究,2008(1):60-75. distribution dynsmics(J.The Economie Journal,1996.106 [15]K Yu,RA Moyeed.Bayeaian quantile regression[J].Statistics and (437):1045-1055. Probability Letters,2001(54):437-447. [5]SN Durlauf,A Kourtellos,A Minkin.The local Solow growth model [16]EG Tsionas.Bayesian quantile inference[J].Journal of Statistical [J].European Economic Review,2001(45):928-940. Computation and Simulation,2003,73(9):659-674. [6]A Kourtellos.Modeling Parameter Heterogeneity in Croes-coury [17]K Yu,P Van Kerm,J Zhang.Bayesian Quantile Regression:An growth regression models[C].University of Cyprus Discussion Application to the Wage Distribution in 1990s J].Britnin. Paper,No.12.2002. Sankhya,2005(67):359-377. 7 T Eicher,A Leukert.Institutions and economic performance: 作者简介 endogeneity and parameter heterogeneity[C].University of Munich 朱慈明,男,1966年生,湖南湘潭人,湖南大学工商管理 Discussion Paper,No.05,2006. 学院教授,博士生导师,研究方向:贝叶斯统计、计量经济 [8]PCB Phillips,DG Sul.Some empiries on economic growth under 模型。 heterogencous technology J].Joural of Macroeconomie,2007 首悫芳,女,1981年生,湖南邵阳人,博士研究生,研究 (29)455-469. 方向:金融工程与风险管理。 9 ]DR Hineline.Parameter heterogeneity in growth regression[J]. 度充明,男,l960年生,专徽安庆人,美国Brunel大摩数 Eeonomie letters,2008,101(2):126-129. [10]A Berard.S Durluaf.Interpreting tests of the convergence 学系教授,研完方向:贝叶斯分位回归统计。 hypothesis[J].Joural of Econometrics,1996(71):161 -173. (责任编辑:周晶) 万方数据
第27卷第7期 朱慧明等:基于MCMC稳态模拟的异质性经济增长模型研究 ·59· 表2 条件收敛参数的贝叶斯分位回归估计 方法 变量 均值 标准差 MC误差 下限 中位数 }:限 0LS回归 b(oh) 一0.1895 O.1025 0.0053 —0.390l 一0.1907 O.0157 6(0.10) 一0.3808 O.0735 0.0034 —0.5117 —0.3866 一O.2180 6(0.25) 一O.1804 O.1212 0.0075 —0.4223 一O.1775 O.0455 分位回归 6(0.50) —0.0652 O.1178 0.0078 —0.3407 —0.0532 O.137l 6(0.75) —0.0503 0.1047 0.0049 —0.2704 —0.0478 O.1526 b(0.90) —0.0731 O.104l O.0029 —0.2758 —0.0766 0.1423 OT5同归 妒l(ols) 0.2479 0.2842 0.0098 —0.3004 0.2529 0.8107 妒。(0.10) 0.3636 O.2177 O.0098 —0.058l 0.3529 0.829l 妒l(O.25) 0.0454 0.3537 0.0188 一0.6742 0.0558 0.693l 分位回归 妒l(0.50) 0.0286 0.2803 O.0126 —0.5078 0.0239 O.6215 妒1(0.75) 0.1763 0.2603 0.0123 一O.2918 O.1556 0.7586 妒,(0.90) 0.7277 0.5250 0.0334 —0.2325 O.7169 1.66lO OLS回归 p2(ols) 一2.7450 0.9297 0.0662 —4.513 —2.7750 一O.9159 p2(0.10) 一3.3920 0.545l 0.0436 —4.455 —3.4050 —2.4610 p2(0.25) —2.0960 L 03】O 0.0807 —4.3900 —2.0450 一O.1607 分位回归 驴2(0.50) —1.6770 1.1530 0.0910 —4.6250 —1.6400 0.3543 妒2(0.75) —2.2560 0.8383 0.0674 —4.2800 —2.2220 —0.7705 妒2(0.90) —2.0290 0.7735 0.0583 —3.6960 —2.0090 —0.3874 OLS同归 妒3(ols) 0.7512 0.3332 0.0119 0.0539 0.7520 1.3980 钆(0.10) 0.8704 0.3500 O.0264 0.2574 0.8387 1.7540 妒3(0.25) 0.7879 0.3264 O.0199 0.2095 0.7649 1.49604l 分位回归 妒3(0.50) 0.7690 0.2450 0.0129 0.3094 0.7646 1.2810 钆(0.75) 0.6789 0.2876 O.0186 0.0943 0.687l 1.2240 吼(0.90) 0.8122 0.5886 0.0434 —0.5780 0.8764 1.7460 注:下限和上限分别表示2.5%的分位数和97.5%的分位数。 参考文献 [1】Barro,x Sala~i Martin.Convergence[J】.Journal of Political Economy。1992(100):223—251. [2]NG Mankiw,D Romer,D Weft.A contribution to the empirics of economic growth[J].Quarterly Journal ofEconomics,1992(107): 407—437. [3】SN Durlauf,PA Johnson.Multiple Begimes and Cross-Country Growth Behavior[J].Journal of Applied Econometrics,1995(10): 365—384. [4]DT Quab.Twin peaks:Growth and convergence in models of distribution dynamics[J】.The Economic Journal,1996,106 (437):1045—1055. [5]SN Durlauf,A Kourtellos,A Minkin.The local Solow growth model [J].European Economic Review,2001(45):928—940. [6]A Kourtellos.Modeling Parameter Heterogeneity in Cross-country growth regression models[c].University of Cyprus Discussion Paper,No.12.2002. [7]T Eicher,A Leukert.Institutions and economic performance: endogeneity and parameter heterogeneity[C].University of Munich Discussion Paper,No.05,2006. [8]PCB Phillips,DG S01.Some empirics on economic growth under heterogeneous technology[J].Journal of Macroeconomic,2007 (29)455—469. [9]DR Hineline.Parameter heterogeneity in growth regression【J]. Economic letters,2008,101(2):126~129. [10]A Bernard,S Durluaf.Interpreting tests of the convergence hypothesis[J].Journal ofEconometrics,1996(71):161—173. [1 1]R Koenker,W Bassett.Regression Quantiles[J].Econometriea, 1978(46):33—50. [12]M Mello,R Perrelli.Growth equations:a quantile regression exploration[J].The quartedy review of economics and finance, 2003(43):643—667. [13】G Canarella,s Pollard.Parameter heterogeneity in the neoclassical growth model:a quantile regression approach[J].Journal of economic development,2004,29(1):1—31. [14]周业安,章泉.参数异质性、经济趋同与中国区域经济发展 [J].经济研究,2008(1):60—75. [1 5]K Yu。RA Moyeed.Bayesian quantile regression[J].Statistics and Probability Letters,2001(54):437—447. [16]EG Tsionas.Bayesian quantile inference[J】.Journal of Statistical Computation and Simulation,2003,73(9):659—674. [17]K Yu。P Van Kerm,J Zhang.Bayesian Quantile Regression:An Application to the Wage Distribution in 1990s[J].Britain. Sankhya,2005(67):359—377. 作者简介 朱慧明,男,1966年生,湖南湘潭人,湖南大学工商管理 学院教授,博士生导师,研究方向:贝叶斯统计、计量经济 模型。 曾惠芳,女,1981年生,湖南邵阳人,博士研究生,研究 方向:金融工程与风险管理。 虞克明,男,1960年生,安徽安庆人,英国Bmnel大学数 学系教授。研究方向:贝叶斯分住回归统计。 (责任编辑:周晶) 万方数据