
2003年10月 系统工程理论与实践 第10期 文章编号:1000-6788(2003)10-0053-06 网上支付系统的风险计量模型及实证分析 赵家敏,刘湘云12 (1.暨南大学金融系,广东广州510632:2.广东商学院金融系,广东广州510632) 摘要:网上支付行为可看作电子货币资产(电子现金、电子支票和数字信用卡等)组合的交易过程,对 网上支付风险进行计量,就是构建一个合适的资产配置模型,使得网上支付系统的效用最大化或交易成 本最小,VR方法提供了一种有效的电子货币资产配置模型.电子货币资产回报的时间序列是一个具有 平稳性的Markov链,因此,采用MCMC方法,通过构造一个平稳分析为π(x)的Markov链得到随机样 本,动态模拟出电子货币资产回报的分布,并通过定价公式得出其损益分布,最终计算出相应的VR值 使用以上构建的网上支付系统风险计量模型,对某商业银行调研后采集有关数据样本作了实证分析,可 为金融机构防范与控制网上支付风险提供参考, 关键词:网上支付系统;风险计量;VaR:MCMC方法 中图分类号:F830.4 文献标识码:A Positive Analysis about the Econometric Modeling on Risks in Online-payment System ZHAO Jia-min',LIU Xiang-yun2 (1.Jinan University.Guangzhou 510632,China:2.Guangdong Commercial College.Guangzhou 5100320,China) Abstract:Since online-parment can be regarded as the exchange process of e-money assets portfolis such as e-cash,e-cheque and digital credit card,the essence of measuring the risks of online-payment is to build up a reasonable asset allocating model which can maximize the utility of the online-paryment system.or minimize the related trading costs,while the VaR methods provides a efficient model for the allocation of e-money assets.The time series of return on the e-money assets is a stationary Markov chain,so the MCMC methods can be used to construct a Markov chain (whose stationary distribution is ()to get stochastic samples.Furthermore,by the MCMC methods we may simulate dynamically the distribution of the retum of e-money assets,and get the distribution of their profit and loss with the pricing formula.lastly compute the correspondent VaR value.Therefore,it would be a good reference for the risk prevention and control of the financial institutions to conduct empirical analysis on the relat- ed data sample of some commercial banks with the above risk measuring model of online-payment sys- tem. Key words:online-payment system;risk measuring:value at risk:markov chain monte carlo method 1问题的提出 就广义而言,网上支付是买卖双方通过开放式的互联网(Internet)或其它公共信息网进行的一种金 融交易,这种交易的对象通常是某种形式的数字金融工具,例如电子现金、电子支票或数字信用卡等,可以 认为,它们是现金货币、存款货币或信贷货币的电子化形式,在网络经济中,它们是一种新型的货币(即电 子货币)资产形式. 收稿日期:2002-08-10 资助项目:国家自然科学基金(79970031) 作者简介:赵家敏(1949-),女,教授,主要研究方向:金融工程,金融风险管理,Email:zhaojmin@pub.guangzhou.gd. :刘湘云2烈据男,湖南衡阳市,博士研究生,主要研究方向:资本市场与证券投资,金融工程
!""#年 $"月 系统工程理论与实践 第 $"期 文章编号%$"""&’())*!""#+$"&"",#&"’ 网上支付系统的风险计量模型及实证分析 赵家敏$ -刘湘云$-! *$.暨南大学金融系-广东 广州 ,$"’#!/!.广东商学院金融系-广东 广州 ,$"’#!+ 摘要% 网上支付行为可看作电子货币资产*电子现金0电子支票和数字信用卡等+组合的交易过程-对 网上支付风险进行计量-就是构建一个合适的资产配置模型-使得网上支付系统的效用最大化或交易成 本最小-123方法提供了一种有效的电子货币资产配置模型4电子货币资产回报的时间序列是一个具有 平稳性的 526789链-因此-采用 5:5:方法-通过构造一个平稳分析为 ;* 文献标识码% ? @8ABCB9D?E2FGABA2H8ICCJDKL8E8MDC6BL58NDFBEO 8E3BA7ABEPEFBED&Q2GMDECRGACDM ST?PUB2&MBE$ -VWX YB2EO&GIE$-! *$.UBE2EXEB9D6ABCG-ZI2EO[J8I,$"’#!-:JBE2/!.ZI2EON8EO:8MMD6LB2F:8FFDOD-ZI2EO[J8I,$""#!"-:JBE2+ \]^_‘ab_% RBELD8EFBED&Q26MDECL2EHD6DO26NDN2ACJDDcLJ2EODQ68LDAA8dD&M8EDG2AADCAQ86Cd8FBA AILJ2AD&L2AJ-D&LJDeID2ENNBOBC2FL6DNBCL26N-CJDDAADELD8dMD2AI6BEOCJD6BA7A8d8EFBED&Q2GMDECBA C8HIBFNIQ26D2A8E2HFD2AADC2FF8L2CBEOM8NDFfJBLJL2EM2cBMB[DCJDICBFBCG8dCJD8EFBED&Q26GMDEC AGACDM-86MBEBMB[DCJD6DF2CDNC62NBEOL8ACA-fJBFDCJD123MDCJ8NAQ689BNDA2DddBLBDECM8NDFd86CJD 2FF8L2CB8E8dD&M8EDG2AADCA.gJDCBMDAD6BDA8d6DCI6E8ECJDD&M8EDG2AADCABA2AC2CB8E26G526789 LJ2BE-A8CJD5:5:MDCJ8NAL2EHDIADNC8L8EAC6ILC2526789LJ2BE*fJ8ADAC2CB8E26GNBAC6BHICB8EBA ;*no+-女-教授-主要研究方向%金融工程-金融风险管理-KM2BF%[J28pMBEqQIH.OI2EO[J8I.ON. LE/刘湘云*$n(!o+-男-湖南衡阳市-博士研究生-主要研究方向%资本市场与证券投资-金融工程 r 问题的提出 就广义而言-网上支付是买卖双方通过开放式的互联网*WECD6EDC+或其它公共信息网进行的一种金 融交易-这种交易的对象通常是某种形式的数字金融工具-例如电子现金0电子支票或数字信用卡等4可以 认为-它们是现金货币0存款货币或信贷货币的电子化形式-在网络经济中-它们是一种新型的货币*即电 子货币+资产形式 sssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssssss 4 万方数据

54 系统工程理论与实践 2003年10月 相对于传统支付系统来说,开放式的Internet能将网上支付风险迅速扩散,且不受时间与地域限制, 因而网上支付系统的总体风险程度会增大。网上支付涉及的经济主体包括交易双方、网上支付中介机构、 认证中心(CA,Certificate Authority)等,风险计量主体发生了变化,但风险种类及各类风险的内涵并未 发生质的改变.网上支付系统中,主要风险类型是信用风险、流动性风险和操作风险,此外还有系统风险、 信誉风险、法律风险、交叉风险和不可抗拒风险等多种形式.在我国,由于商业银行网上支付系统大多属于 封闭型且采取落地模式①,最终的支付由现有的行内支付清算系统或封闭式的电子资金传递(E℉T)系统 来完成,极大地降低了操作风险。因此,目前我国商业银行网上支付系统的主要风险类型仍是信用风险和 流动性风险 网络经济中,电子商务、网上银行、网上证券、网上保险等最终均涉及网上支付,网上支付对金融及经 济发展的影响日益扩大,正成为金融机构新的利润增长点,如上所述,网上支付也带来了许多不同形式的 风险,这些风险一旦发生,在本国金融系统乃至世界范围内会迅速扩散,危及金融机构安全与金融系统稳 定.因此,运用科学而合理的理论与方法对网上支付风险进行测度和实证分析,有利于金融机构和监管当 局防范与化解风险. 2模型假设 首先,网上支付行为可看作电子货币资产的交易过程,在交易中卖出或买入一个包括不同数量的电子 现金、电子支票和数字信用卡的资产组合,因此,网上支付也是资产组合选择行为.对网上支付风险进行计 量,就是构建一个合适的资产配置模型,使得网上支付系统的效用最大化或交易成本最小化,而VR方法 提供了一种有效的资产配置模型.网上支付风险的根源在于电子货币资产的交易过程,其表现形式是各种 电子货币资产现金流的波动性(通常用电子货币资产回报来衡量).国际清算银行在有关风险指导原则中 指出:关于货币资产的风险可以采用VaR方法度量,其市场因子一般由相关现金流表示. 其次,根据我国目前网上支付风险的特点以及为方便风险测度,可对风险计量模型适当简化.本文假 定有关网上支付法律法规健全、社会信用体系完善、安全保密措施得当,网上支付系统设计完整以及社会 政治经济稳定,从而,法律风险、信誉风险、操作风险、交叉风险和不可抗拒风险等可以忽略,本文仅以我国 商业银行网上支付系统的信用风险和流动性风险作为模型的研究对象 最后,假定网络金融市场弱型有效(weak-form efficiency),电子货币资产价格已经反映了全部能从市 场交易数据中得到的信息,即其将来值只与现在值有关,而与过去值无关,因而电子货币资产回报的时间 序列符合Markov特性,是一个Markov链,由于Markov链具有平稳性,因此可动态模拟出电子货币资产 回报的分布,并通过定价公式得出损益分布,从而计算出VaR值. 3网上支付系统风险计量的理论分析 20世纪90年代后,一种新型的风险管理方法一VaR方法得到广泛的应用.VaR的含义是:风险资 产或组合在一个给定的置信区间(Confidence Level)和持有期间(Holding Horizon)时,在正常市场条件下 的最大期望损失].譬如,在给定的持有期间为一个月,给定的置信水平95%,即损失概率为5%时,某投 资组合的VaR等于100万元就意味着:在下一月中有95%的置信度该投资组合的最大期望损失为100万 元,或者说有5%的可能性该组合期望损失将超过100万元 若要精确界定VaR,可令W。为风险资产的初值、R为目标时间区间H上的收益率、W'为给定置信 水平c上资产最低价值,则有: VaR E(W)-W' 其中,W=W[1+R(J)]:W"由下式求得: ①落地模式的基本流程是:企业终端发出电子支付指令,经商业银行·网上银行系统'核验有关密码无误后,通过该银行 内部网将数龄传递到该企业开户行,开户行‘网上银行系统端’自动打印凭证,再由业务人员进行手工处理。银行 采用落地方式处理指令,确保了网上支付的安全
相对于传统支付系统来说!开放式的 "#$%&#%$能将网上支付风险迅速扩散!且不受时间与地域限制! 因而网上支付系统的总体风险程度会增大’网上支付涉及的经济主体包括交易双方(网上支付中介机构( 认证中心)*+!*%&$,-,./$%+0$12&,$34等!风险计量主体发生了变化!但风险种类及各类风险的内涵并未 发生质的改变’网上支付系统中!主要风险类型是信用风险(流动性风险和操作风险!此外还有系统风险( 信誉风险(法律风险(交叉风险和不可抗拒风险等多种形式’在我国!由于商业银行网上支付系统大多属于 封闭型且采取落地模式5!最终的支付由现有的行内支付清算系统或封闭式的电子资金传递)6784系统 来完成!极大地降低了操作风险’因此!目前我国商业银行网上支付系统的主要风险类型仍是信用风险和 流动性风险’ 网络经济中!电子商务(网上银行(网上证券(网上保险等最终均涉及网上支付’网上支付对金融及经 济发展的影响日益扩大!正成为金融机构新的利润增长点’如上所述!网上支付也带来了许多不同形式的 风险!这些风险一旦发生!在本国金融系统乃至世界范围内会迅速扩散!危及金融机构安全与金融系统稳 定’因此!运用科学而合理的理论与方法对网上支付风险进行测度和实证分析!有利于金融机构和监管当 局防范与化解风险’ 9 模型假设 首先!网上支付行为可看作电子货币资产的交易过程!在交易中卖出或买入一个包括不同数量的电子 现金(电子支票和数字信用卡的资产组合!因此!网上支付也是资产组合选择行为’对网上支付风险进行计 量!就是构建一个合适的资产配置模型!使得网上支付系统的效用最大化或交易成本最小化!而 :/;方法 提供了一种有效的资产配置模型’网上支付风险的根源在于电子货币资产的交易过程!其表现形式是各种 电子货币资产现金流的波动性)通常用电子货币资产回报来衡量4’国际清算银行在有关风险指导原则中 指出?-2&@ %--,.,%#.34!电子货币资产价格已经反映了全部能从市 场交易数据中得到的信息!即其将来值只与现在值有关!而与过去值无关!因而电子货币资产回报的时间 序列符合 A/&>2B特性!是一个 A/&>2B链’由于 A/&>2B链具有平稳性!因此可动态模拟出电子货币资产 回报的分布!并通过定价公式得出损益分布!从而计算出 :/;值’ C 网上支付系统风险计量的理论分析 DE世纪 FE年代后!一种新型的风险管理方法GG:/;方法得到广泛的应用’:/;的含义是<风险资 产或组合在一个给定的置信区间)*2#-,H%#.%I%B%J4和持有期间)K2JH,#LK2&,M2#4时!在正常市场条件下 的最大期望损失NOP ’譬如!在给定的持有期间为一个月!给定的置信水平 FQR!即损失概率为 QR时!某投 资组合的 :/;等于 OEE万元就意味着<在下一月中有 FQR的置信度该投资组合的最大期望损失为 OEE万 元!或者说有 QR的可能性该组合期望损失将超过 OEE万元’ 若要精确界定 :/;!可令 SE为风险资产的初值(T为目标时间区间 U 上的收益率(SV为给定置信 水平 W上资产最低价值!则有< :/;X Y)S4Z SV 其中!SXSENO[T)\4P]SV由下式求得< Q^ 系统工程理论与实践 DEE_年 OE月 5 落地模式的基本流程是<企业终端发出电子支付指令!经商业银行‘网上银行系统a核验有关密码无误后!通过该银行 内部网将有关指令传递到该企业开户行!开户行‘网上银行系统端a自动打印凭证!再由业务人员进行手工处理’银行 采用落地方式处理指令!确保了网上支付的安全’ 万方数据

第10期 网上支付系统的风险计量模型及实证分析 55 c f(w)dw 或 1-c=J。f(o)dW=P(w≤W)=p 如上所述,我国商业银行的网上支付系统的主要风险形式是信用风险和流动性风险,而VR在国际 上已被普遍用于度量这两种风险,因此VR方法适用于度量我国商业银行的网上支付系统风险 VaR计算方法主要有四种:正态方法、历史方法、历史模拟方法和随机模拟方法(又称Monte Carlo模 拟方法).这里,我们采用MCMC方法(Markov Chain Monte Carlo方法的简称).它是一种特殊的Monte Carlo模拟方法,它将随机过程中的Markov过程引入到Monte Carlo模拟中,实现了动态模拟(即抽样分 布随模拟的进行而改变).本质上,MCMC方法是使用Markov链的Monte Carlo积分. 假设网上支付系统的电子货币资产回报是一个Markov链,也就是说,设{X,n∈N+}为Markov 链,时间参数集为N+,其状态空间I={1,x2,,xw},其中,x1、x2、x3等分别代表电子现金、电子支票,数 字信用卡等电子货币资产组合中各种支付工具的现金流量,对所有n∈N+,则有 P=(X=x,lxa-=x-1X-”=x-g…,X=,} =P(XO=G-1)=) (1) 式(1)的直观意义是:网上支付系统在现在时刻n一1处于状态x-,那么将来时刻n的状态x,与过去时 刻n一2,n一3,…,1的状态--…,x,无关,仅与现在时刻n一1的状态-有关.即系统的将来只 与现在的状态有关而与过去无关,这种特殊性称为Markov特性. 若在Markov链中,从状态x-,转移到状态x的概率P{X=工,|X-=x-}(x-1.∈I)与n 无关,则称这类Markov链为具有平稳转移概率的Markov链,也称为齐次Markov链.本文所讨论的是连 续状态的Markov链的情况.常假定转移核P(·,·)与t无关,即该Markov链是时间齐次的.两步转移 概率函数为 P2)(x→B)△ p(x',B)dp(x,x') 由此可得步转移概率函数为 p(→B)eJre-t,BdpCr.)6≥1 记Xo的分布为(x)=P(Xo=x),则经过t步后X的边际分布记为 (x)=P(X=x) 如果π(x)满足 p(x,x')π(x)dx=π(x),Hx'∈X 则称π(x)为转移核P(·,·)的平稳分布. 作为初始状态,X)最好具有分布π(x).于是,由平稳分布的定义保证任一X的边际分布也是π(x), 然而实际中无法满足这一点.正因为从π(x)难以直接取样,才需要借助MCMC.事实上,并不需要初始状 态的边际分布就是x(x),从不同的Xo出发,Markov链经过一段时间的迭代后,可以认为各个时刻的 X”边际分布都是平稳分布,此时称它收敛.而在收敛出现以前的一段时间,比如m次迭代中,各状态的边 际分布还不能认为是π(x),因此在使用公式 .=1∑fx) (2) 1-1 估计E(f(x)时,应把前面的m个迭代值去掉,而用后面的n一m个迭代结果估计,即 =之fx) (3) n一m,二m+1 上式称为谫界最热由已知的遍历性定理,有了→E(fX),1∞. 从模拟计算的角度看[),构造的转移核使已知的概率分布π(x)为平稳分布.因此,在采用MCMC时
!"# $ %& ’()*+) 或 ,- !"# %& $ ’()*+% " .()/ %& *" 0 如上所述1我国商业银行的网上支付系统的主要风险形式是信用风险和流动性风险1而 234在国际 上已被普遍用于度量这两种风险1因此 234方法适用于度量我国商业银行的网上支付系统风险5 234计算方法主要有四种6正态方法7历史方法7历史模拟方法和随机模拟方法(又称 89:;?9模 拟方法*@这里1我们采用 8=8=方法(83>A9B=C3D:89:;?9方法的简称*@它是一种特殊的 89:;?9模拟方法1它将随机过程中的 83>A9B过程引入到 89:;?9模拟中1实现了动态模拟(即抽样分 布随模拟的进行而改变*@本质上18=8=方法是使用 83>A9B链的 89:;?9积分@ 假设网上支付系统的电子货币资产回报是一个 83>A9B链1也就是说1设EF(G* 1GHIJ K为 83>A9B 链1时间参数集为 IJ 1其状态空间 L"EM,1MN1O1MIK1其中1M,7MN7MP等分别代表电子现金7电子支票7数 字信用卡等电子货币资产组合中各种支付工具的现金流量5对所有 GHQJ 1则有 ." EF(G*" MRGSM(G-,*" MRG-,1F(G-N*" MRG-N1O1F(,*" MR,K " .EF(G*" MRGSF(G-,*" MRG-,K (,* 式(,*的直观意义是6网上支付系统在现在时刻 G-,处于状态 MRG-,1那么将来时刻 G的状态 MRG 与过去时 刻 G-N1G-P1O1,的状态 MRG-N1MRG-P1O1MR, 无关1仅与现在时刻 G-,的状态 MRG-, 有关5即系统的将来只 与现在的状态有关而与过去无关5这种特殊性称为 83>A9B特性5 若在 83>A9B链中1从状态 MRG-, 转移到状态 MRG 的概率 .EF(G* "MRGSF(G-,* "MRG-,K(MRG-,1MRGHL*与 G 无关1则称这类 83>A9B链为具有平稳转移概率的 83>A9B链1也称为齐次 83>A9B链5本文所讨论的是连 续状态的 83>A9B链的情况5常假定转移核 .(T1T*与 U无关1即该 83>A9B链是时间齐次的5两步转移 概率函数为 .(N* (MV W*X#MYHW 0(MY1W*+0(M1MY* 由此可得 Z步转移概率函数为 .(Z* (MV W*X#MYHW 0Z-, (MY1W*+0(M1MY*1 Z[ , 记 F(\*的分布为 ](M*".(F(\* "M*1则经过 U步后 F(U*的边际分布记为 ]U (M*" .(F(U*" M* 如果 ^(M*满足 #0(M1MY*^(M*+M" ^(MY*1 _MYH F 则称 ^(M*为转移核 .(T1T*的平稳分布5 作为初始状态1F(\*最好具有分布 ^(M*5于是1由平稳分布的定义保证任一 F(U*的边际分布也是^(M*1 然而实际中无法满足这一点5正因为从 ^(M*难以直接取样1才需要借助 8=8=5事实上1并不需要初始状 态的边际分布就是 ^(M*1从不同的 F(\*出发183>A9B链经过一段时间的迭代后1可以认为各个时刻的 F(U*边际分布都是平稳分布1此时称它收敛5而在收敛出现以前的一段时间1比如 ‘次迭代中1各状态的边 际分布还不能认为是 ^(M*1因此在使用公式 ’ aG" , Gb G R", ’(M(R* * (N* 估计 c(’(M**时1应把前面的 ‘个迭代值去掉1而用后面的 G-‘个迭代结果估计1即 ’ a‘G" , G- ‘ b G U"‘J, ’(F(U* * (P* 上式称为遍历平均5由已知的遍历性定理1有 ’ aY ‘GVc(’(F**1GV$d 从模拟计算的角度看eNf 1构造的转移核使已知的概率分布 ^(M*为平稳分布5因此1在采用 8=8=时1 第 ,\期 网上支付系统的风险计量模型及实证分析 gg 万方数据

56 系统工程理论与实践 2003年10月 转移核的构造具有至关重要的作用.不同的转移核的构造方法导致不同的MCMC,如Metropolis方法、 Gibbs抽样方法等. 我们可以把MCMC概括为如下三步: 第一步在X上选一个具有平稳分布的Markov链,使其转移核为P(·,·): 第二步由X中某一点Xo)出发,用第一步中的Markov链产生点序列X》,…,Xm; 第三步对某个m和大的n,任一函数f(x)的期望估计如下: 0x0)≥ f(X) (4) 综上所述,由于网上支付系统中电子货币资产回报的时间序列是一个具有平稳性的Markov链,因此 可采用MCMC方法,通过构造一个平稳分布为π(.x)的Markov链米得到随机样本,从而动态模拟出电子 货币资产回报的分布,并通过定价公式得出其损益分布,最终计算出相应的VR值. 4实证分析 下面以某股份制银行的网上支付系统为研究对象,将MCMC应用于VR的估计,其网上支付系统的 资产组合由电子现金、电子支票和数字信用卡等三种电子货币构成,采用2000年4月至2002年3月共24 个月的数据样本进行实证分析, 4.1MCMC的计算步骤 第一,首先识别网上支付系统中基础的市场因子,并用市场因子表示 市场因子的历史数据 出电子货币资产组合中各种金融工具的盯市价值:第二,假设市场因子的 变化服从的分布(如多元正态分布),运用MCMC估计该分布的参数(如 MCMC法 均值向量和协方差矩阵):第三,根据参数模拟市场因子未来变化的情景, 根据定价公式计算资产组合未来的盯市价值及未来的潜在损益:第四,根 均值向戴 和协方差矩阵 据潜在损益的分布,在给定置信度(如95%)下,计算VaR值.MCMC的计 算流程如图1所示. 拟 4.2市场因子的模拟 市场因子来来的情景 如前所述,对该银行的网上支付系统进行风险分析时,其基础市场因 子就是该系统电子现金、电子支票及数字信用卡等三种电子货币的现金 定价公式 流.运用MCMC法时,所要做的第一步是根据该银行三种电子货币支付 工具的历史交易数据,估计分布的参数(即均值向量和协方差矩阵),这是 资产组合未米 价值的分布 问题的关键所在, 采用的数据集合为2000年4月至2002年3月共24个月电子现金、 图1MCMC流程图 电子支票及数字信用卡的现金流的历史数据。一般说来,金融风险是由于 金融资产价格的波动引起的,在金融经济学中,波动性是用回报的标准差 表1 电子货币资产回报统计量 来度量,而不是用价格的标准差,因此可以通过电子货币 R R R 资产回报来衡量网上支付系统资产组合的损益分布.回 均值 0.000125 报有简单回报、对数回报等多种形式,这里采用对数回 0.000564 0.000523 方 差 报,即在给定第t个月电子货币资产现金流a,的条件下, 0.000165 0.003451 0.004603 标准差 月对数回报为R,=ln(a,/a,-1).首先进行正态性检验(这 0.012864 0.058749 0.067843 偏度 0.586060 1.104853 1.563479 是使用MCMC的前提).经检验可看出,抽样时期三种 峰度 电子货币资产回报(分别用R1、R2,、R3)来表示)的历史 5.684932 8.694532 7.846251 数据近似服从多元正态分布,同时根据历史数据还可以 得到相关的统计量,计算结果如表1所示. 协方养钙蹑黎
转移核的构造具有至关重要的作用!不同的转移核的构造方法导致不同的 "#"#$如 "%&’()(*+,方法- .+//,抽样方法等! 我们可以把 "#"#概括为如下三步0 第一步 在 1上选一个具有平稳分布的 "2’3(4链$使其转移核为 567$789 第二步 由 1中某一点 16:8出发$用第一步中的 "2’3(4链产生点序列 16;8 $和大的 =$任一函数 ?6@8的期望估计如下0 A B6?6188C ; =D > E = FC>G; ?616F8 8 6H8 综上所述$由于网上支付系统中电子货币资产回报的时间序列是一个具有平稳性的 "2’3(4链$因此 可采用 "#"#方法$通过构造一个平稳分布为 I6@8的 "2’3(4链来得到随机样本$从而动态模拟出电子 货币资产回报的分布$并通过定价公式得出其损益分布$最终计算出相应的 J2K值! L 实证分析 下面以某股份制银行的网上支付系统为研究对象$将 "#"#应用于 J2K的估计$其网上支付系统的 资产组合由电子现金-电子支票和数字信用卡等三种电子货币构成$采用 M:::年 H月至 M::M年 N月共 MH 个月的数据样本进行实证分析O LPQ "#"#的计算步骤 图 ; "#"#流程图 第一$首先识别网上支付系统中基础的市场因子$并用市场因子表示 出电子货币资产组合中各种金融工具的盯市价值9第二$假设市场因子的 变 化服从的分布6如多元正态分布8$运用 "#"#估计该分布的参数6如 均值向量和协方差矩阵89第三$根据参数模拟市场因子未来变化的情景$ 根据定价公式计算资产组合未来的盯市价值及未来的潜在损益9第四$根 据潜在损益的分布$在给定置信度6如 RST8下$计算 J2K值O"#"#的计 算流程如图 ;所示O LPU 市场因子的模拟 如前所述$对该银行的网上支付系统进行风险分析时$其基础市场因 子就是该系统电子现金-电子支票及数字信用卡等三种电子货币的现金 流O运用 "#"#法时$所要做的第一步是根据该银行三种电子货币支付 工具的历史交易数据$估计分布的参数6即均值向量和协方差矩阵8$这是 问题的关键所在O 采用的数据集合为 M:::年 H月至 M::M年 N月共 MH个月电子现金- 电子支票及数字信用卡的现金流的历史数据!一般说来$金融风险是由于 金融资产价格的波动引起的!在金融经济学中$波动性是用回报的标准差 表 ; 电子货币资产回报统计量 V6;8 V6M8 V6N8 均 值 :P:::;MS :P:::SWH :P:::SMN 方 差 :P:::;WS :P::NHS; :P::HW:N 标准差 :P:;MXWH :P:SXYHR :P:WYXHN 偏 度 :PSXW:W: ;P;:HXSN ;PSWNHYR 峰 度 SPWXHRNM XPWRHSNM YPXHWMS; 来度量$而不是用价格的标准差$因此可以通过电子货币 资产回报来衡量网上支付系统资产组合的损益分布!回 报有简单回报-对数回报等多种形式$这里采用对数回 报$即在给定第 F个月电子货币资产现金流 ZF的条件下$ 月对数回报为 VFC*[6ZF\ZFD;8!首先进行正态性检验6这 是使用 "#"#的前提8!经检验可看出$抽样时期三种 电子货币资产回报6分别用 V6;8 -V6M8 -V6N8来表示8的历史 数据近似服从多元正态分布$同时根据历史数据还可以 得到相关的统计量$计算结果如表 ;所示P 协方差矩阵为 SW 系统工程理论与实践 M::N年 ;:月 万方数据
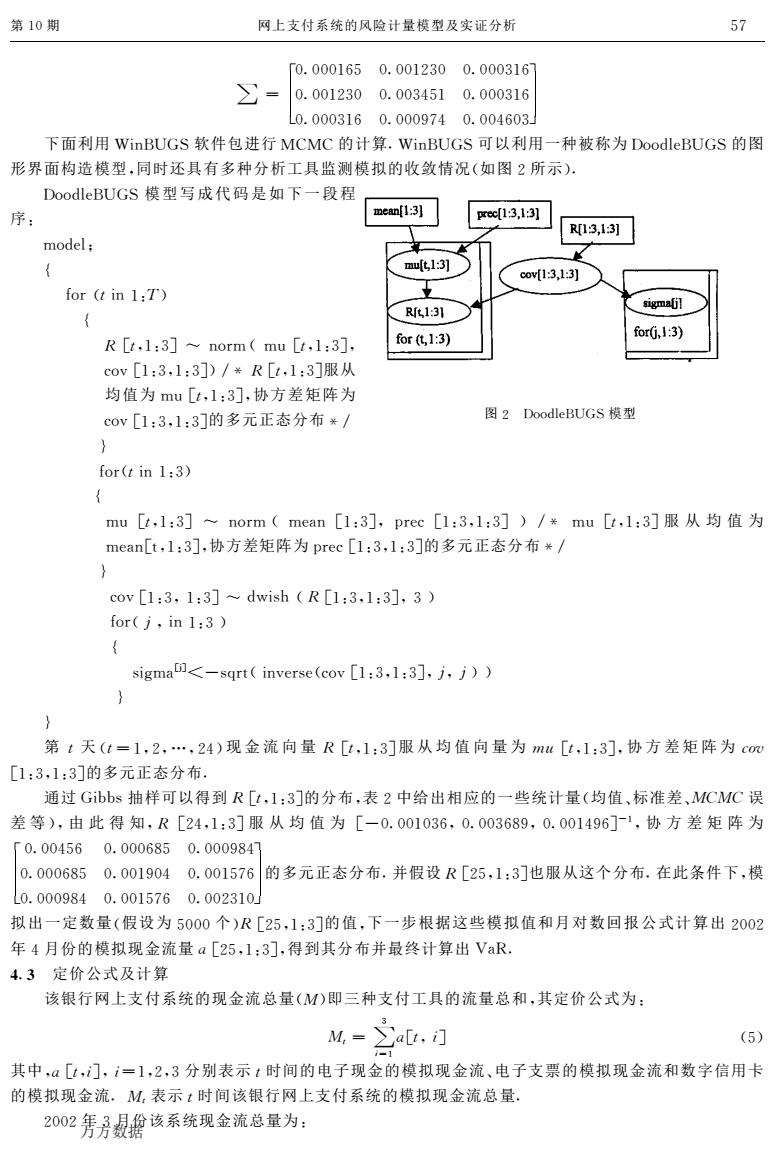
第10期 网上支付系统的风险计量模型及实证分析 57 「0.0001650.0012300.0003167 0.0012300.0034510.000316 0.0003160.0009740.004603 下面利用WinBUGS软件包进行MCMC的计算.WinBUGS可以利用一种被称为DoodleBUGS的图 形界面构造模型,同时还具有多种分析工具监测模拟的收敛情况(如图2所示). DoodleBUGS模型写成代码是如下一段程 序: mean[1:3] ec13,13] R13,1:3] model: mu[t1:3] covf1:3,1:3] for (t in 1:T) R131 sigmaljl for(化1:3) for(j,1:3) R [t,1:3]norm mu [t,1:3], cov[1:3,1:3])/¥R[t,1:3]服从 均值为mu[t,1:3],协方差矩阵为 cov[1:3,1:3]的多元正态分布¥/ 图2 DoodleBUGS模型 } for(t in 1:3) { mu[t,l:3]~norm(mean[1:3],prec[1:3,l:3])/*mu[t,l:3]服从均值为 mean[t,l:3],协方差矩阵为prec[1:3,l:3]的多元正态分布*/ cov[1:3,1:3]~dwish(R[1:3,1:3],3) for(j,in 1:3) sigma<-sqrt inverse(cov [1:3,1:3],j,j)) } } 第t天(t=1,2,…,24)现金流向量R[t,1:3]服从均值向量为mu[t,1:3],协方差矩阵为com [1:3,1:3]的多元正态分布 通过Gibbs抽样可以得到R[t,1:3]的分布,表2中给出相应的一些统计量(均值、标准差、MCMC误 差等),由此得知,R[24,1:3]服从均值为[一0.001036,0.003689,0.001496]-1,协方差矩阵为 「0.004560.0006850.0009847 0.0006850.0019040.001576 的多元正态分布.并假设R[25,1:3]也服从这个分布.在此条件下,模 L0.0009840.0015760.002310 拟出一定数量(假设为5000个)R[25,1:3]的值,下一步根据这些模拟值和月对数回报公式计算出2002 年4月份的模拟现金流量a[25,1:3],得到其分布并最终计算出VaR. 4.3定价公式及计算 该银行网上支付系统的现金流总量(M)即三种支付工具的流量总和,其定价公式为: M,=∑[t,门 (5) 其中,a[t,i门,i=1,2,3分别表示t时间的电子现金的模拟现金流、电子支票的模拟现金流和数字信用卡 的模拟现金流.M,表示t时间该银行网上支付系统的模拟现金流总量, 2002年3,月份该系统现金流总量为: 万方数据
! " #$###%&’ #$##%()# #$###)%& #$##%()# #$##)*’% #$###)%& + , - #$###)%& #$###/0* #$##*&#). 下面利用 1234567软件包进行 8989的计算:1234567可以利用一种被称为 ;?4567的图 形界面构造模型@同时还具有多种分析工具监测模拟的收敛情况A如图 (所示B: 图 ( ;?4567模型 ;?4567模型写成代码是如下一段程 序C DE F G<HAI23%CJB F KLI@%C)MN 3<HDADOLI@%C)M@ P<QL%C)@%C)MBRS KLI@%C)M服从 均值为 DOLI@%C)M@协方差矩阵为 P<QL%C)@%C)M的多元正态分布SR T G<HAI23%C)B F DOLI@%C)M N 3<HDAD?U3L%C)M@VH?PL%C)@%C)M B RS DOLI@%C)M服 从 均 值 为 D?U3LW@%C)M@协方差矩阵为 VH?PL%C)@%C)M的多元正态分布SR T P<QL%C)@%C)MN =X2YZAKL%C)@%C)M@)B G<HA[@23%C)B F Y2\DU L]M ^_Y‘HWA23Q?HY?AP<QL%C)@%C)M@[@[BB T T 第 I天 AI" %@(@a@(*B现 金 流 向 量 K LI@%C)M服 从 均 值 向 量 为 bcLI@%C)M@协 方 差 矩 阵 为 def L%C)@%C)M的多元正态分布g 通过 62hhY抽样可以得到 KLI@%C)M的分布@表 (中给出相应的一些统计量A均值i标准差ijkjk误 差 等 B@由 此 得 知@K L(*@%C)M服 从 均 值 为 L_#$##%#)&@#$##)&l/@#$##%*/&M_% @协 方 差 矩 阵 为 #$##*’& #$###&l’ #$###/l* #$###&l’ #$##%/#* #$##%’0& + , - #$###/l* #$##%’0& #$##()%#. 的多元正态分布g并假设 KL(’@%C)M也服从这个分布g在此条件下@模 拟出一定数量A假设为 ’###个BKL(’@%C)M的值@下一步根据这些模拟值和月对数回报公式计算出 (##( 年 *月份的模拟现金流量 mL(’@%C)M@得到其分布并最终计算出 nUog p$q 定价公式及计算 该银行网上支付系统的现金流总量AjB即三种支付工具的流量总和@其定价公式为C jI" ! ) r"% mLI@rM A’B 其中@mLI@rM@r"%@(@)分别表示 I时间的电子现金的模拟现金流i电子支票的模拟现金流和数字信用卡 的模拟现金流gjI表示 I时间该银行网上支付系统的模拟现金流总量g (##(年 )月份该系统现金流总量为C 第 %#期 网上支付系统的风险计量模型及实证分析 ’0 万方数据
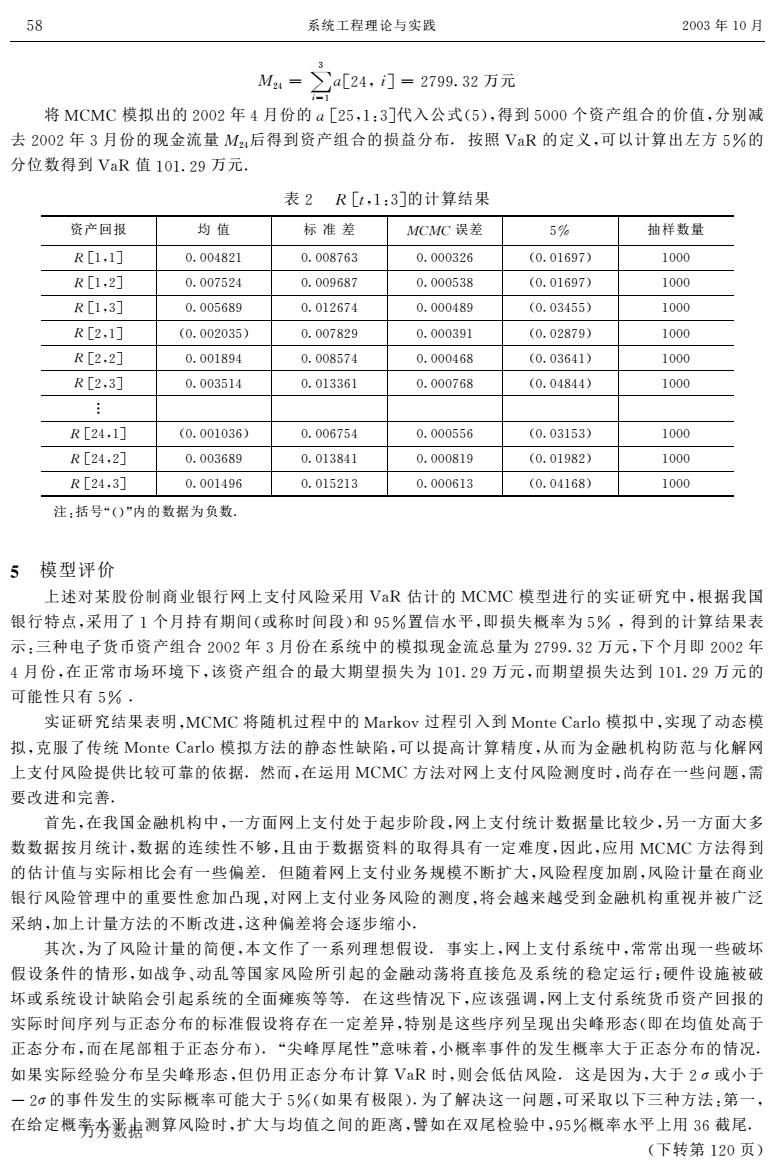
58 系统工程理论与实践 2003年10月 M24= ∑[24,门=279.32万元 = 将MCMC模拟出的2002年4月份的a[25,1:3]代入公式(5),得到5000个资产组合的价值,分别减 去2002年3月份的现金流量M2:后得到资产组合的损益分布.按照VaR的定义,可以计算出左方5%的 分位数得到VaR值101.29万元. 表2R[t,1:3]的计算结果 资产回报 均值 标准差 MCMC误差 5% 抽样数量 R[1,1] 0.004821 0.008763 0.000326 (0.01697) 1000 R[1,2] 0.007524 0.009687 0.000538 (0.01697) 1000 R[1,3] 0.005689 0.012674 0.000489 (0.03455) 1000 R[2,1] (0.002035) 0.007829 0.000391 (0.02879) 1000 R[2,2] 0.001894 0.008574 0.000468 (0.03641) 1000 R[2,3] 0.003514 0.013361 0.000768 (0.04844) 1000 R[24,1] (0.001036) 0.006754 0.000556 (0.03153) 1000 R[24,2] 0.003689 0.013841 0.000819 (0.01982) 1000 R[24,3] 0.001496 0.015213 0.000613 (0.04168) 1000 注:括号“()”内的数据为负数 5模型评价 上述对某股份制商业银行网上支付风险采用VR估计的MCMC模型进行的实证研究中,根据我国 银行特点,采用了1个月持有期间(或称时间段)和95%置信水平,即损失概率为5%,得到的计算结果表 示:三种电子货币资产组合2002年3月份在系统中的模拟现金流总量为2799.32万元,下个月即2002年 4月份,在正常市场环境下,该资产组合的最大期望损失为101.29万元,而期望损失达到101.29万元的 可能性只有5%. 实证研究结果表明,MCMC将随机过程中的Markov过程引入到Monte Carlo模拟中,实现了动态模 拟,克服了传统Monte Carlo模拟方法的静态性缺陷,可以提高计算精度,从而为金融机构防范与化解网 上支付风险提供比较可靠的依据.然而,在运用MCMC方法对网上支付风险测度时,尚存在一些问题,需 要改进和完善 首先,在我国金融机构中,一方面网上支付处于起步阶段,网上支付统计数据量比较少,另一方面大多 数数据按月统计,数据的连续性不够,且由于数据资料的取得具有一定难度,因此,应用MCMC方法得到 的估计值与实际相比会有一些偏差.但随着网上支付业务规模不断扩大,风险程度加剧,风险计量在商业 银行风险管理中的重要性愈加凸现,对网上支付业务风险的测度,将会越来越受到金融机构重视并被广泛 采纳,加上计量方法的不断改进,这种偏差将会逐步缩小, 其次,为了风险计量的简便,本文作了一系列理想假设,事实上,网上支付系统中,常常出现一些破坏 假设条件的情形,如战争、动乱等国家风险所引起的金融动荡将直接危及系统的稳定运行:硬件设施被破 坏或系统设计缺陷会引起系统的全面瘫痪等等.在这些情况下,应该强调,网上支付系统货币资产回报的 实际时间序列与正态分布的标准假设将存在一定差异,特别是这些序列呈现出尖峰形态(即在均值处高于 正态分布,而在尾部粗于正态分布).“尖峰厚尾性”意味着,小概率事件的发生概率大于正态分布的情况. 如果实际经验分布呈尖峰形态,但仍用正态分布计算VR时,则会低估风险.这是因为,大于2。或小于 一2σ的事件发生的实际概率可能大于5%(如果有极限).为了解决这一问题,可采取以下三种方法:第一, 在给定概旁夯轰指测算风险时,扩大与均值之间的距离,譬如在双尾检验中,95%概率水平上用36截尾. (下转第120页)
!"#$ % & ’$( )*"#+’,$ "-../&"万元 将 0101模拟出的 "22"年 #月份的 )*"3+(4&,代入公式536+得到 3222个资产组合的价值+分别减 去 "22"年 &月份的现金流量 !"#后得到资产组合的损益分布7按照 89:的定义+可以计算出左方 3;的 分位数得到 89:值 (2(/".万元7 表 " !>误差 3? 抽样数量 <*(+(, 2/22#@"( 2/22@-A& 2/222&"A 52/2(A.-6 (222 <*(+", 2/22-3"# 2/22.A@- 2/2223&@ 52/2(A.-6 (222 <*(+&, 2/223A@. 2/2("A-# 2/222#@. 52/2Ő (222 <*"+(, 52/22"2&36 2/22-@". 2/222&.( 52/2"@-.6 (222 <*"+", 2/22(@.# 2/22@3-# 2/222#A@ 52/2&A#(6 (222 <*"+&, 2/22&3(# 2/2(&&A( 2/222-A@ 52/2#@##6 (222 B <*"#+(, 52/22(2&A6 2/22A-3# 2/22233A 52/2&(3&6 (222 <*"#+", 2/22&A@. 2/2(&@#( 2/222@(. 52/2(.@"6 (222 <*"#+&, 2/22(#.A 2/2(3"(& 2/222A(& 52/2#(A@6 (222 注4括号C56D内的数据为负数7 E 模型评价 上述对某股份制商业银行网上支付风险采用 89:估计的 0101模型进行的实证研究中+根据我国 银行特点+采用了 (个月持有期间5或称时间段6和 .3;置信水平+即损失概率为 3; +得到的计算结果表 示4三种电子货币资产组合 "22"年 &月份在系统中的模拟现金流总量为 "-../&"万元+下个月即 "22"年 #月份+在正常市场环境下+该资产组合的最大期望损失为 (2(/".万元+而期望损失达到 (2(/".万元的 可能性只有 3; F 实证研究结果表明+0101将随机过程中的 09GHIJ过程引入到 0IKLM19GNI模拟中+实现了动态模 拟+克服了传统 0IKLM19GNI模拟方法的静态性缺陷+可以提高计算精度+从而为金融机构防范与化解网 上支付风险提供比较可靠的依据F然而+在运用 0101方法对网上支付风险测度时+尚存在一些问题+需 要改进和完善F 首先+在我国金融机构中+一方面网上支付处于起步阶段+网上支付统计数据量比较少+另一方面大多 数数据按月统计+数据的连续性不够+且由于数据资料的取得具有一定难度+因此+应用 0101方法得到 的估计值与实际相比会有一些偏差F但随着网上支付业务规模不断扩大+风险程度加剧+风险计量在商业 银行风险管理中的重要性愈加凸现+对网上支付业务风险的测度+将会越来越受到金融机构重视并被广泛 采纳+加上计量方法的不断改进+这种偏差将会逐步缩小F 其次+为了风险计量的简便+本文作了一系列理想假设F事实上+网上支付系统中+常常出现一些破坏 假设条件的情形+如战争O动乱等国家风险所引起的金融动荡将直接危及系统的稳定运行P硬件设施被破 坏或系统设计缺陷会引起系统的全面瘫痪等等F在这些情况下+应该强调+网上支付系统货币资产回报的 实际时间序列与正态分布的标准假设将存在一定差异+特别是这些序列呈现出尖峰形态5即在均值处高于 正态分布+而在尾部粗于正态分布6FC尖峰厚尾性D意味着+小概率事件的发生概率大于正态分布的情况F 如果实际经验分布呈尖峰形态+但仍用正态分布计算 89:时+则会低估风险F这是因为+大于 "Q或小于 R "Q的事件发生的实际概率可能大于 3;5如果有极限6F为了解决这一问题+可采取以下三种方法4第一+ 在给定概率水平上测算风险时+扩大与均值之间的距离+譬如在双尾检验中+.3;概率水平上用 &A截尾F 5下转第 ("2页6 3@ 系统工程理论与实践 "22&年 (2月 万方数据

120 系统工程理论与实践 2003年10月 [5]熊孟英.GM(1,1)在人口预测中的应用[山门.河北大学学报:自然科学版,1995,15(2):50-55. [6]祝精美.规划人口的动态灰色预测[☐].工科数学,1997,13(4):20-23. [7]张启敏.人口迁移的定量研究[U门].宁夏大学学报,1995,16(1):52-55. [8]Pekalski,Andrzej.Model of population dynamics [J].Physica A:Statistical and Theoretical Physics,1998,252(3 -4):325-335. [9]Wazwaz A M,Khuri S A.New ideas for solving size-structured population models [J].Applied Mathematics and Computation (New York),1998,93(1):91-96. [10]Wang Wendi,Fergola P,Tenneriello C.Global attractivity of periodic solutions of population models [J].Journal of Mathematical Analysis and Applications,1997,211(2):498-511. [11]顾朝林,蔡建明.中国大中城市流动人口迁移规律研究[J门.地理学报,1999,54(3):204一212. [12]李如生.非平衡态热力学和耗散结构[M],北京:清华大学出版社,1986.52一64. [13]黄润荣,任光耀.耗散结构与协同学[M].贵阳:贵州人民出版社,1988.190一191. [14]G·尼科利斯,I·普里戈京.非平衡系统的自组织[M].徐锡申,等译.北京:科学出版社,1991.26一64. [15]Wu F.Linguistic cellular automata simulation approach for sustainable land development in a fast growing region [J].Computers,Environment and Urban Systems,1996,20(6):367-387. [16]沈小峰,胡岗,姜璐.耗散结构论[M].上海:上海人民出版社,1987. [17]长沙市统计局编.长沙统计年鉴[2],2001. [18]张文修,梁怡.遗传算法的数学基础[M们.西安:西安交通大学出版社,2000. [19]云庆夏,等.遗传算法和遗传规划:一种搜索寻优技术[M].北京:治金工业出版社,1997. (上接第58页) 第二,用不同的分布表示市场因素的波动,例如“学生”分布(即t分布,“学生”是英国统计学家W.S.G0s- st的笔名)或帕累托稳定分布①.第三,对于极端情形,如金融危机、政治动荡或自然灾害等,MCMC方法 赖以成立的假设和计算的参数会发生巨大变化,而导致MCMC方法估计的结果出现极大误差.为了测量 极端情形下的网上支付系统风险,我们可引入压力试验方法②. 另外,MCMC实证分析的关键在于模拟出市场因子服从何种分布,本文假设市场因子的变动服从联 合正态分布.而实践中,通过正态性检验得出的市场因子往往并不完全服从正态分布,此时需要采取其它 办法拟合市场因子所服从的分布, 参考文献: [1]吴世农,陈斌.风险度量方法与金融资产配置模型的理论和实证研究门.经济研究,1999,(9):30一38. [2]王春峰,等.基于MCM的金融市场风险VaR的估计,管理科学学报,2000,3(2):54一61. [3]Phillippe Jorion.The New Benchmark for Controlling Derivatives Risk[M].The McGraw-Hill Companies,Inc, 1997. [4]Pietro Penza,Vipul K.Bansal,Measuring Market Risk with Value at Risk[M].John Wiley &Sons Ltd,2001. [5]Saunders.A,Credit Risk Measurement:New Approaches to Value at Risk and Other Paradigms[M],John Wiley & Sons Ltd,1999. [6]赵家敏,刘湘云.网络银行信用风险定量分析[门.南方经济,2001,(7):45一47. [7]何光辉.电子货币系统的风险及其控制[].金融研究,2000,(11):34一38. [8]魏先华,李雪松.支付和清算系统的风险分析[J门.金融研究,2001,(12):63一72. [9]戴国强,等,VaR方法对我国金融风险管理的借鉴及应用[J门.金融研究,2000,(7):45一51. ①帕累托(Pareto)发现对97%的人口而言,其收入分布是对数正态的,然而其余的3%人口的收入分布的尾部比预期的 厚得多.这说明存在中心极限定理不适用的分布,这就是帕累托稳定分布 ②压力试跨荷熨称为情景(scenario)分析,它用于衡量一些原本稳定的关系(如相对价格、相关性、波动性等)的稳定性 被打破时对VaR造成的冲击
!"# 熊孟英$%&’()(*在人口预测中的应用!+#$河北大学学报,自然科学版)(--")("’.*,"/0""$ !1# 祝精美$规划人口的动态灰色预测!+#$工科数学)(--2)(3’4*,./0.3$ !2# 张启敏$人口迁移的定量研究!+#$宁夏大学学报)(--")(1’(*,".0""$ !5# 6789:;8?@A7B$&C?7:CDECEF:9G?H>9I?MK7C@7GS;IC?7:;!+#$=EE:? UCIEFG9G’Q7O VC@8*)(--5)-3’(*,-(0-1$ !(/# N9>SN7>?>7@;CDECEF:9GIC?7:;!+#$+CF@>9: CD&9GK7I9G9:H;?=EE:;)(--2).((’.*,4-50"(($ !((# 顾朝林)蔡建明$中国大中城市流动人口迁移规律研究!+#$地理学报)(---)"4’3*,./40.(.$ !(.# 李如生$非平衡态热力学和耗散结构!&#$北京,清华大学出版社)(-51$".014$ !(3# 黄润荣)任光耀$耗散结构与协同学!&#$贵阳,贵州人民出版社)(-55$(-/0(-($ !(4# %Y尼科利斯)ZY普里戈京$非平衡系统的自组织!&#$徐锡申)等译$北京,科学出版社)(--($.1014$ !("# NFW$[<>SF9EE@C9JKDC@;F;G9<>9X:7:9>??7R7:CEI7>G<>9D9;GS@CO<>S@7S !+#$UCIEFG7@;)\>RI7>G9>?]@X9>LH;G7I;)(--1)./’1*,3120352$ !(1# 沈小峰)胡岗)姜璐$耗散结构论!&#$上海,上海人民出版社)(-52$ !(2# 长沙市统计局编$长沙统计年鉴!^#).//($ !(5# 张文修)梁怡$遗传算法的数学基础!&#$西安,西安交通大学出版社).///$ !(-# 云庆夏)等$遗传算法和遗传规划,一种搜索寻优技术!&#$北京,冶金工业出版社 ________________________________________________ )(--2$ ’上接第 "5页* 第二)用不同的分布表示市场因素的波动)例如‘学生a分布’即 b分布)‘学生a是英国统计学家 N$L$%C;T ;7G的笔名*或帕累托稳定分布cd第三)对于极端情形)如金融危机e政治动荡或自然灾害等)&U&U方法 赖以成立的假设和计算的参数会发生巨大变化)而导致 &U&U方法估计的结果出现极大误差d为了测量 极端情形下的网上支付系统风险)我们可引入压力试验方法fd 另外)&U&U实证分析的关键在于模拟出市场因子服从何种分布)本文假设市场因子的变动服从联 合正态分布d而实践中)通过正态性检验得出的市场因子往往并不完全服从正态分布)此时需要采取其它 办法拟合市场因子所服从的分布d 参考文献, !(# 吴世农)陈斌$风险度量方法与金融资产配置模型的理论和实证研究!+#$经济研究)(---)’-*,3/035$ !.# 王春峰)等$基于 &U&U的金融市场风险 g9h的估计$管理科学学报).///)3’.*,"401($ !3# 6K$MK7Q7O i7>JKI9@8DC@UC>G@C::<>Sj7@J) (--2$ !4# 6A9)g;9:)&79;F@<>S&9@87GhN;[G?).//($ !"# L9F>?7@;$=)U@7?G,Q7O=EE@C9JK7;GCg9:F79Gh?mGK7@69@9?N;[G?)(---$ !1# 赵家敏)刘湘云$网络银行信用风险定量分析!+#$南方经济).//()’2*,4"042$ !2# 何光辉$电子货币系统的风险及其控制!+#$金融研究).///)’((*,34035$ !5# 魏先华)李雪松$支付和清算系统的风险分析!+#$金融研究).//()’(.*,1302.$ !-# 戴国强)等$g9h方法对我国金融风险管理的借鉴及应用!+#$金融研究).///)’2*,4"0"($ (./ 系统工程理论与实践 .//3年 (/月 c f 压力试验有时也称为情景’;J7>9@<C*分析)它用于衡量一些原本稳定的关系’如相对价格e相关性e波动性等*的稳定性 被打破时对 g9h造成的冲击d 帕累托’69@7GC*发现对 -2n的人口而言)其收入分布是对数正态的)然而其余的 3n人口的收入分布的尾部比预期的 厚得多d这说明存在中心极限定理不适用的分布)这就是帕累托稳定分布d 万方数据