
第49卷第5期 林 业 科学 Vol.49,No.5 2013年5月 SCIENTIA SILVAE SINICAE May,2013 doi:10.11707/j.1001-7488.20130515 树木位置空间模式建模与预测* 金星姬李凤日'贾炜玮 张连军2 (1.:东北林业大学林学院哈尔滨150040:2.美国纽约州立大学环境科学和林业学院锯拉丘兹NY13210) 摘要:传统的林分生长与收获模型不能为林分和生态系统管理提供准确的空间信息。采用3种配对势函数的 Gibbs点过程模型对美国东北部50块云冷杉样地里树木的空间分布模式进行模拟。该Gibbs模型能够较好地模拟 这50块样地中的82%~84%,但其对完全随机分布和规则分布的样地模拟比对聚集分布的样地模拟效果要好。 使用常用的林分变量如林分密度、公顷断面积、林分平均胸径、平均树高、平均冠幅和冠长建立经验回归模型对 Gbbs模型的2个参数进行预测。结果表明这些回归模型对81%的样地可以得到满意的模拟效果,其中,100%的 完全随机分布样地、71%的规则分布样地和56%的聚集分布样地模拟效果较好。选择3块样地对树木的模拟空间 位置和实际观测位置的相似性进行对比和说明。 关键词:空间点模式;空间点过程:Gibbs模型;Ripley's K--function;马尔可夫链Monte Carlo(MCMC); Metropolis算法;Takacs-Fiksel方法 中图分类号:S711 文献标识码:A 文章编号:1001-7488(2013)05-0110-11 Modeling and Predicting Spatial Patterns of Trees Jin Xingji'Li Fengri'Jia Weiwei'Zhang Lianjun' (1.School of Forestry,Northeast Forestry University Harbin 150040; 2.College of Environmental Science and Forestry.State University of New York (SUNY-ESF)Syracuse,NY13210,USA) Abstract:Traditional forest growth and yield models have been criticized for their inability to provide precise spatial information for forest and ecosystem management.In this study the spatial patterns of trees within 50 spruce-fir plots in the Northeast,USA were modeled by a Gibbs point process model with three pair potential functions.In general,82%-84% of these 50 plots were modeled well by the Gibbs model.However,the complete spatial random CSR)and regular spatial patterns were modeled better than the clustered plots.Further,empirical regression models were developed to predict the two parameters of the Gibbs model using the available stand variables as predictors such as stand density,basal area, mean tree diameter,mean tree height,mean crown length,and mean crown width.The simulation results showed that 81%of the 50 plots were satisfactorily predicted by the empirical regression models.Among them,100%of the CSR plots,71%of the regular plots,and 56%of the clustered plots were predicted well by the empirical regression models. Three example plots were selected to illustrate the similarity between simulated tree locations and observed ones. Key words:spatial point pattern;spatial point process;Gibbs model;Ripley's K-function;Markov Chain Monte Carlo (MCMC);Metropolis algorithm;Takacs-Fiksel method chance success of different species or individuals over 1 Introduction time.The spatial distributions of trees strongly affect Spatial patterns of tree locations in a forest stand competition between neighboring trees,size variability reflect the complex historical and environmental mosaic and distribution,growth and mortality,and crown imposed by initial establishment patterns, structure Kuuluvainen et al.,1987;Kenkel,1988; microenvironment differences,climatic factors, Miller et al.,1989;Hara,1992;Moeur,1993; competing vegetation,management activities,and the Rouvinen et al.,1997;Dovciak et al.,2001 ) Received date:2012-08-06;Revised date:2012-10-12 Foundation project:Supported by the Scientifie Research Funds for Forestry Publie Welfare of China(201004026);Ministry of Education "Overseas Experts and Scholars"project. Corresponding author:Li Fengri. 万方数据
第49卷第5期 2 0 1 3年5月 林 业 科 学 SCIENTIA SILVAE SINICAE VoL 49.No.5 May,2 0 1 3 doi:10.11707/j.1001-7488.20130515 树木位置空间模式建模与预测 金星姬1 李凤日1 贾炜玮1 张连军2 (1.东北林业大学林学院哈尔滨150040;2.美国纽约州立大学环境科学和林业学院锡拉丘兹NYl3210) 摘 要: 传统的林分生长与收获模型不能为林分和生态系统管理提供准确的空间信息。采用3种配对势函数的 Gibbs点过程模型对美国东北部50块云冷杉样地里树木的空间分布模式进行模拟。该Gibbs模型能够较好地模拟 这50块样地中的82%一84%,但其对完全随机分布和规则分布的样地模拟比对聚集分布的样地模拟效果要好。 使用常用的林分变量如林分密度、公顷断面积、林分平均胸径、平均树高、平均冠幅和冠长建立经验回归模型对 Gibbs模型的2个参数进行预测。结果表明这些回归模型对81%的样地可以得到满意的模拟效果,其中,100%的 完全随机分布样地、7t%的规则分布样地和56%的聚集分布样地模拟效果较好。选择3块样地对树木的模拟空间 位置和实际观测位置的相似性进行对比和说明。 关键词: 空间点模式;空间点过程;Gibbs模型;Ripley’S K—function;马尔可夫链Monte Carlo(MCMC); Metropolis算法;Takacs.Fiksel方法 中图分类号:$711 文献标识码:A 文章编号:1001—7488(2013)05—0110—11 Modeling and Predicting Spatial Patterns of Trees Jin Xingji Li Fengri 1 Jia Weiwei Zhang Lianjun2 (1.School of Forestry,Northeast Forestry University Harbin 150040; 2.College ofEnvironmental Science and Forestry,State University ofNew York(SUNY-ESF)Syracuse,NYl3210,USA) Abstract:Traditional forest growth and yield models have been criticized for their inability to provide precise spatial information for forest and ecosystem management.In this study the spatial patterns of trees within 50 spruce·fir plots in the Northeast,USA were modeled by a Gibbs point process model with three pair potential functions.In general,82%一84% of these 50 plots were modeled well by the Gibbs model.However,the complete spatial random(CSR)and regular spatial patterns were modeled better than the clustered plots.Further,empirical regression models were developed to predict the two parameters of the Gibbs model using the available stand variables as predictors such as stand density,basal area, mean tree diameter,mean tree height,mean crown length,and mean crown width.The simulation resuhs showed that 8l%of the 50 plots were satisfactorily predicted by the empirical regression models.Among them.100%of the CSR plots,7 1%of the regular plots,and 56%of the clustered plots were predicted well by the empirical regression models. Three example plots were selected to illustrate the similarity between simulated tree locations and observed ones. Key words: spatial point pattern;spatial point process;Gibbs model;Ripley’S K—function;Markov Chain Monte Carlo (MCMC);Metropolis algorithm;Takacs—Fiksel method 1 Introduction Spatial patterns of tree locations in a forest stand reflect the complex historical and environmental mosaic imposed by initial establishment patterns, microenvironment differences, climatic factors, competing vegetation,management activities,and the chance success Of difierent species or individuals over time.The spatial distributions of trees strongly affect competition between neighboring trees,size variability and distribution,growth and mortality,and crown structure(Kuuluvainen et a1.,1987;Kenkel,1988; Miller et a1.,1989;Hara,1992;Moeur,1993; Rouvinen et a1.,1997;Dovciak et a1.,2001). Received date:2012一08—06;Revised date:2012—10—12, Foundation project:Supported by the Scientific Research Funds for Forestry Public Welfare of China(201004026);Ministry of Education“Overseas Expels and Scholars”project. $Corresponding author:Li Fen96. 万方数据

第5期 金星姬等:树木位置空间模式建模与预测 111 Furthermore,the spatial patterns at tree-scale have One such model is the Gibbs point process model large influences on system-level and community-level or pairwise interaction process model )which properties of ecosystem functions (Pacala et al.,1995; assumes the interaction between two events (e.g., Friedman et al.,2001).In general,positive spatial trees)depends on the relative location of them.It dependence among neighboring trees is mainly due to originates from statistical physics Wood,1968; the effects of the micro-site,whereas inter-tree Landau et al,1980)and has been intensively used in competition tends to create negative spatial dependence spatial statistics (Stoyan et al.,1987;Ogata et al, among neighboring trees Fox et al.,2001). 1981;1984;1985;Diggle et al.,1994).The Gibbs Spatial point pattern analysis is commonly used to point process model with pair potential functions is a study the distributions of the horizontal spacing among class of models for point patterns exhibiting interactions trees within a region of interest.The objective of between the events.These models have been applied spatial point pattern analysis is to measure how in forestry and ecological studies due to their great individual trees are located with respect to each other flexibility and realism in modeling different spatial by using quantitative characteristics and to describe the point patterns (Tomppo,1986;Penttinen et al.,1992; "laws"regulating the locations with mathematical Stoyan et al.,1998;Sarkka et al.,1998;Stoyan et al., models Diggle,1983;Tomppo,1986;Pretzsch, 2000). 1997).There are three fundamental spatial point Different methods have been developed to estimate patterns:complete spatial randomness (CSR ) the parameters of the pair potential functions.Diggle et regularity,and clustering.This classification is over- al.(1994)summarizes three general methods,namely simplified,but useful at an early stage of spatial approximations of maximum likelihood,maximum analysis.It is also helpful to formulate a model for the pseudo-likelihood,and Takacs-Fiksel method.These underlying spatial point process Diggle,1983).A methods can be routinely used in applications and there spatial point pattern is the realization of a spatial point are no restrictions on the parametric form of the pair process (Cressie,1993).Once the spatial point potential functions Tomppo,1986;Stoyan et al., patterns are recognized,it is desirable to fit appropriate 1987;Jensen et al.,1991). point process models to the spatial patterns in order to Spruce-fir stands in the Northeast,USA are understand the mechanisms generating the patterns and traditionally important resources for timber production. to perform analyses of goodness-of-fit for the models. Forest managers and researchers have developed a Detailed review on spatial point process models can be variety of tools for managing these stands.These tools found in the literature (Cressie,1993;Tomppo, include stocking charts and stand density management 1986;Stoyan et al.,2000). diagrams for the pure and mixed softwood stands in the The spatial point process generating CSR is called region (Solomon et al.,2002).However,very little a homogeneous Poisson process,such that the number spatial information is available for these stands to date. of events realized by this process 1)follow a Poisson The objectives of this research were 1)to explore the distribution with mean equal to AA,where A is the spatial structures of the spruce-fir softwood stands in density or intensity of events (e.g.,trees)and A is the Northeast,USA,2)to fit the Gibbs point process the area of the region A;and 2)are independent model with three pair potential functions to the spatial random samples from the uniform distribution on A patterns of trees within the stands,and 3)to develop (Cressie,1993;Diggle,1983).Intuitively,CSR empirical regression models for predicting the means that events are equally likely to occur anywhere parameters of the Gibbs point process model using within A and that events do not interact with each other available stand variables. (Cressie,1993).The homogeneous Poisson point 2 Data and methods process usually serves as a null model Stoyan et al., 2000).If the null model is rejected,more complicated 2.1 Data models are necessary to be tested (Tomppo,1986). Fifty (50)plots were collected from the even- 万方数据
第5期 金星姬等:树木位置空间模式建模与预测 111 Furthermore,the spatial patterns at tree-scale have large influences on system·level and community.1evel properties of ecosystem functions(Pacala et a1.,1 995; Friedman et a1.,200 1).In general,positive spatial dependence among neighboring trees is mainly due to the effects of the micro—site,whereas inter.tree competition tends to create negative spatial dependence among neighboring trees(Fox et a1.,2001). Spatial point pattern analysis is commonly used to study the distributions of the horizontal spacing among trees within a region of interest.The objective of spatial point pattern analysis is to measure how individual trees are located with respect to each other by using quantitative characteristics and to describe the “laws”regulating the locations with mathematical models(Diggle,1983;Tomppo,1986;Pretzsch, 1 997).There are three fundamental spatial point patterns: complete spatial randomness(CSR), regularity,and clustering.This classification is over. simplified,but useful at an early stage of spatial analysis.It is also helpful to formulate a model for the underlying spatial point process(Diggle,1983).A spatial point pattern is the realization of a spatial point process(Cressie,1 993).Once the spatial point patterns are recognized,it is desirable to fit appropriate point process models to the spatial patterns in order to understand the mechanisms generating the patterns and to perform analyses of goodness—of—fit for the models. Detailed review on spatial point process models can be found in the literature(Cressie,1 993;Tomppo, 1986;Stoyan et a1.,2000). The spatial point process generating CSR is called a homogeneous Poisson process,such that the number of events realized by this process 1)follow a Poisson distribution with mean equal to A A l,where A is the density or intensity of events(e.g.,trees)and A|is the area of the region A;and 2)are independent random samples from the uniform distribution on A (Cressie,1993;Diggle,1983).Intuitively,CSR means that events are equally likely to occur anywhere within A and that events do not interact with each other (Cressie,1 993).The homogeneous Poisson point process usually serves as a null model(Stoyan et a1., 2000).If the null model is models are necessary to be rejected,more complicated tested(Tomppo,1986). One such model is the Gibbs point process model (or pairwise interaction process model),which assumes the interaction between two events(e.g., trees)depends on the relative location of them.It originates from statistical physics(Wood,1 968; Landau et a1.,1 980)and has been intensively used in spatial statistics(Stoyan et a1.,1987;Ogata et a1., 1981;1984;1985;Diggle et a1.,1994).The Gibbs point process model with pair potential functions is a class of models for point patterns exhibiting interactions between the events.These models have been applied in forestry and ecological studies due to their great flexibility and realism in modeling different spatial point patterns(Tomppo,1 986;Penttinen et a1.,1 992; Stoyan et a1.,1998;Sarkka et a1.,1998;Stoyan et a1., 2000). Different methods have been developed to estimate the parameters of the pair potential functions.Diggle et a1.(1 994)summarizes three general methods,namely approximations of maximum likelihood, maximum pseudo—likelihood,and Takacs-Fiksel method.These methods can be routinely used in applications and there are no restrictions on the parametric form of the pair potential functions(Tomppo,1986;Stoyan et a1., 1987;Jensen et a1.,1991). Spruce-fir stands in the Northeast,USA are traditionally important resources for timber production. Forest managers and researchers have developed a variety of tools for managing these stands.These tools include stocking charts and stand density management diagrams for the pure and mixed softwood stands in the region(Solomon et a1.,2002).However,very little spatial information is available for these stands to date. The objectives of this research were 1)to explore the spatial structures of the spruce—fir softwood stands in the Northeast,USA,2)to fit the Gibbs point process model with three pair potential functions to the spatial patterns of trees within the stands,and 3)to develop empirical regression models for predicting the parameters of the Gibbs point process model using avai】ab】e stand variables. 2 Data and methods 2.1 Data Fifty(50)plots were collected from the even- 万方数据

112 林业科学 49卷 aged spruce-fir forests in northwestern Maine,USA, trees.The forest plot A is a sampling window within a located in the region between 69 W and 71 W in much larger forest region.Therefore,the events longitude,between 45 N and 46.5 N in latitude,and (trees)are the points of a partial realization of a between 750 m and I 200 m in elevation planar point process within A.For the patterns of N (Kleinschmidt et al.,1980).The plot size ranged from trees in a bounded region A,the pairwise interaction 0.002 5 to 0.02 hm2.The shapes of the plots were processes (i.e.,pair-potential processes)are suitable mostly square with a few rectangular.In each plot,the stochastic models.The joint density for these processes position of each tree over 1.37 m in height was mapped generally takes the form of Li et al,2007).In these plots balsam fir (Abies )=A”。 balsamea)and red spruce (Picea rubens)accounted e即{-A(Ix-xID}, for about 95%of total number of trees and 94%of (1) total volume.Other minor species included black where is the Euclidean distance between trees i cherry (Prunus serotina),eastern white pine (Pinus and j,B is a parameter determining the intensity of the strobus),white spruce Picea glauca),black spruce process,()is a pair potential function,and C is a Picea mariana),and other hardwoods.Tree diameter normalizing constant to make f(x)a density depending at breast height (DBH),total height,crown length on B and中(·). (top to the base of crown),and average crown width The homogeneous Gibbs point process is a special were recorded for each tree (Solomon et al,2002). case of pairwise interaction processes.It is The numbers of trees in each plot ranged from 12 to characterized by the potential functionΦ(·)and 109.Mean tree diameters were from 2.2 to 19.2 cm another parameter a =-log(B).Although the explicit and mean tree total heights were from 2.7 to 17.1 form of the distribution is hard to obtain,the following m (Tab.1). relationship holds for a homogeneous Gibbs point process Diggle et al.,1994) Tab.1 Summary statistics of the stand AE[Z(X)]= variables across the 50 plots Stand variables Mean Std.Min.Max. Number of trees per plot 34.4 17.7 12 109 Efz(X)exp[-a-((2) Stand density/(tree.m2) 0.61 0.54 0.18 2.52 where A is the density of events,Eo is the expectation Stand basal area/(m2.hm-2)50.2 14.3 10.0 79.6 Stand mean DBH/cm 11.53.9 2.2 19.2 with respect to the Palm distribution of the process,E Stand mean height/m 11.63.7 2.7 17.1 is the expectation,and Z(X)is any random function Stand mean crown length/m 4.41.5 1.6 8.4 of the process where X includes all events of the Stand mean crown width/m 1.I 0.3 0.5 1.9 process in the whole plane.For a strict definition of Using the methods of refined nearest neighbor Palm distribution,see Stoyan et al.(1987),Tomppo statistic,Ripley's K-function (Ripely,1976)analysis (1986)and Cressie (1993). and pair correlation function analysis,24 plots were However,when it is conditional on the number of classified as completely spatial random (CSR)point points N,Gibbs distribution can be expressed as pattern,17 plots as regular point pattern,and 9 plots as clustered point pattern out of the 50 plots (Li et al., )=2ep{-会Ax.-XD}.3) where Z is the normalizing constant in the form of 2007).The classification was used as the basis for modeling the spatial patterns in this study z=ep-合点X,-XD],d 2.2 Methods The pair potential function()can be interpreted as 2.2.1 Theoretical background of Gibbs model followings:(d)>0 indicates that the probability pairwise interaction process model)Suppose the density for inter-event distance d is lower than that spatial point pattern in a mapped forest plot A has N under Poisson process and,thus,there is repulsion at events (trees).Denote=X =(u:,v)EA:i=1, distance d;(d)<0 indicates that the probability 2,..,N as the set of coordinates (u:,v)of the density for inter-event distance d is higher than that 万方数据
112 林业科学 49卷 aged spruce—fir forests in northwestern Maine,USA, located in the region between 69。W and 7 1。W in longitude,between 45。N and 46.5。N in latitude,and between 750 m and l 200 m in elevation (Kleinschmidt et a1.,1980).The plot size ranged from 0.002 5 to 0.02 hm2.The shapes of the plots were mostly square with a few rectangular.In each plot,the position of each tree over 1.37 m in height was mapped (Li et a1.,2007).In these plots batsam fir(Abies balsamea)and red spruce(Picea rubens)accounted for about 95%of total number of trees and 94%of total volume.Other minor species included black cherry(Prunus serotina),eastern white pine(Pinus strobus),white spruce(Picea glauca),black spruce (Picea mariana),and other hardwoods.Tree diameter at breast height(DBH),total height,crown length (top to the base of crown),and average crown width were recorded for each tree(Solomon et a1.,2002). The numbers of trees in each plot ranged from 1 2 to 109.Mean tree diameters were from 2.2 to 19.2 am and mean tree total heights were from 2.7 to 17.1 m(Tab.1). Tab.1 Summary statistics of the stand variables across the 50 plots Stand variables Mcan Std. Min. Max. Number oftrees per plot 34.4 17.7 12 109 Stand density/(tree·m一2)0.61 0.54 0.18 2.52 Stand basal area/(m2.hm一2) 50.2 14.3 10.0 79.6 Stand mean DBH/cm 11.5 3.9 2.2 19.2 Stand mean height/m 11.6 3.7 2.7 17.1 Stand mean crown length/m 4.4 1.5 1.6 8.4 Stand mean crown width/m 1.1 0.3 0.5 1.9 Using the methods of refined nearest neighbor statistic.Ripley’s K-function(Ripely,1 976)analysis and pair correlation function analysis,24 plots were classified as completely spatial random(CSR)point pattern,1 7 plots as regular point pattern,and 9 plots as clustered point pattern out of the 50 plots(Li et a1., 2007).The classification was used as the basis for modeling the spatial patterns in this study. 2.2 Methods 2.2.1 Theoretical background of Gibbs model (pairwise interaction process model) Suppose the spatial point pattern in a mapped forest plot A has N events(trees).Denote X={X。=(Mi,口。)∈A:i=1, 2,…,Ⅳ}as the set of coordinates(Mi,u。)of the trees.The forest plot A is a sampling window within a much larger forest region.Therefore,the events (trees)are the points of a partial realization of a planar point process within A.For the patterns of N trees in a bounded region A,the pairwise interaction processes(i.e.,pair—potential processes)are suitable stochastic models.The joint density for these processes generally takes the form of 州=篇唧{-乏。三驯l xi.Xj∽), (1) where㈩I is the Euclidean distance between trees i and j,8 is a parameter determining the intensity of the process,多(·)is a pair potential function,and C is a normalizing constant to make八z)a density depending on口and中(·). The homogeneous Gibbs point process is a special case of pairwise interaction processes. It is characterized by the potential function中(‘)and another parameter a=一log(f1).Although the explicit form of the distribution is hard to obtain,the following relationship holds for a homogeneous Gibbs point process(Diggle et a1.,1994) AE“Z(X)]= E{z(x)exp[一a一萎中(…I)])’(2) where A is the density of events,Eo is the expectation with respect to the Palm distribution of the process,E is the expectation,and Z(X)is any random function of the process where X includes a11 events of the process in the whole plane.For a strict definition of Palm distribution,see Stoyan et a1.(1987),Tomppo (1986)and Cressie(1993). However.when it is conditional on the number of points N,Gibbs distribution can be expressed as 以并)=Z-1exp{-∑∑西(1IXi一划)},(3) where Z is the normalizing constant in the form of z=exp[一乏。三中(IIX;一圳h,…,d‰· The pair potential function多(·)can be interpreted as followings:中(d)>0 indicates that the probability density for inter.event distance d is lower than that under Poisson process and,thus,there is repulsion at distance d;中(d)<0 indicates that the probability density for inter.event distance d is higher than that 万方数据

第5期 金星姬等:树木位置空间模式建模与预测 113 under Poisson process.Thus,there is attraction at length of parameter vector (a,) distance d;and (d)=0 indicates a Poisson process. There is no agreed rule for choosing the function 2.2.2 Pair potential functions The pair potential Z.However,if the test function Z:is chosen to be function ()can be parameterized in various forms. equal to N()Diggle et al,1994),which is the In this study,three parametric models were adopted. number of events i with:-X‖≤rk,where X,(U= The first one is called Very-Soft-Core (VSC)pair 1,2,...,L)is the jth randomly chosen testing point, potential function (Ogata et al,1984): the left side of equation (2)can be estimated as Φ(r)=-lgi1-exp[-(r/6)2]},(4) i.(a,0)=A2K(r), (8) where 6 is a scaling parameter.For the VSC pair where K(r)is Ripley's K-function (Ripley,1976; potential function,the range of interaction is infinite 1977).The right side of equation (2)can be for all distance r.The second one is called Diggle's estimated as pair potential function that has the following form Diggle et al.,1994): 元(e,9)=它N() ()=-lg(1-[1-(/8)2]2),fr≤; N (9) 0, if rx6. exp-&-∑Φ(Ix-X,I)] =1 (5) The choices of L,m and r.are arbitrary although where the scaling parameter 6 defines the range of different values can be tried and compared.For the interaction.The third one is called Ogata and data used in this study,we set the constants as Tanemura's pair potential function (Ogata et al., follows:1)L=2N because we wanted to ensure that 1985): there were enough random points surrounding a tree, (r)=-lg(1+[r(r/8)-1] and 2)m =30 and r=0.Ik which made the exp[-(r/8)2]),r≥0,8>0, (6) maximum value 3.0 m)because we wanted there to be where the scaling parameter 6 defines the range of enough but not too many trees within the plot which are interaction.Notice that equation(4)is a special case of considered interacting with each other. equation(6)when the parameter 7=0.For equation The optimization of equation(7)was performed (5),(r)=0 when r=6 representing the Poisson using a direct search polytope algorithm one available process.For equation(6),(r)=0 when T =5/r, subroutine is the UMPOL in the IMSL Math Library of which represents the Poisson process. Fortran PowerStation 4.0 C 1994-95 Microsoft 2.2.3 Parameter estimation method One of the Corporation).Details of the polytope algorithm can be methods for estimating the parameters of the pair found in the literature (Nelder et al.,1965;Gill et al., 1981). potential functions is the Takacs-Fiksel method (Diggle et al.,1994).It is based on the fundamental 2.2.4 Edge corrections Typically,the study relationship in equation (2).Suppose is the regions would be the sampled plots within a forest stand.Each of these plots covers only a part of the parameter vector of a pair potential function0=8 for entire spatial pattern.Interactions can only be the potential functions(4)and(5)or =(7,)for the potential function(6)).If a series of test functions Z observed among the trees within a plot,while interactions are unobserved between the trees within (k=1,2,...,m)are chosen to estimate both sides of the plot and the trees outside the plots.It is known as equation(2)(denoting the left side as L(a,0)and the edge or boundary effect.If no correction is taken the right side as R(a,0)),the sum of squared for the boundary effect in the point pattern analysis, differences of both sides can be minimized to estimate the estimation of the interactions is biased.In the the model parameters (a,0)as, previous study Li et al.,2007),the toroidal edge S(a,6)=∑[i(a,0)-(a,0)]2,(7) correction method was proven to be simple and satisfactory compared with other available edge where m is some arbitrary number no less than the correction methods such as buffer zone,border 万方数据
第5期 金星姬等:树木位置空间模式建模与预测 113 —————————————————————————————————————————————————一一 under Poisson process.Thus,there is attraction at distance d;and中(d)=0 indicates a Potsson Drocess. 2.2.2 Pair potential functions The pair potential function中(·)can be parameterized in various forms. In this study,three parametric models were adopted. The first one is called Very.Soft.Core(VSC)pair potential function(Ogata et a1.,1 984): 中(r)=一lg{1一exp[一(r俗)2] where 6 is a scaling parameter.For the VSC Dair potential function,the range of interaction is innnite for all distance,.The second one is called Diggle’s pair potential function that has the foliowing form (Diggle et a1.,1994): 西(r):r 19(1~[1一(r/a)2]2),if r≤6; 【 o, if r>占. (5) where the scaling parameter 6 defines the range of interaction.The third one is called Ogata and Tanemura’8 pair potential function(Ogata et a1.. 1985): 西(r)=一lg(1+[丁(r/8)一1] exp[一(r/8)2]),r≥0,6>0, (6) where the scaling parameter 6 defines the range of interaction.Notice that equation(4)is a special case of equation(6)when the parameter 7.=0.For equation (5),中(r)=-0 when r=6 representing the Poisson process.For equation(6),西(r)-=0 when丁=6/r. which represents the Poisson process. 2.2.3 Parameter estimation method 0ne of the methods for estimating the parameters of the pair potential functions is the Takacs—Fiksel method(Diggle et a1.,1994). It is based on the fundamental relationship in equation(2).Suppose 0 is the parameter vector of a pair potential function[0=6 for the potential functions(4)and(5)or 0=(下,∞for the potential function(6)].If a series of test functions Z‘ (k=1,2,…,m)are chosen to estimate both sides of equation(2)(denoting the left side as L^(ot,0)and the right side as R^(ot,0)),the sum of squared differences of both sides can be minimized to estimate the model parameters(ot,0)as, 5(a,口)=∑哦(a,日)一壶。(a,∽]2,(7) t:1 where m is some arbitrary number no less than the length of parameter vector(a,0). There is no agreed rule for choosing the function ZI.However, if the test function Z‘is chosen to be equal to%(r女)(Diggle et a1.,1994),which is the number of events i with lIX。一x,II≤k,where x,(,= 1,2,…,L)is thejth randomly chosen testing point. the left side of equation(2)can be estimated as L^(o/,0) where K(r^)is Ripley’s 1977).The right side estimated as =A 2K(0), (8) K—function(Ripley,1 976; of equation(2)can be 交如∽=÷萎L_㈠) exp[一a一萎4(IIx。一训】. (9) The choices of£,m and^are arbitrary although different values can be tried and cornpared.For the data used in this study, we set the constants as follows:1)L=2N because we wanted to ensure that there were enough random points surrounding a tree, and 2)m=30 and o=0.1七(which made the maximum value 3.0 m)because we wanted there to be enough but not too many trees within the plot which are considered interacting with each other. The optimization of equation(7)was performed using a direct search polytope algorithm(one available subroutine is the UMPOL in the IMSL Math Library of Fortran PowerStation 4.0 c|C 1 994—95 Microsoft Corporation).Details of the polytope algorithm can be found in the literature(Nelder et a1.,1 965;Gill et of.. 1981). 2.2.4 Edge corrections Typically,the study regions would be the sampled plots within a forest stand.Each of these plots covers only a part of the entire spatial pattern. Interactions can only be observed among the trees within a plot, while interactions are unobserved between the trees within the plot and the trees outside the plots.It is known as the edge or boundary effect.If no correction is taken for the boundary effect in the point pattern analysis. the estimation of the interactions is biased.In the previous study(Li et a1.,2007),the toroidal edge correction method was proven to be simple and satisfactory compared with other available edge correction methods such as bufier zone. borde。 万方数据

114 林业科学 49卷 method,and weighting method Moeur,1993;Haase, models are fitted based upon detailed mapped data and 1995)since the plots in this study were all square or individual tree measurements of diameter and height. rectangular in shape,and were small in size.Thus, In forestry practice,however,it is difficult and the toroidal edge correction method was used in expensive to obtain these kinds of data.Therefore,it is estimating the parameters of the pair potential functions desirable to develop empirical regression models for 中(). predicting the parameters of the Gibbs models using the 2.2.5 Simulation of Gibbs models-Metropolis available stand variables as predictors.Since most of algorithm Given a pair potential function,the Gibbs the forest variables are highly correlated (e.g.,tree point process models can be used to simulate an DBH and height),the multicolinearity problem may equilibrium point pattern.One of the methods was exist among the predictor variables.In this study,the originally developed by Metropolis et al.(1953),and principal component PC)regression was used to modified by Wood (1968).The algorithm is a Markov overcome the multicolinearity problem (Neter et al., Chain Monte Carlo (MCMC)procedure and has been 1990). applied in many studies (Ogata et al.,1981;1984; 3 Results 1985;Diggle et al.,1994),which is briefly described in Appendix. 3.1 Parameter estimation and goodness-of-fit 2.2.6 Goodness-of-fit test To evaluate the tests for three pair potential functions goodness-of-fit for each model,500 realizations of the The parameters of three pair potential functions, Gibbs models corresponding to each fitted pair potential namely VSC equation(4)],Diggle's equation(5)] function were performed.Ripley's K-function and Ogata and Tanemura's equation (6)],were converted to L as i(d)=v(d)/i-d)was estimated by the Takacs-Fiksel method (Diggle et al., calculated for each realization,where d is the given 1994)for the 50 plots.The results of the goodness-of- distance of magnitude between paired events.The fit test indicated:overall,82%-84%of the 50 plots 95%confident envelopes were constructed and were satisfactorily fitted by the Gibbs models with three plotted.Then,the observed L statistics from the data pair potential functions (Tab.2).The Diggle's pair were compared with the simulated 95%confident potential function performed best for the CSR plots. envelopes.If model fitting to the data was good,the The VSC pair potential function performed best for the observed L statistics should lie within the simulated regular plots.The Ogata and Tanemura's pair potential 95%confident envelopes Ripley,1976). function was slightly better than the other two for fitting 2.2.7 Predictions of the parameters of Gibbs the clustered plots (Tab.2). point process models The Gibbs point process Tab.2 Summary of goodness-of-fit tests of spatial point patterns for the 50 plots Unaccepted Spatial point pattern Number of plots VSC Diggle Ogata Tanemura Plot Plot Plot % CSR 24 3 12.5 0 0.0 4.2 Cluster 9 4 44.4 4 44.4 3 33.3 Regular 17 2 11.8 4 23.5 J 29.4 Total 50 9 18.0 8 16.0 9 18.0 3.2 Developing prediction models for the functions used in this study. parameters of Gibbs model The Pearson correlation coefficients between the The Gibbs model with the Diggle's pair potential dependent variables (i.e.,the estimated parameters 8 function equation(5)was selected as the spatial and a of the Gibbs model with the Diggle's pair point process model since it had slightly better potential function)and the available stand variables goodness-of-fit results among the three pair potential were computed and tested for Ho:p=0.The 万方数据
114 林业科学 49卷 method,and weighting method(Moeur,1993;Haase, 1 995)since the plots in this study were all square or rectangular in shape,and were small in size.Thus, the toroidal edge correction method was used in estimating the parameters of the pair potential functions 西(·). 2.2.5 Simulation of Gibbs models-Metropolis algorithm Given a pair potential function,the Gibbs point process models can be used to simulate an equilibrium point pattern.One of the methods was originally developed by Metropolis et a1.(1953),and modified by Wood(1 968).The algorithm is a Markov Chain Monte Carlo(MC MC)procedure and has been applied in many studies(Ogata et a1.,1981;1984; 1 985;Diggle et at.,1 994),which is briefly described in Appendix. 2.2.6 Goodness-of-fit test To evaluate the goodness—of-fit for each model,500 realizations of the Gibbs models corresponding to each fitted pair potential function were performed. Ripley’s K—function (convened to L as£(d)= r■————~ √K(d)/竹一d) was calculated for each realization,where d is the given distance of magnitude between paired events.The 95% confident envelopes were constructed and plotted.Then,the observed L statistics from the data were compared with the simulated 95%confident envelopes.If model fitting to the data was good,the observed L statistics should lie within the simulated 95%confident envelopes(Ripley,1 976). 2.2.7 Predictions of the parameters of Gibbs point process models The Gibbs point process models are fitted based upon detailed mapped data and individual tree measurements of diameter and height. In forestry practice,however,it is difficult and expensive to obtain these kinds of data.Therefore,it is desirable to develop empirical regression models for predicting the parameters of the Gibbs models using the available stand variables as predictors.Since most of the forest variables are highly correlated(e.g.,tree DBH and height),the muhicolinearity problem may exist among the predictor variables.In this study,the principal component(PC)regression was used to overcome the muhicolinearity problem(Neter et a1., 1990) 3 Results 3·1 Parameter estimation and goodness-of·fit tests for three pair potential functions The parameters of three pair potential functions, namely VSC[equation(4)],Diggle’s[equation(5)] and Ogata and Tanemura’s[equation(6)],were estimated by the Takacs·Fiksel method(Diggle et a1., 1994)for the 50 plots.The results of the goodness—of— fit test indicated:overall,82%一84%of the 50 plots were satisfactorily fitted by the Gibbs models with three pair potential functions(Tab.2).The Diggle’s pair potential function performed best for the CSR plots. The VSC pair potential function performed best for the regular plots.The Ogata and Tanemura’s pair potential function was slightly better than the other two for fitting the clustered plots(Tab.2). Tab.2 Summary of goodness-of—fit tests of spatial point patterns for the 50 plots Unaeeepted Spatial point pattern Number of plots VSC Diggle Ogata&Tanemura Plot %Plot %Plot % CSR 24 3 12.5 0 0.0 1 4.2 Cluster 9 4 44.4 4 44.4 3 33,3 Regular 17 2 11.8 4 23.5 5 29.4 Total 50 9 18.0 8 16.0 9 18.0 3.2 Developing prediction models for the parameters of Gibhs model The Gibbs model with the Diggle’s pair potential function[equation(5):was selected as the spatial point process model since it had slightly better goodness。。of—fit results among the three pair potential functions used in this study. The Pearson correlation coefficients between the dependent variables(i.e..the estimated parameters 6 and a of the Gibbs model with the Diggte’s pair potential function)and the available stand variables were computed and tested for Ho:P。=0.The 万方数据
第5期 金星姬等:树木位置空间模式建模与预测 115 correlation coefficients and the P-values of the tests shown).Thus,principal component regression was were shown in Tab.3.It was evident that both 6 and a applied to overcome the multicolinearity problem had significant correlations P-value <0.05)with (Neter et al.,1990).The regression coefficients based most of the stand variables. on the principal component regressions for predicting The ordinary least squares regression was first the two parameters (6 and of the Gibbs model on used to regress the two parameters (5 and on the the available stand variables were list in Tab.4.The available stand variables such as stand density,basal model R2 was 0.57 for the 6 model and 0.65 for the a area,mean diameter,mean tree height,mean crown model.Therefore,the Gibbs model parameters can be length,and mean crown width.It was found that predicted using the two empirical regression models multicolinearity existed among the predictor variables, when the values of the six stand variables are available especially among the mean tree diameter,mean tree either observed or estimated). height,and mean of crown length results not Tab.3 Correlations among the two estimated parameters of Gibbs point process model with the Diggle's pair potential function and the available stand variables Density/ Basal area/ Mean a Mean Mean crown Mean crown (tree.m-2) (m-2,hm-2) DBH/cm height/m length/m width/m 8 0.3388 -0.6409 0.3341 0.7194 0.7059 0.5047 0.2730 (P-value) (-)(0.0161) (0.0000) (0.0177) (0.0000) (0.0000) (0.0002) (0.0605) a 1 -0.7882 0,3586 0.7252 0.7301 0.5767 0.3386 (P-value) (-) 0.0000 0.0106 0.0000 0.0000 0.0000 0.0186 Density 1 -0.5415 -0.8759 -0.8918 -0.6512 -0.4732 (P-value) (-) 0.0000 0.0000 0.0000 0.0000 0.0007 Basal area 0.6987 0.6601 0.5985 0.1973 (P-value) (-) 0.0000 0.0000 0.0000 0.1789 Mean DBH 1 0.9686 0.7341 0.4071 (P-value) (-) 0.0000 0.0000 0.0041 Mean height 1 0.6814 0.3794 (P-value) (-) 0.0000 0.0078 Mean crown length 0.2365 (P-value) (-) 0.1055 Mean crown width 1 (P-value) (-) Tab.4 Coefficients of empirical regression models for predicting the two parameters (and )of Gibbs point process model with the Diggle's pair potential function using the available stand variables Dependent Density/Basal area/ Mean Mean Mean crown Mean crown Fit statistics variable Intercept (tree.m-2)(m2.hm-2)DBH/cm height/m length/m width/m P-value Diggle's S -4.21570.2862 -0.03820.18860.22060.0679 -0.11740.572 <0.0001 Diggle's a 0.9208-0.7862 -0.0094 0.0150 0.0279 0.0640 -0.08620.645 <0.0001 3.3 Prediction of the spatial point patterns of the model prediction.First,the observed K-function was 50 plots computed using the tree data for each of the 50 plots. Based on the predicted parameters (6 and &of Then,for each plot,a 95%confident envelope was the Gibbs model with the Diggle's pair potential constructed from 200 simulations using the predicted function,the spatial point patterns of a plot can be parameters of the Gibbs model obtained from the two simulated using the Metropolis algorithm.To evaluate empirical regression models in Tab.4.If the observed the performance of the two empirical regression models K-functions are within the 95%confidence envelope, for predicting the two parameters and a,the Ripley's the prediction of the Gibbs model parameters can be K-function was used to compare the observed data and claimed satisfactory.The results indicated that 100% 万方数据
第5期 金星姬等:树木位置空间模式建模与预测 115 一。————————————————————————————————————————————————————————————一 correlation coefficients and the P.values of the tests were shown in Tab.3.It was evident that both 6 and& had significant correlations(P—value<0.05)with most of the stand variables The ordinary least squares regression was first used to regress the two parameters(6 and&)on the available stand variables such as stand density,basal area.mean diameter,mean tree height,mean crown length.and mean crown width.It was found that multicolinearity existed among the predictor variables, especially among the mean tree diameter,mean tree height,and mean of crown length(results not shown).Thus,principal component regression was applied to overcome the multicolinea“ty problem (Neter et a1.,1990).The regression coefficients based on the principal component regressions for predicting the two parameters(6 and&)of the Gibbs model on the available stand variables were list in Tab.4.The model R2 was 0.57 for the 6 model and 0.65 for the& model.Therefore,the Gibbs model parameters can be predicted using the two empirical regression models when the values of the six stand variables are available (either observed or estimated). Tab.3 Correlations among the two estimated parameters of Gibbs point process model with —————————————————————_————————————————————————_————●_————-—————————————一—— the些墨gle’!旦兰!!旦!!!竺型坐竺!!!竺!苎坚!!!!二兰!!苎!!!!!兰坚二兰!!兰!!竺—— ^ 6 Density/ (tree·m。) Basal area/ (m~·hm一2) Mcan DBH/cm Mcan height/m Mcan crown length/m Mcan crown width/m (P.£lue) (一) (o.016 1) (o.000 o) (o.017 7) (o.000 o) (o.000 o) (o·000 2) (o·060 5) (P—value) Density (P-value) Basal area (P-value) Mean DBH (P-value) Mean height 1 —0.788 2 0.358 6 0.725 2 0.730 1 0.576 7 0-338 6 0.000 0 1 (一) 0.010 6 0.000 0 0.000 0 0.000 0 0.018 6 —0.54l 5 0.000 0 1 (一) 一0.875 9 0.000 O 0.698 7 0.000 0 l (一) 一O.89l 8 0.000 0 0.660 1 0.000 0 0.968 6 0 000 0 l (P.,a1。e) (一) Mean crown length (P—value) 一0.65l 2 0.000 0 0.598 5 0.000 0 0.734 1 0.000 0 0.681 4 0.000 0 —0.473 2 0.000 7 O.197 3 0.178 9 0.407 l 0 004 l 0.379 4 0.007 8 0,236 5 0.105 5 Mean crown width 1 Gibbs point process model with the Diggle’s pair potential fuⅡctlll竺!!竺璺竺!兰二竺!!!!!!!!竺坚:兰!!兰!!!! —’j;::::j::i—。■一‘。。。Density/Basal area/Mean Mean Mean erown Mean cr。wn——————:——!!!』!!竺!竺!!—_ v:riable In忙”。p‘ (tree.m一2) (m2.hm一2)DBH/cm height/m length/m width/m 墨= !:!!!竺 ——jij:ii:ji————:jjjiiii———:l:j;ii—;————酉夏。:;!::’.2。2:0。;:..0。6。7。:-一0。..。1。17。::..5。。7; 监!!:!垒!:!!!!二!::!!!二!:!!!!业!!—型旦L—竺型)_二竺兰2-_竺L—型兰 :。O..。0。0。0: 3.3 Prediction of the spatial point patterns of the 50 plots Based on the predicted parameters(6 and 61)of the Gibbs model with the Diggle’s pair potential function,the spatial point patterns of a plot can be simulated using the Metropolis algorithm.To evaluate the Derfbrmance of the two empirical regression models for predicting the two parameters 6 and&。the Ripley’s K—function was used to compare the observed data and model prediction.First,the observed K—function was computed using the tree data for each of the 50 plots. Then.for each plot,a 95%confident envelope was construeted from 200 simulations using the predicted Darameters of the Gibbs model obtained from the two empirical regression models in Tab.4.If the observed K—functions are within the 95%confidence envelope, the prediction of the Gibbs model parameters can be claimed satisfactory.The results indicated that 100% 万方数据
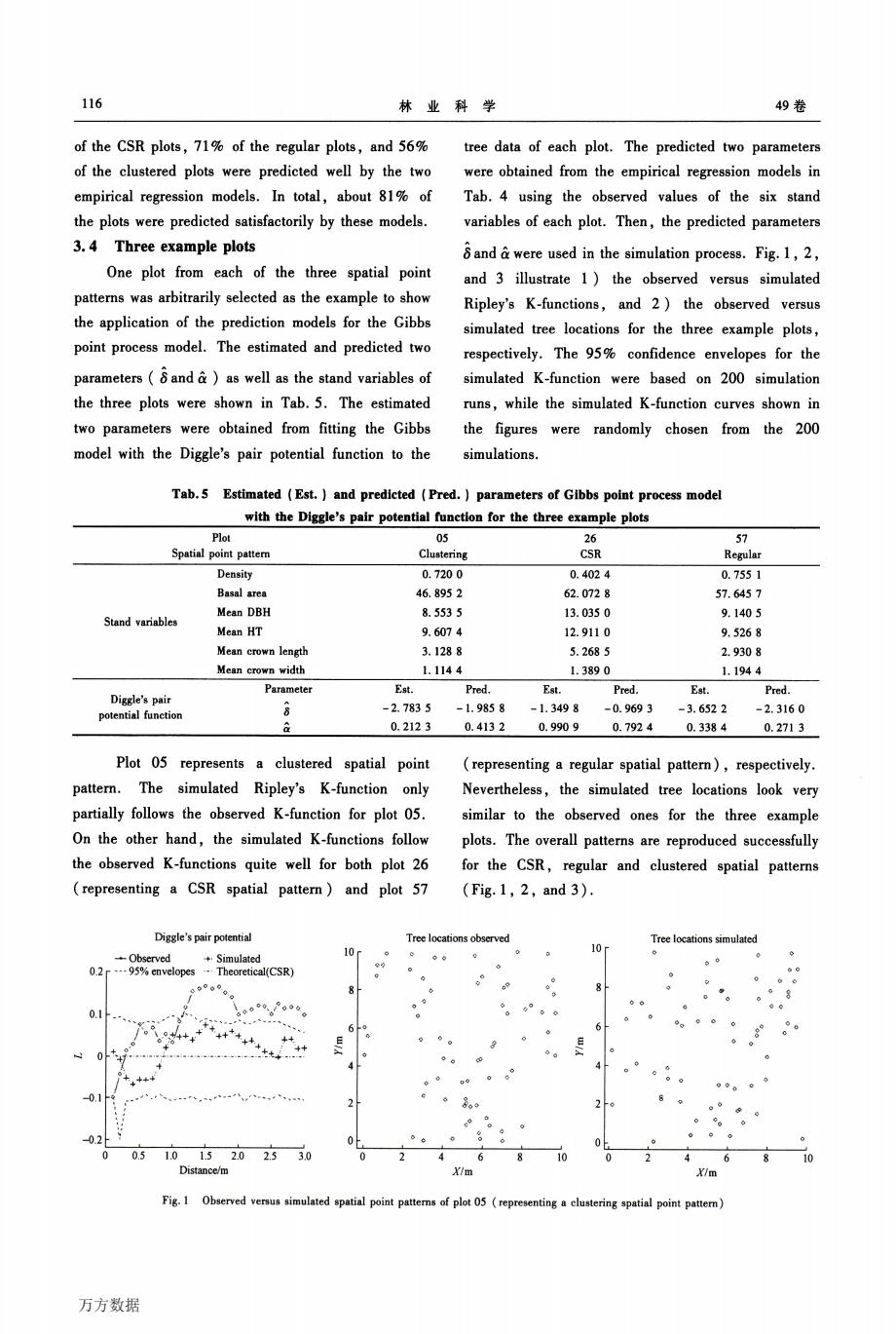
116 林业科学 49卷 of the CSR plots,71%of the regular plots,and 56% tree data of each plot.The predicted two parameters of the clustered plots were predicted well by the two were obtained from the empirical regression models in empirical regression models.In total,about 81%of Tab.4 using the observed values of the six stand the plots were predicted satisfactorily by these models. variables of each plot.Then,the predicted parameters 3.4 Three example plots and were used in the simulation process.Fig.1,2, One plot from each of the three spatial point and 3 illustrate 1)the observed versus simulated patterns was arbitrarily selected as the example to show Ripley's K-functions,and 2)the observed versus the application of the prediction models for the Gibbs simulated tree locations for the three example plots, point process model.The estimated and predicted two respectively.The 95%confidence envelopes for the parameters (6and as well as the stand variables of simulated K-function were based on 200 simulation the three plots were shown in Tab.5.The estimated runs,while the simulated K-function curves shown in two parameters were obtained from fitting the Gibbs the figures were randomly chosen from the 200 model with the Diggle's pair potential function to the simulations. Tab.5 Estimated (Est.and predicted (Pred.parameters of Gibbs point process model with the Diggle's pair potential function for the three example plots Plot 05 26 57 Spatial point pattern Clustering CSR Regular Density 0.7200 0.4024 0.7551 Basal area 46.8952 62.0728 57.6457 Mean DBH 8.5535 13.0350 9.1405 Stand variables Mean HT 9.6074 12.9110 9.5268 Mean crown length 3.1288 5.2685 2.9308 Mean crown width 1.1144 1.3890 1.1944 Parameter Est. Pred. Est. Pred. Est. Pred. Diggle's pair potential function 6 -2.7835 -1.9858 -1.3498 -0.9693 -3.6522 -2.3160 a 0.2123 0.4132 0.9909 0.7924 0.3384 0.2713 Plot 05 represents a clustered spatial point (representing a regular spatial pattern),respectively. pattern. The simulated Ripley's K-function only Nevertheless,the simulated tree locations look very partially follows the observed K-function for plot 05. similar to the observed ones for the three example On the other hand,the simulated K-functions follow plots.The overall patterns are reproduced successfully the observed K-functions quite well for both plot 26 for the CSR,regular and clustered spatial patterns (representing a CSR spatial pattern)and plot 57 (Fig.1,2,and3). Diggle's pair potential Tree locations observed Iree locations simulated 10r 10 -Observed +Simulated 02r -95%envelopes-Theoretical(CSR) 、 0.1 307 -0.1 0 05 1.0152.02.53.0 10 Distance/m /m X/m Fig.1 Observed versus simulated spatial point patters of plot 05(representing a clustering spatial point pattern) 万方数据
116 林业科学 49卷 of the CSR plots,71%of the regular plots,and 56% of the clustered plots were predicted well by the two empirical regression models.In total。about 8 1%of the plots were predicted satisfactorily by these models. 3.4 Three example plots One plot from each of the three spatial point patterns was arbitrarily selected as the example to show the application of the prediction models for the Gibbs point process model.The estimated and predicted two parameters(6 and&)as well as the stand variables of the three plots were shown in Tab.5.The estimated two parameters were obtained from fitting the Gibbs model with the Diggle’S pair potential function to the tree data of each plot.The predicted two parameters were obtained from the empirical regression models in Tab.4 using the observed values of the six stand variables of each plot.Then,the predicted parameters 6 and&were used in the simulation process.Fig.1,2, and 3 illustrate 1)the observed versus simulated Ripley’S K-functions,and 2)the observed versus simulated tree locations for the three example plots, respectively.The 95%confidence envelopes for the simulated K.function were based on 200 simulation Tuns,while the simulated K—function curves shown in the figures were randomly chosen from the 200 simUlations. Tab.5 Estimated(Est.)and predicted(Pred.)parameters of Gibbs point process model with the Dlggle’S pair potential function for the three example plots Plot Spatial point pattern 05 Clustering 26 CSR 57 Regular Diggle’8 pair potential function P”ameter 占 Est.Pred. Est.Pred. Est.Pred. 一2.783 5 —1.985 8 一1.349 8 —0.969 3 —3.652 2 —2.316 0 0.212 3 0.413 2 0.990 9 0.792 4 0.338 4 0.271 3 Plot 05 represents a clustered spatial point pattern.The simulated Ripley’S K—function only partially follows the observed K—function for plot 05. On the other hand,the simulated K-functions follow the observed K-functions quite well for both plot 26 (representing a CSR spatial pattern)and plot 57 Diggle’S pair polential —-·一Observed ·Simulated (representing a regular spatial pattern),respectively. Nevertheless,the simulated tree locations look very similar to the observed ones for the three example plots.The overall patterns are reproduced successfully for the CSR,regular and clustered spatial patterns (Fig.1,2,and 3). Tree locations observed Tree locatiOOS simulated x|m x{m Fig·1 Observed versus simulated spatial point patterns of plot 05(representing a clustering spatial point pattern) 万方数据
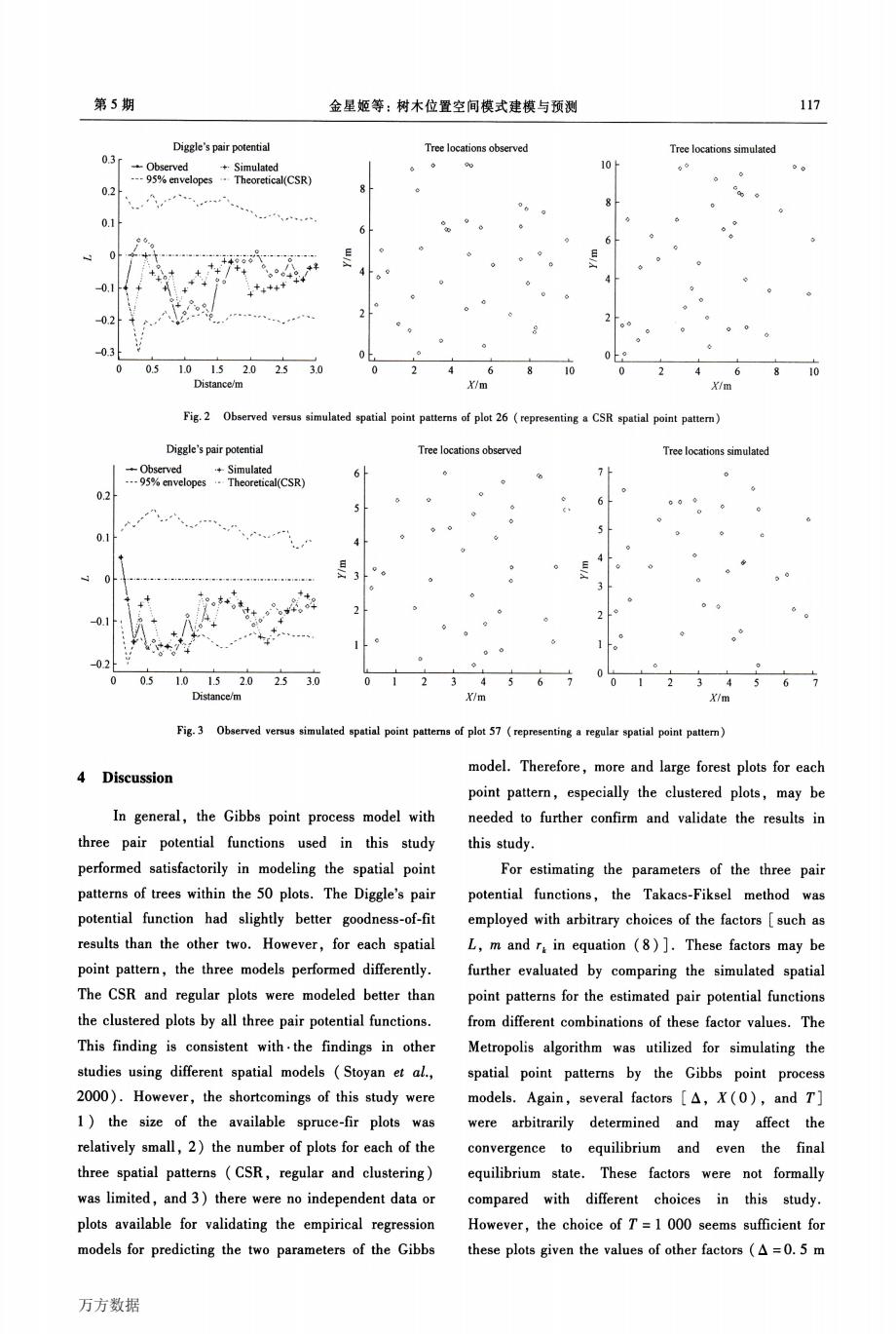
第5期 金星姬等:树木位置空间模式建模与预测 117 Diggle's pair potential Tree locations observed Tree locations simulated 0.3r Observed +Simulated 10 6 03 ---95%envelopesTheoretical(CSR) 0.1 t. + 4 01 0.2 0.3 0 0 05 1.01.52.02.53.0 10 Distance/m X/m X/m Fig.2 Observed versus simulated spatial point patterns of plot 26(representing a CSR spatial point pattern) Diggle's pair potential Tree locations observed Tree locations simulated -Observed +Simulated -95%envelopes Theoretical(CSR) 0.2 0.1 02 05 1.0152.0 2.5 10 Distance/m Y/m Fig.3 Observed versus simulated spatial point patterns of plot 57(representing a regular spatial point patter) 4 Discussion model.Therefore,more and large forest plots for each point pattern,especially the clustered plots,may be In general,the Gibbs point process model with needed to further confirm and validate the results in three pair potential functions used in this study this study. performed satisfactorily in modeling the spatial point For estimating the parameters of the three pair patterns of trees within the 50 plots.The Diggle's pair potential functions,the Takacs-Fiksel method was potential function had slightly better goodness-of-fit employed with arbitrary choices of the factors [such as results than the other two.However,for each spatial L,m and r in equation (8)].These factors may be point pattern,the three models performed differently. further evaluated by comparing the simulated spatial The CSR and regular plots were modeled better than point patterns for the estimated pair potential functions the clustered plots by all three pair potential functions. from different combinations of these factor values.The This finding is consistent with.the findings in other Metropolis algorithm was utilized for simulating the studies using different spatial models (Stoyan et al., spatial point patterns by the Gibbs point process 2000).However,the shortcomings of this study were models.Again,several factors [A,X(0),and T] 1)the size of the available spruce-fir plots was were arbitrarily determined and may affect the relatively small,2)the number of plots for each of the convergence to equilibrium and even the final three spatial patterns (CSR,regular and clustering) equilibrium state.These factors were not formally was limited,and 3)there were no independent data or compared with different choices in this study. plots available for validating the empirical regression However,the choice of T=1 000 seems sufficient for models for predicting the two parameters of the Gibbs these plots given the values of other factors (A=0.5 m 万方数据
第5期 金星姬等:树木位置空间模式建模与预测 117 Diggle’s pair potential Distance/m E k Tree locations observed Tree locations simulated x|m x|m Fig.2 Observed versus simulated spatial point patterns of plot 26(representing a CSR spatial point pattern) Diggle’s pair potential 4 Discussion Distance/m 6 4 吕 ≥3 TI℃e locations observed x}m 7 6 5 E 4 王 3 2 1 0 Tree Iocations simulated x|m Fig.3 Observed versus simulated 8patial point patterns。f plot 57(representing a regular spatial point pattern) In general,the Gibbs point process model with three pair potential functions used in this study performed satisfactorily in modeling the spatial point patterns of trees within the 50 plots.The Diggle’s pair potential function had slightly better goodness-of-fit resuIts than the other two.However,for each spatial point pattern,the three models performed differently. The CSR and regular plots were modeled better than the clustered plots by all three pair potential functions. This finding is consistent with·the findings in other studies using different spatial models(Stoyan et a1., 2000).However,the shortcomings of this study were 1)the size of the available spruce—fir plots was relatively small,2)the number of plots for each of the three spatial patterns(CSR,regular and clustering) was limited,and 3)there were no independent data or plots available for validating the empirical regression models for predicting the two parameters of the Gibbs model.Therefore,more and large forest plots for each point pattern,especially the clustered plots,may be needed to further confirm and validate the results in this study. For estimating the parameters of the three pair potential functions,the Takacs—Fiksel method was employed with arbitrary choices of the factors[such as L,m and“in equation(8)].These factors may be further evaluated by comparing the simulated spatial point patterns for the estimated pair potential functions fjom different combinations of these factor values.The Metropolis algorithm was utilized for simulating the spatial point patterns by the Gibbs point process models.Again,several factors[A,X(0),and T] Were arbitrarily determined and may affect the convergence to equilibrium and even the final eauilibrium state.These factors were not formally compared with different choices in this study. However.the choice of T=1 000 seems sufficient for these plots given the values of other factors(A=0.5 m 万方数据

118 林业科学 49卷 and the initial state as a random pattern of a Poisson Gibbs models.Three example plots were selected to process). illustrate that the patterns of the simulated tree In this study,the Gibbs point process models locations were very similar to the observed ones. were applied to all spatial distributions of trees.It has The spatial structures of a forest stand include its the advantage of being flexible to fit various spatial horizontal and vertical structures.The horizontal point patterns.This is extremely useful if the spatial structure can be characterized by the relative locations pattern of the data is not certain.Because of this of trees over space and the distributions of tree general property,its performance varies among diameters.The vertical structure can be represented by different spatial patterns.For example,in this study,the height distribution and diameter-height it did not fit the clustered pattern as well as it fitted the relationships.The spatial models developed in this CSR or regular patterns.In addition,the empirical study can provide useful information on the horizontal regression models for predicting the two parameters of structures of forest stands,whereas the information on the Gibbs models worked best for the CSR pattern,the vertical structures of forest stands can be obtained followed by the regular pattern,and worst for the from a bivariate distribution model of tree diameter and clustered pattern.This was consistent with the height.The combination of these models will offer goodness-of-fit of the Gibbs point process models for much more information on the three dimensional profile the spatial patterns.Therefore,it would be interesting and dynamics of forest stands to forest managers and to compare the model fitting and prediction,especially researchers. for the clustered plots,using the Gibbs point process 参考文献 model against other spatial models such as Cox process model or Poisson cluster process model Matern, Cressie N A C.1993.Statistics for spatial data:revised edition.John 1971;Cressie,1993)in a future study. Wiley Sons,New York,900. Diggle P J.1983.Statistical analysis of spatial point patterns.Academic 5 Conclusion Press,New York,148. Diggle P J.Fiksel T,Grabarnik P,et al.1994.On parameter estimation The Gibbs point process model with three pair for pairwise interaction point process.Interational Statistical potential functions were used to model the spatial point Review.62(1):99-117. patterns of trees in the 50 spruce-fir plots in the Dovciak M,Frelich L E,Reich P B.2001.Discordance in spatial Northeast,USA.The results indicated that the three patterns of white pine (Pinus strobus)size-classes in a patchy near- pair potential functions fitted 82%-84%of the plots boreal forest.Joumal of Ecology,89(2):280-291. Fox J C,Ades P K,Bi H.2001.Stochastic strueture and individual-tree well.The Diggle's pair potential function performed growth models.Forest Ecology and Management,154(1/2):261- slightly better than the other two pair potential 276. functions (i.e.,VSC and Ogata and Tanemura's).In Friedman S K,Reich P B,Frelich L E.2001.Multiple scale general,the plots of CSR and regular patterns were composition and spatial distribution patterns of the north-eastem Minnesota presettlement forest.Journal of Ecology,89 (4 ) modeled better than the clustered plots by all three pair 538-554. potential functions.Further,empirical regression Gill P E,Murray W,Wright M.1981.Practical optimization.Academic models were developed to predict the two parameters Press,New York. (and)of the Gibbs point process model with the Haase P.1995.Spatial pattern analysis in ecology based on Ripley's K- function:Introduction and methods of edge correction.Journal of Diggle's pair potential function using the available Vegetation Science,6(4):575-582. stand variables as predictors (i.e.,stand density, Hara T.1992.Effects of the mode of competition on stationary size basal area,mean diameter,mean tree height,mean distribution in plant populations.Annals of Botany,69(6): crown length,and mean crown width).The simulation 509-513. results showed that 81%of the 50 plots were predicted Jensen J L,Moller J.1991.Pseudolikelihood for exponential family models of spatial point processes.Annals of Applied Probability,1 satisfactorily by these models,in which 100%of the (3):445-461. CSR plots,71%of the regular plots,and 56%of the Kenkel N C.1988.Pattern of self-thinning in jack pine:testing the clustered plots were predicted satisfactorily by the random mortality hypothesis.Ecology,69(4):1017-1024. 万方数据
118 林业科学 49卷 and the initial state as a random pattern o{a Poisson process). In this study,the Gibbs point process models were applied to all spatial distributions of trees.It has the advantage of being flexible to fit various spatial point patterns.This is extremely useful if the spatial pattern of the data is not certain.Because of this general property, its performance varies among different spatial patterns.For example,in this study, it did not fit the clustered pattern as well as it fitted the CSR or regular patterns.In addition,the empirical regression models for predicting the two parameters of the Gibbs models worked best for the CSR pattern, followed by the regular pattern,and worst for the clustered pattern.This was consistent with the goodness—of-fit of the Gibbs point process models for the spatial patterns.Therefore,it would be interesting to compare the model fitting and prediction,especially for the clustered plots,using the Gibbs point process model against other spatial models such as Cox process model or Poisson cluster process model(Matern, 1971;Cressie,1993)in a future study. 5 Conclusion The Gibbs point process model with three pair potential functions were used to model the spatial point patterns of trees in the 50 spruce—fir plots in the Northeast,USA.The resuhs indicated that the three pair potential functions fitted 82%一84%of the plots well.The Diggle’s pair potential function performed slightly better than the other two pair potential functions(i.e.,VSC and Ogata and Tanemura’s).In general,the plots of CSR and regular patterns were modeled better than the clustered plots by all three pair potential functions. Further, empirical regression models were developed to predict the two parameters (6 and&)of the Gibbs point process model with the Diggle’s pair potential function using the available stand variables as predictors(i.e.,stand density, basal area,mean diameter,mean tree height,mean crown length,and mean crown width).The simulation results showed that 8 1%of the 50 plots were predicted satisfactorily by these models,in which 100%of the CSR plots,71%of the regular plots,and 56%of the clustered plots were predicted satisfactorily by the Gibbs models.Three example plots were selected to illustrate that the patterns of the simulated tree locations were very similar to the observed ones. The spatial structures of a forest stand include its horizontal and vertical structures.The horizontal structure can be characterized by the relative locations of trees over space and the distributions of tree diameters.The vertical structure can be represented by the height distribution and diameter—height relationships.The spatial models developed in this study can provide useful information on the horizontal structures of forest stands,whereas the information on the vertical structures of forest stands can be obtained from a bivariate distribution model of tree diameter and height.The combination of these models will offer much more information oil the three dimensional profile and dynamics of forest stands to forest managers and researchers 参 考 文 献 Crcssie N A C.1993.Statistics for Wiley&Sons.New York.900. Diggle P J.1983.Statistical analysis Press,New York,148. spatial data:revised edition.John of spatial point patterns.Academic Diggle P J,Fiksel T,Grabarnik P,et a1.1 994 On parameter estimation for pairwise interaction point process.International Statistical Review,62(1):99—117. Dovciak M,Frelich L E,Reich P B.2001.Discordance in spatial patterns of white pine(Pinus strobus)size—classes in a patchy near— boreal forest.Journal of Ecology,89(2):280—291. Fox J C,Ades P K,Bi H.2001.Stochastic structure and individual—tree growth models.Forest Ecology and Management,154(1/2):26 1— 276. Friedman S K,Reich P B,Frelich L E.2001.Multiple scale composition and spatial distribution patterns of the noah-eastern Minnesota presettlement forest.Journal of Ecology,89(4): 538—554. Gill P E,Murray W.Wright M.1981.Practical optimization.Academic Press,New York. Haase P.1995 Spatial pattern analysis in ecology based on Ripley’s K· function:Introduction and methods of edge correction.Journal of Vegetation Science,6(4):575—582. Hara T.1992.Effects of the mode of competition on stationary size distribution in plant populations.Annals of Botany,69(6): 509—513. Jensen J L,Moiler J.1991.Pseudolikelihood for exponential family models of spatial point processes.Annals of Applied Probability,1 (3):445—461. Kenkel N C.1988.Pattern of random mortality hypothesis self-thinning in jack pine:testing the Ecology,69(4):1017—1024. 万方数据

第5期 金星姬等:树木位置空间模式建模与预测 119 Kleinschmidt S,Baskerville G L.1980.Foliage weight distribution in method.Biometrics,41(2):421-433 the upper crown of balsam fir.USDA Forest Service Research Paper Pacala S W,Deutschman D H.1995.Details that matter:the spatial NE455,8. distribution of individual trees maintains forest ecosystem function. Kuuluvainen T,Pukkala T.1987.Effect of crown shape and tree 01K05,74(3):357-365 distribution on the spatial distribution of shade.Agricultural and Penttinen A.Stoyan D,Henttonen H M.1992.Marked point processes Forest Meteorology,40(3):215-231. in forest statistics.Forest Science,38(4):806-824. Landau L D,Lifshitz E M.1980.Statistical Physics:Part I.3rd ed. Pretzsch H.1997.Analysis and modeling of spatial stand structure: Revised and enlarged by Lifshitz E M and Pitaevskii L P.Translated Methodological considerations based on mixed beech-larch stands in from Russian by Sykes J B,Kearsley M J.Butterworth-Heinemann, Lower Saxony.Forest Ecology and Management,97 (3 ) Boston. 237-253. Li F,Zhang L.2007.Comparison of point patter analysis methods for Ripley B D.1976.The second-order analysis of stationary point classifying spatial distributions of spruce-fir stands in the Northeast, processes.Journal of Applied Probability,13(2):255-266. U5A.Forestry,80(3):337-349. Ripley B D.1977.Modeling spatial pattems(with discussions).Joural Matern B.1971.Doubly stochastic Poisson processes in the plane//Patil of Royal Statistical Society Series B.39(2):172-192. G P,Pielou E C,Waters W E.Statistical ecology I.Pennsylvania Rouvinen S,Kuuluvainen T.1997.Structure and asymmetry of tree State University Press,College Town,PA,195-213. crowns in relation to local competition in a natural mature Scots pine Metropolis N,Rosenbluth A W,Teller M N,et al.1953.Equation of forest.Canadian Journal of Forest Research,27(6):890-902. state calculations by fast computing machines.Journal of Chemical Sarkka A,Tomppo E.1998.Modeling interaction between trees by Physics,21(6):1087-1092. means of field observations.Forest Ecology and Management,108 Miller T E,Weiner J.1989.Local density variation may mimic effeets of (1/2):57-62. asymmetric competition on plant size variability.Ecology,70(4): Solomon D S,Zhang L.2002.Maximum size-density relationships for 1188-1191. mixed softwoods in the northeastern USA.Forest Ecology and Moeur M.1993.Characterizing spatial patterns of trees using stem- Management,155(1/3):163-170. mapped data.Forest Science,39(4):756-775. Stoyan D,Kendall W S,Mecke J.1987.Stochastic geometry and its Nelder J A,Mead R.1965.A simplex algorithm for function applications.John Wiley Sons,New York. minimization.Computer Journal,7(4):308-313. Stoyan D,Penttinen A.2000.Recent applications of point process Neter J,Kutner M H,Nachtsheim C J,et al.1990.Applied linear methods in forestry statistics.Statistical Science,15(1):61-78. regression models.3 ed.IRWIN,720. Stoyan D,Stoyan H.1998.Non-homogeneous Gibbs process models for Ogata Y.Tanemura M.1981.Estimation of interaction potentials of forestrya case study.Biometrical Joural,40(5):521-531. spatial point patterns through the maximum likelihood procedure. Tomppo E.1986.Models and methods for analysing spatial patterns of Annals of the Institute of Statistical Mathematics Series B,33(2): trees.Seloste:Malleja ja menetelmiae puiden tilajaerjestyksen 315-338 analysoimiseksi.Communicationes Instituti Forestalis Fenniae,138: Ogata Y.Tanemura M.1984.Likelihood analysis of spatial point 65 patterns.Journal of Royal Statistical Society Series B,46(3): Wood WW.1968.Monte Carlo studies of simple liquid models 496-518. Temperly H N,Rowlinson J S,Rushbrooke G S.Physics of Simple Ogata Y,Tanemura M.1985.Estimation of interaction potentials of Liquids.Amsterdam,North-Holland,115-230. marked spatial point patterns through the maximum likelihood Appendix:Simulation procedure of Gibbs models-Metropolis algorithm Suppose there are N trees on a plot A,assuming to have periodic boundaries (i.e.,square or rectangular). These trees interact with each other according to a pair potential function,()Assume the state of the N-tree system is X(t)=X (t),i=1,2,..,N at stage t,where x (t)is the ith tree's location on A.The total potential energy at the stage t is U.(x()=-∑∑Φ(Ix(),-X(),) IsiU.(X(1))and if exp[U (X(t))- 万方数据
第5期 金星姬等:树木位置空间模式建模与预测 119 Kleinschmidt S.Baskerville C L the upper crown of balsam nr NE455.8. 1980. Foliage weight distribution in USDA Forest Service Research Paper Kuuluvainen T, Pukkala T. 1 987. Efkct of crown sha口e and tree dist曲ution on the spatial distributjon of shade. A gricultural and Forest Meteorology,40(3):215—231. Landau L D,Lifshitz E M.1980.Statistical Physic8:Part I.3 rd ed. Revised and enla。ged by Lifshitz E M and Pitaevskii L P.Translated fbm Russian by Sykes J B,Kearsley M J.Bulterworth-Heinemann, Boston. “F,Zha“g L 2007. Comparison of point patte H1 analysis methods for cIassifyi“g 5patial distributions of spnlce-nr stands in the Northeast, uSA.Forestry,80(3):337—349. Matern B. 1971. Doubly stochastic Poisso“processes in th8 plane∥Patil G P,Pielou E C,Waters W E.Statistjcal ecology I.Pennsylvania State University Press,College Town,PA,195—213. Metropolis N,Rosenbluth A W,TeUer M N,甜of.1953.Equa“on of state calculations by fast computi“g machines. Journal of Chemical Physics,21(6):1087—1092. Miller T E,Weiner J.1 989.Local density variation may mimic efkcts of asymmetric competition o”plant size variability. Ecology,70(4): 1188—1191. Moeur M. 1993. Characterizi“g 8patial pattems of trees using stem— m8pped data.Forest Science,39(4):756—775 Nelder J A, Mead R. 1965. A simplex algorichm for function minimization.Computer Journal,7(4):308—313. Neter J,Kutner M H,Nachtsheim C J,甜oZ 1990. Applied linear regression models.3”ed.IRWIN,720. Ogata Y, Tanemura M. 1 98 1. Estimation of interactio” potentials of spatial point patterns thm“gh the maximum 1ikelihood procedure. Annals of the Institute of Statistical Mathematics Se ries B,33(2): 315—338 09ata Y, Tanemura M. 1984. Likelih00d 8naIysis of spatial point pattems.Joumal of Royal Statistical Socie‘y Series B,46(3): 496—518. 09ata Y, Tanemura M. 1985. Estimation of interactio“potentials of marked 8patial point pattems through the maximum 1ikelihood method.Biometrics,4l(2):421—433. Pacala S W,Deutschman D H. 1995. Details that matte。:the spatial distribution of individual trees maintains forest ecosvstem function. OIK0s,74(3):357—365. Penttinen A,Stoyan D,Henttonen H M. 1992 Marked point processes in forest statistics.Forest Science,38(4):806—824. Pretzsch H. 1997. Analysis and modeling of spatial stand stmcture: Methodolo西cal considerations based on mixed beech.1arch stands in Lower Saxony. Forest Ecology and Man39ement, 97 (3): 237—253. Ripley B D. 1976. The second-order analysis of stationary point processes.Journal of Applied Pmbabjlity,13(2):255—266. Ripley B D. 1977. Modeli“g spatial patterns(with discussions).Journal of Royal statistical Society Series B,39(2):172一192. Rouvinen S, Kuuluvainen T. 1997. Structure and asvmmetry of tree crowns in relation to 10cal com”tition in a natural mature Scot8 pine forest. canadian Journal of Forest Research,27(6):890一902. S萏rkk臣A, Tomppo E. 1998. Modeling interaction between trees by means of 6eld obserVati仰s. Forest Ecology and Man89ement, 108 (1/2):57—62 Solomon D S,Zha“g I.. 2002. Maximum size-density relationships for mixed softwoods in the northeastern USA. Foresl Ecology and Management,155(1/3):163—170 Stoyan D,Kendall W S,Mecke J. 1 987. Stochastic geometry and it8 applications.John Wiley&Sons,New York Stoyan D, Penttinen A. 2000. Recent 8pplications of point process methods in forestry statlstics.Statistical Science,15(1):61—78. Stoyan D,Stoyan H. 1998.Non-homogeneous Gibb8 process models for forestry-a case study.Bjomet“cal Joumal,40(5):521—531. Tomppo E. 1986. Models and methods for analysing 8patial pattems of trees. Seloste: Malleja ja menetelmia。 puiden tilajaerjes‘yksen analysoimiseksi. Communicatlones Instituti Forestalis Fenniae,l 38: 65. wood w w.1968.Monte carlo studies of si“ple liquid models∥ Temperly H N,Rowlinson J S,Rushbrooke G S.Physics of Simple Liquids.Amsterdam,North—H011and,1 15—230. Appendix:Simulation procedure of Gibbs models-Metropolis algorithm Suppose there areⅣtrees on a plot A,assuming to haVe periodic boundaries(i.e., square or rectangular). These trees interact with each other according to a pair potential fhnction,中(·). Assume the state of the N-tree system is x(£)={x。(£),i=1,2,…,Ⅳ}at stage f,where菇。(£)is the ith tree’s location on A.The total potential energy at the stage£is u。(x(f))=一∑∑西(||x(£)。一x(£),11). 1≤}(J≤“ Then,a trial state x’(£)={xi(£),i=1,2,…,Ⅳ}is chosen such that a randomly selected tree xj(t)is uniformly distributed within X,(£)±△. It defines a smaU square centered at x,(£)with side length△on』4,while all other trees keep their locations on A the same as at the state f. The total potential energy fbr the trial state is u。(xm))=一∑∑西(∽(f)。一xm)川). I≤‘u。(x(£))and if f≤exp[u。(x(£))一 万方数据