
第21卷第2期 系统工程学报 Vol.21 No.2 2006年4月 JOURNAL OF SYSTEMS ENGINEERING Apr.2006 双指数跳跃扩散模型的McMC估计 胡素华,张世英,张彤 (天津大学管理学院,天津300072) 摘要:使用贝叶斯方法估计了双指数跳跃扩散模型,该方法是使用E方法对连续过程进行离散化,用离散 过程的似然函数做为模型参数的近似后验似然函数.证明了MMC方法是分析双指数跳跃扩散模型的有效工 具,由MMC方法抽样所得的后验分布可以用来进行统计推断,模拟试验表明双指数跳跃扩散模型能够体现 黄产收益的许多经验特狂,尖峰厚尾特征和期权定价中的“波动微笑”, 关键词:双指数跳跃扩散模型;马尔可夫链蒙特卡罗方法;贝叶斯估计 中图分类号: 文献标识码:A文章编号:1000-5781(2006)02-0113-06 Using McMC method to estimate double exponential jump diffusion model HU Su-hua,ZHANG Shi-ying,ZHANG Tong (School of Management,Tianjin University,Tianjin 300072,China) Abstract:In this paper we propose a Bayesian method to estimate the double exponential jump diffusion model(DEJD).The approach is based on the Markov chain Monte Carlo(McMC)method with the likeli- hood of the discredited process as the approximate posterior likelihood.We demonstrate that the MeMC method provides a useful tool in analyzing DEJD diffusion.In particular,quantities of posterior distribu- tions obtained from the McMC outputs can be used for statistical inference.The McMC method is based on Euler scheme.Our simulation shows that the DEJD diffusion exhibits many stylized characters about asset retums such as thick tails,and smiles effect. Key words:double exponential jump diffusion model;Markov chain Monte Carlo method;Bayes estimation 0引言 描述收益分布的尖峰和非对称特征的文献有 Bamdorff等3]和Eberlein等4的广义抛物线模型, 布朗运动和正态分布在期权定价和资产收益 Madan等S)及Andersen等6的时变布朗运动.但 中广泛使用,Black等1及Merton2]成功地用基于 是这些模型的一个共同问题就是很难获得期权定 布朗运动和正态分布建立期权定价模型,但是其 价的解析解.同时也有众多模型来解释波动微笑, 还存在下面两个问题,首先是资产收益经验分布 主要有Hull等]的随机波动模型,Cox等8的 的尖峰和非对称特征;其次是期权定价中的波动 CEV模型,Robert9]的常强度正态跳跃扩散模型 微笑特征.现在的很多研究就是通过解释B$模型 等,但是这些模型没有很好地体现尖峰和非对称 的这两个缺陷来修正Black-Scholes公式. 的特征,特别是尖峰特征. ①收稿日期:2005-04-04:修订日期:2005-10-28. 基金项目:国家自然科学基金资助项目(70301006:70471050) 万方数据
第2l卷第2期 2006年4月 系统工程学报 JOURNAL OF SYSTEMS ENGINEERING V01.21 No.2 Apr.2006 双指数跳跃扩散模型的McMC估计① 胡素华,张世英,张 彤 (天津大学管理学院,天津300072) 摘要:使用贝叶斯方法估计了双指数跳跃扩散模型,该方法是使用Euler方法对连续过程进行离散化,用离散 过程的似然函数做为模型参数的近似后验似然函数.证明了McMC方法是分析双指数跳跃扩散模型的有效工 具,由McMC方法抽样所得的后验分布--J-vX用来进行统计推断.模拟试验表明双指数跳跃扩散模型能够体现 资产收益的许多经验特征,尖峰厚尾特征和期权定价中的“波动微笑”. 关键词:双指数跳跃扩散模型;马尔可夫链蒙特卡罗方法;贝叶斯估计 中图分类号: 文献标识码:A 文章编号:1000—5781(2006)02—0113—06 Using McMC method to estimate double exponential jump diffusion model HU Su-hua,ZHANG Sift·ying,ZHANG Tong (School of Management,Tianjin University,Ti肌jin 300072,China) Abstract:In this paper we propose a Bayesian method to estimate the double exponential jump diffusion model(DEJDl).The approach iS based on the Markov chain Monte Carlo(McMC)method with the likeli— hood of the discredited process as the approximate posterior likelihood.We demonstrate that the McMC method provides a useful tooI in analyzing DEJD diffusion.In particular.quantities of posterior distribu— tions obtained from the McMC outputs can be used for statistical inferenee.The McMC method iS based Oil Euler scheme.Our simulation shows that山e DEJD diffusion exhibits many stylized characters about asset returns such as tllick tails.,and smiles effect. Key words-.double exponential jump diffusion model;narkov chain Monte Carlo method;Bayes estimation 0引 言 布朗运动和正态分布在期权定价和资产收益 中广泛使用,Black等¨J及Menon恻2成功地用基于 布朗运动和正态分布建立期权定价模型,但是其 还存在下面两个问题,首先是资产收益经验分布 的尖峰和非对称特征;其次是期权定价中的波动 微笑特征.现在的很多研究就是通过解释Bs模型 的这两个缺陷来修正Black—Scholes公式. ①收稿日期:2005—04—04;修订日期:21105—10—28. 基金项目:国家自然科学基金资助项目(70301006;70471050) 描述收益分布的尖峰和非对称特征的文献有 Barndorff等[3]和Ebedein等【4J的广义抛物线模型, Madan等[5]及Andersen等[6]的时变布朗运动.但 是这些模型的一个共同问题就是很难获得期权定 价的解析解.同时也有众多模型来解释波动微笑, 主要有Hull等【7J的随机波动模型,Cox等L8 J的 CEV模型,R0bert【91的常强度正态跳跃扩散模型 等,但是这些模型没有很好地体现尖峰和非对称 的特征,特别是尖峰特征. 万方数据

114 系统工程学报 第21卷 为了解决这两个问题,Kou9)提出了一种简 P(x-k=)=P(x-k=-)=0.5(3) 单的跳跃扩散模型,该模型由2部分组成:1)几何 其中:5是双指数变量,的均值为7,方差为72. 布朗运动的连续部分,2)跳跃规模的对数是双指 该模型认为跳跃是市场对外部信息的反映,好 数分布,跳跃时间是泊松过程的事件发生时间的 消息和坏消息以泊松过程到达,资产价格的跳跃也 跳跃部分,正是由于模型的简单性,可以轻易地解 以泊松过程发生.另外为了简单,同时为了取得各种 释模型参数,同时可以得到期权定价的封闭解, 期权定价问题的解析解,假定漂移μ和σ波动为常 关于连续时间的估计,可以采用半参数、 数,但是这个假设可以推广到随机波动模型. GMM,ML等方法,Pedersen将参数的估计值作 1.2双指数跳跃扩散模型的特征 为缺失值,提出了从参数的条件后验分布中抽取 为了更好地体现双指数跳跃扩散模型的特 参数值的McMC方法,虽然这种方法不能适应隐 征,对随机微分方程(1)采用行Euler方法离散, 含因子,但是为McMC技术的发展提供了新的进 可得 展.Eraker2,Elerian等3],Tse等4,胡素华等 =(-2A+(+a)- △S(t) 分别用McMC方法对连续时间模型进行了参数估 N+△) 计.其中Eraker给出了模型中含有隐含变量时,参 》++(+a)- 数估计值和隐含变量估计的McMC方法,所以 =N)+1 McMC方法非常适合Kou的双指数跳跃扩散模 W(t)2≈u△t+Z△t+∑X: i=()+1 型.跳跃因子这个隐含变量的加人,使得模型参数 (4) 的维数大量增加,即有多少个资产价格的样本观 其中:Z:是标准正态随机变量,泊松过程N(t)有 测值,就有多少个跳跃变量,从而就导致了模型参 一次跳跃的概率是λ△t,超过一次的概率是 数估计的困难.本文使用基于贝叶斯方法的 o(△t),因此,如果△t足够小,可以忽略多次跳 McMC方法,从隐含变量的后验分布中抽取样本, 跃,并有 把这个样本作为跳跃因子的观测数据,进而估计 「X:,P=A△t 模型的参数值 X:≈ (5) i=N)+1 l0,P=1-λ△t 总之,当△t很小时,收益可以近似为 1双指数跳跃扩散模型及其特征 △S(t) S(t)≈rAt+GZ,V④t+B,K (6) 1.1双指数跳跃扩散模型 其中:B,为贝努利随机变量,且P(B=1)= Kou为了能够同时体现资产收益分布的尖峰 A△t,P(B,=0)=1-λ△t,X是收益的跳跃规 厚尾和有偏性特征,提出了下面的双指数跳跃扩 模,服从双指数分布,这样收益8装可以用正 散模型 态密度来近似,收益的均值和方差为 假定资产价格为S(t),是下面随机微分方程 的解 8) =μ△t+K以△t+o(△t)≈ ds(t) u△t+k入△t (7) S(t) =dt+odW(t)+o (-1) (1) Va袋8)=a+27aa1-20)+ 其中:W(t)是标准维纳过程,N(t)是强度为入的 o(△t)≈g2△t+2n2λ△t(1-A△t)(8) 泊松过程,且两者相互独立;{}是独立同分布 可以看到这种资产收益分布的一个重要特征 非负随机变量序列,X:=ln(V)是双指数分布, 就是:相对于正态密度而言,这种分布在均值附近 密度为 有更高的峰和两个厚尾,也就是尖峰特征,另外一 个需要提到的是,如果跳跃规模均值心不为0,则 ()=e1n,0<7<1 2 密度是非对称的.实际上,如果K<0,向左偏;反 其中,k是X:的均值,同时 之向右偏 万方数据
一114一 系统工程学报 第21卷 为了解决这两个问题,Kou【10j提出了一种简 单的跳跃扩散模型,该模型由2部分组成:1)几何 布朗运动的连续部分,2)跳跃规模的对数是双指 数分布,跳跃时间是泊松过程的事件发生时间的 跳跃部分.正是由于模型的简单性,可以轻易地解 释模型参数,同时可以得到期权定价的封闭解. 关于连续时间的估计,可以采用半参数、 GMM、ML等方法,Pedersen¨刈将参数的估计值作 为缺失值,提出了从参数的条件后验分布中抽取 参数值的McMC方法,虽然这种方法不能适应隐 含因子,但是为McMC技术的发展提供了新的进 展.Eml(er[12j,Elerian等[13],Tse等[14J,胡素华等 分别用McMC方法对连续时间模型进行了参数估 计.其中Eraker给出了模型中含有隐含变量时,参 数估计值和隐含变量估计的McMC方法,所以 McMC方法非常适合Kou的双指数跳跃扩散模 型.跳跃因子这个隐含变量的加入,使得模型参数 的维数大量增加,即有多少个资产价格的样本观 狈4值,就有多少个跳跃变量,从而就导致了模型参 数估计的困难.本文使用基于贝叶斯方法的 McMC方法,从隐含变量的后验分布中抽取样本, 把这个样本作为跳跃因子的观测数据,进而估计 模型的参数值. 1双指数跳跃扩散模型及其特征 1.1双指数跳跃扩散模型 Kou为了能够同时体现资产收益分布的尖峰 厚尾和有偏性特征,提出了下面的双指数跳跃扩 散模型. 假定资产价格为|S(t),是下面随机微分方程 的解. 谢刊…州¨d(薹(K_1)) (1) 其中:W(t)是标准维纳过程,N(t)是强度为A的 泊松过程,且两者相互独立;{K}是独立同分布 非负随机变量序列,置=ln(K)是双指数分布, 密度为 ^(w)=磊1 e山“I向,0<7<1 (2) 其中,Ⅳ是置的均值,同时 P(戈一此=车)=P(菇一Ⅳ=一手)=0.5(3) 其中:∈是双指数变量,手的均值为叩,方差为叩2. 该模型认为跳跃是市场对外部信息的反映,好 消息和坏消息以泊松过程到达,资产价格的跳跃也 以泊松过程发生.另外为了简单,同时为了取得各种 期权定价问题的解析解,假定漂移岸和仃波动为常 数,但是这个假设可以推广到随机波动模型. 1.2 双指数跳跃扩散模型的特征 为了更好地体现双指数跳跃扩散模型的特 征,对随机微分方程(1)采用行Euler方法离散, 可得 错。(卢一丢盯2 At州嘶+At)一 形(t))+∑Xi+i1仃2(形(£+△t)一 i=N(t)+1 ‘ .】v(I+At) 形(f))2。卢At+必厄+∑置 i=Ⅳ(t)+1 (4) 其中:五是标准正态随机变量,泊松过程Ⅳ(t)有 一次跳跃的概率是AAt,超过一次的概率是 O(At),因此,如果△£足够小,可以忽略多次跳 跃,并有 麓置。睽f:2。芝△。 ㈤ 总之,当At很小时,收益可以近似为 错。础+(7Zt厄+B五 (6) 其中:色为贝努利随机变量,且P(B。=1)= 2At,P(B。=0)=1一aAt,置是收益的跳跃规 模,服从双指数分布.这样收益错就可以用正 态密度来近似,收益的均值和方差为 E(粼)=础+以△t+0(△t)一 AtAt+xAAt (7) Var(错)=仃2At+2772抛(1一擒)+ o(At)。0.2At+2r/2aAt(1一aAt)(8) 可以看到这种资产收益分布的一个重要特征 就是:相对于正态密度而言,这种分布在均值附近 有更高的峰和两个厚尾,也就是尖峰特征.另外一 个需要提到的是,如果跳跃规模均值彤不为0,则 密度是非对称的.实际上,如果彤<0,向左偏;反 之向右偏. 万方数据

第2期 胡素华等:双指数跳跃扩散模型的McMC估计 -115- 另外,还发现,资产收益分布的高峰和厚尾特 0,B,X)r(0) 征随着x|,入,刀的增大而变得更加显著;虽然跳 跳跃时间B,(t=1,2,…,n):π(B:|S, 跃规模的对数为正态分布可以体现收益分布的厚 S:-1,0,X)a p(S:0,S:-1,B:,X:)n(B:) 尾特征,但是它不可能同时有高峰和厚尾的特征 跳跃规模X(t=1,2,…,n):π(X|S,S-1,0, 2模型的估计 B=1)cp(S|0,S-1,B,=1,X)π(X) 对于McMC的MH算法来说,首先要解决的是 2.1跳跃扩散模型的似然函数 建议密度q(|)的选择,具体的讨论可以参见 由式(6)可知 Chib等5],Giks等[16].在本文中使用的是随机游 △S(t) S(i)-MAt-B.X; 走的MH算法,即建议密度为[-0.5,0.5]上的均 ≈Z~N(0,1) (9) 匀分布,参数向量0按照下面的方法更新 aW△t 0'=6+t8 (12) 参数6=(μ,G,心,7)基于观测值集合的对数似 其中ε是在区间上[-0.5,0.5]均匀分布的误差 然函数是 项,π是调和参数,通过π的值可以调整误差项的 lnp(0IS)≈ 方差,一般来说x值应该使接受概率在20%到 30%之间. 1 跳跃扩散模型的McMC估计步骤如下: 1月 (S -S:-1 uAt -B.X. S 1)给定参数的初值0o); 2台 G2△t 10) 2)使用Gibbs算法分别从跳跃时间B和跳跃 2.2 跳跃扩散模型的McMC方法 规模X的后验分布中抽取隐含变量B=(B,t= 马尔可夫链蒙特卡罗方法在众多的统计应用 1,2,…,n)与X=(X,t=1,2,…,n); 中被证明是一种比传统独立取样更有效的取样方 3)给定现在状态0),从建议密度g(0'| 法.在计量经济学和金融学中,McMC方法也被广 0)产生备选值0'; 泛使用.依据贝叶斯原理,参数向量6基于数据S 4)计算接受概率T(0),0) 的条件分布可以通过后验密度p(01S)获得,即 π(01S)=cp(S16)π(0) (11) T())=min( π(01x)g(010) 其中:p(S10)是似然函数,π(0)是参数0的先 (13) 验分布. 5)以概率T(0),0)接受备选值,即 在抛物线扩散跳跃模型中,由于引人了跳跃 0+1)=0';反之拒绝备选值,即0i+)=0; 因子,而这些跳跃因子都是隐含变量,从而参数的 6)重复前面的步骤2)~5),获得0o),01), 估计将更加复杂,要解决参数的估计问题,首先要 02,03),…,剔除前面的d个值,则{0d+”, 解决隐含变量的估计问题;Eraker对含有隐含变 0+2),…都有相同的后验密度π(01x). 量的扩散模型估计提出了相应的解决方案,即在 2.3参数抽样结果的收敛性分析 用McMC的MH算法从参数的后验分布中抽取每 在McMC算法中,取样的样本路线为 一组参数样本的同时,运用McMC的Gibbs算 {0):i=1,2,…,N},输出的遍历均值为 法[2]从隐含变量的后验分布中抽取一组隐含变 量.下面是参数向量0,跳跃时间B=(B,t=1, =为2) (14) 2,…,n)和跳跃规模X=(X,t=1,2,…,n)的 其中函数f(0)是一个实值函数,遍历均值的中 后验分布 心极限定理有 扩散和跳跃参数0:π(0|S,B,X)cxp(S| √N(-E(f0))→N(0,》 (15) 万方数据
第2期 胡素华等:双指数跳跃扩散模型的McMC估计 另外,还发现,资产收益分布的高峰和厚尾特 征随着IⅣl,A,叩的增大而变得更加显著;虽然跳 跃规模的对数为正态分布可以体现收益分布的厚 尾特征,但是它不可能同时有高峰和厚尾的特征. 2模型的估计 2.1 跳跃扩散模型的似然函数 由式(6)可知 登警硝~Ⅳ(叭)(9) G q&t 参数日=(p,盯,彤,叩)基于观测值集合的对数似 然函数是 In P(曰I S)一 一告∑In(a2△t)一 2.2 跳跃扩散模型的McMC方法 吉茎蟹掣 (10) 马尔可夫链蒙特卡罗方法在众多的统计应用 中被证明是一种比传统独立取样更有效的取样方 法.在计量经济学和金融学中,McMC方法也被广 泛使用.依据贝叶斯原理,参数向量0基于数据s 的条件分布可以通过后验密度P(O I.s)获得,即 7r(9 S)=cp(S O)丌(0) (11) 其中:P(.s O)是似然函数,丌(O)是参数O的先 验分布. 在抛物线扩散跳跃模型中,由于引人了跳跃 因子,而这些跳跃因子都是隐含变量,从而参数的 估计将更加复杂.要解决参数的估计问题,首先要 解决隐含变量的估计问题;Eraker对含有隐含变 量的扩散模型估计提出了相应的解决方案,即在 用McMC的MH算法从参数的后验分布中抽取每 一组参数样本的同时,运用McMC的Gibbs算 法u2J从隐含变量的后验分布中抽取一组隐含变 量.下面是参数向量0,跳跃时间B=(B:,t=1, 2,…,n)和跳跃规模x=(Xt,t=1,2,…,n)的 后验分布. 扩散和跳跃参数O:丌(9 Js,B,X)芘P(5 D,B,X)丌(O) 夥I跃时问B。(t=1,2,…,rt):丌(B。J s。, Js;一l,D,置)oc P(s。l 0,S。一l,B;,xt)7r(B;) 跳跃规模五(£=1,2,…,n):丌(五f S,S-1'口, B。=1)。c p(S。I o,S—l,B。=1,五)丌(五) 对于McMC的MH算法来说,首先要解决的是 建议密度q(·I O)的选择,具体的讨论可以参见 Chib等[15],Gilks等[16].在本文中使用的是随机游 走的MH算法,即建议密度为[一0.5,0.5]上的均 匀分布,参数向量8按照下面的方法更新. 口7=9+饨 (12) 其中£是在区间上[一0.5,0.5]均匀分布的误差 项,r是调和参数,通过r的值可以调整误差项的 方差,一般来说r值应该使接受概率在20%到 30%之间. 跳跃扩散模型的McMC估计步骤如下: 1)给定参数的初值日(o’; 2)使用Gibbs算法分别从跳跃时间曰和跳跃 规模x的后验分布中抽取隐含变量B=(B。,t= 1,2,…,n)与x=(Xt,t=1,2,…,n); 3)给定现在状态9(¨,从建议密度g(o7 O(i’)产生备选值O7; 4)计算接受概率丁(9(¨,0’) 删),O,)=min{,,鬟鼎黼} (13) 5)以概率丁(p(¨,07)接受备选值,即 O(i+1):O’;反之拒绝备选值,即O(i+1):O(i’; 6)重复前面的步骤2)。5),获得{9(∞,9(¨, D(∞,9(引,…},剔除前面的d个值,则{O(d+1), 0(。+扪,…}都有相同的后验密度丌(D I戈). 2.3 参数抽样结果的收敛性分析 在McMC算法中,取样的样本路线为 {8“):i=1,2,…,Ⅳ},输出的遍历均值为 五:寺∑,(o(i’) (14) 其中函数.厂(9“’)是一个实值函数,遍历均值的中 心极限定理有 ~/Ⅳ(厶一B(八9)))刚(o,盯}) (15) 万方数据
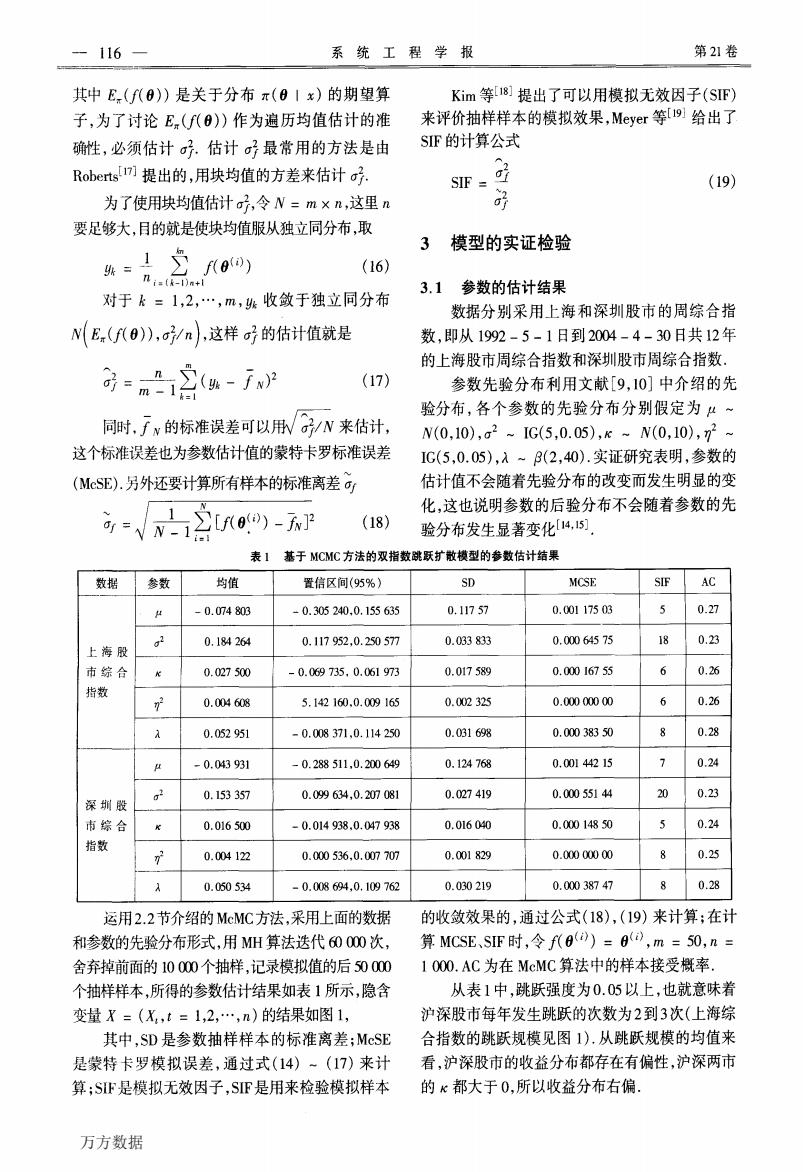
-116 系统工程学报 第2卷 其中E(f(0)是关于分布π(0|x)的期望算 Kim等18]提出了可以用模拟无效因子(SIF) 子,为了讨论En(f(0)作为遍历均值估计的准 来评价抽样样本的模拟效果,Meyer等9]给出了 确性,必须估计σ子.估计σ子最常用的方法是由 SF的计算公式 Roberts7)]提出的,用块均值的方差来估计o子. SIF (19) 为了使用块均值估计o子,令W=m×n,这里n 要足够大,目的就是使块均值服从独立同分布,取 3 模型的实证检验 (16) l i=(k-)a+l 3.1参数的估计结果 对于k=1,2,…,m,张收敛于独立同分布 数据分别采用上海和深圳股市的周综合指 NE.(f(0),o/n),这样o子的估计值就是 数,即从1992-5-1日到2004-4-30日共12年 的上海股市周综合指数和深圳股市周综合指数. G=m12(h-j2 (17) 参数先验分布利用文献[9,10]中介绍的先 验分布,各个参数的先验分布分别假定为:~ 同时,手N的标准误差可以用√G/N来估计, N(0,10),a2-IG(5,0.05),k~N(0,10),72 这个标准误差也为参数估计值的蒙特卡罗标准误差 IG(5,0.05),入~(2,40).实证研究表明,参数的 (McSE).另外还要计算所有样本的标准离差G 估计值不会随着先验分布的改变而发生明显的变 化,这也说明参数的后验分布不会随着参数的先 = 1[f0)-]2 N-1 (18) 验分布发生显著变化4,15] 表1 基于MCMC方法的双指数跳跃扩散模型的参数估计结果 数据 参数 均值 置信区间(95%) SD MCSE SIF AC -0.074803 -0.305240,0.155635 0.11757 0.00117503 5 0.27 0.184264 0.117952,0.250577 0.033833 0.00064575 18 0.23 上海股 市综合 0.027500 -0.069735,0.061973 0.017589 0.00016755 0.26 指数 72 0.004608 5.142160.0.009165 0.002325 0.00000000 0.26 0.052951 -0.008371,0.114250 0.031698 0.00038350 8 0.28 -0.043931 -0.288511,0.200649 0.124768 0.00144215 0.24 2 0.153357 0.099634,0.207081 0.027419 0.00055144 20 0.23 深圳股 市综合 0.016500 -0.014938.0.047938 0.016040 0.00014850 5 0.24 指数 0.004122 0.000536,0.007707 0.001829 0.00000000 0.25 0.050534 -0.008694,0.109762 0.030219 0.00038747 0.28 运用2.2节介绍的McMC方法,采用上面的数据 的收敛效果的,通过公式(18),(19)来计算;在计 和参数的先验分布形式,用MH算法迭代60000次, 算MCsE、Sf时,令f(0)=0),m=50,n= 舍弃掉前面的10000个抽样,记录模拟值的后50000 1O00.AC为在McMC算法中的样本接受概率. 个抽样样本,所得的参数估计结果如表1所示,隐含 从表1中,跳跃强度为0.05以上,也就意味着 变量X=(X,t=1,2,…n)的结果如图1, 沪深股市每年发生跳跃的次数为2到3次(上海综 其中,SD是参数抽样样本的标准离差;McSE 合指数的跳跃规模见图I),从跳跃规模的均值来 是蒙特卡罗模拟误差,通过式(14)~(17)来计 看,沪深股市的收益分布都存在有偏性,沪深两市 算;SF是模拟无效因子,SIF是用来检验模拟样本 的:都大于0,所以收益分布右偏 万方数据
系统工程学报 第21卷 其中B(,(0))是关于分布7I"(0 I∞)的期望算 子,为了讨论E。(八9))作为遍历均值估计的准 确陛,必须估计仃}.估计仃}最常用的方法是由 Robertsr-17]提出的,用块均值的方差来估计仃;. 为了使用块均值估计d;,令N:m×凡,这里n 要足够大,目的就是使块均值服从独立同分布,取 纨:=1∑八∥) (16) ¨i=(k一1)n+1 对于k=1,2,…,m,纨收敛于独立同分布 Ⅳ(E。(厂(p)),仃矽n),这样仃}的估计值就是 扯志圣(纨一歹Ⅳ)2 (17) 一厂i—一 同时,/Ⅳ的标准误差可以刷仃纱Ⅳ来估计, 这个标准误差也为参数估计值的蒙特卡罗标准误差 (McSE).另外还要计算所有样本的标准离差旁 厂—:——]r—————————一 、ar=√志萎[们∽一五]2 (18) Kim等[183提出了可以用模拟无效因子(SIF) 来评价抽样样本的模拟效果,Meyer等[191给出了 SIF的计算公式 SIF:孚 (19) ~^ 口々 3 模型的实证检验 3.1 参数的估计结果 数据分别采用上海和深圳股市的周综合指 数,即从1992—5—1日到2004—4—30 13共12年 的上海股市周综合指数和深圳股市周综合指数. 参数先验分布利用文献[9,10]中介绍的先 验分布,各个参数的先验分布分别假定为/x~ x(o,10),盯2~tC(5,0.05),彤~x(o,10),叩2~ IG(5,0.05),A~/3(2,40).实证研究表明,参数的 估计值不会随着先验分布的改变而发生明显的变 化,这也说明参数的后验分布不会随着参数的先 验分布发生显著变化【14,15 J. 表I 基于MCMC方法的双指数跳跃扩散模型的参数估计结果 数据 参数 均值 置信区间(95%) SD MCSE SIF AC Ⅳ 一0.074 803 —0.305 240.0.155 635 0.117 57 O.001 175 03 5 0.27 上海股 口2 0.184 264 0.117 952,0.250 577 O.033 833 O.Ooo 645 75 18 O.23 市综合 0.027 500 一0.069 735,0.061 973 0.017 589 O.000167 55 6 O.26 指数 叩。 0.004 608 5.142 160.0.009 165 0.002 325 O.000 000 00 6 0.26 A O.052 951 —0.008 371,0.114 250 0.031 698 0.000 383 50 8 0.28 F 一0.043931 —0.288 511,0.200 649 0.124 768 0.00l 442 15 7 0.24 深圳股 d2 0.153 357 0.099 634.0.2ar7 081 0.027 419 0.000 551 44 20 O.23 市综合 0.016 500 —0.014 938,0.047 938 0.016 040 0.000148 50 5 O.24 指数 矿 0.004 122 0.000 536.0.007 70r7 O.001 829 O.000 000 00 8 O.25 A 0.050 534 —0.008 694,0.109 762 0.030 219 O.000 387 47 8 0.28 运用2.2节介绍的MeMC方法,采用上面的数据 和参数的先验分布形式,用MH算法迭代60 0130次, 舍弃掉前面的10 000个抽样,记录模拟值的后50 000 个抽样样本,所得的参数估计结果如表1所示,隐含 变量x=(五,t=1,2,…,n)的结果如图1, 其中,SD是参数抽样样本的标准离差;MeSE 是蒙特卡罗模拟误差,通过式(14)~(17)来计 算;SIF是模拟无效因子,SIF是用来检验模拟样本 的收敛效果的,通过公式(18),(19)来计算;在计 算MCSE、SIF时,令“0“’)=0“,,m=50,n= 1 000.AC为在MeMC算法中的样本接受概率. 从表1中,跳跃强度为0.05以上,也就意味着 沪深股市每年发生跳跃的次数为2到3次(上海综 合指数的跳跃规模见图1).从跳跃规模的均值来 看,沪深股市的收益分布都存在有偏性,沪深两市 的彤都大于0,所以收益分布右偏. 万方数据
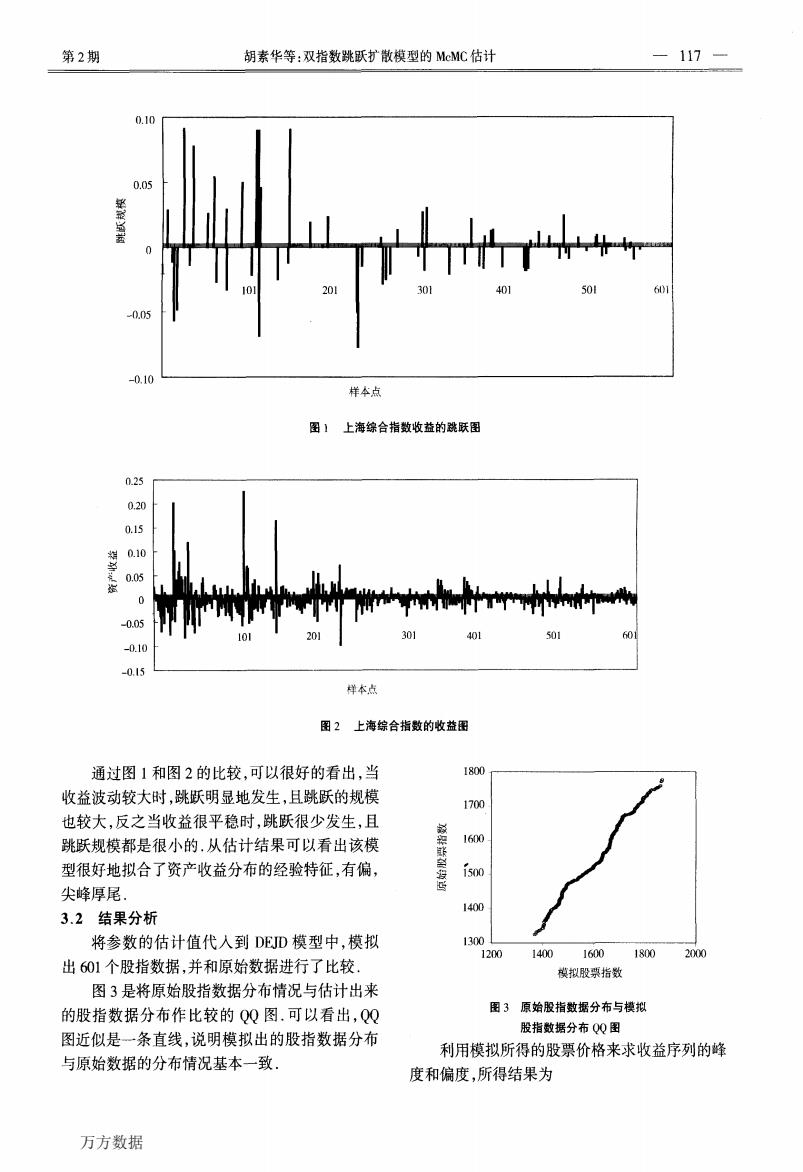
第2期 胡素华等:双指数跳跃扩散模型的McMC估计 117 0.10 0.05 201 401 -0.05 -0.10 样本点 图】上海综合指数收益的跳跃图 0.25 020 0.15 0.10 0.05 -0.05 -0.10 0.15 样本点 图2上海综合指数的收益围 通过图1和图2的比较,可以很好的看出,当 1800 收益波动较大时,跳跃明显地发生,且跳跃的规模 1700 也较大,反之当收益很平稳时,跳跃很少发生,且 跳跃规模都是很小的.从估计结果可以看出该模 1600 型很好地拟合了资产收益分布的经验特征,有偏, i500 尖峰厚尾 1400 3.2结果分析 将参数的估计值代入到DED模型中,模拟 1300 1200 14001600 18002000 出601个股指数据,并和原始数据进行了比较 模拟股票指数 图3是将原始股指数据分布情况与估计出来 的股指数据分布作比较的QQ图.可以看出,QQ 图3原始股指数据分布与模拟 股指数据分布QQ图 图近似是一条直线,说明模拟出的股指数据分布 利用模拟所得的股票价格来求收益序列的峰 与原始数据的分布情况基本一致. 度和偏度,所得结果为 万方数据
第2期 胡素华等:双指数跳跃扩散模型的McMC估计 一117一一 辎 是 毯 美 0.10 O.05 101 样本点 图1 上海综合指数收益的跳跃图 样本点 图2 上海综合指数的收益图 通过图1和图2的比较,可以很好的看出,当 收益波动较大时,跳跃明显地发生,且跳跃的规模 也较大,反之当收益很平稳时,跳跃很少发生,且 跳跃规模都是很小的.从估计结果可以看出该模 型很好地拟合了资产收益分布的经验特征,有偏, 尖峰厚尾. 3.2结果分析 将参数的估计值代入到DEJD模型中,模拟 出601个股指数据,并和原始数据进行了比较. 图3是将原始股指数据分布情况与估计出来 的股指数据分布作比较的QQ图.可以看出,QQ 图近似是一条直线,说明模拟出的股指数据分布 与原始数据的分布情况基本一致. 籁 妲 眺 整 磐 鸶 图3原始股指数据分布与模拟 股指数据分布QQ图 利用模拟所得的股票价格来求收益序列的峰 度和偏度,所得结果为 万方数据

-118 系统工程学报 第21卷 Kurt=19.9876 kew=2.5438 (20) 4结论 从上面的结果我们可以看出,模拟收益序列的蜂度 和偏度远远大于正态分布的峰度和偏度,从而也就 本文中,基于Euler方法获得参数后验分布的 证明了双指数跳跃扩散模型能够很好地同时描述 离散密度,用McMC方法估计了双指数跳跃扩散 资产收益分布的尖峰厚尾和有偏性的特征.另外, 模型及模型中的隐含跳跃变量,发现McMC方法 在用MMC方法对参数进行估计的同时,还估计了 可以很好地估计连续时间模型,特别是含有隐含 跳跃发生的时间和跳跃的规模,而Kou在估计双指 变量的连续时间模型.通过该模型所模拟的股指 数跳跃扩散模型的时候仅仅估计了模型的参数.所 数据和实际数据的分布基本一直,从而说明了 以,模拟结果和估计结果也说明了MMC方法适合 DED扩散可以很好的描述资产收益的分布特征, 估计含有隐含变量的连续时间模型, 参考文献: [1]Merton R C.Theory of rational option opricing[J].Bell Joumal of Economics,1973,4(1):141-183 [2]Black F,Scholes M.The pricing of options and corporate liabilities[J].Joumal of Political Economy,1973,81(3):637-659 [3]Bamdorff N,Shleifer A,Vishny R.A model of investor sentiment[J].Joumal of Financial Economics,1998,49:307-343. [4]Eberlein E,Keller U.Hyperbolic distribution in finance[J].Bemoulli,1995,3(1):281-299. [5]Madan D B,Carr P,Chang EC.The variance gamma process and option pricing[J].European Finance Review,1995,2:79-105. [6]Adersen L,Andreasen J.Jump-diffusion process:Volatility smile fitting and numerical methods for pricing[].Review of Deriva- tives Research,2000,4:231-262. [7]Hull JC,White A.The pricing of options on assets with stochastic volatilities[J].Joural of Finance,1987,42(1):281-300. [8]Cox J C,Ross S.The Valuation of options for alternative stochastic processes[J].Joumal of Financial Economics,1976,3(3): 145-166. [9]Robert M C.Option pricing when underlying stock returns are discontinuous[J].Joumal of Financial Economics,1976,3(3): 125一144. [10]Kou SG.A jump-diffusion model for option pricing[J].Management Science,2002,48(8):1086-1101. [11]Asger P.A new approach to maximum likelihood estimation for stochastic differential equations based on discrete obeervations[]. Scandinavian Joumal of Statistics,1995,22(1):55-71. [12]Eraker B.MeMC analysis of diffusion models with application to finance[].Joumal of Business and Economic Statistics,2001,19 (2):177191. [13]Elerian O,Chib S,Shephard N.Likelihood inference for discretely observed non-linear diffusions[].Econometrica,2001,69 (4):959-993. [14]Tse Y K.Zhang X B,Yu J.Estimation of hyperbolic diffusion using the Markov chain Monte Carlo method[J].Quantitative Fi- nance,2003,3(1):1-12. [15]胡素华,张形,张世英.正态逆高斯扩散模型的McMC估计[J】.系统工程理论方法应用,2005,15(2):41一46. [16]Chibs S,Greenberg E.Understanding the metropolis-hastings algorithm[J].American Statistician,1995,49(2):327-35. [17]Gilks WR,Richardson S,Spiegelhatler D J.Introducing Markov chain Monte Carlo[A].In:Markov Chain Monte Carlo in Prac- tice[M].Gilks WR,Richardson S,Spiegelhalter D J.London:Chapman and Hall,1996.1-20. [18]Roberts GO.Markov chain concepts related to sampling algorithms[A].In:Markov Chain Monte Carlo in Practice[M].Gilks W R,Richardson S,Spiegelhalter D J.London:Chapman and Hall,1996.45-57. [19]Kim S,Shephard N,Chib S.Stochastic volatility:Likelihood inference and comparison with ARCH models[J].Review of Eco- nomic Studies,1998,65(2):361—93. [20]Meyer R,Yu J.BUGS for a Bayesian analysis of stochastic volatility models[J].Econometrics Joumal,2000,3(2):19-215. 作者简介: 胡素华(197一),男,安徽怀宁人,博士生,讲师,研究方向:连续时间金融模型研究,金融波动研究; 张世英(1936一),男,北京人,教授,博士生导师,研究方向:社会经济系统建模与控制; 张形(1968一),女,天津人,副数授,硕士生导师,研究方向:金融分析,公司理财,资产评估. 万方数据
一118一 系统工程学报 第21卷 Kurt=19.987 6 Skew=2.543 8 (20) 从上面的结果我们可以看出,模拟收益序列的峰度 和偏度远远大于正态分布的峰度和偏度,从而也就 证明了双指数跳跃扩散模型能够很好地同时描述 资产收益分布的尖峰厚尾和有偏性的特征.另外, 在用McMC方法对参数进行估计的同时,还估计了 跳跃发生的时问和跳跃的规模,而Kou在估计双指 数跳跃扩散模型的时候仅仅估计了模型的参数.所 以,模拟结果和估计结果也说明了McMC方法适合 估计含有隐含变量的连续时间模型. 参考文献: 4结论 本文中,基于Euler方法获得参数后验分布的 离散密度,用McMC方法估计了双指数跳跃扩散 模型及模型中的隐含跳跃变量,发现McMC方法 可以很好地估计连续时间模型,特别是含有隐含 变量的连续时间模型.通过该模型所模拟的股指 数据和实际数据的分布基本一直,从而说明了 DEJD扩散可以很好的描述资产收益的分布特征. [1 j Menon R C.Theory of rational option opricing[J].Bell Journal of Economics,1973,4(1):141—183. [2]Black F,Scholes M.The pricing of options and corporate liabilities[J].Journal of Political Economy,1973,81(3):637-_659. [3]Barndorff N,Shleifer A,Vishny R.A model of investor sentiment[J].Journal of Financial Economics,1998,49:307—343. [4]Ebedein E,Keller U.Hyperbolic distribution in finance[J].Bernoulli,1995,3(1):281—299. [5]Madan D B,Cart P,c}lang E C.The variance gmlrna process and option砸c崦[J].European Finance Review,1995,2:79—1c15. [6]Adersen L,Andreasen J.Jump-diffusion process_,Volatility smile fitting and numerical methods for pficing[Jj.Renew of Deriva— fives Research,2000,4:231—262. [7]Hull J C,碱te A.ne pricing of options on assets with stochastic volatilities[J].Journal of Finance,1987,42(1):281—300. [8]Cox J C,Ross S.‰Valuation of options for alternative stochastic processes[J].Journal of Financial Economics,1976,3(3): 145—166. [9]Robert M C.Option pricing when underlying stock returns are discontinuous[J].Journal of Financial Economics,1976,3(3): 125—144. [10]Kou S G.A jump.-diffusion model for option pricing[J].Management Science,2002,48(8):108卜1101. [11]Asger P.A new appmach to maximum likelihood estimation for stochastic differential equations based on discrete observations[JJ. Scandinavian Journal of Statistics,1995,22(1):55—71. [12]Eraker B.McMC analysis of diffusion models with application to finance[Jj.Joumal of Business and Economic Statistics,2001,19 (2):177—191. [13]Elerian O,Chib S,Shephard N.Likelihood inference for discretely observed non-linear diffusionslJj.Econometfica,2001,69 (4):959---993. [14]Tse Y K,Zhang X B,Yu J.Estimation of hyperbolic diffusion using the Markov chain Monte Carlo methodlJj.Quantitative Fi— nance,2003,3(1):1--12. [15]胡素华,张彤,张世英.正态逆高斯扩散模型的McMC估计[J].系统工程理论方法应用,2005,15(2):41—46. [16]Chibs S,Greenberg E.Understanding the metropolis-hastings algorithm[J].American Statistician,1995,49(2):327—35. [17]Gilks w R,Richardson S,Spiegelhatler D J.Introducing Markov chain Monte CarlolA].In:Markov Chain Monte Carlo in Prac— flee[M].Gilks W R,Richardson S,Spiegelhalter D J.London:Chapman and Hall,1996.1—20. [18]Roberts G O.Markov chain concepts related to sampling algofithms[A].In:Markov Chain Monte Carlo in Practice[MJ.Gilks W R,Richardson S,Spiegelhaher D J.London:Chapman and Hall,1996.45—57. [19]Kim S,Shephard N,Chib S.Stochastic volatility:Likelihood inference and comparison with ARCH modelslJJ.Review of Eco— nomic Studies,1998,65(2):361—-93. [20]Meyer R,Yu J.BUGS for a Bayesian analysis of stochastic volatility nHlelslJ].Econometrics Journal,2000,3(2):198—215. 作者简介: 胡素华(19r77一),男,安徽怀宁人,博士生,讲师,研究方向:连续时间金融模型研究,金融波动研究; 张世英(1936一),男,北京人,教授,博士生导师,研究方向:社会经济系统建模与控制; 张彤(1968一),女,天津人,副教授,硕士生导师,研究方向:金融分析,公司理财,资产评估. 万方数据