
随机模拟方法与应用--- 期末作业 利用MCMC方法求解生物逆问题 姓名:周东旭 学号:5120309088 专业:电气工程与自动化 写在前面: 本学期的随机模拟方法与应用课程,介绍了许多经典的随机模拟方法,其中,MCMC 方法应用广泛,效果好,在老师所给的参考论文之中,绝大多数也是基于MCMC算法来实 现模拟。受限于专业知识,其中的大部分论文我并不能正确理解,综合考虑理解深度以及 兴趣程度,我最终选择了曹小群,宋君强,张卫民,赵军,张理论等人合著的《MCMC方 法在生物逆问题求解中的应用》这篇论文作为我的参考论文。本文主要是介绍该文献的主 要思想,并给出自己的思考以及部分编程实践,虽已努力尝试在Matlab中实现原文的模拟 结果,但由于能力所限,并且怀疑原文算法有问题,其具体结果可能无法做出来,希望老 师理解。另外,文章前半部分主要是摘录原文,后面则是自己的思考与设计。 问题的引入: 首先我根据自己的理解介绍一下生物逆问题,我们知道,自然界的生物种群变化规律 可以用数学模型来描述,知道了数学模型的参数,便可以推测出接下来的时间里某一地区 某生物种群的数量变化规律,在当今社会,生态的健康程度越来越受到重视,因此,掌握 动植物种群规模的变化规律,对于生态环境保护,珍稀动植物繁衍,生态平衡的保持以及 整个国家的可持续发展战略,都具有重要意义。但是,我们所能监测到的数据都是离散 的,也就是我们只能得到一串样本序列,而无法得到模型的具体参数,那么,如何根据观 察得到的样本来确定模型参数,从而对未来的发展趋势做出预测,这就叫做求解生物逆问 题。 但是,求解这样的问题存在着一些不利因素,与正问题不同,求解逆问题是通过实验 或运行中的观测信息来辨识模型中的未知参数。由于测量信息的不准确、不充分和生态模 型自身的非线性等性质,大大增加了逆问题的求解难度。逆问题的求解一般需要采用特殊 方法,原文中提到,吴自库等采用变分伴随方法估计了一个生态模型中的未知参数:李静 和黄卡玛引入信息熵构造了一个评价因子,有效描述了不同位置测量信息对参数辨识的贡 献。而原文作者则选择基于贝叶斯理论的马尔科夫链蒙特卡罗(MCMC)方法来估计生物动力 学模型中的未知参数。利用MCMC方法求解逆问题,具有以下优点:(1)能方便地将各种先 验信息融入到问题的求解过程中,减小不确定性:(2)获得的是全局最可能解,而通常的最 优化算法可能陷入目标函数局部极小值:(3)能对定义在高维空间且无明确数学表达式的概 率密度函数(PDF),进行数值计算:(4)MCMC算法通过构造Markov链来进行随机模拟,计 算速度高于一般的Monte Carlo方法和模拟退火算法。 算法简介: 贝叶斯理论:
随机模拟方法与应用------期末作业 利用 MCMC 方法求解生物逆问题 姓名:周东旭 学号;5120309088 专业:电气工程与自动化 写在前面: 本学期的随机模拟方法与应用课程,介绍了许多经典的随机模拟方法,其中,MCMC 方法应用广泛,效果好,在老师所给的参考论文之中,绝大多数也是基于 MCMC 算法来实 现模拟。受限于专业知识,其中的大部分论文我并不能正确理解,综合考虑理解深度以及 兴趣程度,我最终选择了曹小群,宋君强,张卫民,赵军,张理论等人合著的《MCMC 方 法在生物逆问题求解中的应用》这篇论文作为我的参考论文。本文主要是介绍该文献的主 要思想,并给出自己的思考以及部分编程实践,虽已努力尝试在 Matlab 中实现原文的模拟 结果,但由于能力所限,并且怀疑原文算法有问题,其具体结果可能无法做出来,希望老 师理解。另外,文章前半部分主要是摘录原文,后面则是自己的思考与设计。 问题的引入: 首先我根据自己的理解介绍一下生物逆问题,我们知道,自然界的生物种群变化规律 可以用数学模型来描述,知道了数学模型的参数,便可以推测出接下来的时间里某一地区 某生物种群的数量变化规律,在当今社会,生态的健康程度越来越受到重视,因此,掌握 动植物种群规模的变化规律,对于生态环境保护,珍稀动植物繁衍,生态平衡的保持以及 整个国家的可持续发展战略,都具有重要意义。但是,我们所能监测到的数据都是离散 的,也就是我们只能得到一串样本序列,而无法得到模型的具体参数,那么,如何根据观 察得到的样本来确定模型参数,从而对未来的发展趋势做出预测,这就叫做求解生物逆问 题。 但是,求解这样的问题存在着一些不利因素,与正问题不同,求解逆问题是通过实验 或运行中的观测信息来辨识模型中的未知参数。由于测量信息的不准确、不充分和生态模 型自身的非线性等性质,大大增加了逆问题的求解难度。逆问题的求解一般需要采用特殊 方法,原文中提到,吴自库等采用变分伴随方法估计了一个生态模型中的未知参数;李静 和黄卡玛引入信息熵构造了一个评价因子,有效描述了不同位置测量信息对参数辨识的贡 献。而原文作者则选择基于贝叶斯理论的马尔科夫链蒙特卡罗(MCMC)方法来估计生物动力 学模型中的未知参数。利用 MCMC 方法求解逆问题,具有以下优点:(1)能方便地将各种先 验信息融入到问题的求解过程中,减小不确定性;(2)获得的是全局最可能解,而通常的最 优化算法可能陷入目标函数局部极小值;(3)能对定义在高维空间且无明确数学表达式的概 率密度函数(PDF),进行数值计算;(4)MCMC 算法通过构造 Markov 链来进行随机模拟,计 算速度高于—般的 Monte Carlo 方法和模拟退火算法。 算法简介: 贝叶斯理论:

贝叶斯统计方法的基本思想是:将未知参数m作为随机量,在对m进行估计时设置 -个先验分布p(m)。在获取观测资料后,使用贝叶斯公式将先验分布改进为后验分布: p(mld)=p(d m)p(m)/p(d) (1) 其中,pm)、pdm)和p(m/d分别表示未知向量的先验、条件和后验PDF。 m=(m1,m2,,mn表示长度为n的未知随机向量,d=(d1,d2,,dM是包含M个观测数据的 列向量。获取观测后,p(d是一个与m无关的常数。 式(1)是进行贝叶斯推理的基础,也是原文利用MCMC算法估计生态模型中未知参数的 出发点。各项意义如下:pm表示未知随机向量的先验信息,从反问题的角度,先验信息 的引入可以克服反问题的不适定性。条件概率密度p(dlm)又称似然函数L(dm,包含了在 所有观测数据条件下未知参数的似然度信息。换言之,表征了估计参数和实际观测数据的 协调程度。先验信息与观测信息相结合,就得到反映未知随机向量综合信息的后验概率 密度:pmd定义在整个解空间,表示了问题的“完全”解,即可能解集合中任意解出现 的概率。获得后验PDF后,理论上可以获得未知参数的任何特征。但实际应用中除了非常 简单的情况,后验PDF都无明确数学表达式。另外,通常的数值积分方法(例如Mote Cao方法)的计算量将随向量维数的增多而呈指数增长。因此。贝叶斯方法很难直接解决 实际问题。 MCMC方法: 上面的分析表明:利用贝叶斯公式可以获得未知参数的后验PDF,但参数估计问题仍 然无法求解。另一方面,随着后验PDF复杂性的增加,单一的“最可能”解如果存在)几 乎没有意义,而利用后验概率的全部信息来对解进行整体推断更具有合理性。换言之,研 究重点不再是通过最优化获得一个单点解,而是对解空间中最可能区域进行重要性抽样 后,然后由样本集对解进行估计。 MCMC方法就是一种直接模拟后验PDF的方法,可以对定义在高维随机向量空间M上 且无明确数学表达式的概率分布P进行抽样。基本思想是产生大量服从分布P的随机向量 序列(m1,m2,,m,其中,1为抽样数。如果向量序列满足马尔可夫性质:向量m*1的产 生仅依赖于前一个向量m,而与过去时刻i-1,i-2,1的状态向量m-1,m-2,…m1都无关, 则该向量序列称为马尔可夫链。马尔科夫性质意味着抽样算法完全可由转移概率矩阵P描 述,矩阵元素Pg表示算法在当前访问m的条件下接着访问的条件概率。按照所用转移 概率矩阵的不同,McMC方法的主要抽样算法有:Gibbs抽样算法、Metropolis-.Hastings算 法和自适应Metropolis算法。 其中,Metropolis算法的动机是推广接受-拒绝抽样方法。在接受拒绝抽样方法中,我 们有目标密度函数、建议密度函数和一个接受准则(概率函数)。同样地我们假设:是全空 间上的离散概率密度函数,人们需要在上按照密度函数产生样本马尔可夫链 原文采用自适应Metropolis算法,以生物模型中未知参数的后验分布为不变极限分布 来构造Markov链。与传统的Metropolis.Hastings算法相比,自适应Metropolis算法不需 要事先确定参数的推荐分布,而是由后验参数的协方差矩阵来估算参数分布。后验参数的 协方差矩阵在每次迭代后都要自适应地调整:由于参数不再需要分组更新,所以计算量大 大减少。如此,第i步参数的推荐分布就是均值为m,、协方差矩阵为C的多元正态分布。 协方差的计算公式如(2)式所示: Co,i≤io CisaCov(mo)+saelaio (2) 在初始io次迭代中,C取固定值Co,之后进行自适应更新。m,是未知参数向量m中某 个分量在第i次迭代的估计值。ε是一个非常小的数,作用是确保C不成为奇异矩阵: C0v(mo,m1,……m二1)是m,m1,m,一1的协方差矩阵:Sa是比例因子,依赖于未知随机
贝叶斯统计方法的基本思想是:将未知参数 m 作为随机量,在对 m 进行估计时设置 —个先验分布 p(m)。在获取观测资料后,使用贝叶斯公式将先验分布改进为后验分布: p(m|d) = p(d|m)p(m)/p(d) (1) 其中,p(m) 、p(d|m) 和 p(m|d)分别表示未知向量的先验、条件和后验 PDF。 mT=(m1,,m2,……,mn)表示长度为 n 的未知随机向量,d T=(d1,,d2,……,dM)是包含 M 个观测数据的 列向量。获取观测后,p(d)是—个与 m 无关的常数。 式(1)是进行贝叶斯推理的基础,也是原文利用 MCMC 算法估计生态模型中未知参数的 出发点。各项意义如下:p(m)表示未知随机向量的先验信息,从反问题的角度,先验信息 的引入可以克服反问题的不适定性。条件概率密度 p(d|m)又称似然函数 L(d|m),包含了在 所有观测数据条件下未知参数的似然度信息。换言之,表征了估计参数和实际观测数据的 协调程度。先验信息与观测信息相结合,就得到反映未知随机向量 m 综合信息的后验概率 密度;p(m|d)定义在整个解空间,表示了问题的“完全”解,即可能解集合中任意解出现 的概率。获得后验 PDF 后,理论上可以获得未知参数的任何特征。但实际应用中除了非常 简单的情况,后验 PDF 都无明确数学表达式。另外,通常的数值积分方法(例如 Monte Carlo 方法)的计算量将随向量维数的增多而呈指数增长。因此。贝叶斯方法很难直接解决 实际问题。 MCMC 方法: 上面的分析表明:利用贝叶斯公式可以获得未知参数的后验 PDF,但参数估计问题仍 然无法求解。另一方面,随着后验 PDF 复杂性的增加,单一的“最可能”解(如果存在)几 乎没有意义,而利用后验概率的全部信息来对解进行整体推断更具有合理性。换言之,研 究重点不再是通过最优化获得一个单点解,而是对解空间中最可能区域进行重要性抽样 后,然后由样本集对解进行估计。 MCMC 方法就是一种直接模拟后验 PDF 的方法,可以对定义在高维随机向量空间 M 上 且无明确数学表达式的概率分布 P 进行抽样。基本思想是产生大量服从分布 P 的随机向量 序列(m1,,m2,……,ml),其中,l 为抽样数。如果向量序列满足马尔可夫性质:向量 mi+1的产 生仅依赖于前一个向量 mi,而与过去时刻 i-1,i-2⋯,l 的状态向量 mi-1,mi-2,……m1都无关, 则该向量序列称为马尔可夫链。马尔科夫性质意味着抽样算法完全可由转移概率矩阵 P 描 述,矩阵元素 Pij 表示算法在当前访问 mj的条件下接着访问 mi的条件概率。按照所用转移 概率矩阵的不同,MCMC 方法的主要抽样算法有:Gibbs 抽样算法、Metropolis-Hastings 算 法和自适应 Metropolis 算法。 其中,Metropolis 算法的动机是推广接受-拒绝抽样方法。在接受-拒绝抽样方法中,我 们有目标密度函数、建议密度函数和一个接受准则(概率函数)。同样地我们假设:是全空 间上的离散概率密度函数,人们需要在上按照密度函数产生样本马尔可夫链 原文采用自适应 Metropolis 算法,以生物模型中未知参数的后验分布为不变极限分布 来构造 Markov 链。与传统的 Metropolis.Hastings 算法相比,自适应 Metropolis 算法不需 要事先确定参数的推荐分布,而是由后验参数的协方差矩阵来估算参数分布。后验参数的 协方差矩阵在每次迭代后都要自适应地调整;由于参数不再需要分组更新,所以计算量大 大减少。如此,第 i 步参数的推荐分布就是均值为𝑚̂𝑖,、协方差矩阵为 Ci的多元正态分布。 协方差的计算公式如(2)式所示: 𝐶𝑖 = { 𝐶0, 𝑖 ≤ 𝑖0 𝑠𝑑𝐶𝑜𝑣(𝑚̂0, 𝑚̂1, … … 𝑚̂𝑖−1 ) + 𝑠𝑑𝜀𝐼𝑑, 𝑖 ≥ 𝑖0 (2) 在初始𝑖0次迭代中,Ci取固定值 C0,之后进行自适应更新。𝑚𝑖 ̂,是未知参数向量 m 中某 个分量在第 i 次迭代的估计值。𝜀是一个非常小的数,作用是确保 Ci不成为奇异矩阵; 𝐶𝑜𝑣(𝑚̂0, 𝑚̂1, … … 𝑚̂𝑖−1 )是𝑚̂0, 𝑚̂1, … … 𝑚̂𝑖−1的协方差矩阵;𝑠𝑑是比例因子,依赖于未知随机

向量的维数d,目的是保证接受率在一个合适的范围内:在文中设定ε=10-6,Sd= 2.42/d。l:为d维单位矩阵。当进行第i+1次迭代时,由公式(2)可导出协方差计算公式 (3) Cui=C+(im+1)+mim ela) (3) 其中m,m-1是前面i,i-1次迭代的参数均值。自适应Metropolis算法的计算步骤如下: (1)设定i=0,对不同变量进行初始化。 (2)随机量的生成和接受,构造Markov链: 利用公式(3)计算协方差矩阵C,并产生服从正态分布的推荐参数m~N(m,C: 利用下式计算接受概率a=min1,(dip二 p(d m)p(mi) 产生服从均匀分布的随机数uU(0,1)小: 若u<a,则接受m+1=m,否则m*1=m. 重复上面的步骤,直到产生预先指定数量的样本为止。 模型简介: 在描述种群的生物模型中,最著名的是Lotka-Volterra方程,该模型能够模拟包括捕食 与被捕食髓个种群的生态系统。Lotka.Volterra生物模型是非线性的,数学模型如下: rdx(-rx(t)+ax(t)y(t)=0 dt (-cy(t)+bx(t)y(t)=0 (4) dt xlt=o =xo,ylt=o=yo, 式中xt),yt)分别为被捕食和捕食种群的数量;r、a、b和c为模型参数;Xo、Yo分别为初 始时刻被捕食和捕食种群的数量。模型(4)为非线性方程,很难得到解析解,为此采用数值 方法求解。原文目标是在已知捕食种群和被捕食种群数量的观测序列情况下,利用MCMC 方法准确估计生态模型参数r、a、b和c 模拟步骤: 首先利用贝叶斯公式来导出未知参数的后验PDF。假设方程(5)中影响种群数量的4个 参数m=r,a,b,c)都是未知的,即对所有模型参数同时进行估计。观测资料为 d=(x),yt)表示只使用部分观测资料。根据贝叶斯公式(1),且不考虑分母常数项,则未知 参数的后验PDF可以通过下式计算: p(r,a,b,cld)=p(dlr,a,b,c)p(r,a,b,c) (5) 其中,式(5)已经假设d=Mg,a,b,c+w,其中Mc,a,b,c表示Lokta-Volterra生态模型的离散数 值模式。w为包含观测误差的独立分布的随机噪声,服从均值为0、标准偏差为σ。的正态 分布。即w-N(O,σ)。同时假设由数值模式M引进的误差远小于观测误差,则可以得到 以下形式的似然函数: L(dlm)= 2n5ne-a-Mra.beP/o响 (6) 式中,n表示观测资料数量。假设参数r、a、b和C分别满足U(m,jl,2,,4表示的
向量的维数 d,目的是保证接受率在—个合适的范围内;在文中设定𝜀 = 10−6,𝑠𝑑 = 2.4 2/𝑑。Id为 d 维单位矩阵。当进行第 i+1 次迭代时,由公式(2)可导出协方差计算公式 (3) 𝐶𝐼+1 = 𝑖−1 𝑖 𝐶𝑖 + 𝑠𝑑 𝑖 (𝑖𝑚̂𝑖−1, 𝑚̂𝑖−1 𝑇 − (𝑖 + 1)𝑚𝑖 ̂, 𝑚̂𝑖 𝑇 + 𝑚𝑖𝑚𝑖 𝑇 + 𝜀𝐼𝑑) (3) 其中𝑚𝑖 ̂, 𝑚̂𝑖−1是前面 i,i-1 次迭代的参数均值。自适应 Metropolis 算法的计算步骤如下: (1)设定 i=0,对不同变量进行初始化。 (2)随机量的生成和接受,构造 Markov 链: 利用公式(3)计算协方差矩阵 C,并产生服从正态分布的推荐参数 m*~N(mi,Ci); 利用下式计算接受概率 α=min{1, 𝑝(𝑑|𝑚∗ )𝑝(𝑚∗ ) 𝑝(𝑑|𝑚)𝑝(𝑚𝑖) }; 产生服从均匀分布的随机数 u~U(0,1); 若 u<α,则接受 mi+1=m* ,否则 mi+1=mi. 重复上面的步骤,直到产生预先指定数量的样本为止。 模型简介: 在描述种群的生物模型中,最著名的是 Lotka-Volterra 方程,该模型能够模拟包括捕食 与被捕食髓个种群的生态系统。Lotka.Volterra 生物模型是非线性的,数学模型如下: { 𝑑𝑥(𝑡) 𝑑𝑡 − 𝑟𝑥(𝑡) + 𝑎𝑥(𝑡)𝑦(𝑡) = 0 𝑑𝑦(𝑡) 𝑑𝑡 − 𝑐𝑦(𝑡) + 𝑏𝑥(𝑡)𝑦(𝑡) = 0 𝑥|𝑡=0 = 𝑥0, 𝑦|𝑡=0 = 𝑦0, (4) 式中 x(t),y(t)分别为被捕食和捕食种群的数量;r、a、b 和 c 为模型参数;X0、Y0分别为初 始时刻被捕食和捕食种群的数量。模型(4)为非线性方程,很难得到解析解,为此采用数值 方法求解。原文目标是在已知捕食种群和被捕食种群数量的观测序列情况下,利用 MCMC 方法准确估计生态模型参数 r、a、b 和 c 模拟步骤: 首先利用贝叶斯公式来导出未知参数的后验 PDF。假设方程(5)中影响种群数量的 4 个 参数 m=(r,a,b,c)都是未知的,即对所有模型参数同时进行估计。观测资料为 d=(x(t),y(t))表示只使用部分观测资料。根据贝叶斯公式(1),且不考虑分母常数项,则未知 参数的后验 PDF 可以通过下式计算: p(r, a, b, c|d) = p(d|r, a, b, c)p(r, a, b, c) (5) 其中,式(5)已经假设 d=M(r,a,b,c)+w,其中 M(r,a,b,c)表示 Lokta-Volterra 生态模型的离散数 值模式。w 为包含观测误差的独立分布的随机噪声,服从均值为 0、标准偏差为σ0的正态 分布。即 w-N(0, σ0 2 )。同时假设由数值模式 M 引进的误差远小于观测误差,则可以得到 以下形式的似然函数: L(d|m) = 1 (2𝜋𝜎0 2 ) 𝑛/2 𝑒 −||𝑑−𝑀(𝑟,𝑎,𝑏,𝑐)|| 2 /(2𝜎0 2 ) (6) 式中,n 表示观测资料数量。。假设参数 r、a、b 和 C 分别满足 U(mj),j=l,2,⋯,4 表示的
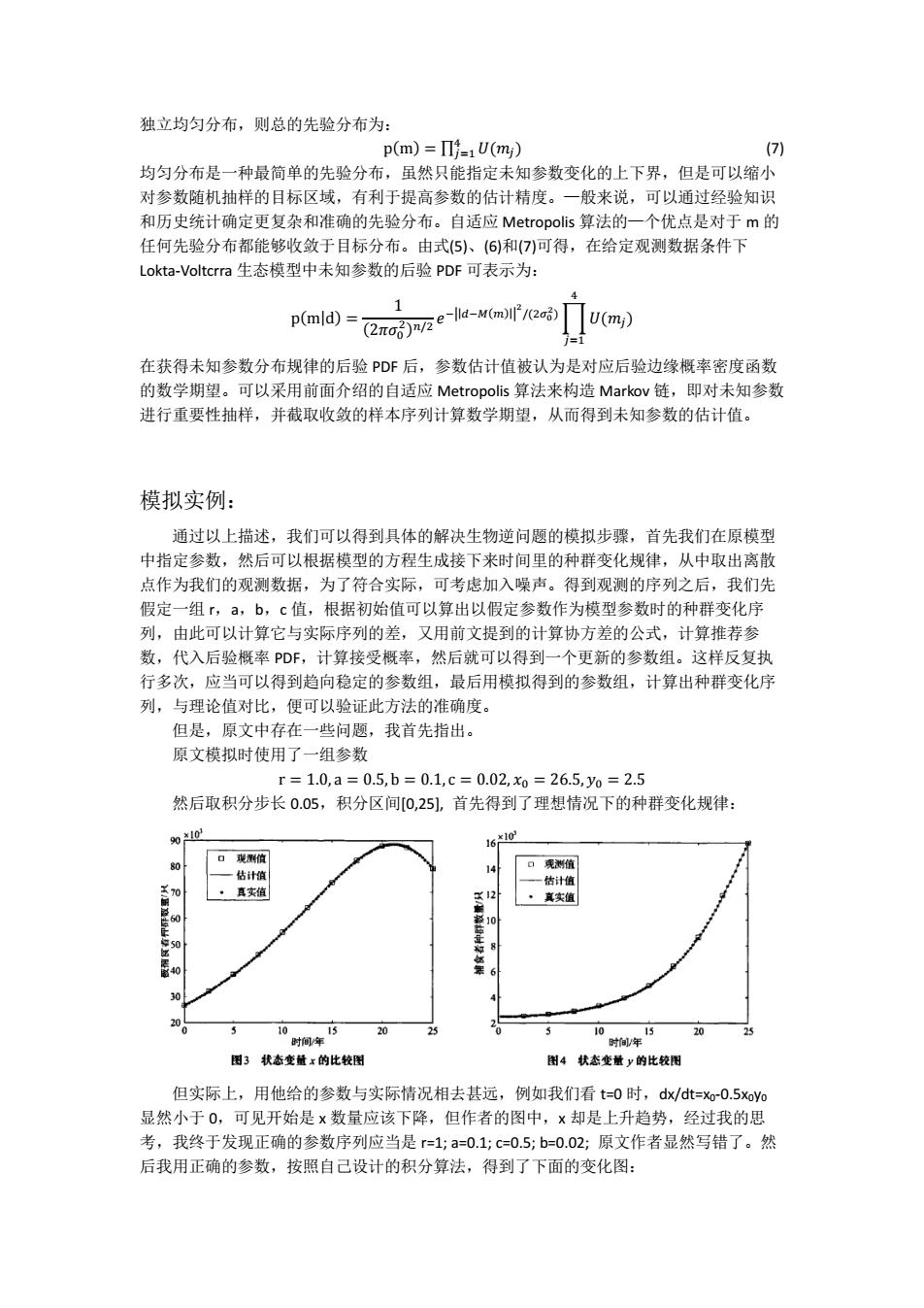
独立均匀分布,则总的先验分布为: p(m)=Π=1U(m) (7) 均匀分布是一种最简单的先验分布,虽然只能指定未知参数变化的上下界,但是可以缩小 对参数随机抽样的目标区域,有利于提高参数的估计精度。一般来说,可以通过经验知识 和历史统计确定更复杂和准确的先验分布。自适应Metropolis算法的一个优点是对于m的 任何先验分布都能够收敛于目标分布。由式(5)、(6)和(7)可得,在给定观测数据条件下 Lokta-Voltcrra生态模型中未知参数的后验PDF可表示为: pml)-2n5元ela-M6mfea响 U(mj) 在获得未知参数分布规律的后验PDF后,参数估计值被认为是对应后验边缘概率密度函数 的数学期望。可以采用前面介绍的自适应Metropolis算法来构造Markov链,即对未知参数 进行重要性抽样,并截取收敛的样本序列计算数学期望,从而得到未知参数的估计值。 模拟实例: 通过以上描述,我们可以得到具体的解决生物逆问题的模拟步骤,首先我们在原模型 中指定参数,然后可以根据模型的方程生成接下来时间里的种群变化规律,从中取出离散 点作为我们的观测数据,为了符合实际,可考虑加入噪声。得到观测的序列之后,我们先 假定一组r,a,b,c值,根据初始值可以算出以假定参数作为模型参数时的种群变化序 列,由此可以计算它与实际序列的差,又用前文提到的计算协方差的公式,计算推荐参 数,代入后验概率PDF,计算接受概率,然后就可以得到一个更新的参数组。这样反复执 行多次,应当可以得到趋向稳定的参数组,最后用模拟得到的参数组,计算出种群变化序 列,与理论值对比,便可以验证此方法的准确度。 但是,原文中存在一些问题,我首先指出。 原文模拟时使用了一组参数 r=1.0,a=0.5,b=0.1,c=0.02,x0=26.5,y0=2.5 然后取积分步长0.05,积分区间[0,25],首先得到了理想情况下的种群变化规律: 0101 80 14 口观湖值 一估计值 一估计值 生0 真实值 ×12 ·真实值 0 20 10 15 20 25 0 5 i年5 10 20 25 时间年 图3状态变量x的比较图 图4状态变量y的比较图 但实际上,用他给的参数与实际情况相去甚远,例如我们看t=0时,dxdt=xo-0.5xoyo 显然小于0,可见开始是x数量应该下降,但作者的图中,×却是上升趋势,经过我的思 考,我终于发现正确的参数序列应当是r=1;a=0.1;c=0.5;b=0.02;原文作者显然写错了。然 后我用正确的参数,按照自己设计的积分算法,得到了下面的变化图:
独立均匀分布,则总的先验分布为: p(m) = ∏ 𝑈(𝑚𝑗) 4 𝑗=1 (7) 均匀分布是一种最简单的先验分布,虽然只能指定未知参数变化的上下界,但是可以缩小 对参数随机抽样的目标区域,有利于提高参数的估计精度。—般来说,可以通过经验知识 和历史统计确定更复杂和准确的先验分布。自适应 Metropolis 算法的—个优点是对于 m 的 任何先验分布都能够收敛于目标分布。由式(5)、(6)和(7)可得,在给定观测数据条件下 Lokta-Voltcrra 生态模型中未知参数的后验 PDF 可表示为: p(m|d) = 1 (2𝜋𝜎0 2 ) 𝑛/2 𝑒 −||𝑑−𝑀(𝑚)|| 2 /(2𝜎0 2 )∏𝑈(𝑚𝑗) 4 𝑗=1 在获得未知参数分布规律的后验 PDF 后,参数估计值被认为是对应后验边缘概率密度函数 的数学期望。可以采用前面介绍的自适应 Metropolis 算法来构造 Markov 链,即对未知参数 进行重要性抽样,并截取收敛的样本序列计算数学期望,从而得到未知参数的估计值。 模拟实例: 通过以上描述,我们可以得到具体的解决生物逆问题的模拟步骤,首先我们在原模型 中指定参数,然后可以根据模型的方程生成接下来时间里的种群变化规律,从中取出离散 点作为我们的观测数据,为了符合实际,可考虑加入噪声。得到观测的序列之后,我们先 假定一组 r,a,b,c 值,根据初始值可以算出以假定参数作为模型参数时的种群变化序 列,由此可以计算它与实际序列的差,又用前文提到的计算协方差的公式,计算推荐参 数,代入后验概率 PDF,计算接受概率,然后就可以得到一个更新的参数组。这样反复执 行多次,应当可以得到趋向稳定的参数组,最后用模拟得到的参数组,计算出种群变化序 列,与理论值对比,便可以验证此方法的准确度。 但是,原文中存在一些问题,我首先指出。 原文模拟时使用了一组参数 r = 1.0, a = 0.5, b = 0.1, c = 0.02, 𝑥0 = 26.5, 𝑦0 = 2.5 然后取积分步长 0.05,积分区间[0,25], 首先得到了理想情况下的种群变化规律: 但实际上,用他给的参数与实际情况相去甚远,例如我们看 t=0 时,dx/dt=x0-0.5x0y0 显然小于 0,可见开始是 x 数量应该下降,但作者的图中,x 却是上升趋势,经过我的思 考,我终于发现正确的参数序列应当是 r=1; a=0.1; c=0.5; b=0.02; 原文作者显然写错了。然 后我用正确的参数,按照自己设计的积分算法,得到了下面的变化图:
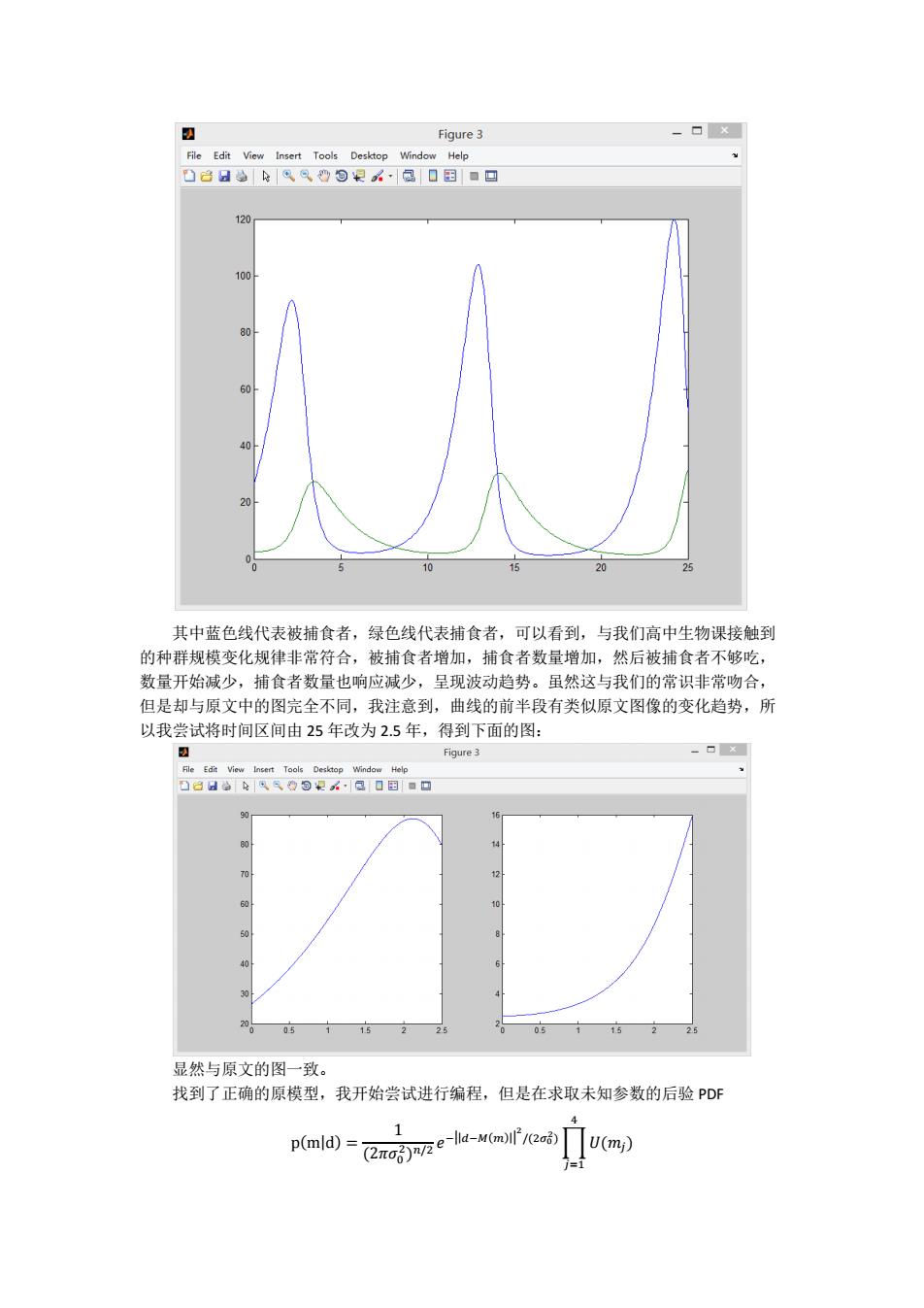
日 Figure 3 File Edit View Insert Tools Desktop Window Help 口名日双只沙包公·岛日田■▣ 120 100 10 20 25 其中蓝色线代表被捕食者,绿色线代表捕食者,可以看到,与我们高中生物课接触到 的种群规模变化规律非常符合,被捕食者增加,捕食者数量增加,然后被捕食者不够吃, 数量开始减少,捕食者数量也响应减少,呈现波动趋势。虽然这与我们的常识非常吻合, 但是却与原文中的图完全不同,我注意到,曲线的前半段有类似原文图像的变化趋势,所 以我尝试将时间区间由25年改为2.5年,得到下面的图: Figure 3 File Edit View Insert Tools Desktop Window Help 日名日公⊙视k,同口国■回 05 15 05 1.5 显然与原文的图一致。 找到了正确的原模型,我开始尝试进行编程,但是在求取未知参数的后验PDF U(mj)
其中蓝色线代表被捕食者,绿色线代表捕食者,可以看到,与我们高中生物课接触到 的种群规模变化规律非常符合,被捕食者增加,捕食者数量增加,然后被捕食者不够吃, 数量开始减少,捕食者数量也响应减少,呈现波动趋势。虽然这与我们的常识非常吻合, 但是却与原文中的图完全不同,我注意到,曲线的前半段有类似原文图像的变化趋势,所 以我尝试将时间区间由 25 年改为 2.5 年,得到下面的图: 显然与原文的图一致。 找到了正确的原模型,我开始尝试进行编程,但是在求取未知参数的后验 PDF p(m|d) = 1 (2𝜋𝜎0 2 ) 𝑛/2 𝑒 −||𝑑−𝑀(𝑚)|| 2 /(2𝜎0 2 )∏𝑈(𝑚𝑗) 4 𝑗=1

的时候遇到了非常不解的问题,原文中设定参数σ=0.1,但是前面又说σ是观测中叠加 的高斯噪声的标准差,噪声的标准差与密度函数的标准差显然没有联系,而且,需要求取 的密度函数为多元正态分布,据我查资料,根本不能这样求取,实际操作中我也发现,以 这个参数进行计算,Matlab结果表明运算过程中基本没有精度可言,已大大超出机器接受 的有效数字范围,所以我自己把它改为一较大的正数,得到了稍好的结果。 然后另一个关键的步骤,求取推荐的参数,需要用到协方差矩阵的概念,我用原文 给的公式 G41s1。 (+兰(mm,-+1m,m+m,m+) 试图计算协方差矩阵,但是,程序运行时却提示随机产生一个服从多元正态分布的参数组 需要半正定的协方差矩阵,由此可见该公式的计算结果存在问题,故我放弃了这个方法, 改用直接求协方差矩阵的方法,获取推荐参数,形成模拟,然而,受限于能力,最终并没 有得到理想的结果,模拟次数已经达到数千次的情况下,参数序列丝毫没有收敛的迹象, 显然,程序算法出现了问题,但是我长时间调试检查仍然没有得到想要的结果,由于专业 知识限制以及时间限制,无法去探索另外的求解方法,所以只好就现在的结果进行分析, 下面的图表明了模拟的结果与实际应该的结果的关系: 2 Figure 1 File Edit View Insert Tools Desktop Window Help 凸3日分®⑨”包捏公·同口国口回 ◆ 90 理想值 80 模拟值 70 50 40 20 理想值 模拟值 0.5 1.5 2.5 ◆ ◆ 可以看到,误差非常大,这是因为估计的参数根本没有收敛。下面是四个估计参数的 变化情况:
的时候遇到了非常不解的问题,原文中设定参数𝜎0 = 0.1,但是前面又说𝜎0是观测中叠加 的高斯噪声的标准差,噪声的标准差与密度函数的标准差显然没有联系,而且,需要求取 的密度函数为多元正态分布,据我查资料,根本不能这样求取,实际操作中我也发现,以 这个参数进行计算,Matlab 结果表明运算过程中基本没有精度可言,已大大超出机器接受 的有效数字范围,所以我自己把它改为一较大的正数,得到了稍好的结果。 然后另一个关键的步骤,求取推荐的参数 m,需要用到协方差矩阵的概念,我用原文 给的公式 𝐶𝐼+1 = 𝑖 − 1 𝑖 𝐶𝑖 + 𝑠𝑑 𝑖 (𝑖𝑚̂𝑖−1, 𝑚̂𝑖−1 𝑇 − (𝑖 + 1)𝑚𝑖 ̂, 𝑚̂𝑖 𝑇 + 𝑚𝑖𝑚𝑖 𝑇 + 𝜀𝐼𝑑) 试图计算协方差矩阵,但是,程序运行时却提示随机产生一个服从多元正态分布的参数组 需要半正定的协方差矩阵,由此可见该公式的计算结果存在问题,故我放弃了这个方法, 改用直接求协方差矩阵的方法,获取推荐参数,形成模拟,然而,受限于能力,最终并没 有得到理想的结果,模拟次数已经达到数千次的情况下,参数序列丝毫没有收敛的迹象, 显然,程序算法出现了问题,但是我长时间调试检查仍然没有得到想要的结果,由于专业 知识限制以及时间限制,无法去探索另外的求解方法,所以只好就现在的结果进行分析, 下面的图表明了模拟的结果与实际应该的结果的关系: 可以看到,误差非常大,这是因为估计的参数根本没有收敛。下面是四个估计参数的 变化情况:
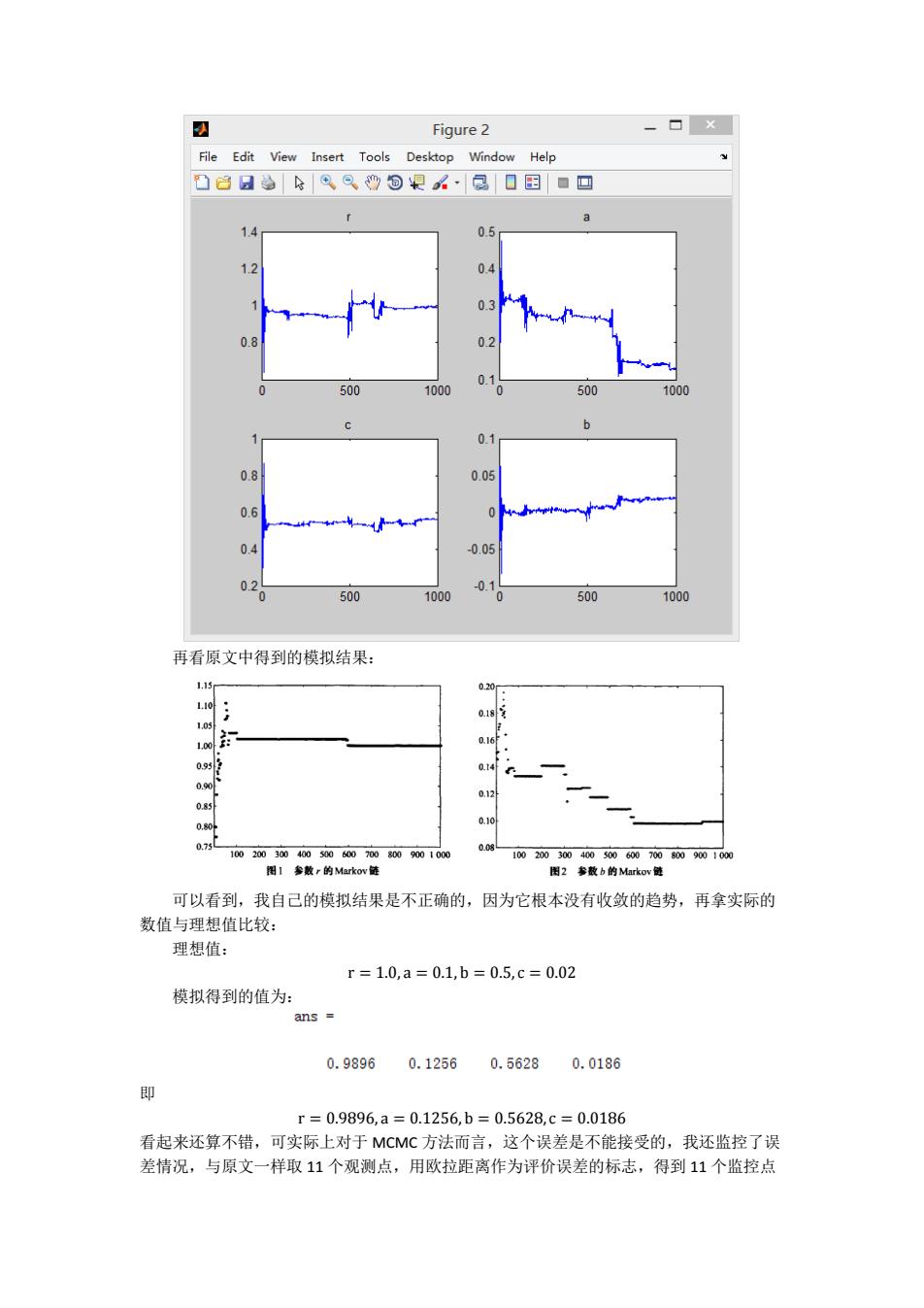
日 Figure 2 File Edit View Insert Tools Desktop Window Help 凸3且动®⑨9回提公,园口国口回 a 1.4 0.5 1.2 0.4 0.8 02 500 1000 500 1000 6 0.1 0.8 0.05 0.6 0 0.4 0.05 02 -0.1 500 1000 500 1000 再看原文中得到的模拟结果: 1.15r 0.20 1.10 1.05 1.0 0.95 0.14 0.12 0.85 0.80 0.10 0.75C 008 1002003004005006007008009001000 1002003004005006007008009001000 图I参数r的Markov 图2参数b的Markov链 可以看到,我自己的模拟结果是不正确的,因为它根本没有收敛的趋势,再拿实际的 数值与理想值比较: 理想值: r=1.0,a=0.1,b=0.5,c=0.02 模拟得到的值为: ans 0.98960.12560.56280.0186 即 r=0.9896,a=0.1256,b=0.5628,c=0.0186 看起来还算不错,可实际上对于MCMC方法而言,这个误差是不能接受的,我还监控了误 差情况,与原文一样取11个观测点,用欧拉距离作为评价误差的标志,得到11个监控点
再看原文中得到的模拟结果: 可以看到,我自己的模拟结果是不正确的,因为它根本没有收敛的趋势,再拿实际的 数值与理想值比较: 理想值: r = 1.0, a = 0.1, b = 0.5, c = 0.02 模拟得到的值为: 即 r = 0.9896, a = 0.1256, b = 0.5628, c = 0.0186 看起来还算不错,可实际上对于 MCMC 方法而言,这个误差是不能接受的,我还监控了误 差情况,与原文一样取 11 个观测点,用欧拉距离作为评价误差的标志,得到 11 个监控点

的总误差的平方和 error2 197.7313 将其除以11再开方,近似得到每点平均误差为4.24,而原文的模拟结果误差极小,可以忽 略,由此可见,对于此生物逆问题的模拟结果不尽如人意,但我认为这其中除了我自己知 识有限,理解能力有限等因素之外,原作者对于某些算法和描述的错误也是一个重要因 素。 写在最后: 本次作业要求对于目前科技研究前沿的论文进行解读并实现,我虽然已经尽力理解并 尝试,但是最终仍然没有得到理想的结果,不过收获依然是很大的,找出原文中的几处错 误,自己花时间编程测试,最终写出这份报告,都凝聚了我的时间与精力,也提升了自己 对于生物逆问题数学模型的理解。最后,感谢老师这一学期精彩的授课与课下辅导! 代码列表: x=1; 设定的参数 a=0.1; c=0.5; b=0.02; t=1 inspace(0,2.5,501);号用于精确绘图的时间点分割 x=zeros(1,501): 号被捕食者种群大小 y=zeros(1,501); 号捕食者种群大小 x0=26.5; 号初始的被捕食者 y0=2.5; 号初始的捕食者x(1)=x0; y(1)=y0: fori=2:501 x(1)=x(1-1)+0.005*(x*×(i-1)-a*x(i-1)*y(i-1)); 冬逐次积分,更新种群 数量 y(i)=y(1-1)+0.005*(-c*y(i-1)+b*x(i-1)*y(i-1)): end figure(1) plot(t,x,t,y) 号画出设定参数情况下种群变化规律nold on samplex0=zeros(1,11); 取观测样本 sampley0=zeros(1,11); for j=1:11 samp1ex0(j)=x(50*j-49); samp1ey0(j)=y(50*j-49); end N=1000:号迭代次数,由于测试显示即使迭代10000次仍无收敛迹象,故设为1000次节省资 源 M=zeros(1000,4); 号存储四个参数,将1000次迭代的过程存储下来
的总误差的平方和 将其除以 11 再开方,近似得到每点平均误差为 4.24,而原文的模拟结果误差极小,可以忽 略,由此可见,对于此生物逆问题的模拟结果不尽如人意,但我认为这其中除了我自己知 识有限,理解能力有限等因素之外,原作者对于某些算法和描述的错误也是一个重要因 素。 写在最后: 本次作业要求对于目前科技研究前沿的论文进行解读并实现,我虽然已经尽力理解并 尝试,但是最终仍然没有得到理想的结果,不过收获依然是很大的,找出原文中的几处错 误,自己花时间编程测试,最终写出这份报告,都凝聚了我的时间与精力,也提升了自己 对于生物逆问题数学模型的理解。最后,感谢老师这一学期精彩的授课与课下辅导! 代码列表: r=1; %设定的参数 a=0.1; c=0.5; b=0.02; t=linspace(0,2.5,501); %用于精确绘图的时间点分割 x=zeros(1,501); %被捕食者种群大小 y=zeros(1,501); %捕食者种群大小 x0=26.5; %初始的被捕食者 y0=2.5; %初始的捕食者x(1)=x0; y(1)=y0; for i=2:501 x(i)=x(i-1)+0.005*(r*x(i-1)-a*x(i-1)*y(i-1)); %逐次积分,更新种群 数量 y(i)=y(i-1)+0.005*(-c*y(i-1)+b*x(i-1)*y(i-1)); end figure(1) plot(t,x,t,y) %画出设定参数情况下种群变化规律hold on samplex0=zeros(1,11); %取观测样本 sampley0=zeros(1,11); for j=1:11 samplex0(j)=x(50*j-49); sampley0(j)=y(50*j-49); end N=1000; %迭代次数,由于测试显示即使迭代10000次仍无收敛迹象,故设为1000次节省资 源 M=zeros(1000,4); %存储四个参数,将1000次迭代的过程存储下来

samplex=zeros(1,11); 冬取样 sampley=zeros(1,11); errorl=0; %误差 error2=0; delta=11; 号标准差 deltal=-1/2/delta/delta; eks1o=10^(-6);号保证协方差矩阵非奇异 M init0=[10.30.50.01];号初始的参数表 M init1=[1.20.20.30.06]; M(1,:)=M inito; M(2,:)=M init1; M_init=[M_init0;M_init1]; xiefangcha=cov(M init); for k=1:N-2 x=y(k,1); a=M(k,2); c=M(k,3): b=M(k,4); fori=2:501 x(1)=x(i-1)+0.005*(r*x(i-1)-a*x(i-1)*y(i-1)); y(i)=y(i-1)+0.005*(-c*y(i-1)+b*×(i-1)*y(i-1)): end error1=0; forj=1:11号计算欧拉距离 samplex (j)=x(50*j-49); sampley(j)=y(50*j-49); errorl=error1+(samplex0(j)-samplex(j))2+(sampley0(j)- sampley(j))2; end pdf1-exp(deltal*error1); 号计算概率密度,考虑到后面会约掉常数故舍去常数 if max (M(k,:))>2 pdf1=1; end M_now=[M(k,:);M(k+1,:)]; 号M_now=M(1:k+1,:): iefangcha=cov(Mnow)+ekslo*eye(4);号计算协方差 1fk==1 m1=M(1,:): else m1=mean(M(1:k,:)); end m2=mean(M(1:k+1,:)): &xiefangcha=k/(k+1)*xiefangcha+ml'*m1-
samplex=zeros(1,11); %取样 sampley=zeros(1,11); error1=0; %误差 error2=0; delta=11; %标准差 delta1=-1/2/delta/delta; ekslo=10^(-6); %保证协方差矩阵非奇异 M_init0=[1 0.3 0.5 0.01]; %初始的参数表 M_init1=[1.2 0.2 0.3 0.06]; M(1,:)=M_init0; M(2,:)=M_init1; M_init=[M_init0;M_init1]; xiefangcha=cov(M_init); for k=1:N-2 r=M(k,1); a=M(k,2); c=M(k,3); b=M(k,4); for i=2:501 x(i)=x(i-1)+0.005*(r*x(i-1)-a*x(i-1)*y(i-1)); y(i)=y(i-1)+0.005*(-c*y(i-1)+b*x(i-1)*y(i-1)); end error1=0; for j=1:11 %计算欧拉距离 samplex(j)=x(50*j-49); sampley(j)=y(50*j-49); error1=error1+(samplex0(j)-samplex(j))^2+(sampley0(j)- sampley(j))^2; end pdf1=exp(delta1*error1); %计算概率密度,考虑到后面会约掉常数故舍去常数 if max(M(k,:))>2 pdf1=1; end M_now=[M(k,:);M(k+1,:)]; %M_now=M(1:k+1,:); xiefangcha=cov(M_now)+ekslo*eye(4); %计算协方差 if k==1 m1=M(1,:); else m1=mean(M(1:k,:)); end m2=mean(M(1:k+1,:)); %xiefangcha=k/(k+1)*xiefangcha+m1'*m1-

m2'*m2*(k+2)/(k+1)+M(k+1,:)"*M(k+1,:)/(k+1)+eks1o*eye(4); M_new=mvnrnd(M(k,:),xiefangcha); 号生成满足取样值得多元正态分布随机数 r=M new(1); a=M new(2); c=M_new(3); b=M new (4); fori=2:501 ×(i)=x(i-1)+0.005*(r*x(i-1)-a*x(i-1)*y(i-1)): y(1)=y(i-1)+0.005*(-c*y(i-1)+b*x(i-1)*y(i-1)); end error2=0; for j=1:11 samplex(j)=x(50*j-49); sampley(j)=y(50*j-49); error2=error2+(samplex0(j)-samplex(j))2+(sampley0(j)- sampley(i))2; end pdf2=exp(deltal*error2); 号建议参数的密度函数 if max(M new)>2 pdf2=0; end alpha=min(1,pdf2/pdf1);号计算接受概率 u=rand;号生成随机数 if u<alpha M(k+2,:)=M_new; 号接受-拒绝法 else M(k+2,:)=M(k,:); end end plot(t,x,t,y) 画出模拟参数对应的种群变化图 hold off M(1000,:) figure(2) ceshi=linspace(1,1000,1000); subp1ot(2,2,1)画出四个参数的变化过程 plot(ceshi,M(:,1)') title('r') subplot(2,2,2) plot (ceshi,M(:,2)') title('a') subplot(2,2,3) plot(ceshi,M(:,3)') title('c')
m2'*m2*(k+2)/(k+1)+M(k+1,:)'*M(k+1,:)/(k+1)+ekslo*eye(4); M_new=mvnrnd(M(k,:),xiefangcha); %生成满足取样值得多元正态分布随机数 r=M_new(1); a=M_new(2); c=M_new(3); b=M_new(4); for i=2:501 x(i)=x(i-1)+0.005*(r*x(i-1)-a*x(i-1)*y(i-1)); y(i)=y(i-1)+0.005*(-c*y(i-1)+b*x(i-1)*y(i-1)); end error2=0; for j=1:11 samplex(j)=x(50*j-49); sampley(j)=y(50*j-49); error2=error2+(samplex0(j)-samplex(j))^2+(sampley0(j)- sampley(j))^2; end pdf2=exp(delta1*error2); %建议参数的密度函数 if max(M_new)>2 pdf2=0; end alpha=min(1,pdf2/pdf1); %计算接受概率 u=rand; %生成随机数 if u<alpha M(k+2,:)=M_new; %接受-拒绝法 else M(k+2,:)= M(k,:); end end plot(t,x,t,y) %画出模拟参数对应的种群变化图 hold off M(1000,:) figure(2) ceshi=linspace(1,1000,1000); subplot(2,2,1) %画出四个参数的变化过程 plot(ceshi,M(:,1)') title('r') subplot(2,2,2) plot(ceshi,M(:,2)') title('a') subplot(2,2,3) plot(ceshi,M(:,3)') title('c')