
上游充通大 SHANGHAI JIAOTONG UNIVERSITY 随机模拟方法及应用 Stochastic Simulation Methods and Its Applications 课程论文 THESIS OF CURRICULUM AI HAO TONG UNIVERS 对流-扩散方程源项识别反问题的MCMC方法论文研读 专 业:材料科学与工程 班 级: F1405101 学 号: 5140519014 学生姓名: 孙密广 指导教师: 当柳青 完成时间:2022年3月11日
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 SHANGHAI JIAOTONG UNIVERSITY 随机模拟方法及应用 Stochastic Simulation Methods and Its Applications 课程论文 THESIS OF CURRICULUM 对流-扩散方程源项识别反问题的 MCMC 方法论文研读 专 业:材料科学与工程 班 级: F1405101 学 号: 5140519014 学生姓名: 孙密广 指导教师: 肖柳青 完成时间:2022 年 3 月 11 日

随机模拟方法及应用 材料科学与工程学院F1405101班孙密广学号:5140519014 对流-扩散方程源项识别反问题的MCMC方法论文研读 材料科学与工程学院 F1405101班孙密广学号:5140519014 目录 1.摘要.… 2 2.MCMC方法基本介绍... 2 3.用Metropolis算法对密度函数进行抽样..2 3.1伽马分布及问题. 3 3.2 matlab程序.... …3 3.3相关图像及图像说明 ……4 4.对流-扩散方程源项识别反问题 4.1对流-扩散方程.... 4.2狄拉克函数....· ..6 4.3反问题的解决思路.....·… ‘、、 4.4个人在研读过程遇到的相关问题..7 5.总结... 6.致谢. 第1页
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 第 1 页 对流-扩散方程源项识别反问题的 MCMC 方法论文研读 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 目录 1.摘要................................................2 2.MCMC 方法基本介绍....................................2 3.用 Metropolis 算法对密度函数进行抽样.................2 3.1 伽马分布及问题.................................3 3.2 matlab 程序....................................3 3.3 相关图像及图像说明.............................4 4.对流-扩散方程源项识别反问题.........................6 4.1 对流-扩散方程....................................6 4.2 狄拉克函数.......................................6 4.3 反问题的解决思路.................................7 4.4 个人在研读过程遇到的相关问题.....................7 5.总结................................................8 6.致谢................................................8

随机模拟方法及应用 材料科学与工程学院F1405101班孙密广学号:5140519014 1.摘要 首先阐述Metropolis算法实现的具体步骤和基本原理,然后证明由此产生的 Markov链满足细致平衡条件,从而以目标分布为不变分布。首先从MCMC进 行密度函数抽样的例子入手,以说明这种算法的高效性和可行性。最后引入实际 中所遇到的对流-扩散方程源项识别反问题,并介绍将其问题建模后转化成可用 MCMC解决问题的过程。展示MCMC方法在一些难以进行实际运算的数学问题 中巨大用处。初步了解数学建模的过程。 关键词:Metropolis算法,MCMC,密度函数抽样,对流-扩散方程源项识别反问题 2.MCMC方法基本介绍 蒙特·卡罗方法,也称统计模拟方法,是指使用随机数(或更常见的伪随机 数)来解决很多计算问题的方法。与它对应的是确定性算法。蒙特·卡罗方法在 金融工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计算、空 气动力学计算)等领域应用广泛。 Metropolis算法是蒙特卡洛方法中最著名的算法,它的应用疆域包括统计物 理、QCD、天体物理、物理化学、数学、计算生物等等,甚至是社会科学。 其基本思想是构造一个遍历的马尔科夫链(状态的转移仅仅依赖当前的状 态,而与以前的状态无关,其基本性质是存在一个不变分布,使得其不变分布成 为人们所需要的抽样分布。 3.用Metropolis算法对密度函数进行抽样 基于上面对于MCMC算法的介绍,运用Metropolis算法从密度函数 fx)=cxe,(0≤x0,从任一点开 始检验分布,相关性及特征量。 第2页
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 第 2 页 1.摘要 首先阐述 Metropolis 算法实现的具体步骤和基本原理,然后证明由此产生的 Markov 链满足细致平衡条件,从而以目标分布为不变分布。首先从 MCMC 进 行密度函数抽样的例子入手,以说明这种算法的高效性和可行性。最后引入实际 中所遇到的对流-扩散方程源项识别反问题,并介绍将其问题建模后转化成可用 MCMC 解决问题的过程。展示 MCMC 方法在一些难以进行实际运算的数学问题 中巨大用处。初步了解数学建模的过程。 关键词:Metropolis 算法,MCMC,密度函数抽样,对流-扩散方程源项识别反问题 2.MCMC 方法基本介绍 蒙特·卡罗方法,也称统计模拟方法,是指使用随机数(或更常见的伪随机 数)来解决很多计算问题的方法。与它对应的是确定性算法。蒙特·卡罗方法在 金融工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计算、空 气动力学计算)等领域应用广泛。 Metropolis 算法是蒙特卡洛方法中最著名的算法,它的应用疆域包括统计物 理、QCD、天体物理、物理化学、数学、计算生物等等,甚至是社会科学。 其基本思想是构造一个遍历的马尔科夫链(状态的转移仅仅依赖当前的状 态,而与以前的状态无关,其基本性质是存在一个不变分布,使得其不变分布成 为人们所需要的抽样分布。 3.用 Metropolis 算法对密度函数进行抽样 基于上面对于 MCMC 算法的介绍,运用 Metropolis 算法从密度函数 f(x)= x cx e 2 ,( 0 x< )取样,x 的领域取为[x , x ] ,存在 >0,从任一点开 始检验分布,相关性及特征量

随机模拟方法及应用 材料科学与工程学院F1405101班孙密广学号:5140519014 3.1伽马分布 伽玛分布是统计学的一种连续概率函数。Gamma分布中的参数a称为形状参数, B称为尺度参数。其概率密度函数如下所示。 1 Ga(x)= xa-le音,x> BT(a 伽玛分布期望是af,方差是4邛2 因此原题中即为满足=3,B=1的伽马分布 3.2 MATLAB程序 =input('从输入的x开始取样x∈[0,+∞)'); f=inline('0.5*x*x*ep(-x)');号未来的版本会删除incline,请使用anonymous functions d=zeros(1,40000); tic fori=1:40000 y=unifrnd(x-0.01,x+0.01):号可在此改变6的大小 if y<0 y=xi end h=min(1,f(y)/f(x);号满足对称化条件的简化 U=rand; if U<h x=yi end d(i)=x; end a=0:0.08:20; hist(d(20001:40000),a)号从后面的20000取样,取点前面“暖场”过程 toc号与前面的tic联合起来测算运行时间 第3页
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 第 3 页 3.1 伽马分布 伽玛分布是统计学的一种连续概率函数。Gamma 分布中的参数α称为形状参数, β称为尺度参数。其概率密度函数如下所示。 伽玛分布期望是 ,方差是 因此原题中即为满足 3, 1的伽马分布 3.2 MATLAB 程序 x=input('从输入的 x 开始取样 x∈[0,+∞)'); f=inline('0.5*x*x*exp(-x)');%未来的版本会删除 incline,请使用 anonymous functions d=zeros(1,40000); tic for i=1:40000 y=unifrnd(x-0.01,x+0.01);%可在此改变δ的大小 if y<0 y=x; end h=min(1,f(y)/f(x));%满足对称化条件的简化 U=rand; if U<h x=y; end d(i)=x; end a=0:0.08:20; hist(d(20001:40000),a)%从后面的 20000 取样,取点前面“暖场”过程 toc %与前面的 tic 联合起来测算运行时间

随机模拟方法及应用 材料科学与工程学院F1405101班孙密广学号:5140519014 3.3相关图像及图像说明 由题意可得X~Ga(3,1)Γ(3)=2!=2,可得c=0.5 取X=10,E(X)=3,DX)=3 6=1, 6=0.5, 6=0.25 00 15 20 取X=2,E(X)=3,D(X)=3 6=1 6=0.5 6=0.25 500 40 第4页
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 第 4 页 3.3 相关图像及图像说明 由题意可得 X~Ga(3,1)Γ(3)=2!=2,可得 c=0.5 取 X=10,E(X)=3,D(X)=3 δ=1, δ=0.5, δ=0.25 取 X=2,E(X)=3,D(X)=3 δ=1 δ=0.5 δ=0.25
随机模拟方法及应用 材料科学与工程学院F1405101班孙密广学号:5140519014 可从上面的实验观察到伽马分布的图像与X的取值基本没关系,只与6的取值 有关系。δ值越小,分布图的峰值越大(峰度),对称性越好(偏度)。由于取 样的范围发生了变化因此会对图形的峰度和偏度产生一定的影响。 最后验证δ值比较大的几个极端情况 8=10, 6=0.01, 0o 15 20 从上面2个较为极端情况的例子可以看出,上面的验证基本符合自己先前的猜想。 继续将模拟进行下去,会看到随着6的不断变大。伽马分布原本的函数图形也发 生了畸变。因此告诉我们在取样的时候样本范围应该尽量小点,从而保证图像的 精确程度,否则就会出现失真现象。 1800 70 50 6=100, 6=1000, 第5页
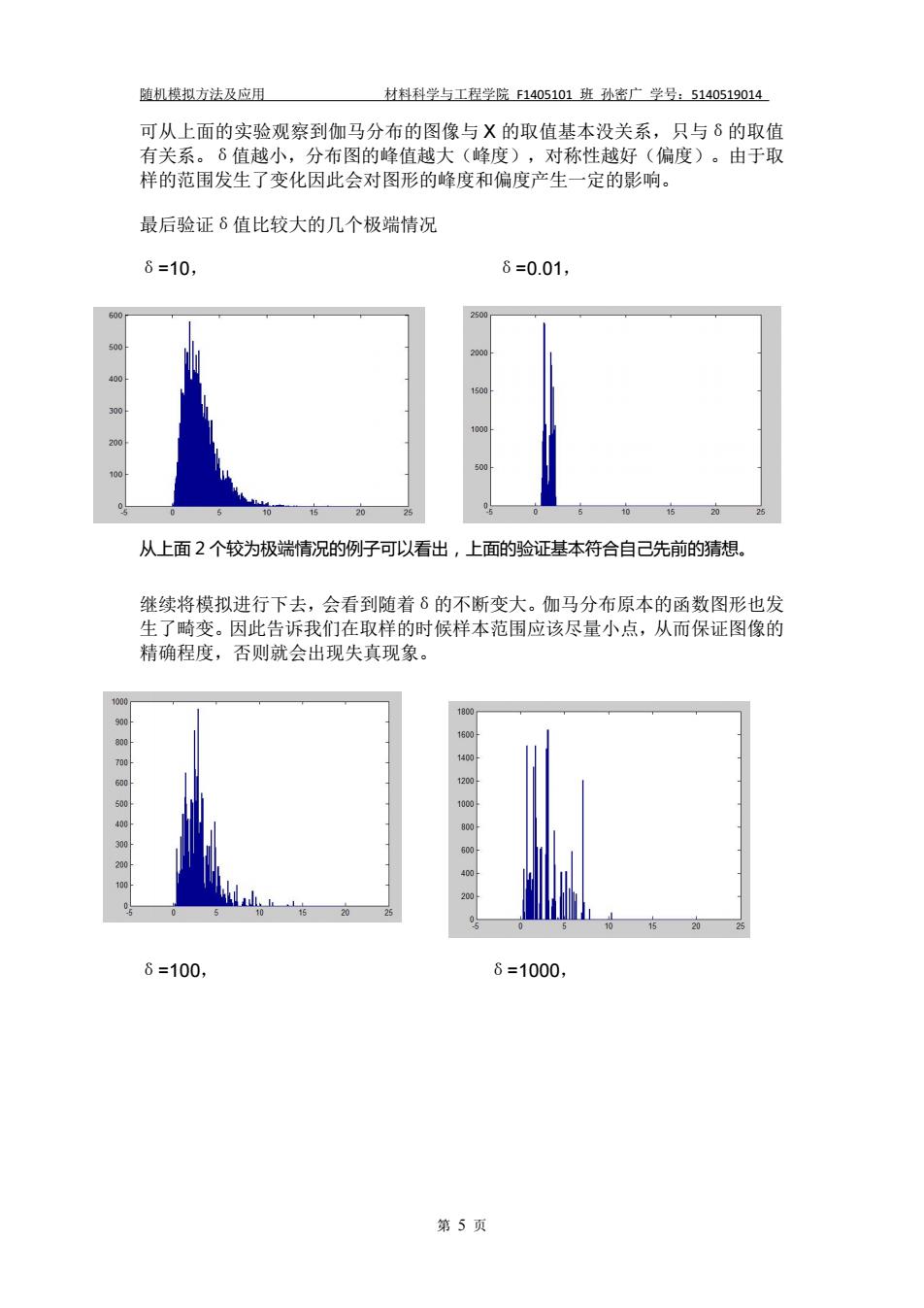
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 第 5 页 可从上面的实验观察到伽马分布的图像与 X 的取值基本没关系,只与δ的取值 有关系。δ值越小,分布图的峰值越大(峰度),对称性越好(偏度)。由于取 样的范围发生了变化因此会对图形的峰度和偏度产生一定的影响。 最后验证δ值比较大的几个极端情况 δ=10, δ=0.01, 从上面 2 个较为极端情况的例子可以看出,上面的验证基本符合自己先前的猜想。 继续将模拟进行下去,会看到随着δ的不断变大。伽马分布原本的函数图形也发 生了畸变。因此告诉我们在取样的时候样本范围应该尽量小点,从而保证图像的 精确程度,否则就会出现失真现象。 δ=100, δ=1000

随机模拟方法及应用 材料科学与工程学院F1405101班孙密广学号:5140519014 4.对流-扩散方程源项识别反问题 4.1对流-扩散方程 对流扩散方程是一类基本的运动方程,它可以用来对流扩散问题数值计算方 法的研究具有重要的理论和实际意义,可用于环境科学、能源开发、流体力学和 电子科学等许多领域。 对流扩散方程是描述粘性流体运动的非线性Bu「gers的线性化模型,它可以 描述水体和大气中污染物的输移、扩散和降解,海水盐度和温度扩散,流体流动 与传热和电化学反应等问题。 以不同数值计算求解对流-扩散方程,以模拟研究对象在时间和空间上的演化 称为正问题。通过所研究的观测资料来估计和识别方程中的参数、原项、边界和 初始条件等成为反问题。 4.2狄拉克函数 由于对流扩散方程中涉及到狄拉克函数,在此做出相关内容补充。 狄拉克δ函数是一个广义函数,在物理学中常用其表示质点、点电荷等理想 模型的密度分布,该函数在除了零以外的点取值都等于零,而其在整个定义域上 的积分等于1。 9% δ(x)=0,(x≠0) δ(x)dx=1 如果函数不在0点取非零值,而在其他地方,可定义 00 6a(x)=6x-a)=0,(x≠a) δa(x)dx=1 其积分运算实际上,只要我们对一个不连续函数取微分,就会出现6函数 1,x≥0 H(x)= 0,x<0 6(x)= dH(x) dx 第6页
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 第 6 页 4.对流-扩散方程源项识别反问题 4.1 对流-扩散方程 对流扩散方程是一类基本的运动方程,它可以用来对流扩散问题数值计算方 法的研究具有重要的理论和实际意义,可用于环境科学、能源开发、流体力学和 电子科学等许多领域。 对流扩散方程是描述粘性流体运动的非线性 Burgers 的线性化模型,它可以 描述水体和大气中污染物的输移、扩散和降解,海水盐度和温度扩散,流体流动 与传热和电化学反应等问题。 以不同数值计算求解对流-扩散方程,以模拟研究对象在时间和空间上的演化 称为正问题。通过所研究的观测资料来估计和识别方程中的参数、原项、边界和 初始条件等成为反问题。 4.2 狄拉克函数 由于对流扩散方程中涉及到狄拉克函数,在此做出相关内容补充。 狄拉克δ函数是一个广义函数,在物理学中常用其表示质点、点电荷等理想 模型的密度分布,该函数在除了零以外的点取值都等于零,而其在整个定义域上 的积分等于 1。 如果函数不在 0 点取非零值,而在其他地方,可定义 其积分运算实际上,只要我们对一个不连续函数取微分,就会出现δ函数

随机模拟方法及应用 材料科学与工程学院F1405101班孙密广学号:5140519014 在对流扩散方程中,利用此函数表示在某个特定位置污染源产生。 4.3反问题的解决思路: (1)首先列出一般性的对流-扩散方程模拟污染物在河道中的扩散,并在实际背 景中得出初边值问题条件下的对流-扩散方程一一是个二阶非线性偏微分方程。 (2)为解方程,将未知参数向量的估计值映射成观测空间的值(从实际的观察 情况入手),引入解算子。利用指数函数的相关函数变换,将原方程化简为等价 的定解问题。 (3)利用特征值和特征函数解化简后的方程组,再利用级数将特征函数进行展 开,在进行相关运算和化简得到在边界条件下原方程组的解。 (4)方程的解其中包括开始引入的解算子(包括时间和空间信息的点污染源位 置和排放强度构成的需要识别的位置向量一一需要对解算子进行截断,基于实际 问题的背景给出特定的解算子) (5)接下来利用MCMC方法将特定的解算子和相应的对流-扩散方程的解一一 对应。 (6)利用贝叶斯公式,将未知参数的先验分布改进为后验分布。通过观测数据 获得参数的统计矩 (7)每个参数的均值、方差和其他高阶统计量的计算由于表达式的不明确以及 计算量会随向量维数增加而呈现指数增长。拟采用MCMC算法对高维随机向量 上无明确数学表达式的概率分布进行模拟抽样。 (8)结合实际问题背景,验证满足马尔科夫性。利用自适应Metropolis算法, 用后验参数的协方差矩阵来估算参数分布一一前0次迭代取为定值以进行自适 应更新。利用数学技巧,导出协方差的计算公式(满足马尔科夫性,当前状态仅 与上一条件有关)数学模型建立,设计并编写程序进行数值模拟,得出相关结论。 (9)优势分析:计算效率较同类的遗传算法更优,对于单个未知参数也只需要 产生4000~5000个样本。 4.4编写程序遇到的问题 (1)matlab运用不够熟练数学模型和程序间的转换,函数关系式的输入等仍需 要进一步的学习。 (2)数学知识的缺乏,相关的演算和处理过程不能很好理解。 (3)大体的步骤基本理解,对于建立模型中的一些细节性的考量不是太理解。 第7页
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 第 7 页 在对流扩散方程中,利用此函数表示在某个特定位置污染源产生。 4.3 反问题的解决思路: (1)首先列出一般性的对流-扩散方程模拟污染物在河道中的扩散,并在实际背 景中得出初边值问题条件下的对流-扩散方程——是个二阶非线性偏微分方程。 (2)为解方程,将未知参数向量的估计值映射成观测空间的值(从实际的观察 情况入手),引入解算子。利用指数函数的相关函数变换,将原方程化简为等价 的定解问题。 (3)利用特征值和特征函数解化简后的方程组,再利用级数将特征函数进行展 开,在进行相关运算和化简得到在边界条件下原方程组的解。 (4)方程的解其中包括开始引入的解算子(包括时间和空间信息的点污染源位 置和排放强度构成的需要识别的位置向量——需要对解算子进行截断,基于实际 问题的背景给出特定的解算子) (5)接下来利用 MCMC 方法将特定的解算子和相应的对流-扩散方程的解一一 对应。 (6)利用贝叶斯公式,将未知参数的先验分布改进为后验分布。通过观测数据 获得参数的统计矩 (7)每个参数的均值、方差和其他高阶统计量的计算由于表达式的不明确以及 计算量会随向量维数增加而呈现指数增长。拟采用 MCMC 算法对高维随机向量 上无明确数学表达式的概率分布进行模拟抽样。 (8)结合实际问题背景,验证满足马尔科夫性。利用自适应 Metropolis 算法, 用后验参数的协方差矩阵来估算参数分布——前 i0 次迭代取为定值以进行自适 应更新。利用数学技巧,导出协方差的计算公式(满足马尔科夫性,当前状态仅 与上一条件有关)数学模型建立,设计并编写程序进行数值模拟,得出相关结论。 (9)优势分析:计算效率较同类的遗传算法更优,对于单个未知参数也只需要 产生 4000~5000 个样本。 4.4 编写程序遇到的问题 (1)matlab 运用不够熟练数学模型和程序间的转换,函数关系式的输入等仍需 要进一步的学习。 (2)数学知识的缺乏,相关的演算和处理过程不能很好理解。 (3)大体的步骤基本理解,对于建立模型中的一些细节性的考量不是太理解

随机模拟方法及应用 材料科学与工程学院F1405101班孙密广学号:5140519014 (4)对于截断,观测概率分布,随机噪声等数学方法和模型的使用不是很理解。 5总结 在对论文的研读中,自己有重新巩固了MCMC算法的基本知识,了解到 MCMC算法的无穷魅力和广泛的应用。同时在论文的研读过程中,深刻认识到 将实际问题转化成数学模型并利用计算机解决问题的过程。对数学建模和 MCMC算法有了更加深刻的认识。虽然,由于自己matlab运用的不熟练和相关 数学知识的缺乏,没有成功把数学模型化成程序,但通过今后进一步的学习相信 自己能收获很多。 6致谢 感谢肖柳青老师一学期的指导和引导,从随机模拟的基本落脚点,向我们介 绍了伊辛模型,信息熵,博弈论,随机游走,股票期权定价等一系列与模拟密切 相关的有趣的生活问题。增长见识,丰富我们视野的同时,让我们感受到在面对 难以解决的数学问题面前,模拟的巨大作用和无穷的魅力。 第8页
随机模拟方法及应用 材料科学与工程学院 F1405101 班 孙密广 学号:5140519014 第 8 页 (4)对于截断,观测概率分布,随机噪声等数学方法和模型的使用不是很理解。 5 总结 在对论文的研读中,自己有重新巩固了 MCMC 算法的基本知识,了解到 MCMC 算法的无穷魅力和广泛的应用。同时在论文的研读过程中,深刻认识到 将实际问题转化成数学模型并利用计算机解决问题的过程。对数学建模和 MCMC 算法有了更加深刻的认识。虽然,由于自己 matlab 运用的不熟练和相关 数学知识的缺乏,没有成功把数学模型化成程序,但通过今后进一步的学习相信 自己能收获很多。 6.致谢 感谢肖柳青老师一学期的指导和引导,从随机模拟的基本落脚点,向我们介 绍了伊辛模型,信息熵,博弈论,随机游走,股票期权定价等一系列与模拟密切 相关的有趣的生活问题。增长见识,丰富我们视野的同时,让我们感受到在面对 难以解决的数学问题面前,模拟的巨大作用和无穷的魅力