
第6章代数系统 第6章代数系统 6.1代数系统的基本概念 6.2二元运算的性质 6.3子代数和积代数 返回总目录
第6章 代数系统 第6章 代数系统 6.1 代数系统的基本概念 6.2 二元运算的性质 6.3 子代数和积代数 返回总目录

第6章代数系统 第6章代数系统 6.1代数系统的基本概念 6.1.1运算 1.运算的定义 定义6.1.1设A是非空集合,从笛卡尔积A×A×…×A到 A的映射f称为集合A上的n元运算。简称为n元运算。 在定义6.1.1中,当n=1时,称为集合A上的一元运算; 当n=2时,称为集合A上的二元运算。 在讨论抽象运算时,"运算”常记为"*”、”。”等。 设*是二元运算,如果a与b运算得到c,记作a*b=c;若*是 元运算,a的运算结果记作*a或*(a)
第6章 代数系统 6.1代数系统的基本概念 6.1.1运算 1.运算的定义 定义6.1.1 设A是非空集合,从笛卡尔积A×A×…×A到 A的映射f称为集合A上的n元运算。简称为n元运算。 在定义6.1.1中,当n=1时,f称为集合A上的一元运算; 当n=2时,f称为集合A上的二元运算。 在讨论抽象运算时,“运算”常记为“*” 、 “ ∘ ”等。 设*是二元运算,如果a与b运算得到c,记作a*b=c;若*是一 元运算,a的运算结果记作*a或*(a)。 第6章 代数系统

第6章代数系统 设A=1,a,1},其中,a是非零实数。A→A,定义 为:a∈A,f孔a)=二。容易看出f是A上的一元运算。 又如,fN×N→N,定义为:m,neN,fm,n)=m+n, f是自然数集合N上的二元运算,它就是普通加法运算。普 通减法不是自然数集合N上的二元运算,因为两个自然数相 减可能得到负数,而负数不是自然数。所以普通的减法不 是自然数集合N上的二元运算。 通过以上讨论可以看出,一个运算是否为集合A上的运 算必须满足以下两点: ①A中任何元素都可以进行这种运算,且运算的结果是 惟一的。 ②A中任何元素的运算结果都属于A。A中任何元素的运 算结果都属于A通常称为运算在A是封闭的
第6章 代数系统 设A=1 , a , ,其中,a是非零实数。f:A→A,定义 为:aA,f(a)= 。容易看出f是A上的一元运算。 又如,f:N×N→N,定义为:m,nN,f(m,n)=m+n, f是自然数集合N上的二元运算,它就是普通加法运算。普 通减法不是自然数集合N上的二元运算,因为两个自然数相 减可能得到负数,而负数不是自然数。所以普通的减法不 是自然数集合N上的二元运算。 通过以上讨论可以看出,一个运算是否为集合A上的运 算必须满足以下两点: ①A中任何元素都可以进行这种运算,且运算的结果是 惟一的。 ②A中任何元素的运算结果都属于A。A中任何元素的运 算结果都属于A通常称为运算在A是封闭的。 a 1 a 1

第6章代数系统 【例6.1】设N为自然数集合,*和是NXW到W映射,规 定为:Vm,neN, m*n=min m.n mon=max m.n 则*和是N上的二元运算。 【例6.2】设N=0,1,…,k1}。Nk上的二元运算+定义为: 对于N中的任意两个元素和,有 *1--ki*2 i+j i+j<k 称二元运算+为模加法
第6章 代数系统 【例6.1】设N为自然数集合,*和∘是N×N到N映射,规 定为:m,nN, m∗n=minm,n m∘n=maxm,n 则∗和∘是N上的二元运算。 【例6.2】设Nk =0,1,…,k-1。Nk上的二元运算+k定义为: 对于Nk中的任意两个元素i和j,有 称二元运算+k为模k加法。 + − + + + + = i j k i j k i j i j k i j k

第6章代数系统 N上的二元运算×定义为:对于N中的任意两个元素和 ,有 ixkj- ixj ixj<k i×除以k的余数 i×ji≥k 称二元运算X为模的乘法。 模加法+和模乘法×是两种重要的二元运算。 在N2=0,1,2,3,4,5,6中,有4+72=6,4+5=2。如果把N7 中的元素:0,1,2,3,4,5,6分别看作是:星期日、星 期一、星期二、星期三、星期四、星期五、星期六。那么 4+,2=6可解释为:星期四再过两天后是星期六;4+,5=2可 解释为:星期四再过五天后是星期二。这是模7加法实际意 义的一种解释
第6章 代数系统 i j k i j k i j k i j i j k = 除以 的余数 称二元运算×k为模k的乘法。 模k加法+k和模k乘法×k是两种重要的二元运算。 在N7 =0,1,2,3,4,5,6中,有4+7 2=6,4+7 5=2。如果把N7 中的元素:0,1,2,3,4,5,6分别看作是:星期日、星 期一、星期二、星期三、星期四、星期五、星期六。那么 4+7 2=6可解释为:星期四再过两天后是星期六;4+7 5=2可 解释为:星期四再过五天后是星期二。这是模7加法实际意 义的一种解释。 Nk上的二元运算×k定义为:对于Nk中的任意两个元素i和 j,有

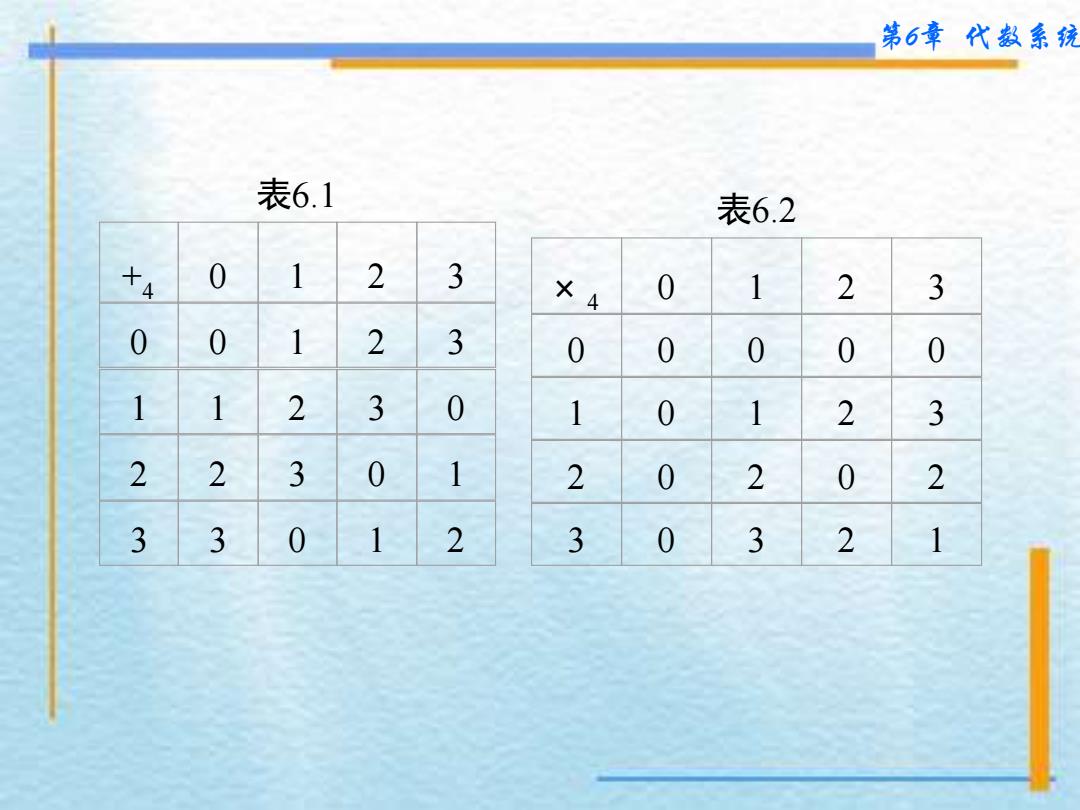
第6章代数系统 2.运算的表示 表示运算的方法通常有两种:解析公式和运算表。 解析公式是指用运算符号和运算对象组成的表达式。如 fa)= itxjij-kitjzk i+j i+j<k 运算表是指运算对象和运算结果构成的二维表。 经常使用运算表来定义有限集合上的二元运算,特别 当有限集合上的二元运算不能用表达式简明地表示时,借 助于运算表来定义二元运算会带来方便。另外,运算表还 便于对二元运算的某些性质进行讨论,更形象地了解二元 运算的有关特征。 设N0,1,2,3},N4上的模4加法+4可以用运算表表示 它的运算表如表6.1所示。N上的模4乘法×,也可以用运算 表表示,它的运算表如表6.2所示
第6章 代数系统 2.运算的表示 表示运算的方法通常有两种:解析公式和运算表。 解析公式是指用运算符号和运算对象组成的表达式。如 f(a)= , a 1 + − + + + + = i j k i j k i j i j k i j k 运算表是指运算对象和运算结果构成的二维表。 经常使用运算表来定义有限集合上的二元运算,特别 当有限集合上的二元运算不能用表达式简明地表示时,借 助于运算表来定义二元运算会带来方便。另外,运算表还 便于对二元运算的某些性质进行讨论,更形象地了解二元 运算的有关特征。 设N4 =0,1,2,3,N4上的模4加法+4可以用运算表表示, 它的运算表如表6.1所示。N4上的模4乘法×4也可以用运算 表表示,它的运算表如表6.2所示
第6章代数系统 表6.1 表6.2 0 1 2 3 × 0 1 2 3 0 0 1 2 3 0 0 0 0 0 1 1 2 3 0 1 0 1 2 3 2 2 3 0 1 2 0 2 0 2 3 3 0 1 2 3 0 3 2 1
第6章 代数系统 表6.1 +4 0 1 2 3 0 0 1 2 3 1 1 2 3 0 2 2 3 0 1 3 3 0 1 2 表6.2 × 4 0 1 2 3 0 0 0 0 0 1 0 1 2 3 2 0 2 0 2 3 0 3 2 1

第6章代数系统 6.1.2代数系统 定义6.1.2 一个非空集合A连同若干个定义在该集合上的 运算*1,*2,…,*所组成的系统称为一个代数系统,记作 构成一个代数系统,该代数系常称 为集合代数。 【例6.4】设R0}是全体非零实数集合,*是R0}上二 元运算,定义为:Va,beR0,a*b=b。则是代 数系统
第6章 代数系统 6.1.2代数系统 定义6.1.2 一个非空集合A连同若干个定义在该集合上的 运算∗ 1 , ∗2 ,…, ∗k 所组成 的系统称为一 个代数系统, 记作 。 根据定义6.1.2,一个代数系统需要满足下面两个条件: ①有一个非空集合A。 ②有一些定义在集合A上的运算。 集合和定义在集合A上的运算是一个代数系统的两个要 素,缺一不可。 【例6.3】设B是一个集合,A=P (B)是A幂集合。集合的 求补运算是A上的一元运算,集合的并和交运算是A上的是二 元运算。于是构成一个代数系统,该代数系常称 为集合代数。 【例6.4】设R-0是全体非零实数集合,*是R-0上二 元运算,定义为:a,b R-0,a*b=b。则是代 数系统

第6章代数系统 6.2二元运算的性质 6.2.1运算的基本性质 1.交换律 定义6.2.1设*是非空集合A上的二元运算,如果对于任意 的a,beA,有a*b=b*a,则称二元运算*在A上是可交换的,也 称二元运算*在A上满足交换律。 例如,设R为实数集合,对于任意的a,b∈R,规定 a*b=(a-b)2 aob=a2+b2 ab=a+b-ab 则运算*、和都是可交换的 2.结合律 定义6.2.2设*是非空集合A上的二元运算,如果对于任意 的a,b,c∈A,有(a*b)*c=a*(b*c),则称二元运算*在A上是可结 合的,也称二元运算*在A上满足结合律 返回章目录
第6章 代数系统 6.2 二元运算的性质 6.2.1运算的基本性质 1.交换律 定义6.2.1 设*是非空集合A上的二元运算,如果对于任意 的a,bA,有a∗b=b∗a,则称二元运算∗在A上是可交换的,也 称二元运算*在A上满足交换律。 例如,设R为实数集合,对于任意的a,bR,规定 a∗b=(a–b) 2 a∘b=a2+b 2 a·b=a+b–ab 则运算∗、∘和·都是可交换的。 2.结合律 定义6.2.2 设*是非空集合A上的二元运算,如果对于任意 的a,b,cA,有(a*b)*c=a*(b*c),则称二元运算*在A上是可结 合的,也称二元运算∗在A上满足结合律 返回章目录

第6章代数系统 实数集合上的普通加法和乘法是二元运算,满足结合律; 矩阵的加法和乘法也是二元运算,也满足结合律;向量的内 积、外积是二元运算,但不满足结合律。 【例6.5】设*是非空集合A上的二元运算,定义为: Va,beA,a*b=b。证明运算*是可结合的。 证明:对于任意的a,b,ceA, 有(a*b)*c=c,而a*(b*c)=a*c=C,故有(a*b)*c=a*(b*C), 即运算*是可结合的。 当二元运算*在A上适合结合律时,在只有该运算符的表 达式中,表示运算顺序的括号常被省略。所以将(x*y)*z =*0y*z)常写成x**z。这样,可以令 n个 a”=1*米..米L
第6章 代数系统 实数集合上的普通加法和乘法是二元运算,满足结合律; 矩阵的加法和乘法也是二元运算,也满足结合律;向量的内 积、外积是二元运算,但不满足结合律。 【例6.5】设*是非空集合A上的二元运算,定义为: a,bA,a∗b=b。证明运算*是可结合的。 证明:对于任意的a,b,cA, 有(a∗b)∗c=c,而a∗(b∗c)=a∗c=c,故有(a∗b)∗c=a∗(b∗c), 即运算∗是可结合的。 当二元运算*在A上适合结合律时,在只有该运算符的表 达式中,表示运算顺序的括号常被省略。所以将(x*y)*z =x*(y*z)常写成x*y*z。这样,可以令 n个 n a = a a a