
《随机模拟方法与应用》课程大作业 2015年度春季学期 对MCMC方法在瑞利分布样本采集及一元线性回归模型参 数估计中应用的思考与研究 学号:5110109140 姓名:吴凯斌 授课老师:肖柳青 1.全文内容概要 本文基于统计学中有关瑞利分布及一元线性回归分析的参考文献,主要对马尔可夫链蒙 特卡罗方法(即MCMC方法)在瑞利分布样本采集以及一元线性回归模型参数估计中的应 用进行了思考与研究。全文共分为三大部分:首先,简单介绍了马尔科夫链的数学概念,并 通过提出一个具体的模型来说明其表示方法:其次,介绍了MCMC方法在电子工程中常用 的一个数学分布一一瑞利分布中随机采集若干个样本的具体应用,并将算法通过matlab加 以实现:最后,介绍了MCMC算法在一元线性回归模型参数估计中的应用思想,并将其与 最小二乘法进行了对比。 2.马尔可夫链的概念及其表示方式 无论是世界上重大的政治局势变化,还是我们每个人生活中的一些非常琐碎的事情,它 们之间绝大多数都是有着一定的因果关系的,也就是说每件事情的发生都会对接下来出现的 事情产生一定的影响,这种影响可以是有形的,也可以是无形的,其最终将反映到接下来每 件事发生的概率上。事实上,从当前一件事的发生转变到受其影响的接下来的另一件事的发 生,如果这样一个转变过程仅与当前这件事有关,这样就产生了一个简单的马尔可夫过程。 下面举一个简单的例子加以说明,如果我好好复习准备考试周,各门功课都拿到A的概率 是0.6:经过一般准备各门功课都拿到A的概率是0.3:而不好好复习,各门功课都拿到A 的概率是0.1。显然,这样的假设基于:我各门功课最终是否都能拿到A仅与当前我是否认 真准备考试周有关。另一方面,假如我各门功课都能拿到A,我暑假期间选择和同学一起去 旅游的概率为0.6,而选择上小学期的概率为0.4:假如我没能各门功课都拿到A,暑假期间 和同学一起去旅游的概率是0.3,而上小学期的概率则为0.7。显然,此时我们的假设基于: 我暑假是和同学出去旅游还是上小学期仅与我各门功课是否都拿到A有关。从我是否好好 准备考试周的当前状态一直转移到暑假我是和同学出去旅游还是上小学期的将来状态,这样 一整个过程就是一个简单的马尔可夫过程。 如果记我好好复习准备考试周为事件A,作一般准备为事件B,而不好好准备为事件 C,则2(A,B,C)组成了当前所有可能的事件空间。若记我所有课程都拿到A为事件D, 未能所有课程都拿A为事件D,则由题意,知: P(D|A)=0.6,P(D1B)=0.3,P(D|C)=0.1 (1) 又由我各门功课都拿到A和不能都拿到A为互斥事件,故有:
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 1 对 MCMC 方法在瑞利分布样本采集及一元线性回归模型参 数估计中应用的思考与研究 学号:5110109140 姓名:吴凯斌 授课老师:肖柳青 1.全文内容概要 本文基于统计学中有关瑞利分布及一元线性回归分析的参考文献,主要对马尔可夫链蒙 特卡罗方法(即 MCMC 方法)在瑞利分布样本采集以及一元线性回归模型参数估计中的应 用进行了思考与研究。全文共分为三大部分:首先,简单介绍了马尔科夫链的数学概念,并 通过提出一个具体的模型来说明其表示方法;其次,介绍了 MCMC 方法在电子工程中常用 的一个数学分布——瑞利分布中随机采集若干个样本的具体应用,并将算法通过 matlab 加 以实现;最后,介绍了 MCMC 算法在一元线性回归模型参数估计中的应用思想,并将其与 最小二乘法进行了对比。 2.马尔可夫链的概念及其表示方式 无论是世界上重大的政治局势变化,还是我们每个人生活中的一些非常琐碎的事情,它 们之间绝大多数都是有着一定的因果关系的,也就是说每件事情的发生都会对接下来出现的 事情产生一定的影响,这种影响可以是有形的,也可以是无形的,其最终将反映到接下来每 件事发生的概率上。事实上,从当前一件事的发生转变到受其影响的接下来的另一件事的发 生,如果这样一个转变过程仅与当前这件事有关,这样就产生了一个简单的马尔可夫过程。 下面举一个简单的例子加以说明,如果我好好复习准备考试周,各门功课都拿到 A 的概率 是 0.6;经过一般准备各门功课都拿到 A 的概率是 0.3;而不好好复习,各门功课都拿到 A 的概率是 0.1。显然,这样的假设基于:我各门功课最终是否都能拿到 A 仅与当前我是否认 真准备考试周有关。另一方面,假如我各门功课都能拿到 A,我暑假期间选择和同学一起去 旅游的概率为 0.6,而选择上小学期的概率为 0.4;假如我没能各门功课都拿到 A,暑假期间 和同学一起去旅游的概率是 0.3,而上小学期的概率则为 0.7。显然,此时我们的假设基于: 我暑假是和同学出去旅游还是上小学期仅与我各门功课是否都拿到 A 有关。从我是否好好 准备考试周的当前状态一直转移到暑假我是和同学出去旅游还是上小学期的将来状态,这样 一整个过程就是一个简单的马尔可夫过程。 如果记我好好复习准备考试周为事件 A ,作一般准备为事件 B ,而不好好准备为事件 C ,则( , , ) A B C 组成了当前所有可能的事件空间。若记我所有课程都拿到 A 为事件 D , 未能所有课程都拿 A 为事件 D ,则由题意,知: P D A P D B P D C ( | ) 0.6, ( | ) 0.3, ( | ) 0.1 (1) 又由我各门功课都拿到 A 和不能都拿到 A 为互斥事件,故有:

《随机模拟方法与应用》课程大作业 2015年度春季学期 P(D|A)=0.4,P(D|B)=0.7,P(D1C)=0.9 (2) 同样由于是互斥事件,若设暑假我和同学一起旅游为事件E,则上小学期为事件E。 若记我所得成绩的事件集合为:G(D,D),暑期所做的事件集合为:(E,瓦)。那么: 2(A,B,C)→oD,D→0E,E) (3) 这样一整个转移过程即为马尔可夫链,不难发现,在整个转移过程中,决定事件走向, 或者说决定马尔可夫链走向的关键就是其转移概率。 马尔科夫链的精髓,其实就是简化了系统从一个时刻到下一个时刻的随机演化方式,也就是 假定系统的下一步状态仅取决于当前时刻的系统状态,而与其整个发展历史无关,或者说, 马尔可夫链具有遗忘性。 马尔科夫链也可以用转移矩阵的形式来表示,以上面的模型为例,则转移矩阵的形式如 下: E 0.6 0.4 (4) E 0.3 0.7D 而其中,又有: A D 0.6 0.3 0. (5) D 0.4 0.7 0.9 C 观察可知, 转移矩阵中每一行之和均满足归一性条件:∑P=1。 3.MCMC方法在瑞利分布中采集样本的应用 3.1瑞利分布简介 瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接收包括统计时 变特性的一种分布类型。当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态 分布时,这个向量的模呈瑞利分布,其在电子工程、通信系统等学科中有着极为广泛的应用。 因此,对其进行相关研究是非常有必要的。 3.2瑞利分布 若能机变量X的分布商数影式为:F闲=1-ep-.其中≥0.0>0。 则称随机变量服从瑞利分布,同时不难看出其对应的密度函数为:)=二ep( 3.3特征数 2
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 2 P D A P D B P D C ( | ) 0.4, ( | ) 0.7, ( | ) 0.9 (2) 同样由于是互斥事件,若设暑假我和同学一起旅游为事件 E ,则上小学期为事件 E 。 若记我所得成绩的事件集合为: ( , ) D D ,暑期所做的事件集合为: ( , ) E E 。那么: ( , , ) , ( , ) A B C D D E E (3) 这样一整个转移过程即为马尔可夫链,不难发现,在整个转移过程中,决定事件走向, 或者说决定马尔可夫链走向的关键就是其转移概率。 马尔科夫链的精髓,其实就是简化了系统从一个时刻到下一个时刻的随机演化方式,也就是 假定系统的下一步状态仅取决于当前时刻的系统状态,而与其整个发展历史无关,或者说, 马尔可夫链具有遗忘性。 马尔科夫链也可以用转移矩阵的形式来表示,以上面的模型为例,则转移矩阵的形式如 下: 0.6 0.4 0.3 0.7 E D E D (4) 而其中,又有: 0.6 0.3 0.1 0.4 0.7 0.9 A D B D C (5) 观察可知,转移矩阵中每一行之和均满足归一性条件: 1 ij p 。 3.MCMC 方法在瑞利分布中采集样本的应用 3.1 瑞利分布简介 瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接收包括统计时 变特性的一种分布类型。当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态 分布时,这个向量的模呈瑞利分布,其在电子工程、通信系统等学科中有着极为广泛的应用。 因此,对其进行相关研究是非常有必要的。 3.2 瑞利分布 若随机变量 X 的分布函数形式为: 2 2 ( ) 1 exp( ) 2 x F x ,其中 x 0, 0 。 则称随机变量服从瑞利分布,同时不难看出其对应的密度函数为: 2 2 2 ( ) exp( ) 2 x x f x 。 3.3 特征数

《随机模拟方法与应用》课程大作业 2015年度春季学期 x=fh-j亭p -r -2 -x2 =-∫xde2a)=-xe2a+∫e2dk (6) 2J√2πb Ex-Jxx exp(x =-rde)=-e6+2jeh (7) =-2b2∫de2a)=2o2 Dx-EX-(EXY-2- (8) 3.4参数的极大似然估计 似然函数为: L(a)=e (9) 对数似然函数为: x h4o)=-2mlna+宫n-2a (10) 对上式求导,得: dInL(o)2n +1 (11) do 令上式为0,得参数的极大似然估计为: (12) 2n 3.5MCMC方法在瑞利分布中随机采集样本的应用及matlab模拟 3
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 3 2 2 2 2 2 2 2 2 2 2 2 0 0 2 2 2 0 0 0 2 ( ) exp( ) 2 ( ) | 2 1 2 2 2 x x x x x x EX xf x dx x dx xd e xe e dx b e dx b b (6) 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 0 0 0 2 2 2 0 exp( ) 2 ( ) | 2 2 ( ) 2 x x x x x x EX x dx x d e x e xe dx b d e (7) 2 2 2 2 2 4 ( ) 2 ( ) 2 2 DX EX EX (8) 3.4 参数的极大似然估计 似然函数为: 2 2 2 2 2 2 2 2 1 1 ( ) i i x x n n i n i i i x L e x e (9) 对数似然函数为: 2 1 2 1 ln ( ) 2 ln ln 2 n n i i i i x L n x (10) 对上式求导,得: 2 1 3 ln ( ) 2 n i i x d L n d (11) 令上式为 0,得参数的极大似然估计为: 2 1 2 2 n i i x n 。 (12) 3.5 MCMC 方法在瑞利分布中随机采集样本的应用及 matlab 模拟

《随机模拟方法与应用》课程大作业 2015年度春季学期 -x2 考忠如下瑞利分布,其概率密度面数为:)产后,我首先考志了从该分 布中随机产生l000个样本来近似该概率密度分布函数的情形,若取总循环次数total number 为500,000,g=1,每隔500次收集一次,共得到最终样本数为1000。其matlab源代码如 下: c1eara11;号5110109140吴凯斌《随机模拟方法与应用》大作业程序辅导老师:肖柳青 close all; sigma=l;号给定分布中sigma的数值 j=1; total Num=500000; 号定义模拟总次数和样本总数 sample num=5000; sample=zeros(1,total Num); 号设置样本存储空间 =5*rand(1); sample(j)=x; for i=1:total Num 号设置建议密度函数 &fy=1/sqrt (2*pi)*exp(-(y-x)2/2) z=randn(1)+sample(j); u=rand(1); 号计算alpha的值,alpha=pi(y)*g(y,x)/(pi()*g(,y) 1f(z>=0) alpha=z/sigma2*exp(-z2/2/sigma2)/(sample(j)/sigma2*exp (-sample (j) ^2/2/sigma^2)); else alpha=0; end alpha=min(1,alpha); if(u<=alpha) sample(j+1)=z; else sample(j+1)=sample(j); end j=j+1; 4
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 4 考虑如下瑞利分布,其概率密度函数为: 2 2 2 ( ) exp( ) 2 x x f x ,我首先考虑了从该分 布中随机产生 1000 个样本来近似该概率密度分布函数的情形,若取总循环次数 total_number 为 500,000, 1,每隔 500 次收集一次,共得到最终样本数为 1000。其 matlab 源代码如 下: clear all; %5110109140_吴凯斌 《随机模拟方法与应用》大作业程序 辅导老师:肖柳青 close all; sigma=1; %给定分布中sigma的数值 j=1; total_Num=500000; %定义模拟总次数和样本总数 sample_num=5000; sample=zeros(1,total_Num); %设置样本存储空间 x=5*rand(1); sample(j)=x; for i=1:total_Num %设置建议密度函数 %fy=1/sqrt(2*pi)*exp(-(y-x)^2/2) z=randn(1)+sample(j); u=rand(1); %计算alpha的值, alpha=pi(y)*q(y,x)/(pi(x)*q(x,y)) if(z>=0) alpha=z/sigma^2*exp(-z^2/2/sigma^2)/(sample(j)/sigma^2*exp(-sample(j) ^2/2/sigma^2)); else alpha=0; end alpha=min(1,alpha); if(u<=alpha) sample(j+1)=z; else sample(j+1)=sample(j); end j=j+1;
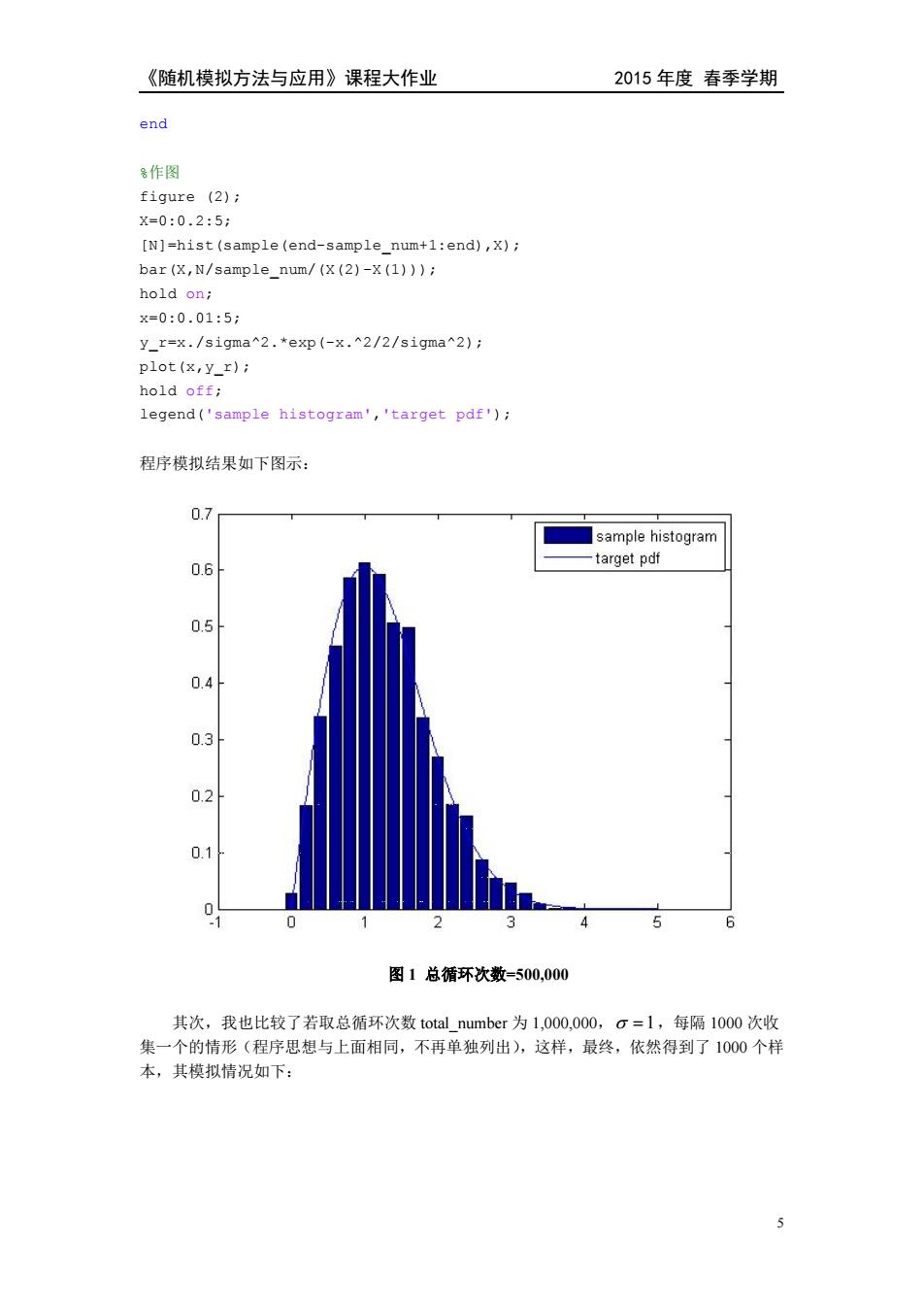
《随机模拟方法与应用》课程大作业 2015年度春季学期 end 各作图 figure (2); X=0:0.2:5; [N]=hist (sample(end-sample_num+1:end),x); bar(X,N/sample_num/(X (2)-x (1))); hold on; x=0:0.015; y_r=x./sigma2.*exp (-x.2/2/sigma2) plot(x,y_r); hold off; legend('sample histogram','target pdf'); 程序模拟结果如下图示: 0.7 ■sample histogram 0.6 target pdf 0.5 0.4 0.3 0.2 0.1 0 -1 0 3 6 图1总循环次数=500,000 其次,我也比较了若取总循环次数total number为1,000,000,g=1,每隔1000次收 集一个的情形(程序思想与上面相同,不再单独列出),这样,最终,依然得到了1000个样 本,其模拟情况如下: 5
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 5 end %作图 figure (2); X=0:0.2:5; [N]=hist(sample(end-sample_num+1:end),X); bar(X,N/sample_num/(X(2)-X(1))); hold on; x=0:0.01:5; y_r=x./sigma^2.*exp(-x.^2/2/sigma^2); plot(x,y_r); hold off; legend('sample histogram','target pdf'); 程序模拟结果如下图示: 图 1 总循环次数=500,000 其次,我也比较了若取总循环次数 total_number 为 1,000,000, 1,每隔 1000 次收 集一个的情形(程序思想与上面相同,不再单独列出),这样,最终,依然得到了 1000 个样 本,其模拟情况如下:
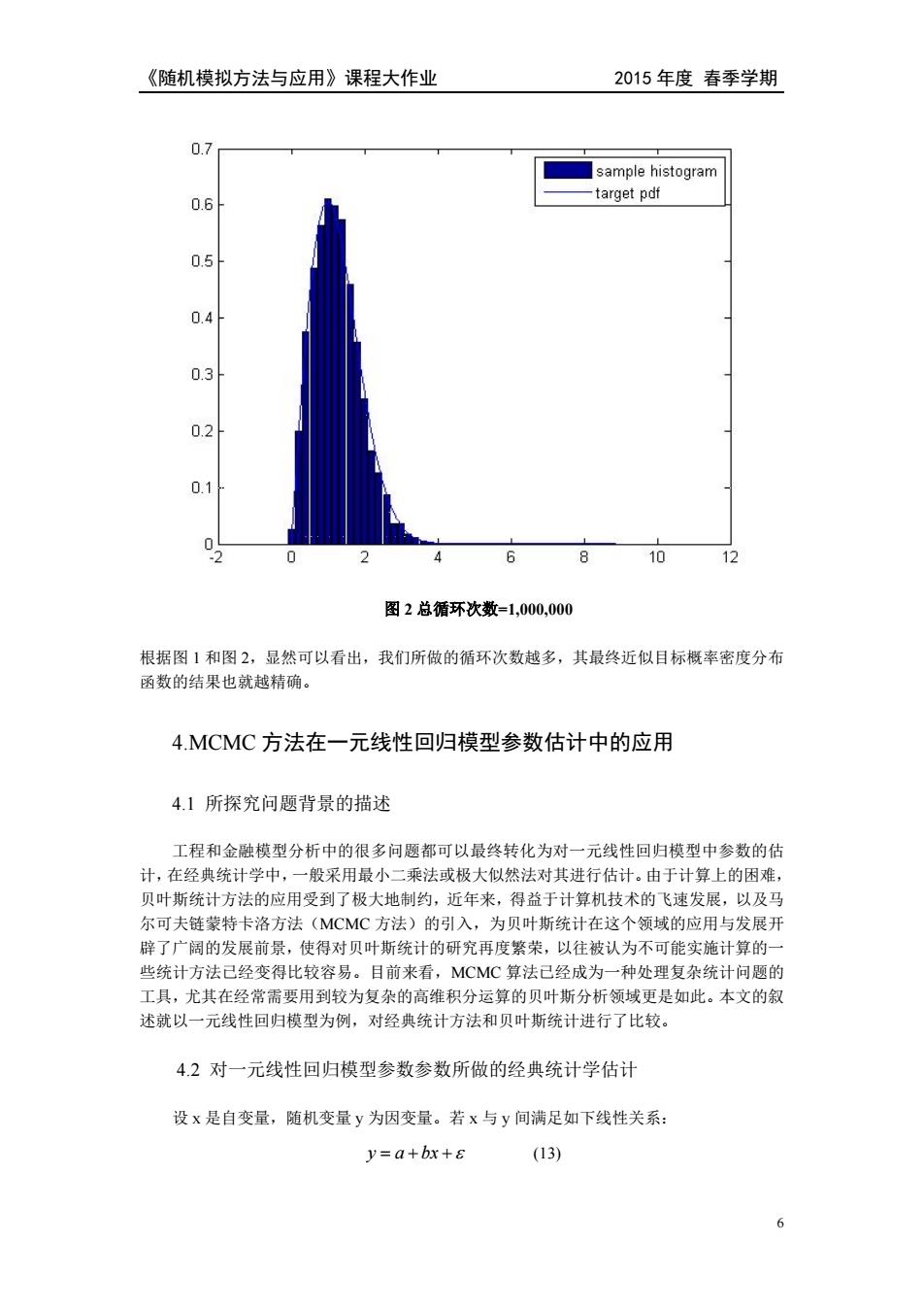
《随机模拟方法与应用》课程大作业 2015年度春季学期 0.7 sample histogram 0.6 target pdf 0.5 0.4 0.3 0.2 0.1 0 10 12 图2总循环次数=1,000,000 根据图1和图2,显然可以看出,我们所做的循环次数越多,其最终近似目标概率密度分布 函数的结果也就越精确。 4.MCMC方法在一元线性回归模型参数估计中的应用 4.1所探究问题背景的描述 工程和金融模型分析中的很多问题都可以最终转化为对一元线性回归模型中参数的估 计,在经典统计学中,一般采用最小二乘法或极大似然法对其进行估计。由于计算上的困难, 贝叶斯统计方法的应用受到了极大地制约,近年来,得益于计算机技术的飞速发展,以及马 尔可夫链蒙特卡洛方法(MCMC方法)的引入,为贝叶斯统计在这个领域的应用与发展开 辟了广阔的发展前景,使得对贝叶斯统计的研究再度繁荣,以往被认为不可能实施计算的一 些统计方法已经变得比较容易。目前来看,MCMC算法已经成为一种处理复杂统计问题的 工具,尤其在经常需要用到较为复杂的高维积分运算的贝叶斯分析领域更是如此。本文的叙 述就以一元线性回归模型为例,对经典统计方法和贝叶斯统计进行了比较。 4.2对一元线性回归模型参数参数所做的经典统计学估计 设x是自变量,随机变量y为因变量。若x与y间满足如下线性关系: y=a+bx+8 (13) 6
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 6 图 2 总循环次数=1,000,000 根据图 1 和图 2,显然可以看出,我们所做的循环次数越多,其最终近似目标概率密度分布 函数的结果也就越精确。 4.MCMC 方法在一元线性回归模型参数估计中的应用 4.1 所探究问题背景的描述 工程和金融模型分析中的很多问题都可以最终转化为对一元线性回归模型中参数的估 计,在经典统计学中,一般采用最小二乘法或极大似然法对其进行估计。由于计算上的困难, 贝叶斯统计方法的应用受到了极大地制约,近年来,得益于计算机技术的飞速发展,以及马 尔可夫链蒙特卡洛方法(MCMC 方法)的引入,为贝叶斯统计在这个领域的应用与发展开 辟了广阔的发展前景,使得对贝叶斯统计的研究再度繁荣,以往被认为不可能实施计算的一 些统计方法已经变得比较容易。目前来看,MCMC 算法已经成为一种处理复杂统计问题的 工具,尤其在经常需要用到较为复杂的高维积分运算的贝叶斯分析领域更是如此。本文的叙 述就以一元线性回归模型为例,对经典统计方法和贝叶斯统计进行了比较。 4.2 对一元线性回归模型参数参数所做的经典统计学估计 设 x 是自变量,随机变量 y 为因变量。若 x 与 y 间满足如下线性关系: y a bx (13)

《随机模拟方法与应用》课程大作业 2015年度春季学期 其中:6~N(0,σ2),且a,b都是不依赖于x的未知参数。 则称(6)式为一元线性回归模型。另设有n组样本观测值(x,y),i=1,2,…n,令: 0=∑y-a-bx,)。 求Q关于a,b的偏导数,并令其为零,则可得: 80 (y,-a-bx,) =0 Ba Ba (14) 80 a(y,-a-bx,)2 i= =0 ab ab a=y-b 解此方程,易得: A 2(x-xX0y-月 b= (15) 2(x-x 其中:x=2x,少=2y·由(8)式所得到的参数a,b使得Q的值最小,故称a,b为 n i=l ni=1 a,b的最小二乘估计值,上述方法就是经常用到的最小二乘法。 事实上,我们可以将每一个统计样本都看做随机变量来处理,由(6)知, y~N(a+bx,o2),因此,每个样本均服从概率分布: 1 f(x;:y;a,b)=- xpl 2o2 (16) i=1,2,…n 由于n组样本观测值(x,y)可看做n个相互独立的随机变量,故似然函数为: L=L(a,b)=IIf(x;,y,,a,b) (17) 又由: aL -0 Ba (18) aL =0 ab 故可以计算参数a,b的估计值,这就是极大似然估计法的大致思路。式(I1)解的结果就 即为式(8)。与公式(7)一样,据此可知,最小二乘法与极大似然法虽然出发点不一样, 但方程组求解结果相同,这说明它们在本质上是一样的。 7
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 7 其中: 2 ~ (0, ) N ,且 a,b 都是不依赖于 x 的未知参数。 则称(6)式为一元线性回归模型。另设有 n 组样本观测值 ( , ), 1, 2, , i i x y i n 令: 2 1 ( ) n i i i Q y a bx 。 求 Q 关于 a,b 的偏导数,并令其为零,则可得: 2 1 2 1 ( ) 0 ( ) 0 n i i in i i i y a bx Q a a y a bx Q b b (14) 解此方程,易得: ^ ^ ^ 1 1 1 2 1 ( )( ) ( ) n i n i i a y b x x y y b x x (15) 其中: 1 1 1 1 , n n i i i i x x y y n n 。由(8)式所得到的参数 ^ ^ a b, 使得 Q 的值最小,故称 ^ ^ a b, 为 a,b 的最小二乘估计值,上述方法就是经常用到的最小二乘法。 事实 上,我 们可以 将每一个 统计样 本都看 做随机 变量来 处理, 由(6)知 , 2 y N a bx ~ ( , ) ,因此,每个样本均服从概率分布: 2 2 1 ( ) ( , , , ) exp[ ] 2 2 1, 2, . i i i i y a bx f x y a b i n (16) 由于 n 组样本观测值 ( , ) i i x y 可看做 n 个相互独立的随机变量,故似然函数为: 1 ( , ) ( , , , ) n i i i L L a b f x y a b (17) 又由: 0 0 L a L b (18) 故可以计算参数 a,b 的估计值,这就是极大似然估计法的大致思路。式(11)解的结果就 即为式(8)。与公式(7)一样,据此可知,最小二乘法与极大似然法虽然出发点不一样, 但方程组求解结果相同,这说明它们在本质上是一样的

《随机模拟方法与应用》课程大作业 2015年度春季学期 4.3 Gibbs抽样方法 目前,Gibbs抽样方法在贝叶斯分析中应用最为广泛。Gibbs抽样是由Geman在1984 年提出来的,最早用于图像的处理分析、人工智能和神经网络等大型复杂数据的分析,后经 Gelfand和Smith(1990)引入贝叶斯模型研究中,通过模拟进行积分运算,这给贝叶斯方 法的实际应用产生了深刻影响。Gibs抽样方法的思路很直观:它通过一系列步骤,构建了 一条具有π-不变性的马尔可夫链。若设0=(日,…B)为k维向量,它的概率密度为p(), 显然,这是一个联合概率密度。若令日,表示0的第i个分量,日,表示0中除去0之后剩 下的(k-1)个分量,记转移核函数为: p(8,A)=P,(8,A)=p8∈A|B,) (19) i=1,2,…k. 其中A为k维可测向量空间。令初始点为0o)=(0,…),考虑如下循环: (1)从条件分布P(0|0-,…0-)中抽样得到8: (j)从条件分布P(8,1,…-)中抽样得到巴: … (k)从条件分布P(9|日,…9-)中抽样得到: 上述(1)-(k)步抽样完成了一轮循环,这就是Gibbs抽样。在(1)·(k)步过程中,每 一步只抽一个变量,同时其他变量保持不变。一轮循环结束后,再以该循环所得变量值为起 点进行下一轮循环,如此往复,得到日=(,…),=1,2,.。这显然是一条马尔可夫 链。 4.4一元线性回归模型参数的贝叶斯估计 在(6)式中,变量x和y均为可观察的已知量,未知量为参数α,b,σ2。根据贝叶斯原 理,给定y和x时,a,b,o2的后验联合分布为: p(a,b,o21y,x)cp(a,b.o2)IIp(y,la,b,o2,x) (20) <pa.b.a)expa)] 假定参数变量α,b,σ2之间相互独立,且它们的先验分布分别取为: 8
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 8 4.3 Gibbs 抽样方法 目前,Gibbs 抽样方法在贝叶斯分析中应用最为广泛。Gibbs 抽样是由 Geman 在 1984 年提出来的,最早用于图像的处理分析、人工智能和神经网络等大型复杂数据的分析,后经 Gelfand 和 Smith(1990)引入贝叶斯模型研究中,通过模拟进行积分运算,这给贝叶斯方 法的实际应用产生了深刻影响。Gibbs 抽样方法的思路很直观:它通过一系列步骤,构建了 一条具有 不变性的马尔可夫链。若设 1 ( , ) k 为 k 维向量,它的概率密度为 p( ) , 显然,这是一个联合概率密度。若令i 表示 的第 i 个分量, i 表示 中除去i 之后剩 下的(k-1)个分量,记转移核函数为: ( , ) ( , ) ( | ) 1, 2, . i i i p A p A p A i k (19) 其中 A 为 k 维可测向量空间。令初始点为 (0) (0) (0) ( , ) i k ,考虑如下循环: (1) 从条件分布 ( 1) ( 1) 1 1 2 ( | , ) t t P k 中抽样得到 1 t ; (j)从条件分布 ( ) 1 1 ( | , ) t t Pj j k 中抽样得到 t j ; (k)从条件分布 ( ) 1 1 ( | , ) t t Pk k k 中抽样得到 t k ; 上述(1)-(k)步抽样完成了一轮循环,这就是 Gibbs 抽样。在(1)-(k)步过程中,每 一步只抽一个变量,同时其他变量保持不变。一轮循环结束后,再以该循环所得变量值为起 点进行下一轮循环,如此往复,得到 ( ) ( ) ( ) 1 ( , ) t t t k ,t=1,2,。这显然是一条马尔可夫 链。 4.4 一元线性回归模型参数的贝叶斯估计 在(6)式中,变量 x 和 y 均为可观察的已知量,未知量为参数 2 a b, , 。根据贝叶斯原 理,给定 y 和 x 时, 2 a b, , 的后验联合分布为: 2 2 2 1 2 2 2 1 ( , , | , ) ( , , ) ( | , , , ) 1 ( , , ) exp [ ( ) ] 2 n i i i n i i i p a b y x p a b p y a b x p a b y a bx (20) 假 定 参 数 变 量 2 a b, , 之 间 相 互 独 立 , 且 它 们 的 先 验 分 布 分 别 取 为 :

《随机模拟方法与应用》课程大作业 2015年度春季学期 p(a)c1,p(b)=N(0,2),p(o2)c11o2,p(o2)c1/o2 (21) 由共轭分布法,可算得参数a的条件后验分布为N(a,s),其中: a=1/m)2(y-a-bx,) (22) s=o2In (23) 同理,b的条件后验分布为N(b,s2),其中: 万=(2x)2x0y-a) 24) =(2x))o2 (25) 而σ2的条件后验分布仍为逆卡平方分布,并具有: 2-()20y-a-bx, (26) i=l 4.5一元线性回归模型参数的MCMC算法 下一步就可以根据之前推导出的各参数后验分布,采用MCMC模拟算法对模型(1) 中各个参数进行估计,其步骤如下: (1)给参数(a,b,o2)赋初值(ao,b,o20) (2)根据公式(15)、(16)更新a。 (3)根据公式(17)、(18)更新b。 (4)根据公式(19)更新σ2。 (5)根据σ~b/更新σ,其中是从一个自由度为1的X2分布中抽出的一个随 机数。 (6) 重复(2)~(4)t轮: (7) 分析样本(a四,b0,o20)(a2),b2),σ22),…,(a0,b,σ2)计算各个参数的估 计值。 4.6实例分析 下面分析的数据摘自刘嘉煜,王家生,张玉环的《应用概率统计》,其主要来描述合成 纤维抽丝工段第一导丝盘速度与电流周波之间的关系,现由生产记录得到下面十组数据: 9
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 9 2 2 2 2 1 1 p a p b N p p ( ) 1, ( ) (0, 2), ( ) 1/ , ( ) 1/ (21) 由共轭分布法,可算得参数 a 的条件后验分布为 2 0 N a s ( , ) ,其中: 1 (1/ ) ( ) n i i i a n y a bx (22) 2 2 0 s n / (23) 同理,b 的条件后验分布为 2 1 N b s ( , ) ,其中: 2 1 1 1 ( ) ( ) n n i i i i i b x x y a 24) 2 2 1 2 1 1 ( ) n i i s x (25) 而 2 的条件后验分布仍为逆卡平方分布,并具有: 2 2 2 1 1 ~ ( ) ( ) n i i i n y a bx (26) 4.5 一元线性回归模型参数的 MCMC 算法 下一步就可以根据之前推导出的各参数后验分布,采用 MCMC 模拟算法对模型(1) 中各个参数进行估计,其步骤如下: (1) 给参数 2 ( , , ) a b 赋初值 (0) (0) 2(0) ( , , ). a b (2) 根据公式(15)、(16)更新 a。 (3) 根据公式(17)、(18)更新 b。 (4) 根据公式(19)更新 2 。 (5) 根据 2 2 1 1 ~ / b 更新 2 1 ,其中 2 1 是从一个自由度为 1 的 2 分布中抽出的一个随 机数。 (6) 重复(2)~(4)t 轮; (7) 分析样本 (1) (1) 2(1) ( , , ) a b (2) (2) 2(2) ( , , ) a b ,, ( ) ( ) 2( ) ( , , ) t t t a b 计算各个参数的估 计值。 4.6 实例分析 下面分析的数据摘自刘嘉煜,王家生,张玉环的《应用概率统计》,其主要来描述合成 纤维抽丝工段第一导丝盘速度与电流周波之间的关系,现由生产记录得到下面十组数据:

《随机模拟方法与应用》课程大作业 2015年度春季学期 周波49.2 50.0 49.3 49.049.0 49.549.8 49.950.2 50.2 盘速16.7 17.0 16.8 16.6 16.7 16.8 16.9 17.0 17.0 17.1 度 根据表中所给的电流周波与第一导丝盘速度的10对数据,求线性回归方程。 解法1: 选用最小二乘法,先计算出: 0 10 x,=496.1,∑y=168.6, isl i=l 2-24613512=8364,92 10 代入式(8),则有:a=0.04,b=0.339,所求线性回归方程为: y=0.04+0.339x (27) 下面的解法2考虑,若基于MCMC方法,取循环次数t=200000,每一轮循环都收集a,b 两个参数,去除前2000轮未收敛的循环,剩余的循环中每隔50个收集一个,这样共得到 3960个数据,将各统计数作柱形图。由柱形图看出,a,b分布是左右对称的,因此分别以其 平均数0.039和0.342估计相应的参数,从而得到回归方程: y=0.039+0.342x (28) 比较不难发现,此结果与应用最小二乘法求解的结果非常一致。 4.7对结果的分析与思考 在经典的统计学理论中,对于较简单的一元线性回归模型参数的估计,无论是最小二乘 法还是极大似然方法,都仅利用了所采集数据的样本信息和总体信息。而贝叶斯估计,不仅 仅利用了已有数据的样本信息和总体信息,而且还利用了先验信息,即在抽样前有关已有参 数的一些信息,由于这些先验信息参与到了统计推断中来,无疑提高了统计推断的质量。 近年来,随着现代统计学的迅猛发展,利用MCMC方法处理复杂的统计问题,己经获 得令人瞩目的成功,在经济、物理、生物技术、工业自动化等诸多领域都得到了日益广泛的 应用,并成为这些学科中一些重要原理与方法的依据之一。在许多较为复杂的情况下, MCMC算法比经典数理统计方法能更直接地解决问题,且可有效整合部分先验信息,但因 其需要高强度计算的特性曾一度限制了其应用与推广。随着高性能计算机的发展,贝叶斯统 计方法已被广泛用于科学研究的各个领域。 虽然贝叶斯方法并未给出参数估计的具体表达式,但是它可以推导出参数估计的后验分 布,借助于计算机进行概率抽取,同样可以对参数进行估计。在简单模型参数估计上,两者 方法效果相差不大,在复杂模型参数估计上,贝叶斯方法较经典统计方法显示出更大的优越 性。 o
《随机模拟方法与应用》课程大作业 2015 年度 春季学期 10 周波 49.2 50.0 49.3 49.0 49.0 49.5 49.8 49.9 50.2 50.2 盘 速 度 16.7 17.0 16.8 16.6 16.7 16.8 16.9 17.0 17.0 17.1 根据表中所给的电流周波与第一导丝盘速度的 10 对数据,求线性回归方程。 解法 1: 选用最小二乘法,先计算出: 10 10 1 1 10 10 2 1 1 496.1, 168.6, 24613.51, 8364.92 i i i i i i i i i x y x x y 代入式(8),则有: ^ ^ a b 0.04, 0.339 ,所求线性回归方程为: ^y x 0.04 0.339 (27) 下面的解法 2 考虑,若基于 MCMC 方法,取循环次数 t=200000,每一轮循环都收集 a,b 两个参数,去除前 2000 轮未收敛的循环,剩余的循环中每隔 50 个收集一个,这样共得到 3960 个数据,将各统计数作柱形图。由柱形图看出,a,b 分布是左右对称的,因此分别以其 平均数 0.039 和 0.342 估计相应的参数,从而得到回归方程: ^y x 0.039 0.342 (28) 比较不难发现,此结果与应用最小二乘法求解的结果非常一致。 4.7 对结果的分析与思考 在经典的统计学理论中,对于较简单的一元线性回归模型参数的估计,无论是最小二乘 法还是极大似然方法,都仅利用了所采集数据的样本信息和总体信息。而贝叶斯估计,不仅 仅利用了已有数据的样本信息和总体信息,而且还利用了先验信息,即在抽样前有关已有参 数的一些信息,由于这些先验信息参与到了统计推断中来,无疑提高了统计推断的质量。 近年来,随着现代统计学的迅猛发展,利用 MCMC 方法处理复杂的统计问题,己经获 得令人瞩目的成功,在经济、物理、生物技术、工业自动化等诸多领域都得到了日益广泛的 应用,并成为这些学科中一些重要原理与方法的依据之一。在许多较为复杂的情况下, MCMC 算法比经典数理统计方法能更直接地解决问题,且可有效整合部分先验信息,但因 其需要高强度计算的特性曾一度限制了其应用与推广。随着高性能计算机的发展,贝叶斯统 计方法已被广泛用于科学研究的各个领域。 虽然贝叶斯方法并未给出参数估计的具体表达式,但是它可以推导出参数估计的后验分 布,借助于计算机进行概率抽取,同样可以对参数进行估计。在简单模型参数估计上,两者 方法效果相差不大,在复杂模型参数估计上,贝叶斯方法较经典统计方法显示出更大的优越 性