
水 利 学 报 2013年8月 SHUILI XUEBAO 第44卷第8期 文章编号:0559-9350(2013)08-0942-08 基于广义极值分布和Metropolis-Hastings抽样算法的 贝叶斯MCMC洪水频率分析方法 鲁帆,严登华 (中国水利水电科学研究院流域水循环模拟与调控国家重点实验室,北京100038) 摘要:广义极值(GEV)分布是国内外洪水频率分析建模中广泛应用的一种概率分布。本文将水文频率分布线型的 未知参数看作随机变量,通过基于Metropolis--Hastings抽样算法的贝叶斯MCMC方法估计GEV分布参数和设计洪 水的后验分布:并据此进行极值洪水的频率分析。汉江流域丹江口水库年最大1日(3日、5日、7日)洪量和年最 大洪峰流量频率分析结果表明,基于Metropolis-Hastings抽样的MCMC模拟在GEV分布参数的贝叶斯估计计算中 行之有效;由于利用了与似然函数渐近性质无关的先验信息,贝叶斯估计方法得到的高分位数设计洪量的后验分 布比经典统计方法得到的设计洪量能包含更多的信息,从而能表达由于参数不确定性而引起的预测不确定性。该 方法能显著地通过分位数图、PPCC法、均方根误差法、K-S法等多种拟合优度检验方法,拟合效果不亚于矩 法、极大似然估计法等常用的经典统计方法。 关键词:洪水频率分析;贝叶斯估计;广义极值分布;Metropolis--Hastings抽样;拟合优化度检验 中图分类号:P333 文献标识码:A 1研究背景 极值洪水是一类非常典型的极值事件,其发生频率小,而一旦发生却影响巨大。相对于一般样 本而言,极值洪水的观测数据比较缺乏,这导致洪水频率分析中分布参数和分位数的估计存在较大 的不确定性。因此,极值洪水的频率计算及不确定性评估方法一直是水文领域的一个研究热点。 贝叶斯估计是一种综合考虑未知总体分布参数的先验信息与样本信息的统计方法,其依据贝叶 斯定理,先求出后验分布,再根据后验分布推断未知总体分布参数。它与矩法、权函数法、极大似 然法等经典统计之间的主要区别在于:它认为未知参数可以看作是随机变量,在关于总体分布参数 的任何统计推断问题中,除了使用样本所提供的信息外,还必须在抽样之前就依据经验或历史资料 规定一个总体分布参数先验信息的概率表述,即先验分布。在洪水频率分析中,如果有其他信息可 以利用,并能表示成先验分布的形式,则即使样本系列较短,也可以获得相对比较精确的推断。此 外,利用贝叶斯估计得到的高分位数的后验分布,由于考虑了模型的不确定性和参数的随机性,通 常比经典统计方法估计的高分位数包含更多的信息。近年来,贝叶斯估计方法逐步被引入到水文频 率分析研究中。例如:Daniel R.H.O'Connell研究了一种新颖的非参数贝叶斯洪水频率估计方法a, W Femandes等s利用贝叶斯方法和具有上界的分布函数研究极值洪水的概率。应用贝叶斯方法的最 大障碍在于后验统计推断中分母积分的计算。虽然选择好的先验分布族可以简化后验分布中的积分 计算,但对于具有高维参数向量的复杂总体分布,即便是用数值积分方法,后验分布计算式中分母 的计算也比较困难。模拟方法的新近发展使这一难题得到了有效的解决,其中的马尔科夫链蒙特卡 罗(MCMC)方法就是较好的方法。 收稿日期:2012-10-30 基金项目:国家自然科学基金项目(51109224):国家重点基础研究发展计划课题(2013CB036406、2010CB951102) 作者简介:鲁帆(1981-),男,湖北天门人,博士,高级工程师,主要从事水文水资源研究。E-mail:19805320@163.com -942-
收稿日期:2012-10-30 基金项目:国家自然科学基金项目(51109224);国家重点基础研究发展计划课题(2013CB036406、2010CB951102) 作者简介:鲁帆(1981-),男,湖北天门人,博士,高级工程师,主要从事水文水资源研究。E-mail:lf9805320@163.com 2013 年 8 月 第 44 卷 第 8 期 文章编号:0559-9350(2013)08-0942-08 水 利 学 报 SHUILI XUEBAO 基于广义极值分布和 Metropolis-Hastings抽样算法的 贝叶斯 MCMC 洪水频率分析方法 鲁 帆,严登华 (中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038) 摘要:广义极值(GEV)分布是国内外洪水频率分析建模中广泛应用的一种概率分布。本文将水文频率分布线型的 未知参数看作随机变量,通过基于 Metropolis-Hastings 抽样算法的贝叶斯 MCMC 方法估计 GEV 分布参数和设计洪 水的后验分布,并据此进行极值洪水的频率分析。汉江流域丹江口水库年最大 1 日(3 日、5 日、7 日)洪量和年最 大洪峰流量频率分析结果表明,基于 Metropolis-Hastings 抽样的 MCMC 模拟在 GEV 分布参数的贝叶斯估计计算中 行之有效;由于利用了与似然函数渐近性质无关的先验信息,贝叶斯估计方法得到的高分位数设计洪量的后验分 布比经典统计方法得到的设计洪量能包含更多的信息,从而能表达由于参数不确定性而引起的预测不确定性。该 方法能显著地通过分位数图、PPCC 法、均方根误差法、K-S 法等多种拟合优度检验方法,拟合效果不亚于矩 法、极大似然估计法等常用的经典统计方法。 关键词:洪水频率分析;贝叶斯估计;广义极值分布;Metropolis-Hastings抽样;拟合优化度检验 中图分类号:P333 文献标识码:A 1 研究背景 极值洪水是一类非常典型的极值事件,其发生频率小,而一旦发生却影响巨大。相对于一般样 本而言,极值洪水的观测数据比较缺乏,这导致洪水频率分析中分布参数和分位数的估计存在较大 的不确定性[1-2] 。因此,极值洪水的频率计算及不确定性评估方法一直是水文领域的一个研究热点。 贝叶斯估计是一种综合考虑未知总体分布参数的先验信息与样本信息的统计方法,其依据贝叶 斯定理,先求出后验分布,再根据后验分布推断未知总体分布参数[3] 。它与矩法、权函数法、极大似 然法等经典统计之间的主要区别在于:它认为未知参数可以看作是随机变量,在关于总体分布参数 的任何统计推断问题中,除了使用样本所提供的信息外,还必须在抽样之前就依据经验或历史资料 规定一个总体分布参数先验信息的概率表述,即先验分布。在洪水频率分析中,如果有其他信息可 以利用,并能表示成先验分布的形式,则即使样本系列较短,也可以获得相对比较精确的推断。此 外,利用贝叶斯估计得到的高分位数的后验分布,由于考虑了模型的不确定性和参数的随机性,通 常比经典统计方法估计的高分位数包含更多的信息。近年来,贝叶斯估计方法逐步被引入到水文频 率分析研究中。例如:Daniel R.H. O’Connell 研究了一种新颖的非参数贝叶斯洪水频率估计方法[4] , W Femandes 等[5] 利用贝叶斯方法和具有上界的分布函数研究极值洪水的概率。应用贝叶斯方法的最 大障碍在于后验统计推断中分母积分的计算。虽然选择好的先验分布族可以简化后验分布中的积分 计算,但对于具有高维参数向量的复杂总体分布,即便是用数值积分方法,后验分布计算式中分母 的计算也比较困难[6] 。模拟方法的新近发展使这一难题得到了有效的解决,其中的马尔科夫链蒙特卡 罗(MCMC)方法就是较好的方法[7] 。 — 942 —

GEV分布用统一的形式表示Gumbel分布、Frechet分布和Weibull分布等3种极值分布类型,是分 析随机变量极端变异性的一个重要分布,广泛应用于水文、气象、保险和金融等领域。GEV分布 常用的参数估计方法包括极大似然估计法、线性矩法和矩法等,其中以极大似然估计法最为常用四。 然而,虽然极大似然估计法从考虑不确定性出发,可以计算极值变量分位数的置信区间,但由于极大 似然估计量以渐近正态性为基础,所以除非样本系列足够长,否则不能充分说明这种不确定性。 Martins和Stedinger的研究也表明,当样本系列较短时,极大似然估计法估计的形状参数有时会偏 小,这导致观测值与分位数值之间的均方根误差会偏大。 本文将GEV分布作为洪水频率分布线型,选取基于Metropolis-Hastings:抽样的MCMC模拟方法, 研究极值洪水的贝叶斯MCMC频率分析方法,并应用于南水北调中线工程水源地丹江口水库入库洪 水的频率分析中。 2贝叶斯洪水频率分析的基本原理 对于给定的水文要素样本系列x=(X,·,X)和选定的水文频率分布线型,洪水频率分析中贝 叶斯估计方法的基本原理如图1所示,可概括成如下4步。 先验 分布 MCMC模拟后验 参数估计 水文频率 片斯 及设计洪 分布线型 公式 分布 水计算 似然 函数 图1贝叶斯估计方法基本原理 (1)先验分布选择与似然函数计算。首先需要依据经验或历史资料来构建一个总体分布参数先验 信息的概率表述,即先验分布。先验分布的确定具有一定的主观性,也可能会对贝叶斯估计的效率 及参数估计结果的可靠性产生一定的影响。例如,若已知0≤≤1,且此区间内的任何值都有相等的 概率,即可认为的先验分布是(0,1)上的均匀分布U(0,1)。如果相信是一个任意实值,且可能取 较小值,而不是较大值,则可用一个方差很大的正态分布表示,比如N(0,50)。对于未知的总体分 布参数向量9,用π(0)表示其先验分布的密度。由于X是相互独立的,所以样本=(X,·,X)的似 然函数∫(x9)可用下式计算: f(xB)=Πf(:) (1) (2)后验分布计算。由贝叶斯公式将关于的先验密度π(0)的信息转化为含有由数据提供的附加信 息的后验分布密度∫(0x),用下式计算: π(0)f(xl9) f(0x)= (2) nπ(6)f(x9)d9 (3)总体分布参数估计。后验分布是贝叶斯统计推断的基础。对的任何统计推断完全基于且仅 基于这个后验分布。例如,可以取后验分布的均值6=E(日)=旷(Br)d作为的估计值或将使得 后验密度最大的6=m路∫(k)作为的估计值。 (4)设计洪水计算。如果z表示密度函数为∫(z9)的随机变量的未来观测,∫(日x)表示观测值为 x时的后验分布,则 (=k)=fr(=0)f(0k)d0 (3) 即为给定x下z的预测密度。与其他的预测方法相比,预测密度的优点在于它包含了反映模型不确定 —943-
GEV 分布用统一的形式表示 Gumbel分布、Fréchet分布和 Weibull分布等 3 种极值分布类型,是分 析随机变量极端变异性的一个重要分布,广泛应用于水文、气象、保险和金融等领域[8-10] 。GEV 分布 常用的参数估计方法包括极大似然估计法、线性矩法和矩法等,其中以极大似然估计法最为常用[11-12] 。 然而,虽然极大似然估计法从考虑不确定性出发,可以计算极值变量分位数的置信区间,但由于极大 似然估计量以渐近正态性为基础,所以除非样本系列足够长,否则不能充分说明这种不确定性[13-14] 。 Martins 和 Stedinger 的研究也表明,当样本系列较短时,极大似然估计法估计的形状参数有时会偏 小,这导致观测值与分位数值之间的均方根误差会偏大[15] 。 本文将 GEV 分布作为洪水频率分布线型,选取基于 Metropolis-Hastings 抽样的 MCMC 模拟方法, 研究极值洪水的贝叶斯 MCMC 频率分析方法,并应用于南水北调中线工程水源地丹江口水库入库洪 水的频率分析中。 2 贝叶斯洪水频率分析的基本原理 对于给定的水文要素样本系列 x=(X1,…,Xn )和选定的水文频率分布线型,洪水频率分析中贝 叶斯估计方法的基本原理如图 1 所示,可概括成如下 4 步。 (1)先验分布选择与似然函数计算。首先需要依据经验或历史资料来构建一个总体分布参数先验 信息的概率表述,即先验分布。先验分布的确定具有一定的主观性,也可能会对贝叶斯估计的效率 及参数估计结果的可靠性产生一定的影响。例如,若已知 0≤θ≤1,且此区间内的任何值都有相等的 概率,即可认为θ的先验分布是(0,1)上的均匀分布 U(0,1)。如果相信θ是一个任意实值,且可能取 较小值,而不是较大值,则可用一个方差很大的正态分布表示,比如 N(0,50)。对于未知的总体分 布参数向量θ,用π(θ )表示其先验分布的密度。由于 Xi是相互独立的,所以样本 x=(X1,…,Xn )的似 然函数 f ( x |θ )可用下式计算: f ( x |θ ) = Õi = 1 n f ( x ) i ;θ (1) (2)后验分布计算。由贝叶斯公式将关于θ的先验密度π(θ )的信息转化为含有由数据提供的附加信 息的后验分布密度 f (θ |x ),用下式计算: f (θ |x ) = π(θ ) f ( x |θ ) Θ π(θ ) f ( x |θ )dθ (2) (3)总体分布参数估计。后验分布是贝叶斯统计推断的基础。对θ的任何统计推断完全基于且仅 基于这个后验分布。例如,可以取后验分布的均值θ̂ = E (θ |x ) = Θθf (θ |x )dθ 作为θ的估计值或将使得 后验密度最大的θ̂ = max θ ∈ Θ f (θ |x )作为θ的估计值。 (4)设计洪水计算。如果 z 表示密度函数为 f (z |θ )的随机变量的未来观测, f (θ |x )表示观测值为 x 时θ的后验分布,则 f (z |x ) = Θ f (z |θ ) f (θ |x )dθ (3) 即为给定 x 下 z 的预测密度。与其他的预测方法相比,预测密度的优点在于它包含了反映模型不确定 图 1 贝叶斯估计方法基本原理 — 943 —

性的∫(旧x),以及反映未来观测值变异性的∫(z9)。 由式(3)得 Pr(Z≤zx)=Pr(Z≤zP)/(0r)d (4) 式(4)给出了水文要素样本的未来分布,其中含有参数的不确定性和未来观测值的随机性。 解方程Pr(Z≤zx)=1-1/m,就可得到m年重现水平的设计洪水值(即1-1/m分位数),本文包 含了由于模型估计引起的不确定性。其中:式(4)的估计值可以用MCMC模拟方法估计后验分布得 到。在删除了模拟序列前面一些数值之后,剩下的序列01,…,日,就可看作来自平稳分布∫(6) 的观测值。 3后验分布随机样本的MCMC模拟 MCMC方法的目的是模拟产生服从式(2)中后验分布的随机样本,然后用模拟样本来估计后验分 布。例如,用模拟样本的均值估计后验均值,用模拟样本的直方图估计后验分布的密度等。该方法 产生的模拟序列0。,0,82,…为一阶马尔科夫链,其中0。为任意初始值,6:由条件分布q(9)产 生,即01只依赖于当前的0,与以前的9。,9,…,0-1无关。记p(0,0)=q(0+1=0'9:=0)称为转 移核,它表示当0,=0时,经一步迭代后的马尔科夫链的边缘分布,且假定与i无关,即马尔科夫 链是时间齐次。若后验分布∫(0x)满足 Jp(0,9)f(ex)d0=f(0'),0'eΘ (5) 则称∫(0x)为转移核p(0,0)的平稳分布。因此,如果能使得0。的分布就是∫(日x),则由平稳 分布的定义可保证任一,的边缘分布也是∫(0x)。但实际上,这是难以实现的。之所以要用MCMC 方法,就是因为后验分布∫(日x)的抽样比较麻烦。实际证明,不同的,对日,的分布并没有显著影响。 对不同的初值。,虽然其实际分布并不一定是∫(旧x),但经过一段时间的迭代后,可以认为此时的日 的边缘分布就是平稳分布∫(0x),称为收敛0。只需抛掉收敛之前的6,…,,用以后的01,…, 0作为后验分布∫(6x)的抽样即可。 在采用MCMC方法时,条件分布q(~9:)对马尔科夫链的影响非常重要,只有合适的转移核才能满 足式(5),使∫(0x)为平稳分布。不同的转移核相应于不同的MCMC方法。Metropolis--Hastings算法 是较早出现且最有名的MCMC方法,它由Metropolis等人提出,之后由Hastings对其加以推广而形 成。此外,还有Gibbs?算法等,Gibbs算法是Metropolis-Hastings算法的一个特例。近年来,一些学者 尝试将贝叶斯MCMC方法引入水文频率分析和水文预报领域-o。本文采用Metropolis--Hastings算法 进行后验分布随机样本的MCMC模拟,选定建议分布g(9:)和初值日。,第i次迭代的具体步骤如下: (1)由q(9)产生一个新的建议值0: (2)根据选择的似然函数、先验分布和转移核,计算接受概率 f(x9)π(09(lB) a;min, (6) f(xa.)π(a,)9(oe) (3)以概率a接受0为下一个9:+即 0,u≤&a: 0:+1= (7) 8,u>a 其中,u是[0,1]均匀分布随机数。 -944-
性的 f (θ |x ),以及反映未来观测值变异性的 f (z |θ )。 由式(3)得 Pr (Z ≤ z |x ) = Θ Pr (Z ≤ z |θ ) f (θ |x )dθ (4) 式(4)给出了水文要素样本的未来分布,其中含有参数的不确定性和未来观测值的随机性。 解方程Pr (Z ≤ z |x ) = 1 - 1 m,就可得到 m 年重现水平的设计洪水值(即1 - 1 m分位数),本文包 含了由于模型估计引起的不确定性。其中:式(4)的估计值可以用 MCMC 模拟方法估计后验分布得 到。在删除了模拟序列前面一些数值之后,剩下的序列θk+1,…,θk+s就可看作来自平稳分布 f (θ |x ) 的观测值。 3 后验分布随机样本的 MCMC 模拟 MCMC 方法的目的是模拟产生服从式(2)中后验分布的随机样本,然后用模拟样本来估计后验分 布。例如,用模拟样本的均值估计后验均值,用模拟样本的直方图估计后验分布的密度等。该方法 产生的模拟序列θ0,θ1,θ2,…为一阶马尔科夫链,其中θ0 为任意初始值,θi+1 由条件分布q (∙ |θ )i 产 生,即θi+1只依赖于当前的θi ,与以前的θ0,θ1,…,θi-1无关。记 p (θ,θ ′) = q (θi + 1 = θ ′ |θi = θ )称为转 移核[6,16] ,它表示当θi = θ 时,经一步迭代后的马尔科夫链的边缘分布,且假定与 i 无关,即马尔科夫 链是时间齐次。若后验分布 f (θ |x )满足 p (θ,θ ′) f (θ |x )dθ = f (θ ′ |x ),∀θ ′ ∈ Θ (5) 则称 f (θ |x )为转移核 p (θ,θ ′)的平稳分布。因此,如果能使得θ0的分布就是 f (θ |x ),则由平稳 分布的定义可保证任一θi的边缘分布也是 f (θ |x )。但实际上,这是难以实现的。之所以要用 MCMC 方法,就是因为后验分布 f (θ |x )的抽样比较麻烦。实际证明,不同的θ0对θi的分布并没有显著影响。 对不同的初值θ0,虽然其实际分布并不一定是 f (θ |x ),但经过一段时间的迭代后,可以认为此时的θi 的边缘分布就是平稳分布 f (θ |x ),称为收敛[6] 。只需抛掉收敛之前的θ1,…,θk,用以后的θk+1,…, θn作为后验分布 f (θ |x )的抽样即可。 在采用 MCMC 方法时,条件分布q (∙ |θ )i 对马尔科夫链的影响非常重要,只有合适的转移核才能满 足式(5),使 f (θ |x )为平稳分布。不同的转移核相应于不同的 MCMC 方法。Metropolis-Hastings 算法 是较早出现且最有名的 MCMC 方法,它由 Metropolis 等人提出,之后由 Hastings 对其加以推广而形 成。此外,还有 Gibbs 算法等,Gibbs 算法是 Metropolis-Hastings 算法的一个特例。近年来,一些学者 尝试将贝叶斯 MCMC 方法引入水文频率分析和水文预报领域[17-20] 。本文采用 Metropolis-Hastings 算法 进行后验分布随机样本的 MCMC 模拟,选定建议分布q (∙ |θ )i 和初值θ0,第 i次迭代的具体步骤如下: (1)由q (∙ |θ )i 产生一个新的建议值θ * ; (2)根据选择的似然函数、先验分布和转移核,计算接受概率αi αi = min ì í î ï ï ü ý þ ï ï 1, f ( x |θ ) * π(θ ) * q (θi |θ ) * f ( x |θ )i π(θ )i q (θ | ) * θi (6) (3)以概率αi接受θ * 为下一个θi + 1 ,即 θi + 1 = ì í î θ * ,μ ≤ αi θi,μ > αi (7) 其中,μ是[0,1]均匀分布随机数。 — 944 —

通过迭代重复上述步骤。这样对足够大的k值,序列日41,02,…可以认为是后验分布(2)的抽 样。和独立样本一样,可以用这个序列来估计一些数字特征,比如后验均值。这种方法可以完全不 考虑所选的g(当然必须服从某些正则条件)。从极限意义上讲,式(7)给出的拒绝步骤确保了模拟序 列的平稳分布具有所需的边缘分布。 4实例分析 丹江口水库是汉江中下游防洪和水资源开发的关键水利枢纽工程,也是南水北调中线工程的水 源工程。枢纽控制流域面积9.52万km2,约占汉江集水面积的60%,多年平均入库径流量约363亿m。 根据该水库建库后1969一2008年的入库径流资料,分别选取设计时段(1、3、5、7d)的年最大洪量系 列和年最大洪峰流量系列作为洪水频率计算的样本数据。 4.1GEV分布参数与设计洪水的估计GEV分布的分布函数为: ≠0 F(x)= (8) x-) exp-exp =0 其中:μ、σ、分别为GEV分布模型的位置参数、尺度参数和形状参数,并满足4∈R,σ>0,∈R, 1+(x-u)/o>0。 为计算方便,洪量系列的单位统一为万m/s,以下类同。分别对丹江口水库设计时段(1、3、5、7d) 的年最大洪量值系列和年最大洪峰流量系列建立GEV分布模型。令中=Iog0,以保证σ>0。选择先验 密度函数为π(u,中,)=π(u)π(中)π()。其中π(日、(日和π,(均值为零,方差分别为4、6和E 的正态密度函数,参数、中和之间是独立的。选择足够大的方差使密度函数相当平坦,取u=。=10,三 100,这样就确定了先验密度。 根据Metropolis--Hastings方法原理,对向量(w,中,)的每个分量分别应用式(7),且每个建议分 布g选为各自坐标轴上的随机游动,即u=4+e4,中=中+e。,=(+e,其中,ee、e。、e是均值 为0,方差分别为w4、"。、”的正态变量。"。、"b、0,的数值根据试验确定。 限于篇幅,仅给出年最大1日洪量GEV分布模型每个参数20O00次迭代产生的MCMC序列,见 图2。其中,令σ,=,得到尺度参数σ后验分布的模拟样本。在除去前面不稳定的模拟值后,其余 比较稳定的模拟值就认为是要求的后验分布的观测。 从图2可以看出,左边的序列大约在3000次迭代后趋于稳定,右边的序列大约在1000次迭代后 趋于稳定。但左边图中显示各参数的收敛值与右边图中显示各参数的收敛值非常接近。这说明参数 0a、06、w,的选择并不影响计算的模型参数,只是影响算法的效率。 将向量(4,0,)的每个模拟值代入式(9) 4--(g-p以门5≠0 X1-p= (9) u-log-log(1-p),=0 就得到相应的1p年重现期的设计洪量值的后验分布样本。图3给出了选取参数w.=0.01、心。= 025、心=0.25的情况下,年最大1日洪量GEV分布模型的参数u、o、和百年一遇设计洪量xo9的后 验密度估计。其中,百年一遇设计洪量的单位为万m/s。 表1列出了贝叶斯估计方法和极大似然估计方法估计的不同极值系列GEV模型的分布参数值及 百年一遇设计洪量值。 -945-
通过迭代重复上述步骤。这样对足够大的 k 值,序列θk+1,θk+2,…可以认为是后验分布(2)的抽 样。和独立样本一样,可以用这个序列来估计一些数字特征,比如后验均值。这种方法可以完全不 考虑所选的 q(当然必须服从某些正则条件)。从极限意义上讲,式(7)给出的拒绝步骤确保了模拟序 列的平稳分布具有所需的边缘分布。 4 实例分析 丹江口水库是汉江中下游防洪和水资源开发的关键水利枢纽工程,也是南水北调中线工程的水 源工程。枢纽控制流域面积 9.52 万 km2 ,约占汉江集水面积的 60%,多年平均入库径流量约 363 亿 m3 。 根据该水库建库后 1969—2008 年的入库径流资料,分别选取设计时段(1、3、5、7d)的年最大洪量系 列和年最大洪峰流量系列作为洪水频率计算的样本数据。 4.1 GEV 分布参数与设计洪水的估计 GEV 分布的分布函数为: F ( x ) = ì í î ï ï ï ï ï ï ï ï exp ì í î ï ï ü ý þ ï ï - é ë êê ù û úú 1 + ξ ( x - μ ) σ -1 ξ ξ ≠ 0 exp ì í î ü ý þ -exp é ë êê ù û - úú ( x - μ ) σ ξ = 0 (8) 其中:μ、σ、ξ分别为 GEV分布模型的位置参数、尺度参数和形状参数,并满足 μ ∈ R,σ > 0,ξ ∈ R , 1 + ξ ( x - μ ) σ > 0。 为计算方便,洪量系列的单位统一为万 m3 /s,以下类同。分别对丹江口水库设计时段(1、3、5、7d) 的年最大洪量值系列和年最大洪峰流量系列建立 GEV 分布模型。令ϕ = logσ ,以保证σ > 0。选择先验 密度函数为π ( μ,ϕ,ξ ) = πμ ( μ )πϕ (ϕ )πξ (ξ )。其中πμ (⋅)、πϕ (⋅)和πξ (⋅)均值为零,方差分别为 vμ、vϕ和 vξ 的正态密度函数,参数μ、ϕ和ξ之间是独立的。选择足够大的方差使密度函数相当平坦,取vμ=vϕ=104 ,vξ = 100,这样就确定了先验密度。 根据 Metropolis-Hastings 方法原理,对向量(μ,ϕ,ξ)的每个分量分别应用式(7),且每个建议分 布 q 选为各自坐标轴上的随机游动,即 μ* = μ + εμ,ϕ* = ϕ + εϕ,ξ * =ξ + εξ,其中,εμ、εϕ、εξ是均值 为 0,方差分别为wμ、wϕ、wξ的正态变量。wμ、wϕ、wξ的数值根据试验确定。 限于篇幅,仅给出年最大 1 日洪量 GEV 分布模型每个参数 20 000 次迭代产生的 MCMC 序列,见 图 2。其中,令σi = e ϕi ,得到尺度参数σ后验分布的模拟样本。在除去前面不稳定的模拟值后,其余 比较稳定的模拟值就认为是要求的后验分布的观测。 从图 2 可以看出,左边的序列大约在 3 000 次迭代后趋于稳定,右边的序列大约在 1000 次迭代后 趋于稳定。但左边图中显示各参数的收敛值与右边图中显示各参数的收敛值非常接近。这说明参数 wμ、wϕ、wξ的选择并不影响计算的模型参数,只是影响算法的效率。 将向量(μi ,σi ,ξi )的每个模拟值代入式(9) x1 - p = ì í î ï ï μ - σ ξ é ë ù û 1 - {-log (1 - p )} -ξ ,ξ ≠ 0 μ - σlog {-log (1 - p )}, ξ = 0 (9) 就得到相应的 1/p 年重现期的设计洪量值的后验分布样本。图 3 给出了选取参数wμ=0.01、wϕ = 0.25、wξ=0.25 的情况下,年最大 1 日洪量 GEV 分布模型的参数μ、σ、ξ和百年一遇设计洪量 x0.99的后 验密度估计。其中,百年一遇设计洪量的单位为万 m3 /s。 表 1 列出了贝叶斯估计方法和极大似然估计方法估计的不同极值系列 GEV 模型的分布参数值及 百年一遇设计洪量值。 — 945 —
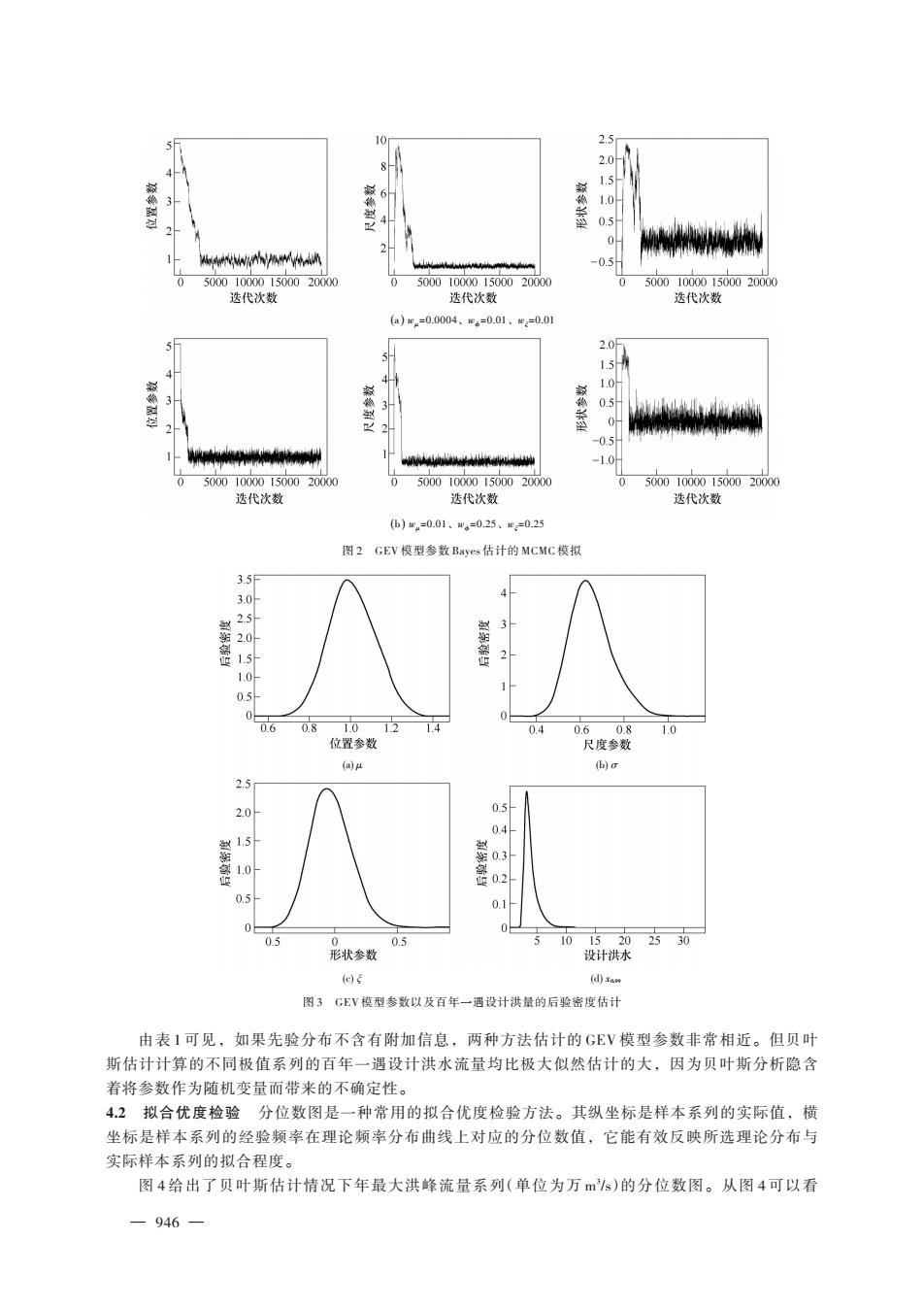
10 2.5 3 6以 1.0 0.5 构州NN/W4aM 0.5 0 5000100001500020000 0 5000100001500020000 5000100001500020000 迭代次数 迭代次数 运代次数 (a).=0.0004、=0.01、=0.01 5 2.0 1.5 4 4-1 1.0- 3/ 0.5 -0.5 1 Mhaw -1.0 05000100001500020000 05000100001500020000 5000100001500020000 迭代次数 迭代次数 迭代次数 ()w.=0.01、w4=0.25、0=0.25 图2GEV模型参数Bayes估计的MCMC模拟 3.5F 30 3 2.0 1.0 05 0 0 0.6 0.81.012 14 0.4 0.608 1.0 位置参数 尺度参数 (a)4 b)o 2.5 2.0 0.5 0.4 1.5 0.3 1.0 0.2 0.5 0.1 0.5 0 0.5 5 1015202530 形状参数 设计洪水 (e) (d)xaw 图3GEV模型参数以及百年一遇设计洪量的后验密度估计 由表1可见,如果先验分布不含有附加信息,两种方法估计的GEV模型参数非常相近。但贝叶 斯估计计算的不同极值系列的百年一遇设计洪水流量均比极大似然估计的大,因为贝叶斯分析隐含 着将参数作为随机变量而带来的不确定性。 4.2拟合优度检验分位数图是一种常用的拟合优度检验方法。其纵坐标是样本系列的实际值,横 坐标是样本系列的经验频率在理论频率分布曲线上对应的分位数值,它能有效反映所选理论分布与 实际样本系列的拟合程度。 图4给出了贝叶斯估计情况下年最大洪峰流量系列(单位为万m/s)的分位数图。从图4可以看 -946-
(a) μ (c) ξ (d) x0.99 (b) σ 图 3 GEV 模型参数以及百年一遇设计洪量的后验密度估计 (a ) wμ=0.0004、wϕ=0.01、wξ=0.01 (b ) wμ=0.01、wϕ=0.25、wξ=0.25 图 2 GEV 模型参数 Bayes估计的 MCMC 模拟 由表 1 可见,如果先验分布不含有附加信息,两种方法估计的 GEV 模型参数非常相近。但贝叶 斯估计计算的不同极值系列的百年一遇设计洪水流量均比极大似然估计的大,因为贝叶斯分析隐含 着将参数作为随机变量而带来的不确定性。 4.2 拟合优度检验 分位数图是一种常用的拟合优度检验方法。其纵坐标是样本系列的实际值,横 坐标是样本系列的经验频率在理论频率分布曲线上对应的分位数值,它能有效反映所选理论分布与 实际样本系列的拟合程度。 图 4 给出了贝叶斯估计情况下年最大洪峰流量系列(单位为万 m3 /s)的分位数图。从图 4 可以看 — 946 —

表1GEV分布参数及设计洪量 GEV分布参数 极值系列 参数估计方法 百年一遇设计洪水流量 (万m/s) 贝叶斯估计 0.972 0.645 -0.036 3.879 最大1日洪量 极大似然估计 1.005 0.615 -0.067 3.439 贝叶斯估计 0.733 0.466 0.038 3.281 最大3日洪量 极大似然估计 0.733 0.435 0.020 2.828 贝叶斯估计 0.571 0.340 0.105 2.781 最大5日洪量 极大似然估计 0.573 0.321 0.085 2.380 贝叶斯估计 0.495 0.280 0.112 2338 最大7日洪量 极大似然估计 0.495 0.261 0.099 2.016 贝叶斯估计 1.183 0.773 -0.114 4.151 年最大洪峰流量 极大似然估计 1.206 0.735 -0.148 3.661 出,所有的分位数图都近似为直线,说明所选分布比较适合实际样本系列。此外,两种不同参数的 分位数图非常接近,这也说明了参数0、心。、心,的选择并不影响理论分布的拟合效果。设计时段 (1、3、5、7)的年最大洪量值系列的分位数图也有相同结论。 35 35F 3.0 3.0 50 2.5 2.5 20- 1s 1.0 1.0 0.5 0.5 0.51.01.52.02.53.03.5 0.51.01.52.02.53.03.5 分位数值 分位数值 (a)w.=0.0004、e4=0.01、1r=0.01 ()m.=0.01、w6=0.25、w=0.25 图4GEV模型贝叶斯估计的分位数 采用PPCC法和均方根误差法、Kolmogrov--Smirnow(简称K-S)法等3种拟合优度检验方法对贝叶 斯估计方法的效果进行了检验。其中,PPCC法依据实测样本序列排序后的观测值与GEV分布曲线上 经验频率分布相应的分位数值之间的相关系数,均方根误差法依据上述观测值与分位数值之间的均 方根误差,K-$法依据样本经验分布与理论极值分布计算柯尔莫哥洛夫统计量,详细原理可参见文 献[6]。在显著性水平0.05下,本文所研究贝叶斯估计方法能显著地通过上述3种方法的检验。以 PPCC相关系数和均方根误差为检验指标,比较贝叶斯估计方法、GEV分布参数估计中最常用的极大 似然估计法、皮尔逊Ⅲ型分布参数估计中最常用的矩法等3种频率分析方法的拟合效果,计算结果 列于表2中。 由表2可见,贝叶斯估计方法计算的PPCC相关系数总体上大于另外两种方法的对应值,而其计 算的均方根误差总体上小于另外两种方法的对应值。这说明贝叶斯估计方法的拟合效果可能略优于 另外两种方法。 5结论 本文基于GEV分布与Metropolis--Hastings算法进行贝叶斯MCMC洪水频率分析研究,并应用于汉 -947-
出,所有的分位数图都近似为直线,说明所选分布比较适合实际样本系列。此外,两种不同参数的 分位数图非常接近,这也说明了参数wμ、wϕ、wξ的选择并不影响理论分布的拟合效果。设计时段 (1、3、5、7d)的年最大洪量值系列的分位数图也有相同结论。 (a ) wμ=0.0004、wϕ=0.01、wξ=0.01 (b ) wμ=0.01、wϕ=0.25、wξ=0.25 图 4 GEV 模型贝叶斯估计的分位数 采用 PPCC 法和均方根误差法、Kolmogrov-Smirnow(简称 K-S)法等 3 种拟合优度检验方法对贝叶 斯估计方法的效果进行了检验。其中,PPCC 法依据实测样本序列排序后的观测值与 GEV 分布曲线上 经验频率分布相应的分位数值之间的相关系数,均方根误差法依据上述观测值与分位数值之间的均 方根误差,K-S 法依据样本经验分布与理论极值分布计算柯尔莫哥洛夫统计量,详细原理可参见文 献[6]。在显著性水平 0.05 下,本文所研究贝叶斯估计方法能显著地通过上述 3 种方法的检验。以 PPCC 相关系数和均方根误差为检验指标,比较贝叶斯估计方法、GEV 分布参数估计中最常用的极大 似然估计法、皮尔逊 III 型分布参数估计中最常用的矩法等 3 种频率分析方法的拟合效果,计算结果 列于表 2 中。 由表 2 可见,贝叶斯估计方法计算的 PPCC 相关系数总体上大于另外两种方法的对应值,而其计 算的均方根误差总体上小于另外两种方法的对应值。这说明贝叶斯估计方法的拟合效果可能略优于 另外两种方法。 5 结论 本文基于 GEV 分布与 Metropolis-Hastings 算法进行贝叶斯 MCMC 洪水频率分析研究,并应用于汉 极值系列 最大 1 日洪量 最大 3 日洪量 最大 5 日洪量 最大 7 日洪量 年最大洪峰流量 参数估计方法 贝叶斯估计 极大似然估计 贝叶斯估计 极大似然估计 贝叶斯估计 极大似然估计 贝叶斯估计 极大似然估计 贝叶斯估计 极大似然估计 GEV 分布参数 μ 0.972 1.005 0.733 0.733 0.571 0.573 0.495 0.495 1.183 1.206 σ 0.645 0.615 0.466 0.435 0.340 0.321 0.280 0.261 0.773 0.735 ξ -0.036 -0.067 0.038 0.020 0.105 0.085 0.112 0.099 -0.114 -0.148 百年一遇设计洪水流量 (/ 万 m3 /s) 3.879 3.439 3.281 2.828 2.781 2.380 2.338 2.016 4.151 3.661 表 1 GEV 分布参数及设计洪量 — 947 —
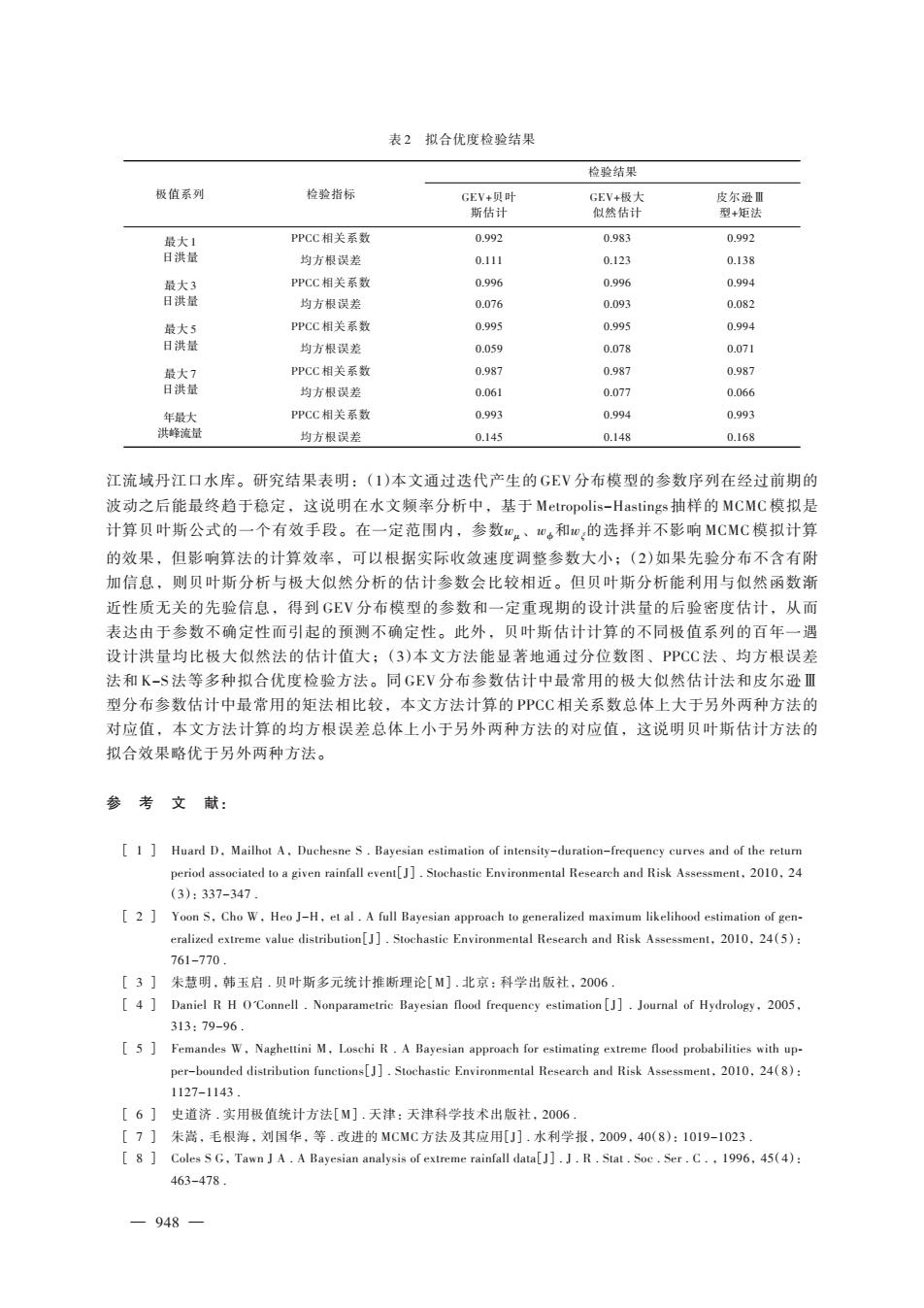
表2拟合优度检验结果 检验结果 极值系列 检验指标 GEV+贝叶 GEV+极大 皮尔逊Ⅲ 斯估计 似然估计 型+矩法 最大1 PPCC相关系数 0.992 0.983 0.992 日洪量 均方根误差 0.111 0.123 0.138 最大3 PPCC相关系数 0.996 0.996 0.994 日洪量 均方根误差 0.076 0.093 0.082 最大5 PPCC相关系数 0.995 0.995 0.994 日洪量 均方根误差 0.059 0.078 0.071 最大7 PPCC相关系数 0.987 0.987 0.987 日洪量 均方根误差 0.061 0.077 0.066 年最大 PPCC相关系数 0.993 0.994 0.993 洪蜂流量 均方根误差 0.145 0.148 0.168 江流域丹江口水库。研究结果表明:(1)本文通过迭代产生的GEV分布模型的参数序列在经过前期的 波动之后能最终趋于稳定,这说明在水文频率分析中,基于Metropolis--Hastings抽样的MCMC模拟是 计算贝叶斯公式的一个有效手段。在一定范围内,参数We、w和u的选择并不影响MCMC模拟计算 的效果,但影响算法的计算效率,可以根据实际收敛速度调整参数大小;(2)如果先验分布不含有附 加信息,则贝叶斯分析与极大似然分析的估计参数会比较相近。但贝叶斯分析能利用与似然函数渐 近性质无关的先验信息,得到GEV分布模型的参数和一定重现期的设计洪量的后验密度估计,从而 表达由于参数不确定性而引起的预测不确定性。此外,贝叶斯估计计算的不同极值系列的百年一遇 设计洪量均比极大似然法的估计值大;(3)本文方法能显著地通过分位数图、PPCC法、均方根误差 法和K-S法等多种拟合优度检验方法。同GEV分布参数估计中最常用的极大似然估计法和皮尔逊Ⅲ 型分布参数估计中最常用的矩法相比较,本文方法计算的PPCC相关系数总体上大于另外两种方法的 对应值,本文方法计算的均方根误差总体上小于另外两种方法的对应值,这说明贝叶斯估计方法的 拟合效果略优于另外两种方法。 参考文献: [1 Huard D,Mailhot A.Duchesne S.Bayesian estimation of intensity-duration-frequency curves and of the return period associated to a given rainfall event[J].Stochastic Environmental Research and Risk Assessment,2010,24 (3):337-347. 2 Yoon S.Cho W.Heo J-H,et al.A full Bayesian approach to generalized maximum likelihood estimation of gen- eralized extreme value distribution[J].Stochastic Environmental Research and Risk Assessment,2010,24(5): 761-770. [3]朱慧明.韩玉启.贝叶斯多元统计推断理论[M].北京:科学出版社,2006. [4 Daniel R H OConnell.Nonparametric Bayesian flood frequency estimation[J].Journal of Hydrology,2005, 313:79-96. [5 Femandes W.Naghettini M,Loschi R.A Bayesian approach for estimating extreme flood probabilities with up- per-bounded distribution functions[]].Stochastic Environmental Research and Risk Assessment.2010.24(8): 1127-1143 [6]史道济.实用极值统计方法[M].天津:天津科学技术出版社,2006. [7]朱嵩,毛根海,刘国华,等.改进的MCMC方法及其应用[J].水利学报,2009,40(8):1019-1023 [8 Coles SG,Tawn JA.A Bayesian analysis of extreme rainfall data[J].J.R.Stat.Soc.Ser.C..1996,45(4): 463-478. -948-
极值系列 最大 1 日洪量 最大 3 日洪量 最大 5 日洪量 最大 7 日洪量 年最大 洪峰流量 检验指标 PPCC 相关系数 均方根误差 PPCC 相关系数 均方根误差 PPCC 相关系数 均方根误差 PPCC 相关系数 均方根误差 PPCC 相关系数 均方根误差 检验结果 GEV+贝叶 斯估计 0.992 0.111 0.996 0.076 0.995 0.059 0.987 0.061 0.993 0.145 GEV+极大 似然估计 0.983 0.123 0.996 0.093 0.995 0.078 0.987 0.077 0.994 0.148 皮尔逊Ⅲ 型+矩法 0.992 0.138 0.994 0.082 0.994 0.071 0.987 0.066 0.993 0.168 表 2 拟合优度检验结果 江流域丹江口水库。研究结果表明:(1)本文通过迭代产生的 GEV 分布模型的参数序列在经过前期的 波动之后能最终趋于稳定,这说明在水文频率分析中,基于 Metropolis-Hastings 抽样的 MCMC 模拟是 计算贝叶斯公式的一个有效手段。在一定范围内,参数wμ、wϕ和wξ的选择并不影响 MCMC 模拟计算 的效果,但影响算法的计算效率,可以根据实际收敛速度调整参数大小;(2)如果先验分布不含有附 加信息,则贝叶斯分析与极大似然分析的估计参数会比较相近。但贝叶斯分析能利用与似然函数渐 近性质无关的先验信息,得到 GEV 分布模型的参数和一定重现期的设计洪量的后验密度估计,从而 表达由于参数不确定性而引起的预测不确定性。此外,贝叶斯估计计算的不同极值系列的百年一遇 设计洪量均比极大似然法的估计值大;(3)本文方法能显著地通过分位数图、PPCC 法、均方根误差 法和 K-S 法等多种拟合优度检验方法。同 GEV 分布参数估计中最常用的极大似然估计法和皮尔逊Ⅲ 型分布参数估计中最常用的矩法相比较,本文方法计算的 PPCC 相关系数总体上大于另外两种方法的 对应值,本文方法计算的均方根误差总体上小于另外两种方法的对应值,这说明贝叶斯估计方法的 拟合效果略优于另外两种方法。 参 考 文 献: [ 1 ] Huard D,Mailhot A,Duchesne S . Bayesian estimation of intensity-duration-frequency curves and of the return period associated to a given rainfall event[J]. Stochastic Environmental Research and Risk Assessment,2010,24 (3):337-347 . [ 2 ] Yoon S,Cho W,Heo J-H,et al . A full Bayesian approach to generalized maximum likelihood estimation of gen⁃ eralized extreme value distribution[J]. Stochastic Environmental Research and Risk Assessment,2010,24(5): 761-770 . [ 3 ] 朱慧明,韩玉启 . 贝叶斯多元统计推断理论[M]. 北京:科学出版社,2006 . [ 4 ] Daniel R H O'Connell . Nonparametric Bayesian flood frequency estimation[J]. Journal of Hydrology,2005, 313:79-96 . [ 5 ] Femandes W,Naghettini M,Loschi R . A Bayesian approach for estimating extreme flood probabilities with up⁃ per-bounded distribution functions[J]. Stochastic Environmental Research and Risk Assessment,2010,24(8): 1127-1143 . [ 6 ] 史道济 . 实用极值统计方法[M]. 天津:天津科学技术出版社,2006 . [ 7 ] 朱嵩,毛根海,刘国华,等 . 改进的 MCMC 方法及其应用[J]. 水利学报,2009,40(8):1019-1023 . [ 8 ] Coles S G,Tawn J A . A Bayesian analysis of extreme rainfall data[J]. J . R . Stat . Soc . Ser . C . ,1996,45(4): 463-478 . — 948 —

9 Walshaw D.Modelling extreme wind speeds in regions prone to hurricanes[J].J.R.Stat.Soc.Ser.C..2000, 49(1):51-62. 10 Huang W,Xu S.Nnaji S.Evaluation of GEV model for frequency analysis of annual maximum water levels in the coast of United States[J].Ocean Eng.2008.35(11-12):1132-1147. [11 Prescott P,Walden A T.Maximum likelihood estimation of the parameters of the generalized extreme-value distri- bution[J].Biometrika,1980,67(3):723-724. 12 Madsen H.Rasmussen PF.Rosbjerg D.Comparison of annual maximum series and partial duration series meth- ods for modeling extreme hydrologic events,1.At-site modeling[J].Water Resour.Res .1997.33(4): 746-757. 13 Coles S.An introduction to statistical modeling of extreme values[Z].Springer,London.2001. [14 Katz R W,Parlange M B,Naveau P.Statistics of extremes in hydrology [J].Adv.Water.Resour.,2002,25 (8-12):1287-1304. 15 Martins E S,Stedinger J R.Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data[J].Water Resour.Res.,2000,36(3):737-744. [16]刘次华,随机过程[M].武汉:华中科技大学出版社,2001. [17]邢贞相,芮孝芳,崔海燕,等.基于AM-MCMC算法的贝叶斯概率洪水预报模型[J].水利学报,2007,38 (12):1500-1506. [18]李向阳,程春田,林剑艺,等,基于BP神经网络的贝叶斯概率水文预报模型[J].水利学报,2006,37(3): 354-359. [19 Dirceu S,Reis Jr.Jery R.Stedinger.Bayesian MCMC flood frequency analysis with historical information[]]. Joural of Hydrology,2005,313(1-2):97-116. 20 LiangZ M.Li B Q.YuZ B.et al.Application of Bayesian approach to hydrological frequency analysis[J].Sei- ence China Technological Sciences,2011,54(5):1183-1192. Bayesian MCMC flood frequency analysis based on generalized extreme value distribution and Metropolis-Hastings algorithm LU Fan,YAN Deng-hua (State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin.China Institute of Water Resources and Hydropower Research,Beijing 100038,China) Abstract:The generalized extreme value (GEV)distribution has been widely used for modeling the distri- bution of flood flows.In this paper,the unknown parameters of hydrologic frequeney distribution linetype are considered as random variables.and Bayesian Markov chain Monte Carlo (MCMC)method based on Metropolis-Hastings algorithm is used to evaluate the posterior distributions of GEV distribution parameters and flood quantiles.The application example was conducted with flood data from the Han River basin, near the Danjiangkou reservoir.in Hubei,China.The results indicate that MCMC methods based on Me- tropolis-Hastings algorithm are useful tools for parameter estimation of GEV distribution.Due to effective us- ing of prior information unrelated to asymptotic property of likelihood function.posterior distribution of up- per quantile obtained from Bayesian estimation includes more information compared with classical statistical methods in flood frequency analysis.Thus uncertainty of forecasting caused by uncertainty of parameters can be quantificationally expressed.Moreover,the proposed Bayesian method can significantly pass several gener- al goodness-of-fit tests,such as quantile plot,probability plot correlation coefficient method,root mean square error method.and Kolmogrov-Smirnow method.The capabilities and utility of the method in more re- liable estimates of extreme floods is illustrated. Key words:flood frequency analysis;Bayesian statistics:GEV distribution;Metropolis-Hastings algorithm; Goodness-of-fit test (责任编辑:王成丽) -949-
[ 9 ] Walshaw D . Modelling extreme wind speeds in regions prone to hurricanes[J]. J . R . Stat . Soc . Ser . C . ,2000, 49(1):51-62 . [ 10] Huang W,Xu S,Nnaji S . Evaluation of GEV model for frequency analysis of annual maximum water levels in the coast of United States[J]. Ocean Eng . ,2008,35(11-12):1132-1147 . [ 11] Prescott P,Walden A T . Maximum likelihood estimation of the parameters of the generalized extreme-value distri⁃ bution[J]. Biometrika,1980,67(3):723-724 . [ 12] Madsen H,Rasmussen P F,Rosbjerg D . Comparison of annual maximum series and partial duration series meth⁃ ods for modeling extreme hydrologic events,1,At-site modeling[J]. Water Resour . Res . ,1997,33(4): 746-757 . [ 13] Coles S . An introduction to statistical modeling of extreme values[Z]. Springer,London,2001 . [ 14] Katz R W,Parlange M B,Naveau P . Statistics of extremes in hydrology[J]. Adv . Water . Resour . ,2002,25 (8-12):1287-1304 . [ 15] Martins E S,Stedinger J R . Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data[J]. Water Resour . Res . ,2000,36(3):737-744 . [ 16] 刘次华 . 随机过程[M]. 武汉:华中科技大学出版社,2001 . [ 17] 邢贞相,芮孝芳,崔海燕,等 . 基于 AM-MCMC 算法的贝叶斯概率洪水预报模型[J]. 水利学报,2007,38 (12):1500-1506 . [ 18] 李向阳,程春田,林剑艺,等 . 基于 BP 神经网络的贝叶斯概率水文预报模型[J]. 水利学报,2006,37(3): 354-359 . [ 19] Dirceu S,Reis Jr,Jery R,Stedinger . Bayesian MCMC flood frequency analysis with historical information[J]. Journal of Hydrology,2005,313(1-2):97-116 . [ 20] Liang Z M,Li B Q,Yu Z B,et al . Application of Bayesian approach to hydrological frequency analysis[J]. Sci⁃ ence China Technological Sciences,2011,54(5):1183-1192 . Bayesian MCMC flood frequency analysis based on generalized extreme value distribution and Metropolis-Hastings algorithm LU Fan,YAN Deng-hua (State Key Laboratory of Simulation and Regulation of Water Cycle in River Basin,China Institute of Water Resources and Hydropower Research,Beijing 100038,China) Abstract:The generalized extreme value (GEV) distribution has been widely used for modeling the distri⁃ bution of flood flows. In this paper, the unknown parameters of hydrologic frequency distribution linetype are considered as random variables, and Bayesian Markov chain Monte Carlo (MCMC) method based on Metropolis-Hastings algorithm is used to evaluate the posterior distributions of GEV distribution parameters and flood quantiles. The application example was conducted with flood data from the Han River basin, near the Danjiangkou reservoir, in Hubei, China. The results indicate that MCMC methods based on Me⁃ tropolis-Hastings algorithm are useful tools for parameter estimation of GEV distribution. Due to effective us⁃ ing of prior information unrelated to asymptotic property of likelihood function,posterior distribution of up⁃ per quantile obtained from Bayesian estimation includes more information compared with classical statistical methods in flood frequency analysis. Thus uncertainty of forecasting caused by uncertainty of parameters can be quantificationally expressed. Moreover,the proposed Bayesian method can significantly pass several gener⁃ al goodness-of-fit tests, such as quantile plot, probability plot correlation coefficient method, root mean square error method,and Kolmogrov-Smirnow method. The capabilities and utility of the method in more re⁃ liable estimates of extreme floods is illustrated. Key words:flood frequency analysis;Bayesian statistics;GEV distribution;Metropolis-Hastings algorithm; Goodness-of-fit test (责任编辑:王成丽) — 949 —