
第15卷第2期 系统工程理论方法应用 Vol.15 No.2 2006年4月 SYSTEMS ENGINEERING-THEORY METHODOLOGY APPLICATIONS Apr.2006 文章编号:1005-2542(2006)02-0133-06 正态逆高斯扩散模型的MCMC估计 胡素华,张形,张世英 (天津大学管理学院,天津300072) 【摘要】使用贝叶斯方法估计了正态逆高斯扩散模型,该方法首先使用Eulr方法对连续过程进行离散 化,用离散过程的似然函数做为模型参数的近似似然函数。证明了MCMC方法是分析正态逆高斯扩散模型 的有效工具,由MCMC方法抽样所得的后验分布可以用来进行统计推断。模拟试验表明:正态逆高斯扩散 能够体现资产收益的许多经验特征,如泰勒效应、尖峰厚尾等。 关键词:MCMC;正态逆高斯扩散;广义抛物线扩散;贝叶斯方法 中图分类号:F830.91 文献标识码:A Estimation of Normal Inverse Gaussian Diffusion Using MCMC Method HU Su-hua,ZHANG Tong,ZHANG Shi-ying (School of Management,Tianjin Univ.,Tianjin 300072,China) [Abstract]In this paper we propose a Bayesian method to estimate the normal inverse Gaussian(NIG)dif- fusion model.The approach is based on the Markov chain Monte Carlo(MCMC)method with the likeli- hood of the discredited process as the approximate posterior likelihood.We demonstrate that the MCMC method provides a useful tool in analyzing NIG diffusion.In particular,quantities of posterior distribu- tions obtained from the MCMC outputs can be used for statistical inference.The MCMC method is based on Euler scheme.Our simulation study shows that the NIG diffusion exhibits many of the stylized facts about asset returns documented in the discrete-time financial econometrics literature,such as the Taylor effect,a slowly declining autocorrelation function of the squared returns,and thick tails. Key words:Markov chain Monte Carlo;normal inverse Gaussian diffusion;generalized hyperbolic diffu- sion;Bayes method 在金融学文献中,几何布朗运动被用来描述股 散过程也得到了重视,NIG(正态逆高斯)扩散过程 票价格运动,虽然在期权定价和其他理论中具有重和抛物线扩散过程都是GH(广义抛物线)扩散过程 要的作用,但是几何布朗运动不能很好地描述股票 的特殊情况,Rydberg]用NIG扩散过程作为金融 收益的经验统计特征,如高峰、波动集聚和长记忆 数据建模,在用NIG模型拟合一些股票数据上取得 性。为了反映这些特征,有跳跃扩散模型、随机波动 了良好的效果,并将NIG扩散模型运用到期权定价 模型、随机波动加跳跃模型以及时变列维过程。作为 中。但是,目前国内使用非线性连续时间扩散过程为 非线性扩散过程,Bibby和S+rensen]的抛物线扩 资产收益建模的研究还处在一个起步阶段,关于这 方面的研究成果还不多。 收璃日期:2004-11-05 虽然NIG扩散过程的稳定分布服从抛物线分 基多项目:国家自然科学基金资助项目(70301006) 布并有封闭形式表达式,但是转移密度没有封闭形 作者简介:胡素华(1977-),男,博士生,主要从事连续时间金融 式的解。由于缺少转移密度的知识,使用准确似然方 模型研究与金融波动研究。 法进行模型的计量经济估计是不可行的。Rydberg 万方数据
第15卷第2期 系统工程理论方法应用 V01.15 No.2 2006年4月 SYSTEMS ENGINEERING—THEORY METHODOLOGY APPLICATl0NS Apr.2006 文章编号:1005—2542(2006)02—0133一06 正态逆高斯扩散模型的MCMC估计 胡素华, 张彤, 张世英 (天津大学管理学院,天津300072) 【摘要】使用贝叶斯方法估计了正态逆高斯扩散模型,该方法首先使用Euler方法对连续过程进行离散 化,用离散过程的似然函数做为模型参数的近似似然函数。证明了MCMC方法是分析正态逆高斯扩散模型 的有效工具,由MCMC方法抽样所得的后验分布可以用来进行统计推断。模拟试验表明:正态逆高斯扩散 能够体现资产收益的许多经验特征,如泰勒效应、尖峰厚尾等。 关键词:MCMC;正态逆高斯扩散;广义抛物线扩散;贝叶斯方法 中图分类号:F 830.91 文献标识码:A Estimation of Normal Inverse Gaussian Diffusion Using MCMC Method HU Su-hua, ZHANG Tong, (School of Management,Tianjin Univ. ZHANG Shi-ying ,Tianjin 300072,China) [Abstract]In this paper we propose a Bayesian method to estimate the normal inverse Gaussian(NIG)dif— fusion model.The approach iS based on the Markov chain Monte Carlo(MCMC)method with the likeli— hood of the discredited process as the approximate posterior likelihood.We demonstrate that the MCMC method provides a useful tool in analyzing NIG diffusion.In particular,quantities of posterior distribu— tions obtained from the MCMC outputs can be used for statistical inference.The MCMC method iS based on Euler scheme.0ur simulation study shows that the NIG diffusion exhibits many of the stylized facts about asset returns documented in the discrete—time financial econometrics literature,such as the Taylor effect,a slowly declining autocorretation function of the squared returns,and thick tails. Key words:Markov chain Monte Carlo;normal inverse Gaussian diffusion;generalized hyperbolic diffu— sion;Bayes method 在金融学文献中,几何布朗运动被用来描述股 票价格运动,虽然在期权定价和其他理论中具有重 要的作用,但是几何布朗运动不能很好地描述股票 收益的经验统计特征,如高峰、波动集聚和长记忆 性。为了反映这些特征,有跳跃扩散模型、随机波动 模型、随机波动加跳跃模型以及时变列维过程。作为 非线性扩散过程,Bibby和S夺rensenu o的抛物线扩 收稿日期:2004—11—05 基多项目:国家自然科学基金资助项目(70301006) 作者简介:胡素华(1977一),男,博士生。主要从事连续时间金融 模型研究与金融波动研究。 散过程也得到了重视,NIG(正态逆高斯)扩散过程 和抛物线扩散过程都是GH(广义抛物线)扩散过程 的特殊情况,Rydberg[21用NIG扩散过程作为金融 数据建模,在用NIG模型拟合一些股票数据上取得 了良好的效果,并将NIG扩散模型运用到期权定价 中。但是,目前国内使用非线性连续时间扩散过程为 资产收益建模的研究还处在一个起步阶段,关于这 方面的研究成果还不多。 虽然NIG扩散过程的稳定分布服从抛物线分 布并有封闭形式表达式,但是转移密度没有封闭形 式的解。由于缺少转移密度的知识,使用准确似然方 法进行模型的计量经济估计是不可行的。Rydberg 万方数据

134 系统工程理论方法应用 第15卷 采用鞅估计函数方程方法来估计NIG扩散过程,然 本文中,选择v(x)满足: 而基于鞅函数估计方程的估计值存在且是非对称正 v(x)=aexp- g6(x-4) 态分布,同时估计值不是有效的;另外,估计值的标 K(ags(z-)) 准差的计算非常复杂。 (5) 本文通过将扩散过程的离散似然作为近似后 式中:g(x)=√8十x2;a,B,6,是分布参数,满足 验,使用MCMC方法来估计抛物线扩散过程,与在 a>|B≥0,6>0.8是标度参数,4是位置参数,B决 经典框架中的ML方法一样,MCMC方法提供了一 定对称性,α决定分布的倾斜度。 个基于贝叶斯分析的全似然推断。在抛物线扩散,离 用MCMC方法估计NIG模型时,首先总结在 散化近似ML方法在数值收敛方面存在困难,然 众多金融文献中关于资产收益序列的经验特征,定 而,MCMC方法提供了从后验分布中抽取参数样本 义r为股票收益,Ryden总结了r,的下列动态性 的方法避免了数值优化的问题,并使借助蒙特卡罗 质: 方法的准确有限样本的推断可行。 (1),是不相关的: 1NIG模型 (2)1r,,的自相关函数缓慢衰诚,衰减的速 度较稳定ARMA自相关函数要慢的多; NIG分布和抛物线分布都是广义抛物线分布 (3)收益绝对值的自相关在幂-1时最大,这 的两种特例,NIG扩散过程较抛物线扩散过程具有 就是泰勒效应,即 更厚的尾部,从而更有利于描述股票价格,为其建 模。 corr(Ir:l,r-)>corr(r,r) 中≠1 (4)收益常常表现出厚尾的边际分布特征。 假定股票价格满足: S,=exp(kt+X:) (1) 2NIG扩散过程的离散化 式中:x为股票价格对数随时间变化系数:S,为股票 使用广泛应用的Euler方法对广义扩散过程 价格:X,为股票价格对数除趋势项后的状态变量, dX,=4(·)dt十o(·)近似,其表达式为: X,=X。+o(X,)dW (2) X+a=X,+u(X,)△t+(X,0)△W,(6) 通过伊藤公式,有 式中,△W,=e√,e~idN(0,1),给定X,的观测 ds,-++ 值集合X={,:t=0,1,…,n},则参数0基于观测 值集合的对数似然函数为 v(logS.kt)dw. (3) logPe(01X)= 是21ogoz,0a)- 注意到,如果函数(·)是一个常数,关于S,的模型 是一个在BS公式中使用的几何布朗运动。过程X: 空 3--1-(,)△)2 (7) G(x,0)△t 是一个时变维纳过程,这样式(3)就是一个简单的 B-S模型广义形式。关于logS,的漂移项是一个时间 式中,ps(0X)是基于Euler离散方法的似然函数。 的线性函数t的假定不是必须的,做这样的假定是 3借助MCMC方法估计NIG扩散 为了简单和尽可能的不改变几何布朗运动模型。在 本文中,要讨论的就是当1ogS,有一个确定性漂移 3.1MCMC方法 时的情况。 MCMC方法已经成功应用到统计学中,且相对 通过选择合适的v(x)可以得到几个有趣的模 于传统的独立取样方法具有很多优势,Gewekets]提 型,但是在此仅仅考虑一个特殊而常见的情况,并推 出了使用后验模拟方法完成贝叶斯推断,并强调了 广到一般情况。经验研究表明,股票收益logS+a一 基于贝叶斯推断的MCMC模拟的重要性。Giks[6) logS:的分布不是正态的,分布的尾部趋向于对数线 总结了MCMC算法的应用。MCMC方法在计量经 性。若选择式(4)形式,就是Bibby和Serensen的抛 济学和金融学中的广泛应用可以参见文献[7~9]。 物线扩散过程: 基于数据集合X参数向量日的贝叶斯推断后 [a+u--8x-四] 「 验可以借助后验密度p(|X)得到,通过贝叶斯原 v(t)=oexp 理,有 (4) π(01X)=cp(8川X)π() (8) 万方数据
系 统 工 程 理 论 方 法 应 用 第15卷 采用鞅估计函数方程方法来估计NIG扩散过程,然 而基于鞅函数估计方程的估计值存在且是非对称正 态分布,同时估计值不是有效的;另外,估计值的标 准差的计算非常复杂。 本文通过将扩散过程的离散似然作为近似后 验,使用MCMC方法来估计抛物线扩散过程;与在 经典框架中的ML方法一样,MCMC方法提供了一 个基于贝叶斯分析的全似然推断。在抛物线扩散,离 散化近似ML方法在数值收敛方面存在困难,然 而,MCMC方法提供了从后验分布中抽取参数样本 的方法避免了数值优化的问题,并使借助蒙特卡罗 方法的准确有限样本的推断可行。 1 NIG模型 NIG分布和抛物线分布都是广义抛物线分布 的两种特例,NIG扩散过程较抛物线扩散过程具有 更厚的尾部,从而更有利于描述股票价格,为其建 模‘引。 假定股票价格满足: S。一exp(彤£+X。) (1) 式中:彤为股票价格对数随时间变化系数;S,为股票 价格;X。为股票价格对数除趋势项后的状态变量, Ct X,一X。+I u(X,)dW, (2) J 0 通过伊藤公式,有 ,广 1 1 dS。一s。{i盯+寺可2(109S。一tot)ldt+ 、L 厶 J 、 勘(109S,+/ct)dW。} (3) , 注意到,如果函数口(·)是一个常数,关于S。的模型 是一个在B—S公式中使用的几何布朗运动。过程X。 是一个时变维纳过程,这样式(3)就是一个简单的 B—S模型广义形式。关于logS。的漂移项是一个时间 的线性函数彤£的假定不是必须的,做这样的假定是 为了简单和尽可能的不改变几何布朗运动模型。在 本文中,要讨论的就是当logs;有一个确定性漂移 时的情况。 通过选择合适的u(z)可以得到几个有趣的模 型,但是在此仅仅考虑一个特殊而常见的情况,并推 广到一般情况。经验研究表明,股票收益logS件。一 logS。的分布不是正态的,分布的尾部趋向于对数线 性。若选择式(4)形式,就是Bibby和Sq,rensen的抛 物线扩散过程: u(f)=aexpl告a怕可可习一去卢(T一∥)l L厶 厶 J (4) 本文中,选择秽(z)满足: m,一一“一号触一产,)√赢舞筹b (5) 式中:ga(z)一√艿2+z2;a,卢,占,卢是分布参数,满足 口>l卢I≥o,8>0。艿是标度参数,∥是位置参数,卢决 定对称性,口决定分布的倾斜度。 用MCMC方法估计NIG模型时,首先总结在 众多金融文献中关于资产收益序列的经验特征,定 义^为股票收益,Ryden[43总结了n的下列动态性 质: (1)n是不相关的; (2)h I,r;的自相关函数缓慢衰减,衰减的速 度较稳定ARMA自相关函数要慢的多; (3)收益绝对值的自相关在幂一1时最大,这 就是泰勒效应,即 corr(h I,∽一^I)>corr(h l’,I rf一^I 9) j5≠1 (4)收益常常表现出厚尾的边际分布特征。 2 NIG扩散过程的离散化 使用广泛应用的Euler方法对广义扩散过程 dX,一∥(·)dt+盯(·)近似,其表达式为: X件血一X。+∥(X,,0)zXt+盯(X,,O)AW。(6) 式中,/xW。一岛~/&,gt~iid N(0,1),给定x,的观测 值集合X一{z。:t一0,1,…,,2),则参数0基于观测 值集合的对数似然函数为 logpE(0Ix)一一丢∑log(a(x,,疗)2At)一 丢塞虹±a(南x拶At ㈩ 2纠 。,口)2 … 式中,PE(护fX)是基于Euler离散方法的似然函数。 3 借助MCMC方法估计NIG扩散 3.1 MCMC方法 MCMC方法已经成功应用到统计学中,且相对 于传统的独立取样方法具有很多优势,Geweke[51提 出了使用后验模拟方法完成贝叶斯推断,并强调了 基于贝叶斯推断的MCMC模拟的重要性。Gilks[63 总结了MCMC算法的应用。MCMC方法在计量经 济学和金融学中的广泛应用可以参见文献[7~9]。 基于数据集合X参数向量0的贝叶斯推断后 验可以借助后验密度P(臼lX)得到,通过贝叶斯原 理,有 7l"(护IX)一cp(咿IX)7r(0) (8) 万方数据

第2期 胡素华,等:正态逆高斯扩散模型的MCMC估计 135 式中:c是标准化常数;p(X|)是以0为条件的似然 式中,函数f(·)是一个实值函数,遍历均值的中心 函数;π()是0的先验密度。贝叶斯方法要求统计推 极限定理有: 断必须是基于参数的后验分布,然而直接处理后验 √/N(fN-E.(f(0))P+N(0,a)(12) 是很困难的.但是,如果可从后验分布抽取参数向量 E,(·)是关于分布π(θ|X)的期望算子,为讨论 的样本,关于参数向量的统计推断就可以使用一般 E.(f()做为遍历均值估计的准确性,必须估计 的蒙特卡罗方法实现。MCMC方法的目的就是提供 a形。估计o形最普遍的方法就是由Roberts提出的 一种从参数后验分布中抽取样本的一种机制。由于 块均值。 从后验中直接取样是很困难的,从而可以用MCMC 为了使用块均值估计σ子,MCMC算法运行N= 方法建立马尔可夫链,使它的稳定分布和后验分布 m×n,这里n足够大,取: 相同,当马尔可夫链收敛时,模拟值可以看作是从后 验分布中抽取的样本。 y= f() (13) n;-(使)+1 关于MCMC方法有Gibbs取样和MH算法二 对于=1,2,…,m,y近似于独立同分布 类。本文采用MH算法,需要注意的是:①接受概率 N(E,(f()),/n),这样a的估计值为 的计算不需要后验函数中正规化常量的知识;②建 议密度的选择。 所-m” Fm二12-fw)2 (14) MH算法从建议密度q(·I)生成备选0,该 同时,fx的标准误差可以用√σ/N来估计,该标准 建议密度必须满足一定的性质1。备选&以概率 误差也成为参数估计值的蒙特卡罗标准误差 T(0,8)被接受,而接受概率11为 (MCSE)。另外还要计算所有样本的标准离差: T(0,0)=min1,rg901f) π(0x)q(0T0) (9) 算法如下: =√2f0)-1 (15) (1)给定现在状态,从建议密度g(·|) Kim2]提出了可以用模拟无效因子(SIF)来评 生成备选值日; 价抽样样本的模拟效果,Meyer和Yu1a]给出了SIF (2)按照式(9)计算接受概率T(0,0): 的计算公式: (3)以概率T(0,8)接受备选值,即+”= SIF=G/所 (16) 8;反之,拒绝备选值,即+》=: 4 实证研究 (4)重复前面的步骤,获得{,1,…,剔除 前面的d个值,则{0d+》,d+》,…}都具有相同的后 4.1参数的估计结果 验密度π(X)。 使用MCMC方法来估计NIG扩散模型,数据 3.2经验结果 分别采用上海和深圳股市的周综合指数,即从 假定参数的联合先验信息是π(),基于Euler 1992-05-03~2004-04-30共12年的上海和深圳股 似然函数为E(0|X),则联合后验为r(0|X)心 市周综合指数。 π()pe(O1X)。在随机游走MH算法中,建议密度是 参数先验分布利用文献[3,9]中介绍的先验分 在[一0.5,0.5]上的均匀分布,参数向量0按照下面 布,各个参数的先验分别假定为:心~N(0,10),a~T 的方法更新: (1,20),82~T(0.05,20),4~N(5,10),~ 8=8+re (10) U(-a,a),a2~IG(5,0.05)。 式中:e是在区间上[一0.5,0.5]生成的随机数;x是 按照随机游走MH算法对NIG扩散模型进行 调和参数,因此,x的选择应使参数被接受的概率 参数估计,每个参数共产生60000个样本,剔除前 在20%~30%。一般来说,如果参数之间是弱相关 面的10000个模拟样本,记录的模拟样本为后面的 的,π就可以是一个常数:否则,π应是一个常向量。 50000个。其中,上海综指参数的样本曲线见图1, 3.3参数模拟的收敛性分析 上海和深圳综合指数的参数估计结果为表1所示。 在MCMC算法中,取样的样本路线为{: 表1总结了各个参数的遍历平均(Mean)、标准 i=1,2,…,N},并且输出的遍历均值有下列形式: 离差(SD)、95%的贝叶斯置信区间(CI)、蒙特卡罗 标准误差(MCSE)和SIF:贝叶斯置信区间说明了 (11) 各参数估计的有效性。 万方数据
第2期 胡素华,等:正态逆高斯扩散模型的MCMC估计 式中:f是标准化常数;p(X I曰)是以0为条件的似然 函数;丌(曰)是口的先验密度。贝叶斯方法要求统计推 断必须是基于参数的后验分布,然而直接处理后验 是很困难的。但是,如果可从后验分布抽取参数向量 的样本,关于参数向量的统计推断就可以使用一般 的蒙特卡罗方法实现。MCMC方法的目的就是提供 一种从参数后验分布中抽取样本的一种机制。由于 从后验中直接取样是很困难的,从而可以用MCMC 方法建立马尔可夫链,使它的稳定分布和后验分布 相同,当马尔可夫链收敛时,模拟值可以看作是从后 验分布中抽取的样本。 关于MCMC方法有Gibbs取样和MH算法二 类。本文采用MH算法,需要注意的是:①接受概率 的计算不需要后验函数中正规化常量的知识;②建 议密度的选择。 MH算法从建议密度q(·l口)生成备选曰7,该 建议密度必须满足一定的性质[1…。备选口’以概率 T(O,07)被接受,而接受概率[1叩为 算法如下: 丁㈣∽一叫,,篙揣)㈤ (1)给定现在状态0“’,从建议密度q(·|0“’) 生成备选值07; (2)按照式(9)计算接受概率T(O“’,0’); (3)以概率71(护“’,07)接受备选值,即0“+1’一 07;反之,拒绝备选值,即0“+1’一护“’; (4)重复前面的步骤,获得{0∞’,0n’,…},剔除 前面的d个值,则{0叫+1’,0叫+2’,…)都具有相同的后 验密度7r(口lX)。 3.2经验结果 假定参数的联合先验信息是玎(臼),基于Euler 似然函数为Ps(口I x),则联合后验为7r(0 X)。C 丌(护)户E(伊|X)。在随机游走MH算法中,建议密度是 在[一0.5,0.5]上的均匀分布,参数向量臼按照下面 的方法更新: 07—0+r£ (10) 式中:e是在区间上[一0.5,0.5]生成的随机数;r是 调和参数,因此,r的选择应使参数07被接受的概率 在20%~30%。一般来说,如果参数之间是弱相关 的,r就可以是一个常数;否则,r应是一个常向量。 3.3参数模拟的收敛性分析 在MCMC算法中,取样的样本路线为{0“’: i一1,2,…,Ⅳ),并且输出的遍历均值有下列形式: 1旦 ^一寺>:f(o“’) (11) 式中,函数厂(·)是一个实值函数,遍历均值的中心 极限定理有: √Ⅳ(/'Ⅳ一E。(厂(臼)))D—N(O,仃;) (12) E。(·)是关于分布丌(口I X)的期望算子,为讨论 E。(厂(护))做为遍历均值估计的准确性,必须估计 盯}。估计盯}最普遍的方法就是由Roberts E113提出的 块均值。 为了使用块均值估计d},MCMC算法运行Ⅳ一 优×72,这里n足够大,取: 1 kn yk=土2 i厶八∥J y厂(∥) (13) L J ’‘,=(女一1)n+1 对于是=1,2,…,m,弘近似于独立同分布 Ⅳ(E。(厂(伊)),唠/咒),这样盯}的估计值为 ;多一—∑∑(挑一兀)z 仃,一而垄‘挑一-,Ⅳ)‘ (14) 同时,7Ⅳ的标准误差可以用√a}/N来估计,该标准 误差也成为参数估计值的蒙特卡罗标准误差 (MCSE)。另外还要计算所有样本的标准离差: 厂—■——]r—————————一 爵一√南圣[,(0“’)一九]2(15) Kim[121提出了可以用模拟无效因子(SIF)来评 价抽样样本的模拟效果,Meyer和yuE133给出了SIF 的计算公式: SIF一仃}/d} (16) 4实证研究 4.1参数的估计结果 使用MCMC方法来估计NIG扩散模型,数据 分别采用上海和深圳股市的周综合指数,即从 1992—05—03~2004—04—30共12年的上海和深圳股 市周综合指数。 参数先验分布利用文献[3,9]中介绍的先验分 布,各个参数的先验分别假定为:Ⅳ~Ⅳ(O,10),a~r (1,20),艿2~r(0.05,20),产~N(5,10),p~ U(一a,a),盯2~JG(5,0.05)。 按照随机游走MH算法对NIG扩散模型进行 参数估计,每个参数共产生60 000个样本,剔除前 面的10 000个模拟样本,记录的模拟样本为后面的 50 000个。其中,上海综指参数的样本曲线见图1, 上海和深圳综合指数的参数估计结果为表1所示。 表1总结了各个参数的遍历平均(Mean)、标准 离差(SD)、95%的贝叶斯置信区间(CI)、蒙特卡罗 标准误差(MCSE)和SIF;贝叶斯置信区间说明了 各参数估计的有效性。 万方数据
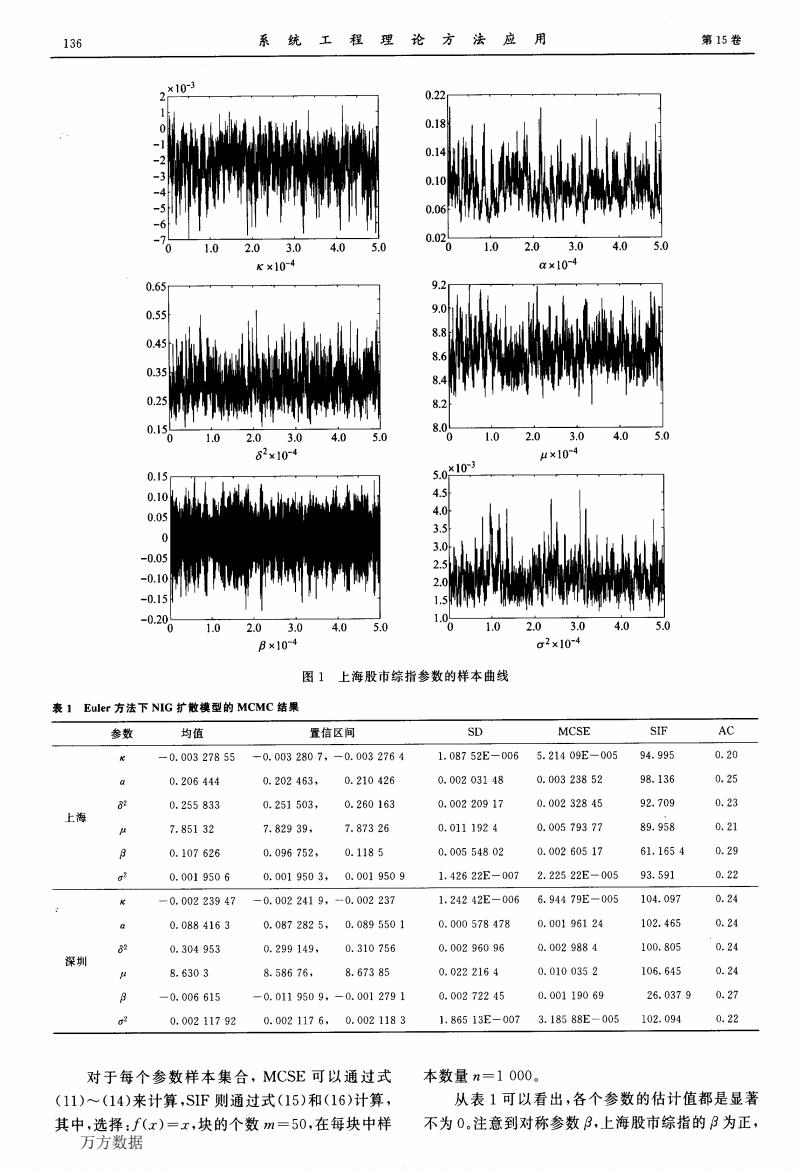
136 系统工程理论方法应用 第15卷 2*103 0.22 0.10 0.06 0.02 2.0 3.0 0 1.0 2.0 3.0 50 K×10-4 a×10-4 0.65 9.2 0.55 9.0 8.8 8.6 0.35 25 8.2 0.15 8.0 1.0 2.03.0 4.0 5.0 1.0 2.03.0 4.0 5.0 2x10-4 A×104 5.0*103 4.5 0.05 4.0 0 3.0 -0.05 时 2.5 -0.10 2.0 -0.15 02% 1.0 1.0 2.03.0 4.05.0 1.0 2.0 3.0 5 B×104 σ2×104 图1上海股市综指参数的样本曲线 表1 Euler方法下NIG扩散模型的MCMC结果 参数 均值 置信区间 SD MCSE SIF AC -0.00327855 -0.0032807,-0.0032764 1.08752E-006 5.21409E-005 94.995 0.20 a 0.206444 0.202463, 0.210426 0.00203148 0.00323852 98.136 0.25 0.255833 0.251503, 0.260163 0.00220917 0.00232845 92.709 0.23 上海 7.85132 7,82939, 7.87326 0.0111924 0.00579377 89,958 0.21 0.107626 0.096752, 0.1185 0.00554802 0.00260517 61.1654 0.29 0.0019506 0.0019503, 0.0019509 1.42622E-007 2.22522E-005 93.591 0.22 -0.00223947 -0.0022419,-0.002237 1.24242E-006 6.94479E-005 104.097 0.24 0.0884163 0.0872825, 0.0895501 0.000578478 0.00196124 102.465 0.24 82 0.304953 0.299149, 0.310756 0.00296096 0.0029884 100.805 0.24 深圳 8.6303 8.58676, 8.67385 0.0222164 0.0100352 106.645 0.24 B -0.006615 -0.0119509,-0.0012791 0.00272245 0.00119069 26.0379 0.27 0.00211792 0.0021176,0.0021183 1.86513E-007 3.18588E-005 102.094 0.22 对于每个参数样本集合,MCSE可以通过式 本数量n=1000。 (11)~(14)来计算,SIF则通过式(15)和(16)计算, 从表1可以看出,各个参数的估计值都是显著 其中,选择:f(x)=x,块的个数m=50,在每块中样 不为0.注意到对称参数B,上海股市综指的阝为正, 万方数据
136 系 统 工 程 理 论 方 法 应 用 第15卷 2 1 O 一1 —2 —3 —4 —5 —6 -7 ×10—3 0 1.O 0.65 O.55 0.45 O.35 0.25 0.15 2.O 3.0 4.0 5.0 K×10-4 0 1.0 2.0 3.0 4.0 5.0 占2×10一4 8×10—4 表1 Euler方法下NIG扩散模型的MCMC结果 a×lO一4 图1 上海股市综指参数的样本曲线 盯2×lO。4 对于每个参数样本集合,MCSE可以通过式 (11)~(14)来计算,SIF则通过式(15)和(16)计算, 其中,选择:厂(z)一z,块的个数m一50,在每块中样 本数量咒一1 000。 从表1可以看出,各个参数的估计值都是显著 不为0。注意到对称参数卢,上海股市综指的p为正, 万方数据
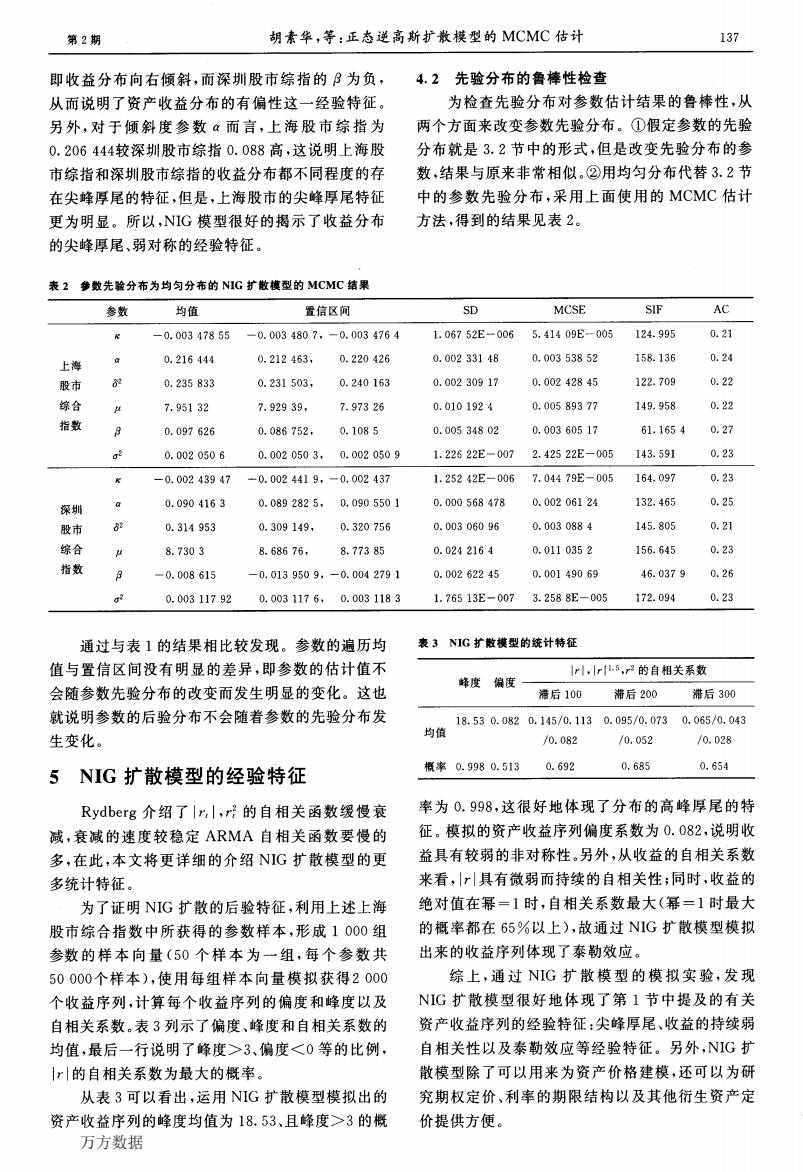
第2期 胡素华,等:正态逆高斯扩散模型的MCMC估计 137 即收益分布向右倾斜,而深圳股市综指的B为负,4.2先验分布的鲁棒性检查 从而说明了资产收益分布的有偏性这一经验特征。 为检查先验分布对参数估计结果的鲁棒性,从 另外,对于倾斜度参数a而言,上海股市综指为 两个方面来改变参数先验分布。①假定参数的先验 0.206444较深圳股市综指0.088高,这说明上海股 分布就是3.2节中的形式,但是改变先验分布的参 市综指和深圳股市综指的收益分布都不同程度的存 数,结果与原来非常相似。②用均匀分布代替3.2节 在尖蜂厚尾的特征,但是,上海股市的尖峰厚尾特征 中的参数先验分布,采用上面使用的MCMC估计 更为明显。所以,NIG模型很好的揭示了收益分布 方法,得到的结果见表2。 的尖蜂厚尾、弱对称的经验特征。 表2参数先验分布为均匀分布的NIG扩散模型的MCMC结果 参数 均值 置信区间 SD MCSE SIF AC R -0.00347855 -0.0034807,-0.0034764 1.06752E-0065.41409E-005 124.995 0.21 0.00233148 0.00353852 158.136 0.24 上海 0.216444 0.212463, 0.220426 股市 0.235833 0.231503, 0.240163 0.00230917 0.00242845 122.709 0.22 综合 7.95132 7.92939. 7.97326 0.0101924 0.00589377 149.958 0.22 指数 0.097626 0.086752, 0.1085 0.00534802 0.00360517 61.1654 0.27 0.0020506 0.0020503,0.0020509 1.22622E-0072.42522E-005 143.591 0.23 -0.00243947 -0.0024419,-0.002437 1.25242E-006 7.04479E-005 164.097 0.23 深圳 0.0904163 0.0892825,0.0905501 0.000568478 0.00206124 132.465 0.25 股市 82 0.314953 0.309149, 0.320756 0.00306096 0.0030884 145.805 0.21 综合 8.7303 8.68676, 8.77385 0.0242164 0.0110352 156.645 0.23 指数 -0.008615 -0.0139509,-0.0042791 0.00262245 0.00149069 46.0379 0.26 0.00311792 0.0031176,0.0031183 1.76513E-0073.2588E-005 172.094 0.23 通过与表1的结果相比较发现。参数的遍历均 表3NIG扩散模型的统计特征 值与置信区间没有明显的差异,即参数的估计值不 r,r5,r2的自相关系数 蜂度偏度 会随参数先验分布的改变而发生明显的变化。这也 滞后100 滞后200 滞后300 就说明参数的后验分布不会随着参数的先验分布发 18.530.0820.145/0.1130.095/0.0730.065/0.043 生变化。 均值 /0.082 /0.052 /0.028 概率0.9980.5130.692 0.685 0.654 5NIG扩散模型的经验特征 Rydberg介绍了r,|,r2的自相关函数缓慢衰 率为0.998,这很好地体现了分布的高峰厚尾的特 减,衰减的速度较稳定ARMA自相关函数要慢的 征。模拟的资产收益序列偏度系数为0.082,说明收 多,在此,本文将更详细的介绍NIG扩散模型的更 益具有较弱的非对称性。另外,从收益的自相关系数 多统计特征。 来看,具有微弱而持续的自相关性;同时,收益的 为了证明NIG扩散的后验特征,利用上述上海 绝对值在幂=1时,自相关系数最大(幂=1时最大 股市综合指数中所获得的参数样本,形成1000组 的概率都在65%以上),故通过NIG扩散模型模拟 参数的样本向量(50个样本为一组,每个参数共 出来的收益序列体现了泰勒效应。 50000个样本),使用每组样本向量模拟获得2000 综上,通过NIG扩散模型的模拟实验,发现 个收益序列,计算每个收益序列的偏度和峰度以及 NIG扩散模型很好地体现了第1节中提及的有关 自相关系数。表3列示了偏度、峰度和自相关系数的 资产收益序列的经验特征:尖峰厚尾、收益的持续弱 均值,最后一行说明了峰度>3、偏度3的概 价提供方便。 万方数据
第2期 胡素华,等:正态逆高斯扩散模型的MCMC估计 即收益分布向右倾斜,而深圳股市综指的卢为负, 从而说明了资产收益分布的有偏性这一经验特征。 另外,对于倾斜度参数口而言,上海股市综指为 0.206 444较深圳股市综指0.088高,这说明上海股 市综指和深圳股市综指的收益分布都不同程度的存 在尖峰厚尾的特征,但是,上海股市的尖峰厚尾特征 更为明显。所以,NIG模型很好的揭示了收益分布 的尖峰厚尾、弱对称的经验特征。 表2参数先验分布为均匀分布的NIG扩散模型的MCMC结果 4.2先验分布的鲁棒性检查 为检查先验分布对参数估计结果的鲁棒性,从 两个方面来改变参数先验分布。①假定参数的先验 分布就是3.2节中的形式,但是改变先验分布的参 数,结果与原来非常相似。②用均匀分布代替3.2节 中的参数先验分布,采用上面使用的MCMC估计 方法,得到的结果见表2。 参数 均值 置信区间 SD MCSE SIF AC Ⅳ 一0.003 478 55 —0.003 480 7,一0.003 476 4 1.067 52E一006 5.414 09E一005 124.995 0.21 E海 8 0·216 444 0·212 463,0-220 426 0·002 331 48 O·003 538 52 158·136 0·24 股市 d2 0.235 833 0.231 503,0.240 163 0.002 309 17 0·002 428 45 122·709 0·22 综合 11 7.951 32 7.929 39, 7.973 26 0.010 192 4 0.005 893 77 149.958 0.22 指数 口 o.097 626 0.086 752,0.108 5 O.005 348 02 0.003 605 17 61.165 4 0.27 0,2 0.002 050 6 0.002 050 3,0.002 050 9 1.226 22E一007 2.425 22E一005 143.591 0.23 K 一0.002 439 47 —0.002 441 9,一0.002 437 1.252 42E一006 7.044 79E一005 164.097 0.23 深tJII 。0·090 416 3 0·089 282 5,0·090 550 1 O·000 568 478 O·002 061 24 132·465 O·25 股市 d2 0.314 953 0.309 149,0.320 756 0.003 060 96 0·003 088 4 145·805 0·21 综合 /1 8.730 3 8.686 76,8.773 85 0.024 216 4 0.011 035 2 156.645 0.23 指数 口 --0.008 615 —0.013 950 9,一0.004 279 1 0.002 622 45 0.001 490 69 46.037 9 0.26 d2 0.003 117 92 0.003 1】7 6.0.003 1】8 3 1.765 13E一007 3.258 8E一005 172.094 0.23 通过与表1的结果相比较发现。参数的遍历均 值与置信区间没有明显的差异,即参数的估计值不 会随参数先验分布的改变而发生明显的变化。这也 就说明参数的后验分布不会随着参数的先验分布发 生变化。 5 NIG扩散模型的经验特征 Rydberg介绍了h I,r;的自相关函数缓慢衰 减,衰减的速度较稳定ARMA自相关函数要慢的 多,在此,本文将更详细的介绍NIG扩散模型的更 多统计特征。 为了证明NIG扩散的后验特征,利用上述上海 股市综合指数中所获得的参数样本,形成1 000组 参数的样本向量(50个样本为一组,每个参数共 50 000个样本),使用每组样本向量模拟获得2 000 个收益序列,计算每个收益序列的偏度和峰度以及 自相关系数。表3列示了偏度、峰度和自相关系数的 均值,最后一行说明了峰度>3、偏度3的概 表3 NIG扩散模型的统计特征 lr J,Irl n 峰度偏度—— s,rz的自相关系数 滞后100 滞后200 滞后300 率为0.998,这很好地体现了分布的高峰厚尾的特 征。模拟的资产收益序列偏度系数为0.082,说明收 益具有较弱的非对称性。另外,从收益的自相关系数 来看,…具有微弱而持续的自相关性;同时,收益的 绝对值在幂一1时,自相关系数最大(幂一1时最大 的概率都在65%以上),故通过NIG扩散模型模拟 出来的收益序列体现了泰勒效应。 综上,通过NIG扩散模型的模拟实验,发现 NIG扩散模型很好地体现了第1节中提及的有关 资产收益序列的经验特征:尖峰厚尾、收益的持续弱 自相关性以及泰勒效应等经验特征。另外,NIG扩 散模型除了可以用来为资产价格建模,还可以为研 究期权定价、利率的期限结构以及其他衍生资产定 价提供方便。 万方数据

138 系统工程理论方法应用 第15卷 [6]Gilks W R.Richardson S,Spiegelhatler D J.Intro- 6结语 ducing Markov chain Monte Carlo in Practice [M]. 本文基于用Euler方法获得参数后验分布的离 Gilks W R,Richardson S.Spiegelhaiter D J,eds. 散密度,使用MCMC方法来估计NIG扩散,相对于 London:Chapman and Hall,1996:45-57. [7]Eraker B.MCMC analysis of diffusion models with 其他估计方法,如ML估计,可以发现MCMC方法 application to finance [J].J Business Economic 可以提供更好的经验结果。除了说明MCMC方法 Statistics,2001,19:177-91. 是估计NIG扩散和进行统计推断的有效工具外,还 [8 Elerian O,Chib S,Shephard N.Likelihood infer- 说明了NIG扩散可以体现资产收益的不相关性和 ence for discretely observed non-linear diffusions[J]. 泰勒效应以及收益分布的尖峰厚尾、弱有偏等。 Econometrica,2001,69:959-93. [9]Tse Y K,Zhang Xibin,Yu Jun.Estimation of hy- 参考文献: perbolic diffusion using the Markov chain Monte [1 Bibby B M,S4rensen M,A hyperbolic diffusion Carlo method[J].Quantitative Finance,2003,3:1- model for stock prices.Finance and Stochastic, 12. 1997(1):25-41. [10]Chibs S,Greenberg E.Understanding the Metropo- [2 Rydberg T H.Generalized hyperbolic diffusion pro- lis-Hastings algorithm [J.Am Statistician,1995, cesses with applications in fiance[J].Mathematical 49:327-35. Finance,1999,9(2):183-201. [11] Roberts G O,Markov chain concepts related to sam- [3]Rydberg T H.The normal inverse Gaussian levy pling algorithms Markov Chain Monte Carlo in Prac- process:Simulation and approximation [J].Commo tice[M].Gilks W R,Richardson S,Spiegelhalter D Stat:Stoch Models,1997,13:887-910. J,eds.London:Chapman and Hall,1996:45-57. [4 Ryden T,Terasverta T.Asbrink S.Stylized facts of [12]Kim S,Shephard N,Chibs.Stochastic volatility: daily return series and the Hidden Markov modelJ]. Likelihood inference and comparison with ARCH J Appl Econometrics,1998,13:217-44. models[]].Rev Econ Stud,1998,65:361-93. [5]Geweke J.1999 Using simulation methods for [13] Meyer R,Yu J.BUGS for a Bayesian analysis of Bayesian econometric models:Inference,develop- stochastic volatility models [J].Econometrics J, ment,and communication [J].Econometric Rev, 2000,3:198-215. 1999,18:1-73. (上接第132页) 6结语 Journal of Operational Research,1978,2(4):429- 本文将DEA评价方法应用于物流园区投资规 444. 模规划的评价中,结果表明,DEA评价方法能做到 [4]Charnes A,Cooper WW.Lewin A Y,et al.Data en- 对所有被评价物流园区规划方案的充分评价,且能 velopment analysis [M].Boston,Dordrecht,Lon- 提出进一步的目标改进措施,为规划决策者进行规 don:Kluwer Academic Publisher,1994. [5]Wei QL.Sun D B,Xiao Z J.Measuring technical 划和决策提供了更加全面的信息。因此,通过应用 progress with data envelopment analysis [J].Euro- DEA方法评价,能够显著地改善目前物流园区规划 pean Journal of Operational Research,1995,80(3): 的质量。 691-702. 参考文献: [6]魏权龄.评价相对有效性的DEA方法[M们.北京:中国 人民大学出版社,1988. [1]李旭宏,毛海军.开发区专业物流园区规划[门交通运 [7]同济大学,南京现代物流产业发展规划研究[R], 输工程学报,2002,2(3):81-84. 2002. [2]王战权,杨东援.物流园区规划初探[U门.系统工程, [8]吴文江,用数据包络分析进行规模收益分析的探讨 2001,19(1):79-83. [J],系统工程理论方法应用,2000,9(3):248-251. [3]Charnes A.Cooper WW,Rhodes E.Measuring the [9]东南大学交通学院.连云港市现代物流业发展规划 efficiency of decision-making units [J].European [R],2003. 万方数据
138 系 统 工 程理 论 方 法 应 用 第15卷 6 结 语 本文基于用Euler方法获得参数后验分布的离 散密度,使用MCMC方法来估计NIG扩散。相对于 其他估计方法,如ML估计,可以发现MCMC方法 可以提供更好的经验结果。除了说明MCMC方法 是估计NIG扩散和进行统计推断的有效工具外,还 说明了NIG扩散可以体现资产收益的不相关性和 泰勒效应以及收益分布的尖峰厚尾、弱有偏等。 参考文献: [1] [2] [3] [4] [5] Bibby B M,S中rensen M, model for stock prices[J]. 1997(1):25—41. A hyperbolic diffusion Finance and Stochastic, Rydberg T H.Generalized hyperbolic diffusion pro— cesses with applications in fiance[J].Mathematical Finance,1999,9(2):183—201. Rydberg T H.The normal inverse Gaussian levy process:Simulation and approximation[J].Commo Stat:Stoch Models,1997,13:887—910. Ryden T,Terasverta T,Asbrink S.Stylized facts of daily return series and the Hidden Markov model[J]. J Appl Econometrics,1998,13:217—44. Geweke J. 1 999 Using simulation methods for Bayesian econometric models:Inference,develop— ment,and communication[J].Econometric Rev, 1999,18:1—73. [6] [7] [8] [9] [10] [11] [12] [13] Gilks W R.Richardson S,Spiegelhatler D J.Intro— ducing Markov chain Monte Carlo in Practice IN]. Gilks W R,Richardson S,Spiegelhatter D J,eds. London:Chapman and I-k.1l,1996:45--57. Eraker B.MCMC analysis'.'of diffusion models with application to finance[J].J Business Economic 、 Statistics,2001,19:177—91. Elerian O,Chib S,Shephard N.Likelihood infer— ence for discretely observed non—linear diffusions[J-]. Econometrica,2001,69:959—93. Tse Y K,Zhang Xibin,Yu Jun.Estimation of hy— perbolic diffusion using the Markov chain Monte Carlo method[J].Quantitative Finance,2003,3:1— 12. Chibs S,Greenberg E.Understanding the Metropo— lis—Hastings algorithm[J].Am Statistician,1995, 49:327—35. Roberts G 0,Markov chain concepts related to sam— piing algorithms Markov Chain Monte Carlo in Prac— tice[-M-].Gilks WR,Richardson S,Spiegelhalter D J,eds.London:Chapman and Hall,1996:45—57. Kim S,Shephard N,Chibs.Stochastic volatility: Likelihood inference and comparison with ARCH models[J].Rev Econ Stud,1998,65:361—93. Meyer R,Yu J.BUGS for a Bayesian analysis of stochastic volatility models[J].Econometrics J, 2000,3:198—215. (t-接第132页) 6 结 语 本文将DEA评价方法应用于物流园区投资规 模规划的评价中,结果表明,DEA评价方法能做到 对所有被评价物流园区规划方案的充分评价,且能 提出进一步的目标改进措施,为规划决策者进行规 划和决策提供了更加全面的信息。因此,通过应用 DEA方法评价,能够显著地改善目前物流园区规划 的质量。 参考文献: [1] [2] [33 李旭宏,毛海军.开发区专业物流园区规划[J].交通运 输工程学报,2002,2(3):81—84. 王战权,杨东援.物流园区规划初探[J].系统工程, 2001.19(1):79—83. Charnes A,Cooper W W,Rhodes E.Measuring the efficiency of decision—making units[J].European [4] [5] [6] [7] [8] [93 Journal of Operational Research,1978,2(4):429— 444. Charnes A,Cooper W W,Lewin A Y,et a1.Data an— velopment analysis[M].Boston,Dordrecht,Lon— don:Kluwer Academic Publisher,1994. Wei Q L,Sun D B,Xiao Z J.Measuring technical progress with data envelopment analysis[J].Euro— pean Journal of Operational Research,1 995,80(3): 691—702. 魏权龄.评价相对有效性的DEA方法[M].北京:中国 人民大学出版社,1988. 同济大学.南京现代物流产业发展规划研究[R]. 2002. 吴文江,用数据包络分析进行规模收益分析的探讨 [J],系统工程理论方法应用,2000,9(3):248—251. 东南大学交通学院.连云港市现代物流业发展规划 [R],2003. 万方数据