
2006年3月 数理统计与管理 Mar.,2006 第25卷第2期 Application of Statistics and Management Vol.25 No.2 文章编号:1002一1566(2006)02-0161一05 基于蒙特卡洛一马尔科夫链 (MCMC)的ARMA模型选择 赵昕东 (吉林大学数量经济研究中心长春市130012) 摘要:AIC与SIC等准则函数方法是ARMA模型选择过程中经常使用的方法。但是,当模型的阶 数很高时,无法计算并比较每一个备选模型的准则函数值。本文提出了一个基于蒙特卡洛一马尔 科夫链方法的随机模型生成方法,以产生准则函数值最小的备选模型。实际应用表明本文的方法 在处理拥有大量备选模型的ARMA模型选择问题时有很好的效果。 关键词:模型选择:MCMC方法:吉伯斯样本生成:随机模型生成方法 中图分类号:0212 文献标识码:A ARMA Model Selection Based on Monte Carlo Markov-Chain ZHAO Xin-dong (Center for Quantitative Economics Jilin University Changchun,130012,China) Ahstract:Several criteria such as AIC and SIC are usually used in ARMA model selection.However,when the order of ARMA model is very high,to compare every candidate model's criterion value is computationally infeasible.In this paper I suppose an MCMC random model generating procedure that can generate a model with the lowest crite- rion value.A practiced study shows this method is quite efficient in ARMA model selection with large number of candidate model. Key words:model selection:MCMC:Gibbs sampling:random model generating procedure 1问题的提出 在时间序列分析中,自回归移动平均(ARMA)模型是应用最为广泛的模型之一。关于 ARMA模型的一个重要课题是模型选择(Model Selection),即找到能够真实反映时间序列变 动规律的ARMA模型,我们称之为真实模型(True Model),模型选择就是要确定模型的具体 函数形式,包括自回归阶数、移动平均阶数以及在确定的阶数下哪些自回归参数为零,哪些移 动平均参数为零。 模型选择的方法很多,最简单的就是比较所有备选模型的R,将R2最大的模型作为最 优模型,但这种方法的弊端是R2通常随着变量数量的增加而增加,因此将导致过度拟合的出 现。博克期-詹金期方法(Box-Jenkins,1976)是通过观察时间序列的自相关函数与偏相关函数 确定模型阶数,但显然这种方法过于粗略,无法处理阶数较高结构复杂的模型。随着信息理论 收稿日期:2004年08月10日 万方数据
文章编号:!""#—!$%%(#""%)"#&"!%!—"$ 收稿日期:#""’年"(月!"日 基于蒙特卡洛&马尔科夫链 ()*)*)的 +,)+模型选择 赵昕东 (吉林大学数量经济研究中心 长春市!-""!#) 摘要:+.*与/.*等准则函数方法是+,)+模型选择过程中经常使用的方法。但是,当模型的阶 数很高时,无法计算并比较每一个备选模型的准则函数值。本文提出了一个基于蒙特卡洛&马尔 科夫链方法的随机模型生成方法,以产生准则函数值最小的备选模型。实际应用表明本文的方法 在处理拥有大量备选模型的+,)+模型选择问题时有很好的效果。 关键词:模型选择;)*)*方法;吉伯斯样本生成;随机模型生成方法 中图分类号:0#!# 文献标识码:+ !"#!#$%&’(&’&)*+$,-./&%$,#$,*&0.1’$#.12$3405.+, 12+034567859 (*:5;:?@5;4;@;4A:BC858D4CEF4G45H54A:<E4;I*J@59CJ?5,!-""!#,*J45@) !6/*1.)*:/:A:<@GC<4;:<4@E?CJ@E+.*@57/.*@<:?E?@GGI?E:745+,)+D87:GE:G:C;485K28L:A:<,LJ:5;J:8<7:< 8=+,)+D87:G4EA:<IJ49J,;8C8DM@<::A:<IC@5747@;:D87:GNEC<4;:<485A@G?:4EC8DM?;@;485@GGI45=:@E4OG:K.5 ;J4EM@M:<.E?MM8E:@5)*)*<@578DD87:G9:5:<@;459M<8C:7?<:;J@;C@59:5:<@;:@D87:GL4;J;J:G8L:E;C<4;:6 <485A@G?:K+M<@C;4C:7E;?7IEJ8LE;J4ED:;J874EP?4;::==4C4:5;45+,)+D87:GE:G:C;485L4;JG@<9:5?DO:<8= C@5747@;:D87:GK 7&89$1%/:D87:GE:G:C;485;)*)*;Q4OOEE@DMG459;<@578DD87:G9:5:<@;459M<8C:7?<: ! 问题的提出 在时间序列分析中,自回归移动平均(+,)+)模型是应用最为广泛的模型之一。关于 +,)+模型的一个重要课题是模型选择()87:G/:G:C;485),即找到能够真实反映时间序列变 动规律的+,)+模型,我们称之为真实模型(R<?:)87:G),模型选择就是要确定模型的具体 函数形式,包括自回归阶数、移动平均阶数以及在确定的阶数下哪些自回归参数为零,哪些移 动平均参数为零。 模型选择的方法很多,最简单的就是比较所有备选模型的 !#,将 !# 最大的模型作为最 优模型,但这种方法的弊端是!#通常随着变量数量的增加而增加,因此将导致过度拟合的出 现。博克期"詹金期方法(S8T6F:5U45E,!VW%)是通过观察时间序列的自相关函数与偏相关函数 确定模型阶数,但显然这种方法过于粗略,无法处理阶数较高结构复杂的模型。随着信息理论 #""%年 -月 第#$卷 第#期 数理统计与管理 +MMG4C@;4858=/;@;4E;4CE@57)@5@9:D:5; )@<K,#""% X8GK#$ Y8K# 万方数据

162 数理统计与管理 第25卷第2期2006年3月 的发展,二十世纪七十年代以来,准则函数方法被广泛使用,通过比较所有备选模型的准则函 数值,选择准则函数值最小的模型。较为常用的准则函数有AIC(Akaike,1974),SIC (Schwarz,1978)等,这两种准则函数分别为: A1C=log.g+2p+g+1)/八n-p) SIC=logg+(p+q+1)logn-p)/八n-p) 这里。=含Y,-Y,(n一p力与g分别为自回归阶数与移动平均阶数,n是时间 序列样本个数。 当前,随着计算机技术的发展,在模型阶数不是很高时,可以通过计算所有备选模型的准 则函数值进行模型选择。但是在某些情况下,真实模型的自回归阶数或移动平均的阶数可能 很高,这样备选的模型相当多,如果计算每个备选模型的准则函数值,计算量将非常大。例如, 如果自回归阶数与移动平均阶数最高分别可能达到10阶,称ARMA(10,10)为全模型(full mode),模型选择就是从ARMA(10,10)中选择正确的模型,那么备选模型个数将会高达220, 我们无法计算每一个模型的准则函数值。为了克服这一困难,本文给出了一个基于蒙特卡洛 马尔科夫链(MCMC)方法的吉伯斯随机样本生成方法(Gibbs sampler)[Casella,G.and George, E.I,1992],使计算量大大减少。 2吉伯期样本生成方法 吉伯斯样本生成方法是一种计算技术,在不须要计算多元随机变量的联合密度函数的条 件下,只通过多元随机变量中每一个随机变量的条件分布,生成多元随机变量的样本。该方法 利用了马尔科夫链的基本性质。 假定(X1,X2,…X)是K维随机变量,(x0),x0,…x0)是(X1,X2,…X)的一个样本 (初值),吉伯斯样本生成方法就是根据下面的条件概率生成(X1,X2,“,X)的随机样本的方 法。 X’~fx11X2=x9-1,X3=x9-D,…,Xk=x{-1D) Xy’~fx21X1=x9,X3=x9-D,…,X=x9-D) X9》~f|X1=x9’,X2=xy,…,X-1=x2) 这样在不须要计算联合分布的密度函数的条件下,可以得到联合分布的随机样本,并通过 随机样本了解联合分布的特征。 3基于MCMC随机模型生成方法的模型选择 对给定的全模型ARMA(p,q), Y:=a1 Yi-1++apY-p+e-B1e-1--Be-g (1) 模型选择就是要确定(α1,…,ap)以及(B1,…,B。)中哪些元素的值应该取零,我们定义两 组向量U1×p=(u1…,ub)与V1×g=(1,…,6)分别对应(a1,…,ap)与(月1,…,月,),如果 (α1,…,ap)与(A,…,B)中的元素不等于零,则U与V中对应的元素取值为1,否则取值为 零。然后我有院授M=w=(u1…ug01…)}为U,V)中元素的所有可能组合,那么M
的发展,二十世纪七十年代以来,准则函数方法被广泛使用,通过比较所有备选模型的准则函 数值,选 择 准 则 函 数 值 最 小 的 模 型。较 为 常 用 的 准 则 函 数 有 !"#(!$%&$’,()*+),,"# (,-./%01,()*2)等,这两种准则函数分别为: !"# $345%!6 &,’(6(&(’(()/()*&) +"# $345%!6 &,’((&(’(()345 ()*&)/()*&) 这里%!6 &,’7 ! )8& ,7( (-,8%-,)/()8&),&与’分别为自回归阶数与移动平均阶数,) 是时间 序列样本个数。 当前,随着计算机技术的发展,在模型阶数不是很高时,可以通过计算所有备选模型的准 则函数值进行模型选择。但是在某些情况下,真实模型的自回归阶数或移动平均的阶数可能 很高,这样备选的模型相当多,如果计算每个备选模型的准则函数值,计算量将非常大。例如, 如果自回归阶数与移动平均阶数最高分别可能达到(9阶,称 !:;!((9,(9)为全模型(4?’3),模型选择就是从!:;!((9,(9)中选择正确的模型,那么备选模型个数将会高达669, 我们无法计算每一个模型的准则函数值。为了克服这一困难,本文给出了一个基于蒙特卡洛@ 马尔科夫链(;#;#)方法的吉伯斯随机样本生成方法(A&BBCC%>D3’0)[#%C’33%,AE%F?A’405’, GE",())6],使计算量大大减少。 6 吉伯期样本生成方法 吉伯斯样本生成方法是一种计算技术,在不须要计算多元随机变量的联合密度函数的条 件下,只通过多元随机变量中每一个随机变量的条件分布,生成多元随机变量的样本。该方法 利用了马尔科夫链的基本性质。 假定(.(,.6,…./)是 0 维随机变量,(1 (9) ( ,1 (9) 6 ,…1 (9) / )是(.(,.6,…./)的一个样本 (初值),吉伯斯样本生成方法就是根据下面的条件概率生成(.(,.6,…,./)的随机样本的方 法。 . (2) ( "3(1(4.6 $1 (2*() 6 ,.H $1 (2*() H ,…,./ $1 (2*() / ) . (2) 6 "3(164.( $1 (2) ( ,.H $1 (2*() H ,…,./ $1 (2*() / ) . (2) / "3(1/4.( $1 (2) ( ,.6 $1 (2) 6 ,…,./*( $1 (2) /*() 这样在不须要计算联合分布的密度函数的条件下,可以得到联合分布的随机样本,并通过 随机样本了解联合分布的特征。 H 基于 !"!"随机模型生成方法的模型选择 对给定的全模型!:;!(D,I), -5 $#(-5*((…(#&-5*&($5*%($5*(*…*%’$5*’ (() 模型选择就是要确定(#(,…,#&)以及(%(,…,%’)中哪些元素的值应该取零,我们定义两 组向量 6(J&7(7(,…,7&)与 8(J’7(9(,…,9&)分别对应(#(,…,#&)与(%(,…,%’),如果 (#(,…,#&)与(%(,…,%’)中的元素不等于零,则 6 与8 中对应的元素取值为(,否则取值为 零。然后我们定义 :7{&7(7(,…7’,9(,…9’)}为(6,8)中元素的所有可能组合,那么 ; 6K( 数理统计与管理 第6L卷 第6期 699K年H月 万方数据

赵昕东:基于蒙特卡洛-马尔科夫链(MCMC)的ARMA模型选择 163 就代表了(1)式中全模型所包含的所有的备选模型,w=(u1,…ug,v1,…,)可以代表任意一 个备选模型。 考虑到AIC与SC都具有共同的形式: S(u,o)=log2.。+c(u,v) 这里u和分别表示向量U与V中最后一个“1”的位置,分别等于自回归阶数与移动平均阶 数。 我们首先定义一个M上的概率分布 P(w)=T exp(-S(u,v)) ∈Mexp(-S(u,u) 进一步定义w0为真实模型,显然S(uo,o)为S(u,v)所有可能取值中的最小值,并且P (ω)在w0取得最大值。假设有一组备选模型(:i=1,…,K),令 fk=之Iw,=u/K i=l 为模型。在该组备选模型中出现的频率,我们有 limf,k=P(wo)=maP(a) (2) u∈M 的概率为1。因此,只要K足够大,真模型0将以最高的频率出现在备选模型中。 为便于表达。我们定义向量 W=(w1,…,,…,wp+g),i=1,…,p+9 以表示模型w=(u1…,up'v1,…,g)。 我们将W=(w1…,心,…,p+g),i=1,…,p+q看成p+q维随机变量的联合分布, 每个随机变量的条件分布服从二项分布,这样就可以应用吉伯斯样本生成方法生成W1)= (D,…,wg),W2》=(2,…,g),…,W=(w,…,wg)一组随机样本,即随 机产生一组备选模型。因为该组模型是随机产生的,当模型足够多时,根据(2)式,真实模型出 现的次数将最多。 根据吉伯斯样本生成方法,为计算P(W)我们需要计算条件概率P(|1,“,-1' +1…,p+g),i=1,…,p+qP(w|1,…,-1+1…,p+g) P(;l1,…,;-1+1…,p+g) p(w1,…,;-1'=1,5+1’…,p+g)+P(1,…,w-1'5=0,+1…,wp+g) P(W) P(W,:=1)+P(W,;=0) exp(-S(W)) ≥m∈Mexp-S(W)) exp(-S(W,e;=1))exp(-S(W,,=0) S.ewexp(-s(W))+Srexp(-s(W)) exp(-S(W)) exp(-S(W,,=1)+exp(-S(W,,=0) 在备选模型的数量很多时,∑∈Mexp(一S(u,v)的值是难以计算的,而本文的模型选择 方法无须计算∑∈Mexp(-S(u,v)的值。 以下塞据伯斯样本生成方法的ARMA模型选择算法:
就代表了(!)式中全模型所包含的所有的备选模型,!"(!!,…!",#!,…#")可以代表任意一 个备选模型。 考虑到#$%与&$%都具有共同的形式: $(!,#)%’()&"* !,#’((!,#) 这里!和#分别表示向量) 与* 中最后一个“!”的位置,分别等于自回归阶数与移动平均阶 数。 我们首先定义一个 + 上的概率分布 +(!)% ,-. (,$(!,#)) !!"-,-. (,$(!,#)) 进一步定义!/为真实模型,显然$(!/,#/)为$(!,#)所有可能取值中的最小值,并且+ (!)在!/取得最大值。假设有一组备选模型(!.:."!,…,/),令 0!/ % ! / .%! 1(!. %!)// 为模型! 在该组备选模型中出现的频率,我们有 ’01/#2 0!// %+(!/)% 13-!"- +(#) (*) 的概率为!。因此,只要 4足够大,真模型!/将以最高的频率出现在备选模型中。 为便于表达。我们定义向量 2 %(3!,…,3.,…,34’"),.%!,…,4’" 以表示模型!"(!!,…,!4,#!,…,#")。 我们将 2"(3!,…,3.,…,345"),."!,…,45"看成45"维随机变量的联合分布, 每个随机变量的条件分布服从二项分布,这样就可以应用吉伯斯样本生成方法生成 2(!) " (3(!) ! ,…,3(!) 45"),2(*) "(3(*) ! ,…,3(*) 45"),…,2(5) "(3(5) ! ,…,3(5) 45")一组随机样本,即随 机产生一组备选模型。因为该组模型是随机产生的,当模型足够多时,根据(*)式,真实模型出 现的次数将最多。 根据吉伯斯样本生成方法,为计算$+(2)我们需要计算条件概率$+(3.%3!,…,3.6!, 3.5!,…,345"),."!,…,45",$+(3.%3!,…,3.6!,3.5!,…,345") " $+(3.%3!,…,3.6!,3.5!,…,345") $+(3!,…,3.6!,3."!,3.5!,…,345")5$+(3!,…,3.6!,3."/,3.5!,…,345") " $+(2) $+(2,3."!)5$+(2,3."/) " ,-. (6$(2)) !!"-,-. (6$(2)) ,-. (6$(2,3."!)) !!"-,-. (6$(2))5 ,-. (6$(2,3."/)) !!"-,-. (6$(2)) " ,-. (6$(2)) ,-. (6$(2,3."!))5,-. (6$(2,3."/)) 在备选模型的数量很多时,!!"-,-. (6$(!,#))的值是难以计算的,而本文的模型选择 方法无须计算!!"-,-. (6$(!,#))的值。 以下是基于吉伯斯样本生成方法的#7+#模型选择算法: 赵昕东:基于蒙特卡洛6马尔科夫链(+%+%)的#7+#模型选择 !98 万方数据
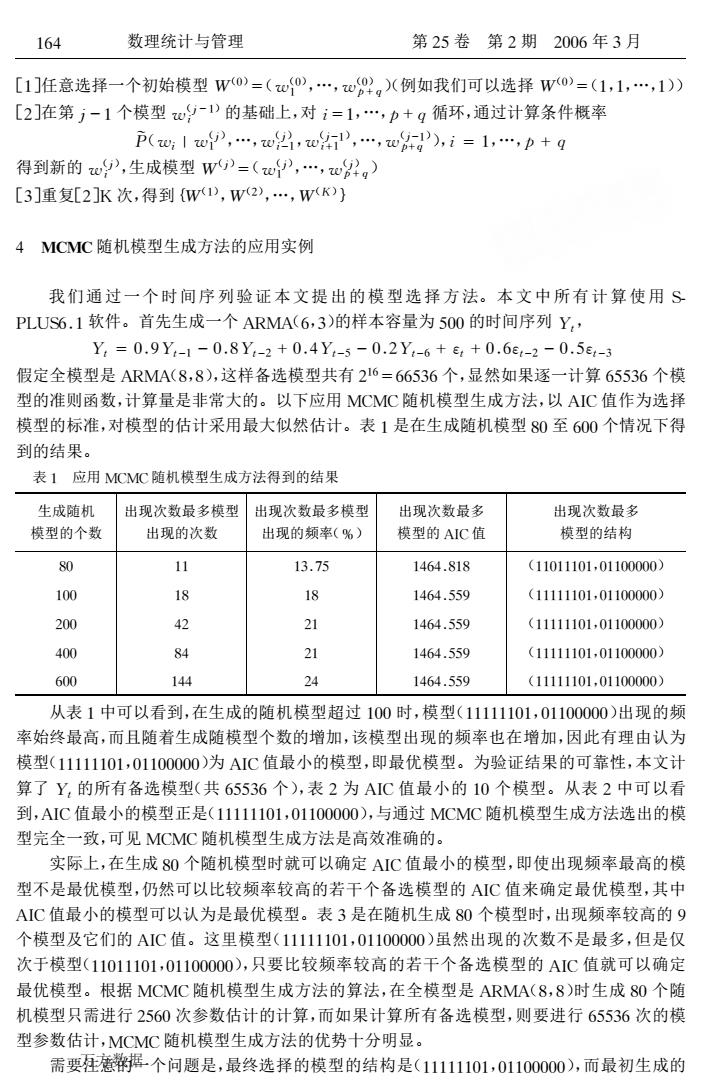
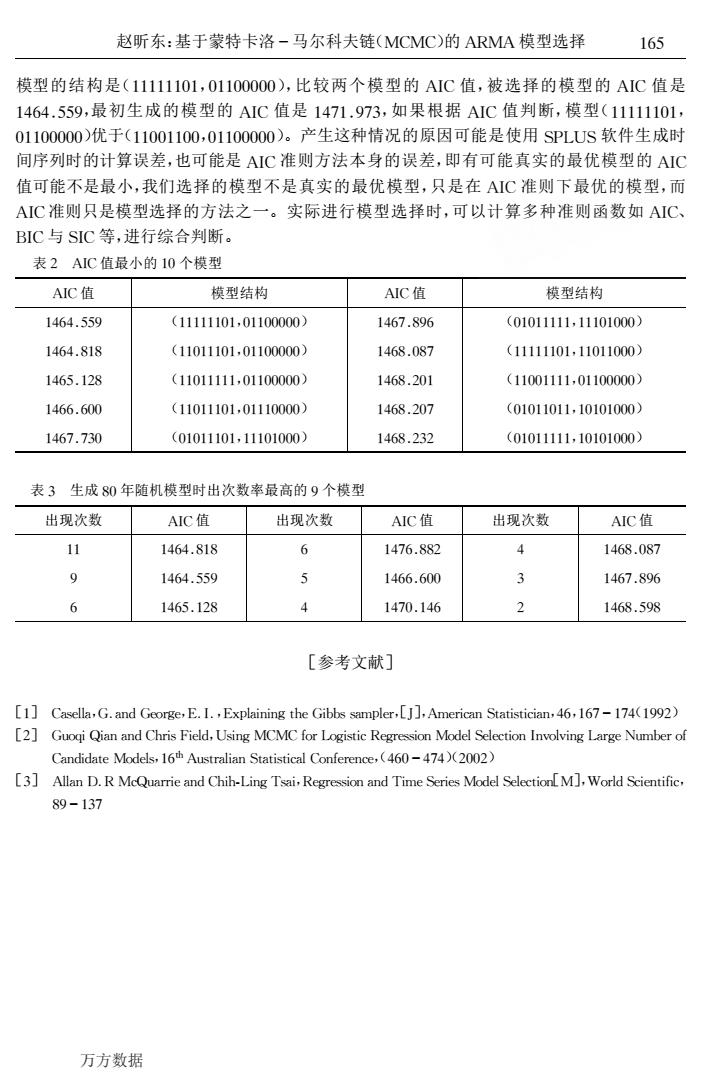
164 数理统计与管理 第25卷第2期2006年3月 [1]任意选择一个初始模型W0)=(心0,…,心0g)(例如我们可以选择W0)=(1,1,…,1) [2]在第j-1个模型9-1D的基础上,对i=1,…,p+q循环,通过计算条件概率 P(1o,…,w,,…,wg),i=1,…,p+q 得到新的,生成模型w》=(,,g) [3]重复[2]K次,得到W1,W2),…,WK)) 4 MCMC随机模型生成方法的应用实例 我们通过一个时间序列验证本文提出的模型选择方法。本文中所有计算使用S PLUS6.1软件。首先生成一个ARMA(6,3)的样本容量为500的时间序列Y, Y,=0.9Y-1-0.8Y-2+0.4Y-5-0.2Y-6+e+0.6e-2-0.5e-3 假定全模型是ARMA(8,8),这样备选模型共有216=66536个,显然如果逐一计算65536个模 型的准则函数,计算量是非常大的。以下应用MCMC随机模型生成方法,以AIC值作为选择 模型的标准,对模型的估计采用最大似然估计。表1是在生成随机模型80至600个情况下得 到的结果。 表1应用MCMC随机模型生成方法得到的结果 生成随机 出现次数最多模型 出现次数最多模型 出现次数最多 出现次数最多 模型的个数 出现的次数 出现的频率(%) 模型的AIC值 模型的结构 80 11 13.75 1464.818 (11011101,01100000) 100 18 18 1464.559 (11111101,01100000) 200 42 21 1464.559 (11111101,01100000) 400 84 21 1464.559 (11111101,01100000) 600 144 24 1464.559 (11111101,01100000) 从表1中可以看到,在生成的随机模型超过100时,模型(11111101,01100000)出现的频 率始终最高,而且随着生成随模型个数的增加,该模型出现的频率也在增加,因此有理由认为 模型(11111101,01100000)为AIC值最小的模型,即最优模型。为验证结果的可靠性,本文计 算了Y,的所有备选模型(共65536个),表2为AIC值最小的10个模型。从表2中可以看 到,AIC值最小的模型正是(11111101,01100000),与通过MCMC随机模型生成方法选出的模 型完全一致,可见MCMC随机模型生成方法是高效准确的。 实际上,在生成80个随机模型时就可以确定AIC值最小的模型,即使出现频率最高的模 型不是最优模型,仍然可以比较频率较高的若干个备选模型的AC值来确定最优模型,其中 AIC值最小的模型可以认为是最优模型。表3是在随机生成80个模型时,出现频率较高的9 个模型及它们的AIC值。这里模型(11111101,01100000)虽然出现的次数不是最多,但是仅 次于模型(11011101,01100000),只要比较频率较高的若干个备选模型的AIC值就可以确定 最优模型。根据MCMC随机模型生成方法的算法,在全模型是ARMA(8,8)时生成80个随 机模型只需进行2560次参数估计的计算,而如果计算所有备选模型,则要进行65536次的模 型参数估计,MCMC随机模型生成方法的优势十分明显。 需要狂意据个问题是,最终选择的模型的结构是(11111101,01100000),而最初生成的
[!]任意选择一个初始模型 !(") #("(") ! ,…,"(") #$$)(例如我们可以选择 !(") #(!,!,…,!)) [%]在第%&!个模型 "(%&!) & 的基础上,对&#!,…,#$$循环,通过计算条件概率 !’("&("(%) ! ,…,"(%) &)!,"(%)!) &*! ,…,"(%)!) #*$ ),&+!,…,#*$ 得到新的 "(%) & ,生成模型 !(%) #("(%) ! ,…,"(%) #$$) [’]重复[%](次,得到{!(!),!(%),…,!(,)} ) !"!"随机模型生成方法的应用实例 我们通过一个时间序列验证本文提出的模型选择方法。本文中所有计算使用 *+ ,-.*/0!软件。首先生成一个1231(/,’)的样本容量为4""的时间序列-., -. +"05-.)!)"06-.)%*"0)-.)4)"0%-.)/*!.*"0/!.)%)"04!.)’ 假定全模型是1231(6,6),这样备选模型共有%!/#//4’/个,显然如果逐一计算/44’/个模 型的准则函数,计算量是非常大的。以下应用 3737随机模型生成方法,以187值作为选择 模型的标准,对模型的估计采用最大似然估计。表!是在生成随机模型6"至/""个情况下得 到的结果。 表! 应用 3737随机模型生成方法得到的结果 生成随机 模型的个数 出现次数最多模型 出现的次数 出现次数最多模型 出现的频率(9) 出现次数最多 模型的187值 出现次数最多 模型的结构 6" !! !’0:4 !)/)06!6 (!!"!!!"!,"!!""""") !"" !6 !6 !)/)0445 (!!!!!!"!,"!!""""") %"" )% %! !)/)0445 (!!!!!!"!,"!!""""") )"" 6) %! !)/)0445 (!!!!!!"!,"!!""""") /"" !)) %) !)/)0445 (!!!!!!"!,"!!""""") 从表!中可以看到,在生成的随机模型超过!""时,模型(!!!!!!"!,"!!""""")出现的频 率始终最高,而且随着生成随模型个数的增加,该模型出现的频率也在增加,因此有理由认为 模型(!!!!!!"!,"!!""""")为187值最小的模型,即最优模型。为验证结果的可靠性,本文计 算了-.的所有备选模型(共/44’/个),表%为 187值最小的!"个模型。从表%中可以看 到,187值最小的模型正是(!!!!!!"!,"!!"""""),与通过 3737随机模型生成方法选出的模 型完全一致,可见 3737随机模型生成方法是高效准确的。 实际上,在生成6"个随机模型时就可以确定187值最小的模型,即使出现频率最高的模 型不是最优模型,仍然可以比较频率较高的若干个备选模型的 187值来确定最优模型,其中 187值最小的模型可以认为是最优模型。表’是在随机生成6"个模型时,出现频率较高的5 个模型及它们的187值。这里模型(!!!!!!"!,"!!""""")虽然出现的次数不是最多,但是仅 次于模型(!!"!!!"!,"!!"""""),只要比较频率较高的若干个备选模型的 187值就可以确定 最优模型。根据 3737随机模型生成方法的算法,在全模型是 1231(6,6)时生成6"个随 机模型只需进行%4/"次参数估计的计算,而如果计算所有备选模型,则要进行/44’/次的模 型参数估计,3737随机模型生成方法的优势十分明显。 需要注意的一个问题是,最终选择的模型的结构是(!!!!!!"!,"!!"""""),而最初生成的 !/) 数理统计与管理 第%4卷 第%期 %""/年’月 万方数据
赵昕东:基于蒙特卡洛-马尔科夫链(MCMC)的ARMA模型选择 165 模型的结构是(11111101,01100000),比较两个模型的AIC值,被选择的模型的AIC值是 1464.559,最初生成的模型的AIC值是1471.973,如果根据AIC值判断,模型(11111101, 01100000)优于(11001100,01100000)。产生这种情况的原因可能是使用SPLUS软件生成时 间序列时的计算误差,也可能是AIC准则方法本身的误差,即有可能真实的最优模型的AIC 值可能不是最小,我们选择的模型不是真实的最优模型,只是在AC准则下最优的模型,而 AIC准则只是模型选择的方法之一。实际进行模型选择时,可以计算多种准则函数如AC、 BIC与SIC等,进行综合判断。 表2AIC值最小的10个模型 AIC值 模型结构 AIC值 模型结构 1464.559 (11111101,01100000) 1467.896 (01011111,11101000) 1464.818 (11011101,01100000) 1468.087 (11111101,11011000) 1465.128 (11011111,01100000) 1468.201 (11001111,01100000) 1466.600 (11011101,01110000) 1468.207 (01011011,10101000) 1467.730 (01011101,11101000) 1468.232 (01011111,10101000) 表3生成80年随机模型时出次数率最高的9个模型 出现次数 AIC值 出现次数 AIC值 出现次数 AIC值 11 1464.818 6 1476.882 4 1468.087 9 1464.559 5 1466.600 3 1467.896 6 1465.128 4 1470.146 2 1468.598 [参考文献] [1]Casella,G.and George,E.I.Explaining the Gibbs sampler,[J],American Statistician,46,167-174(1992) [2]Guogi Qian and Chris Field,Using MCMC for Logistic Regression Model Selection Involving Large Number of Candidate Models,16th Australian Statistical Conference,(460-474)(2002) [3]Allan D.R McQuarrie and Chih-Ling Tsai,Regression and Time Series Model Selection[M],World Scientific, 89-137 万方数据
模型的结构是(!!!!!!"!,"!!"""""),比较两个模型的 #$%值,被选择的模型的 #$%值是 !&’&())*,最初生成的模型的 #$%值是!&+!(*+,,如果根据 #$%值判断,模型(!!!!!!"!, "!!""""")优于(!!""!!"","!!""""")。产生这种情况的原因可能是使用-./0-软件生成时 间序列时的计算误差,也可能是 #$%准则方法本身的误差,即有可能真实的最优模型的 #$% 值可能不是最小,我们选择的模型不是真实的最优模型,只是在 #$%准则下最优的模型,而 #$%准则只是模型选择的方法之一。实际进行模型选择时,可以计算多种准则函数如 #$%、 1$%与-$%等,进行综合判断。 表2 #$%值最小的!"个模型 #$%值 模型结构 #$%值 模型结构 !&’&())* (!!!!!!"!,"!!""""") !&’+(3*’ ("!"!!!!!,!!!"!""") !&’&(3!3 (!!"!!!"!,"!!""""") !&’3("3+ (!!!!!!"!,!!"!!""") !&’)(!23 (!!"!!!!!,"!!""""") !&’3(2"! (!!""!!!!,"!!""""") !&’’(’"" (!!"!!!"!,"!!!"""") !&’3(2"+ ("!"!!"!!,!"!"!""") !&’+(+," ("!"!!!"!,!!!"!""") !&’3(2,2 ("!"!!!!!,!"!"!""") 表, 生成3"年随机模型时出次数率最高的*个模型 出现次数 #$%值 出现次数 #$%值 出现次数 #$%值 !! !&’&(3!3 ’ !&+’(332 & !&’3("3+ * !&’&())* ) !&’’(’"" , !&’+(3*’ ’ !&’)(!23 & !&+"(!&’ 2 !&’3()*3 [参考文献] [!] %456774,894:;866,?9$9,?@A74B:B:>CD68BEE554FA76=[,G],#F6=BH4:-C4CB5CBHB4:,&’,!’+I!+&(!**2) [2] 8JN%N%OB5CBHP6>=655B/4=>6RJFE6=U54B,P6>=655B<:4:;UBF6-6=B65N<;67-676HCB<:[N],V<=7;-HB6:CBOBH, 3*I!,+ 赵昕东:基于蒙特卡洛I马尔科夫链(N%N%)的#PN#模型选择 !’) 万方数据