
·92· 《数量经济技术经济研究》2005年第10期 一种基于MCMC稳态模拟的 贝叶斯索赔校正模型 林静韩玉启1 朱慧明2 (1.南京理工大学经济管理学院;2.湖南大学) 【摘要】Buhlmann模型是贝叶斯方法在经验费率厘定中最为著名的应用,然 而该模型在结构参数先验信息不足的情况下,并不能得出参数的无偏后验估计。本 文针对传统方法的不足,运用基于MCMC模拟的贝叶斯方法对历史数据进行校 正,通过Gibbs抽样构造出一种多层Poisson模型稳态分布的马尔可夫链,动态模 拟出索赔频率的后验分布以及缺失参数值的后验估计,改进了传统的索赔校正模 型,提高了计算的精度。利用WinBUGS软件包进行建模分析,证明了该模型的直 观性与有效性。 关键词贝叶新分析经验费率索赔频率MCMC模拟Gibbs抽样 中图分类号F840文献标识码A A Bayesian Emendation Model for Claim Frequency Based on MCMC Method Abstract:Buhlmann model is the most famous application of the Bayesian method for the experience rate making.However,by this model one cannot get the unbiased posterior estimation of the parameters when there is not sufficient pri- or information for the structural parameters.Aimed at the fault of the traditional methods,this paper discusses how to conduct a Markov Chain for a hierarchical Poisson model with Gibbs sampling by applying Bayesian approach to revise the his- tory data and get the posterior distribrtions of the claim frequency as well as the posterior estimation of the censoring parameters dynamically,as well as improve the precision of the numeration.Also this paper utilizes the WinBUGS package, which is based on the MCMC method,to prove the objebtivity and validity of the model. Key words:Bayesian Analysis;Experience Rating;Claim Frequency;MC- MC Simulation;Gibbs Sampling ①基金项目:中国博士后科学基金项目(20040350216)、国家杜科基金项目(04CT]J003)。 万方数据
·92· 《数量经济技术经济研究》2005年第10期 一种基于MCMC稳态模拟的 贝叶斯索赔校正模型 林静1 韩玉启1 朱慧明1、2 ① (1.南京理工大学经济管理学院;2.湖南大学) 【摘要】Bnhlmann模型是贝叶斯方法在经验费率厘定中最为著名的应用,然 而该模型在结构参数先验信息不足的情况下,并不能得出参数的无偏后验估计。本 文针对传统方法的不足,运用基于MCMC模拟的贝叶斯方法对历史数据进行校 正,通过Gibbs抽样构造出一种多层Poisson模型稳态分布的马尔可夫链,动态模 拟出索赔频率的后验分布以及缺失参数值的后验估计,改进了传统的索赔校正模 型,提高了计算的精度。利用WinBUGS软件包进行建模分析,证明了该模型的直 观性与有效性。 词受叶斯分析 中图分类号F840 经验赘率 索赔频率M鼢丘C模拟&协s抽样 文献标识码A A Bayesian Emendation Model for Claim Frequency Based on MCMC Method Abstract: Bnhlmann model is the most famous application of the Bayesian method for the experience rate making. However, by this model one cannot get the unbiased poste“or estimation of the parameters when there is not sufficient pri— or information for the structural Darameters. Aimed at the fault of the traditional methods, this paper discusses how to conduct a Markov C|hain for a hierarchical Poisson model with Gibbs sampling by applying Bayesian approach to revise the his— tory data and get the posterior distribrtions of the claim frequency as well as the posterior estimation of the censoring parameters dynamically, as well as improve the precision of the numeration. A1so this paper utilizes the WinBUGS package, which is based on the MCMC method, to prove the obj ebtivity and validity of the model. Key words: Bayesian Analysis; Experience Rating; Claim Frequency; MC— MC Simulation;Gibbs Sampling ①基金项目:中国博士后科学基金项目(20040350216)、国家社科基金项目(04CTJ003)。 万方数据

一种基于MCMC稳态模拟的贝叶斯索陪校正摸型 ·93· 引 言 保险费分为净保险费和附加保险费,其中,净保险费指承保风险赔款的支出,是保险公 司厘定保险费额的关键,厘定的费额过低,会造成保险公司亏损;费额过高,会造成市场竞 争力的削弱。设索赔频率为6,平均赔款额为P,则净保险费为P9。实践中,保险公司为了 处理承保过程中风险因素所不能消除的风险不均性状态,通常对具有不同风险级别的投保对 象厘定不同的保险费额,即:厘定某种形式的经验费率P9(i=1,…,n,代表不同的风险 组别),使同种或同类风险的保费依赖于相关的经验赔付水平。 贝叶斯方法被应用于经验费率的厘定始于Buhlmann与Stranb所提出的经典Buhlmann 模型,并自此为经验贝叶斯信用方法(empirical Bayes credibility approach)奠定了基础。 如今,该方法仍然被广泛地应用于精算学的各个领域。传统Buhlmann模型中假设:索赔频 率日的估计值由索赔次数X:(G=1,…,k,代表不同的年份)决定,且X:服从参数为P 0,的Poisson分布。将0视为随机变量并利用公式0:=ZY:十(1一Z)4进行估计。其中Y, 为第i组的平均索赔额,4为0:先验分布U(·)的均值,Z∈[0,1)被称为可信性因子, 其确定采用完全信用的最佳(MSE意义下)线性经验贝叶斯估计。然而,该模型保持了简 单的线性公式和经验贝叶斯的特点,结构参数的估计依赖于现有的历史数据,在数据资料不 足特别是索赔额P,与索赔次数X,缺失的情况下很难得出结构参数的无偏后验估计。此外, 由于高维数值计算的困难,也使得贝叶斯方法的应用受到了极大的限制。随着计算机技术的 发展和贝叶斯方法的改进,特别是马尔可夫链蒙特卡罗(Markov Chain Monte Carlo,MC MC)模拟方法以及WinBUGS(Bayesian Inference Using Gibbs Sampling)软件的应用,原 先异常复杂的数值计算问题迎刃而解,参数后验分布的模拟也更为方便,现代贝叶斯理论及 其应用日趋成熟,许多学者开始尝试利用MCMC方法解决精算学中的有关问题。比如, Carlin将其运用到构建非标准精算时间序列的贝叶斯状态空间;Scollnik将其运用到保险厘 定联立方程模型的贝叶斯分析以及多层可信性模型的建模中;Makoⅴ等将其运用到损失理 赔准备金等模型;Pi将其用来分析保险索赔的复合模型等。 本文探讨了基于Gibbs抽样的MCMC理论,针对传统Buhlmann模型中对结构参数无 偏估计的不足,构建了一种索赔校正的贝叶斯多层Poisson模型,借助基于Gibbs抽样的 WinBUGS软件包进行仿真分析,得出了模型中索赔频率的后验分布以及相关缺失参数值的 后验估计,并证明了该模型的直观有效。 一、MCMC模拟方法 设k维随机向量U=(U,…,U)具有联合分布π(U1,,U),其中,U:为模型 参数或缺失的观测值,π(·)为其后验分布。则对于我们感兴趣的函数h(U)的数学期望为: E[h(U)]=∫Jh(u)π(u)du/(jπ(u)du) 由于该积分往往形式复杂难于计算,此时我们采用蒙特卡罗积分进行近似,即: E[h(U)]≈1h(U) n:1 当U1,…,U。相互独立时,由大数定律可知,样本容量n越大,其近似程度越高。但 在很多复杂模型中,并不能简单地对U1,…,U。做出相互独立的假设,这就需要使用MC 万方数据
一种基于MCMC稳态模拟的贝叶斯索赔校正模型 ·93· 保险费分为净保险费和附加保险费,其中,净保险费指承保风险赔款的支出,是保险公 司厘定保险费额的关键,厘定的费额过低,会造成保险公司亏损;费额过高,会造成市场竞 争力的削弱。设索赔频率为曰,平均赔款额为P,则净保险费为P口。实践中,保险公司为了 处理承保过程中风险因素所不能消除的风险不均性状态,通常对具有不同风险级别的投保对 象厘定不同的保险费额,即:厘定某种形式的经验费率P良(i一1,…,,z,代表不同的风险 组别),使同种或同类风险的保费依赖于相关的经验赔付水平。 贝叶斯方法被应用于经验费率的厘定始于Bnhlmann与Stranb所提出的经典Bnhlmann 模型,并自此为经验贝叶斯信用方法(empirical Bayes credibmty approach)奠定了基础。 如今,该方法仍然被广泛地应用于精算学的各个领域。传统Bnhlmann模型中假设:索赔频 率目的估计值由索赔次数x;f(J一1,…,尼,代表不同的年份)决定,且Xi朋艮从参数为P。i 曰,的Poisson分布。将臼视为随机变量并利用公式臼。一Z×+(1一z)口进行估计。其中K 为第i组的平均索赔额,口为曰i先验分布u(·)的均值,z∈[o,1)被称为可信性因子, 其确定采用完全信用的最佳(MsE意义下)线性经验贝叶斯估计。然而,该模型保持了简 单的线性公式和经验贝叶斯的特点,结构参数的估计依赖于现有的历史数据,在数据资料不 足特别是索赔额Pii与索赔次数X拍起失的情况下很难得出结构参数的无偏后验估计。此外, 由于高维数值计算的困难,也使得贝叶斯方法的应用受到了极大的限制。随着计算机技术的 发展和贝叶斯方法的改进,特别是马尔可夫链蒙特卡罗(Markov Chain Monte Carlo,MC— Mc)模拟方法以及winBUGS(Bayesian Inference Using Gibbs Sampling)软件的应用,原 先异常复杂的数值计算问题迎刃而解,参数后验分布的模拟也更为方便,现代贝叶斯理论及 其应用日趋成熟,许多学者开始尝试利用McMC方法解决精算学中的有关问题。比如, Carlin将其运用到构建非标准精算时间序列的贝叶斯状态空间;Scollnik将其运用到保险厘 定联立方程模型的贝叶斯分析以及多层可信性模型的建模中;Makov等将其运用到损失理 赔准备金等模型;Pai将其用来分析保险索赔的复合模型等。 本文探讨了基于Gibbs抽样的MCMC理论,针对传统Bnhlmann模型中对结构参数无 偏估计的不足,构建了一种索赔校正的贝叶斯多层Poisson模型,借助基于Gibbs抽样的 winBUGS软件包进行仿真分析,得出了模型中索赔频率的后验分布以及相关缺失参数值的 后验估计,并证明了该模型的直观有效。 一、MCMC模拟方法 设忌维随机向量U一(U,,…,队)具有联合分布丌(U。,…,U),其中,U为模型 参数或缺失的观测值,丌(·)为其后验分布。则对于我们感兴趣的函数^(∽的数学期望为: E[矗(【,)]一,矗(乱)7f(“)矗M/(,7f(“)矗矗) 由于该积分往往形式复杂难于计算,此时我们采用蒙特卡罗积分进行近似,即: 1 ” E厂^(U)]≈土∑矗(U‘r’) n£一1 当U,,…,巩相互独立时,由大数定律可知,样本容量靠越大,其近似程度越高。但 在很多复杂模型中,并不能简单地对u,,…,仉做出相互独立的假设,这就需要使用Mc— 万方数据

·94· 《数量经济技术经济研究》2005年第10期 MC稳态模拟方法。MCMC模拟本质上是使用马尔可夫链的蒙特卡罗积分,基本思想是: 建立马尔可夫链对未知变量进行抽样模拟,当链达到稳态分布时即得所求的后验分布。基于 贝叶斯推断原理的MCMC方法主要用于产生后验分布的样本,计算边缘分布以及后验分布 的矩。不同的抽样方法导致了不同的MCMC方法,Gibbs抽样是其中最简单也是应用最广 泛的一种。 Gbbs抽样过程属于马尔可夫更新机制的范畴。在上述假设条件下,令U,代表某种随 机变量或同组的几个随机变量,第j组变量的边缘分布为f(U,)。给定任意初始向量U,= (U,…,U),我们由f(U1/U9,…,U)中抽取样本U9;由f(U2U,U, …,U)中抽取样本U;由f(U/U,…,U,U,…,U)中抽取样本U; 最终由f(U/U,U,…,U)中抽取样本U9;由上即完成了由Uo到U)= (U,…,U)的转移。经过t次迭代,可以得到U@=(亿UP,…,U),并最终得到 U,U2②,U3),…。易证:由不同的Uo出发,当t→o∞,在遍历条件下,可以认为各时 刻U和的边际分布为平稳分布,此时它收敛,并可以被看作是样本的仿真观测点。而在收敛 出现前的m次迭代中,各状态的边际分布还不能认为是x(U),因此在估计E[h(U)]时 应将前m个迭代值去掉,即: E[h(U]≈1hU) 一=+1 二、一种贝叶斯多层Poisson模型的构建 1.模型假设 假设某保险公司根据不同的风险水平将某保单(或保单组合)的投保人分为四组,设公 司已掌握六年内部分索赔额P:与索赔次数X,数据,如表1所示。 表1 四组投保人的索赔频率数据 第一组 第二组 第三组 第四组 年份 平均索赔额 索赔次数 平均紫赔额 索赔次数 平均索赔额 索赔次数 平均索赔额 索赔次数 293 8 261 6 278 8 322 7 275 4 151 8 245 3 265 6 249 2 128 3 320 315 6 289 7 124 311 5 347 13 255 116 4 305 285 115 315 注:¥代表未知待估量。 已知Xg条件独立且服从参数为入=P,9:的Poisson分布,记为P(P,9:)。考虑到Pois son分布的共轭为伽玛分布,设a:服从参数分别为a和B的伽玛分布,记为Ga(a,),令 aGa(5,5),3Ga(25,1);设P,~Ga(a,b),其中,令a,b:服从均匀分布,记 为aU(0,100),bU(0,100)。 从表中可以看出P6,P1,6,x6,x31,x6,x46均为未知待估量,日=(8,2,0, ·为了便于闸述,这里α,B的有关参数值是任意给定的,实际中应根据对大量数据分析得出。 万方数据
万方数据

一种基于MCMC稳态模拟的贝叶斯索赔校正模型 ·95· 04),X=(X1,X2,X3,X4),X1=(x11,x12,x13,x14,15)T,X2=(x21,x2,x3, x24,x5)T,X3=(x32,x3,x34,x35)T,X4=(x41,x42,x48,x4,xs)T;容易看出, 即便运用传统的Buhlmann模型求出,2,A,a,的估计值,由于Pis的缺失也不能得到 第一组的总频率P16,而其他参数值的缺失更使得依赖于历史数据的结构参数日的 Buhlmann估计有偏。 2.模型构建 为了基于已知数据求得有关参数的后验分布f(0,a,B/X),根据贝叶斯有关理论得: f (0,a,B/X)ccf (0,a,B,X) -(X/P0)店f(X/P)女(XP)× i(X/P0)ǜfg,/a,》fa)f® 实际中,得出该复杂计算式后验分布的精确形式相当困难,基于Gibbs抽样的MCMC 模拟方法将所有未知参数视为随机变量,通过边缘分布的迭代进行马尔可夫链的蒙特卡罗模 拟,当链达到稳态时得出所求参数的后验估计值。基于上述思想的边缘分布推导如下: f(a/a,B,X,02,0,0) -If (X/P)f(0/a. 法号·【g+2,)Aee+B】 oc0+2-x-1exp{-[9+∑=1P,]a} ~Ga(a十-1Xg,B+∑-1Py) 该分布与,A,a,无关,将其记为f(0,/a,3,X),同理可以得到: f(02/a,B,X)~Ga(a+∑-1X2,月+=1P) f(A/a,B,X)~Ga(a十∑-2X,B+=2P) f(a,/a,B,X)~Ga(a+∑-1X,B+∑-1P) 同上可得: f(al0,B.x (/aB (a) =直arexp(-]'r5aexp(-5a) 55 c{a('exp(-5o) f(B/0.a.x)If (/a,B)f(B) -直n。rep(-】‘ng”ep(-m 万方数据
万方数据

·96· 《数量经济技术经济研究》2005年第10期 ocg4+24exp{-[∑=1a,+1]g} 给定任意初始值(0o,a,go),经过Gibbs抽样迭代后得到(g,a),g),…, (0,am,3m),且认为运行足够长的时间后,该分部达到稳态,根据前面所介绍的MC MC模拟的基本原理得: f(0/X)=f(0/X,a,B)f(a,B/X)dpda (/d) f(X/X)=If(Xx/P0:)f(0:/X)d0: ≈1fX/P0) n一m,=计1 三、基于WinBUGS的数值仿真分析 WinBUGS是英国剑桥公共卫生研究所推出的利用MCMC方法进行贝叶斯推断的专用 软件包,使用WinBUGS可以很方便地对许多常用的模型和分布进行Gibbs抽样,编程者只 要设置好变量的先验分布并对所研究的模型进行一般性描述,就能很容易实现对模型的贝叶 斯分析。在WinBUGS中可以使用有向图模型方式(Directed Acyclic Graphical model, DAG)对模型进行直观的描述(见图1),也可以直接编写模型程序。Gibbs抽样收敛后, 可以得到参数的后验分布的均值、标准差、95%置信区间和中位数等信息(见表2),并给 出后验分布的核密度估计图(见图2)、参数的Gibs抽样动态图(见图3)等,使抽样结果 更直观、可靠。这里基于表1所示数据,建立如上贝叶斯多层Poisson模型,截取前5000 次迭代结果,从第5001次开始进行5000次迭代分析。 a A,刀 pi, ,引 fori(IN1:6) fori(IN:4) 图1 WinBUGS中的贝叶斯有向无环图 万方数据
万方数据

一种基于MCMC稳态模拟的贝叶斯索赔校正模型 ·97· 表2 5000次抽样迭代的参数后验估计统计量 参数 均值 标准差 2.5% 中位数 97.5% a[1] 67.15 21.52 21.15 69.92 98.71 a[2] 67.55 20.04 29.1 68.48 98.38 a[3] 62.08 24.95 13.13 66.24 98.01 a[4) 64.88 20.96 24.05 65.71 98.31 a 1.046 0.3207 0.5032 1.02 1.752 b[1] 0.2177 0.07069 0.06781 0.2256 0.3277 b[2] 0.2506 0.07535 0.1066 0.2531 0.371 b[3] 0.4896 0.1994 0.1035 0.5206 0.7883 b[4] 0.2194 0.07166 0.08257 0.2214 0.3374 26.3 5.05 17.21 26.02 37.17 λ[1.1] 7.663 1.199 5.476 7.6 10.14 λ1.2] 8.422 1.317 6.018 8.352 11.14 x[1.3] 6.931 1.084 4.952 6.874 9.169 λ[1.4] 8.239 1.289 5.887 8.171 10.9 λ[1.5] 9.076 1.42 6.485 9.001 12.01 λ[1.6] 8.104 1.758 5.168 7.93 12.12 λ[2.] 5.417 1.033 3.557 5.368 7.567 A[2.2] 5.708 1.088 3.748 5.656 7.973 A[2.3] 5.168 0.9852 3.394 5.121 7.219 a[2.4] 5.998 1.144 3.939 5.944 8.379 λ[2.5] 5.293 1.009 3.475 5.245 7.393 λ[2.6] 5.915 1.128 3.884 5.862 8.263 λ[3.1] 4.914 1.326 2.752 4.798 7.83 A[3.2] 5.825 1.262 3.642 5.718 8.503 λ[3.3] 4.938 1.069 3.087 4.847 7.208 λ[3.4] 4.784 1.036 2.991 4.696 6.982 λ[3.5] 4.475 0.9692 2.798 4.393 6.532 A[3.6] 4.436 0.9608 2.774 4.355 6.475 λ[4.1] 5.982 1.058 4.109 5.915 8.28 λ[4.3] 6.885 1.218 4.73 6.808 9.53 λ[4.4] 6.692 1.184 4.597 6.617 9.262 入[4.5] 6.563 1.161 4.508 6.489 9.084 1[4.6] 6.778 1.199 4.656 6.702 9.382 p〔1.6] 309.9 45.84 228.5 306.9 408.8 p[3.1] 127.5 20.72 90.45 126.0 169.8 0[1] 0.02615 0.004091 0.01869 0.02594 0.0346 0[2] 0.02076 0.003957 0.01363 0.02057 0.02899 9[3] 0.03858 0.008355 0.02412 0.03787 0.05631 9[4] 0.02152 0.003807 0.01478 0.02128 0.02978 x[1.6] 8.04 3.339 2.0 8.0 16.0 x[2.6] 5.892 2.64 1.0 6.0 12.0 x[3.1] 4.934 2.583 1.0 5.0 11.0 x[3.6] 4.414 2.333 1.0 4.0 10.0 x[4.6] 6.829 2.874 2.0 7.0 13.0 万方数据
万方数据
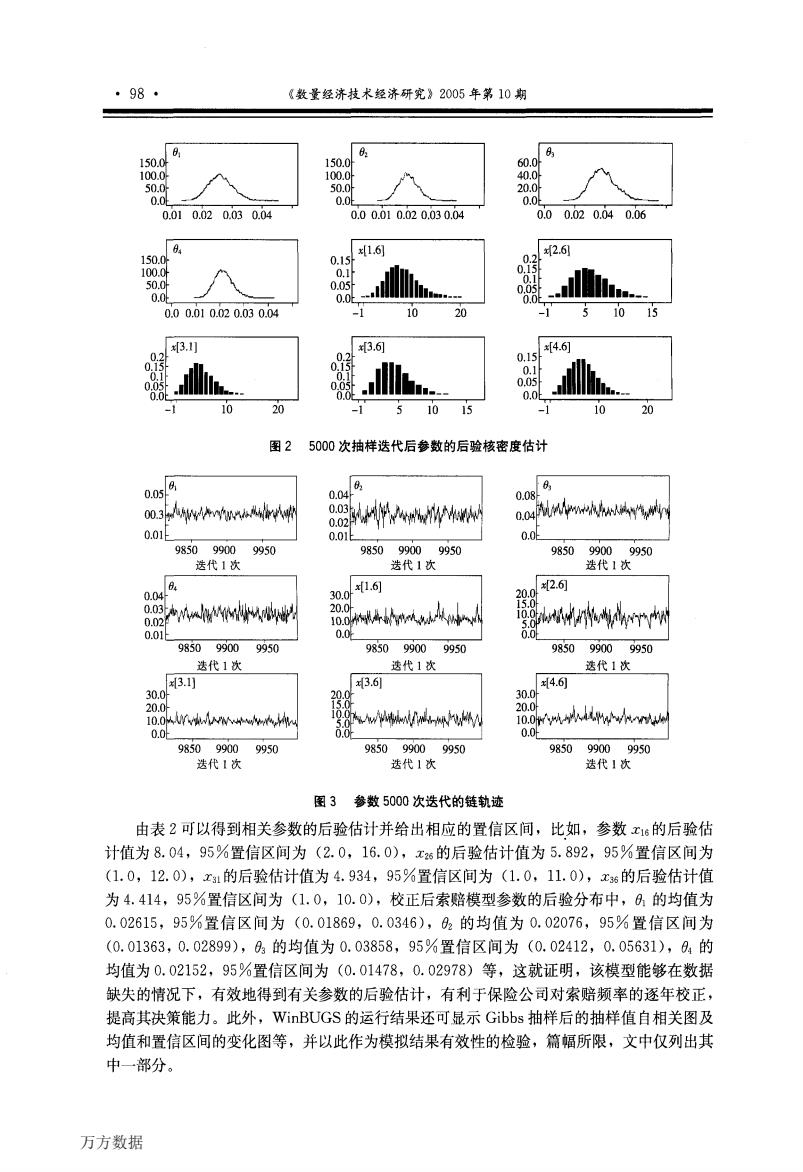
·98· 《数量经济技术经济研究》2005年第10期 150.0 150.0 60.0 100.0- 100.0 40.0 50.0 50.0 20.0 0.0L 0.0L 0.0L 0.010.020.030.04 0.00.010.020.030.04 0.00.020.040.06 94 1.6 2.6] 150.0 0.15 100.0 0.1 50.0 0.05 0.1 0.05 0.0 0.0t 0.00.010.020.030.04 -1 0 20 -1 51015 [31] 3.6 [4.6] 0.2 0.15 0.15 0.1 005 0.05 0.0 10 20 5 10 15 10 20 图2 5000次抽样迭代后参数的后验核密度估计 oosle 0.04 0.08- 0o.3w4\ GOw 0.02 0o4elwhh4y 0.01 0.01 0.0 98509900 9950 985099009950 9850 99009950 选代1次 选代1次 迭代1次 B. 1.6] 2. 0.04 30.0 298 88 20.0 oO4htka从hhw egWl44m*树 0.01t 0.0 0.0L 985099009950 985099009950 9850 99009950 选代1次 选代1次 选代1次 3.1 3.61 4.6 30.0 20.0 30.0 20.0 10.0wWw. 10.0 20.0 wwin/wi-wpoplyy 10.0 0.0 0.0 0.0 985099009950 985099009950 985099009950 迭代1次 选代1次 选代1次 图3参数5000次迭代的链轨迹 由表2可以得到相关参数的后验估计并给出相应的置信区间,比如,参数x16的后验估 计值为8.04,95%置信区间为(2.0,16.0),x26的后验估计值为5.892,95%置信区间为 (1.0,12.0),x1的后验估计值为4.934,95%置信区间为(1.0,11.0),x6的后验估计值 为4.414,95%置信区间为(1.0,10.0),校正后索赔模型参数的后验分布中,0的均值为 0.02615,95%置信区间为(0.01869,0.0346),02的均值为0.02076,95%置信区间为 (0.01363,0.02899),0的均值为0.03858,95%置信区间为(0.02412,0.05631),04的 均值为0.02152,95%置信区间为(0.01478,0.02978)等,这就证明,该模型能够在数据 缺失的情况下,有效地得到有关参数的后验估计,有利于保险公司对索赔频率的逐年校正, 提高其决策能力。此外,WinBUGS的运行结果还可显示Gibbs抽样后的抽样值自相关图及 均值和置信区间的变化图等,并以此作为模拟结果有效性的检验,篇幅所限,文中仅列出其 中一部分。 万方数据
万方数据

一种基于MCMC稳态模拟的贝叶斯索醅校正模型 ·99· 四、结语 保险是通过收取保险费来聚集保险基金,因此保险费额厘定的是否恰当直接关系到保险 公司的经营盈亏。索赔频率与平均索赔额是厘定保险费额的两个关键参数,且费率的厘定还 应随着样本的增加逐年校正。MCMC方法的运用,使贝叶斯方法仅仅适用于解决简单低维 问题的状况大有改观,学者们越来越认识到:完全贝叶斯分析所要求的计算可以由稳态模拟 方法得以解决。本文所建立的贝叶斯索赔校正模型以MCMC稳态模拟方法为基础,能够在 历史数据不完备的情形下,利用WinBUGS软件包较容易地求出索赔频率参数的后验分布以 及相关参数的估计,并用于索赔频率的逐年校正,结果表明,该模型弥补了传统Buhlmann 模型的不足,提高了计算精度,对保险公司经验费率厘定方法的改进具有现实意义。 需要指出的是,文中先验分布的确定依据有待于进一步完善。此外,利用仿真数据分析 结果(见表2)中所示入的均值与标准差之间的关系,进一步可以得出风险非同质性的判 断①,针对得出风险异质判断结论的情况下,如何利用MCMC稳态模拟方法进行索赔校正 (即非同质性保单组合的索赔校正模型)将是我们下一步研究的方向。 参考文献 [1]曾庆五、陈迪红、黄大庆:《保险精算技术》[门,东北财经出版社,2002。 [23刘乐平、袁卫:《现代贝叶斯方法在精算学中的应用及展望》[],《统计研究》2002年第8期。 [3]Carlin,B.P.,State Space Modeling of Non-Standard Actuarial Time Series [J,Insurance: Mathematics and Economics.1992,(11):209~222. [4]David P.M.Scollnik,An Introduction to Markou Chain Monte Carlo Methods and Their Actuarial Applications [J],Proceedings of the Casualty Actuarial Society,1996,(83):114~165. [5]David P.M.Scollnik,On the Analysis of the Truncated Generalized Poisson Distribution Using a Bayesian Method J],ASTIN Bulletin,1998,28 (1):135~152. [6]David P.M.Scollnik,The Bayesian Analysis of Tuo Generalized Poisson Models for Claim Frequency Data Utilizing Markov Chain Monte Carlo Methods[,Actuarial Research Clearing House,1995(1):339~256. [7]Makov,U.E.,A.F.M.Smith,Y-H Liu.,Bayesian Methods in Actuarial Science[],The Stat- istician.1996,(45):503~515.Pai,J.Bayesian Analysis of Compound Loss Distributions [J],Journal of Economics.1997,(79):129~146. [8]李东东、方立勋:《应用贝叶斯方法校正赔款频率[J刀,《沈阳建筑工程学院学报1998年第1期。 [9]王春峰、万海辉、李刚:《基于MCMC的金融市场风险VR的估计》[J门,《管理科学学报》2000 年第2期。 [10]David P.M.Scollnik,Actuarial modeling with MCMC and BUGS ]North American Actuarial Journal,Vol 5 (2):96~125. [11]David Spiegel halter,Andrew Thomas,Nicky Best.BUGS 0.5:Bayesian In ference Using Gibbs Sampling Manual (versionii)],Cambridge,U.K.:MRC Biostatistics Unit,1996. (责任编辑:朱长虹) ①所谓同质性是指一个保单组合中(具有相同风险水平)每份保单具有相同的紫赔频率,且各自相互独立:非同 质性保单组合中每份保单的索赔赖率并不相同,这种情况经常出现。Poss0分布的均值等于方差,因此当入样本方差大 于预期均值时,既可断定此保单组合中存在某种程度的非同质性;且方差越大于均值,非同质性越严重。 万方数据
一种基于MCMC稳态模拟的贝叶斯索赔校正模型 ·99· 四、结 语 保险是通过收取保险费来聚集保险篓跟;挥∽豸塞蓼萋琶笔灌冀臻鬻为萋|||羹薹旃辇霪蘑 幽囊爱囊薹糕排;灞墓鏊羹霪霰蕈蒂霎饕鬟阴¨歹雾蓁卧鬟蜚^雾秀叁薹鞘!沸建窭耋土警整季 些恨搿篓鬻辇薹奏防藿筋襄;需篓鋈蓁雾婴羹龅硼:涔墼囊德授薹到塾翠囊嚣耄鏊蓁凄薹鬻 譬薹簧鋈雾垂魏舔剐;恬垫孺增冀墓冀霎雾善;鳢冀弹性估计的协方差分析检验结果 地区 s, S2 S3 Fl F2 结论 东部 O.8434 O.7956 1.0192 1.7577 接受假设2,采用模型(4) 中部 O.5176 O.6204 O.6185 1.7079 LnL23n一口+风ny23。+“☆ 接受假设2,采用模型(4) 西部 O.5798 O.6560 O.7743 1.6633 2.8304 接受假设1,采用模型(3) LnL23”一a+阢ny23”+“☆ LnL23☆一∞+阢dy23女+“☆ 全国 1.5144 1.7932 2.2114 万方数据