
第30卷第2期 经济数学 Vol.30,No.2 2013年6月 JOURNAL OF QUANTITATIVE ECONOMICS Jun.2013 基于贝叶斯MCMC算法的美式期权定价 熊炳忠,马柏林 (嘉兴学院数理与信息工程学院,浙江嘉兴314000) 摘要鉴于美式期权的定价具有后向选代搜索特征,本文结合L,ongstaff和Schwartz提出的美式期 权定价的最小二乘模拟方法,研究基于马尔科夫链蒙特卡洛算法对回归方程系数的估计,实现对美式期权 的双重模拟定价,通过对无红利美式看跌股票期权定价进行大量实证模拟,从期权价值定价误差等方面同 著名的最小二乘蒙特卡洛模拟方法进行对比分析,结果表明基于MCMC回归算法给出的美式期权定价具 有更高的精确度.模拟实证结果表明本文提出的对美式期权定价方法具有较好的可行性,有效性与广泛的 适用性,该方法的不足之处就是类似于一般的蒙特卡洛方法,会使得求解的计算量有所加大。 关键词美式期权;MCMC回归;方差减少技术;蒙特卡洛模拟 中图分类号F830 文献标识码A Pricing American-Style Options Based on Bayesian Markov Chain Monte Carlo Algorithm XIONG Bing-zhong,MA Bo-lin (Institute of Mathematics,Physics and Information Engineering,JiaXing University,ZheJiang,JiaXing 314001,China) Abstract Based on the backward feature of iterative search of American-style options pricing,and combining with the i- dea of least-squares Monte-Carlo pricing American-style options by Longstaff and Schwartz,we proposed a new method,in which the coefficient of the regression equation was estimated by the Markov Chain Monte-Carlo method to price American- style options by double simulation.The methodology is extensively tested on simulated data of pricing American-style stock put option with no dividend.Comparing the option value and relative error with the well-known least-squares Monte Carlo algo- rithm for pricing American-style options,the precision based on MCMC regression method is better than it.It can be concluded that MCMC regression method for pricing American-style options is much more feasible and effective by empirical simulation. This method has extensive applicability as well.The drawback of the method is potentially heavy computation demand,which is the same as the general Monte Carlo method. Key words American-style option:MCMC regression;variance reduction techniques;Monte Carlo simulation 重要且最具活力的方向之一·美式期权的显著特点 1引言 是合约在有效期内的任意时刻都可以执行该合约, 使得投资者可以更加方便地处理其投资组合,受到 对美式期权的合理定价一直是数量金融中最为 广大投资者的欢迎,因此它在金融衍生品市场中使 收稿日期:2013-04-05 基金项目:渐江省教育厅2012年度科研计划项目(Y201225300):浙江省自然科学基金(Y6100810):2010年嘉兴学院科研重点项目 (70110096) 作者简介:熊炳忠(1971一),男,江西玉山人,讲师,硕士 E-mail xiongbzh@mail.zjxu.edu.cn 万方数据
第30卷 2 O l 3 第2期 年6月 经 济 数 学 JOURNAL 0F QUANTITATIVE ECONOMICS Vol-30,No.2 Jun.2 O l 3 基于贝叶斯MCMC算法的美式期权定价+ 熊炳忠,马柏林 (嘉兴学院数理与信息工程学院,浙江嘉兴314000) 摘要鉴于美式期权的定价具有后向迭代搜索特征,本文结合Longstaff和Schwartz提出的美式期 权定价的最小二乘模拟方法,研究基于马尔科夫链蒙特卡洛算法对回归方程系数的估计,实现对美式期权 的双重模拟定价.通过对无红利美式看跌股票期权定价进行大量实证模拟,从期权价值定价误差等方面同 著名的最小二乘蒙特卡洛模拟方法进行对比分析,结果表明基于MCMC回归算法给出的美式期权定价具 有更高的精确度.模拟实证结果表明本文提出的对美式期权定价方法具有较好的可行性、有效性与广泛的 适用性.该方法的不足之处就是类似于一般的蒙特卡洛方法,会使得求解的计算量有所加大. 关键词 美式期权;MCMC回归;方差减少技术;蒙特卡洛模拟 中图分类号F830 文献标识码A Pricing American—Style options Based on Bayesian MarkoV Chain Monte Carlo Algorithm X10NG Bing—zhong,MA Bo—lin (J挖盯如“把。厂』垭2£^棚fics,P^j塔if5 n以d J行,0,7,硷fi伽Ekgi埘碧一ng,.,缸Xi玎g Uhit肥巧缸y。Zh已.,谊行g..,谊Xi以g 314001。(冼i,搬) Abstract Based on the backward feature of iterative search of American—style options pricing,and combining with the i— dea of least—squares Mont}Carlo pricing American—style options by Longstaff and Schwartz,we proposed a new method,in which the coefficient of the regression equation was estimated by the Markov Chain Mont}Carlo method to price Americanf style options by double simulation. The methodology is extensively tested on simulated data of pricing American—style stock put option with no dividend. Comparing the option value and reIative error with the well—known least—squares IⅥonte Carlo algo— rithm for pricing American—style options,the precision based on MCMC regression method is better than it.It can be concluded that MCMC regression method for p“cing Ame“can-styIe options is much more feasible and effective by empirical simulation. This method has extensive applicability as well_ The drawback of the method is potentially heavy computation demand,which is the same as the general Monte Carlo method. Key words American—style option;MCMC regression;variance reduction techniques;Monte Carlo simulation 引 言 对美式期权的合理定价一直是数量金融中最为 重要且最具活力的方向之一.美式期权的显著特点 是合约在有效期内的任意时刻都可以执行该合约, 使得投资者可以更加方便地处理其投资组合,受到 广大投资者的欢迎,因此它在金融衍生品市场中使 收稿日期:2013一04一05 基金项目:浙江省教育厅2012年度科研计划项目(Y201225300);浙江省自然科学基金(Y6100810);2010年嘉兴学院科研重点项且 (70110096) 作者简介:熊炳忠(1971一),男,江西玉山人,讲师,硕士 E—mail:xiongbzh@mail.zjxu.edu.cn 万方数据

-56 经济数学 第30卷 用也最为广泛.鉴于美式期权行权时间点的不确定 从几何布朗运动: 性,金融工程师一殷无法直接给出其解析定价公 ds(t)/S(t)=rdt++odw(t), (1) 式,业界只能通过数值求解方法为其定价.一般 其中,和。分别表示无风险利率和标的资产波动 地,期权定价的数值解法主要有二叉树模型)、三 率,w(t)是布朗运动,S(t)为标的价格过程,dS(t) 叉树模型、有限差分以及蒙特卡洛模拟等方法[).由 表示标的微分,dw(t)=e√dte表示标准正态分 于蒙特卡洛模拟方法简单、直观、易于操作,不需要 复杂的数学知识以及适合处理复杂的随机过程、复 布.用Ito引理计算得到 杂的终值计算等,使得该方法越来越广泛使用与解 dln S(t)=(r-0.5a2)dt +odw(t). (2) 决对复杂期权的定价问题.但由于传统的蒙特卡洛 记0表示初始时刻,t表示到期时刻,将[0,t] 方法难以处理期权提前执行的问题,一段时期以来, 进行N等分,△t=t-t1,i=1,…,N. 使其在美式期权定价上受到极大的限制.自Long 对式(1)离散化后得到: staff and Schwartz在文献[4]提出最小二乘蒙特卡 lnS(t)-lnS(t-1)=(r-0.5a2)△t+g√△ei, 洛方法(Least Squares Monte Carlo Approach, (3) LSM)以来,使用蒙特卡洛方法给美式期权定价越 由此可得标的资产在任意时刻t:的价格为: 来越引起人们的重视.LSM方法不仅能处理常用的 二叉树、三叉树和有限差分方法所能处理的复杂衍 S(t:)=S(t-1){exp(r-0.5a2)△t+g√△te:)}, (4) 生品定价问题,而且还能给出以上方法都无法解决 的依赖多种因素的美式期权的定价).但是,LSM 即 方法存在系统低估美式期权的价值问题;在实值路 S(t)=S(0){exp(r-0.5o)iat+gV△∑e, 径数量较少下给出的回归很不稳定以及如果存在少 数的奇异点时会对回归模型带来的比较大的影响, (5) 从而引起较大的定价误差.近年来,在ISM基础上 这样就可以给出标的一条样本路径{S(0),S(t), 国内外学者对美式期权的定价方法改进进行了大力 …,S(tw)},若模拟M条路径,便可以得到各条路 的研究与发展[6],加权最小二乘模拟]、偏最小二 径的价格矩阵 乘模拟]、广义矩方法、拟蒙特卡洛方法、粒子滤波 S(0)S(t)…S(tx) 方法山等相继用来给复杂的美式期权定价上:考 S(0)S2(t)…S2(tw) 虑基函数的各种不同选取1町、标的资产价格模型的各 种不同1)设定;波动率模型的各种不同选取、引入带跳 S(0)SM(t1)..SM(tN)KN+D 因子、考虑收益率模型的厚尾分布;将统计中的稳健估 从而得到美式看张和美式看跌期权的收益分别为: 计方法、贝叶斯后验分布估计方法、样条估计方法以及 max(S-K,0),max(K一Se,0),这里的Sm表 融入各种方差减少技术4.5]等现代有效、高级统计方 示在心时刻执行期权时标的资产价格,K表示期权 法等.本文提出将现代统计模拟计算的实用而强大的 的执行价格. 基于马尔科夫链蒙特卡洛方法1]融合到美式期权定 2.2LSM方法美式期权定价原理 价的最优停时决策1,)的条件期望计算中来,使得在 设定美式期权在[0,]内有效,在0<1<… 每次求解回归方程系数时尽可能利用已有的先验、市 <tw=t时刻可以执行期权.同样设置相等时间间 场中已有的美式期权的价格、市场中对应的标的资产 隔△t=t一t1,t:时刻标的价格S(t:),另记y:表 实时价格数据等各个方面的有效信息,利用现代计算 机的快速、高性能的随机取样和强大的计算能力,同时 示在t时刻美式看跌期权的收益.则在[0,t]时间 进行后验参数分布的马尔科夫链1)和标的资产价格路 内一直持有该美式期权所得到的收益为: 径有效的双重模拟,实现对美式期权既更加稳健又更 yN max (K-S(ty),0) 加合理的模拟定价 在tw-1时刻有: 「K一S(tw-1),在tw1时刻执行期权; yN-1= 2LSM美式期权定价 e yN, 在tv1时刻继续持有期权. (6) 2.1标的资产价格过程 类似地,对任意时刻t:,美式看跌期权持有者的 在风险中性条件下,假定标的资产价格过程服 收益: 万方数据
一56一 经济数学 第30卷 用也最为广泛.鉴于美式期权行权时间点的不确定 性,金融工程师一般无法直接给出其解析定价公 式L1 J,业界只能通过数值求解方法为其定价.一般 地,期权定价的数值解法主要有二叉树模型比]、三 叉树模型、有限差分以及蒙特卡洛模拟等方法[3].由 于蒙特卡洛模拟方法简单、直观、易于操作,不需要 复杂的数学知识以及适合处理复杂的随机过程、复 杂的终值计算等,使得该方法越来越广泛使用与解 决对复杂期权的定价问题.但由于传统的蒙特卡洛 方法难以处理期权提前执行的问题,一段时期以来, 使其在美式期权定价上受到极大的限制.自Long— staff and schwartz在文献[4]提出最小二乘蒙特卡 洛方法(Least Squares Monte Carlo Approach, LSM)以来,使用蒙特卡洛方法给美式期权定价越 来越引起人们的重视.LSM方法不仅能处理常用的 二叉树、三叉树和有限差分方法所能处理的复杂衍 生品定价问题,而且还能给出以上方法都无法解决 的依赖多种因素的美式期权的定价[5].但是,LSM 方法存在系统低估美式期权的价值问题;在实值路 径数量较少下给出的回归很不稳定以及如果存在少 数的奇异点时会对回归模型带来的比较大的影响, 从而引起较大的定价误差.近年来,在LSM基础上 国内外学者对美式期权的定价方法改进进行了大力 的研究与发展[6’7],加权最小二乘模拟[8]、偏最小二 乘模拟[9]、广义矩方法、拟蒙特卡洛方法、粒子滤波 方法口0’11 3等相继用来给复杂的美式期权定价上;考 虑基函数的各种不同选取[12。、标的资产价格模型的各 种不同[13]设定;波动率模型的各种不同选取、引入带跳 因子、考虑收益率模型的厚尾分布;将统计中的稳健估 计方法、贝叶斯后验分布估计方法、样条估计方法以及 融人各种方差减少技术n4 J印等现代有效、高级统计方 法等.本文提出将现代统计模拟计算的实用而强大的 基于马尔科夫链蒙特卡洛方法[161融合到美式期权定 价的最优停时决策[17’181的条件期望计算中来,使得在 每次求解回归方程系数时尽可能利用已有的先验、市 场中已有的美式期权的价格、市场中对应的标的资产 实时价格数据等各个方面的有效信息,利用现代计算 机的快速、高性能的随机取样和强大的计算能力,同时 进行后验参数分布的马尔科夫链[1朝和标的资产价格路 径有效的双重模拟,实现对美式期权既更加稳健又更 加合理的模拟定价. 2 LSM美式期权定价 2.1标的资产价格过程 在风险中性条件下,假定标的资产价格过程服 从几何布朗运动: dS(})/S(})一rd£+仃d∞(£), (1) 其中r和盯分别表示无风险利率和标的资产波动 率,叫(£)是布朗运动,S(f)为标的价格过程,dS(£) 表示标的微分,d叫(f)一∈~/df £表示标准正态分 布.用It6引理计算得到 dln S(£)=(r一0.5盯2)d£+口d∞(f). (2) 记。表示初始时刻,f表示到期时刻,将[o,£] 进行N等分,出一£。一fH,i一1,…,N. 对式(1)离散化后得到: In S(£:)一ln s(£i_I)一(,.一o.5盯2)△£+盯√△楚:, (3) 由此可得标的资产在任意时刻f。的价格为: S(£,)一S(£i_1){exp(,.一o.5d2)△£+仃~/△廷。)}, (4) 即 J s(£。)一s(o){exp(r—o.5盯2)i&+仃伍∑eJ)' J=l (5) 这样就可以给出标的一条样本路径{S(O),S(f。), …,S(£N)),若模拟M条路径,便可以得到各条路 径的价格矩阵 S(O) S1(f1) S(O) S2(£.) S(0) SM(≠.) S1(£N) S2(£N) ● : SM(£N) 从而得到美式看张和美式看跌期权的收益分别为: max(S。一K,0),max(K—S。,0),这里的S。表 示在劬时刻执行期权时标的资产价格,K表示期权 的执行价格. 2.2 LSM方法美式期权定价原理 设定美式期权在[o,£]内有效,在o<£。<… <£~一£时刻可以执行期权.同样设置相等时间间 隔出一£。一£,。,£。时刻标的价格S(£:),另记y。表 示在£。时刻美式看跌期权的收益.则在[o,f]时间 内一直持有该美式期权所得到的收益为: 了N—max(K—S(£N),O), 在fN一。时刻有: f K—S(£N一,), 在£N。时刻执行期权; ’肛1—1e哪ryN, 在£N一。时刻继续持有期权. (6) 类似地,对任意时刻£,,美式看跌期权持有者的 收益: 万方数据

第2期 熊炳忠等:基于贝叶斯MCMC算法的美式期权定价 57 K-S(t), 在t,时刻执行期权; 第三步:对选出的实值路径折现现金流到前一 y:= le-roy-1, 在t,时刻继续持有期权 个执行点: (7) 第四步:用第三步算得的实值路径折现现金流 按照上述迭代过程直至1时刻,求出回报y,,如此 关于前一时刻标的资产价格用普通最小二乘做回 运行M条路径,可得到{y,…,y},这样美式看 归,求出回归方程 跌期权的风险中性定价为: 第五步:用步骤四的方程计算继续持有期权的 PA(0,S(0)=[eay1|S=S(0] 价值: 分e1. 第六步:比较当前时刻继续持有价值与期权内 M台 (8) 在价值的大小确定最优停时策略; 现在就是要在每一时刻t:决定是执行还是继续持有 第七步:按当前时刻调整基于第六步的计算结 期权,也就是要比较K一S(t:)与ey+1的大小关 果得到当前时刻的现金流: 系,但由于在t,时刻无法知道t41时刻的y1,现在 第八步:重复步骤三至七,直至算到初始时刻; 改用比较基于S(t,)下的条件期望的折现f,(S(t,) 第九步:求出第八步各条路径结果的平均值. 与K一S()的大小来决定是执行期权还是继续持 2.3.2LSM方法美式期权算法实例 有期权.即 例1设标的资产初始价格为10,无风险利率 IK-S(t,),若K-S(t)≥f(S(t), 0.03,波动率0.4,给一个到期期限为1年的美式看 y:= {ey+1, 其他, 跌期权定价.为说明原理方便,假定在t=1/3,2/3, (9) 1时刻决定是否执行该合约.第一步,按照(5)式模 此处f,(S(t)=E[eay1|S=S(t)门,LSM的 拟产生在t=1/3,2/3,1时刻8条路径的资产价格、 核心就是用最小二乘方法来估计f,(S(:)函数, 分别计算出在1时刻的收益y,数据为表1所示, 基于f,(S(t,)= ∑ap(S(u,)和较大数量的路 表1模拟标的各路径价格 路径 1/3 2/3 y3=max( 径数估计出a,其中p(x)表示基函数.常用的基 K-S(1),0) 函数选取有Hermite,Laguerre,Legendre和Jacobi 8.41 9.93 6.82 5.18 多项式.对于在不同基函数下对美式期权定价影响 2 11.99 13.98 13.38 0 的数值检验可查看文献[12],文献[12]中的结果表 3 13.23 17.51 12.87 0 明,基于最小二乘估计方法下美式看跌期权对基函 6.81 7.82 10.67 1.33 数的各种选取相当的稳健,文献中常常采用最简单 5 7.14 9.22 7.55 4.45 的二次多项式函数,即 11.22 8.38 9.38 2.62 f(S(t)=a+aS(t:)+aS(t,)i=1,…,N. 7 8.92 8.97 9.35 2.65 (10) 11.54 10.99 8.73 3.27 本文在进行蒙特卡洛美式看跌期权定价使用 Laguerre多项式,其定义为: 第二步,计算出yexp(一r△)的值,并且在实 l (x)exp ((exp ()(1-), 值路径上估计出其关于S(2/3),S2(2/3)的回归方 (11) 程为: 4(x)=exp(受)1-2r+x2/2), (12) Lexp(-m)/S号] )-ewp学)号re. (13) =-81.28+16.99s(号)-0.98S(号), 3 2.3LSM方法美式期权算法 定义其为f2(S), 2.3.1LSM方法美式期权算法步骤 第三步,依据 根据上文的LSM方法原理,描述成算法步骤 如下: K-S号,K-s号≥5号》, 第一步:随机模拟标的资产多条价格路径,算出 y2= 各条路径期权到期时间点上的现金流; e即←r,K-5号)<fS号. 3 第二步:根据第一步的现金流,选出实值路径; 给出在2/3时刻的收益,具体数据如表2所示 万方数据
第2期 熊炳忠等:基于贝叶斯MCMc算法的美式期权定价 f K—S(£,), 在£,时刻执行期权; 以 l e1甜y。, 在f,时刻继续持有期权. (7) 按照上述迭代过程直至£。时刻,求出回报y。.如此 运行M条路径,可得到{y;,…,yr}.这样美式看 跌期权的风险中性定价为: PA(o,S(o)一E[e心y。l S—S(o)] , M 圭击∑豇e一州]. (8) 一M刍“卜 川小 ~7 现在就是要在每一时刻f。决定是执行还是继续持有 期权,也就是要比较K—S(£,)与e一。歹川的大小关 系,但由于在£:时刻无法知道£H时刻的y…,现在 改用比较基于S(£。)下的条件期望的折现^(S(£。)) 与K—S(£,)的大小来决定是执行期权还是继续持 有期权.即 f K—S(£。), 若K—S(£。)≥厂。(S(£:)), 。‘ I e出2了斗1, 其他, (9) 此处厂,(s(£。))一定[e出‘y.+。I S—s(£。)],LSM的 核心就是用最小二乘方法来估计^(S(£,))函数, 基于^(s(f。))一∑at鼽(s(f,))和较大数量的路 径数估计出口。,其中织(z)表示基函数.常用的基 函数选取有Hermite,Laguerre,Legendre和Jacobi 多项式.对于在不同基函数下对美式期权定价影响 的数值检验可查看文献[12],文献[12]中的结果表 明,基于最小二乘估计方法下美式看跌期权对基函 数的各种选取相当的稳健,文献中常常采用最简单 的二次多项式函数,即 ^(S(£:))一a0+a1S(£。)+a2 S2(£:)i一1,…,N. (10) 本文在进行蒙特卡洛美式看跌期权定价使用 Laguerre多项式,其定义为: zo(z)一exp(寺)z1(z)一exp(鲁)(1一z), (11) z2(z)=exp(妻)(1—2z+z2/2), (12) “z)=eXp(专)着为(扼飞 (13) 2.3 LSM方法美式期权算法 2.3.1 LSM方法美式期权算法步骤 根据上文的LSM方法原理,描述成算法步骤 如下: 第一步:随机模拟标的资产多条价格路径,算出 各条路径期权到期时间点上的现金流; 第二步:根据第一步的现金流,选出实值路径; 第三步:对选出的实值路径折现现金流到前一 个执行点; 第四步:用第三步算得的实值路径折现现金流 关于前一时刻标的资产价格用普通最小二乘做回 归,求出回归方程. 第五步:用步骤四的方程计算继续持有期权的 价值; 第六步:比较当前时刻继续持有价值与期权内 在价值的大小确定最优停时策略; 第七步:按当前时刻调整基于第六步的计算结 果得到当前时刻的现金流; 第八步:重复步骤三至七,直至算到初始时刻; 第九步:求出第八步各条路径结果的平均值. 2.3.2 LSM方法美式期权算法实例 例1设标的资产初始价格为10,无风险利率 o.03,波动率o.4,给一个到期期限为1年的美式看 跌期权定价.为说明原理方便,假定在£一1/3,2/3, 1时刻决定是否执行该合约.第一步,按照(5)式模 拟产生在£一1/3,2/3,1时刻8条路径的资产价格、 分别计算出在1时刻的收益了。,数据为表1所示. 表l模拟标的各路径价格 路径 1/3 2/3 1 芝嚣‰ 9.93 13.98 1 7.5l 7.82 9.22 8.38 8.97 10.99 第二步,计算出y。exp(一r△£)的值,并且在实 值路径上估计出其关于S(2/3),S2(2/3)的回归方 程为: E[了3exp(一订)/s(妻)] =一81.28+16.99s(号)一o.98s2(号), 定义其为,。(S). 第三步,依据 f K—sc号,,K~sc号,≥^(sc号,,, 弛一1。xp c一,△。,y。,K—sc号,<^csc号,,. 给出在2/3时刻的收益,具体数据如表2所示. 万方数据

-58 经济数学 第30卷 表2在2/3时刻的最优决策 02,…,0。的任意初始值,则Gibbs抽样如下: 路径 K-S(2/3) f2(S(2/3) yaexp (-n) 改 第一步:从f1(G/,,…,,D,M)中抽取一 1 2.07 4.64 5.17 5.17 个随机样本,记抽取出的随机数为; 2 0 0 第二步:从f2(02/,,…,,D,M)中抽取一 0 一 0 0 个随机样本,记抽取出的随机数为; 4,18 1.05 1.35 4.18 2.78 4.23 4.51 4.51 第n步:从fn(0./,,…,01,D,M)中抽取 6 3.62 2.76 2.68 3.62 个随机样本,记抽取出的随机数为; 7 3.03 3.71 2.89 2.89 每完成一次Gibbs抽样,后验参数从(,, 1.01 3.51 3.28 3.28 …,)变为(,,…,),再以这组参数为初 值如此继续迭代N次,得到一系列的随机抽取: 第四步,类似第二步计算出y2exp(-r△t)的 (,,…,),…,(,,…,0),在正则条件下, 值,并且在实值路径上估计出其关于S(号,S(分) 当N充分大,(,%,…,)渐近等价于来自这n 个参数的联合分布f(8,02,,0.,D,M)的随机抽 的回归方程为: 取,丢掉前m个预烧随机样本,建立一个Gibbs样 E[y2exp(-t)/S(1/3)] 本(+1,1,…,1),…,(,路,…,0),把这些 =-896+3.55S(号)-0.23S(宁, 样本看作是从参数的联合分布f(8,2,…,0n,D, 定义其为f(S) M)中随机抽取的,然后利用这些预烧后的随机样 第五步,依据 本进行各种统计推断,如进行参数的估计、极值问题 的求解等 K-s号.K-s号≥fs号: 3.2线性回归模型参数的贝叶斯分析 y1= 设一般的线性回归模型为: exp (-rAt)y2, K-s0号)<fs号》. Y=a+月X:+…+B1X-1+e, (14) 给出在1/3时刻的期权收益,具体如表3所示. 其中Y表示因变量,X表示解释变量,B,是回归系 表3在1/3时刻的最优决策 数,e是扰动项.假设有n次观察的数据, 路径 K-S(1/3) f1(S(1/3) 2e即(-H) y=a十3t1:十… (15) 3.59 4.54 5.12 5.12 +B。1x(g1:十e(i=1,…,n). 2 0.01 1.47 0 0 3 0 0 0 记Y=[y1y2,…yn]B=[a,,…,f。1] 4 5.19 4.15 4.13 5.19 e=[e1,e2,…,en] 5 4.86 4.27 4.41 4.86 1 x1.1… Ip-1.1 6 0.78 2.56 3.58 3.58 1 X= x1.2…xp12 7 3.08 4.38 2.84 2.84 (16) 0.46 2.16 3.22 3.22 1 工1, Ig-l.n 则上式可表示为:Y=X8+e,e~N(0,d2In)其中I. 3 回归模型的MCMC分析 是n阶单位矩阵.设定B的先验分布 x(B)~N(A,∑,, 马尔科夫链蒙特卡洛(下文简称为MCMC)方 (17) 法的基本思想就是建立一个平稳分布的马尔科夫链 π(d2)=lnv-x2(w,c6), 的来得到所需抽样分布的样本,基于这些样本做出 其中风,∑g,c都是超参数.依照贝叶斯法则可 各种统计推断,执行该方法的常用的有两种算法, 以得到两个参数B,2的后验分布为: Gibbs抽样算法和Metropolis-Hastings算法. pB|Y,X,c)~N(g,∑i)B 3.1 Gibbs抽样算法 设n个需要估计的参数依次为01,2,…,0,,D =∑i(∑,A+XX8)∑g 为可用的数据集,M表示接受的模型.在给定其他 =(∑,+o2XX), (18) 参数和已知的数据集下,推出某个参数的后验条件 p(a2|B,Y,X)~nv-x2(o¥,c2·), (19) 分布,再在这个分布下抽取随机数.设,…,是 其中 万方数据
一58一 经济数学 第30卷 表2在2/3时刻的最优决策 路径 K—S(2/3) ^(S(2/3)) ∞eXp(一,f) y2 第四步,类似第二步计算出了。exp(一r出)的 值,并且在实值路径上估计出其关于s({),sz(妻) o .) 的回归方程为: E[y2exp(一疗)/S(1/3)] 1 1 一一8.96+3.55s(÷)一o.23s2(÷), o O 定义其为厂,(S). 第五步,依据 K—s(÷),K—s(÷)≥厂。(s(÷)); 0 0 J exp(一r△f)y。,K—s(÷)<^(s(÷)). 给出在1/3时刻的期权收益,具体如表3所示. 表3在l/3时刻的最优决策 路径 K—s(1/3) ,1(s(1/3)) y2exp(一疗) j,l 3 回归模型的MCMC分析 马尔科夫链蒙特卡洛(下文简称为MCMC)方 法的基本思想就是建立一个平稳分布的马尔科夫链 的来得到所需抽样分布的样本,基于这些样本做出 各种统计推断,执行该方法的常用的有两种算法, Gibbs抽样算法和Metropolis—Hastings算法. 3.1 Gibbs抽样算法 设咒个需要估计的参数依次为口-,晚,…,六,D 为可用的数据集,M表示接受的模型.在给定其他 参数和已知的数据集下,推出某个参数的后验条件 分布,再在这个分布下抽取随机数.设镀,…,镀是 口。,…,臼。的任意初始值,则Gibbs抽样如下: 第一步:从,。(乱/鹊,鹄,…,锑,D,M)中抽取一 个随机样本,记抽取出的随机数为口i; 第二步:从^(臼:/臼},鳄,…,锑,D,M)中抽取一 个随机样本,记抽取出的随机数为出; 第起步:从^(曰。/曰;,眺,…,畦。,D,M)中抽取 一个随机样本,记抽取出的随机数为饿; 每完成一次Gibbs抽样,后验参数从(贷,畿, …,成)变为(卵1,移1,…,甜1),再以这组参数为初 值如此继续迭代N次,得到一系列的随机抽取: (钭,钙,…,以),…,(卯,鲋,…,鳄),在正则条件下, 当N充分大,(甜,掣,…,甜)渐近等价于来自这押 个参数的联合分布厂(执,臼:,…,六,D,M)的随机抽 取,丢掉前m个预烧随机样本,建立一个Gibbs样 本(旷1,矿1,…,铲1),…,(蚪,鲋,…,甜),把这些 样本看作是从参数的联合分布厂(矾,曰:,…,曰。,D, M)中随机抽取的,然后利用这些预烧后的随机样 本进行各种统计推断,如进行参数的估计、极值问题 的求解等. 3.2线性回归模型参数的贝叶斯分析 设一般的线性回归模型为: y一口+肺X1+…+胁。X旷。+e, (14) 其中y表示因变量,X表示解释变量,&是回归系 数,e是扰动项.假设有理次观察的数据, y,一口+佛zl:+… +肛lz(旷Ⅲ+£,(i一1,…,行). (15) 记y一[y。了z,…y。] 卢一[a,卢。,…,J8_旷。]。 £一[£l,£2,…,£。]’ X一 (16) 则上式司表不为:y一郧+£,£~N(O,盯2j。)其中J。 是咒阶单位矩阵.设定口的先验分布 丌(p~N(胁,∑ph (17) 丌(仃2)=而u—z2(勘。,f5), 其中岛,∑。,铆。,cj都是超参数.依照贝叶斯法则可 以得到两个参数卢,叮2的后验分布为: 户(p Y,x,口2)~N(卢’,∑:)卢’ 一∑;(∑;1|;8。+厂2x’冲)∑; 一(∑:1+厂2x7x)~, (18) 夕(盯2 I卢,y,X)~如口一Z2(可*,f2‘), (19) 其中 1 2 ∞丑;A n 1●J 1...1 他,,”U嬲跗匏 5 4 4 3 2 码∞,均踮飓吣蛎 3 3 0 5 4 O 3 0 万方数据

第2期 熊炳忠等:基于贝叶斯MCMC算法的美式期权定价 -59- v'=n+w,c2·=[oc+(Y-X3)'(Y- 卡洛积分.这种积分是基于大量的随机抽样,利用这 X3)]/w 些随机样本进行各种概率分析,作出估计、预测等. 根据Gibbs算法从式(13)和(14)中依次采样得到3 设g(x)是一个可积函数,记 和。2的随机样本,估计各个参数后验值. -E()]d (20) 4美式期权MCMC线性回归算法 根据大数定律可以将 (21) 根据上文介绍的LSM的算法原理和MCMC 9=1/M∑g(X,) i-I 算法中Gibbs抽样原理,将MCMC算法中的Gibbs 作为0的一个估计. 抽样嵌套在LSM方法中,对回归方程系数的进行 如果a1,a2是参数6的两个估计量,且ar(01) 估计,其计算的原理不在是普通最小二乘估计,而是 <var(02),则使用0,比使用02方差的减少百分比 基于对各个参数的无信息先验分布,对模拟标的资 为: 产价格数据的后验分布的随机取样来对回归方程系 一般增加样本量可以减少方差,但是会极大提 数进行统计推断.它能够比较好地克服经典最小二 高计算成本.如果要使得标准差至多为e,var 乘方法的对数据量小和数据有奇异点时对回归模型 (g(X)=a2则样本量至少为a2/e2,即标准差缩小 的估计的诸多不足之处.MCMC回归算法步骤如 为1%,样本量就要提高10000倍.常用的方差减少 下: 技术有,对偶变量法、控制变量法、分层抽样法以及 第一步:随机模拟标的资产多条价格路径,从最 重要抽样方法等. 后一个时间点开始倒推计算出各条路径期权到期时 5.2对偶变量方法的基本原理 间点上的现金流; 在进行最小二乘法美式期权定价、MCMC回归 第二步:根据第一步的现金流,选出实值路径; 的美式期权定价以及标准欧式期权定价时,为提高 第三步:把选出的实值路径的现金流折现到前 模拟的精度、尽可能地减少模拟样本量,我们采用最 一个执行时间点上; 为常用的对偶变量技术来实现对标的资产的路径模 第四步:按回归方程系数无信息先验分布规则, 拟.考虑两个随机变量X,Y,因为 设置好回归方程中各参数的初始值 var[(X+Y)/2]=0.25[var(X) 第五步:用第三步算得的实值路径折现现金流 +var (Y)+2cov (X,Y), (22) 关于前一时刻标的资产价格的函数采用MCMC随 当X,Y负相关时,(X+Y)/2的方差就要比他们相 机采样的算法,求出每一步的回归方程; 互独立时要小,这就是考虑使用负相关的随机表里 第六步:用步骤五求得的方程求出继续持有该 来减少方差的原理.一般地,如果X1,X2,…,X。是 期权合约的价值: 由变换产生的,即对任意X:(i=1,…,n),有,X: 第七步:比较当前时刻继续持有期权的价值与 =Fx(U,),其中U服从标准均匀分布,则1一U, 期权本身的内在价值的大小确定最优停时策略,即 也服从标准均匀分布,且U:与1一U:互为负相关. 是否继续持有该期权, 记 第八步:按当前时刻调整基于第七步的计算结 Y;=g(X)=g(Fx(U),....Fx(Ui)) 果得到当前时刻的现金流; (23) 第九步:重复步骤三至八,直至算到初始时刻: Y,=g(X)=g(Fx(1-U),…, 第十步:求出第九步中各条路径结果的平均值. Fx(1-U)) (24) 则Y,与Y,具有相同的分布,当它们负相关时就可 5蒙特卡洛模拟方差减少的对偶变量技术 以同时使用这两个样本来减少抽样的方差.下面给 出它们互为负相关的条件. 5.1蒙特卡洛积分的基本原理 定义1对任意的j=1,…,n,如果有x,≤ 期权的模拟定价技术最根本的就是要进行蒙特 y,则称(x1,…,xn)≤(y,…,yn);如果对一个n 万方数据
第2期 熊炳忠等:基于贝叶斯MCMC算法的美式期权定价 一59一 u+一72+u,f2。一[uoci+(y一邵)(y一 邪)],7u’ 根据Gibbs算法从式(13)和(14)中依次采样得到口 和仃2的随机样本,估计各个参数后验值. 4美式期权MCMC线性回归算法 根据上文介绍的LsM的算法原理和MCMc 算法中Gibbs抽样原理,将MCMC算法中的Gibbs 抽样嵌套在LSM方法中,对回归方程系数的进行 估计,其计算的原理不在是普通最小二乘估计,而是 基于对各个参数的无信息先验分布,对模拟标的资 产价格数据的后验分布的随机取样来对回归方程系 数进行统计推断.它能够比较好地克服经典最小二 乘方法的对数据量小和数据有奇异点时对回归模型 的估计的诸多不足之处.MCMC回归算法步骤如 下: 第一步:随机模拟标的资产多条价格路径,从最 后一个时间点开始倒推计算出各条路径期权到期时 间点上的现金流; 第二步:根据第一步的现金流,选出实值路径; 第三步:把选出的实值路径的现金流折现到前 一个执行时间点上; 第四步:按回归方程系数无信息先验分布规则, 设置好回归方程中各参数的初始值. 第五步:用第三步算得的实值路径折现现金流 关于前一时刻标的资产价格的函数采用MCMC随 机采样的算法,求出每一步的回归方程; 第六步:用步骤五求得的方程求出继续持有该 期权合约的价值; 第七步:比较当前时刻继续持有期权的价值与 期权本身的内在价值的大小确定最优停时策略,即 是否继续持有该期权. 第八步:按当前时刻调整基于第七步的计算结 果得到当前时刻的现金流; 第九步:重复步骤三至八,直至算到初始时刻; 第十步:求出第九步中各条路径结果的平均值. 5 蒙特卡洛模拟方差减少的对偶变量技术 5.1 蒙特卡洛积分的基本原理 期权的模拟定价技术最根本的就是要进行蒙特 卡洛积分.这种积分是基于大量的随机抽样,利用这 些随机样本进行各种概率分析,作出估计、预测等. 设g(z)是一个可积函数,记 r+∞ 口一E[g(x)]一l g(z)厂(z)dz. (20) J一∞ 根据大数定律可以将 M 舀一1/M∑g(x:) (21) j 作为臼的一个估计. 如果a。,舀。是参数目的两个估计量,且啦r(a,) <var(扫。),则使用a。比使用舀:方差的减少百分比 为: 一般增加样本量可以减少方差,但是会极大提 高计算成本.如果要使得标准差至多为P,var (g(X))一盯2则样本量至少为口2/P2,即标准差缩小 为1%,样本量就要提高10000倍.常用的方差减少 技术有,对偶变量法、控制变量法、分层抽样法以及 重要抽样方法等. 5.2对偶变量方法的基本原理 在进行最小二乘法美式期权定价、MCMC回归 的美式期权定价以及标准欧式期权定价时,为提高 模拟的精度、尽可能地减少模拟样本量,我们采用最 为常用的对偶变量技术来实现对标的资产的路径模 拟.考虑两个随机变量X,y,因为 var[(x+y)/2]一o.25[var(x) +var(y)+2cov(X,y)], (22) 当X,y负相关时,(X+y)/2的方差就要比他们相 互独立时要小.这就是考虑使用负相关的随机表里 来减少方差的原理.一般地,如果X。,X:,…,X。是 由变换产生的,即对任意X。(i一1,…,行),有,X。 一氐1(U。),其中Ui服从标准均匀分布,则1一U, 也服从标准均匀分布,且U。与1一U互为负相关. 记 E—g(X‘,’)一g(氏1(阴),…,瓦1(U:)) (23) E—g(x‘’’)一g(瓦1(1一∽),…, 氐1(1一U:)) (24) 则E与y,具有相同的分布,当它们负相关时就可 以同时使用这两个样本来减少抽样的方差.下面给 出它们互为负相关的条件. 定义1 对任意的歹一1,…,行,如果有t≤ y,,则称(z1,.一,z。)≤(了。,…,y。);如果对一个行 万方数据

—60 经济数学 第30卷 元函数g=g(x1,…,x)每一个变量都是增函数, 故Y与Y互为负相关, 则称g=g(x1,…,xn)是增函数.类似地,如果对每 5.3对偶变量技术的应用 个变量g是减函数,则g是递减的函数;若果g是增 若要产生m个随机样本,则先产生m/2个样 函数或者是减函数,则称g是单调函数 本,记 定理1设X=(X,…,X)各个分量相互独 Yj g(Fx(U),.,Fx(U)), (38) 立,∫和g函数为同方向单调函数(即同增或者同 Y,=g(Fx(1-U月),…,Fx(1-U).(39) 减),则 计算另外m/2个样本,其中U表示标准均匀分布, E[f(X)g(X)]E[f(X)E[g(X)].(25) 从而由对偶变量方法所得到的估计量为 证明不妨设f,g同时为增函数,现在对n作 0=(Y1+Y{+…+Ym2+Ym2)/m 数学归纳法证明.假设n=1,则对所有的 两/2 x,y∈R,(f(x)-f(y)(g(x)-g(y)≥0. ,+y)m, (40) (26) 相比于一般蒙特卡洛估计,使用对偶变量方法会使 因此 得模拟的方差极大减少, E[(f(X)-f(Y))(g(X)-g(Y))]≥0, (27) 6模拟实证 即有 E[f(X)g(X)]+E[(f(Y))(g(Y)] 下面考虑标的资产只有一种标的资产进行模拟 >E[f(X)g(Y)]+E[f(Y)g(X)]. (28) 实证,分别采用著名的LSM方法和本文提出的 又因为X,Y独立同分布,上式左边等于 MCMCLRM方法来计算美式看跌期权价格.期权 2E[f(X)g(X)]2E[f(X)E(g(X)],(29) 定价的基本假设为:「)标的资产价格遵循几何布朗 对n=1时成立;现在假设对n一1时成立,因为 运动;ⅱ)无市场摩擦,即不考虑交易费、税收等;而) E[f(X)g(X)/X.=x] 市场无套利机会;V)不需支付红利;V)无风险利率 ≥ELfX…,X1xn)]E[g(X,…,X1x)] 为常数.设置模拟数据的各项指标为:标的资产价格 =E[f(X/X,=zn]E[g(X/X=x].(30) 路径数量为10000条,期权有效期按分别为1年和 上式对每个X,为增函数,由n一1时成立可以得到: 两年,时间间隔为1/252年,相当于在一年所有交易 E[f(X)g(X)]=E(E[f(X)g(X)/X.]) 日内都可以交易一次.市场无风险利率为0,03,标 =E[f(X)E[g(X)]E(E[f(X/X. 的资产初始价格为10元,标的资产交割价格为12 =xn)]}E{E[g(X/X.=xn)]}. (31) 元,其波动率分别取0.4和0.5.在进行MCM- 推论1设g=g(x,…,xn)是单调函数,令 CLRM方法时,参数后验分布的MCMC抽样总次 Y=g(X)=g(Fx(U),…,Fx'(U.),(32) 数为50000次抽样,预烧(burn-in)样本量为 Y=g(Fx(1-U1),…,Fx(1-Un),(33) 30000.由于股票价格是模拟的,为避免因股票价格 则Y与Y互为负相关 模拟的可能不稳定性对美式期权定价所造成的不利 证明不妨设g函数是单调递增的函数,则 影响,在运行LSM和MCMCLRM中分别同时插入 Y=g(X)=g(Fx'(U),....,Fx'(U.))(34) 在模拟价格下的对应的标准欧式看跌期权价格数 与-Y=-g(Fx(1-U1),…,Fx'(1-Um)△f 据.具体运行结果列于表4~表7. 都是递增函数.因此下式成立. 表4 MCMCLRM与LSM方法美式看跌期权定价对比 E[f(U)g(U)]>E[f(U)]E[g(U)]. (35) MCMCLRM EUI LSM EU2 又因为: 期权价格 2.72795 2.658098 2.741095 2.656499 E[YY]≤E[Y]E[Y], (36) 标准差 0.01395 0.116029 0.0139541 0.1145386 所以 相对误差 0.02628 0.03845 cov (Y,Y)=E(YY)-E(Y)E(Y)<0. 本表使用数据:S0=10,K=12,r=0.03,0=0.4,T=1. (37) 万方数据
一60一 经济数学 第30卷 元函数g—g(z。,…,z。)每一个变量都是增函数, 则称g—g(zl,.“,z。)是增函数.类似地,如果对每 个变量g是减函数,则g是递减的函数;若果g是增 函数或者是减函数,则称g是单调函数. 定理1 设X=(X。,…,x。)各个分量相互独 立,.厂和g函数为同方向单调函数(即同增或者同 减),则 E[,(X)g(X)]≥E[,(X)]E[g(X)]. (25) 证明不妨设厂,g同时为增函数,现在对以作 数学归纳法证明.假设理一1,则对所有的 z,y∈R,(,(z)一厂(y))(g(z)一g(y))≥O. (26) 因此 E[(,(X)一,(y))(g(X)一g(y))]≥o, (27) 即有 E[厂(X)g(X)]+E[(厂(y))(g(y)] ≥E[,(X)g(y)]+E[厂(y)g(X)]. (28) 又因为X,y独立同分布,上式左边等于 2E[,(x)g(x)]≥2E[厂(x)E(g(x)], (29) 对,z一1时成立;现在假设对咒一1时成立,因为 E[厂(X)g(X)/X。一z。] ≥E[厂(X1,…,k。,毛)]E[g(x1,…,k。,z。)] 一E[厂(x/X。=z。]E[g(x/X。一z。].(30) 上式对每个X。为增函数,由行一1时成立可以得到: E【f(x)g(x)]一EIE【f(x)g(X)/X,]1 =E[厂(X)]E[g(X)]≥E{E[,(X/X。 一z。)])E{E[g(x/x。一z。)]). (31) 推论1 设g—g(z,,…,z。)是单调函数,令 y—g(X)一g(Fil(U1),…,氏1(U。)),(32) y—g(氐1(1~U1),…,Fil(1一U。)), (33) 则y与y互为负相关. 证明不妨设g函数是单调递增的函数,则 y—g(X)=g(Fjl(己,1),…,Fil(U。)) (34) 与一y一一g(氐1(1一U。),…,瓦1(1一U。))全厂 都是递增函数.因此下式成立. E[厂(U)g(U)]≥E[厂(U)]E[g(u)]. (35) 又因为: E[yy]≤E[y]E[y], (36) 所以 cov(y,y)一E(∥)一E(y)E(/)≤o. (37) 故y与y互为负相关. 5.3对偶变量技术的应用 若要产生优个随机样本,则先产生m/2个样 本,记 y,=g(氐1(U{),…,氏1(U:)), (38) E—g(瓦1(1一u{),…,氐1(1一u:)).(39) 计算另外m/2个样本,其中U表示标准均匀分布, 从而由对偶变量方法所得到的估计量为 臼一(y。+yi+…+y。:+y:,。)/研 m/2 一∑(y,+巧)/m, (40) J=1 相比于一般蒙特卡洛估计,使用对偶变量方法会使 得模拟的方差极大减少. 6 模拟实证 下面考虑标的资产只有一种标的资产进行模拟 实证,分别采用著名的LSM方法和本文提出的 MCMCLRM方法来计算美式看跌期权价格.期权 定价的基本假设为:i)标的资产价格遵循几何布朗 运动;ii)无市场摩擦,即不考虑交易费、税收等;iii) 市场无套利机会;jv)不需支付红利;v)无风险利率 为常数.设置模拟数据的各项指标为:标的资产价格 路径数量为10 000条,期权有效期按分别为1年和 两年,时间间隔为1/252年,相当于在一年所有交易 日内都可以交易一次.市场无风险利率为o.03,标 的资产初始价格为10元,标的资产交割价格为12 元,其波动率分别取o.4和o.5.在进行MCM— CLRM方法时,参数后验分布的MCMC抽样总次 数为50 000次抽样,预烧(burn—in)样本量为 30000.由于股票价格是模拟的,为避免因股票价格 模拟的可能不稳定性对美式期权定价所造成的不利 影响,在运行LSM和MCMCI.RM中分别同时插入 在模拟价格下的对应的标准欧式看跌期权价格数 据.具体运行结果列于表4~表7. 表4 MCMCLRM与LSM方法美式看跌期权定价对比 本表使用数据:so=10,K=12,r:o.03,口=o.4,丁=1 万方数据
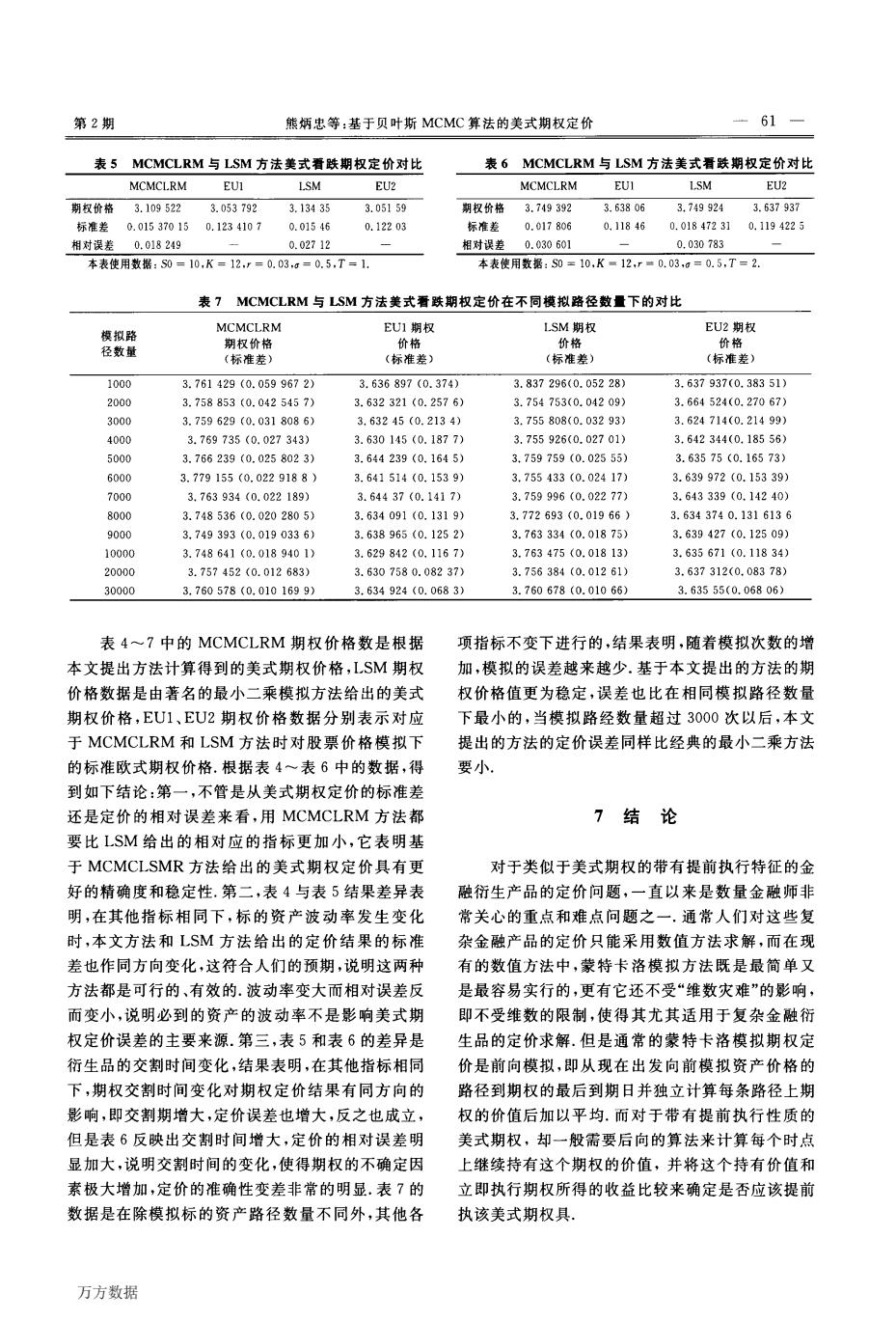
第2期 熊炳忠等:基于贝叶斯MCMC算法的美式期权定价 61 表5 MCMCLRM与LSM方法美式看跌期权定价对比 表6 MCMCLRM与LSM方法美式看跌期权定价对比 MCMCLRM EUI LSM EU2 MCMCLRM EUI LSM EU2 期权价格3.109522 3.053792 3.13435 3.05159 期权价格 3.749392 3.63806 3.749924 3.637937 标准差0.01537015 0.1234107 0.01546 0.12203 标准差 0.017806 0.11846 0.01847231 0.1194225 相对误差0.018249 0.02712 相对误差0.030601 0.030783 本表使用数据:S0=10,K=12,r=0.03,g=0.5,T=1. 本表使用数据:S0=10,K■12,r■0.03,0=0.5,T=2. 表7 MCMCLRM与LSM方法美式看跌期权定价在不同模拟路径数量下的对比 MCMCLRM LSM期权 EU2期权 模拟路 EU1期权 期权价格 价格 价格 径数量 价格 (标准差) (标准差) (标准差) (标准差) 1000 3.761429(0.0599672) 3.636897(0.374) 3.837296(0.05228) 3.637937(0.38351) 2000 3.758853(0.0425457) 3.632321(0.2576) 3.754753(0.04209) 3.664524(0.27067) 3000 3.759629(0.0318086) 3,63245(0.2134) 3.755808(0.03293) 3.624714(0.21499) 4000 3.769735(0.027343) 3.630145(0.1877) 3.755926(0.02701) 3.642344(0.18556) 5000 3.766239(0.0258023) 3.644239(0.1645) 3.759759(0.02555) 3.63575(0.16573) 6000 3.779155(0.0229188) 3.641514(0.1539) 3.755433(0.02417) 3.639972(0.15339) 7000 3.763934(0.022189) 3.64437(0.1417) 3.759996(0.02277) 3.643339(0.14240) 8000 3.748536(0.0202805) 3.634091(0.1319) 3.772693(0.01966) 3.6343740.1316136 9000 3.749393(0.0190336) 3.638965(0.1252) 3.763334(0.01875) 3.639427(0.12509) 10000 3.748641(0.0189401) 3.629842(0.1167) 3.763475(0.01813) 3.635671(0.11834) 20000 3.757452(0.012683) 3.6307580.08237) 3.756384(0.01261) 3.637312(0.08378) 30000 3.760578(0.0101699) 3.634924(0.0683) 3.760678(0.01066) 3.63555(0.06806) 表4~7中的MCMCLRM期权价格数是根据 项指标不变下进行的,结果表明,随着模拟次数的增 本文提出方法计算得到的美式期权价格,LSM期权 加,模拟的误差越来越少,基于本文提出的方法的期 价格数据是由著名的最小二乘模拟方法给出的美式 权价格值更为稳定,误差也比在相同模拟路径数量 期权价格,EU1、EU2期权价格数据分别表示对应 下最小的,当模拟路经数量超过3000次以后,本文 于MCMCLRM和LSM方法时对股票价格模拟下 提出的方法的定价误差同样比经典的最小二乘方法 的标准欧式期权价格.根据表4~表6中的数据,得 要小 到如下结论:第一,不管是从美式期权定价的标准差 还是定价的相对误差来看,用MCMCLRM方法都 7结论 要比LSM给出的相对应的指标更加小,它表明基 于MCMCLSMR方法给出的美式期权定价具有更 对于类似于美式期权的带有提前执行特征的金 好的精确度和稳定性,第二,表4与表5结果差异表 融衍生产品的定价问题,一直以来是数量金融师非 明,在其他指标相同下,标的资产波动率发生变化 常关心的重点和难点问题之一,通常人们对这些复 时,本文方法和LSM方法给出的定价结果的标准 杂金融产品的定价只能采用数值方法求解,而在现 差也作同方向变化,这符合人们的预期,说明这两种 有的数值方法中,蒙特卡洛模拟方法既是最简单又 方法都是可行的、有效的.波动率变大而相对误差反 是最容易实行的,更有它还不受“维数灾难”的影响, 而变小,说明必到的资产的波动率不是影响美式期 即不受维数的限制,使得其尤其适用于复杂金融衍 权定价误差的主要来源.第三,表5和表6的差异是 生品的定价求解.但是通常的蒙特卡洛模拟期权定 衍生品的交割时间变化,结果表明,在其他指标相同 价是前向模拟,即从现在出发向前模拟资产价格的 下,期权交割时间变化对期权定价结果有同方向的 路径到期权的最后到期日并独立计算每条路径上期 影响,即交割期增大,定价误差也增大,反之也成立, 权的价值后加以平均.而对于带有提前执行性质的 但是表6反映出交割时间增大,定价的相对误差明 美式期权,却一般需要后向的算法来计算每个时点 显加大,说明交割时间的变化,使得期权的不确定因 上继续持有这个期权的价值,并将这个持有价值和 素极大增加,定价的准确性变差非常的明显.表7的 立即执行期权所得的收益比较来确定是否应该提前 数据是在除模拟标的资产路径数量不同外,其他各 执该美式期权具. 万方数据
第2期 熊炳忠等:基于贝叶斯MCMC算法的美式期权定价 一61一 表5 MCMCLRM与LSM方法美式看跌期权定价对比 表6 McMcLRM与LsM方法美式看跌期权定价对比 本表使用数据:so=10,K=1 2,r=o.03,J=o.5,丁=1. 本表使用数据:so=10,K=12,r=o.03,口=o.5,T=2 表7 McMcLRM与LsM方法美式看跌期权定价在不同模拟路径数量下的对比 表4~7中的MCMCLRM期权价格数是根据 本文提出方法计算得到的美式期权价格,LSM期权 价格数据是由著名的最小二乘模拟方法给出的美式 期权价格,EUl、EU2期权价格数据分别表示对应 于MCMCLRM和LSM方法时对股票价格模拟下 的标准欧式期权价格.根据表4~表6中的数据,得 到如下结论:第一,不管是从美式期权定价的标准差 还是定价的相对误差来看,用MCMCLRM方法都 要比LSM给出的相对应的指标更加小,它表明基 于MCMCLSMR方法给出的美式期权定价具有更 好的精确度和稳定性.第二,表4与表5结果差异表 明,在其他指标相同下,标的资产波动率发生变化 时,本文方法和LSM方法给出的定价结果的标准 差也作同方向变化,这符合人们的预期,说明这两种 方法都是可行的、有效的.波动率变大而相对误差反 而变小,说明必到的资产的波动率不是影响美式期 权定价误差的主要来源.第三,表5和表6的差异是 衍生品的交割时间变化,结果表明,在其他指标相同 下,期权交割时间变化对期权定价结果有同方向的 影响,即交割期增大,定价误差也增大,反之也成立, 但是表6反映出交割时间增大,定价的相对误差明 显加大,说明交割时间的变化,使得期权的不确定因 素极大增加,定价的准确性变差非常的明显.表7的 数据是在除模拟标的资产路径数量不同外,其他各 项指标不变下进行的,结果表明,随着模拟次数的增 加,模拟的误差越来越少.基于本文提出的方法的期 权价格值更为稳定,误差也比在相同模拟路径数量 下最小的,当模拟路经数量超过3000次以后,本文 提出的方法的定价误差同样比经典的最小二乘方法 要小. 7 结 论 对于类似于美式期权的带有提前执行特征的金 融衍生产品的定价问题,一直以来是数量金融师非 常关心的重点和难点问题之一.通常人们对这些复 杂金融产品的定价只能采用数值方法求解,而在现 有的数值方法中,蒙特卡洛模拟方法既是最简单又 是最容易实行的,更有它还不受“维数灾难”的影响, 即不受维数的限制,使得其尤其适用于复杂金融衍 生品的定价求解.但是通常的蒙特卡洛模拟期权定 价是前向模拟,即从现在出发向前模拟资产价格的 路径到期权的最后到期日并独立计算每条路径上期 权的价值后加以平均.而对于带有提前执行性质的 美式期权,却一般需要后向的算法来计算每个时点 上继续持有这个期权的价值,并将这个持有价值和 立即执行期权所得的收益比较来确定是否应该提前 执该美式期权具. 万方数据

62 经济数学 第30卷 利用马尔科夫链的样本作为对不变分布或者是 7th Ed.New Jersey:Pearson Prentice Hall Upper Saddle Riv- 样本空间非常大的离散分布等的随机采样,是动态 er,2009 的蒙特卡洛模拟方法,其能生成非常复杂的随机数; [4]Longstaff F A,Schwartz E S.Valuing American options by simulation:A simple least-squares approach[J.The Review 对高维甚至是超高维分布实现采样;实行被估计参 of Financial Studies,2001.14(1):113-147. 数的贝叶斯后验估计;实现重要性采样等, [5]P GLASSERMAN.Monte Carlo Methods in Financial Engi- 本文提出融合贝叶斯MCMC算法到美式期权 neering[M].New York:Springer-Verlag,2004:200-275. 的模拟定价中,就是将统计中的基于贝叶斯后验分 [6]Broadie M,Glasserman P.Pricing American-style securities u- 布的随机抽样算法替代LSM算法中的普通最小二 sing simulation[J].Journal of Economic Dynamics and Con- trol,2004,21(8):1323-1352. 乘方法用于估计LSM算法中每次进行回归方程系 [7]L ROGERS.Monte carlo valuation of american options[J] 数的更加有效估计,利用解出的回归方程求出预测 Mathematical Finance,2002,12(3):271-286. 值,将其折现后再来同立即执行该期权的现金流进 [8]杨海军,雷杨.基于加权最小二乘拟蒙特卡罗的美式期权定价 行对比,然后决定是执行该期权还是继续持有.利用 [J门.系统工程学报:2008,23(5):532-538. 贝叶斯MCMC算法,特别是在模拟标的资产价格 [9] 郑承利,韩立岩,基于偏最小二乘回归的美式期权仿真定价方 法[J].应用概率统计2004,20(3):295一300. 路径又采用方差减少技术后,一方面能实现对标的 [10]B A RAMBHARAT,A E BROCKEWLL.Sequential monte 资产的模拟价格数据更充分地利用;另一方面也能 carlo Pricing of american-style options under stochastic volatili 充分结合实际市场中的衍生品对应产品的价格交易 ty models[J].Annals of Applied Statistics.2010,4(1):222 数据信息.实证结果表明使用本文方法对美式期权 -265. 定价比经典LSM中进行普通最小二乘估计上减少 [11]Bhojnarine R.Rambharat R.American Option Valuation with 各种计算上的误差,减少奇异数据点对模型的较大 Particle Filters[M].New York:Numberical Mehhods in Fi- nance Springer Proceedings in Mathematics,2012,12:51-82. 影响.经大量模拟实证表明,在同等条件下,对美式 [12]L STENTOFT.Assessing the least squares monte-carlo ap- 期权定价的定价标准差和定价的相对误差采用 proach to american option valuationJ.Review of Derivatives MCMCLRM方法要比LSM方法给出的都要小,说 Research,2004a,7(2):129-148. 明采用MCMC方法后,能够较大程度上提高对美 [13]邓国和,杨向群.随机波动率与双指数跳扩散组合模型的美式 式期权定价合理性和精确度;还有,MCMC回归方 期权定价[J门.应用数学学报2009,32(2):236-255. [14]马俊海,张维,刘凤琴,期权定价的蒙特卡罗模拟综合性方差减 法能提供一个最优停时问题的更加有效而稳健的 少技术[J门.管理科学学报2005,8(4):68一73. 解,能给出美式期权的更加精确且合理的定价.该方 [15]M BROADIE,P GLASSERMAN.Jain G Enhanced Monte 法的不足之处就是类似于一般的蒙特卡洛方法下使 Carlo estimates for American options prices[J],Journal of D 得计算量可能有所加大,但是随着现代计算机技术 erivatives,1997,5(1):25-44. 的飞速发展,计算量的问题不在是困扰模拟技术的 [16]D PETER.Hoff A First Course in Bayesian Statistical Meth- ods[M].Springer Dordrecht Heidelberg London New York: 难题 2010:105-130. 参考文献 17]N CLARKE,K PARROTT.Multigrid for american option pri- cing with stochastic volatility.Applied Mathematical Finance [1]M J BRENNAN,E S SCHWARTZ.The valuation of Ameri- [J],1999,6(3):177-195. can put optionsJ.The Journal of Financel977,32(2):449- [18]L TIERNEY.Markov chains for exploring posterior distribu- 462. tions (with discussion)[J]the Analysis of Statistics,1994 22 [2]J Cox S A ROSS,M RUBINSTEIN.Option pricing:A sim- (4):1701-1762. plified approach[J].Journal of Financial Economies 1979,7: [19]D GAMERMAN,H F LOPES.Markov chain monte carlo: 229-263. Stochastic simulation for bayesian inference[M].2nd ed.New [3]John C HULL.Options,Futures,and Other Derivatives[M]. York:Chapman&.Hall/CRC:2006. 万方数据
一62~ 经济数学 第30卷 利用马尔科夫链的样本作为对不变分布或者是 样本空间非常大的离散分布等的随机采样,是动态 的蒙特卡洛模拟方法,其能生成非常复杂的随机数; 对高维甚至是超高维分布实现采样;实行被估计参 数的贝叶斯后验估计;实现重要性采样等. 本文提出融合贝叶斯MCMC算法到美式期权 的模拟定价中,就是将统计中的基于贝叶斯后验分 布的随机抽样算法替代LSM算法中的普通最小二 乘方法用于估计LSM算法中每次进行回归方程系 数的更加有效估计,利用解出的回归方程求出预测 值,将其折现后再来同立即执行该期权的现金流进 行对比,然后决定是执行该期权还是继续持有.利用 贝叶斯MCMC算法,特别是在模拟标的资产价格 路径又采用方差减少技术后,一方面能实现对标的 资产的模拟价格数据更充分地利用;另一方面也能 充分结合实际市场中的衍生品对应产品的价格交易 数据信息.实证结果表明使用本文方法对美式期权 定价比经典LSM中进行普通最小二乘估计上减少 各种计算上的误差,减少奇异数据点对模型的较大 影响.经大量模拟实证表明,在同等条件下,对美式 期权定价的定价标准差和定价的相对误差采用 MCMCLRM方法要比LSM方法给出的都要小,说 明采用MCMC方法后,能够较大程度上提高对美 式期权定价合理性和精确度;还有,MCMC回归方 法能提供一个最优停时问题的更加有效而稳健的 解,能给出美式期权的更加精确且合理的定价.该方 法的不足之处就是类似于一般的蒙特卡洛方法下使 得计算量可能有所加大,但是随着现代计算机技术 的飞速发展,计算量的问题不在是困扰模拟技术的 难题. [1] [2] [3] 参考文献 M J BRENNAN,E S SCHWARTZ.The valuation of Amer卜 can put 0ptions[J].The Joumal of Financel977,32(2):449— 462. J Cox S A ROSS,M RUBINSTEIN.0ption p“cing:A sim— plified approach[J].Journal of Flnancial Economics 1979,7: 229—263. John C HULL.0ptions,Futures,and Other Derivatives[M]. [4] [5] [6] [7] [8] [9] [10] 7th Ed.New Jersey:Pearson Prentice Hall Upper Saddle Riv— er,2009. Longstaff F A,Schwartz E S.Valuing Ame“can options by simulation:A simple 1east—squares approach[J]. The Review of Financial Studies,2001,14(1):11 3 147. P GLASSERMAN.Monte Carlo Methods in Financial Engi— neering[M].NewYork:Springer—Verlag,2004:200一275. Broadie M,Glasserman P.Pricing American—style secu“ties u— sing simulation[j]. Journal of Economic Dynamics and con— trol,2004,21(8):1323—1352. L ROGERs. Monte carlo valuation of ame“can options[J]. Mathematical Finance,2002,1 2(3):271—286. 杨海军,雷杨.基于加权最小二乘拟蒙特卡罗的美式期权定价 [J].系统工程学报:2008,23(5):532—538. 郑承利,韩立岩.基于偏最小二乘回归的美式期权仿真定价方 法口].应用概率统计2004,20(3):295—300. B A RAMBHARAT,A E BR()CKEWI,I,.Sequential monte carlo Pricing of american—style options under stochastic volatjli— ty models口].Annals of AppIied statistics,2010,4(1):222 —265. [11]Bhojnarine R.Rambharat R.American()ption Valuation with Particle Filters[M].New York:Numbe“cal Mehhods in Fi— nance Springer Proceedings in Mathematics,20 1 2,1 2:5 1—82. [12]L sTENTOFT.Assessing the Ieast squares monte-carlo ap— proach to american option valuation[J]. Review of De“vatives Research,2004a,7(2):129—148. [13]邓国和,杨向群.随机波动率与双指数跳扩散组合模型的美式 期权定价[J].应用数学学报2009,32(2):236—255. [14]马俊海,张维,刘凤琴.期权定价的蒙特卡罗模拟综合性方差减 少技术[J].管理科学学报2005,8(4):68—73. [15]M BROADIE,P GI,AssERMAN.Jain G Enhanced Monte carlo estimates for American options p rices[J],Journal of D e“vatives,1997,5(1):25 44. [16]D PETER.Hoff A First course in Bayesian statistical Meth— ods[M].Springer Dordrecht Heidelberg I。ondon New York: 2010:105—130. 1 7]N cLARKE,K PARRoTT.Multig“d for american option pri— cing with stochastic v01atility. Applied Mathematical Finance [J],1999,6(3):177—195. [18]L TIERNEY.Markov chains for exploring posterior dist“bu一 [19] tions(with discussion)[J]the Analysis of statistics,1994 22 (4):1701—1762. D GAMERMAN,H F L()PES. Markov chain monte carlo: stochastic simulation for bayesian inference[M].2nd ed.New York:Chapman&Hall/CRC:2006. 万方数据