
第20卷第3期 管理科学 Vol.20 No.3 2007年6月 JOURNAL OF MANAGEMENT SCIENCES June,2007 黛 基于贝叶斯MCMC的POT模型 一低频高损的操作风险度量 刘睿,詹原瑞,刘家鹏 天津大学管理学院,天津300072 嫡要:对低频率高损失的操作风险进行量化非常困难,其特点为较少发生,而一旦发生通 常都会造成巨额损失,因此数据匮乏是一个严重的挑战,内部欺诈风险是此类风险的典型代 表,也是中国商业银行有代表性的重大操作风险类型。在损失分布法的框架下,通过极值理 论对内部欺诈风险进行度量:考虑到使用损失数据对频率直接拟合带来的问题,待助POT模 型的重要性质对内部欺诈风险强度和顿率进行估计;在此基础上,使用基于吉布斯抽样的贝 叶斯MCMC方法估计POT模型的参数,以解决样本数据不足时极大似然估计中误差增大的问 题。在这一方法柜架下,以中国商业银行的内部欺诈损失数据为样本,对中国商业银行的内 部欺诈风险进行度量,并估计了相应的经济资本。 关键词:低顿高损:损失分布法;贝叶斯MCMC;POT模型;经济资本 中图分类号:830.4 文献标识码:A 文章编号:1672-0334(2007)03-0076-08 The Pot Model Based on Bayesian MCMC Method: Measuring Low Frequency/High Severity Operational Risk LIU Rui,ZHAN Yuan-rui,LIU Jia-peng School of Management,Tianjin University,Tianjin 300072.China Abstract:Internal fraud is the significantly representative loss type in China banking industry.For this low frequency/high severity loss,however,risk measurement and the corresponding economic capital estimation is very difficult,due to the lack of adequate loss data.This paper makes use of the POT Model,which proved to be effective in extreme loss measurement,to deal with the loss severity and frequency under the Loss Distribu- tion Method framework.A Bayesian MCMC model with Gibbs sampling is established to estimate the parameters required in POT.Furthermore,based on some internal fraud loss data from Chinese banks,the paper gives the estimation to the intemal fraud risk of an assumed moderate-size bank and the corresponding risk capital for the first time. Keywords:low frequency/high severity;internal fraud;Bayesian MCMC:POT Model:economie capital 1引曹 高损失强度和高发生频率低损失强度两种类型,前 操作风险的度量及其经济资本的估计已经成为 者一般指很少发生的极端事件,后者往往成为日常 银行风险管理的核心问题之一。从操作风险损失发 风险管理的一部分。 生的特点看,可以将操作风险事件分为低发生频率 在新巴赛尔协议规定的7种操作风险损失类型 收稿日期:2007-04-20 金项目:国家自然科学基金(70573076):高等学校博士学科专项科研基金(20050056057) 作者简介:刘管(1976-),男,云南人,天神大学管理学院博士研究生,研究方向:风险管理等。 万方数据
第20卷第3期 管理科学 v01.20 No.3 2 O 0 7年6月 JOURNAL 0F MANAGEMENT SCIENCES June.2 O 0 7 ⑩ 基于贝叶斯MCMC的POT模型 低频高损的操作风险度量 刘 睿,詹原瑞,刘家鹏 天津大学管理学院,天津300072 摘要:对低频率高损失的操作风险进行量化非常困难,其特点为较少发生,而一旦发生通 常都会造成巨额损失,因此数据匮乏是一个严重的挑战,内部欺诈风险是此类风险的典型代 表,也是中国商业银行有代表性的重大操作风险类型。在损失分布法的框架下.通过极值理 论对内部欺诈风险进行度量;考虑到使用损失数据对频率直接拟合带来的问题,借助POT模 型的重要性质对内部欺诈风险强度和频率进行估计;在此基础上,使用基于吉布斯抽样的贝 叶斯McMc方法估计POT模型的参数,以解决样本数据不足时极大似然估计中误差增大的问 题。在这一方法框架下,以中国商业银行的内部欺诈损失数据为样本,对中国商业银行的内 部欺诈风险进行度量,并估计了相应的经济资本。 关键调:低频高损;损失分布法;贝叶斯McMc;POT模型;经济资本 中图分类号:R30.4 文献标识码:A 文章编号:1672—0334(2007)03—0076—08 The P0t Model Based on Bayesian MCMC Method: Measuring Low Frequency/High SeVerity operational Risk LIU Rui,ZHAN Yuan—nIi,UU Jia—peng School of Management,Tianjin University,Tianjin 300072,China Abstract:Intemal fraud is the significantly representative loss type in China banking industry. For this low frequenc)∥high severity 10ss,however,risk measuI℃ment and the corresponding economic capital estimation is very difficult,due to the lack of adequate loss data.This paper makes use of the POT Model,which pmved to be efkctiVe in extreme loss measurement,to deal with the loss severity and fbquency under the Loss Distribu— tion Method framework.A Bayesian MCMC model with Gibbs sampling is established to estimate the pammeters required in POT. FunheHIlore,based on some internal fI乜ud loss data f而m Chinese banks,the paper gives the estimation to the intemal fhud risk of an assumed moderate—size bank and the corresponding risk capital fbr the first time. Keywords:low frequency/high sevedty;intemal fhud;Bayesian MCMC;POT Model;economic capital 1 引言 操作风险的度量及其经济资本的估计已经成为 银行风险管理的核心问题之一。从操作风险损失发 生的特点看,可以将操作风险事件分为低发生频率 高损失强度和高发生频率低损失强度两种类型,前 者一般指很少发生的极端事件,后者往往成为日常 风险管理的一部分。 在新巴赛尔协议规定的7种操作风险损失类型 收稿日期:2007一04—20 基金项目:国家自然科学基金(70573076);高等学校博士学科专项科研基金(20050056057) 作者简介:刘睿(1976一),男,云南人,天津大学管理学院博士研究生,研究方向:风险管理等。 万方数据

第3期 刘容等:基于贝叶斯MCMC的POT模型-一低频高损的操作风险度量 中,内部欺诈是一种典型的低颜高损的操作风险事。 收集数据不全面带来的估计误差,只要极值有代表 件。新巴赛尔协议将内部欺诈定义为由打算欺骗、 性,数据问题对于尾部分布影响相对较小。更重要 盗用资产或规避监管、法律或公司规章的行为引起 的是,对于损失强度与频率间的关系(一般是未知 的损失,其中至少涉及到内部的某一方,典型的内 的),P0T模型提供了一个性质良好的处理途径(关 部欺诈事件包括偷窃、信用诈骗和未授权交易等。 于极值理论的详细讨论参见文献[4])。POT模型可 在中国特殊的制度环境下,内部欺诈事件给中国银 以用简明的解析方法合并处理损失强度与损失频 行业造成的损失是相当惊人的,内部欺诈已经对以 率,从而获得总和损失的尾部估计。这不但降低了 银行为核心的中国金融系统构成了异常严重的威 直接模拟带来的计算成本,更重要的是诚少了模拟 胁。 误差,这种误差往往来源于对两类分布及其关系的 针对中国银行业面临的极高的内部欺诈风险, 假设与真实状况间的差异,而这种差异在模拟中经 到目前为止还没有一个合理的估计方法,本研究将 常筱放大。当然,小样本问题对POT的估计也会产 对此类风险进行单独度量并计算相应的经济资本。 生影响,在下一部分将讨论这个问题。 对低频率高损失的风险进行度量往往比较困难,对 2.1损失麗部和损失顿率的处理 于内部欺诈风险更是如此,其本质特征决定了此类 POT模型主要基于广义帕累托分布(GPD),即 事件的损失数据非常匮乏。由于案发隐秘、造成的 f£—0 损失严重,能否恰当度量极端损失及其频率就成为 (x) (2) 关键的问题。另外,在小样本条件下,通常的估计方 -e(-合) f5=0 法可能是很不可靠的,需要使用更有效的技术。 本研究在损失分布法的框架下,借助POT(peaks 其中,x为随机变量,5为形状参数,B为广义帕累托 over threshold)模型的重要性质对内部欺诈风险强度 分布的尺度参数。当E0时(2)式对 贝叶斯马尔可夫链蒙特卡罗模拟(Markov Chain 应于普通帕累托分布,ParetoⅡ分布为厚尾的,其有 Monte Carlo,MCMC)方法估计POT模型的参数,最后 以收集到的部分内部欺诈损失数据为样本,对中国 尾郎指数a=可以通过加一个位置参数扩展以 商业银行的内部欺诈风险经济资本进行估计。 上分布形式,GPDa(x)定义为GPDa(x-u)。 Balkema-De Haan和Pickands证明,对于充分高的 2 基于POT模型的内部欺诈损失估计 阔值4,超额值y的分布收敛于GPDa(x),y=x-。 在量化操作风险资本的高级计量法中,损失分 同样,对x一4≥0,设F,(x)是随机变量x的未知分布 布法是最常用、最重要的方法之一,它通常在对损失 函数(其右端点为x,可能是无限的),“为某特定阀 值,则超额分布函数为 事件频率和损失强度建立相关假设的基础上,对各 业务线/损失类型的操作风险损失进行估计,其一般 F(y)=P(X-u≤ylX>u) 模型可表示为 F.(x)-F.(u) 1-F() (I) y x-u 0 (3) 对于随机变量x,如果能对高于某阙值的超额值 其中,L为损失强度,N为损失频率,S为总和损失, 的条件分布用GPD拟合,就可以得到原分布的尾部 各自对应的分布为强度分布、频度分布和总和损失 (高于阚值“)部分的拟合,即对x>4有 分布。一般情况下,假设损失强度L独立同分布,且 每个L,独立于N。因此,为了量化内部欺诈风险,需 F(x)=P(X≤x) 要评估损失的两个维度,进而得到内部欺诈的总和 =(1-P号X≤u)F(x-)+PX≤u}(4) 损失分布。Klugman等认为,总和损失分布S可以用 对足够大的圆值“有尾部估计为 Fourier转换、蒙特卡罗模拟或者解析近似的方法获 F(x)=[1-F.(4)]G,n(x)+F.(u)(5) 得),蒙特卡罗模拟是实践中最常用的方法,樊欣、 杨晓光用此方法对中国银行业的操作风险进行了模 其中,F,(“)是在阈值4处的经验分布函数,n为超过 拟估计。但是,在小样本条件下,由于损失的发生 觸值的损失个数,口为尾部估计中的尺度参数。(5) 式中的尾部估计也是GPD分布,其形状参数E相同, 非常稀少,直接用样本数据对强度和频率拟和很难 奏效,此时蒙特卡罗模拟可能带来很高的误差。 并有以下位置和尺度参数1,即 对于内部欺诈而言,数据稀少是一个本质的问 u=4+E-{[1-F,(u)]-1| 题,针对其数据量少,极端值高的特点,本研究将使 o=1-F(u)] (6) 用POT模型进行损失强度的估计,POT模型用于处 对于低频率的极端损失而言,频率估计往往是 理极端数据是常见而有效的。选择POT模型可以将 很难处理的,POT模型提供了一个有效的途径。按 注意力集中在极端损失上,这将减少由于数据不足、 照Leadbetter等的证明,对于足够大的阀值u,超过u 万方数据
第3期 刘睿等:基于贝叶斯MCMc的POT模型——低频高损的操作风险度量 77 中,内部欺诈是一种典型的低频高损的操作风险事 件。新巴赛尔协议将内部欺诈定义为由打算欺骗、 盗用资产或规避监管、法律或公司规章的行为引起 的损失,其中至少涉及到内部的某一方…,典型的内 部欺诈事件包括偷窃、信用诈骗和未授权交易等。 在中国特殊的制度环境下,内部欺诈事件给中国银 行业造成的损失是相当惊人的,内部欺诈已经对以 银行为核心的中国金融系统构成了异常严重的威 胁。 针对中国银行业面临的极高的内部欺诈风险, 到目前为止还没有一个合理的估计方法,本研究将 对此类风险进行单独度量并计算相应的经济资本。 对低频率高损失的风险进行度量往往比较困难,对 于内部欺诈风险更是如此,其本质特征决定了此类 事件的损失数据非常匮乏。由于案发隐秘、造成的 损失严重,能否恰当度量极端损失及其频率就成为 关键的问题。另外,在小样本条件下,通常的估计方 法可能是很不可靠的,需要使用更有效的技术。 本研究在损失分布法的框架下,借助POT(peaks over threshold)模型的重要性质对内部欺诈风险强度 和频率进行估计,并使用基于吉布斯(Gibbs)抽样的 贝叶斯马尔可夫链蒙特卡罗模拟(Markov chain Monte cado,MCMc)方法估计POT模型的参数,最后 以收集到的部分内部欺诈损失数据为样本,对中国 商业银行的内部欺诈风险经济资本进行估计。 2基于PoT模型的内部藏诈损失估计 在量化操作风险资本的高级计量法中,损失分 布法是最常用、最重要的方法之一,它通常在对损失 事件频率和损失强度建立相关假设的基础上,对各 业务线/损失类型的操作风险损失进行估计,其一般 模型可表示为 s=∑L。 (I) 其中,厶为损失强度,Ⅳ为损失频率,s为总和损失, 各自对应的分布为强度分布、频度分布和总和损失 分布。一般情况下,假设损失强度L独立同分布,且 每个厶独立于Ⅳ。因此,为了量化内部欺诈风险,需 要评估损失的两个维度,进而得到内部欺诈的总和 损失分布。Klugman等认为,总和损失分布s可以用 Fourier转换、蒙特卡罗模拟或者解析近似的方法获 得¨1,蒙特卡罗模拟是实践中最常用的方法,樊欣、 杨晓光用此方法对中国银行业的操作风险进行了模 拟估计|3 J。但是,在小样本条件下,由于损失的发生 非常稀少,直接用样本数据对强度和频率拟和很难 奏效,此时蒙特卡罗模拟可能带来很高的误差。 对于内部欺诈而言,数据稀少是一个本质的问 题,针对其数据量少、极端值高的特点,本研究将使 用POT模型进行损失强度的估计,POT模型用于处 理极端数据是常见而有效的。选择POT模型可以将 注意力集中在极端损失上,这将减少由于数据不足、 收集数据不全面带来的估计误差,只要极值有代表 性,数据问题对于尾部分布影响相对较小。更重要 的是,对于损失强度与频率间的关系(一般是未知 的),POT模型提供了一个性质良好的处理途径(关 于极值理论的详细讨论参见文献[4])。POT模型可 以用简明的解析方法合并处理损失强度与损失频 率,从而获得总和损失的尾部估计。这不但降低了 直接模拟带来的计算成本,更重要的是减少了模拟 误差,这种误差往往来源于对两类分布及其关系的 假设与真实状况间的差异,而这种差异在模拟中经 常被放大。当然,小样本问题对POT的估计也会产 生影响,在下一部分将讨论这个问题。 2.1损失尾部和损失频率的处理 POT模型主要基于广义帕累托分布(GPD),即 G‰㈩:r。《言’了孵刘 G加f舅(戈)={ (2) 一 (2) 【l—exp(一音) 孵=o 其中,算为随机变量,f为形状参数,卢为广义帕累托 分布的尺度参数。当f0时(2)式对 应于普通帕累托分布,ParetoⅡ分布为厚尾的,其有 尾部指数a=÷。可以通过加一个位置参数p扩展以 上分布形式,GP哝。p(茹)定义为GP4.口(菇一p)。 Balkem.De Haan和Pick粕ds证明,对于充分高的 阈值Ⅱ,超额值y的分布收敛于G雌.口(茹),y=算一“。 同样,对菇一肛≥O,设殳(z)是随机变量膏的未知分布 函数(其右端点为z。可能是无限的),u为某特定阈 值,则超额分布函数为 F。(y)=尸(X—u s y X>“) t(x)一t(u) l—t(珏) y=茗一Ⅱ>0 (3) 对于随机变量茁,如果能对高于某阈值的超额值 的条件分布用GPD拟合,就可以得到原分布的尾部 (高于阈值“)部分的拟合,即对茁>p有 F(x)=P(爿≤戈) =(1一P{x s u})F。(z—u)+尸{x s u} (4) 对足够大的阈值“有尾部估计为 F(戈)=[1一F,,(u)]G“..,(石)+F。(“) (5) 其中,t(u)是在阈值“处的经验分布函数,n为超过 阈值的损失个数,盯为尾部估计中的尺度参数。(5) 式中的尾部估计也是GPD分布,其形状参数亭相同, 并有以下位置和尺度参数H J,即 p:¨+膳“{[1一F。(“)]‘一1} 盯=口[1一F。(“)]5 (6) 对于低频率的极端损失而言,频率估计往往是 很难处理的,POT模型提供了一个有效的途径。按 照Leadbetter等的证明,对于足够大的阈值u,超过M 万方数据

78 管理科学 2007年6月 的随机变量x(以下称为超额数,x的个数称为超额 以下部分将使用(10)式进行估计。需要指出,以上 数数量)序列逐渐收敛于一个强度为入(入>0)的泊 超额均值函数是定义在形状参数专小于1的条件下。 松过程5,1。这样泊松极限近似可以帮助我们处理超 对于专大于1的情况,可以使用中值超额函数,具体 额值y。(即x-u)的发生频率,相关研究参见文献 的讨论参见文献[4]。中值超额函数定义为 [7,8]。 (12) 可以进行如下的假设:超过阈值“的超额数x发 med()=[Fr.(分J 生时间服从强度为A(A>0)的泊松过程,参数A度 综上,T时期内超过某特定阈值的超额损失 量在囡值“处单位时间内超额数x的发生强度:相应 (EL)资本和操作风险经济资本分别为 的各超额值y.相互独立,并服从GPD分布:y。与超额 数数量N。相互独立。后面两个假设是常见的,并且 ca=A7月9 (13) 对于本研究的内部欺诈问题是合理的。关于尾部服 CARs=&+A,TB+丝 1- (14) 从GPD的问题可以使用经验数据进一步检验。 一觳的,在损失数据平稳的情况下,令入。为超过 阀值“的频率,从尾部估计中可得 3POT横型参数的贝叶斯MCMC估计 从以上分析可知,参数的确定对于POT和经济 A,=1-P1X≤u=(1+专“-)t (7) r 资本的估计至关重要,通常的POT参数估计方法有 需要指出,如果有证据表明损失是时间相依的, 极大似然法、矩估计和概率加权矩方法。已有的研 模型将是一个非齐次泊松过程,如强度系数随时间 究证明极大似然法在大样本条件下比其他方法(如 而改变,即入=入()。对此类相依数据仍然可以处理, 概率加权矩方法)更加有效2:矩估计和概率加权 保持模型稳健性的惟一假定是超额值近似服从GPD 矩方法容易计算,但仅在F(u),相 应的VaR值可得 h,Be)=-g+(合-)2n1-合(15) aR.=F'(1-a) 其中,k=-。(15)式随着是接近x…趋近于无穷。 =u+2)4- (8) 对于内部欺诈事件而言,低频率高损失是其本 质的特点,大量的样本往往难以获得。在确定阈值 本研究将采用期望短缺(expected shortfall,ES)作 后,当超额数数量较少时(如少于30个),使用极大 为期望损失强度的衡量,作为一致性风险度量指标 似然法估计将很不可靠。此外,在尾部推断中,对估 ES在本研究方法中具有优势。由于满足次可加性, 计的范围进行评价是很重要的,需要给出置信区间。 在整合不同类别的操作凤险损失的过程中,ES更便 针对内部欺诈数据稀少损失强度大的特点,本研究 于考量银行整体的操作风险经济资本。另外,对于典 将采用一种有效的方法,即贝叶斯模拟。Medova用 型的低颜率高损失事件(如内部欺诈)需要进一步 此类方法对由俄罗斯金融危机引发的金融机构交易 考虑损失特征的因素。正如下文所述,内部欺诈的损 损失进行了估计。本研究表明,使用贝叶斯估计 失样本具有右偏的、尖峰厚尾的分布(这符合内部欺 的POT模型参数比较稳定,支持尾部近似GPD的假 诈风险的特点),为了评估损失的总体状况,S比作 设。另外,该方法能提供比极大似然法更多的信息, 为分位数的VaR能提供更全面的信息。于是对于特 如参数的核密度估计及其置信区间。 定的损失水平L潜在损失规模为 限于本文研究的问题,这里只对有代表性的厚 ES(L)=L +E(X -LI X L) 尾损失分布(即>0,下一部分中本研究的数据是厚 L+MEF(L) (9) 尾的)进行讨论,对于ξ0,设?=日则 GPD模型可表示为1 ⑧.=L+B+丝 GPD(xl5,r)=1-(1+6r)言 1- x>0 (16) L=u (10) 设T专相互独立,并有以下先验分布,即 成‘成 专-Pareto I(a,c) >0,e>0 T -Gamma(a,b)a >0,b >0 (17) L VaR>u (11) 其中,a,c为帕累托分布的参数,a、b为伽马分布参 万方数据
78 管理科学 2007年6月 的随机变量戈(以下称为超额数,戈的个数称为超额 数数量)序列逐渐收敛于一个强度为A(A>0)的泊 松过程∞’61。这样泊松极限近似可以帮助我们处理超 额值y。(即x—u)的发生频率,相关研究参见文献 [7,8]。 可以进行如下的假设:超过阈值u的超额数z发 生时间服从强度为A(A>o)的泊松过程,参数A度 量在阈值M处单位时间内超额数并的发生强度;相应 的各超额值y。相互独立,并服从GPD分布;y。与超额 数数量,v。相互独立。后面两个假设是常见的,并且 对于本研究的内部欺诈问题是合理的。关于尾部服 从GPD的问题可以使用经验数据进一步检验。 一般的,在损失数据平稳的情况下,令A。为超过 阈值u的频率,从尾部估计中可得 A。=1一P{x≤“}=(1+亭堡二世)一古 (7) (J 需要指出,如果有证据表明损失是时间相依的, 模型将是一个非齐次泊松过程,如强度系数随时间 而改变,即A=A(£)。对此类相依数据仍然可以处理, 保持模型稳健性的惟一假定是超额值近似服从GPD 分布。有关的研究如chavez—Demoulin等使用平滑技 术对模型中的趋势整合旧J,Ferm等使用了对数据聚 集去除(declustering)的方法[…]。 2.2损失强度和经济资本估计 对于损失强度,若给定的置信水平a>F。(M),相 应的地尺值可得 ,o’、 忱|R。=F“(1一d) =M+等[(与羔)~一1] (8) f ^ 本研究将采用期望短缺(expected shortfau,Es)作 为期望损失强度的衡量,作为一致性风险度量指标 E.s在本研究方法中具有优势。由于满足次可加性, 在整合不同类别的操作风险损失的过程中,Es更便 于考量银行整体的操作风险经济资本。另外,对于典 型的低频率高损失事件(如内部欺诈)需要进一步 考虑损失特征的因素。正如下文所述,内部欺诈的损 失样本具有右偏的、尖峰厚尾的分布(这符合内部欺 诈风险的特点),为了评估损失的总体状况,删比作 为分位数的忱R能提供更全面的信息。于是对于特 定的损失水平£潜在损失规模为 .ES(L)=L+E(X一£I x>L) =L+MEF(L) (9) 其中,肘EF为超额均值函数。(9)式用参数为f、卢的 GPD模型可表示为…J 瓜一,+旦±趣 Es。=£+气二等 I一言 L=“ (10) 恳:f土+—卫二兰L]谂。 嬲。=[亡+—卫-卫]阮尺。 1一; (1一手)比尺。 £=比R。>“ (11) 以下部分将使用(10)式进行估计。需要指出,以上 超额均值函数是定义在形状参数孝小于l的条件下。 对于f大于1的情况,可以使用中值超额函数,具体 的讨论参见文献[4]。中值超额函数定义为 med叭H)=[F。(÷)]。 (12) 综上,r时期内超过某特定阈值的超额损失 (EL)资本和操作风险经济资本分别为 cA%吐。7T等葺 (13) cA%:M+A。71譬粤 (14) 3 POT模型参数的贝叶斯McMC估计 从以上分析可知,参数的确定对于POT和经济 资本的估计至关重要,通常的POT参数估计方法有 极大似然法、矩估计和概率加权矩方法。已有的研 究证明极大似然法在大样本条件下比其他方法(如 概率加权矩方法)更加有效¨21;矩估计和概率加权 矩方法容易计算,但仅在f0,下一部分中本研究的数据是厚 尾的)进行讨论,对于孝o,设丁=÷,则 卢 GPD(戈I f,下)=l一(1+亭丁戈)了 戈>0 (16) 设r、f相互独立,并有以下先验分布,即 f~Pore£o I(d,c) d>0,c>0 r~Gn,n,nn(n,6) 血>0,6>0 (17) 其中,a、c为帕累托分布的参数,。、6为伽马分布参 万方数据

第3期 刘容等:基于贝叶斯MCMC的POT模型-一低频高损的操作风险度量 79 数。具体米说,形状参数服从帕累托先验分布,其 数的联合后验分布中获得样本,从而得到需要的边 密度函数为 际分布。总的来说,在给定损失数据后,使用MCMC fela,c)ac"g(() 模拟产生一个与条件后验参数分布相近似的经验参 z∈A 数分布,最后使用这个经验分布的均值作为最终的 1(z)= (18) lo 估计值。需要注意的是,实施Gibbs抽样要求知道估 zA 计参数的满条件分布的信息。在薄尾条件下(E0,c>0l4(z)为示性函数,仅在变量z属于 区域A时为1,否则为0。帕累托先验的一个优点是 0),A小于x.的限制令Winbugs实施采样很困难, 帕累托分布有一个正的下限c,这样可避免模拟中由 此时只能运用Gilks等提出的ARMS(adaptive rejection 于样本较小导致形状参数过分通近0。需要指出, metropolis sampling)方法,该方法使用高级的Metropo- 这个先验不是必须的,采用正态分布进行模拟,结果 1is采样,具有更广的适用性6。 与此类:由于B是GPD的尺度参数,t=日故设, 服从Gamma分布。关于贝叶斯方法中先验及其稳健 4数据来源、分析及实证结果 性问题参见Berger的研究I。 内部欺诈事件的历史数据十分稀少,单一机构 无法提供足够的数据,因此外部数据是银行一个重 根据贝叶斯法则,参数和?的联合后验分布为 )=(f) 要的补充。由于中国商业银行目前尚未建立内部操 (19) J∬L(x15,rjE)r)dkdr 作风险损失数据收集的制度,也没有类似国外的行 业数据库和专门的商业数据库,本研究的数据来源 其中,L(x!专,r)为似然函数,样本信息通过似然函数 有两类,大部分取自公开的信息渠道,有少部分数据 进人估计的过程。(19)式可表示为 来源于一些地方商业银行的内部资料。样本数据中 f八5,r1x)gL(xI,r)f八E)f(r) (20) 包括工,农、中、建四大银行和其他全国性股份制银 以表示成比例,这样参数的后验分布为 行的各级分支机构以及地方商业银行、信用社(改制 p(671 x)cg expl-(1+L)In(1+ 前)、邮政储蓄机构等多家地方金融机构,其中涉及 四大国有银行的损失事件数量过半,都是源于各地 T5-br]I(r>0).1(5>0) (21) 方分支机构的损失。 其中,(r>0).(5>0)均为示性函数,仅在参数大 从实践上看,规模因素可能会对损失频率有一 于0时存在。由(20)式可知,参数专和T的边际分布 定的影响,而四大银行的规模远大于中国其他银行。 (Ix)(rlx)非已知的分布,不能从封闭形式获 为了减少规模因素的影响,使样本中的数据具有可 得,但可以通过马尔可夫链蒙特卡罗模拟得到。关 比性,将四大银行的各省级分行作为被估计的单位, 于MCMC方法的具体讨论参见文献[14]和[15],其 这其中不再考虑规模的差异。于是就可以把某个分 基本思想是模拟一条马尔可夫链的样本路径,链的 行视为一个研究对象,而将所有的其他损失数据视 状态空间是被估计参数的值,链的极限分布为被估 为引人的外部数据。这样,研究的结果就可以看作 参数的贝叶斯后验分布。在充分的迭代后,马尔可 类似规模银行的内部欺诈风险的度量,其代表的内 夫链将忘记原始状态而收敛于一个平稳的目标分布 部欺诈风险水平可以大致反映出中国同等规模商业 厂x,而不依赖于原始状态a。或时间t。将前面测试期 银行的一般水平,这与本研究的目标是一致的。 阶段的n个状态滤去,剩下的链将作为目标后验分 4.1样本猫述及阈值确定 布的样本。 样本共包括102个损失数据,具体的损失频率及 本研究使用Winbugs软件进行Gibbs抽样,从参 相应损失强度分布见表【。 表1各年内部欺诈损失数据 Table 1 Internal Fraud Loss Data in Each Year 1999年前 2000年 2001年 2002年 2003年 2004年 2005年 损失事件数量 42 9 8 12 9 14 8 损失金额(亿元) 81.39 5.78 11.36 16.08 40.49 37.73 12.73 设计机构数量 4 7 7 6 7 损失事件平均数 3.0 1.3 1.6 1.7 1.5 2.0 1.1 平均损失金额(亿元) 5.81 0.83 2.27 2.3 6.75 5.39 1.81 万方数据
第3期 刘睿等:基于贝叶斯McMc的POT模型——低频高损的操作风险度量 79 数。具体来说,形状参数f服从帕累托先验分布,其 密度函数为 灭毒I理,c)=ac。f。。“’L。(f) rl z∈A L(z)={ (18) 【0 。芭A 其中,理>0,c>O。厶(z)为示性函数,仅在变量。属于 区域A时为l,否则为0。帕累托先验的一个优点是 帕累托分布有一个正的下限c,这样可避免模拟中由 于样本较小导致形状参数f过分逼近0。需要指出, 这个先验不是必须的,采用正态分布进行模拟,结果 与此类似。由于p是G阳的尺度参数,丁=—},故设下 p 服从Gamma分布。关于贝叶斯方法中先验及其稳健 性问题参见Berger的研究¨“。 根据贝叶斯法则,参数f和-『的联合后验分布为 只f,rl茗):了址且d筮址(19) |J£(戈I孝,r玳亭)八丁)蟛d下 其中,£(引孝,f)为似然函数,样本信息通过似然函数 进入估计的过程。(19)式可表示为 ,(孝,f I茗)。c£(戈I f,丁I“亭I厂(下) (20) 。c表示成比例,这样参数的后验分布为 1 n p(f,r I茗)*7.…’‘1P“’exp[一(1+÷)∑1n(1+ 下缸。一6l下],(下>0).,(亭>0) (21) 其中,,(下>0).,(f>0)均为示性函数,仅在参数大 于。时存在。由(20)式可知,参数f和r的边际分布 以亭l z)以Jr I算)非已知的分布,不能从封闭形式获 得,但可以通过马尔可夫链蒙特卡罗模拟得到。关 于McMc方法的具体讨论参见文献[14]和[15],其 基本思想是模拟一条马尔可夫链的样本路径,链的 状态空间是被估计参数的值,链的极限分布为被估 参数的贝叶斯后验分布。在充分的迭代后,马尔可 夫链将忘记原始状态而收敛于一个平稳的目标分布 厶。而不依赖于原始状态吼或时间£。将前面测试期 阶段的n个状态滤去,剩下的链将作为目标后验分 布的样本。 本研究使用winbugs软件进行Gibbs抽样,从参 数的联合后验分布中获得样本,从而得到需要的边 际分布。总的来说,在给定损失数据后,使用MCMC 模拟产生一个与条件后验参数分布相近似的经验参 数分布,最后使用这个经验分布的均值作为最终的 估计值。需要注意的是,实施Gibbs抽样要求知道估 计参数的满条件分布的信息。在薄尾条件下(f< 疗 o),号小于戈…的限制令winbugs实施采样很困难, 言 此时只能运用Cilks等提出的ARMs(ad印tive rejection metropo】is sampling)方法,该方法使用高级的Metropo— lis采样,具有更广的适用性¨…。 4数据来源、分析及实证结果 内部欺诈事件的历史数据十分稀少,单一机构 无法提供足够的数据,因此外部数据是银行一个重 要的补充。由于中国商业银行目前尚未建立内部操 作风险损失数据收集的制度,也没有类似国外的行 业数据库和专门的商业数据库,本研究的数据来源 有两类,大部分取自公开的信息渠道,有少部分数据 来源于一些地方商业银行的内部资料。样本数据中 包括工、农、中、建四大银行和其他全国性股份制银 行的各级分支机构以及地方商业银行、信用社(改制 前)、邮政储蓄机构等多家地方金融机构,其中涉及 四大国有银行的损失事件数量过半,都是源于各地 方分支机构的损失。 从实践上看,规模因素可能会对损失频率有一 定的影响,而四大银行的规模远大于中国其他银行。 为了减少规模因素的影响,使样本中的数据具有可 比性,将四大银行的各省级分行作为被估计的单位, 这其中不再考虑规模的差异。于是就可以把某个分 行视为一个研究对象,而将所有的其他损失数据视 为引入的外部数据。这样,研究的结果就可以看作 类似规模银行的内部欺诈风险的度量,其代表的内 部欺诈风险水平可以大致反映出中国同等规模商业 银行的一般水平,这与本研究的目标是一致的。 4.1样本描述及阈值确定 样本共包括102个损失数据,具体的损失频率及 相应损失强度分布见表l。 表l各年内部欺诈损失数据 TabIe 1 Internal Fraud Lo鸽Data in Each Year 万方数据
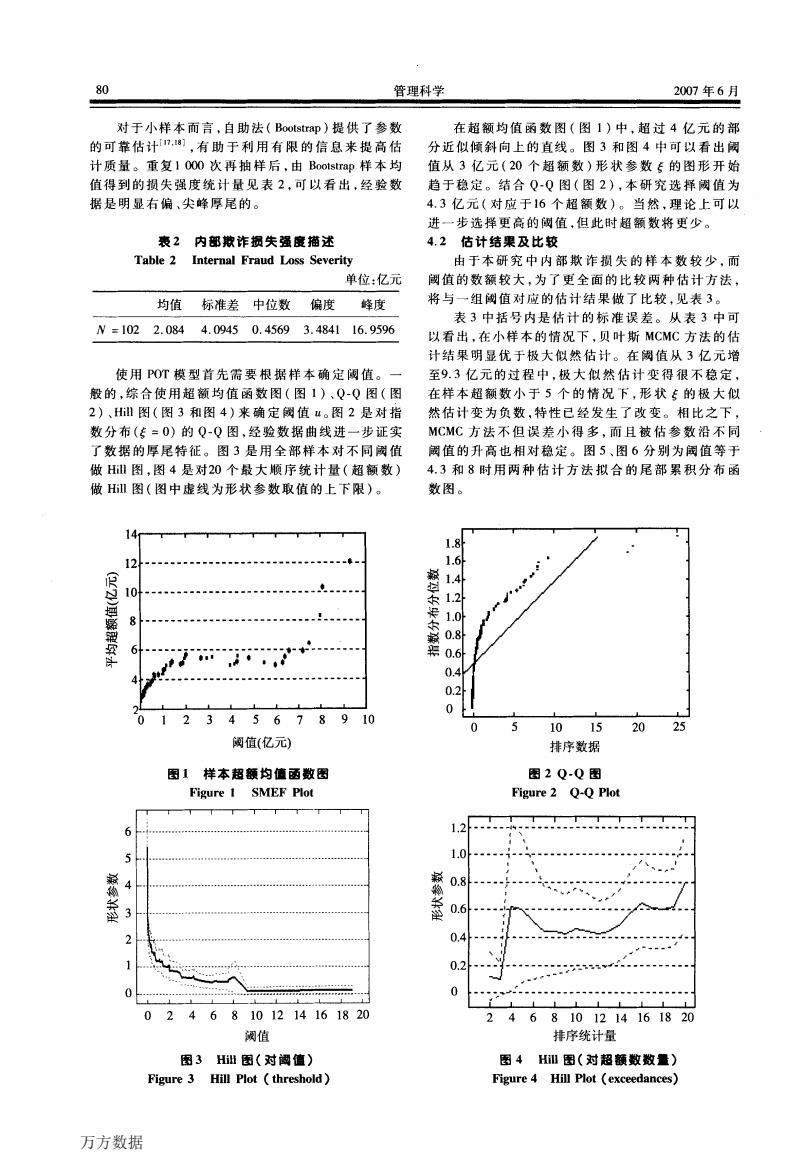
80 管理科学 2007年6月 对于小样本而言,自助法(Bootstra即)提供了参数 在超额均值函数图(图1)中,超过4亿元的部 的可靠估计.],有助于利用有限的信息来提高估 分近似倾斜向上的直线。图3和图4中可以看出阀 计质量。重复】000次再抽样后,由Bootstrap样本均 值从3亿元(20个超额数)形状参数专的图形开始 值得到的损失强度统计量见表2,可以看出,经验数 趋于稳定。结合QQ图(图2),本研究选择阔值为 据是明显右偏、尖峰厚尾的。 4.3亿元(对应于16个超额数)。当然,理论上可以 进一步选择更高的阈值,但此时超额数将更少。 表2内部撒诈损失强度描述 4.2估计结果及比较 Table 2 Internal Fraud Loss Severity 由于本研究中内部欺诈损失的样本数较少,而 单位:亿元 阈值的数额较大,为了更全面的比较两种估计方法, 均值标准差中位数偏度 峰度 将与一组阈值对应的估计结果做了比较,见表3。 表3中括号内是估计的标准误差。从表3中可 N=1022.0844.09450.45693.484116.9596 以看出,在小样本的情况下,贝叶斯MCMC方法的估 计结果明显优于极大似然估计。在阅值从3亿元增 使用POT模型首先需要根据样本确定阀值。一 至9.3亿元的过程中,极大似然估计变得很不稳定, 般的,综合使用超额均值函数图(图1)、Q-Q图(图 在样本超额数小于5个的情况下,形状专的极大似 2)、Hl图(图3和图4)来确定镯值u。图2是对指 然估计变为负数,特性已经发生了改变。相比之下, 数分布(传=0)的Q-Q图,经验数据曲线进一步证实 MCMC方法不但误差小得多,而且被估参数沿不同 了数据的厚尾特征。图3是用全部样本对不同威值 值的升高也相对稳定。图5、图6分别为阈值等于 做H图,图4是对20个最大顺序统计量(超额数) 4.3和8时用两种估计方法拟合的尾部累积分布函 做H图(图中虚线为形状参数取值的上下限)。 数图。 14 1.8 12 1.6h 翰 1.4 10 1.2 8 1.0h 0.8 0.6 0.4 0.2 0 12345678910 1015 20 25 阅值(亿元) 排序数据 图1样本超额均值函数因 图2Q-Q图 Figure 1 SMEF Plot Figure 2 Q-Q Plot 1.2 10---1- 、 0.8 0.6 0.4 0.2 02468101214161820 68101214161820 阅值 排序统计量 图3Hi出图(对阁值) 图4H图(对超额数数量) Figure 3 Hill Plot threshold) Figure 4 Hill Plot (exceedances) 万方数据
管理科学 2007年6月 对于小样本而言,自助法(Bootstrap)提供了参数 的可靠估计m,博1,有助于利用有限的信息来提高估 计质量。重复1 Ooo次再抽样后,由Bootstrap样本均 值得到的损失强度统计量见表2,可以看出,经验数 据是明显右偏、尖峰厚尾的。 表2内部欺诈损失强度描述 Table 2 Intemal F翰ud L0蟠SeVerity 单位:亿元 使用POT模型首先需要根据样本确定阈值。一 般的,综合使用超额均值函数图(图1)、Q—Q图(图 2)、Hin图(图3和图4)来确定阈值u。图2是对指 数分布(亭=0)的Q—Q图,经验数据曲线进一步证实 了数据的厚尾特征。图3是用全部样本对不同阈值 做Hill图,图4是对20个最大顺序统计量(超额数) 做Hill图(图中虚线为形状参数取值的上下限)。 1R 迥 埋 鞴 剐 蜜 鼬 6 5 慧4 垂s 2 1 O 阈值(亿元) 图1样本超额均值函数图 Figure l SMEF PlOt …辩. ….j±~:一 ,1- 、-.冬≮::::::.:.人 、。‘~t。一.. \ …。‘’。“ 0 2 4 6 8 10 12 14 16 18 20 阈值 图3 Hill图(对阈值) Figure 3 Hm Plot(thr髂hom) 在超额均值函数图(图1)中,超过4亿元的部 分近似倾斜向上的直线。图3和图4中可以看出阈 值从3亿元(20个超额数)形状参数f的图形开始 趋于稳定。结合Q—Q图(图2),本研究选择阈值为 4.3亿元(对应于16个超额数)。当然,理论上可以 进一步选择更高的阈值,但此时超额数将更少。 4.2估计结果及比较 由于本研究中内部欺诈损失的样本数较少,而 阈值的数额较大,为了更全面的比较两种估计方法, 将与一组阈值对应的估计结果做了比较,见表3。 表3中括号内是估计的标准误差。从表3中可 以看出,在小样本的情况下,贝叶斯MCMc方法的估 计结果明显优于极大似然估计。在阈值从3亿元增 至9.3亿元的过程中,极大似然估计变得很不稳定, 在样本超额数小于5个的情况下,形状f的极大似 然估计变为负数,特性已经发生了改变。相比之下, McMc方法不但误差小得多,而且被估参数沿不同 阈值的升高也相对稳定。图5、图6分别为阈值等于 4.3和8时用两种估计方法拟合的尾部累积分布函 数图。 籁 迥 求 挺 求 籁 避 籁 弧 篓 避 排序数据 图2 Q·Q图 ngure 2 Q·Q Plot 排序统计量 图4 Hm图(对超额数数量) Figure 4 HⅢPlot(exc∞dances) 万方数据
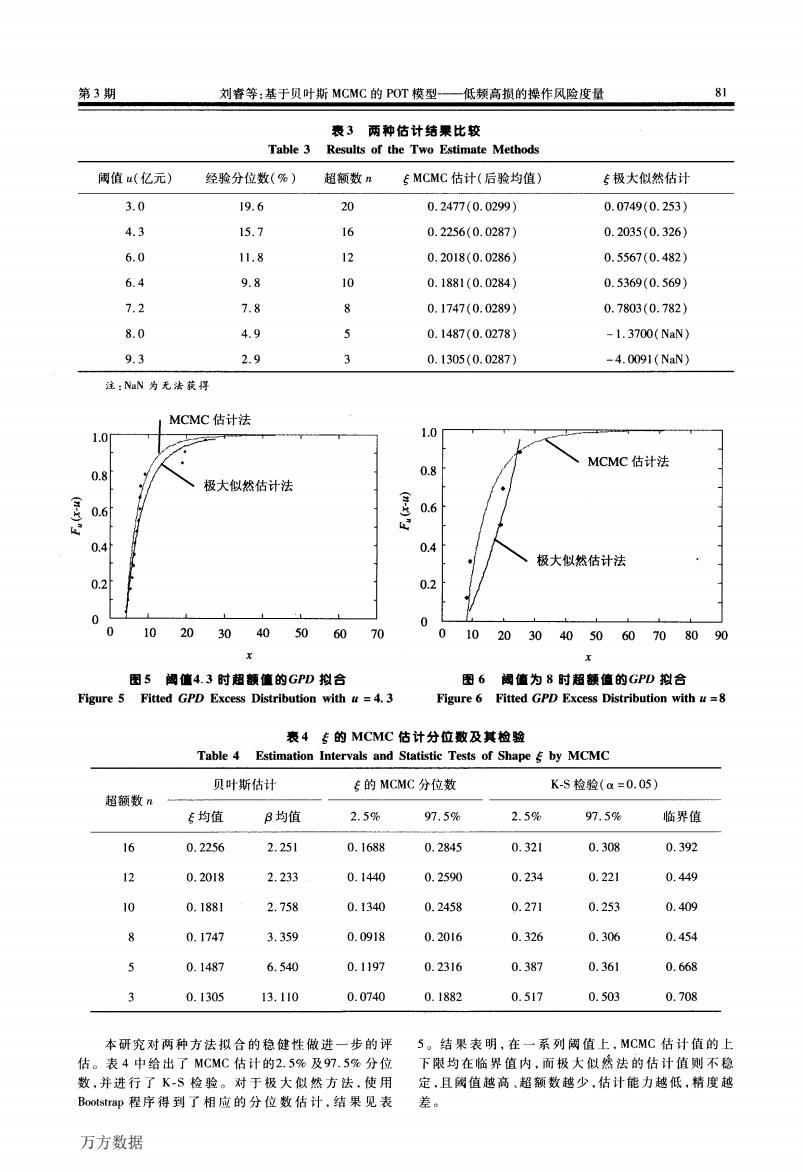
第3期 刘睿等:基于贝叶斯MCMC的POT模型—低频高损的操作风险度量 表3两种估计结聚比较 Table 3 Results of the Two Estimate Methods 阈值u(亿元) 经验分位数(%) 超额数n EMCMC估计(后验均值) 极大似然估计 3.0 19.6 20 0.2477(0.0299) 0.0749(0.253) 4.3 15.7 16 0.2256(0.0287) 0.2035(0.326) 6.0 11.8 12 0.2018(0.0286) 0.5567(0.482) 6.4 9.8 10 0.1881(0.0284) 0.5369(0.569) 7.2 7.8 8 0.1747(0.0289) 0.7803(0.782) 8.0 4.9 5 0.1487(0.0278) -1.3700(NaN) 9.3 2.9 3 0.1305(0.0287) -4.0091(NaN) 注:NaN为无法获得 MCMC估计法 1.0 1.0 MCMC估计法 0.8 0.8 极大似然估计法 0.6 0.6 0.4 0.4 极大似然估计法 0.2 0.2 0 0 102030405060 70 0 10 2030405060708090 x 图5阈值4.3时超额值的GPD拟合 图6阈值为8时超额值的GPD拟合 Figure 5 Fitted GPD Excess Distribution with u=4.3 Figure 6 Fitted GPD Excess Distribution with u=8 表4专的MCMC估计分位数及其检验 Table 4 Estimation Intervals and Statistic Tests of Shape by MCMC 贝叶斯估计 E的MCMC分位数 K-S检验(a=0.05) 超额数n 5均值 B均值 2.5% 97.5% 2.5% 97.5% 临界值 16 0.2256 2.251 0.1688 0.2845 0.321 0.308 0.392 12 0.2018 2.233 0.1440 0.2590 0.234 0.221 0.449 10 0.1881 2.758 0.1340 0.2458 0.271 0.253 0.409 0.1747 3.359 0.0918 0.2016 0.326 0.306 0.454 0.1487 6.540 0.1197 0.2316 0.387 0.361 0.668 3 0.1305 13.110 0.0740 0.1882 0.517 0.503 0.708 本研究对两种方法拟合的稳健性做进一步的评 5。结果表明,在一系列阑值上,MCMC估计值的上 估。表4中给出了MCMC估计的2.5%及97.5%分位 下限均在临界值内,而极大似然法的估计值则不稳 数,并进行了K-S检验。对于极大似然方法,使用 定,且阈值越高、超额数越少,估计能力越低,精度越 Bootstrap程序得到了相应的分位数估计,结果见表 差。 万方数据
笙二墨2一.一. 型童箜:茎王!!竺±斯McMc的PoT模型——低频高损的操作风险度量 81 表3两种估讨结粟比较 Table 3 Results of the Two Estimate Methods ——————————————————————————————————————————————————一一 阈值M(亿元) 经验分位数(%) 超额数凡 fMcMc估计(后验均值) f极大似然估计 j-u 19·6 20 0.2477(0.0299) 0.0749(0.253) q‘j I,·7 16 0.2256(0.0287) 0.2035(0.326) 6.0 6.4 7.2 11.8 9.8 7.8 12 10 8 0.2018(0.0286) 0.5567(0.482) 0.188l(0.0284) 0.5369(0.569) 0.1747(0.0289) 0.7803(0.782) 8·O 4-9 5 O.1487(0.0278) 一1.3700(NaN) 9·3 2.9 3 O.1305(O.0287) 一4.009l(NaN) ———————————————————————————————————————————————一 注:NaN为无法获得 § 3 心 图5 阈值4.3时超额值的础D拟合 FigIlre 5 ntted船D Exce豁Distribution诮th“=4.3 § 6 心 X 图6 阈值为8时超额值的凹D拟合 Figure 6 Fitted G肋Excess Distmuti蛐with“=8 表4孝的McMc估计分位数及其检验 TabIe 4 Estimation Inter、,als and Statistic Tests of Shape f by MCMC ——————————————————————————————————————————————————————二_ 超额数n——~——————————————二——~一 .。.. 贝叶斯估计 亭的McMc分位数 K.s检验(0【:O.05) 亭均值 卢均值 2.5% 97.5% 2.5% 97.5% 临界值 ———————————————————————————————————————————————————————————一 16 0.2256 2.25l 0.1688 0.2845 O.321 0.308 0.392 12 10 8 5 0.2018 0.188l 0.1747 0.1487 2.233 2.758 3.359 6.540 0.1440 0.1340 0.0918 0.1197 0.2590 0.2458 0.2016 0.2316 0.234 0.271 0.326 0.387 0.221 0.253 0.306 0.361 0.449 0.409 0.454 0.668 3 0.1305 13.110 0.0740 0.1882 0.517 0.503 0.708 ——————————————————————————————————————————————————————一 本研究对两种方法拟合的稳健性做进~步的评 估。表4中给出了MCMC估计的2.5%及97.5%分位 数,并进行了K—s检验。对于极大似然方法,使用 Bootstrap程序得到了相应的分位数估计,结果见表 5。结果表明,在一系列阈值上,McMc估计值的上 下限均在临界值内,而极大似然法的估计值则不稳 定,且阈值越高、超额数越少,估计能力越低,精度越 差。 万方数据
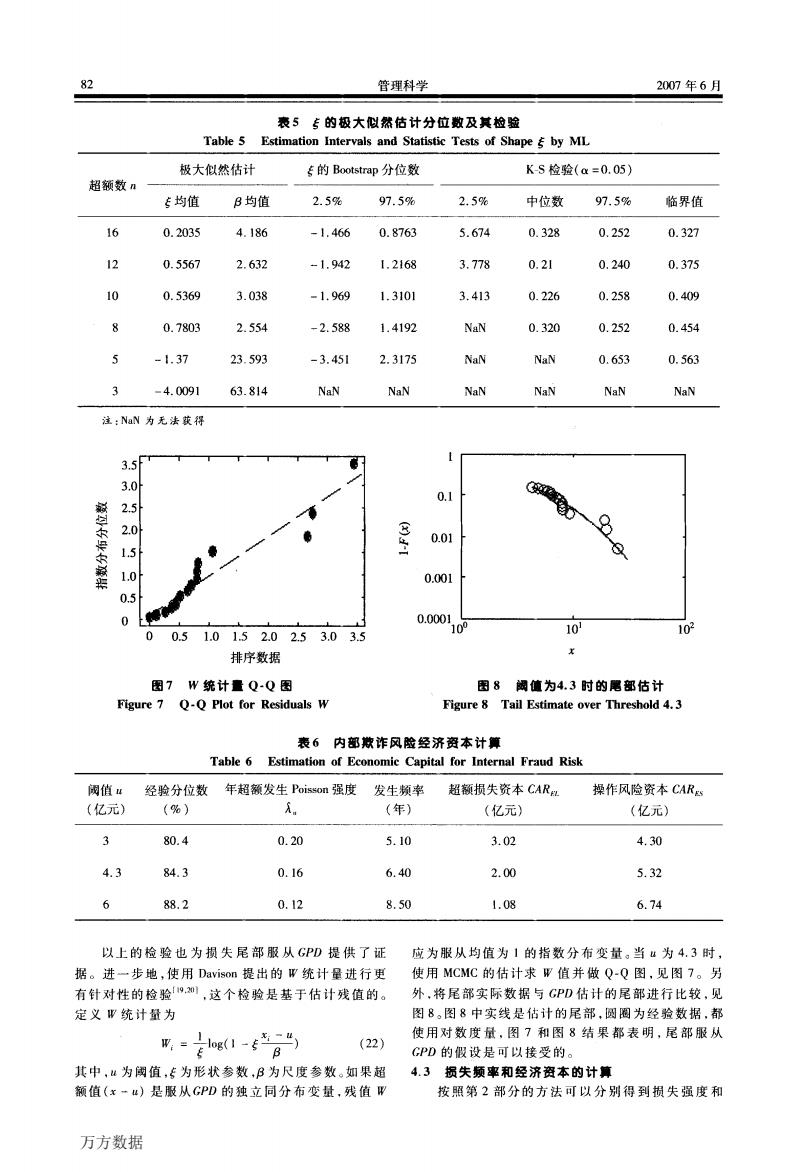
82 管理科学 2007年6月 表5专的极大似然估计分位数及其检验 Table 5 Estimation Intervals and Statistic Tests of Shape by ML 极大似然估计 专的Bootstrap分位数 KS检验(=0.05) 超额数n 专均值 B均值 2.5% 97.5% 2.5% 中位数 97.5% 临界值 16 0.2035 4.186 -1.466 0.8763 5.674 0.328 0.252 0.327 12 0.5567 2.632 -1.942 1.2168 3.778 0.21 0.240 0.375 10 0.5369 3.038 -1.969 1.3101 3.413 0.226 0.258 0.409 0.7803 2.554 -2.588 1.4192 NaN 0.320 0.252 0.454 5 -1.37 23.593 -3.451 2.3175 NaN NaN 0.653 0.563 -4.0091 63.814 NaN NaN NaN NaN NaN NaN 注:NaN为无法获得 3.5 3.0 0.1 0 2 8 0.01 1.0 0.001 0.5 0.000 10 00.51.01.52.02.53.03.5 10 102 排序数据 图7W统计置Q-Q图 图8锅值为4.3时的吧部估计 Figure 7 Q-O Plot for Residuals w Figure 8 Tail Estimate over Threshold 4.3 表6内部欺诈风险经济资本计算 Table 6 Estimation of Economic Capital for Internal Fraud Risk 阀值4 经验分位数 年超额发生Poisson强度 发生频率 超额损失资本CAR, 操作风险资本CARg (亿元) (%) A。 (年) (亿元) (亿元) 80.4 0.20 5.10 3.02 4.30 4.3 84.3 0.16 6.40 2.00 5.32 6 88.2 0.12 8.50 1.08 6.74 以上的检验也为损失尾部服从GPD提供了证 应为服从均值为1的指数分布变量。当u为4.3时, 据。进一步地,使用Davison提出的W统计量进行更 使用MCMC的估计求W值并做Q-Q图,见图7。另 有针对性的检验,,这个检验是基于估计残值的。 外,将尾部实际数据与GPD估计的尾部进行比较,见 定义W统计量为 图8。图8中实线是估计的尾部,圆圈为经验数据,都 属=e1-6角的) 使用对数度量,图7和图8结果都表明,尾部服从 (22) GPD的假设是可以接受的。 其中,“为阈值,专为形状参数,B为尺度参数。如果超 4.3损失频率和经济资本的计算 额值(x一u)是服从GPD的独立同分布变量,残值W 按照第2部分的方法可以分别得到损失强度和 万方数据
82 管理科学 2007年6月 注:NaN为无法获得 籁 q 求 忙 求 籁 靼 排序数据 图7 w统计量Q·Q圈 Figure 7 Q-Q Hot for Residuals W S ‰ 二 图8 阈值为4.3时的尾部估计 Figure 8 Tail Estimate over Threshold 4.3 表6 内部欺诈风险经济资本计算 Table 6 Estimation of Econolllic Capital for Inter眦I Fraud硒sk 以上的检验也为损失尾部服从GPD提供了证 据。进一步地,使用Davison提出的形统计量进行更 有针对性的检验¨9’2…,这个检验是基于估计残值的。 定义形统计量为 1 z—H 阢2言109(1一f‘广) (22) 其中,H为阈值,f为形状参数,卢为尺度参数。如果超 额值(x一“)是服从GPD的独立同分布变量,残值形 应为服从均值为1的指数分布变量。当¨为4.3时, 使用McMc的估计求形值并做Q—Q图,见图7。另 外,将尾部实际数据与GPD估计的尾部进行比较,见 图8。图8中实线是估计的尾部,圆圈为经验数据,都 使用对数度量,图7和图8结果都表明,尾部服从 GPD的假设是可以接受的。 4.3损失频率和经济资本的计算 按照第2部分的方法可以分别得到损失强度和 万方数据

第3期 刘睿等:基于贝叶斯MCMC的POT模型一低频高损的操作风险度量 83 频率的估计,进而根据(13)式得到经济资本的估计, [6 V Chavez-Demoulin,P Embrechts,J Neslehova. 具体结果见表6。 Quantitative Models for Operational Risk:Extremes, 表6中第3列是估计的超额损失发生强度,最后 Dependence and Aggregation[J].Journal of Banking 一列是以ES为强度计算的欺诈风险经济资本。可 &Finance,2006,30(10):2635-2658 以看出,國值的较大变化对风险资本的估计有一定 [7]MeNeil A,Frey R,Embrechts P.Quantitative Risk 影响,但小于阈值的变化幅度。实际的估算中可以 Management:Concepts,Techniques and Tools[M]. 根据银行的规模,经营范围、内控状况等因素对选定 Princeton:Princeton University Press,2005. 的阔值加以修正。 [8]Pfeifer D,Neslehova J.Modeling and Generating De- 从结果中可以看出,一个中等规模的中国商业 pendent Risk Process for IRM and DFA[J].ASTIN 银行平均5年就发生一起损失在3亿元以上的巨额 Bulletin,2004,34(2):333-360. 内部欺诈事件,这个频率是惊人的,证明中国商业银 [9]Chavez-Demoulin V,Embrechts P.Smooth Extremal 行具有相当巨大的内部欺诈风险。为了防御内部欺 Models in Finance and Insurance J].Joumal of 诈损失,相应的银行经济资本接近了5亿元,这对于 Risk and Insurance,2003,71(2):183-199. 一个中等规模的中国商业银行而言是极端沉重的负 [10]Ferro C.Segers J.Inference for Clusters of Extreme 担。 Values[J].Journal of the Royal Statistical Society, 2003,65(2):545-556. 5结论 [1I Medova E A.Measuring Risk by Extreme Values POT模型对低频高损的内部欺诈风险进行估计 [J].Risk,2000,(11):20-25. 时具有简单明确的优势,它不需要对两者之间的关 [12]P de Zea Bermudez,M A Amaral Turkman.Bayesian 系(往往是未知的)进行假定,也不需要用模拟米合 Approach to Parameter Estimation of the Generalized 成操作风险总额损失分布,可以直接通过对POT参 Pareto Distribution J].Test (Joumal of Statistics 数的估计得到经济资本的估计,这大大提高了损失 and Probability),2003,12(1):259-277. 分布法的使用效率,也便于对估计的误差进行控制。 [13]Berger James O.Statistical Decision Theory and 但是,针对内部欺诈这种典型的低频率高强度的损 Bayesian Analysis second ed.)M ]Beijing: 失类型,数据稀少是一个本质的问题。引人Bayesian World Publishing Corporation,1998. MCMC方法对POT模型进行估计是一个有效的办 [14]Siddhartha Chib.Markov Chain Monte Carlo Meth- 法。研究表明,在小样本情况下贝叶斯MCMC方法 ods:Computation and Inference[C】∥Heckman J 比极大似然估计更稳定,误差更小。使用样本损失 J,Leamer E.Handbook of Econometrics.V North- 数据对中国商业银行的内部欺诈风险进行估算,结 Holland.Amsterdam Springer-Verlag,2001:3569- 果证实,银行的内部欺诈风险相当惊人,为此银行需 3649. 要配备大量的经济资本,这个问题的严重性已经令 [15]Siddhartha Chib,Nardari F,Shephard N.Markov 我们无法回避。 Chain Monte Carlo Methods for Stochastic Volatility Models J].Journal of Econometrics,2002,108(2): 参考文献: 281-316. [1]Basel II.International Convergence of Capital Meas- [16]Gilks W R,Best N G,Tan KK C.Adaptive Rejec- urement and Capital Standards[R].Switzerland:Ba- tion Metropolis Sampling within Gibbs Sampling[J]. sel Committee on Banking Supervision,2004 Applied Statistics,1995,44(4):455-472. [2]Klugman Stuart A,Harry H Panjer,Gordon E Will- [17]Efron B,Tibshirani R.An Introduction to the Boot- mot.Loss Models:From Data to Decisions second strap M ]London:Chapman and Hall,1993. ed.)M ]New York:John Wiley Sons,Ine.. [18]Cheng-Der Fuh,Edward H Ip.Bootstrap and Bayes- 2004. ian Bootstrap Clones for Censored Markov Chains [3]樊欣,杨晓光.我国银行业操作风险的蒙特卡 [J].Journal of Statistical Planning and Inference, 罗模拟估计[J].系统工程理论与实践,2005, 2005,128(2):459-474. (5):12-19 [19]Davison A C,Smith R L.Models for Exceedances o- [4]Reiss R,Thomas M.Statistical Analysis of Extreme ver High Thresholds with Discussion )J].Joural Values from Insurance,Finance,Hydrology and Other of the Royal Statistical Society B),1990.52(3): Fields second ed.)[M].Basel:Birkhauser Ver- 393-442. ag,2001. [20]Jan Beirlant,Yuri Goegebeur.Local Polynomial Maxi- [5]Leadbetter M R.On a Basis for Peaks over Thresh mum Likelihood Estimation for Pareto-type Distribu- old'Modeling J].Statistics Probability Letters, tions[J].Journal of Multivariate Analysis,2004,89 1991,12(4):357-362, (1):97-118. 万方数据
第3期 刘睿等:基于贝叶斯McMc的POT模型——低频高损的操作风险度量 83 频率的估计,进而根据(13)式得到经济资本的估计, 具体结果见表6。 表6中第3列是估计的超额损失发生强度,最后 一列是以ES为强度计算的欺诈风险经济资本。可 以看出,阈值的较大变化对风险资本的估计有一定 影响,但小于阈值的变化幅度。实际的估算中可以 根据银行的规模、经营范围、内控状况等因素对选定 的阈值加以修正。 从结果中可以看出,一个中等规模的中国商业 银行平均5年就发生一起损失在3亿元以上的巨额 内部欺诈事件,这个频率是惊人的,证明中国商业银 行具有相当巨大的内部欺诈风险。为了防御内部欺 诈损失,相应的银行经济资本接近了5亿元,这对于 一个中等规模的中国商业银行而言是极端沉重的负 担。 5结论 POT模型对低频高损的内部欺诈风险进行估计 时具有简单明确的优势,它不需要对两者之间的关 系(往往是未知的)进行假定,也不需要用模拟来合 成操作风险总额损失分布,可以直接通过对POT参 数的估计得到经济资本的估计,这大大提高了损失 分布法的使用效率,也便于对估计的误差进行控制。 但是,针对内部欺诈这种典型的低频率高强度的损 失类型,数据稀少是一个本质的问题。引入Bayesian McMc方法对POT模型进行估计是一个有效的办 法。研究表明,在小样本情况下贝叶斯MCMC方法 比极大似然估计更稳定,误差更小。使用样本损失 数据对中国商业银行的内部欺诈风险进行估算,结 果证实,银行的内部欺诈风险相当惊人,为此银行需 要配备大量的经济资本,这个问题的严重性已经令 我们无法回避。 参考文献: [1] Basel II.Intemational convergence of capital Meas— urement and capital standards[R].switzerland:Ba— sel Committee on Banking Supendsjon,2004. [2] Klugman stuan A,Harry H Panjer,Gordon E will一 Ⅱlot.Loss Mode】s:From Data to Decjsjons (second ed.)[M].New York:John wiley&sons,Inc., 2004. [3]樊欣,杨晓光.我国银行业操作风险的蒙特书 罗模拟估计[J].系统工程理论与实践,2005, (5):12一19, 『4] Reiss R.Thomas M.Statistical Analvsis of Extreme Values fI.om Insurance,Finance,Hydmlogy and 0ther Fields(second ed.)[M].Basel:Birkh冱user Ver— lag,2001. 『5]Leadbetter M R.0n a Basis for Peaks over ThI.esh. old’Modeling[J].statistics&Proha}Jility Letters, 199l,12(4):357—362. [6] V Chavez—Demoulin,P Embrechts,J Ne吾lehov矗. Quantitative Models for 0perational Risk:Extremes, Dependence and Aggregation[J].Joumal of Banking &Finance,2006,30(10):2635—2658. [7] McNeil A,Frey R,Embrechts P.Quantitative Risk Management:concepts,’rechniques and Tools[M]. Princetoll:Princeton University PI℃ss,2005. [8] Pfeifer D,Ne茑lehov丘J.Modeling and cenerating De— pendent Risk Pmcess for IRM and DFA[J].AsTIN Bulletin,2004,34(2):333—360. 9 Ch8vez.Demoubn V,Embrechts P.smooth Extremal Models in Financ套 and Insurance『J], Joumal of Risk and Insurance,2003,7l(2):183一199. [10]Fbrro c,segers J.IrIference for clusters of Extreme Values[J].Joumal o“he Royal statistical society, 2003,65(2):545—556. [1 1] Medova E A.Measuring Risk by Extreme VaIues [J].Risk,2000,(11):20—25. [12]P de zea Be丌11udez,M A Amaral Turkman.Bayesian Appmach to Parameter Estimation of the Generalized Pareto Distribution[J].Test (Joumal 0f statistics and Pmbability),2003,12(I):259—277. [1 3] Berger James 0.statistical Decision‘I’heory and Bayesian Analysis(second ed.)[M].Beijing: World Publishing Corporation,1998. 『14]Siddhartha Chib.Markov Chain Monte Cado Meth— ods:computation and InfeIIence[c]∥Heckman J J.Leamer E.Handbook of Econometrics.V Nonh. Honand.Amsterdam:Springer—Verlag,2001:3569— 3649. [15] Siddhanha chib,Nardari F,Shephard N.Markov Chain Monte Carlo Methods for Stochastic Volatility Mod≤lsl J].Joumal“Econometrics,2002,108(2): 281—316. [16]Gilks w R,Best N G,Tan K K c.Adaptive Rejec— tion Metmpolis sampli“g within Gibbs sampling[J]. Applied Statistics,1995,44(4):455—472. [1 7] Ef而n B,Tibshirani R.An Introduction to the Boot— slrap[M].London:chapman and Han,1993. [18]cheng—Der Fuh,Edward H Ip.Bootstrap and Bayes— ian Bootstrap Clones for Censored Markov Chains [J].Joumal of sta“s“cal Planning and Inference, 2005,128(2):459—474. [19]Da“son A c,smith R L.Models for Exceedances o. ver High Thresholds(with Discussion)[J].Joumal of the Royal Statistical Society(B),1990,52(3): 393—442. [20]Jan Beirlant,Yuri Goegebeur.Local Polynomial Maxi— mum Likelihood Estimatjon for Pareto—type Distrihu— tions[J].Jounlal of Multivariate Analysis,2004,89 (1):97一118, 口 万方数据