《随机模拟方法与应用 Stochastic Simulation Methods and Its Applications》教学资源（论文资料）48 中国商业银行操作风险损失分布甄别与分析——基于贝叶斯MCMC频率方法.pdf_大学文库

第32卷第173期财经理论与实践（双月刊） Vol.32 No.173 2011年9月 THE THEORY AND PRACTICE OF FINANCE AND ECONOMICS Sep.2011 ·金融与保险· 中国商业银行操作风险损失分布甄别与分析：基于贝叶斯MCMC频率方法吴俊，宾建成2 (1.厦门大学经济学院，瓶建厦门361005,2.上海对外贸易学院国际贸易系，上海201620)· 摘要：确切的操作风险损失分布保障了风险度量的准确性。对银行操作风险损失数据的分析，国外学者一致认为操作风险分布近似泊松分布或负的贝奴里分布。基于中国商业银行1994~2008年的操作风险损失数据，通过对操作风险损失分布的检险、贝叶斯马尔科夫蒙神卡洛颜平分析，发现中国商业银行操作风险损失分布近似服从广义极值分布(Generalized Extreme,Value), 关键词：操作损失；贝叶斯：马尔科夫链：蒙特卡洛中田分类号：F832.33 文献标识码：A文章编号：1003一7217(2011)05一0008-07 操作风险度量的模型与分布假定是为了能反映要满足一定的比率。根据损失分布方法估计操作风操作风险损失频率与操作风险损失事件，而分布的险资本需要评估总的损失分布，而总损失分布在风假定无疑是最基础和最重要的。新巴塞尔资本协议险理论中是最基本的问题。风险理论中的总风险模 (BaselⅡ、BaselⅢ)未规定银行应假定其操作风险型(Collective risk model).的缺点是损失参数和分布分布类型，但BaselⅢ中规定：银行假定的操作风险具有不确定性。在风险模型中，闭式解(Closed一损失分布能反映确实存在的、阀值之上的操作风险 form solutions)不适合操作风险典型的分布特征。数据特征，该假定应与潜在的操作损失数据及监管然而，随着现代计算机处理能力的强大，这些分布可者的期望一致(B1IS,2010))。可见，精准的操作风用数值方法直接计算。Shevchennko(20l0)的研究险损失分布为建立操作损失模型、完善操作风险计发现，数值算法能成功地计算总损失分布，这些数值量方法、操作风险管理提供确实的依据。算法可用蒙特卡洛(Monte Carlo)、Panjer recursion 一、文献回顾和傅里叶转换(Fourier transformation).方法[)。目前，国内学者基于中国银行业的操作风险损失在操作风险分析方法中，BaselⅡ就操作风险数据对操作风险进行了定量研究。樊欣、杨晓光分布假定未特别做出规定，给予银行较大的自主权， (2003)根据国内外媒体公开报道，收集了1990~2003 但银行必须能够说明操作风险分析方法能“捕获”损年的71起操作风险损失事件，并对各项业务的损失失事件的厚尾部特征(BIS,2006)2)。为了能反映操情况进行了初步分析0。李志辉(2005)介绍了国内作风险损失的厚尾部特征，在实践中，操作风险分布外商业银行操作风险损失数据的收集和主要操作风用的最多的是泊松分布，其次是负的贝奴里分布险损失数据库，并分析了商业银行内、外操作风险损 (Negative Binomial))(BIS,20l0)。随着人们对操失数据的区别们。袁德磊、赵定涛(2007)基于对国内作风险的认识，新巴塞尔资本协议(BaselⅢ)对操银行业的操作风险损失历史数据收集，从业务类型、作风险分布的假定给出了“一致性”原则，银行假定损失类型和地区分布等方面，对操作损失频度和强度的操作风险损失分布能反映确实存在的、阀值之上进行了定量分析。他们认为，内部欺诈和外部欺诈是的操作风险数据特征，该假定与潜在的操作损失数引起损失事件的主要类型)。刘容、詹原瑞、刘家鹏据及监管者的期望一致(BIS,2010) (2007)借助POT模型，基于吉布斯抽样的贝叶斯依据新巴塞尔资本协议，操作风险资本要求需 MCMC方法，对中国商业银行的内部欺诈风险进行收稿日期：2011一04一13；修回日期：2011-05-28 作者葡介：吴(1982一)，男，江西抚州人，厦门大学经济学院世界经济博士研究生，研究方向：国际金融：宾建成(1966一)，男，潮南东安人，上海对外贸易学院国际贸易系教授，博士生导师，研究方向：国际贸易与国际投资。万方数据

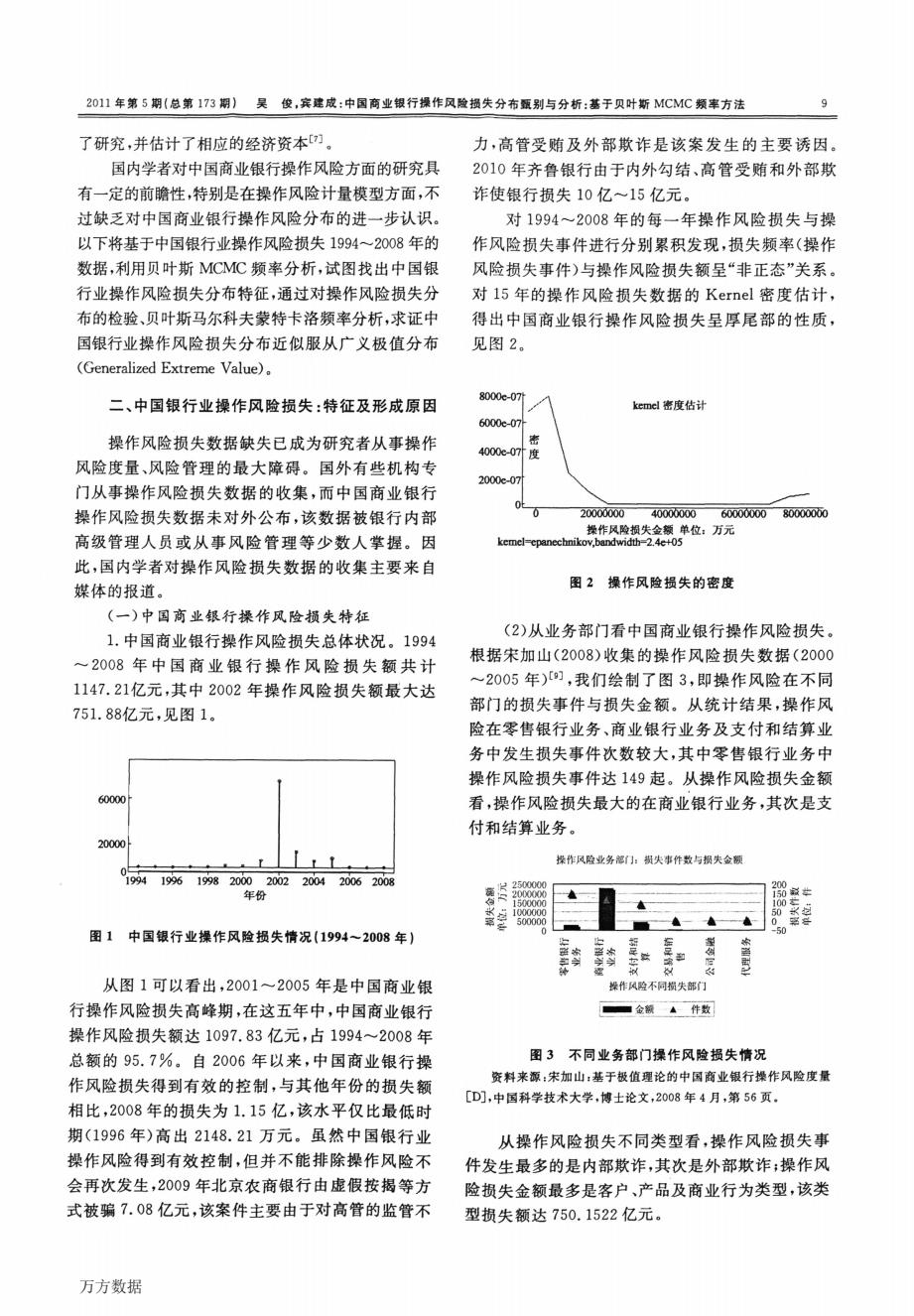
2011年第5期（总第173期）吴俊，宾建成：中国商业银行操作风险损失分布甄别与分析：基于贝叶斯MCMC频率方法 9 了研究，并估计了相应的经济资本) 力，高管受贿及外部欺诈是该案发生的主要诱因。国内学者对中国商业银行操作风险方面的研究具 2010年齐鲁银行由于内外勾结、高管受贿和外部欺有一定的前瞻性，特别是在操作风险计量模型方面，不诈使银行损失10亿~15亿元。过缺乏对中国商业银行操作风险分布的进一步认识。对1994~2008年的每一年操作风险损失与操以下将基于中国银行业操作风险损失1994~2008年的作风险损失事件进行分别累积发现，损失频率（操作数据，利用贝叶斯MCMC频率分析，试图找出中国银风险损失事件)与操作风险损失额呈“非正态”关系。行业操作风险损失分布特征，通过对操作风险损失分对l5年的操作风险损失数据的Kernel密度估计，布的检验、贝叶斯马尔科夫蒙特卡洛频率分析，求证中得出中国商业银行操作风险损失呈厚尾部的性质，国银行业操作风险损失分布近似服从广义极值分布见图2。 (Generalized Extreme Value). 二、中国银行业操作风险损失：特征及形成原因 8000e-07t kemel密度估计 6000e-07 操作风险损失数据缺失已成为研究者从事操作 4000e-07度风险度量、风险管理的最大障碍。国外有些机构专 2000e-07 门从事操作风险损失数据的收集，而中国商业银行操作风险损失数据未对外公布，该数据被银行内部 20000000 40000000 60000000 80000000 操作风险损失金额单位：万元高级管理人员或从事风险管理等少数人掌握。因 kemel-epanechnikov,bandwidth-2.4e+05 此，国内学者对操作风险损失数据的收集主要来自媒体的报道。图2操作风险损失的密度 (一)中国商业银行操作风险损失特征 1.中国商业银行操作风险损失总体状况。1994 (2)从业务部门看中国商业银行操作风险损失。 ~2008年中国商业银行操作风险损失额共计根据宋加山(2008)收集的操作风险损失数据(2000 1147.21亿元，其中2002年操作风险损失额最大达 ~2005年)们，我们绘制了图3，即操作风险在不同 751.88亿元，见图1。部门的损失事件与损失金额。从统计结果，操作风险在零售银行业务、商业银行业务及支付和结算业务中发生损失事件次数较大，其中零售银行业务中操作风险损失事件达149起。从操作风险损失金额 60000 看，操作风险损失最大的在商业银行业务，其次是支付和结算业务。 20000 操作风险业务部：损失事件数与损失金额 019941996199820002002200420062008 200 年份 500000 图1中国银行业操作风险损失情况(1994~2008年) 从图1可以看出，2001~2005年是中国商业银操作风险不同损失部门行操作风险损失高峰期，在这五年中，中国商业银行 ■金额▲件数操作风险损失额达1097.83亿元，占1994~2008年总额的95.7%。自2006年以来，中国商业银行操图3不同业务部门操作风险损失情况作风险损失得到有效的控制，与其他年份的损失额资料来源：宋加山：基于极值理论的中国商业银行操作风险度量 [D],中国科学技术大学，博士论文，2008年4月，第56页。相比，2008年的损失为1.15亿，该水平仅比最低时期(1996年)高出2148.21万元。虽然中国银行业从操作风险损失不同类型看，操作风险损失事操作风险得到有效控制，但并不能排除操作风险不件发生最多的是内部欺诈，其次是外部欺诈；操作风会再次发生，2009年北京农商银行由虚假按揭等方险损失金额最多是客户、产品及商业行为类型，该类式被骗7.08亿元，该案件主要由于对高管的监管不型损失额达750.1522亿元。万方数据

10 财经理论与实践（双月刊） 2011年第5期操作风验损失类型，损失率件数与损失金额测的信念程度及计算事件已发生后推测的信念程 150梦 422 度。这里要解答的是在观察到操作风险损失已经发 4000000 2000000 生的情况下，频率函数P,参数为日的概率是多少。内部章市外多素诈客户，产品经营中断有形贵产以及商业行为成系统出帽婴失贝叶斯理论可用公式表示为：操失类型 p(0lD)=(Dla)·p() (D) (1) 金额▲案件次数式(1)中，p(1D)表示在给定D情况下，关于0 图4不同损失类型操作风险损失情况的条件概率，p(8)为先验概率，p(D)表示在给定日资料来源：根据收樂资料整理而得。情况下，关于D的条件概率，p(D)为先验概率，通 (二)中国商业银行操作风险形成诱因：监管制过该值为常数。因此，式(1)表示了在观察到了D 度缺陷后对0的修正。从监管制度看，中国商业银行操作风险的形成有由于一些复杂模型，贝叶斯分析不能得到闭式其特殊的背景，即在商业银行改革过程中，监管当局解，因此，在对这些复杂模型进行分析时，需要用对商业银行监管制度的疏忽。 MCMC方法。 1.商业银行监管制度漏洞，人为因素是操作风 (二)贝叶斯MCMC算法险泛滥的主要诱因。主要表现为风险管理体制不完马尔科夫蒙特卡洛(MCMC)方法是以构建马善，降低了作案成本，滋生了银行内部员工利用职务尔科夫链为基础的抽样概率分布算法，该方法得到之便进行的违法行为（员工内部欺诈、内外勾结）。的分布较接近真实分布。简单的贝叶斯MCMC过 2.产权制度不明晰。商业银行的产权属于国家程有以下几个步骤： (人民所有)，而在执行过程中，中央政府和各级地方 (1)在参数空间⊙上构建马尔科夫链，其均衡政府作为国家的代表执行所有权。中央政府和地方分布是p(lD); 政府对商业银行的管理可能会偏离一般金融企业目 (2)运行马尔科夫链抽样过程；标，而侧重转向发展经济和社会稳定。从信息经济 (3)构建马尔科夫链均衡分布算法。本文用学角度，商业银行可视为委托人，商业银行的管理人 Metropolis--Hasting(MH)算法。可视为代理人。在实践中，委托人与代理人的目标 MH算法是一类常用的构造马尔科夫链的方不一致，代理人的策略偏离委托人的最优目标。产法。MCMC方法的精髓在于构造合适的马尔科夫权制度不明晰易导致监管当局对银行风险监管不链，因此，算法的主要目的是对马尔科夫链{X,|t= 力，代理人的行为或策略得不到有力的监督，从而埋 0,1,2,…},在给定一个X所处的状态下，产生下下了操作风险滋生的种子。一步的状态X+1。MH算法构造如下： 3.内控制度缺失易滋生操作风险。加强银行内 (1)构造合适的提议分布g(·|X+:): 部操作风险的控制，必须完普银行系统内部控制制 (2)从g(·|X+1)中产生Y；度。在中国特殊国情下，中国商业银行的稳健目标 (3)若Y被接受，则X+1=Y,否则X+1=X:。不一致，因此，内部控制制度未起到实质性作用。从提议分布的选择要使得产生的马尔科夫链的平岗位职责角度来看，还没有形成完整、科学、有效的稳分布为目标抽样分布，需要满足的正则化条件包岗位职责体系，部门之间、岗位之间普遍存在界面不括不可约、正常返、非周期。以下验证通过MH方法清、职责不明现象，无法建立起持续监控和改进的内得到马尔科夫链分布f为平稳分布。验证如下： (1)从g(·|X+1)中产生Y; 控机制。 (2)从U(0,1)中产生U; 4.缺乏有效的操作风险管理框架。以信息披露为例，一旦操作风险发生，对风险损失的确定等需要 ③活U<g代爱则接受￥，并令X=Y, 经过层层向上披露，信息披露机制不灵活。否则X+1=X; 三、操作损失分析模型：贝叶斯MCMC频率模型 (4)增加t,返回到(1)。上述算法接受概率为： (一)贝叶斯推断 f(Y)g(X.IY) (2) 贝叶斯推断即用数值方法估计事件未发生时推 a(X,Y)=min （1,X)gYx 万方数据

2011年第5期（总第173期）吴使，宾建成：中国商业银行操作风险损失分布甄别与分析：基于贝叶斯MCMC频率方法 11 通过以上可以看出，通过MH算法构造的链满第t十1步迭代的第i步中，使用MH算法更新Xt。足马尔科夫性质，因为X+1仅依赖于X。但MH 做法如下：算法构造的链是否非周期不可约则取决于提议分布对i=1,…k,从第i个提议分布q:(·|X, 的选取，如果是非周期不可约则链具有唯一的平稳 X:-)中产生Y,这里，X-=（X+11,X1…, 性。事实上，当r≠s时，转移核为： X,t),然后以概率a(X,-4,Xd,Y)=min K(r,s)=p(s|X.=r)≈ P(XH1∈s±h,TA|X,=T)/2h= 红完》者檬接是则令X+1d=Y:否则令X+i=Xi。 g(y I r)a(r,y)dy/2h- 四、实证分析 g(s I r)a(r,s),h-0 (一)操作风险损失分布的甄选当r=s时，假定操作风险损失服从正态分布、对数正态分 K(r,s)=p(s|X,=r)≈ 布、广义极值分布、泊松分布中的某一种分布，其分 P(X+1∈r±h,TAIX,=r)/2h+ 布函数形式分别为： P(X+任r土h,TA|X,=r)= (1)正态分布：N(40).随机变量X服从正态分布 3 a(r,y)g(y I r)dy/2h+ ~Nuo,fx）=与ep(-22)d>0, 2 [1-a(r,y)]g(y I r)dy- μ∈R,x∈R;期望、方差分别表示为：E[门=u, yh Var[X幻=d。 a(r,rgr|r）+1-a(r,]g(y|r）dy,h→0 (2)对数正态分布：LN(u,a),随机变量X服从对数正态分布记为X~LN(μ，c),概率密度函数表因此有：K(r,)=a(r,s)g(s|r）+I(r=[1- “V2ap←血2，d> 示为：fx)=1 2a2 a(r,y)]g(y|r）d,从而对r=s时，方程成立，对任意r ≠s时有： 0,4∈R,x>0;期望、方差分别表示为：E[X]= K(r,s)f(r)=a(r,s)g(sI r)= et,Var[x]=eim(e-1). m(8)a1- (3)泊松分布：P(a),随机变量X服从泊松分布记为X~P(a),概率密度函数表示为：Pr(N=k) min (g(s I r)f(r),f(s)g(rIs))= a(s,r)g(r Is)f(s)=K(s,r)f(s) -行eA>0,∈《01,2，…期望、方卷分别表因此，f满足平衡方程，从而f为平稳分布。示为：E[N]=λ，Var[N]=。 (三)单一组成MH算法 (4)广义极值分布：GPV(u,o,)。表示为随机当状态空间为多维时，不整体更新X,而是对其分变量X服从广义极值分布记为X~GEV(4,o,), 量进行逐个更新，即称为单一组成H算法概率密度函数表示为：fx)-(x)。心其中， (Single-component Metropolis Hastings Algorithms) (1+(E二)-ei迁E≠0 样做更方便和更有效率。记： t(x)= A∈R, X=（X1,…X) e mle if话=0 X,-4=（X.1,…X1,X.1…X,k）分别表示在第t步链的状态，以及在第t步除第。>0,∈R;期望，方差分别为：E式X灯一u-号+ i个分量外其他分量的状态。f(x)=f(x1,…x)为是g,Var[X灯=(8：-i). 目标分布，f八xx+1)= f(x)一表示工利用以上分布函数，对中国1994~2008年间商 f(x1,…,x)dxi 业银行操作风险损失数据进行拟合，数据拟合结果对其他分量的条件密度。见图5。图5表示，广义极值分布(GEV能较好地则逐分量的MH算法更新X,是由k步构成：令拟合中国银行业操作风险损失”。 X:表示在第t次迭代后X,第i个分量的状态，则在万方数据

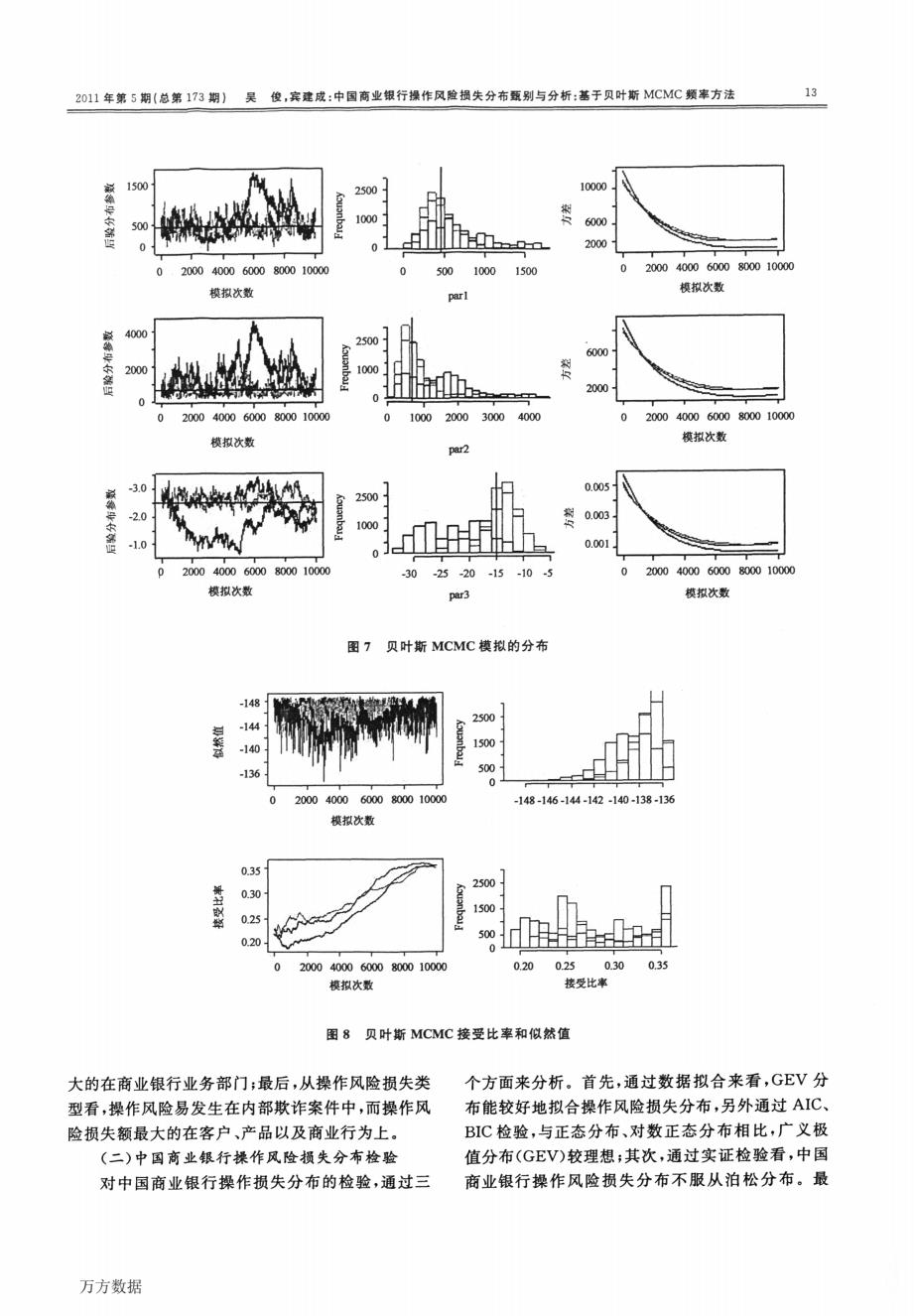
财经理论与实践（双月刊） 2011年第5期 0.90 Kolmogorov-Smirnov goodness-of--fit假设检验方法。原假设：中国商业银行操作风险损失分布服从率0.50 泊松分布；备择假设：中国商业银行操作风险损失分 0.25 00s2 -是v 布不服从泊松分布。K一S检验即随机变量X是否 100200 500100020005000100002000050000 服从已假设的分布。对泊松分布的检验见表1。表操作风险损失单位：万元 1显示，中国商业银行操作风险损失分布不服从泊图5正态分布、对数正态分布、广义极值分布松分布。另外，中国商业银行操作风险损失累积分对操作风险的拟合布不支持中国商业银行操作风险损失数据服从泊松分布，见图6。从图6可以看出，对操作风险损失金 (二)操作损失分布的检验额的经验分布与泊松分布完全不相关。因此，可以 1.泊松分布的检验。对泊松分布的检验基于认为在有限数据情况下，中国商业银行操作风险损失分布不适合采用泊松分布。表1对泊松分布的检验 =1.5 1=2.5 A=5 A=10 A=20 A=mean(x) H 1 1 1 1 1 1.797e-0141.797e-014 1.797e-014 1.797e-0141.797e-014 2.048e-009 注：P表示概率 2.AIC、BIC判别。图5表明，从GEV分布对收集较困难，大部分学者操作风险损失数据基于媒操作风险损失有较好的拟合。从AIC、BIC判断标体报道的资料。因此，从收集媒体报道的数据模拟准看，与NORM、LN分布相比，GEV分布更好，见操作风险损失分布具有不可靠性。为了更好捕抓操表2。作风险损失分布的准确性，我们采用贝叶斯MCMC 频率方法。经验累积分布 3.贝叶斯MCMC频率分析。基于1994~2008 1.0 0.9 年收集的操作风险数据，采用贝叶斯MCMC频率 0.8 方法分析GEV分布是否符合中国商业银行操作风 0.7 险损失分布。在贝叶斯MCMC频率分析中，迭代常06 密0.5 的次数为10000次，得到了相应的后验分布参数、后度04 验分布图及模拟的参数方差(partl、part2,part3), 0.3 经整分布见图7。从图7可以看出，对于模拟出的参数分布 02 0.1 图符合厚尾部分布特征，并且随着模拟次数的增加， 0.0 参数间的方差逐渐减小。 0 损失额 X10 在贝叶斯MCMC频率分析中，我们检验了 MCMC的可接受率，结果表示随着模拟次数的增图6 商业银行操作风险损失分布的经验累计分布与泊松分布比较加，接受比率逐渐增加，见图8。五、结论表2NORM,LN、GEV的AIC、BIC判别 NORM LN GEV (一)中国商业银行操作风险损失分布特征 AIC 341.3 276.9 274.3 以上基于中国商业银行1994~2008年操作风 BIC 342.7 278.3 276.4 险损失数据，分析了操作风险损失在银行业间的分布情况，具体体现在以下几个方面：首先，从总体看，根据上面的分析，中国商业银行操作风险损失 2001~2005年是中国商业银行操作风险损失高峰分布较符合GEV分布，然而，由于操作风险损失具期；其次，从操作风险损失业务部门看，操作风险损有低频率、高损失的特点，操作风险损失数据在中国失事件发生最多的是零售银行业部门，损失金额最万方数据

14 财经理论与实贱（双月刊） 2011年第5期后，通过贝叶斯MCMC方法对GEV分布的可靠性进行检验，我们发现随着模拟次数的增加，操作风险的GEV分布的可靠性逐渐增加。注释： (三)加强商业银行操作风险管理措施 ①文中的操作风险损失数据来源于钱艺平博士论文中所涉及的中国商业银行操作风险损失金额及事件(1994~2008年). 风险管理提高效益，创造价值。自巴塞尔提倡 ②由于泊松分布考虑到需要对1的估计，因此，我们单独对泊松分全面风险管理框架以来，我国银行业对全面风险管布进行检验。理的理念还不到位，仍以信用风险管理为主，对市场参考文献：风险、操作性风险等重视不够。因此，应该从以下几 [1]BIS(2010),Consultative Document:Operational Risk-Supervi- 个方面完善对操作风险的管理： sory Guidelines for the Advanced Measurement Approaches [OL].www.bis.org. (1)与新巴塞尔资本协议要求一致，建立完善操 [2]BIS(2006).International Convergenceof Capital Measuremen- 作风险管理框架。鉴于单个银行的资产规模、业务 tand Capital Standards:A Revised FrameworkComprehensive 范围，单个银行应该建立自己的操作风险管理框架。 Version[OL].www.bis.org. [3]Pavel V.Shevchenko.Calculation of aggregate loss distributions 银行应严格按照各自的操作风险风险框架执行，并 [J].The Journal of Operational Risk,2010,5(2):3-40. 配合相关部门对操作风险进行监控。 [4幻樊旭，杨晓光.从煤体报道看中国银行业操作风险状况[U].管理评论，2003，(11)：43-47. (2)在操作风险管理框架内，建立一套自我持续 [5]李志辉.商业银行操作风险损失数据分析[J门.国际金融研究，改进的操作风险管理机制。操作风险管理机制对业 2005,(12):55-61. 务和管理流程进行实时、连续监控，不断主动识别风 [6]袁德磊，赵定涛.基于媒体报道的国内银行业操作风险损失分布研究[J].国际金融研究，2007，(2)：22一29. 险、评估风险、控制风险，实现对风险的有效控制。 [?]刘膏，詹原瑞，刘家鹏.基于贝叶斯MCMC的POT模型一低 (3)营造良好氛围的操作风险管理文化。目前，频高损失的操作风险度量[J门.管理科学，2007，(3)：76一83. 中国银行业操作风险管理停留在风险管理流程环 [8]钱艺平，VaR约束的商业银行风险管理研究[D].中南大学博士论文，2009一12. 节，缺乏体制上的风险管理或风险控制的氛围。因 [9]宋加山.基于极值理论的中国商业银行操作风险度量[D].中国此，应积极推动引导把操作风险管理问题从操作风科学技术大学博士论文，2008一04：56. 险管理的流程层面不断推向操作风险管理制度层 (责任编辑：宁晓青) 面，逐步形成以领导带头，人人参与操作风险管理的文化。 Screen and Analysis of the Operational Loss Distribution Commercial Banks in China:Based on Bayesian MCMC Algorithm Method WU Jun',BIN Jian-cheng? 1.School of Economics,Xiamen University,Xiamen,Fujian 461005,China; 2.Internatiaonal Business School,Shanghai Institute of Foreign Trade,Shanghai 201620,China) Abstract:The accuracy of operational risk loss distribution is one of the safeguards to the pre- cision of risk measurement.Scholars abroad believe that operational loss distribution of commer- cial banks is poisson or bernoulli distribution.Using the data from commercial banks in china, based on the Bayesian MCMC algorithm method,it is found that the operational risk loss distri- bution in china is the generalized extreme value distribution. Key words:Operational loss;Bayesian;Markov Chain:Monta Carlo 万方数据