计算机类本科规划教材：《离散数学》课程配套电子教案（PPT课件讲稿）第5章 函数

第5章品数 第5章函数 5.1函数的基本概念 5.2反函数和复合函数 5.3集合的基数 返回总目录

第5章 函数 第5章 函数 5.1 函数的基本概念 5.2 反函数和复合函数 5.3 集合的基数 返回总目录

第5章品数 第5章函数 5.1函数的基本概念 定义5.1.1设A和B是两个任意集合，f是A到B的二元关 系，如果对于A中的每一个元素x,都存在B中惟一元素y, 使得∈∫，则称f是A到B的函数或映射。记为fA→B。 ∈常记为y=孔x),x称为自变元或像源，y称为在作 用下x的函数值或像。 由函数的定义可以看出，函数是一种特殊的二元关 系。若f是A到B的函数。它与一般二元关系的区别如下： ①函数的定义中强调A中的每一个元素x有像，所以 A=domf。这称为像的存在性。 ②函数的定义中还强调像y是唯一的，称做像的惟一 性。像的惟一性可以描述为：设x)戶y1且x2)戶y2。如果 x=x2,那么yy2。或者，如果yy2,那么x12

第5章 函数 5.1函数的基本概念 定义5.1.1设A和B是两个任意集合，f是A到B的二元关 系，如果对于A中的每一个元素x，都存在B中惟一元素y， 使得x,yf，则称f是A到B的函数或映射。记为f：A→B。 x,yf，常记为y=f(x)，x称为自变元或像源，y称为在f作 用下x的函数值或像。 由函数的定义可以看出，函数是一种特殊的二元关 系。若f是A到B的函数。它与一般二元关系的区别如下： ①函数的定义中强调A中的每一个元素x有像，所以 A=dom f。 这称为像的存在性。 ②函数的定义中还强调像y是唯一的，称做像的惟一 性。像的惟一性可以描述为：设f(x1 )=y1且f(x2 )=y2。如果 x1 =x2，那么y1 =y2。或者，如果y1≠y2，那么x1≠x2。 第5章 函 数

第5章品数 【例5.2】设N为自然数集合，下列N上的二元关系是 否为函数？ A|x∈N〉 解：和g都是从自然数集合W到自然数集合W的函数， 常记为fN→N,孔x)=2x和g:N→N,gx)=2。 设A和B是两个任意集合，AXB任意子集是A到B的二 元关系，但不一定是A到B的函数。当A和B是有限集时， 由定理4.1.1的证明过程可以看出，A到B的二元关系共有 2MB个，A到B的函数有多少个呢？以下研究这个问题。 设A和B是两个任意的集合，ff:A→B是A到B的所 有函数构成的集合，常记为B4。读作B上A

第5章 函数 【例5.2】设 N为自然数集合，下列N上的二元关系是 否为函数？ f=x,2x | xN  g=x,2 | xN  解：f和g都是从自然数集合N到自然数集合N的函数， 常记为f：N→N，f(x)=2x和g：N→N，g(x)=2。 设A和B是两个任意集合，A×B任意子集是A到B的二 元关系，但不一定是A到B的函数。当A和B是有限集时， 由定理4.1.1的证明过程可以看出，A到B的二元关系共有 2 |A||B|个，A到B的函数有多少个呢？以下研究这个问题。 设A和B是两个任意的集合，f |f：A→B是A到B的所 有函数构成的集合，常记为B A。读作B上A

第5章品数 【例5.3】设A=1,2,3,B=a,b},求B4。 解：由A到B的函数有以下8个： f67 f2=,,t f4=,7 f5-,7 f6=,,,,} BA6fi3,5,45,f6,方} A到B的函数共8个，8=23=BM。 当A和B都是有限集时，这个结论可以推广。一般地 说，若A=m,BFn,则B4=nm=B4

第5章 函数 【例5.3】设 A=1,2,3，B=a,b，求B A 。 解：由A到B的函数有以下8个： f0 =1,a,2,a,3,a f1 =1,a,2,a,3,b f2 =1,a,2,b,3,a f3 =1,a,2,b,3,b f4 =1,b,2,a,3,a f5 =1,b,2,a,3,b f6 =1,b,2,b,3,a f7 =1,b,2,b,3,b B A= f0 , f1 , f2 , f3 , f4 , f5 , f6 , f7  A到B的函数共8个，8=23=|B| |A|。 当A和B都是有限集时，这个结论可以推广。一般地 说，若|A|=m，|B|=n，则|B A |=n m=|B| |A|

第5章品数 定义5.1.2设A和B是两个任意的集合，A→B, A1cA,集合x)x∈A1称为集合A1在f下的像，记为A1)。 集合A在f下的像孔A)=孔x)x∈A}称为函数f的像。显然， 函数f的像fA)就是二元关系f的值域，即几A)=ranf。 【例5.4】设f〈1,2,3→a,b}, f=,A1日1,2， 试求A1在f下的像A1)和函数f的像孔A). 解：几A1)=x)xeA11),f2)=a} A)=x)x∈A=f1),2),f3)=a,b}

第5章 函数 定义5.1.2 设A和B是两个任意的集合，f：A→B， A1A，集合f(x) |xA1称为集合A1在f下的像，记为f(A1 )。 集合A在f下的像 f(A)= f(x) |xA称为函数f的像。显然， 函数f的像f(A)就是二元关系f的值域，即f(A)=ran f。 【例5.4】设f：1,2,3 →a,b， f=1,a,2,a,3,b，A1 =1,2， 试求A1在f下的像f(A1 )和函数f的像f(A)。 解：f(A1 )= f(x) |xA1=f(1), f(2)=a f(A)= f(x) |xA=f(1), f(2), f(3)=a,b

第5章品数 定义5.1.3设fA→B,g:C→D,若A=C,B=D且 Vx∈A,有x)=g(x),则称函数f和g相等，记为f=g。 例如，函数f:N→N,x)=x3 函数g:1,2,3→N,g(x)=x3 虽然函数和g有相同的表达式x3,但是它们是两个不 同的函数。 如果把和g看成二元关系， fNXN,用列举法表示为： ,,,,,…} g1,2,3×N,用列举法表示为： ,,,7 按二元关系相等的条件衡量，它们也是不等的。函 数相等和二元关系相等是一致的

第5章 函数 定义5.1.3 设f：A→B，g：C→D，若A=C，B=D且 xA，有f(x)=g(x)，则称函数f和g相等，记为f =g。 例如，函数f：N→N，f(x)= x 3 函数g：1,2,3 →N，g(x)=x 3 虽然函数f和g有相同的表达式x 3，但是它们是两个不 同的函数。 如果把f和g看成二元关系， fN×N，用列举法表示为： 0,0,1,1,2,8,3,27, 4,64, … g1,2,3 ×N，用列举法表示为： 0,0,1,1,2,8,3,27 按二元关系相等的条件衡量，它们也是不等的。函 数相等和二元关系相等是一致的

第5章品数 定义5.1.4设fA→B,若f的值域ranf=B,则称f为满射。 设f是A到B的函数，由定义不难看出，如果yeB,都存 在x∈A,使得x)=y,则f是满射函数。 例如，Aa,b,cd},B=1,2,3},f是由A到B的函数， 定义为：f=,,,7 因为ran戶孔A)1,2,3=B,所以是满射。图5.2是f的示 意图。由图5.2可得出如下的结论： 若A、B是有限集，f:A→B 是满射，在的示意图中，B中每 个元素至少是一个有向边的终点 b 且A企B1 图5.2

第5章 函数 定义5.1.4 设f：A→B，若f的值域ran f =B，则称f为满射。 设f是A到B的函数，由定义不难看出，如果yB，都存 在xA，使得f(x)=y，则f是满射函数。 例如，A=a,b,c,d，B=1,2,3，f是由A到B的函数， 定义为：f =a,1,b,1,c,3,d,2 因为ran f=f(A)=1,2,3=B，所以f是满射。图5.2是f的示 意图。由图5.2可得出如下的结论： 若A、B是有限集，f：A→B 是满射，在f的示意图中，B中每 个元素至少是一个有向边的终点 且|A|≥|B|

第5章品数 定义5.1.5设fA→B,若Vyeranf,存在惟一的xeA, 使得x)=y,则称f为单射。 设f是A到B的函数，由定义不难看出，如果对于x∈A, x2∈A,x1)y1,x2)y2。 ①当y2时，一定有x=x2,则是单射函数。 ②当x2时，一定有yy2,则是单射函数。 【例5.5】设fa,b7→2,4,67，定义 f=,7 函数是否为单射？隄否为满射？

第5章 函数 定义5.1.5 设f：A→B，若yran f，存在惟一的xA， 使得f(x)=y，则称f为单射。 设f是A到B的函数，由定义不难看出，如果对于x1A， x2A，f(x1 )=y1，f(x2 )=y2。 ①当y1 =y2时，一定有x1 =x2，则f是单射函数。 ②当x1≠x2时，一定有y1≠y2，则f是单射函数。 【例5.5】设f：a,b→2,4,6，定义 f =a,2,b,6 函数f是否为单射？f是否为满射？

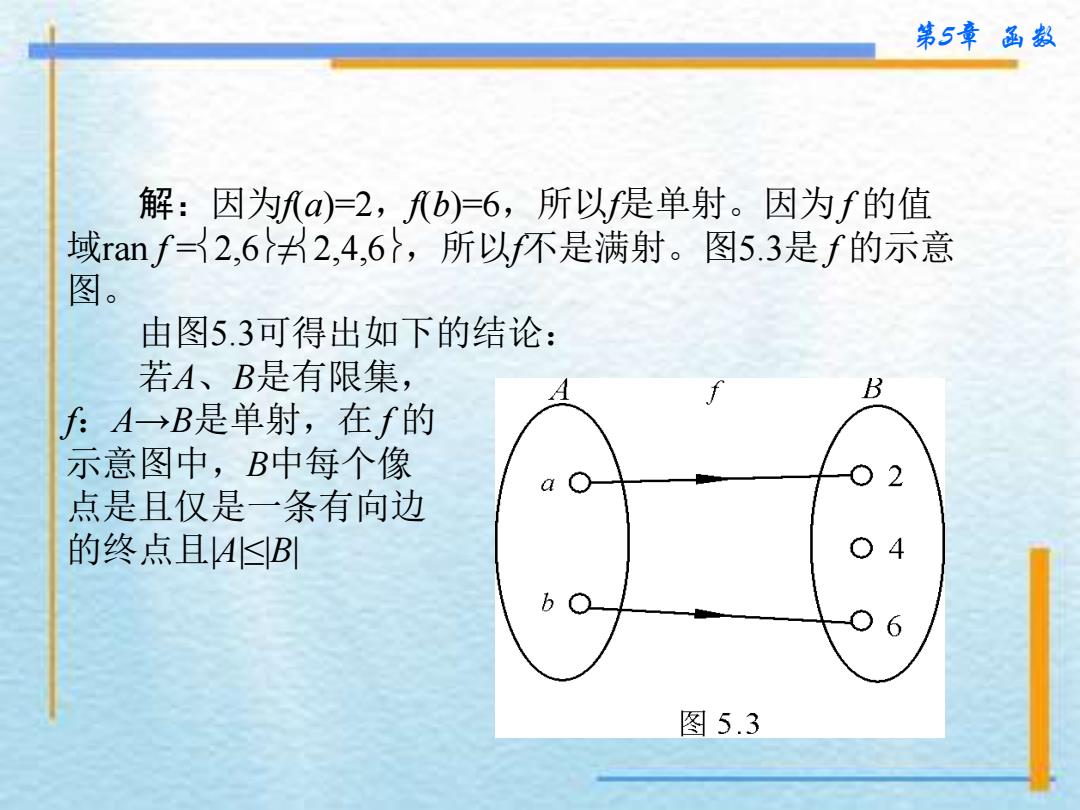
第5章品数 解：因为)=2，b)=6,所以f是单射。因为f的值 域ranf2,6书2,4,67，所以f不是满射。图5.3是f的示意 图。 由图5.3可得出如下的结论： 若A、B是有限集， B f:A→B是单射，在f的 示意图中，B中每个像 点是且仅是一条有向边 的终点且AB 4 b 图5.3

第5章 函数 解：因为f(a)=2，f(b)=6，所以f是单射。因为 f 的值 域ran f =2,6≠2,4,6，所以f不是满射。图5.3是 f 的示意 图。 由图5.3可得出如下的结论： 若A、B是有限集， f：A→B是单射，在 f 的 示意图中，B中每个像 点是且仅是一条有向边 的终点且|A|≤|B|

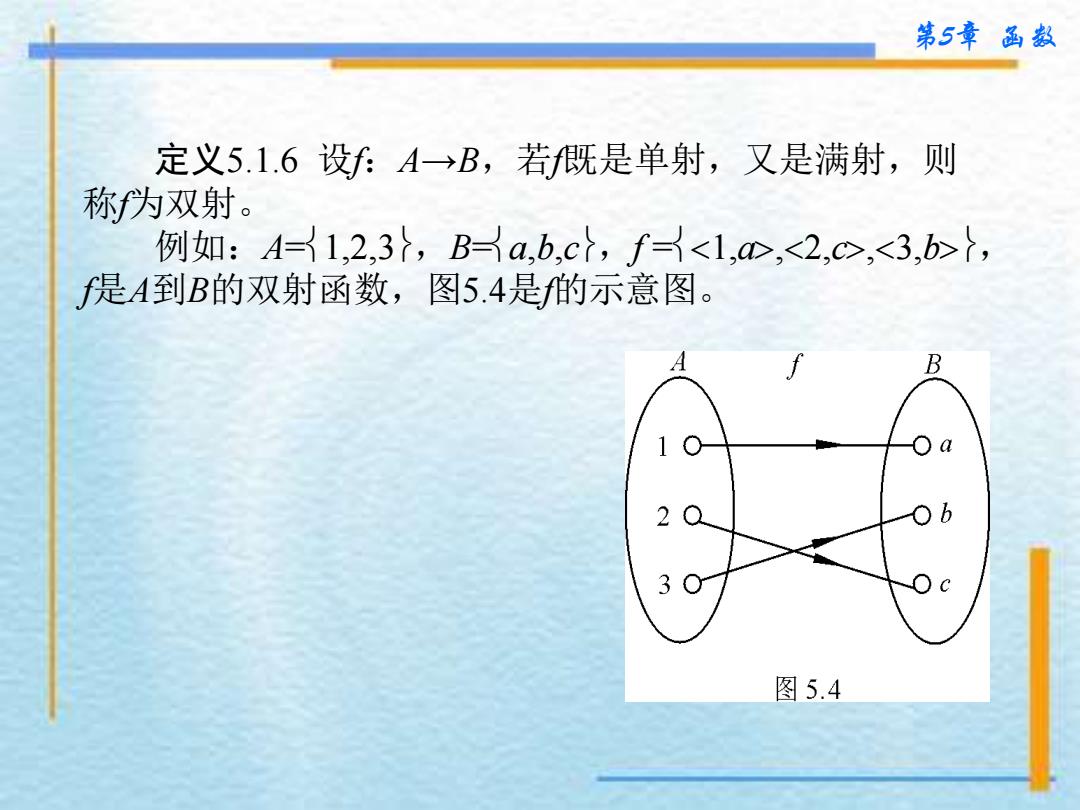
第5章品数 定义5.1.6设fA→B,若f既是单射，又是满射，则 称为双射。 例如：A=1,2,3},Ba,b,c},f, f是A到B的双射函数，图5.4是的示意图。 B 1 2 b 3 图5.4

第5章 函数 定义5.1.6 设f：A→B，若f既是单射，又是满射，则 称f为双射。 例如：A=1,2,3，B=a,b,c，f =1,a,2,c,3,b， f是A到B的双射函数，图5.4是f的示意图