
第8章格与布尔代数 第8章格与布尔代数 8.1格 8.2布尔代数 返回总目录
第8章 格与布尔代数 第8章 格与布尔代数 8.1 格 8.2 布尔代数 返回总目录

第章格与布尔代数 第8章格与布尔代数 8.1格 8.1.1格的概念和性质 定义8.1.1设是偏序集,如果x,yeX,集合x,y 都有最小上界和最大下界,则称是格 【例8.1】设S12=1,2,3,4,6,12是12的因子构成的集合。 其上的整除关系Rlx∈S12∧yeS12∧x整除y,R是S2 上的偏序关系,,,,, ,7, 哈斯图如图8.1所示。从哈斯图中可看出,集合S12的任意两 个元素都有最小上界和最大下界,故偏序集是格
第8章 格与布尔代数 第8章 格与布尔代数 8.1格 8.1.1格的概念和性质 定义8.1.1 设X,≼是偏序集,如果x,yX,集合x,y 都有最小上界和最大下界,则称X,≼是格。 【例8.1】设S12 =1,2,3,4,6,12是12的因子构成的集合。 其上的整除关系R=x,y| xS12∧yS12∧x整除y,R是S12 上的偏序关系,S12,R是偏序集。写出S12上的盖住关系 COV S12,画出哈斯图,验证偏序集S12,R是格。 解:S12上的盖住关系 COV S12 =1,2,1,3,2,4,2,6,3,6, 4,12,6,12, 哈斯图如图8.1所示。从哈斯图中可看出,集合S12的任意两 个元素都有最小上界和最大下界,故偏序集S12,R是格
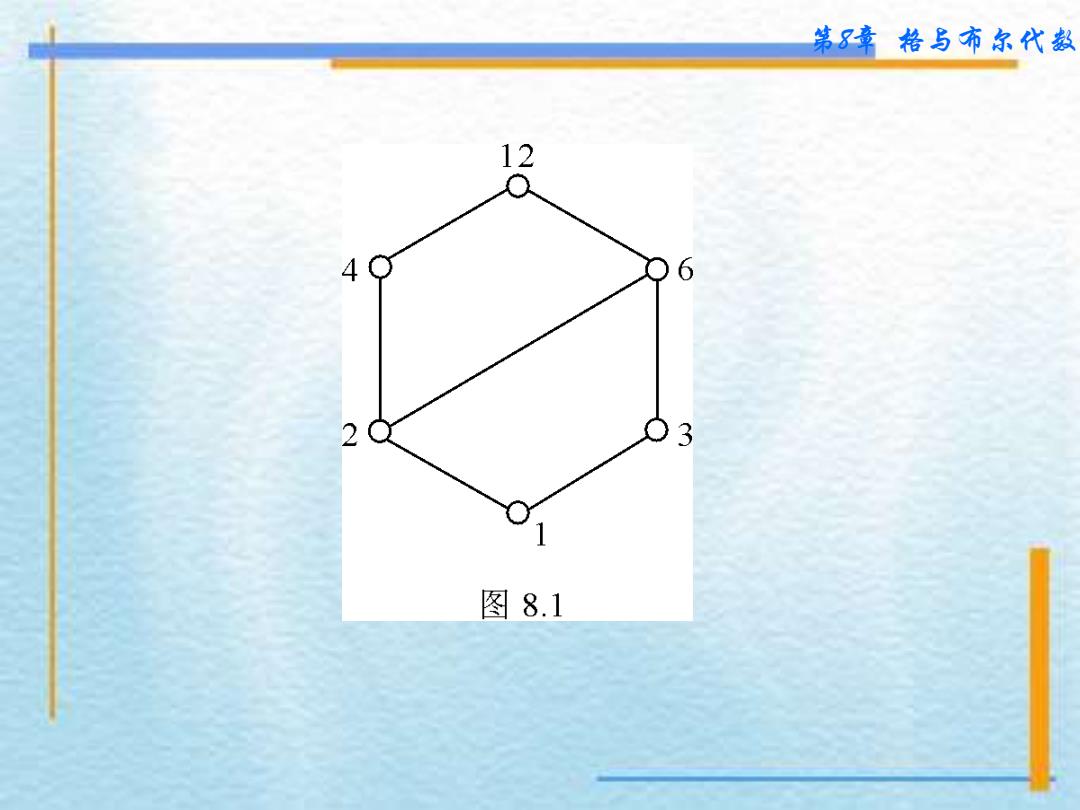
第章格与布尔代数 12 4 6 2 3 1 图8.1
第8章 格与布尔代数

第8章 格与布尔代数 【例8.2】图8.2中给出了一些偏序集的哈斯图,判断它 们是否构成格。 解:它们都不是格。在(a)中,子1,2没有下界,因而没 有最大下界。在(b)中,了2,4虽有两个上界,但没有最小上 界。在(c)中,了1,3没有下界,因而没有最大下界。在(d)中, 2,3}虽有三个上界,但没有最小上界。 (a) (b) (c) (d) 图8.2
第8章 格与布尔代数 【例8.2】图8.2中给出了一些偏序集的哈斯图,判断它 们是否构成格。 解:它们都不是格。在(a)中,1,2没有下界,因而没 有最大下界。在(b)中,2,4虽有两个上界,但没有最小上 界。在(c)中,1,3没有下界,因而没有最大下界。在(d)中, 2,3虽有三个上界,但没有最小上界

第8章 格与布尔代数 设是格,x,yEX,今后用xVy表示集合x,y的最 小上界,二元运算V称为并运算;用x个y表示集合x,y的最 大下界,二元运算∧称为交运算。 定义81.2设是格,V是X上的并运算,∧是X上 的交运算。则称是格导出的代数系统。 在例4.28中,根据图4.14,集合a},b的最小上界为 a,b,即aVba,b=a}Ub;它的最大下界为E, 即a}∧b=E=anb}。这个结果可以推广到一般情况。 x,yeP(A),xVy=xUy,x∧y=xny。这样,格导 出的代数系统实际就是代数系统, 所以,二元运算V和个的运算表如表8.1和表8.2所示。 在例8.1中,根据图8.1,集合4,6}的最小上界为12,即 4V6=12=4和6的最小公倍数;它的最大下界为2,即 4∧6=2=4和6的最大公约数。同样,这个结果也可以推广到 一 般情况。即在格中,二 元运算V是求最小公倍数;二元运算个是求最大公约数
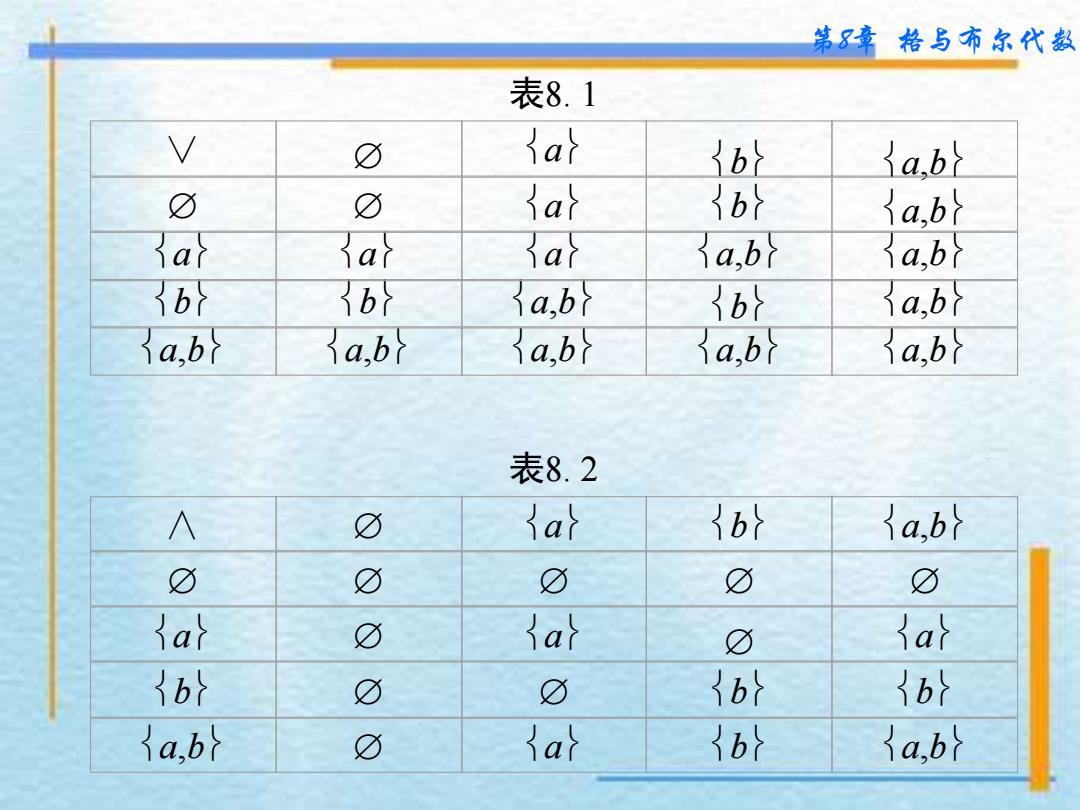
第8章 格与布尔代数 设X,≼是格,x,yX,今后用x∨y表示集合x,y的最 小上界,二元运算∨称为并运算;用x∧y表示集合x,y的最 大下界,二元运算∧称为交运算。 定义8.1.2 设X,≼是格,∨是X上的并运算,∧是X上 的交运算。则称X,∨,∧是格X,≼导出的代数系统。 在例4.28中,根据图4.14,集合a,b的最小上界为 a,b,即a∨b=a,b=a∪b;它的最大下界为Æ, 即a∧b=Æ=a∩b。这个结果可以推广到一般情况。 x,yP (A),x∨y=x∪y,x∧y=x∩y。这样,格P (A),R 导 出的代数系统P (A),∨,∧实际就是代数系统P (A),∪,∩, 所以,二元运算∨和∧的运算表如表8.1和表8.2所示。 在例8.1中,根据图8.1,集合4,6的最小上界为12,即 4∨6=12=4 和 6 的最小公倍数;它的最大下界为 2 , 即 4∧6=2=4和6的最大公约数。同样,这个结果也可以推广到 一般情况。即在格S12,R导出的代数系统S12,∨,∧中,二 元运算∨是求最小公倍数;二元运算∧是求最大公约数
第章格与布尔代数 表8.1 V 0 a 3bt {a,b} 0 0 Rar b {a,b} a a a Rabr fabi bi b Rabi 3bi Rabi Rabi Rabr Rabr Rabr abi 表8.2 ∧ 0 Rai 3bi Rabi 0 0 0 0 0 Rai ☑ Rar 0 {a} 3bi 0 0 3br 3bi Rabi 0 Rar b Rabi
第 8 章 格与布尔代数 表8. 1 表8. 2 ∨ a a b b a , b a a a a , b a , b a , b b b a , b a , b a , b a , b a , b b a , b a , b ∧ a b a , b a a a b b b a , b a b a , b

第8章格与布尔代数 下面介绍格的对偶原理 设是偏序集,在X上定义二元关系 ≥-kb,a心e≤7 可以证明也是偏序集 定义8.1.3设f是含有格中元素以及符号=,≤,,V和∧的 命题。将中的≤替换成>,≥替换成≤,V替换成个,∧替 换成V,得到一个新命题,所得的命题叫做的对偶命题, 记为f*。 例如,在格中,f为a∧(bVc)≤a,则f的对偶命题f*为 aV(b∧c)≥a 命题和它的对偶命题f*遵循下列的规则,这规则叫做 格的对偶原理。 设f是含有格中元素以及符号=,≤,,V和∧的命题 若f对一切格为真,则的对偶命题∫*也对一切格为真。 格的许多性质都是互为对偶命题的。有了格的对偶原 理,在证明格的性质时,只需证明其中的一个就可以了
第8章 格与布尔代数 下面介绍格的对偶原理。 设X,≼是偏序集,在X上定义二元关系 ≽=a,b|b,a≼ 可以证明X,≽也是偏序集。 定义8.1.3 设f是含有格中元素以及符号=,≼,≽,∨和∧的 命题。将f中的≼替换成≽,≽替换成≼,∨替换成∧,∧替 换成∨,得到一个新命题,所得的命题叫做f的对偶命题, 记为f * 。 例如,在格中,f为a∧(b∨c)≼a,则f的对偶命题f *为 a∨(b∧c)≽a 命题f和它的对偶命题f *遵循下列的规则,这规则叫做 格的对偶原理。 设f是含有格中元素以及符号=,≼,≽,∨和∧的命题。 若f对一切格为真,则f的对偶命题f *也对一切格为真。 格的许多性质都是互为对偶命题的。有了格的对偶原 理,在证明格的性质时,只需证明其中的一个就可以了

第8章格与布尔代数 定理8.1.1设是格,是格导出的 代数系统。则Va,b,ceX有 (1)aVb=bVa,a∧b=b∧a (交换律) (2)(aVb)Vc=av(bVc) (a∧b)∧c=a∧(b∧c) (结合律) (3)ava=a, a∧a=a (幂等律) (4)aV(a∧b)=a a∧(aVb)=a (吸收律) 证明:(1)Va,beX,{a,b=b,a,所以它们的最小上界 相等。即aVb=bVa,同理可证a∧b=b个a (2)a和b的最大下界一定是a、b的下界,即a个b≤a, 同理,(a个b)∧c≤a∧b,所以,(a∧b)∧c≤a∧b≤a 同理有(a∧b)∧c≤a∧b<b和(a∧b)∧c<c
第8章 格与布尔代数 定理8.1.1 设X,≼是格,X,∨,∧是格X,≼导出的 代数系统。则a,b,cX有 ⑴ a∨b=b∨a, a∧b=b∧a (交换律) ⑵ (a∨b)∨c=a∨(b∨c) (a∧b)∧c=a∧(b∧c) (结合律) ⑶ a∨a= a, a∧a= a (幂等律) ⑷ a∨(a∧b)=a a∧(a∨b)=a (吸收律) 证明:⑴a,bX,a,b=b,a,所以它们的最小上界 相等。即a∨b=b∨a,同理可证a∧b=b∧a ⑵ a和b的最大下界一定是a、b的下界,即a∧b≼a, 同理,(a∧b)∧c≼a∧b,所以,(a∧b)∧c≼a∧b≼a 同理有 (a∧b)∧c≼a∧b≼b 和 (a∧b)∧c≼c

第8章格与布尔代数 由以上3式得 (a∧b)∧c≤b∧c和(a∧b)∧c≤a∧(b∧c) 类似地可证 a∧(b∧c)≤(a∧b)∧c 根据偏序关系的反对称性有(a∧b)∧c-a∧(b∧c) 由对偶原理得 (aVb)Vc=av(bVc) (3)显然a≤aVa,又由≤的自反性得a≤a,从而推出 aVa≤a,根据偏序关系的反对称性有aVa=a 由对偶原理得a∧a=a (4)显然a≤aV(a∧b), 又由a≤a,a∧b≤a得aV(a个b)≤a,从而得 aV(a∧b)=a。 由对偶原理得a∧(aVb)=a
第8章 格与布尔代数 由以上3式得 (a∧b)∧c≼b∧c和(a∧b)∧c≼a∧(b∧c) 类似地可证 a∧(b∧c)≼(a∧b)∧c 根据偏序关系的反对称性有(a∧b)∧c= a∧(b∧c) 由对偶原理得 (a∨b)∨c= a∨(b∨c) ⑶ 显然a≼a∨a,又由≼的自反性得a≼a,从而推出 a∨a≼a,根据偏序关系的反对称性有a∨a=a 由对偶原理得a∧a=a ⑷显然 a≼a∨(a∧b), 又由a≼a,a∧b≼a得a∨(a∧b)≼a,从而得 a∨(a∧b)=a。 由对偶原理得a∧(a∨b)=a

第8章 格与布尔代数 定理8.1.2设是代数系统,其中V,∧都是二元 运算。如果V和∧满足吸收律,则V和个满足幂等律。 证明:aVa=aV(a个(aVb)=a,同理可证a个a=a 定理8.1.3设是代数系统,其中V,∧都是二元 运算,满足交换律、结合律和吸收律,则可适当定义X的偏 序关系≤,使构成一个格。 证明:定义X上的一个二元关系 ≤=la,beX且a个b=aY (1)证明≤是X上的偏序关系 。 由定理8.1.2知个满足幂等律,即a个a=a,所以a≤a。故 ≤是自反的。 设a≤b且b≤a,则a∧b=a且b∧a=b,于是=a个b=b∧a =b。 所以≤是反对称的。 设a≤b且b≤c,则a∧b=a且b个c=b,于是a∧c-(a∧b)个c =a个(b个c)=a个b=a,即a≤c,故≤是传递的。 这就证明了≤是X上的偏序关系
第8章 格与布尔代数 定理8.1.2 设X,∨,∧是代数系统,其中∨,∧都是二元 运算。如果∨和∧满足吸收律,则∨和∧满足幂等律。 证明:a∨a=a∨(a∧(a∨b))=a,同理可证a∧a=a 定理8.1.3 设X,∨,∧是代数系统,其中∨,∧都是二元 运算,满足交换律、结合律和吸收律,则可适当定义X的偏 序关系≼,使X,≼构成一个格。 证明:定义X上的一个二元关系 ≼=a,b|a,bX且a∧b=a ⑴ 证明≼是X上的偏序关系。 由定理8.1.2知∧满足幂等律,即a∧a=a,所以a≼a。故 ≼是自反的。 设a≼b且b≼a,则a∧b=a且b∧a=b,于是a=a∧b=b∧a =b。所以≼是反对称的。 设a≼b且b≼c,则a∧b=a且b∧c=b,于是a∧c=(a∧b)∧c =a∧(b∧c)=a∧b=a,即a≼c,故≼是传递的。 这就证明了≼是X上的偏序关系